2. 同济大学 机械与能源工程学院 机器人技术与多体系统实验室 上海 201804
2. Laboratory of Robotics and Multibody System, School of Mechanical Engineering, Tongji University, Shanghai 201804, China
由于地形复杂、环境恶劣等原因,自主式水下航行器(Autonomous Underwater Vehicle, AUV)日益成为代替人类开发利用海洋资源的重要工具,例如近海养殖[1]、石油钻井平台检测[2]、海洋科学探索[3]等。
微型AUV具有高度非线性和耦合性,工作环境存在复杂的海流扰动和不确定的模型参数等特征,同时为了降低系统能耗、成本和质量等,往往采用欠驱动的方式,从而提高其运动控制的难度。微型AUV的轨迹跟踪控制[4]是AUV从给定的初始位置出发,在控制器的持续激励下能到达并跟随空间中人为给定的定义在时间域上的光滑几何轨迹。目前,国内外专家学者对于微型AUV轨迹跟踪控制主要采用PID控制方法、反步控制方法、神经网络控制方法以及滑模控制方法等。PID控制方法由于其结构简单且具有良好性能,在机器人领域具有广泛应用,但是PID控制器在非线性模型中表现不佳[5]。反步法通过递归构造闭环系统的Lyapunov函数获得反馈控制器,从而选取控制律并不断修正,保证闭环系统轨迹的有界性且收敛到平衡点[6],但控制器设计过程中需要对虚拟控制量进行求导,出现的微分项膨胀问题会导致控制系统难以到达稳定。神经网络控制方法可应用在绝大多数复杂的非线性对象中,但需要大量的输入、输出样本数据进行训练[7]。因此,滑模控制凭借快速响应、较强的抗干扰性、无需系统在线辨识及物理实现简单等特性,在AUV的轨迹跟踪控制中不断推广应用并取得了一些成果。Chen等[8]基于Hölder不等式和有限时间稳定性理论,为多AUV系统设计了一个分布式有限时间观察器。以Zhang等[9]提出了一种预测滑模级联控制并应用于AUV的跨域转换,特别是通过前馈控制补偿浮力变化的影响。最后通过与PID控制器的对比仿真结果验证了所提出控制方案的可行性和鲁棒性。尽管国内外对于滑模控制有了广泛研究,但因其本质上不连续开关特性导致的抖振始终是实际系统应用的突出障碍[10],针对该问题主要方法有准滑动模态方法、滤波方法、趋近律方法、连续切换方法等。其中准滑动模态方法将一定范围内的状态点吸引至滑模切换面的某一邻域内,从而有效解决系统惯性引起的抖振问题。
本文针对微型AUV在三维水下环境中轨迹精确跟踪问题,建立Frenet坐标系下的运动误差模型,设计基于准滑动模态的滑模控制器,并证明该控制系统在Lyapunov函数下全局渐进稳定的。最后,通过仿真验证了该控制策略的可行性。
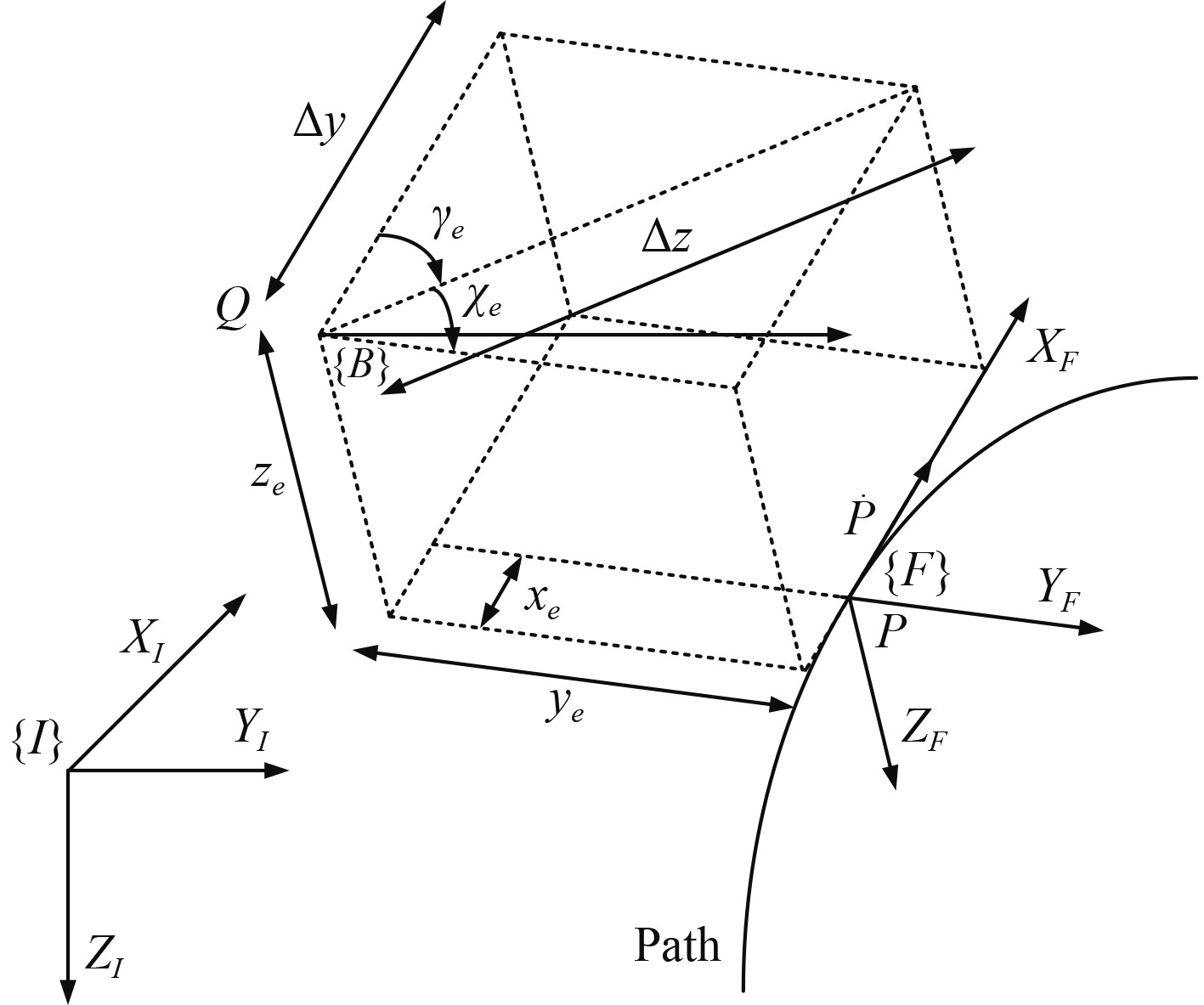
1 微型自主式水下航行器建模本文微型AUV的执行机构由1个推进器和4个舵板组成,以实现艇体进退、俯仰及偏航3个自由度方向上的控制。没有配备垂直方向和水平方向的推进器,不能直接对艇体的升沉和横移运动进行控制。自主式水下航行器的运动学模型及受力分析在艇体坐标系和惯性坐标系下表示,如图1所示。基于多体动力学理论和牛顿-欧拉公式可得:
|
图 1 微型AUV坐标系及轨迹跟踪 Fig. 1 Coordinate system and trajectory tracking of micro AUV |
| $ \left\{ \begin{gathered} \dot \eta = J(\eta )\mu ,\\ {\boldsymbol{M}}(\mu )\dot \mu + {\boldsymbol{C}}(\mu ,\dot \mu )\mu + {\boldsymbol{D}}(\mu ,\dot \mu )\mu + g(\eta ) = \tau - {\tau _d}。\\ \end{gathered} \right. $ | (1) |
式中,
期望轨迹是给定的三维螺旋下潜轨迹,点
由于AUV几何外形对称,质量均匀分布,且长时间处于中性浮力状态,可默认其重力与浮力大小相等,方向相反。此外,4个舵机两两之间实现近同步转动,且由于扶正力矩的存在,可忽视艇体的部分横滚运动。简化模型可得:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot x = {U_B}\cos {\gamma _Q}\cos {\chi _Q}},\\ {\dot y = {U_B}\sin {\gamma _Q}\cos {\chi _Q}} ,\\ {\dot z = {U_B}\sin {\chi _Q}} ,\\ {{{\dot \chi }_Q} = q + \dot \alpha },\\ {{{\dot \gamma }_Q} = r/\cos \theta + \dot \beta } 。\end{array}} \right. $ | (2) |
式中:航迹角
为了便于建立跟踪误差方程,引入惯性坐标系
| $ {R_P} = \left[ {\begin{array}{*{20}{c}} {\cos {\gamma _P}\cos {\chi _P}}&{ - \sin {\gamma _P}}&{\cos {\gamma _P}\sin {\chi _P}} \\ {\sin {\gamma _P}\cos {\chi _P}}&{\cos {\gamma _P}}&{\sin {\gamma _P}\sin {\chi _P}} \\ { - \sin {\chi _P}}&0&{\cos {\chi _P}} \end{array}} \right] \text{。} $ | (3) |
式中:
可得微型AUV点
| $ \varepsilon = R_P^{\rm{T}}(Q - P) \text{,} $ | (4) |
式中,
| $ \dot \varepsilon = \dot R_P^{\rm{T}}(Q - P) + R_P^{\rm{T}}(\dot Q - \dot P) \text{,} $ | (5) |
式中,
根据式(5)可得微型AUV在Frenet下的位置误差方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_e} = {y_e}{{\dot \gamma }_P}\cos {\chi _P} - {z_e}{{\dot \chi }_P} + {U_{{B}}}\cos {\gamma _e}\cos {\chi _e} - {U_P}} ,\\ {{{\dot y}_e} = - {x_e}{{\dot \gamma }_P}\cos {\chi _P} - {z_e}{{\dot \gamma }_P}\sin {\chi _P} + {U_{{B}}}\sin {\gamma _e}\cos {\chi _e}},\\ {{{\dot z}_e} = {x_e}{{\dot \chi }_P} - {y_e}{{\dot \gamma }_P}\sin {\chi _P} - {U_{{B}}}\sin {\chi _e}},\\ {{{\dot \theta }_e} = q + {{\dot \alpha }_e} - {{\dot \chi }_P}},\\ {{{\dot \psi }_e} = r/\cos \theta + {{\dot \beta }_e} - {{\dot \gamma }_P}} 。\end{array}} \right. $ | (6) |
为保证微型AUV的运动学误差模型稳定,设计虚拟速度为:
| $ {U_P} = {U_{{B}}}\cos {\psi _e}\cos {\theta _e} + \kappa {x_e} \text{,} $ | (7) |
式中,
| $ \dot \mu = \frac{{{U_{\text{B}}}\cos {\psi _e}\cos {\theta _e} + \kappa {x_e}}}{{\sqrt {\dot x_P^2 + \dot y_P^2 + \dot z_P^2} }} \text{。} $ | (8) |
将
| $ {U_P} = {U_{\text{B}}}\frac{{\Delta y}}{{\sqrt {y_e^2 + \Delta {y^2}} }}\frac{{\Delta z}}{{\sqrt {z_e^2 + \Delta {z^2}} }} + \kappa {x_e} \text{。} $ | (9) |
式中,
根据该微型自主式水下航行器的特性,分别针对其推进器、俯仰舵和方向舵设计滑模控制器,相应的滑模面分别为
针对微型AUV的纵向位移偏差
| $ \left\{ \begin{gathered} {s_{11}}({x_e}) = {k_{11}}{\text{sat}}({k_{12}}{x_e}) + {{\dot x}_e},\\ {s_{12}}({s_{11}}) = {k_{13}}{\text{sat}}({k_{14}}{s_{11}}) + {{\dot s}_{11}}。\\ \end{gathered} \right. $ | (10) |
设计反馈控制律:
| $ \dot n = - {k_{15}}{s_{12}} - {k_{16}}{{\rm{sgn}}} ({s_{12}}) \text{,} $ | (11) |
式中,
在实际推进器建模过程中,往往采用一阶惯性模型来描述其特征:
| $ \dot n = {K_M}({n_r} - n)/{T_M} \text{。} $ | (12) |
式中:
根据该推进器的水动力性能计算结果可知,推力公式为:
| $ {X_{{\text{prop}}}} = \rho {n^2}Df\left( {J,{R_e},{F_n}} \right) \text{。} $ | (13) |
式中:
由式(11)和式(12)可得推进器旋转速度的输入指令为:
| $ {n_r} = n - {T_M}[{k_{15}}{s_{12}} + {k_{16}}{{\rm{sgn}}} ({s_{12}})] 。$ | (14) |
基于Lyapunov稳定性理论考虑微型AUV系统运动学方程和轨迹跟踪控制器,为了使纵向轨迹跟踪到达条件且满足误差稳定性要求,选取Lyapunov函数为:
| $ {V_1} = \frac{{s_{12}^2}}{2} \text{。} $ | (15) |
求导可得:
| $ {\dot V_1} = {s_{12}}{\dot s_{12}} = {s_{12}}\frac{{\partial {s_{12}}}}{{\partial n}}\dot n \text{。} $ | (16) |
对滑模面
| $ \frac{{\partial {s_{12}}}}{{\partial n}} = \frac{{\partial {{\ddot x}_e}}}{{\partial n}} = \frac{\partial }{{\partial n}}({\dot v_t}\cos {\theta _e}) \geqslant {\text{0}} \text{。} $ | (17) |
式中,
由式(11)和式(14)可得:
| $ {s_{12}}\dot n = - {k_{15}}s_{12}^2 - {k_{16}}|{s_{12}}| \leqslant {\text{0}} \text{,} $ | (18) |
进而由式(16)~式(18)可得:
| $ {\dot V_1} = {s_{12}}{\dot s_{12}} \leqslant {\text{0}} \text{,} $ | (19) |
易证得仅当
针对微型AUV的垂向位移偏差
| $ \left\{ \begin{gathered} {s_{21}}({z_e}) = {k_{21}}{\text{sat}}({k_{22}}{z_e}) + {{\dot z}_e},\\ {s_{22}}({s_{21}},{\theta _e}) = {\theta _e} + {k_{23}}\int {{\text{sat}}({s_{21}}){\text{d}}t},\\ {s_{23}}({s_{22}}) = {k_{24}}{\text{sat}}({s_{22}}) + {{\dot s}_{22}},\\ {s_{24}}({s_{23}}) = {k_{25}}{\text{sat}}({s_{23}}) + {{\dot s}_{23}} 。\\ \end{gathered} \right. $ | (20) |
设计反馈控制律:
| $ {\dot \delta _s} = - {k_{26}}{s_{24}} - {k_{27}}{{\rm{sgn}}} ({s_{24}}) \text{,} $ | (21) |
式中,
在微型AUV实际运动过程中,其俯仰舵机的转动角度受到执行机构的约束,由此数学模型可建立为:
| $ {\delta _{{{r,}}{{{s}}_{{\text{real}}}}}} = \left\{ \begin{gathered} {{\dot \delta }_{{{r,s}}}}t - {\delta _{{{r,s,{\rm{max}}}}}} < {{\dot \delta }_{{{r,s}}}}t < {\delta _{{{r,s,\max}}}} ,\\ \delta _{{{r,s,\max}}}^2 < {{\dot \delta }_{{{r,s}}}}t,\\ - {\delta _{{{r,s,\max}}}}{{\dot \delta }_{{{r,s}}}}t < - {\delta _{{{r,s,\max}}}} 。\\ \end{gathered} \right. $ | (22) |
| $ {\dot \delta _{{{r,s}}}} = {\delta _{{{r,s}},\max }}/{T_{{{r,s}}}} \text{,} $ | (23) |
式中:
| $ {M_{{\text{prop}}}} = \left[ {\begin{array}{*{20}{l}} X \\ Y \\ Z \\ K \\ M \\ N \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} 0&{{X_{\delta s\delta s}}}&{{X_{\delta r\delta r}}}&0&{{X_{\delta s}}}&0 \\ 0&0&0&0&0&{{Y_{\delta r}}} \\ 0&0&0&0&{{Z_{\delta s}}}&0 \\ 0&0&0&0&0&{{K_{\delta r}}} \\ 0&0&0&0&{{M_{\delta s}}}&0 \\ 0&0&0&0&0&{{N_{\delta r}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} 0 \\ {\delta _s^2} \\ {\delta _r^2} \\ 0 \\ {{\delta _s}} \\ {{\delta _r}} \end{array}} \right] 。$ | (24) |
由式(21)和式(23)可得俯仰舵角角度的输入指令为:
| $ {\delta _{sd}} = {\delta _s} - {T_{{{r,s}}}}[{k_{26}}{s_{24}} + {k_{27}}{{\rm{sgn}}} ({s_{24}})] 。$ | (25) |
为了使垂向轨迹跟踪到达条件且满足误差稳定性要求,选取Lyapunov函数为:
| $ {V_2} = \frac{{s_{24}^2}}{2} \text{,} $ | (26) |
求导可得:
| $ {\dot V_2} = {s_{24}}{\dot s_{24}} = {s_{24}}\frac{{\partial {s_{24}}}}{{\partial {\delta _s}}}{\dot \delta _s} \text{,} $ | (27) |
对式滑模面
| $ \frac{{\partial {s_{24}}}}{{\partial {\delta _s}}} = \frac{{\partial {M_{{\text{prop}}}}}}{{\partial {\delta _s}}} + {k_{23}}\frac{{\partial \{{{1/[(\dot z}}_e^2/\sqrt {{{\dot x}}_e^2 + {{\dot y}}_e^2} {)^2} + 1]\} }}{{\partial {\delta _s}}} \text{,} $ | (28) |
存在
| $ \frac{{\partial {k_{24}}}}{{\partial {\delta _s}}} > 0 。$ | (29) |
由式(20)和式(21)可得:
| $ {s_{24}}{\dot \delta _s} = - {k_{26}}s_{24}^2 - {k_{27}}{s_{24}}{{\rm{sgn}}} ({s_{24}}) \leqslant {\text{0}} \text{,} $ | (30) |
进而由式(27)、式(29)和式(30)可得:
| $ {\dot V_2} = {s_{24}}{\dot s_{24}} \leqslant {\text{0}} \text{。} $ | (32) |
易证得仅当
为验证上述轨迹跟踪控制器的有效性和鲁棒性,在Matlab中建立仿真环境,对微型AUV进行仿真实验分析。仿真对象为实验室自主研制的微型AUV,仿真对象三维模型如图2所示。
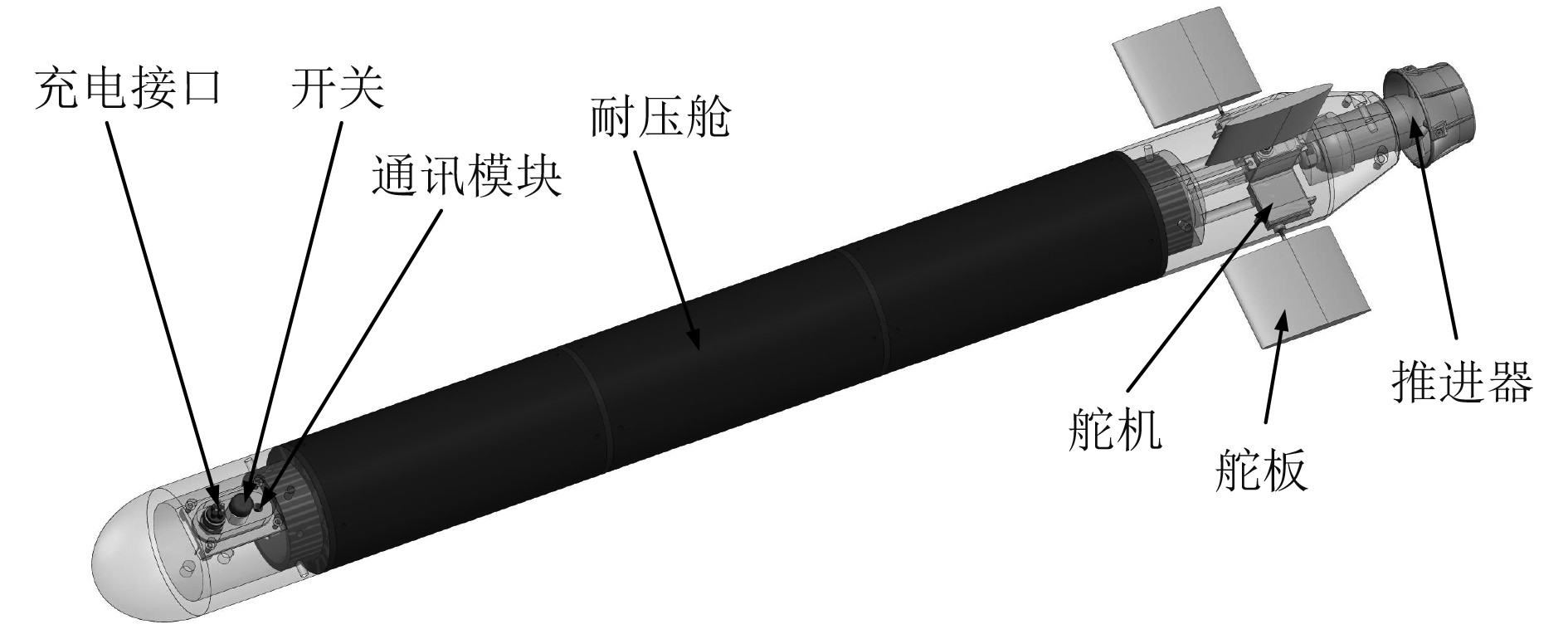
|
图 2 微型AUV三维模型 Fig. 2 3D model of micro AUV |
根据自主研制的微型AUV各参数计算,其质量和惯性参数如表1所示。
|
|
表 1 微型AUV质量和惯性参数 Tab.1 Mass and inertial parameters of minor AUV |
微型AUV质心期望轨迹为水下三维螺旋下潜运动,其中下潜轨迹为

|
图 3 微型AUV螺旋下潜空间运动轨迹跟踪 Fig. 3 Trajectory tracking of micro AUV in spiral diving |
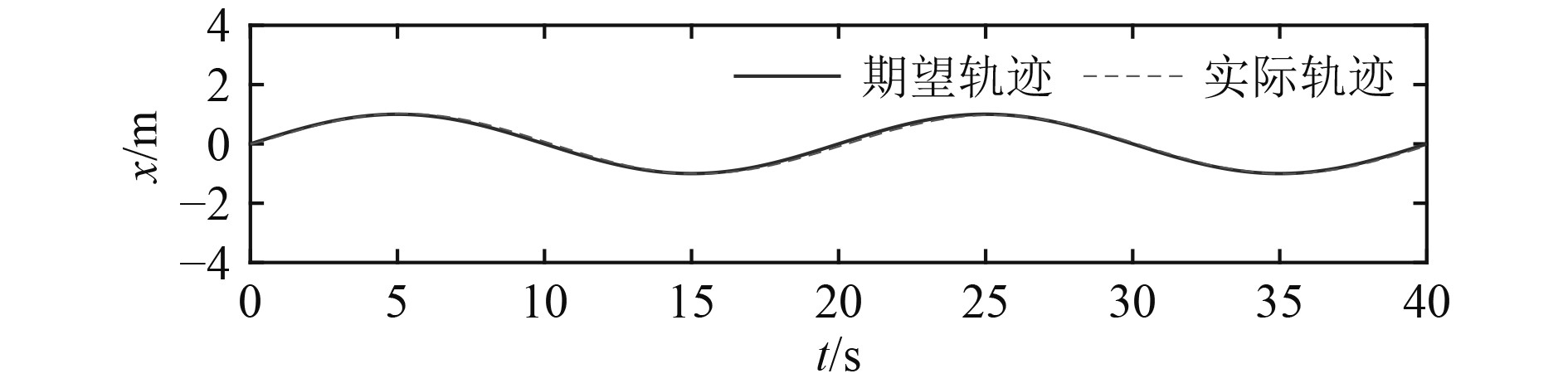
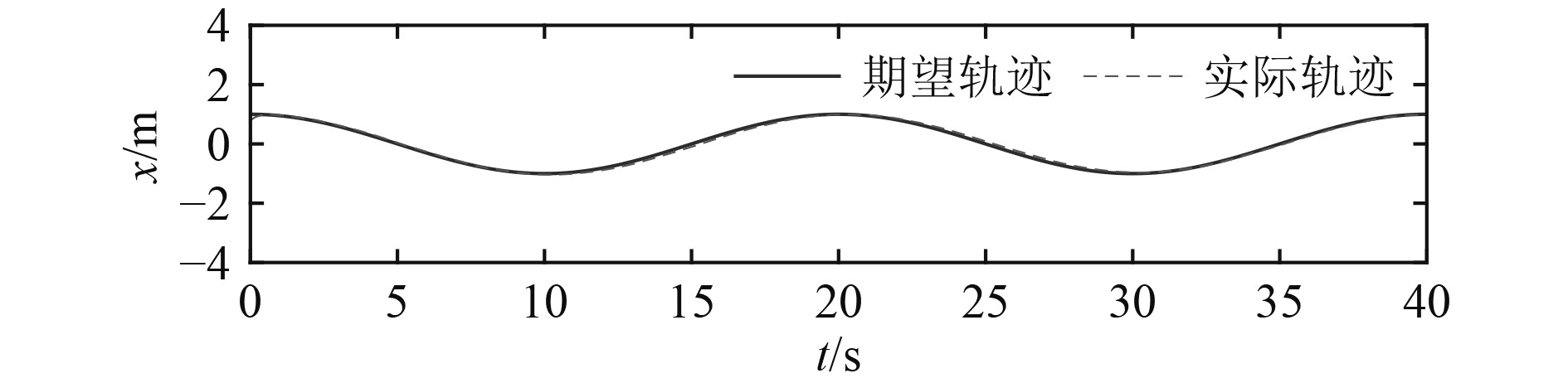
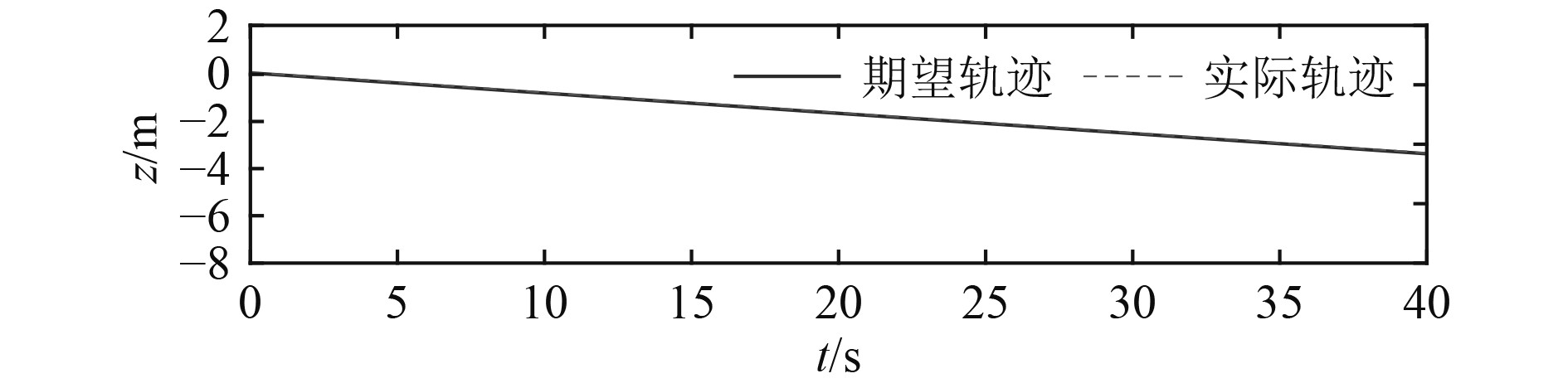
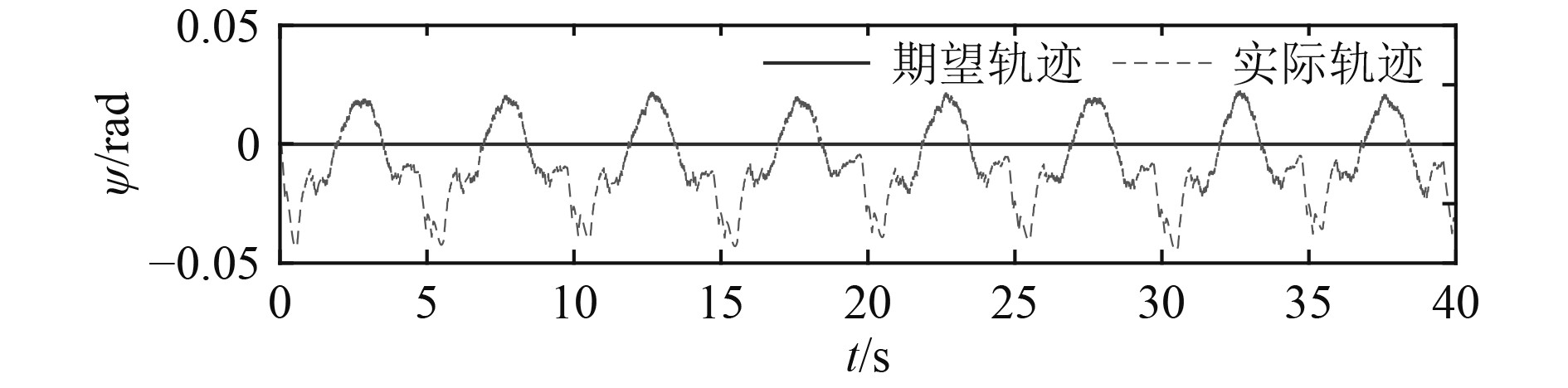
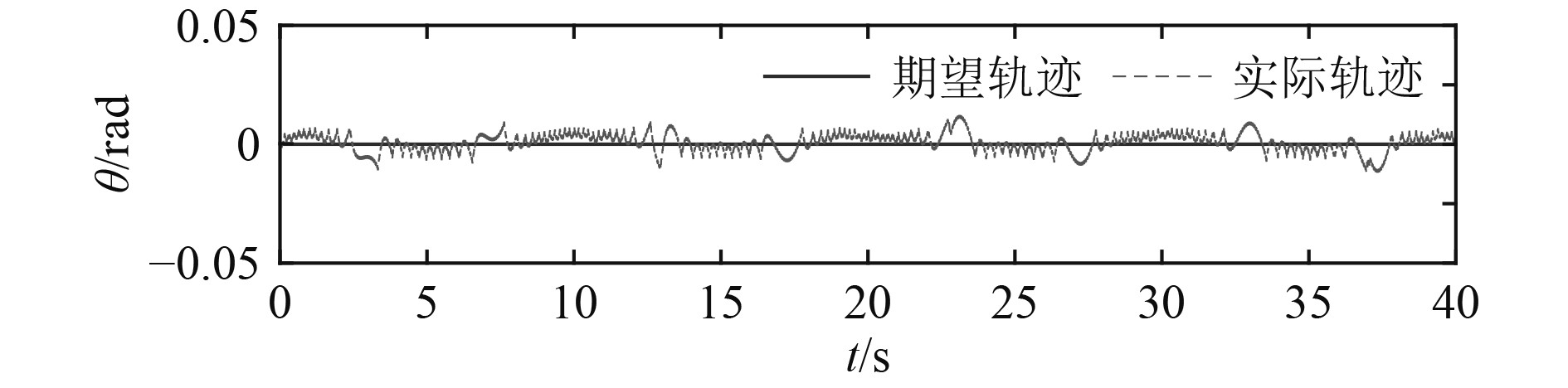
微型AUV在纵向、横向和垂向的运动轨迹跟踪结果如图4~图6所示,其偏航角、纵倾角和横滚角姿态控制如图7~图9所示。从仿真结果曲线可知,所设计的滑模控制器跟踪效果较好,能够以较高的精度实现微型AUV的轨迹跟踪效果,由于微型AUV结构特性和外界干扰的不确定性,在偏航角姿态控制上存在一定抖振。
|
图 4 微型AUV纵向运动轨迹跟踪 Fig. 4 Trajectory tracking of micro AUV in forward motion |
|
图 5 微型AUV横向运动轨迹跟踪 Fig. 5 Trajectory tracking of micro AUV in lateral motion |
|
图 6 微型AUV垂向运动轨迹跟踪 Fig. 6 Trajectory tracking of minor AUV in vertical motion |
|
图 7 微型AUV姿态偏航角控制 Fig. 7 Yaw angle control of micro AUV attitude |
|
图 8 微型AUV姿态纵倾角控制 Fig. 8 Pitch angle control of micro AUV attitude |

|
图 9 微型AUV姿态横滚角控制 Fig. 9 Roll angle control of micro AUV attitude |
本文针对自行研制的微型AUV特性,开展三维空间内的轨迹跟踪研究,建立了纵向、垂向及横向的动力学模型,并设计了基于准滑动模态的滑模控制律。仿真结果表明,所设计的控制器能精确实现微型AUV空间螺旋下潜运动的轨迹跟踪。由于微型AUV的结构特性和存在较强的不确定干扰,在偏航角控制上存在一定抖振问题。后续将导入更精确的艇体参数及干扰项进行仿真,并在实体上对其进行试验验证。
| [1] |
CHEN Y, QIAO J, LIU J, et al. Three-dimensional path following control system for net cage inspection using bionic robotic fish[J]. Information Procdssing in Agriculture, 2022, 9(1): 110-111. |
| [2] |
KIMURA R, UKITA M, KAMEZUKA K, et al. construction of guidance and control system and GUI of an autonomous underwater robot SOTAB-I[J]. IFAC Proceedings Volumes, 2013, 46(33): 13-18. DOI:10.3182/20130918-4-JP-3022.00007 |
| [3] |
BOUKEZZOULA R, JAULIN L, DESROCHERS B, et al. Thick gradual sets and their computations: Application for determining the uncertain zone explored by an underwater robot[J]. Engineering Applications of Artificial Intelligence, 2021, 102: 104287. DOI:10.1016/j.engappai.2021.104287 |
| [4] |
MARCIN M, ADAM S, JERZY Z, et al. Fish-like shaped robot for underwater surveillance and reconnaissance–Hull design and study of drag and noise[J]. Ocean Engineering, 2020, 217: 107889. DOI:10.1016/j.oceaneng.2020.107889 |
| [5] |
HASSAN M W, ABBAS N H. Disturbance Rejection for Underwater robotic vehicle based on adaptive fuzzy with nonlinear PID controller[J]. ISA Transactions, 2022.
|
| [6] |
KANELLAKOPOULOS I, KOKOTOVIC P V, MORSE A S. Systematic design of adaptive controllers for feedback linearizable systems[C]//1991 American control conference. IEEE, 1991: 649-654.
|
| [7] |
赵杰梅, 胡忠辉. 基于动态反馈的AUV水平面轨迹跟踪控制[J]. 浙江大学学报(工学版), 2018, 52(8): 1467-1473+1481. |
| [8] |
CHEN B, HU J, ZHAO Y, et al. Finite-time observer based tracking control of uncertain heterogeneous underwater vehicles using adaptive sliding mode approach[J]. Neurocomputing, 2022, 481: 322-332. DOI:10.1016/j.neucom.2022.01.038 |
| [9] |
ZHANG H, ZENG Z, YU C, et al. Predictive and sliding mode cascade control for cross-domain locomotion of a coaxial aerial underwater vehicle with disturbances[J]. Applied Ocean Research, 2020, 100: 102183. DOI:10.1016/j.apor.2020.102183 |
| [10] |
刘金琨. 滑模变结构控制Matlab仿真[M]. 北京: 清华大学出版社, 2005.
|
 2023, Vol. 45
2023, Vol. 45
