2. 闽西职业技术学院,福建 龙岩 364021
2. Minxi Vocational and Technical College, Longyan 364021, China
泵产品在船舶行业的应用非常广泛,涉及船舶推进系统、发电系统等方方面面。其中,离心泵是船舶中最常见的泵之一。离心泵是一种常见的动力泵,它通过旋转叶轮产生离心力来将液体输送到所需的位置。离心泵通常由马达、叶轮和泵壳组成。马达提供动力,使叶轮旋转,液体被吸入并在离心力的作用下被推送到泵的出口。船舶离心泵主要用于输送海水、燃油、润滑油等介质,被广泛应用于海水循环系统、消防系统、油料输送系统、排水系统等。
离心泵的模态分析是指对离心泵进行振动分析,找出其固有频率及振动模态,以评估其结构的稳定性、可靠性和耐久性。离心泵的振动问题是离心泵故障的主要原因之一,因此进行模态分析可以更好地了解离心泵的结构特点,预测其可能出现的振动问题,从而采取相应的措施进行改进和优化。
由于离心泵的工作介质是流体,因此进行离心泵的力学分析时需要重点考虑流体和固体的耦合作用,本文介绍流体力学的基础理论,研究一种流固耦合求解算法,并结合Workbench进行了船舶离心泵转子的有限元模态分析。
1 流体力学的湍流理论和壁面函数理论 1.1 湍流模型计算流体力学(CFD)是联系数理模型和流动现象的重要手段,船舶离心泵的流体力学特性分析必须要引入湍流模型,才能使流场求解方程组收敛。
本文主要介绍3种湍流模型[1],分别为涡粘模型、
1)涡粘模型
涡粘模型的基础是引入湍流粘度参数
| $ \overline {\rho {u_i}^\prime u_j^\prime } = - \mu \left( {\frac{{ \partial {{\bar u}_i}}}{{ \partial {x_j}}} + \frac{{ \partial {{\bar u}_j}}}{{ \partial {x_i}}}} \right) + \frac{2}{3}\left( {\rho k + {\mu _t}\frac{{ \partial {{\bar u}_ + }}}{{ \partial {x_i}}}} \right){\delta _{ij}} \text{。} $ |
式中:
2)
| $ \varepsilon = \frac{\mu }{\rho }\overline {\left( {\frac{{ \partial u_i^{}}}{{ \partial {x_k}}}} \right)\left( {\frac{{ \partial {u_j}}}{{ \partial {x_k}}}} \right)} \text{。} $ |
用
| $ {\mu _t} = \rho {C_\mu }\frac{{{\kappa ^2}}}{\varepsilon } 。$ |
式中,
| $ \begin{gathered} \frac{{ \partial (\rho k)}}{{ \partial t}} + \frac{{ \partial \left( {\rho {u_i}k} \right)}}{{ \partial {x_i}}} = \frac{ \partial }{{ \partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{ \partial k}}{{ \partial {x_j}}}} \right] + {G_k} - \rho \varepsilon \text{,} \\ \frac{{ \partial (\rho \varepsilon )}}{{ \partial t}} + \frac{{ \partial \left( {\rho {u_j}\varepsilon } \right)}}{{ \partial {x_i}}} = \frac{ \partial }{{ \partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _r}}}{{{\sigma _s}}}} \right)\frac{{ \partial \varepsilon }}{{ \partial {x_j}}}} \right] + \frac{\varepsilon }{k}\text{。} \\ \end{gathered} $ |
3)
| $ \begin{gathered} \rho \frac{{{{\rm{D}}_k}}}{{{{\rm{D}}_t}}} = \frac{ \partial }{{ \partial {x_i}}}\left( {{a_k}{\mu _{eff}}\frac{{ \partial k}}{{ \partial {x_i}}}} \right) + {G_k} - \rho \varepsilon n\text{,} \\ \rho \frac{{{{\rm{D}}_l}}}{{{{\rm{D}}_t}}} = \frac{ \partial }{{ \partial {x_i}}}\left( {{a_t}{\mu _{eft}}\frac{{ \partial \varepsilon }}{{ \partial {x_i}}}} \right) + \frac{\varepsilon }{k}{G_l} - \rho \frac{{{\varepsilon ^2}}}{k} \text{。} \\ \end{gathered} $ |
式中:
壁面函数理论的基本假设是:在靠近壁面处,流体中的速度分布主要由摩擦力控制,而在远离壁面处,速度分布主要由惯性力控制。因此,可以将流场分成2个区域:壁面附近的边界层和远离壁面的外层。在边界层内,壁面函数通过一些经验公式来计算速度和剪切应力的分布,而在外层,可以使用更简单的流动模型来计算速度和压力的分布。
壁面函数是一种在计算流体力学(CFD)中常用的模拟流体在壁面附近的速度和剪切应力的方法。壁面函数理论是基于边界层理论的,边界层理论是描述流体在靠近壁面处,速度剖面变化的一种理论。在CFD模拟中,由于计算网格的限制,通常无法将壁面附近的流场细化到足够小的尺度,因此需要使用壁面函数来模拟壁面附近的流场。
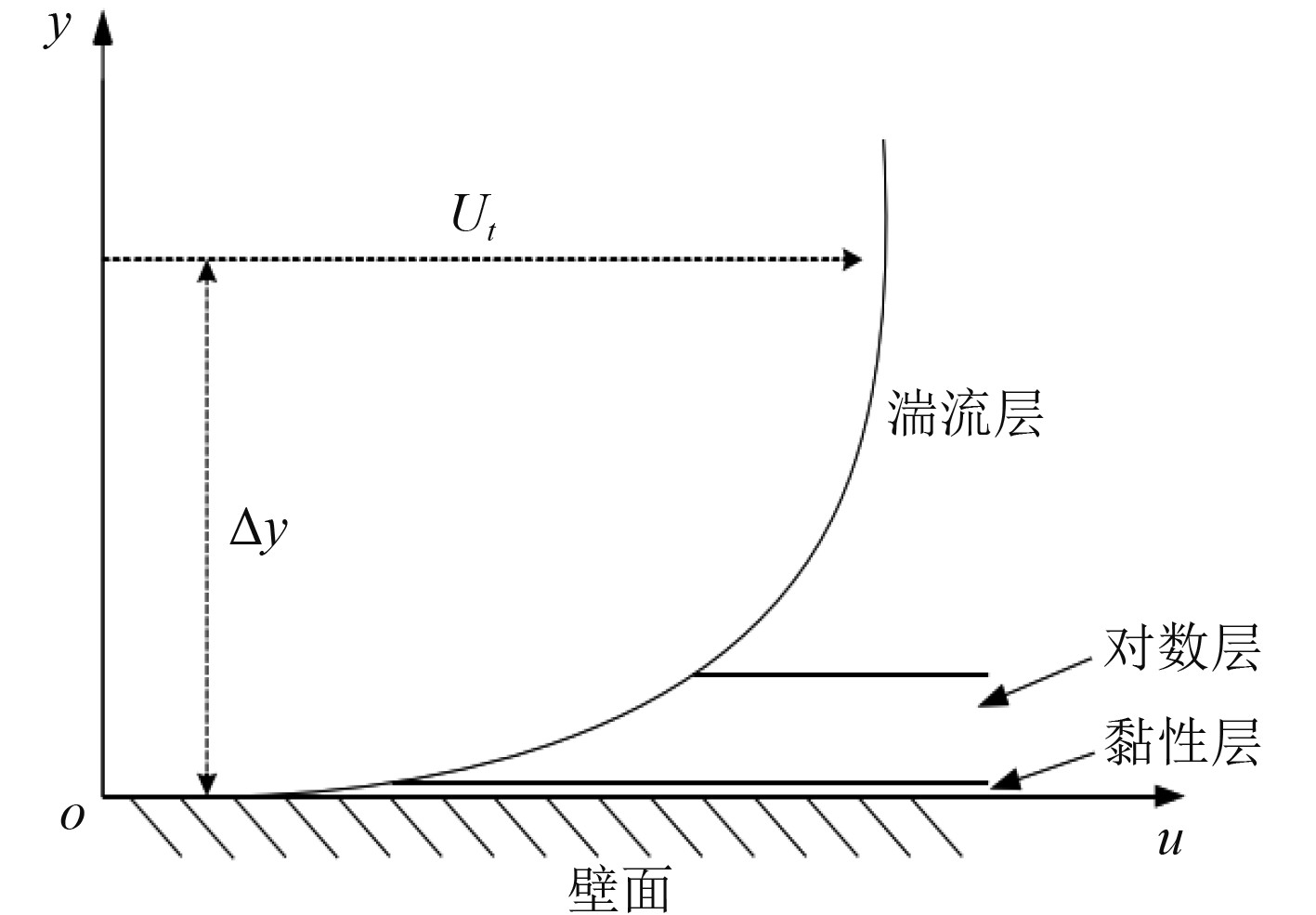
壁面函数理论的示意图如图1所示。
|
图 1 壁面函数理论的示意图 Fig. 1 Diagram of wall function theory |
流场与壁面之间的层次划分包括黏性层、对数层、湍流层。
对数层区域,流体的切向速度和剪切应力
| $ \begin{gathered} {U_t} = \frac{1}{k}\ln \left( {{y_t}} \right) + C \text{,} \\ {y_t} = \frac{{\rho \Delta {u_s}}}{\mu }\text{,} \\ {u_s} = {\left( {\frac{{{\tau _p}}}{\rho }} \right)^{\frac{1}{2}}}\text{。} \\ \end{gathered} $ |
常见的流固耦合求解方法包括:
1)前沿耦合法(Front-Coupling Method)[3]。该方法将流体和固体的运动方程分别求解,然后通过界面条件将两者耦合起来。这种方法的优点是能够处理复杂的流体和固体结构,但计算量较大,适用于小规模问题。
2)后沿耦合法(Back-Coupling Method)。该方法将流体和固体的运动方程同时求解,通过界面条件将两者耦合起来。这种方法的优点是计算效率高,适用于大规模问题,但对于复杂的流体和固体结构可能不够准确。
3)有限元法。该方法分别建立流体和固体的网格,然后通过耦合方程将两者结合起来。这种方法的优点是适用于复杂的流体和固体结构,这也是本文使用的方法。
流固耦合的有限元法原理如图2所示。

|
图 2 流固耦合的有限元法原理 Fig. 2 Principle of fluid-structure coupling finite element method |
可知,需要对流体和固体进行力学特性分析,然后通过载荷和程序耦合环节,将流体和固体的求解联系起来。
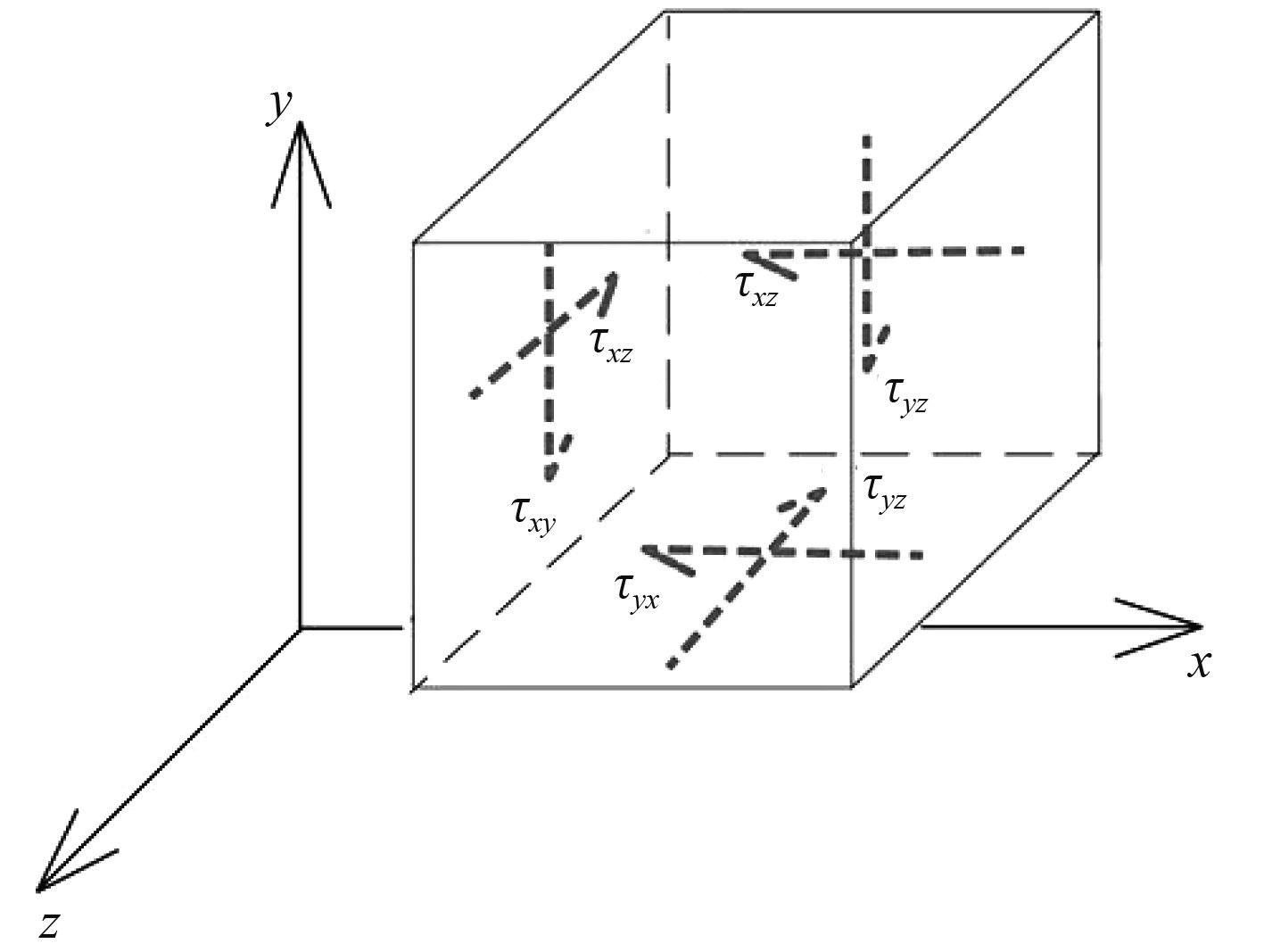
流固耦合过程首先进行固体(泵)的静力学分析,建立固体的空间弹性体应力模型如图3所示。
|
图 3 固体的空间弹性体应力模型 Fig. 3 Spatial elastomer stress model of solid |
刚体的基本变量包括位移向量
| $ \left\{ {\begin{array}{*{20}{l}} {\{ {\boldsymbol{u}}\} = {{[u,v,w]}^{\rm{T}}}} \text{,}\\ {\{ {\bf{\varepsilon }}\} = {{\left[ {{\varepsilon _x},{\varepsilon _y},{\varepsilon _z},{\gamma _{xy}},{\gamma _{xx}},{\gamma _{xx}}} \right]}^{\rm{T}}}}\text{,} \\ {\{ {\bf{\sigma }}\} = {{\left[ {{\sigma _x},{\sigma _y},{\sigma _z},{\tau _{xy}},{\tau _x},{\tau _{zx}}} \right]}^{\rm{T}}}} \text{。} \end{array}} \right. $ |
系统的平衡方程为:
| $ \left[ A \right]\{ {\bf{\sigma }}\} + \{ {{R}}\} = 0 \text{,} $ |
其中,
| $ [{\boldsymbol{A}}] = \left[ {\begin{array}{*{20}{c}} {\dfrac{ \partial }{{ \partial x}}}&0&0&{\dfrac{ \partial }{{ \partial y}}}&{}&{\dfrac{ \partial }{{ \partial z}}} \\ {}&{\dfrac{ \partial }{{ \partial y}}}&{}&{\dfrac{ \partial }{{ \partial x}}}&{\dfrac{ \partial }{{ \partial z}}}&{} \\ {}&{\dfrac{ \partial }{{ \partial z}}}&{}&{\dfrac{ \partial }{{ \partial y}}}&{\dfrac{ \partial }{{ \partial x}}}&{} \end{array}} \right] \text{。} $ |
式中,
刚体的力学特性边界条件如下式:
| $ \left\{ {\begin{array}{*{20}{l}} {{T_x} = {n_x}{\sigma _x} + {n_y}{\tau _{yx}} + {n_z}{\tau _{zx}}}\text{,} \\ {{T_y} = {n_x}{\tau _{xy}} + {n_y}{\sigma _y} + {n_z}{\tau _{zy}}}\text{,} \\ {{T_z} = {n_x}{\tau _{xz}} + {n_y}{\tau _{xy}} + {n_z}{\sigma _z}} \text{。} \end{array}} \right. $ |
式中:
模态分析是指通过理论计算和数学模型推导的方法,对结构或系统的振动特性进行分析。这种分析方法通常用于预测结构在固有频率和振型方面的特性。本文基于有限元方法对船舶离心泵结构进行模态分析[4]。
建立结构的运动学微分方程如下:
| $ [{\boldsymbol{M}}]\{ {\boldsymbol{\ddot x}}\} + [{\boldsymbol{C}}]\{ {\boldsymbol{\dot x}}\} + [{\boldsymbol{K}}]\{ {\boldsymbol{x}}\} = \{ {\boldsymbol{F}}({\boldsymbol{t}})\} \text{。} $ |
式中:
对微分方程进行拉普拉斯变换可得:
| $ \begin{gathered} \left( {{s^2}[{\bf{M}}] + s[{\bf{C}}] + [{\bf{K}}]} \right)\{ X(s)\} = \{ F(s)\}\text{,} \\ X(s) = \int_{ - \infty }^{ + \infty } X (t){e^{ - st}}{\rm{d}}t\text{,} \\ F(s) = \int_{ - \infty }^{ + \infty } F (t){e^{ - st}}{\rm{d}}t\text{。} \\ \end{gathered} $ |
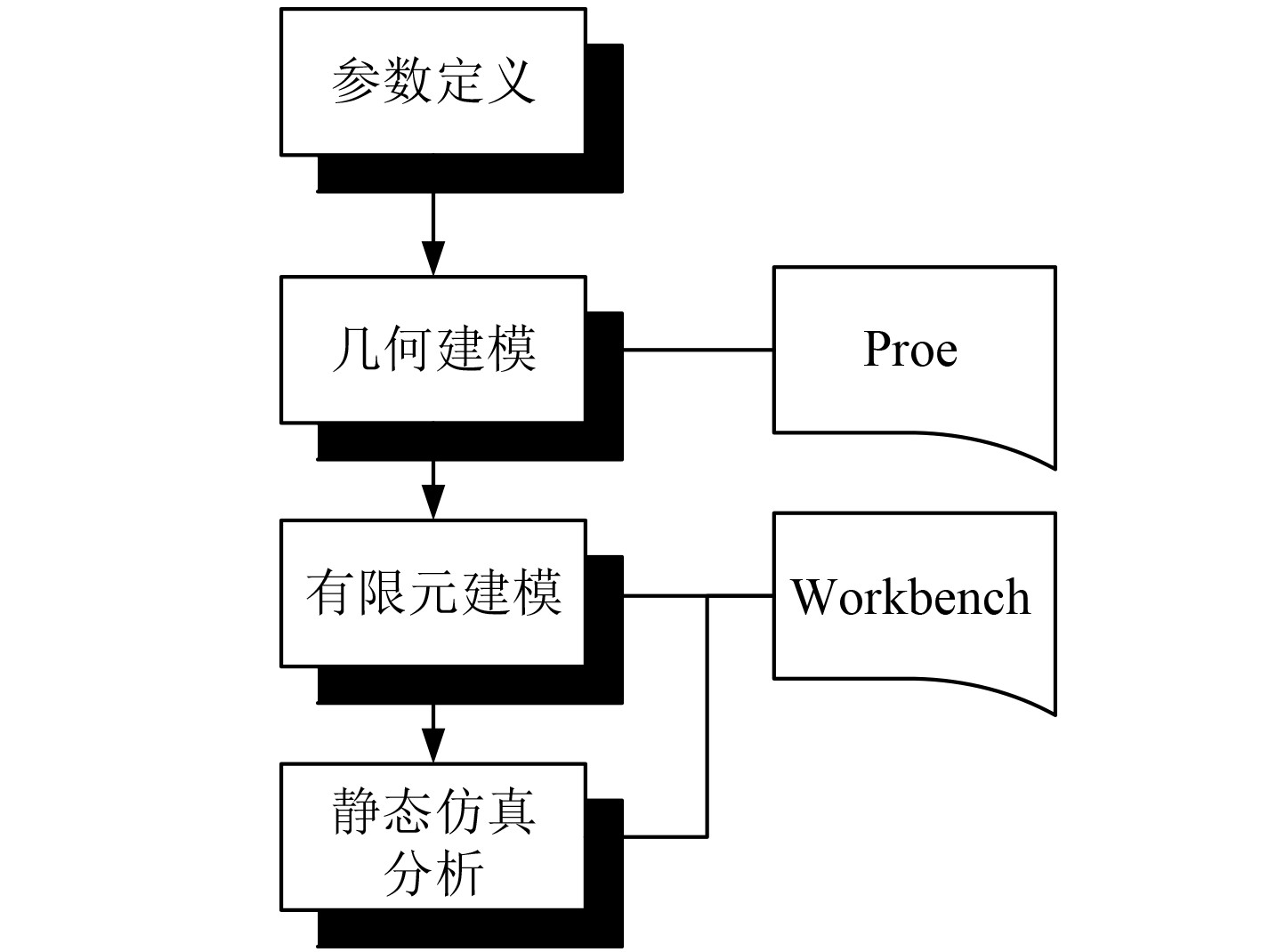
基于有限元软件的模态分析流程如图4所示。
|
图 4 基于有限元软件的模态分析流程 Fig. 4 Modal analysis process based on finite element software |
基于有限元分析的船舶离心泵转子流固耦合模态分析环节包括:
1)三维建模
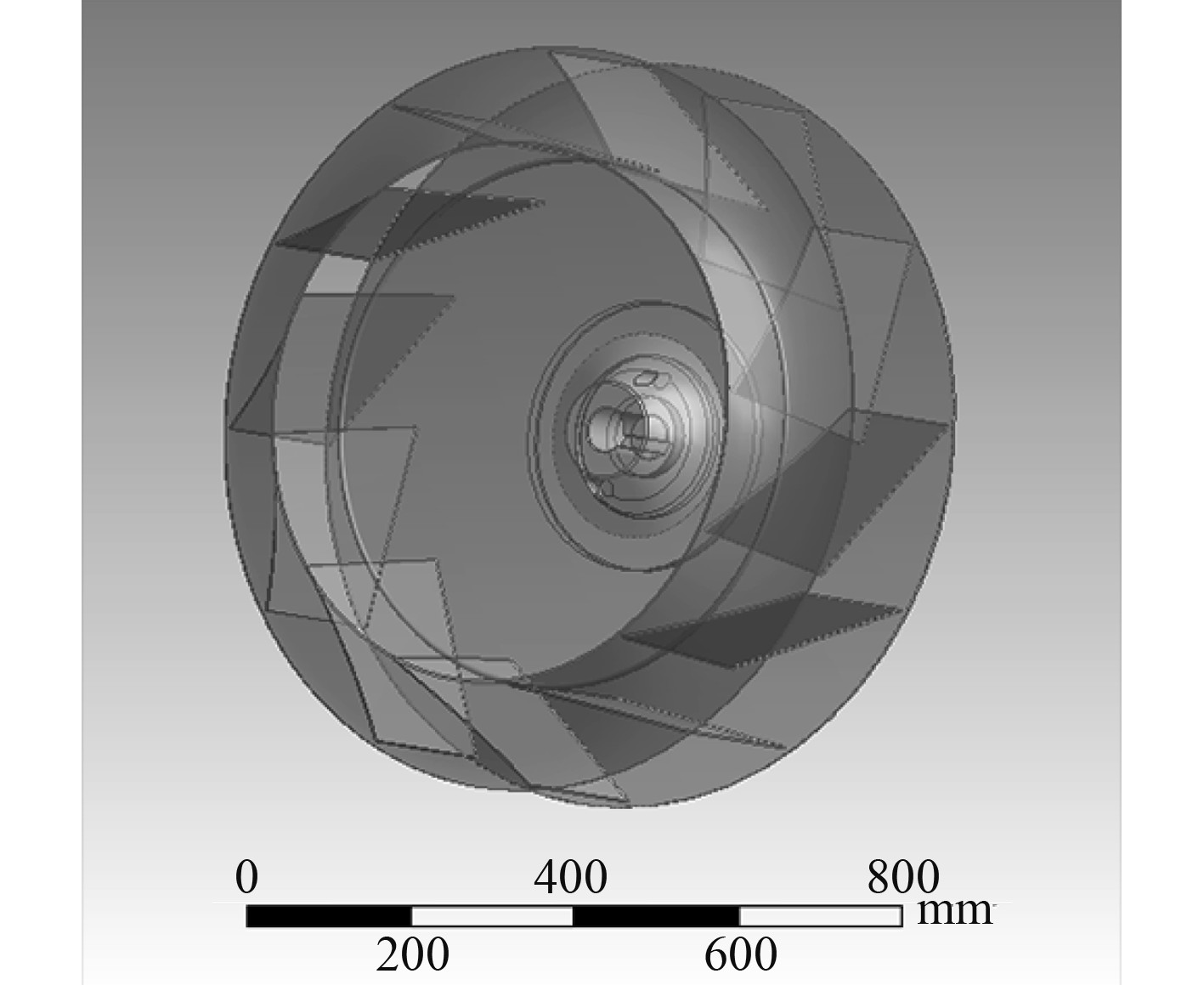
离心泵转子的三维建模基于CREO软件,如图5所示。
|
图 5 离心泵转子的三维建模 Fig. 5 Three-dimensional modeling of centrifugal pump rotor |
2)有限元建模
由于离心泵转子结构模型较为复杂,网格的划分方法选用四面体自动划分网格法,有限元网格在workbench软件中完成,网格单元的尺寸设置为5 mm,生成网格数为124964,有限元模型如图6所示。
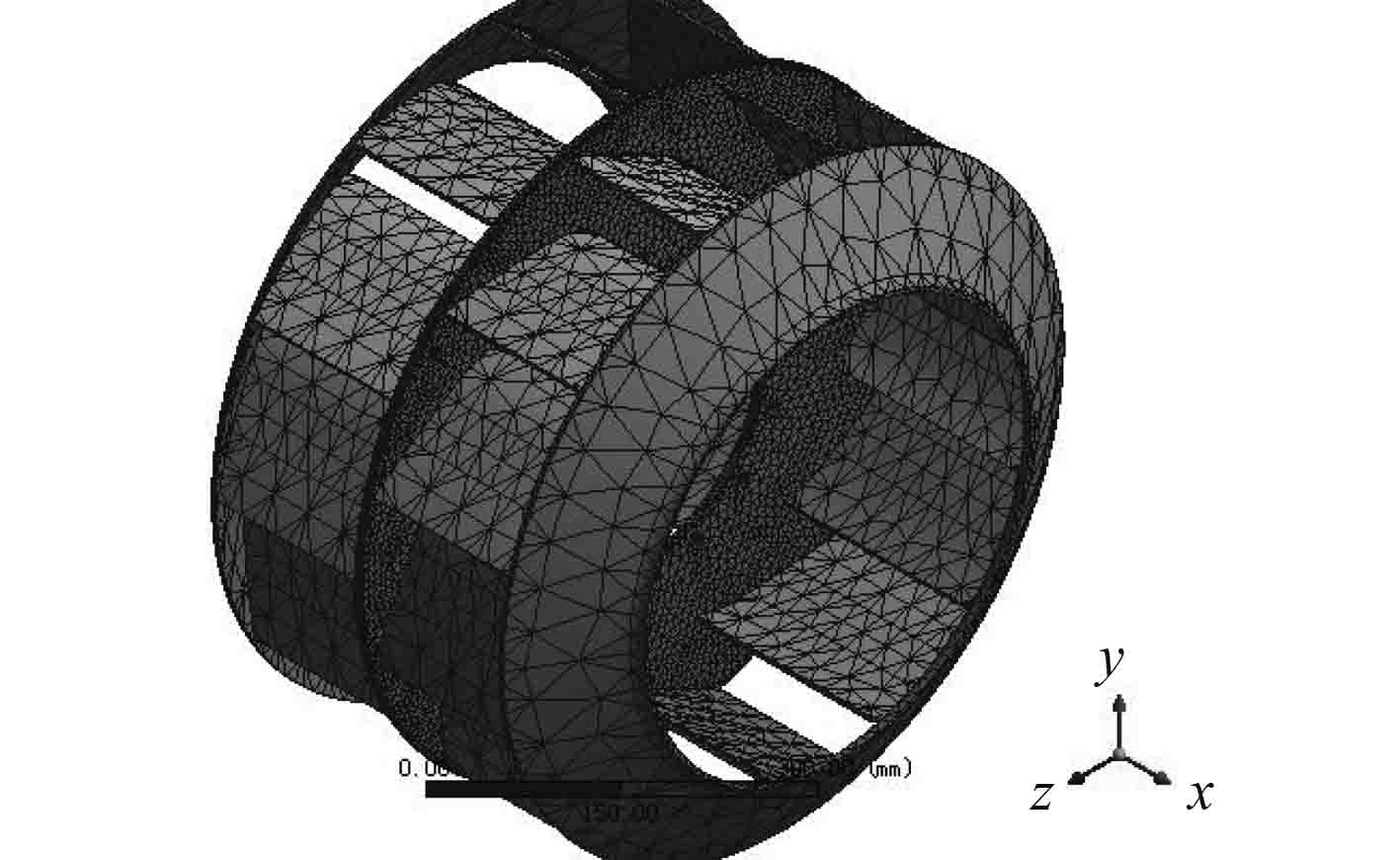
|
图 6 离心泵转子结构有限元模型 Fig. 6 Centrifugal pump rotor structure |
3)载荷与求解
载荷及边界条件包括:进口压力值为1个标准大气压,湍流强度设置为4500;出口流量设置为标准流量;壁面采用无滑移壁面。
图7为基于流固耦合分析的离心泵转子模态仿真云图。
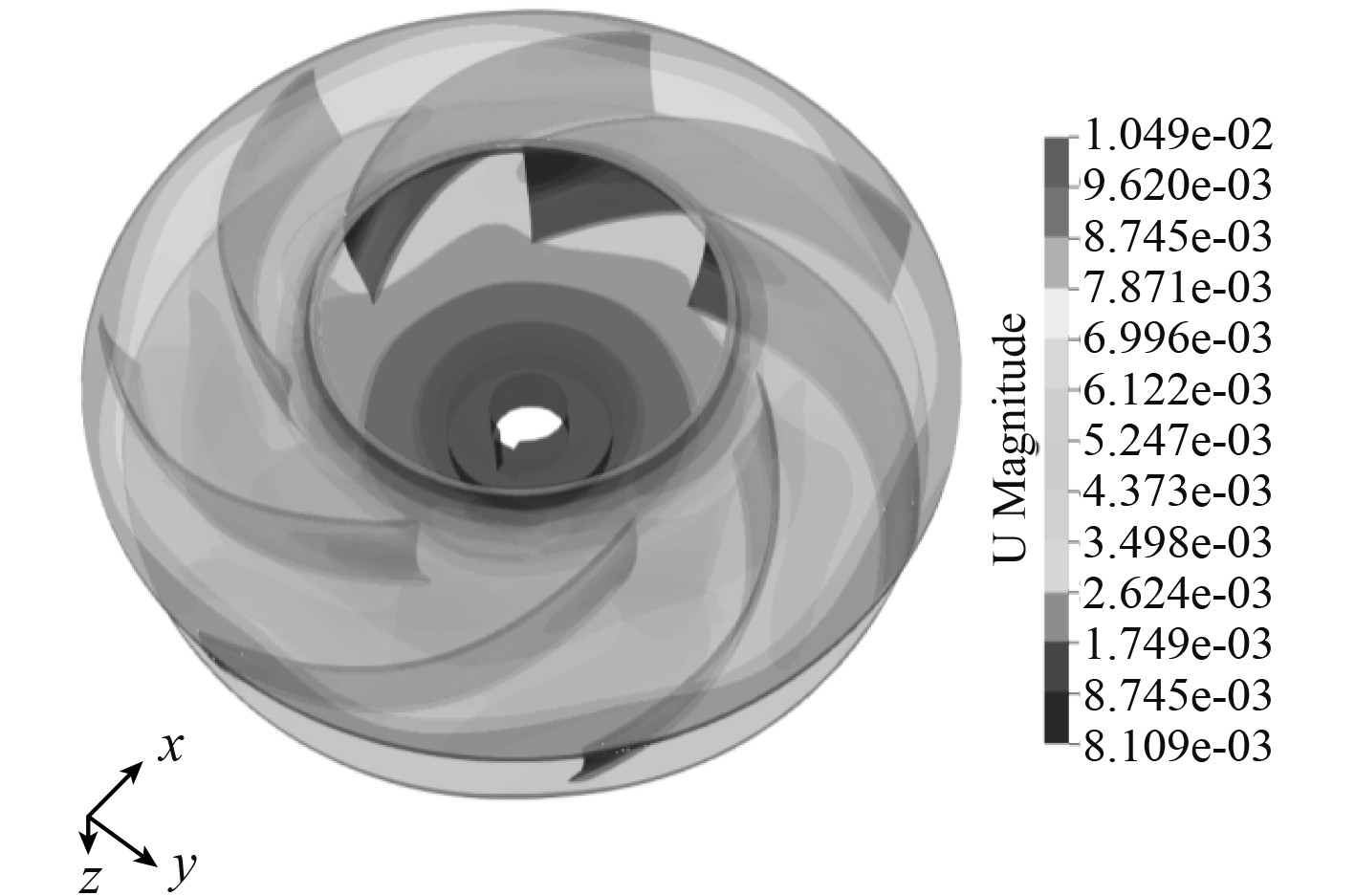
|
图 7 离心泵转子模态仿真云图 Fig. 7 Cloud image of rotor mode simulation of centrifugal pump |
可知,离心泵转子最大振幅为1.049E-02,位于扇叶根部位置。
3 结 语船舶离心泵转子的优化设计是一个复杂的工程问题,涉及到流体力学、结构力学和振动特性等多个领域。本文基于流固耦合分析进行船舶离心泵转子的仿真和优化设计,通过计算流体动力学(CFD)方法,对离心泵内部的流场进行分析,采用有限元分析(FEA)等方法,对离心泵转子的结构进行分析,将流场分析和结构分析进行耦合,并在Workbench中进行了结构仿真。
| [1] |
李春光, 阎慧东, 张华栋, 等. 基于振动阈值的船舶离心泵系统建造阶段声学故障诊断方法[J]. 船舶, 2019, 33(3): 116-125. LI Chun-guang, YAN Hui-dong, ZHANG Hua-dong, et al. Acoustic fault diagnosis method of marine centrifugal pump system during construction based on vibration threshold[J]. Ships, 2019, 33(3): 116-125. |
| [2] |
陈海燕, 许丽华, 罗兆伟. 流固耦合技术在船舶离心泵转子的模态分析[J]. 船舶科学技术, 2017, 39(22): 79-81. CHEN Hai-yan, XU Li-hua, LUO Zhao-wei. Modal Analysis of fluid-structure coupling technology in marine centrifugal pump rotor[J]. Ship Science and Technology, 2017, 39(22): 79-81. |
| [3] |
邱勇, 王辉. 船舶用立式离心泵轴封的设计优化[J]. 液压气动与密封, 2015, 35(4): 52-54. QIU Yong, WANG Hui. Design optimization of shaft Seal for marine vertical centrifugal pump[J]. Hydraulics Pneumatics & Seals, 2015, 35(4): 52-54. |
| [4] |
吴仁荣. 船舶系统用离心泵的应用场合和结构特点[J]. 船舶辅助机电设备, 1976(3): 30-37. WU Ren-rong. Application and structural characteristics of centrifugal pump for marine system[J]. Ship Auxiliary Electrical and Mechanical Equipment, 1976(3): 30-37. |
 2023, Vol. 45
2023, Vol. 45
