船舶在水面上航行过程中,船首推开的水流会通过船体的侧面以及船体的底部回流,以补足船体尾部的空间[1]。但是水流经过船体底部回流之后,其水流速度加快,导致水流对船体底部的作用力变小,在这种情况下,为了能够确保船体自身的重力和水流对船体的浮力相互平衡,船体则会出现整体垂直下沉,并且由于船体首部和尾部受到的压力存在差异,造成船体纵倾产生变化,这2个因素一起构成了船体下沉现象[2]。根据船体下沉位置的不同,船体下沉可以分为船首、船中以及船尾3种下沉[3]。船舶在浅水域航行时,因为受到浅水效应的影响,船体的下沉现象更为明显,这会减小船舶的富余水深,降低船体的操控性能,甚至造成船舶搁浅,因此浅水域的船体下沉现象会对船体的安全造成严重的威胁[4]。近年来,随着船舶大型化以及高速化的发展,船体的吃水深度也逐渐变大,因此,先前建设的港口以及巷道等设施的相对吃水深度降低,这些水域进而变成浅水域[5]。船舶在水面上航行过程中,由于驾驶人员对船体下沉量的错误预估而导致船体触浅等事故时有发生,因此对船舶航行过程中的下沉量进行精确预估,对船舶正常航行有着十分重要的意义。
1 船舶航行过程分析 1.1 船舶运动学模型的构建船舶受到的水流阻力大小及方向和阻力系数存在一定的关系,而水流的阻力系数会随着水深和船舶吃水深度之间比值的变化而变化[6]。当船舶在深海中航行时,船舶的吃水深度和海水深度之比可以看成是0,当船舶在浅水区域航行时,船舶受到的水流阻力系数则不可忽略,这即为浅水效应,并且当船体的吃水深度和海水的深度之比大于1/2时,浅水效应十分明显[7]。把船舶当作短翼时,其展弦比的计算公式为:
| $ {\lambda _H} = \frac{{2d}}{L}\text{。} $ | (1) |
当船舶处于斜流环境下时,水流和船舶的运动方向相反,并且水流和船舶之间的冲角为β,则升力L的计算公式为:
| $ L = \frac{{{C_L}\rho {V^2}Ld}}{2} \approx \frac{{{C_L}\rho {V^2}Ld}}{2}\text{。} $ | (2) |
根据短翼原理,小冲角情况下,其升力系数的计算公式为:
| $ {C_L} = \frac{{2{\text{π}} }}{{1 + \frac{2}{{{\lambda _H}}}}}\left| \beta \right|\text{。} $ | (3) |
在对浅水区域的船舶运动数学模型进行研究过程中,本文以常规深水下的分离型船舶数学模型为基础,并分辨出浅水和深水区域之间的差异,如阻力系数、伴流系数等,经过整理之后,则可以得到回归公式,其基本方程如下式:
| $ \left\{ {\begin{array}{*{20}{l}} {X = m\left( {\dot u - vr} \right)}\text{,} \\ {Y = m\left( {\dot v + ur} \right)} \text{,}\\ {N = Y \cdot {x_C} + {I_{zz}}\dot r} \text{。} \end{array}} \right. $ | (4) |
浅水区域中的船舶,纵向流体动力学模型和深水中的一致,可以采用下式来描述:
| $ {X_H} = X\left( u \right) + {X_{vv}}{v^2} + {X_{vr}}vr + {X_{rr}}{r^2}\text{。} $ | (5) |
船舶在浅水区域航行时,由于水底对船舶四周的水流运动存在一定影响,即存在阻塞效应,因此船舶的直行系数会产生一定的变化,如下式:
| $ \left\{ {\begin{array}{*{20}{l}} {X\left( u \right) = \dfrac{1}{2}\rho {V^2}Ld{{X'}_{uu}}{{u'}^2}} \text{,}\\ {{{X'}_{uu}}{{u'}^2} = \dfrac{S}{{Ld}}{C_{dh}}} \text{。} \end{array}} \right. $ | (6) |
式中的船舶航行的总阻力系数Cdh的值会受到浅水效应的影响,根据浅水区域的影响,对船舶航行的阻力系数进行修正,其计算公式为:
| $ \frac{{{C_{dh}}}}{{{C_\infty }}} = A + \frac{B}{{h/d}}\text{。} $ | (7) |
式中,A和B为试验系数。为了简化计算,对A和B两个参数进行回归拟合计算,如下式:
| $ \hat A = 1 + 0.97{F_h} - 1.592F_h^2\text{,} $ | (8) |
| $ \hat B = - 121.87{F_h} + 585.9F_h^2 - 928.4F_h^3\text{。} $ | (9) |
经过解算则可以得到水流阻力系数和水深之间的关系,如下式:
| $ y = 1 + 0.47\frac{d}{h} - 1.7{\left( {\frac{d}{h}} \right)^2} + 6.6{\left( {\frac{d}{h}} \right)^3}\text{。} $ | (10) |
作用在船体上的风力Fa的计算方法如下式:
| $ {F_a} = \frac{1}{2}{\rho _a}{C_a}v_a^2\left( {{A_a}{{\cos }^2}\theta + {B_a}{{\sin }^2}\theta } \right)\text{。} $ | (11) |
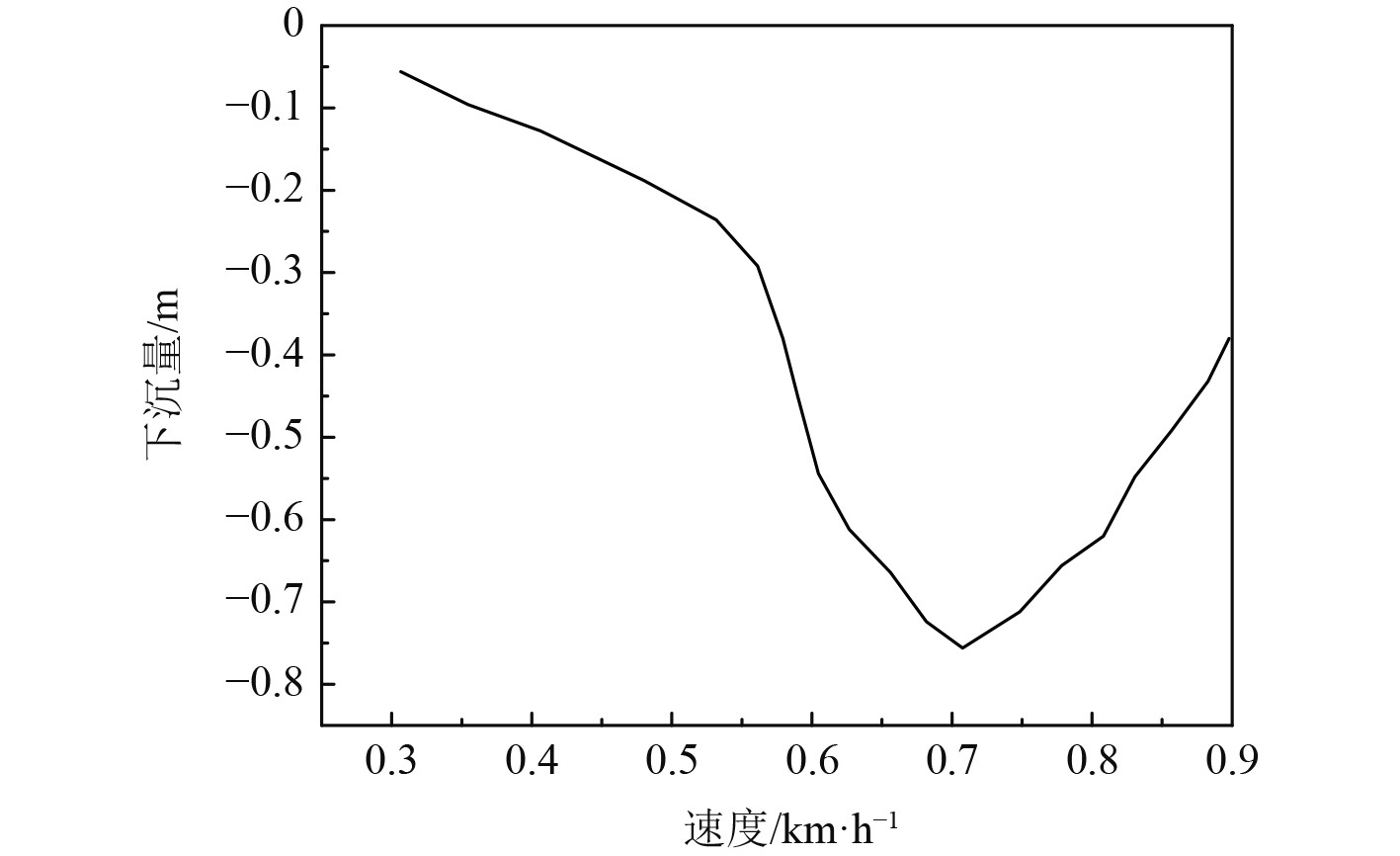
在浅水区域中,船舶的下沉量和船舶的速度存在一定的关系,变化曲线如图1所示。可以看出,在速度为0.7 km/h时,下沉量出现最小值。
|
图 1 船舶下沉量随速度变化曲线 Fig. 1 Curve of ship sinking with speed |
水深傅汝德数船体在亚临界区域中的下沉量和纵倾量的计算方法分别如下式:
| $ {F_{nh}} = \frac{V}{{\sqrt {gh} }}\text{,} $ | (12) |
| $ \frac{s}{L} = {C_s}\frac{{F_{nh}^2}}{{\sqrt {\left| {1 - F_{nh}^2} \right|} }}\text{,} $ | (13) |
| $ \frac{t}{L} = {C_t}\frac{{F_{nh}^2}}{{\sqrt {\left| {1 - F_{nh}^2} \right|} }}\text{。} $ | (14) |
在对船舶下沉量进行数值分析时,为了能够得到精确的结果,需要对CFD模型中的初始数值以及运动方式等参数进行配置。在本文的数值分析试验中,为了能够更加清晰显示船舶航行过程中下沉量的变化情况,对船舶采用自由运动的模式,并且将释放时间配置成1 s,缓冲时间配置成5 s。由于船舶存在升沉以及纵倾2个自由度,因此对这2个自由度进行开放,分别围绕坐标系中的y轴和z轴进行运动,船体的质心、惯性矩以及质量,可以利用CFD的惯性矩阵以及实际船体的排水量进行计算。
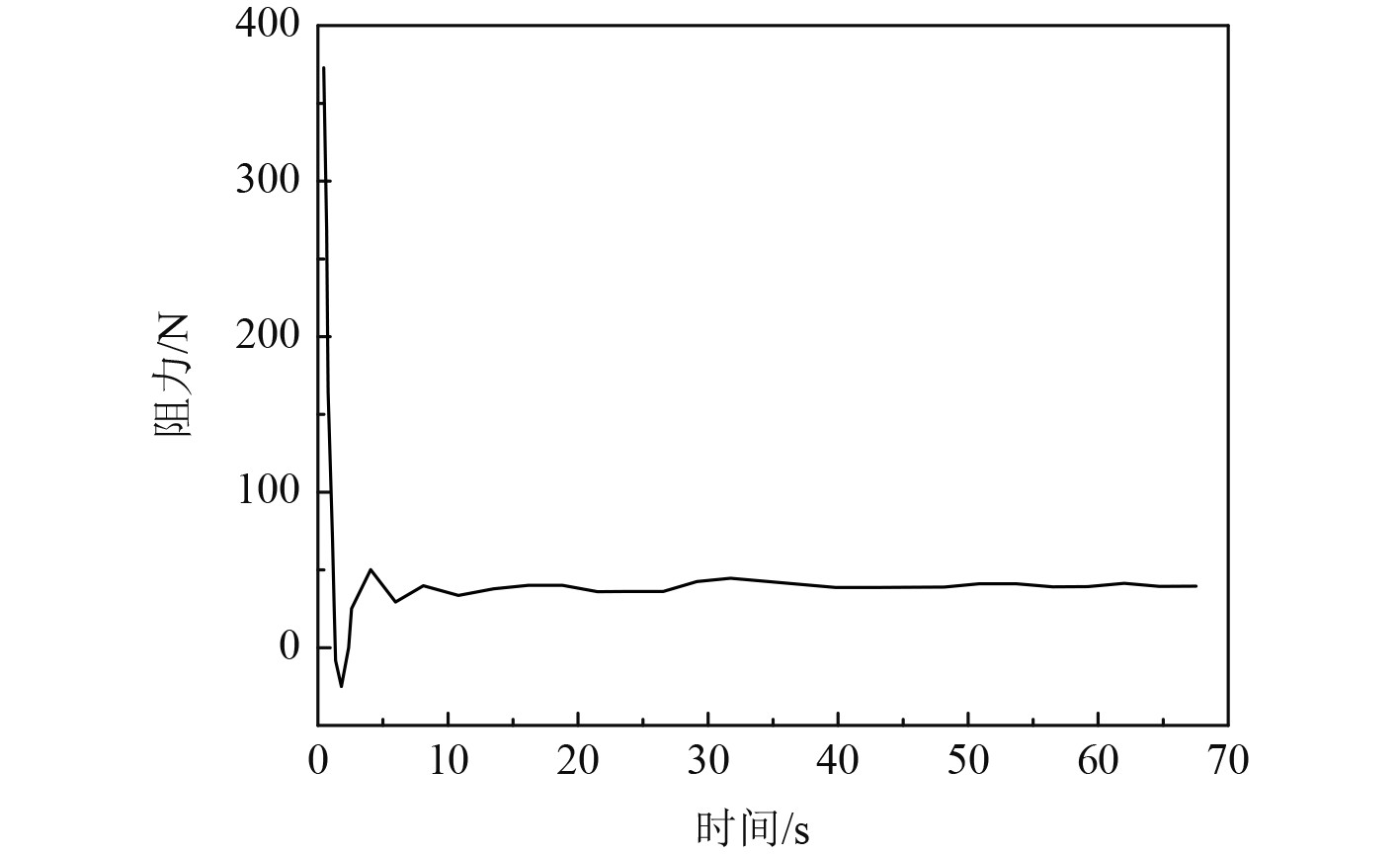
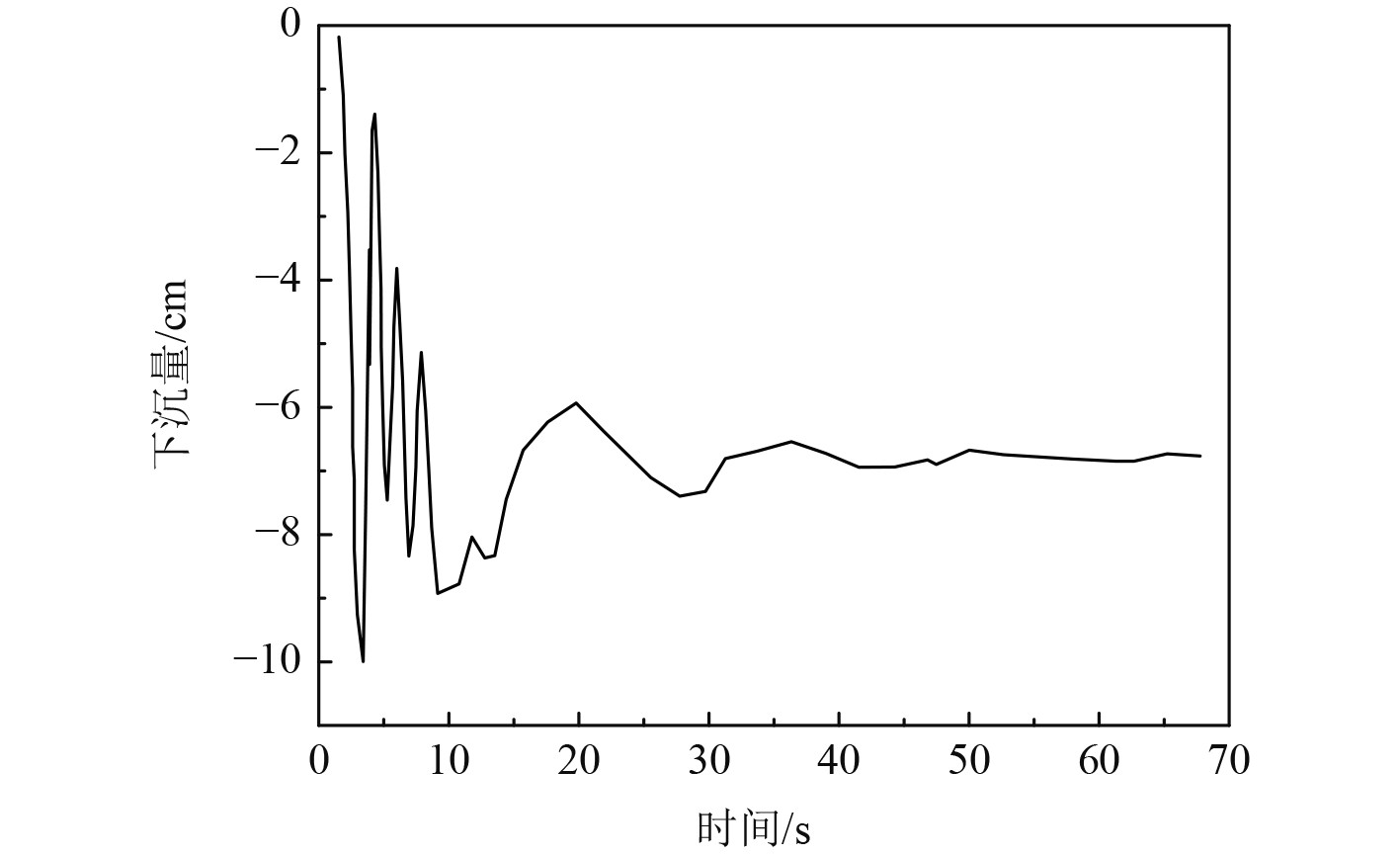
在傅汝德数为0.142的情况下,对船舶的阻力以及下沉量进行CFD数值模拟分析,仿真得到的船舶阻力数值模拟曲线如图2所示,仿真得到的船舶下沉量数值模拟曲线如图3所示。从图2可以看出,在仿真初期船舶受到的阻力会随着时间的推移迅速下降,然后趋于稳定。从图3可以看出,船舶下沉量一开始存在较大的震荡,随着时间的推移船舶下沉量区域稳定。
|
图 2 船舶阻力数值模拟曲线 Fig. 2 Numerical simulation curve of ship resistance |
|
图 3 船舶下沉量数值模拟曲线 Fig. 3 Numerical simulation curve of ship sinking |
由于船舶下沉量对船舶的安全航行有着很大的影响,因此通过大量的试验得到了船体下沉量的估算公式,该估算公式是在船模水池试验中,以大量的试验数据作为基础,并根据船体的长度、宽度以及吃水深度等参数估算得到的。本文通过浅水域中船舶的下沉量公式,对178000 GT的船体下沉量进行估算,其估算公式如下式:
| $ S = \left( {61.7 \cdot {C_B}\frac{B}{L} - 0.6} \right) \cdot \frac{{F_{rh}^2}}{{\sqrt {1 - F_{rh}^2} }}\text{。} $ | (15) |
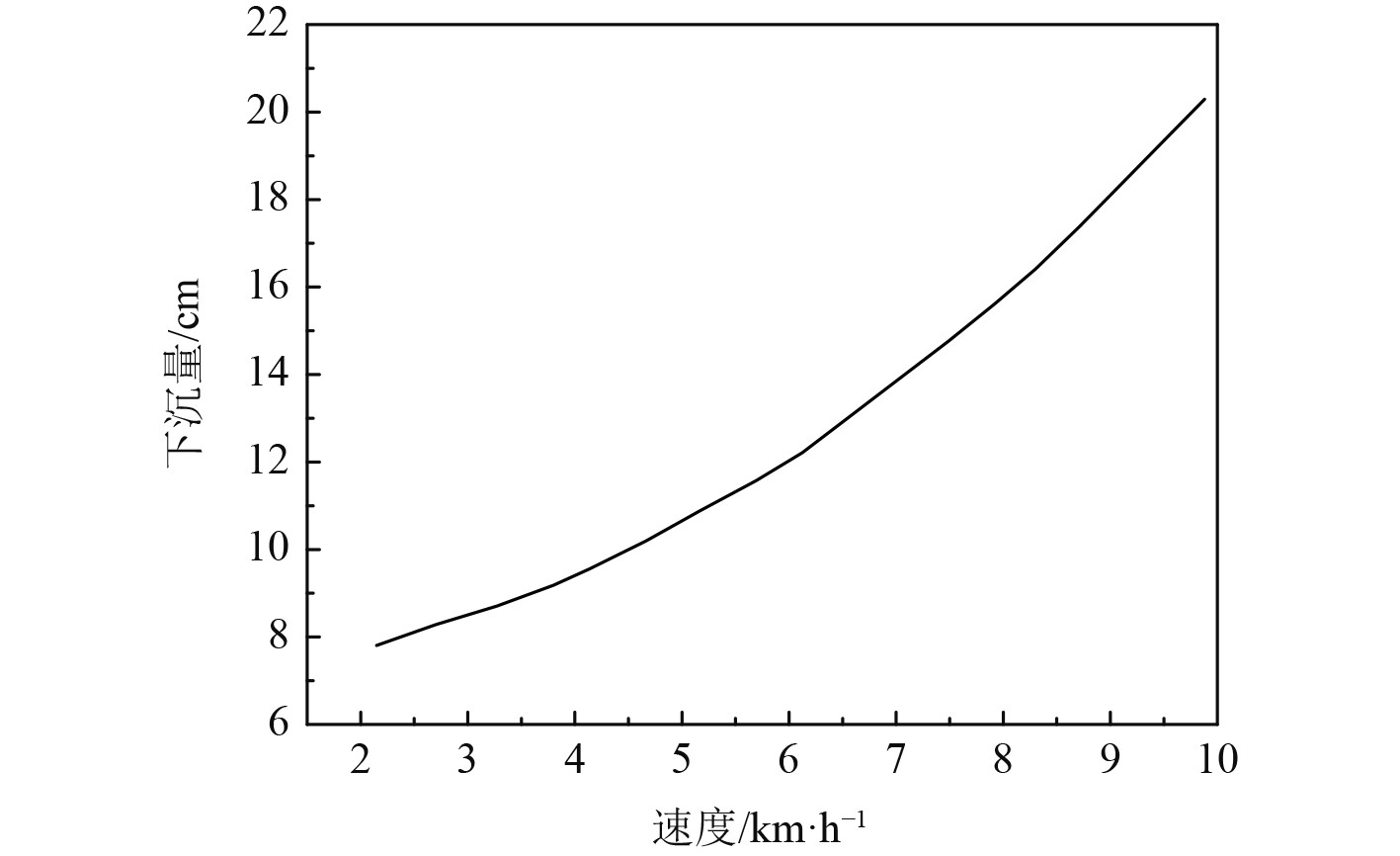
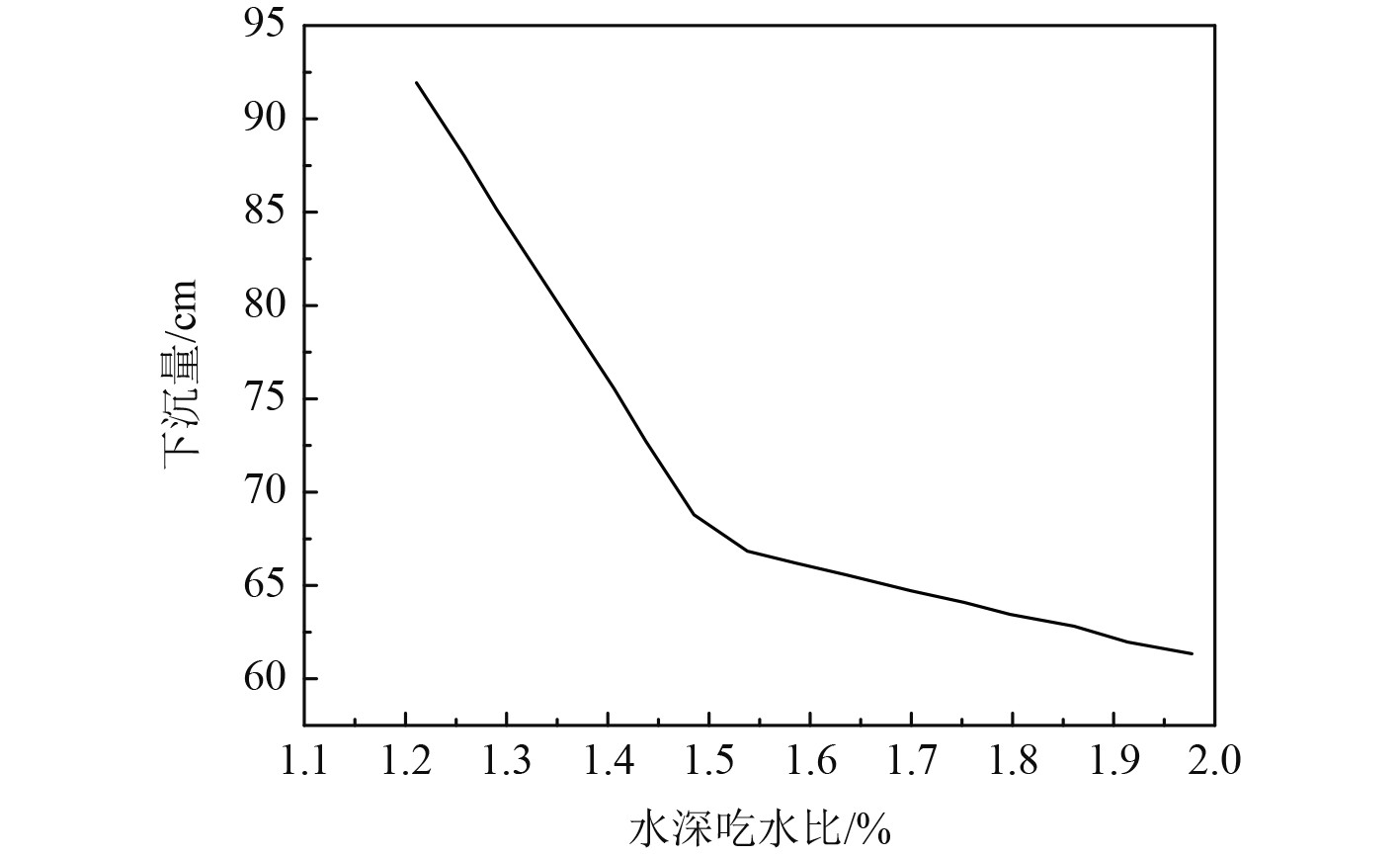
在水深吃水比等于15的情况下,随着流速的增加,船体的下沉量也会增加,如图4所示。船舶的下沉量随水深吃水比的变化情况如图5所示。可以看出,船体的下沉量会随着水深吃水比值的升高而降低。
|
图 4 船舶下沉量和流速之间的关系 Fig. 4 The relationship between ship sinking and flow velocity |
|
图 5 船体下沉量随水深吃水比的变化曲线 Fig. 5 Curve of the variation of ship sinking with water depth and draft ratio |
本文对不同水深以及速度下的船舶下沉量的CFD仿真进行分析,并通过回归的方法得到船舶纵倾角的变化方程。船体下沉量在不同水深下的无量纲化处理方法如下式:
| $ {S'_{{M_0}}} = \frac{{{S_{{M_0}}}}}{d}\text{。} $ | (16) |
式中,
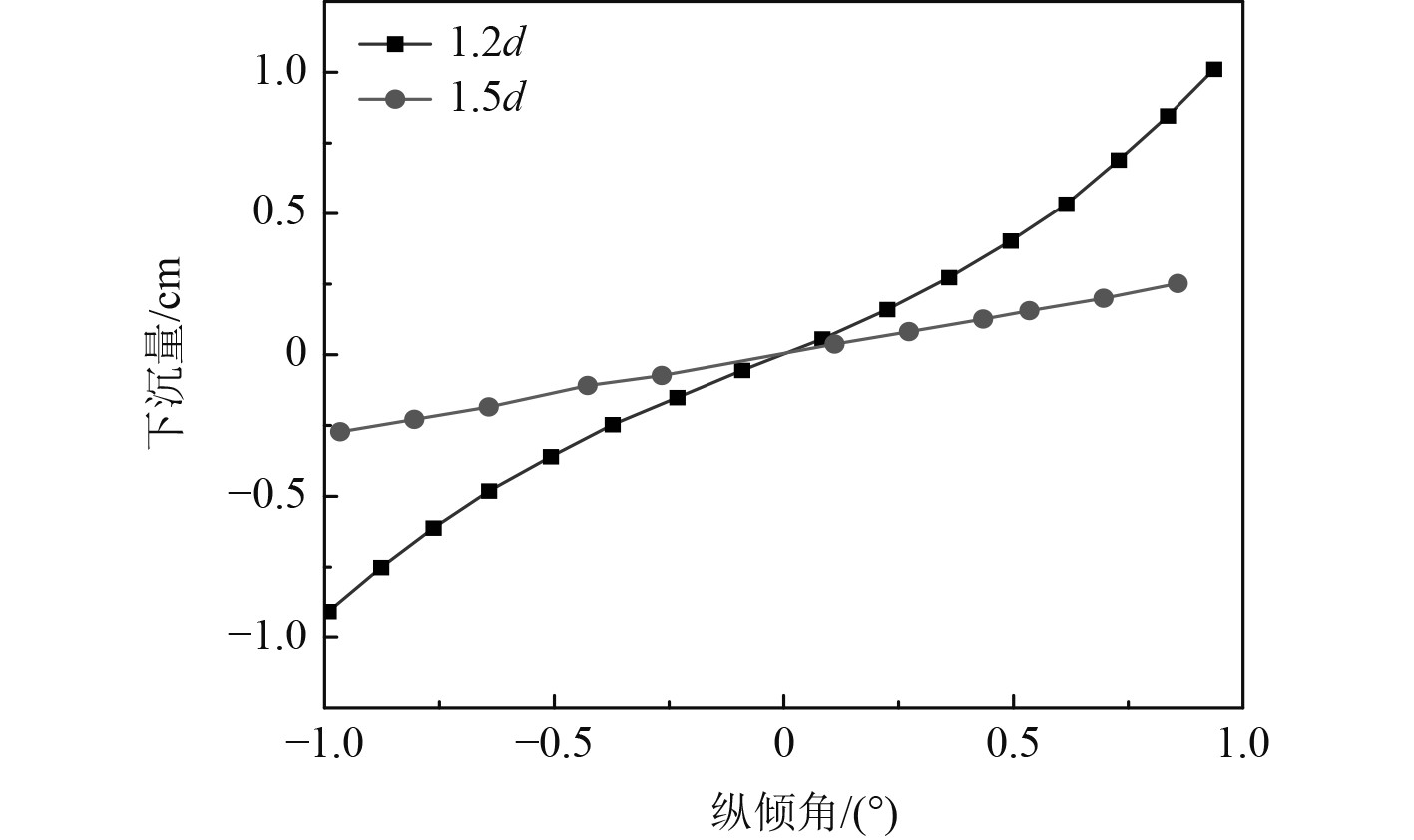
船中下沉量的变化量随纵倾角的变化曲线如图6所示。可以看出,随着船体纵倾角的逐步增大,船中下沉量的变化也不断增大,因此船体在不同的纵倾角的情况下,船中下沉量和船体吃水变化量之间属于正相关关系。在水深吃水比等于1.5的情况下,船舶的浅水效应不是很明显,船中下沉量的变化量相对较小;在水深吃水比等于1.2的情况下,船舶的浅水效应十分明显,船体受到的压力降低,此时船中的下沉量和船体的纵倾角之间不属于正比例关系,则此时船中下沉量的回归预测方法需要采用三次形式,船中的下沉量可以通过多项式进行回归预测,如下式:
|
图 6 船中下沉量随纵倾角的变化曲线 Fig. 6 Curve of the variation of the sinking amount in the ship with the longitudinal inclination angle |
| $ \Delta {S'_M} = a \cdot \varphi _0^3 + b \cdot \varphi _0^2 + c \cdot {\varphi _0}\text{。} $ | (17) |
经过不同水深吃水比下船中下沉量的分析可以看出,水深吃水比等于1.2的时有十分明显的浅水效应,因此船体下沉量具备高阶系数,该高阶系数可以通过回归预测得到,如下式:
| $ c = 39.1 \cdot {e^{ - 7.78 \cdot \frac{h}{d}}} + 0.009 \cdot {e^{ - 0.69 \cdot \frac{h}{d}}}\text{。} $ | (18) |
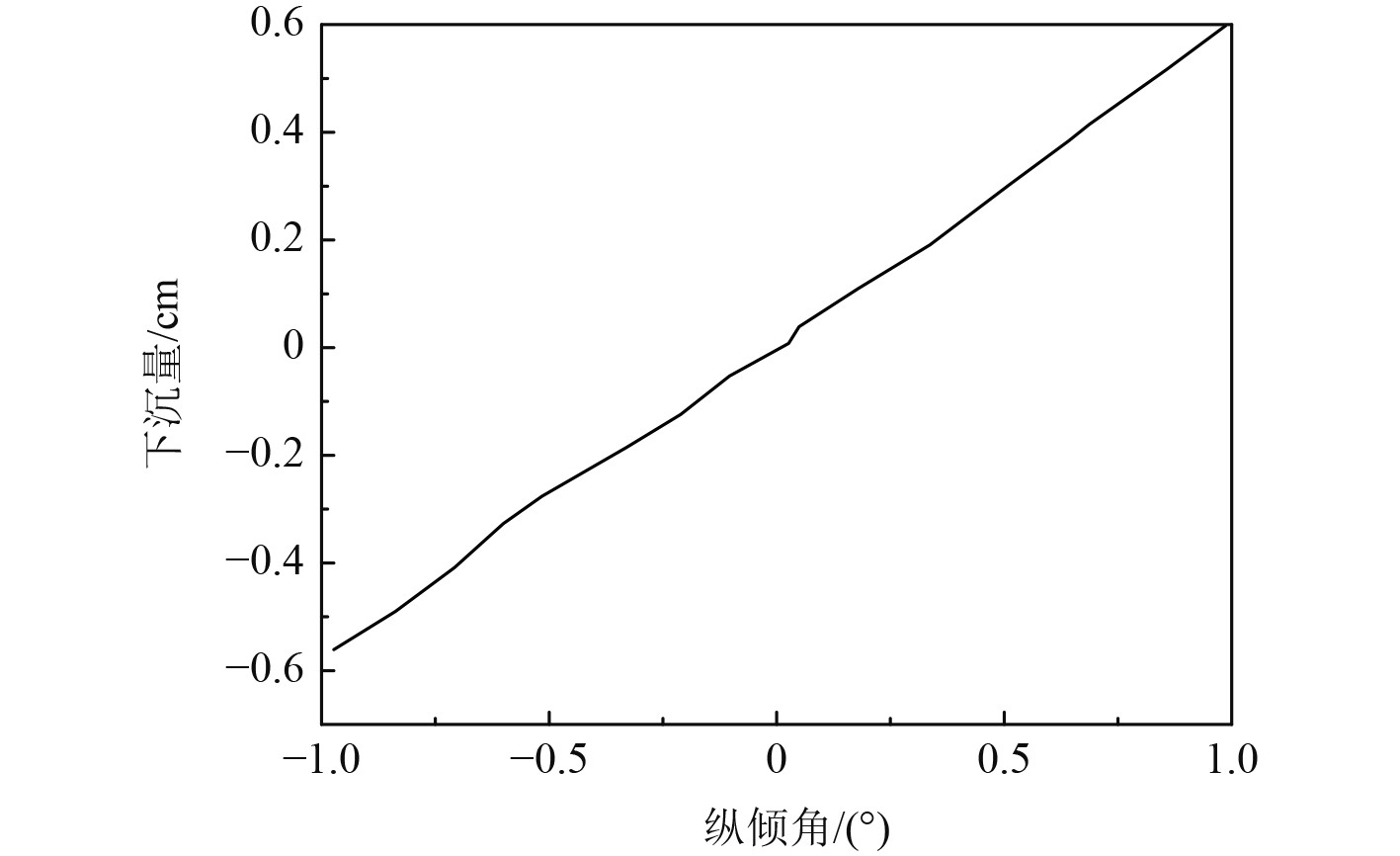
图7给出了船尾下沉量随纵倾角的变化曲线。可以看出,船尾下沉量和船体初始纵倾角之间属于正比例关系,因此通过一次方程可以对船尾下沉量和船体初始纵倾角之间的关系进行线性拟合,如下式:
|
图 7 船尾下沉量随纵倾角变化曲线 Fig. 7 Curve of stern settlement with longitudinal inclination angle |
| $ \Delta {S'_\varphi } = k_1 \cdot {\varphi _0}\text{。} $ | (19) |
式中,k1为系数,可以基于水深吃水比进行回归计算而得到。
| $ k_1 = 0.001\;9 \cdot {\left( {\frac{h}{d}} \right)^{ - 1.085}} + 0.000\;187\text{。} $ | (20) |
随着船舶朝着大型以及快速化方向发展,在港口等水域容易受到流的影响,因此船体出现一定程度的下沉现象,并且随着水深吃水比的降低,会进一步减小船底到水底的距离,船舶周围水流速度则会进一步增加,因此船体受到的水的压力会变大,最终使得船体在浅水域出现更加明显的下沉现象。本文对船舶航行过程中的下沉量进行预测,对船舶技术的发展有积极的促进作用。
| [1] |
丁水汀, 宋越, 杜发荣, 等. 柴-燃混合循环系统发展综述及航空适用分析[J]. 北京理工大学学报, 2023(43): 1-17. DING Shui-ting, SONG Yue, DU Fa-rong, et al. Review of combined cycle power system and analysis of key research points for aviation application[J]. Transactions of Beijing Institute of Technology, 2023(43): 1-17. |
| [2] |
冯德银. 大型船舶行驶过程沉量可靠性预测[J]. 船舶科学技术, 2018(40): 40-42. FENG De-yin. Reliability prediction of heavy load on large ships[J]. Ship Science and Technology, 2018(40): 40-42. |
| [3] |
严心池, 安伟光, 陈卫东, 等. 大型船舶结构的可靠性研究[J]. 哈尔滨工程大学学报, 2004(25): 147-152. YAN Xin-chi, AN Wei-guang, CHEN Wei-dong, et al. reliability analysis for large ship structure[J]. Journal of Harbin Engineering University, 2004(25): 147-152. |
| [4] |
沈建国. 非线性回归分析的船舶装备动态环境模拟研究[J]. 船舶科学技术, 2020(42): 214-216. SHEN Jian-guo. Research on dynamic environment simulation of ship equipment by nonlinear regression analysis[J]. Ship Science and Technology, 2020(42): 214-216. |
| [5] |
郭兴华, 李伟, 刘芳武, 等. 基于数据挖掘的船舶航线自动控制技术[J]. 船舶科学技术, 2022(44): 132-135. GUO Xing-hua, LI Wei, LIU Fang-wu, et al. Research on automatic control technology of ship navigation line based on data mining[J]. Ship Science and Technology, 2022(44): 132-135. |
| [6] |
刘学军, 田树科. 船舶电力系统中DC-DC变换器的建模与控制[J]. 船舶科学技术, 2019(41): 94-96. LIU Xue-jun, TIAN Shu-ke. Research on modeling and control of DC-DC converter in ship power system[J]. Ship Science and Technology, 2019(41): 94-96. |
| [7] |
鲁晓丽, 赵泽旭, 史英杰. 现代统计学理论的船舶交通数据特征分析[J]. 船舶科学技术, 2018(40): 31-33. LU Xiao-li, ZHAO Ze-xu, SHI Ying-jie. Characteristics analysis of ship and ship traffic data based on modern statistical theory[J]. Ship Science and Technology, 2018(40): 31-33. |
 2023, Vol. 45
2023, Vol. 45
