2. 上海交通大学 高新船舶与深海开发装备协同创新中心,上海 200240;
3. 中国船舶及海洋工程设计研究院,上海 200011
2. Collaborative Innovation Center for Advanced Ship and Deep-sea Exploration, Shanghai Jiaotong University, Shanghai 200240, China;
3. Marine Design and Research Institute of China, Shanghai 200011, China
尾轴架主要用于支撑伸出船体的尾轴,尾轴架系统的强度需要能够承受船舶在航行中复杂的载荷。计算尾轴架强度时,可采用理论计算方法[1],而有限元法相较于理论计算方法有着较高精度。利用有限元法计算时,需建立尾轴及尾轴架的有限元模型,采用不同单元来模拟结构以及不同的构件间连接简化方式需耗费的时间不同,同时也影响到计算精度,因此有必要对尾轴架系统强度计算时的建模方法进行研究。
有限元法计算时,尾轴架及尾轴的模拟可采用梁单元或实体单元,而对于尾轴与轴毂间的连接也有不同处理方式。Dedy等[2]为了研究载荷传递到单、双臂尾轴架的规律以及初始变形对尾轴架应力大小及变形的影响,采用实体单元对尾轴架及尾轴进行建模,计算模型范围仅包括尾轴架、尾轴以及与尾轴架相接触的船底板。Firmandha等[3]在研究计算尾轴架设计载荷的咬合法以及螺旋桨断叶法时,仅对尾轴架及尾轴采用体单元进行模拟,在尾轴架端部和尾轴与船体相交处施加约束。祁玉荣[4]对船舶结构模型的分析与简化进行一定研究,在计算尾轴架断叶强度时建立的有限元模型范围:船长方向取169 # 肋位-225 # 肋位,船宽方向取船中-舷侧,尾轴架及尾轴均采用实体单元模拟。王滨[5]采用实体单元建立了某船轴系各个结构的有限元模型,分别研究了尾轴上各处轴承的刚度对尾轴轴系振动特性的影响。研究显示,尾轴架轴承刚度对振动频率的影响最大,而推力轴承等也会在一定程度上影响轴系的振动特性。罗晨等[6]在研究有限元模型建立方式对尾轴架系统振动特性计算的影响时,基于梁单元模型分别考虑了尾轴承刚度、尾轴架建模采用的单元类型以及建模范围等因素,对单、双臂尾轴架及尾轴的横向振动特性进行了计算分析,与试验结果比较发现建模时,尾轴架系统的边界处理方式以及轴承的支撑刚度对尾轴架固有频率计算结果的影响很大。唐宇航等[7]对规范中尾轴架简化计算方法进行研究,分析了尾轴架的刚度对强度计算的影响,将规范方法、考虑尾轴架刚度方法得到的尾轴架应力与有限元结果进行对比,对比中采用体单元模型模拟尾轴架及尾轴,但未对尾轴承刚度展开研究。王高祥[8]对比了美国、苏联舰船设计手册和国内规范中尾轴架强度计算时的设计载荷,分别使用传统静力学方法以及有限元方法计算了某船尾轴架在规范载荷下的强度,其中尾轴架与尾轴采用实体单元模拟,构件连接局部部位采用了更小网格尺寸。许学强等[9]分析了国内外各船级社对双臂尾轴架尺寸设计所提出的要求,选取CCS规范以及与CCS差距最大的船级社规范分别设计了符合要求的最小尺寸尾轴架,采用Hypermesh中的SOLID单元建立了2个尾轴架的模型,并进行加载计算。
本文针对尾轴架系统强度计算以及建模方法展开研究,对比不同的设计载荷选取方法;研究了尾轴系统不同单元类型模拟、不同连接处理方式以及模拟方式及单元模拟尾轴、不同简化方式模拟尾轴轴毂与尾轴间的连接建立船舶尾轴架系统有限元模型进行计算,分析不同模型建立方式应力结果的差异。
1 尾轴架系统强度计算设计载荷及工况 1.1 设计载荷选取尾轴架系统位于船尾下部,会受到不同的载荷作用,如水动力载荷、波浪载荷以及因事故而产生的螺旋桨断叶及尾轴折断载荷等。强度计算时需选取较为典型的载荷以使得设计出的尾轴架系统具有足够的强度,目前常用的载荷计算方法有咬合法、尾轴折断法和螺旋桨断叶法。
船舶航行中,尾轴受主机的驱动旋转从而带动螺旋桨,当尾轴与轴毂之间由于装配等原因而产生意外咬合时,主机的扭矩传递到尾轴架上。咬合法力矩
| $ M = \frac{{60}}{{2{\text{π}} }} \cdot \frac{P}{N} 。$ | (1) |
式中:
尾轴架会受到尾轴传递而来的螺旋桨载荷,《船舶实用设计手册》[11]中规定:即使尾轴在受到螺旋桨转动或损坏时的作用力而发生损坏时,尾轴架也能保持不发生破坏。设计时取能使尾轴折断的力作为尾轴架系统设计载荷,作用力
| $ F = 0.1{\sigma _s}\frac{{{d^3}}}{a}。$ | (2) |
式中:
另外,国军标[12-13]中规定尾轴架以及尾轴架与船体相连区域结构的计算载荷取为最大转速下螺旋桨断叶载荷,即离心力
| $ \left\{ \begin{aligned} & C = 1.63(2n{\text{π}} )Rq ,\\ & {P_r} = 4{P_1}s 。\end{aligned} \right. $ | (3) |
式中:
3种设计载荷的选取均是基于实船可能会发生的事故。实际上,船舶航行过程中发生螺旋桨断叶事故更为常见。因此,本文设计载荷采用螺旋桨断叶法计算得到,外载荷离心力C= 3.5×106 N,偏心力矩Pr= 1×106 N·m。
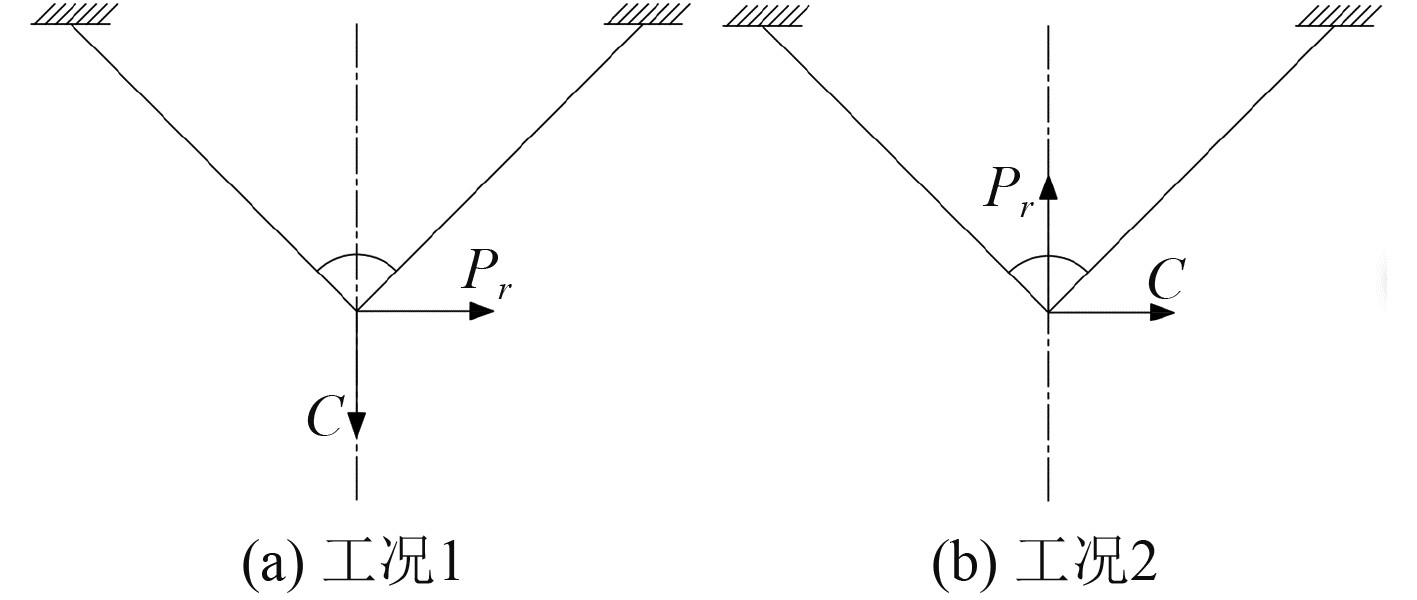
1.2 计算工况选取尾轴架系统强度计算时,通常选取最极端的2个工况,即工况1离心力和偏心弯矩作用于双支臂夹角平分线与尾轴轴线所构成的平面内;工况2离心力和偏心弯矩垂直于双支臂夹角平分线与尾轴轴线所构成的平面,两工况如图1所示。
|
图 1 尾轴架系统计算工况 Fig. 1 Load cases for strength assessment of shaft bracket system |
由于尾轴架支臂通常为实心且轴毂的厚度也较大,在建立尾轴架系统有限元模型时,为了达到更高的计算精度,尾轴架支臂和轴毂通常会采用实体单元进行模拟,本文研究中也是采用尾轴架支臂和轴毂模拟。由于尾轴通常为空心圆柱,在建立尾轴的有限元模型时,可采用实体单元或梁单元。为了研究尾轴模拟方式对尾轴架强度计算的影响,在此分别采用实体单元(方案1)及梁单元(方案2)模拟尾轴建立尾轴架系统有限元模型。
方案1尾轴承与尾轴架轴毂材料相同且长度一致,即忽略尾轴承刚度和长度的影响,同时关联尾轴与轴毂、尾轴承6个方向的自由度,忽略轴毂与尾轴间的转动。方案2建立尾轴架系统模型时,将尾轴简化为梁单元,尾轴架轴毂与尾轴间采用MPC刚性连接,该方案无法考虑尾轴承刚度和长度影响。
尾轴架支臂与船体的连接处以及尾轴出口处的边界条件为刚性固定,方案1和方案2的模型如图2和图3所示。

|
图 2 尾轴架系统有限元模型(方案1) Fig. 2 The FE model of shaft bracket system (Scheme 1) |

|
图 3 尾轴架系统有限元模型(方案2) Fig. 3 The FE model of shaft bracket system (Scheme 2) |
尾轴架通过轴毂支承尾轴,实际结构中尾轴与轴毂间可靠轴承实现相对转动,建模时若忽略这一约束条件,直接将尾轴与轴毂连接,可能会有一定误差。为研究连接方式对计算结果的影响,在方案1的基础上建立方案3模型,将尾轴与轴毂间采用滑动MPC连接并设置为接触,同时考虑实船轴毂内部有卡槽,会限制尾轴在轴向运动,使用MPC关联轴毂端面与尾轴间的相对轴向位移,如图4所示。

|
图 4 尾轴架系统有限元模型(方案3) Fig. 4 The FE model of shaft bracket system (Scheme 3) |
因为尾轴与轴毂之间实际并非直接接触,二者由尾轴承相连接,本船使用的是赛龙轴承,其材料属性及尺寸参数见表1。可看出,赛龙轴承的弹性模量远小于钢,泊松比也与钢相差较多,并且实际轴承的长度也小于轴毂的长度。为考察轴承刚度及长度的影响,建立方案4模型进行分析。
|
|
表 1 尾轴承参数 Tab.1 Parameters of bearings |
由于轴承的结构较为复杂,方案4将其简化为同尺寸的实体进行模拟,采用表1材料属性。为了模拟尾轴与轴毂间的相对转动,采用滑动MPC关联尾轴承与轴毂接触面并设置为接触,尾轴承与轴间直接相连。使用MPC关联轴毂端面与尾轴承间的相对轴向位移,同时考虑尾轴相对转动及尾轴承刚度的有限元计算模型(方案4)如图5所示。

|
图 5 尾轴架系统有限元模型(方案4) Fig. 5 The FE model of shaft bracket system (Scheme 4) |
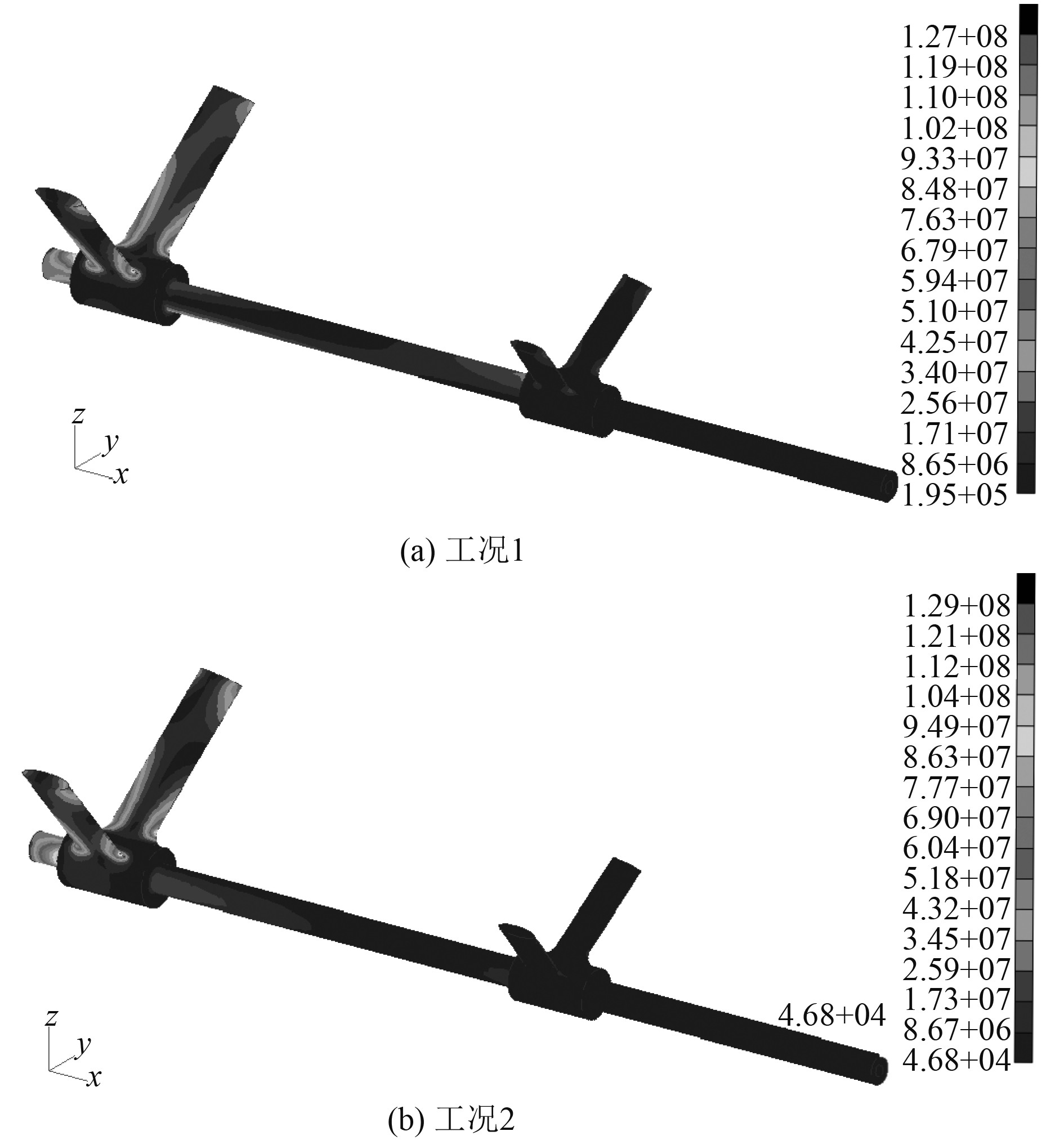
设计载荷以集中力的形式施加在尾轴后端部,计算得到各方案2种工况下的Von Mises应力云图,如图6~图9所示。
|
图 6 尾轴架系统Von Mises应力云图(方案1) Fig. 6 The Von Mises nephogram of shaft bracket system (Scheme 1) |
|
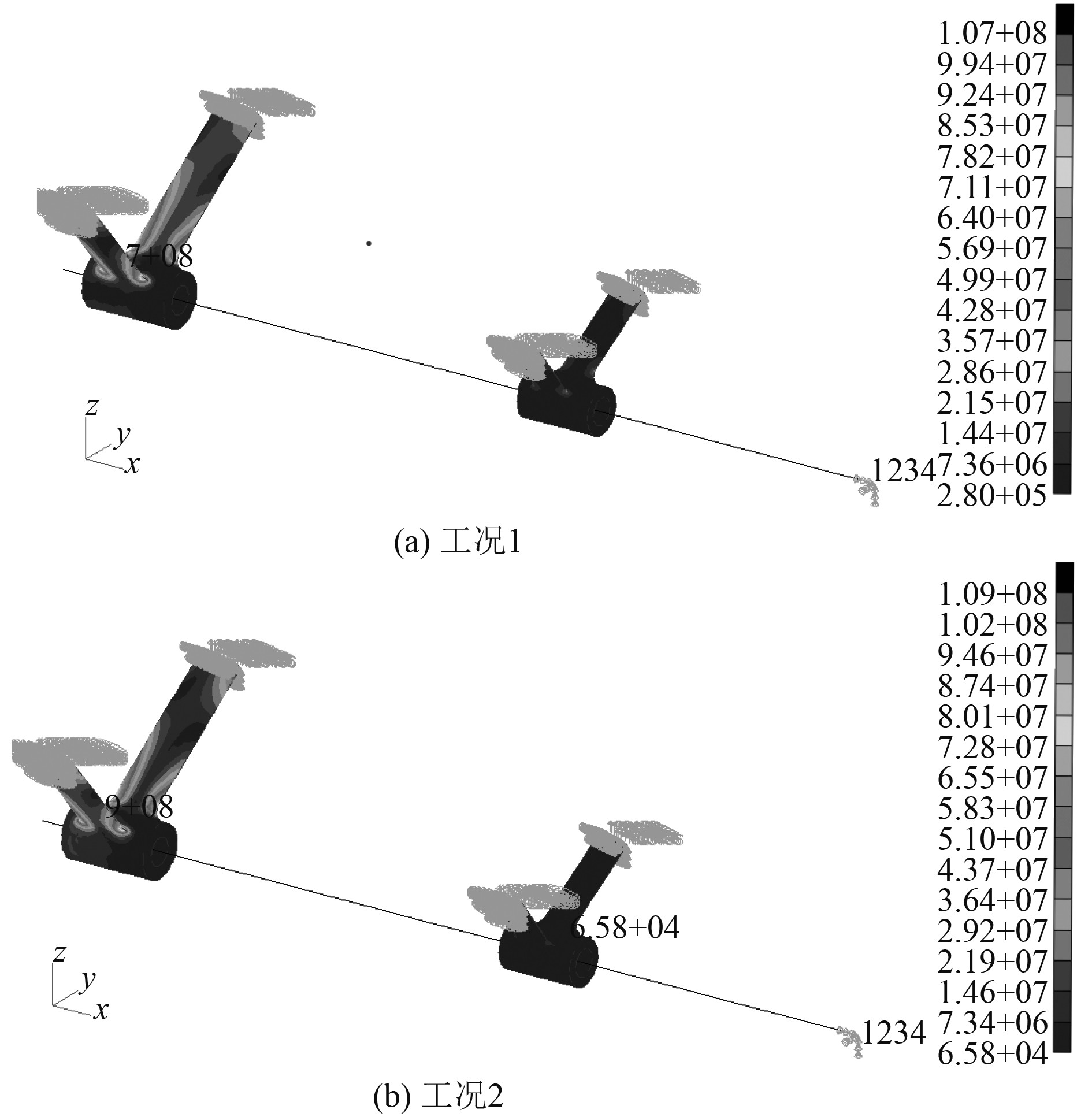
图 7 尾轴架系统Von Mises应力云图(方案2) Fig. 7 The Von Mises nephogram of shaft bracket system (Scheme 2) |
|
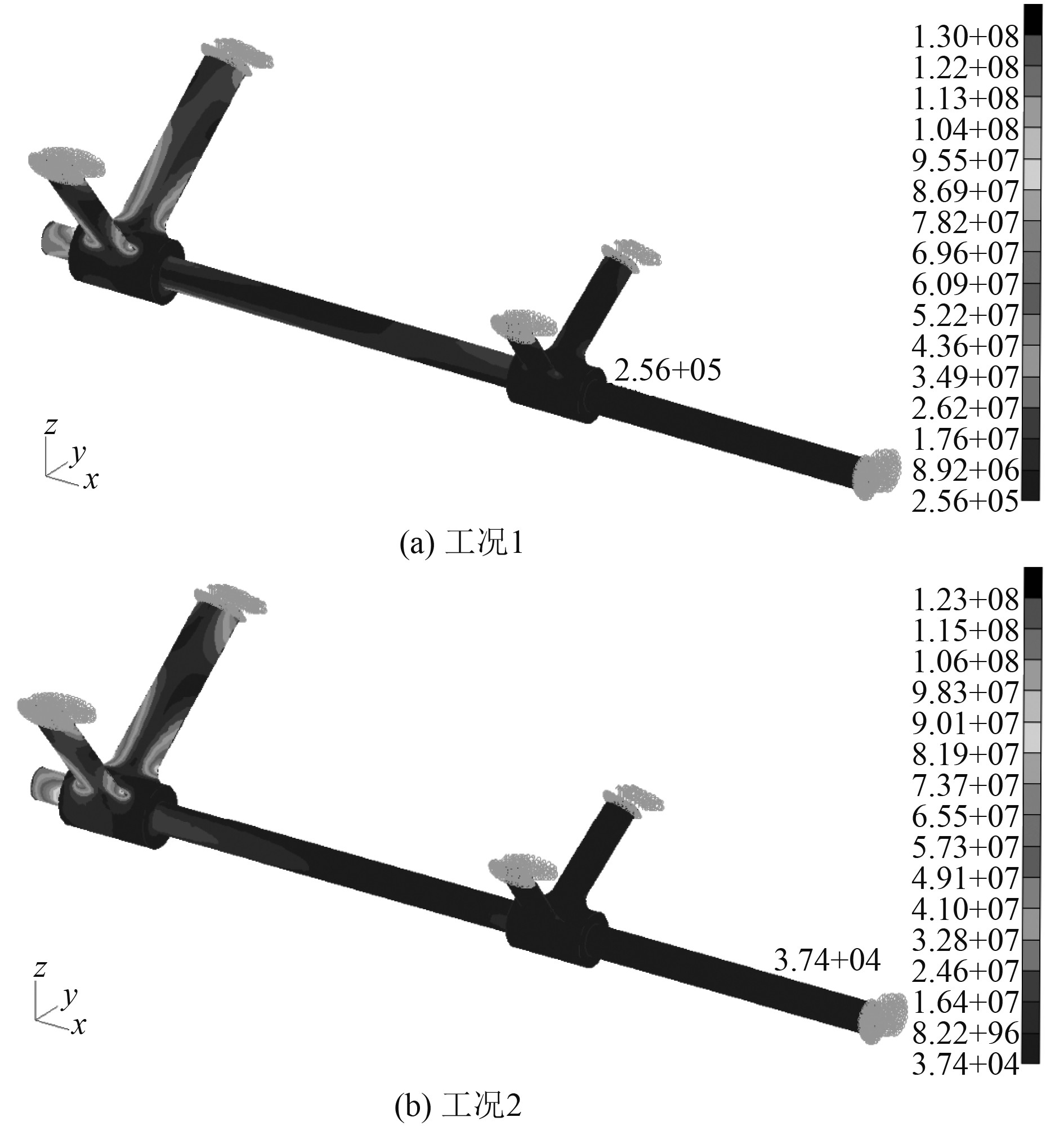
图 8 尾轴架系统Von Mises应力云图(方案3) Fig. 8 The von mises nephogram of shaft bracket system (Scheme 3) |

|
图 9 尾轴架系统Von Mises应力云图(方案4) Fig. 9 The Von Mises nephogram of shaft bracket system (Scheme 4) |
将4个方案计算得到的前、后尾轴架以及尾轴最大Von Mises应力列于表2中,方案2尾轴采用梁单元模拟无法读取Von Mises应力,故不列出,且本文设计载荷主要用于校核尾轴架,表中尾轴的应力仅作方案对比的参考。表2中,
|
|
表 2 尾轴架系统Von Mises应力汇总 Tab.2 Von Mises stress of shaft bracket system |
两工况下不同方案计算结果对比表明,尾轴采用不同的单元进行模拟以及对尾轴与轴毂间连接方式,采用不同的简化方式对于后尾轴架的最大Von Mises应力影响较小,4种方案计算结果接近;前尾轴架应力相差较大,采用梁单元模拟尾轴的方案2时,前尾轴架应力远高于其余3种方案,方案2工况1前尾轴架最大应力为方案4的3.26倍;两工况下方案4前尾轴架应力小于其余3种方案。
对比尾轴与轴毂间采用相同连接方式的方案1与方案2,尾轴采用实体单元的方案1应力结果更接近方案4;对比采用相同单元模拟结构的方案1与方案3,考虑了尾轴与轴毂间相对转动的方案3计算结果更接近方案4,但计算精度的提高有限,尾轴与轴毂间可相对转动这一条件的简化对于计算结果的影响较小。另外,不考虑轴承刚度会导致前尾轴架应力计算结果明显偏大,方案3工况1前尾轴架最大应力为方案4的2.16倍,工况2也达到了1.43倍。
3 结 语本文总结了尾轴架系统的设计载荷计算方法,通过对比选取了本文计算所使用的载荷及2种工况。分别采用梁单元及实体单元模拟尾轴建立计算模型,同时对尾轴与轴毂间的连接采用不同的简化方式进行模拟并建立了相应的模型。对建立的4种模型分别进行了2种工况的加载计算,读取尾轴架及尾轴的应力进行对比分析。分析表明,采用不同方案对后尾轴架的应力计算影响不大(各方案差距在6%以内);采用梁单元模拟尾轴会导致前尾轴架计算应力偏高,不考虑尾轴承刚度以及尾轴与轴毂间相对滑动的简化也会导致前尾轴架应力计算结果明显偏大,若要求较高的计算精度,需采用实体单元建立尾轴并考虑尾轴承的刚度以及尾轴与轴毂间的相对转动。
| [1] |
于善御. 水面舰艇艉轴架强度的设计与计算[J]. 舰船科学技术, 1982(9): 47-53. YU S Y. Design and calculation of the strength of the shaft bracket of the surface warship[J]. Ship Science and Technology, 1982(9): 47-53. |
| [2] |
DEDY W, RENDRA R, TOTOK Y. (2016). Strength structural analysis of the shaft bracket propeller on fast patrol boats[J]. Light, 2016, 7(2): 997-1001. |
| [3] |
FIRMANDHA T, YUDI O M, ANGGARA S. Shaft bracket strength assessment based on seizing and blade loss methods[J]. Chinese Journal of Ship Research, 2019, 14(2): 47-53. DOI:10.19693/j.issn.1673-3185.01483 |
| [4] |
祁玉荣. 舰船艉轴架强度、模态与冲击响应分析研究[D]. 上海: 上海交通大学, 2004.
|
| [5] |
王滨. 轴承刚度对船舶轴系振动特性的影响研究[J]. 齐齐哈尔大学学报(自然科学版), 2009, 25(6): 55-60. WANG B. Research on the effect of bearing stiffness on the vibration characteristics of ship shafting[J]. Journal of Qiqihar University(Philosophy & Social Science Edition), 2009, 25(6): 55-60. |
| [6] |
罗晨, 邹春平, 李增光, 等. 船舶艉轴架系统建模及振动特性分析[J]. 中国舰船研究, 2014, 9(2): 55-61. LUO C, ZOU C P, LI Z G, et al. Numerical simulation of vibration characteristics of ship shaft bracket systems[J]. Chinese Journal of Ship Research, 2014, 9(2): 55-61. DOI:10.3969/j.issn.1673-3185.2014.02.010 |
| [7] |
唐宇航, 陈志坚, 段振斌. 考虑艉轴架结构刚度耦合的艉轴架强度计算[J]. 中国舰船研究, 2015, 10(4): 71-78. TANG Y H, CHEN Z J, DUAN Z B. Strength calculation considering structural stiffness coupling of shaft bracket[J]. Chinese Journal of Ship Research, 2015, 10(4): 71-78. DOI:10.3969/j.issn.1673-3185.2015.04.011 |
| [8] |
王高祥. 艉轴架载荷与强度分析[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [9] |
许学强, 李天匀, 张旭, 等. 基于不同规范的双臂艉轴架轻量化分析[J]. 中国舰船研究, 2019, 14(4): 67-73. XU X Q, LI T Y, ZHANG X, et al. Lightweight analysis on double-arm propeller shaft bracket on basis of different rules[J]. Chinese Journal of Ship Research, 2019, 14(4): 67-73. DOI:10.19693/j.issn.1673-3185.01369 |
| [10] |
OBERG E, JONES F D. Machinery's handbook[M]. 26th ed. New York: Industrial Press, 2012.
|
| [11] |
中国船舶工业集团公司. 船舶设计实用手册(结构分册)[M]. 第3版. 北京: 国防工业出版社, 2013.
|
| [12] |
中国船舶科学研究中心. 水面舰艇结构设计计算方法: GJB/Z 119-1999[S]. 北京: 国防科学技术工业委员会, 1999.
|
| [13] |
中国船舶科学研究中心. 舰船通用规范: GJB 4000-2000[S]. 北京: 国防科学技术工业委员会, 2000.
|
 2023, Vol. 45
2023, Vol. 45
