0 引　言

船舶中央冷却系统仅中央冷却器使用海水冷却，具有腐蚀性的海水不直接接触和冷却各种散热设备，可有效提高各设备的可靠性和寿命，已成为各型船舶冷却系统设计的首要选择。作为全船冷却系统，在实际应用过程中，因淡水侧各支路流量分配不均导致设备不能得到有效冷却的现象经常出现^[1]。因此，有必要对船舶中央冷却系统水力特征进行分析。

刘方等^[2]以传统的管路流量计算为基础，提出多分枝管路流量分配迭代补偿计算方法。宋振国^[3]以图论为抓手，建立了船舶管网水力计算的数学模型，并通过实船试验，验证了数学模型的正确性。贾志强等^[4]将SIMPLE算法应用到水力管网进行动态模拟，实现了瞬态计算。陆蕾^[5]分析了钻井平台冷却水系统达到流量平衡的关键技术，并使用标准矩阵求解技术等方法对冷却系统进行优化。多数研究在对中央冷却系统计算过程中进行简化，并且需要代入特定模型进行求解，为实际工程应用带来了不便。

本文对中央冷却系统进行介绍，从简单管路的特性出发，提出基于阻抗平衡法的管路特性及流量分配计算方法，对冷却水管路进行定量分析，并采用Flowmaster软件对计算方法进行验证，最后利用阻抗平衡法反向计算了设计流量状态下的各支管阻抗以及局部阻力系数，可在实际工程中进行应用。

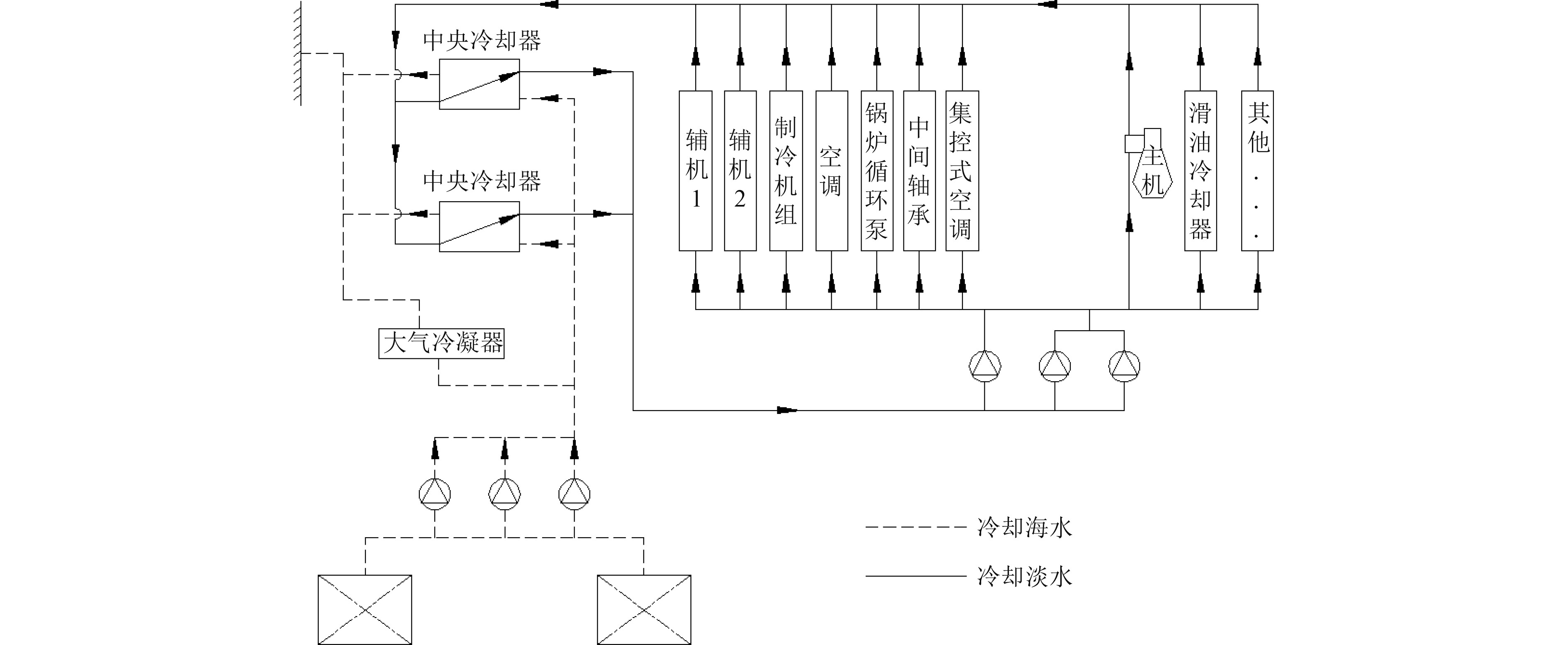
1 船舶中央冷却系统介绍

船舶中央冷却系统属于闭式冷却水系统的一种，利用海水冷却泵从海水门中抽取海水并送至中央冷却器，对中央冷却器的淡水回路进行冷却，海水升温后流出舷外，完成海水侧循环。经中央冷却器冷却后的低温淡水，经淡水冷却泵加压后沿各冷却支管流至主机、空调等设备的冷却器，带走舱内各设备产生的热量，随后经冷却总管汇集至中央冷却器，完成淡水侧循环。中央冷却水系统使用海水冷却的冷却器仅1套，材料要求低；需耐腐蚀的管路也较短；同时舱内管路不直接承压，提高了管路及其附件的安全性。船舶中央冷却系统可分为混流式中央冷却水系统、独立式中央冷却水系统、自流式中央冷却水系统^[6]。图1为某PLG船中央冷却系统原理图^[7]。

2 冷却管路水力及流量分配计算

如图1所示，中央冷却系统海水侧管路形式单一，不存在流量分配不均问题。淡水侧由淡水冷却泵统一向各冷却用户输送冷却水，由于各冷却支管通径、长度以及所使用的管路附件不同，在阻抗平衡的原则下，管内实际流量与设计流量会有较大差别，必须进行支管阻力匹配计算和设计。中央冷却系统淡水侧为闭式循环，流体的位能与压力能、速度能互相转化，因此在计算过程中可不考虑各管路空间走向，视为平面系统进行计算。

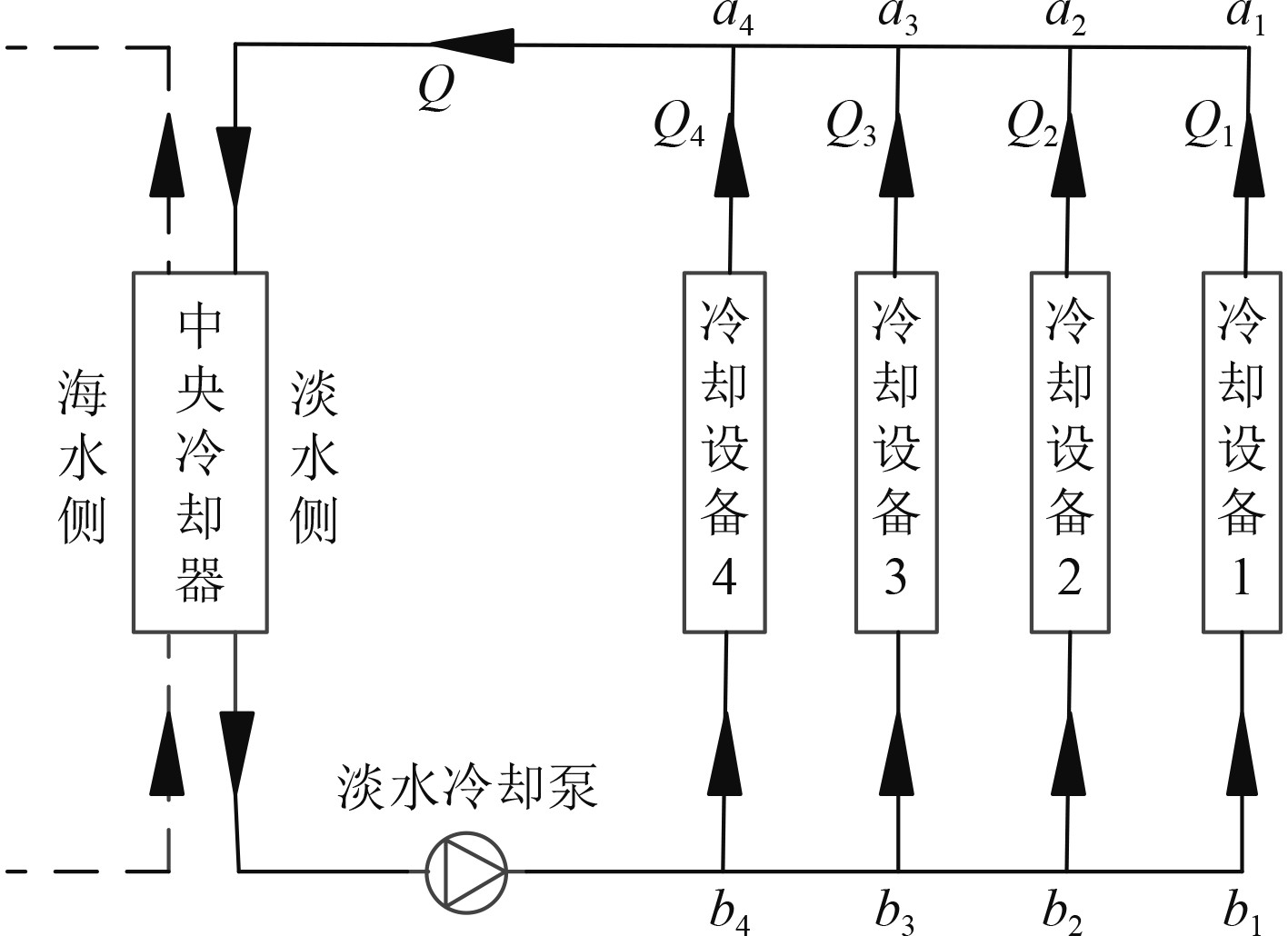
2.1 物理模型

以4台冷却设备为例，将中央冷却系统淡水侧计算模型简化，如图2所示。各冷却设备的流量分别为Q₁~Q₄，总流量为Q，分析可得：

$\left\{ \begin{aligned} & {Q_{{b_2}{b_1}}} = {Q_{{a_1}{a_2}}} = {Q_1}，\\ & {Q_{{b_3}{b_2}}} = {Q_{{a_2}{a_3}}} = {Q_1} + {Q_2}，\\ & {Q_{{b_4}{b_3}}} = {Q_{{a_3}{a_4}}} = {Q_1} + {Q_2} + {Q_3}，\\ & Q = {Q_1} + {Q_2} + {Q_3} + {Q_4}。\end{aligned} \right.$

(1)

冷却管路在船舱内多沿舷侧布置，${a_1}{a_2}$、${a_2}{a_3}$、${a_3}{a_4}$等管段距离普遍较长，存在较多数量的弯头、阀门、滤器等管路附件，阻抗不同并且流量不同，其也不符合并联管路定义特征，因此图2不可使用各冷却支路简单并联的计算方法。

黏性流体管道计算的伯努利方程为：

${z_1} + \frac{{{p_1}}}{\gamma } + \frac{{u_1^2}}{{2g}} = {z_2} + \frac{{{p_2}}}{\gamma } + \frac{{u_2^2}}{{2g}} + {H_{{w}}}。$

(2)

式中：${z_1}$、${z_2}$为管道内1-1与2-2截面中心至基准水平面的垂直距离，m；${p_1}$、${p_2}$为1-1与2-2截面上的流体压力，Pa；${u_1}$、${u_2}$为1-1与2-2截面上的流体平均速度，m/s；$\gamma$为管路内流体的重度，N/m³；${H_{{w}}}$为管路内流体在1-1与2-2截面间的压头损失，m。

压头损失可分为沿程压力损失和局部阻力损失，对于简单管路计算如下：

${H_{{w}}} = \lambda \frac{L}{d} \times \frac{{{u^2}}}{{2g}} + \Sigma \zeta \frac{{{u^2}}}{{2g}} = (\lambda \frac{L}{d} + \Sigma \zeta )\frac{{{u^2}}}{{2g}}。$

(3)

式中：$\lambda$为沿程阻力系数；L为管路长度，m；d为管路内径，m；u为管路内流体平均速度，m/s；$\zeta$为局部阻力系数。

将$u = \frac{Q}{{\displaystyle\frac{{\text{π}} }{4}{d^2}}}$代入式(3)，有

${H_{{w}}} = \frac{{8(\lambda \displaystyle\frac{L}{d} + \sum \zeta )}}{{{{\text{π}} ^2}{d^4}g}}{Q^2} 。$

(4)

定义管路阻抗^[8]：

$S = \frac{{8(\lambda \displaystyle\frac{L}{d} + \sum \zeta )}}{{{{\text{π}} ^2}{d^4}g}}。$

(5)

在冷却系统实际应用中，由于管路附件的布置、管路腐蚀等原因，管路内流体基本处于完全湍流区，雷诺数对阻力影响很小，此时可视为局部阻力系数$\lambda$与Re无关，只是绝对粗糙度$\Delta$与管径d的函数。在管路系统型号规格确定情况下，采用尼古拉兹公式，即可计算出相应管段的$\lambda$，即

$\lambda = \frac{1}{{{{(1.74 + 2\lg \displaystyle\frac{d}{{2\Delta }})}^2}}} 。$

(6)

依据式(5)及式(6)可计算出各分支管路的阻抗，结合式(4)，则有：

${H_{{w}}} = S{Q^2}。$

(7)

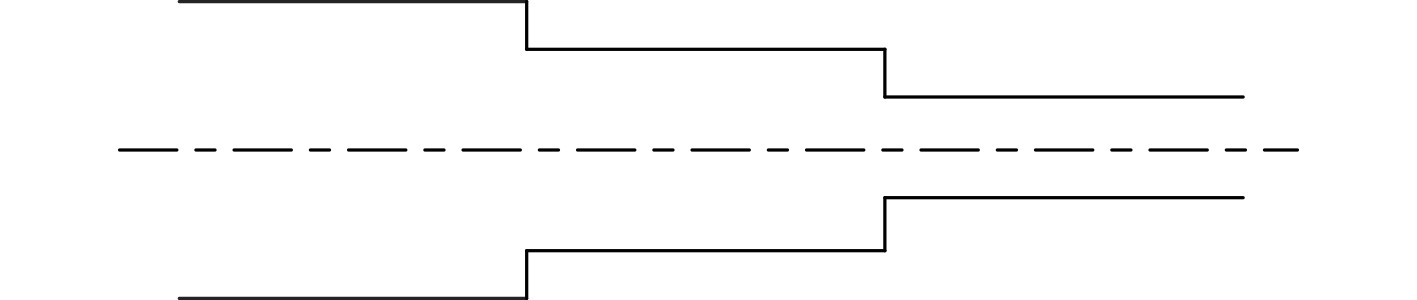
船舶冷却管路为简单管路经过串联和并联组成的管网。由不同管径或不同粗糙度的简单管路头尾相连组成串联管路，如图3所示，其各管段中流量相同，总压头损失等于串联各管段压头损失之和，总阻抗为串联各管段阻抗之和，即

$\left\{ \begin{aligned} & Q = {Q_1} + {Q_2} + {Q_3}，\\ & {H_w} = {H_{w1}} + {H_{w2}} + {H_{w3}}，\\ & S = {S_1} + {S_2} + {S_3}。\end{aligned} \right.$

(8)

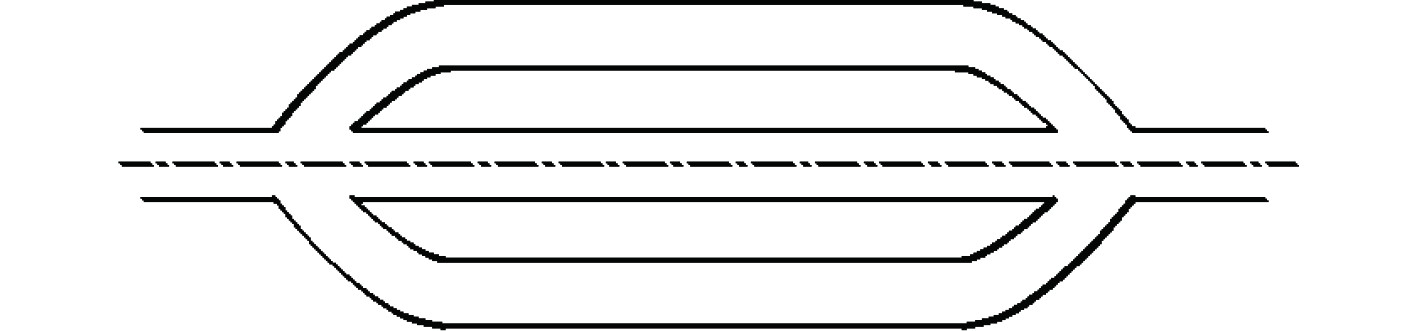
由2个或2个以上简单管路入口与入口相连接、出口与出口相连接组成并联管路，如图4所示。可知，其总流量等于各分支管段流量之和，总压头损失等于各分支管段压头损失，总阻抗的平方根倒数等于各分支管段阻抗的平方根倒数之和，即

$\left\{ \begin{aligned} & Q = {Q_1} + {Q_2} + {Q_3}，\\ & {H_w} = {H_{w1}} = {H_{w2}} = {H_{w3}}，\\ &\frac{1}{{\sqrt S }} = \frac{1}{{\sqrt {{S_1}} }} + \frac{1}{{\sqrt {{S_2}} }} + \frac{1}{{\sqrt {{S_3}} }}。\end{aligned} \right.$

(9)

由式(9)可进一步推导出，并联各分支管段流量之比等于阻抗的平方根倒数之比，即

${Q_1}:{Q_2}:{Q_3} = \frac{1}{{\sqrt {{S_1}} }}:\frac{1}{{\sqrt {{S_2}} }}:\frac{1}{{\sqrt {{S_3}} }} 。$

(10)

2.2 求解过程

在冷却管路已设计完成的情况下，利用阻抗平衡法对淡水侧进行水力计算，参考图2，计算步骤如下：

步骤1　首先计算${b_1}{a_1}$、${b_2}{a_2}$、${b_2}{b_1}$、${a_1}{a_2}$等各分支管段的阻抗；

步骤2　计算管段${b_2}{b_1}{a_1}{a_2}$阻抗，根据串联管路规律，可得：

${S_{{b_2}{b_1}{a_1}{a_2}}} = {S_{{b_2}{b_1}}} + {S_{{b_1}{a_1}}} + {S_{{a_1}{a_2}}}。$

(11)

步骤3　将管段${b_2}{b_1}{a_1}{a_2}$与管段${b_2}{a_2}$并联，计算并联后的阻抗${S_{1,2}}$：

$\frac{1}{{\sqrt {{S_{1,2}}} }} = \frac{1}{{\sqrt {{S_{{b_2}{b_1}{a_1}{a_2}}}} }} + \frac{1}{{\sqrt {{S_{{b_2}{a_2}}}} }} 。$

(12)

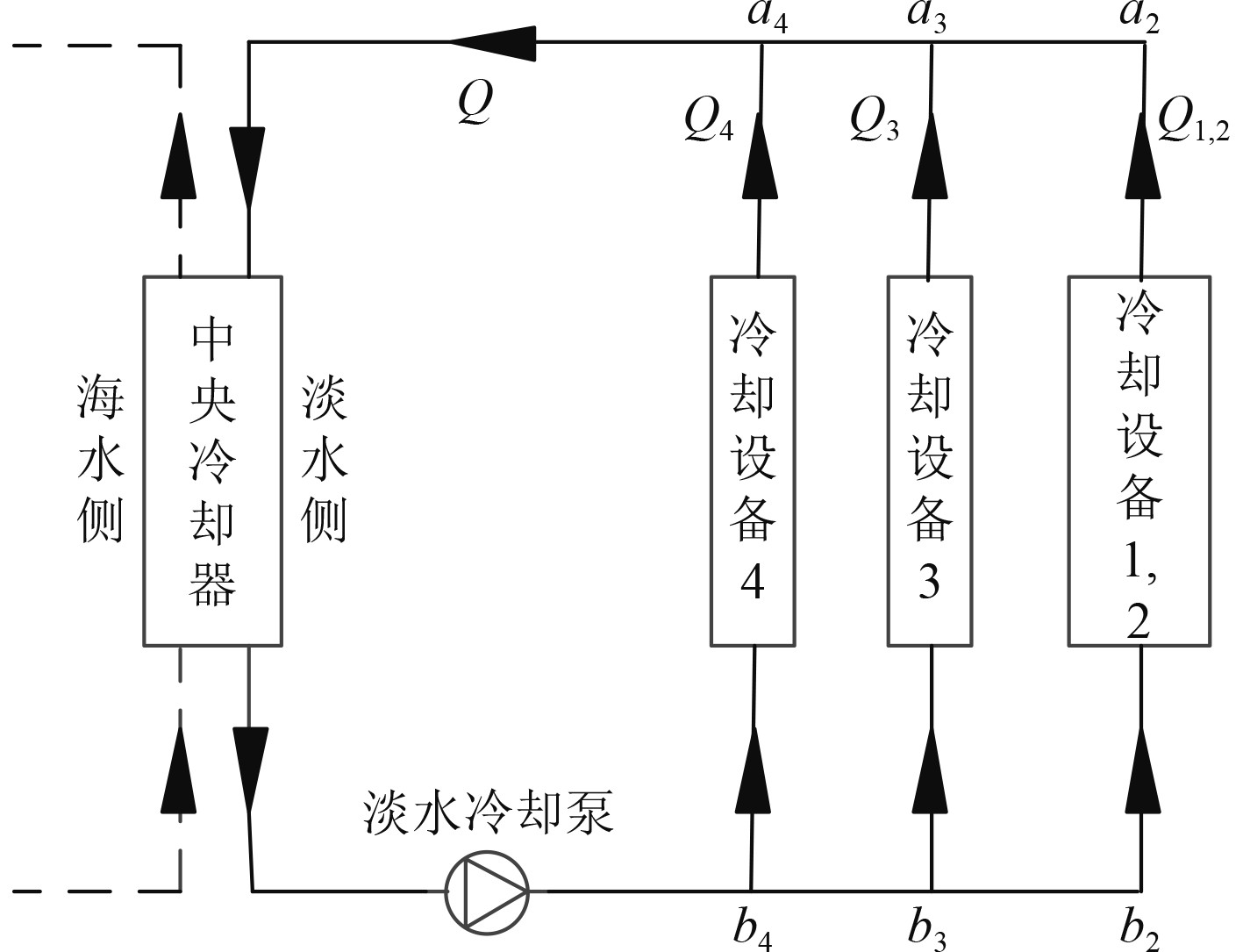
经过上述步骤后，冷却系统计算模型可简化为图5所示。

步骤4　参考图5，计算管段${b_3}{b_2}{a_2}{a_3}$阻抗，根据串联管路规律，可得：

${S_{{b_3}{b_2}{a_2}{a_3}}} = {S_{{b_3}{b_2}}} + {S_{1,2}} + {S_{{a_2}{a_3}}} 。$

(13)

步骤5　将管段${b_3}{b_2}{a_2}{a_3}$与管段${b_3}{a_3}$并联，计算并联后的阻抗${S_{1,2,3}}$：

$\frac{1}{{\sqrt {{S_{1,2,3}}} }} = \frac{1}{{\sqrt {{S_{{b_3}{b_2}{a_2}{a_3}}}} }} + \frac{1}{{\sqrt {{S_{{b_3}{a_3}}}} }}。$

(14)

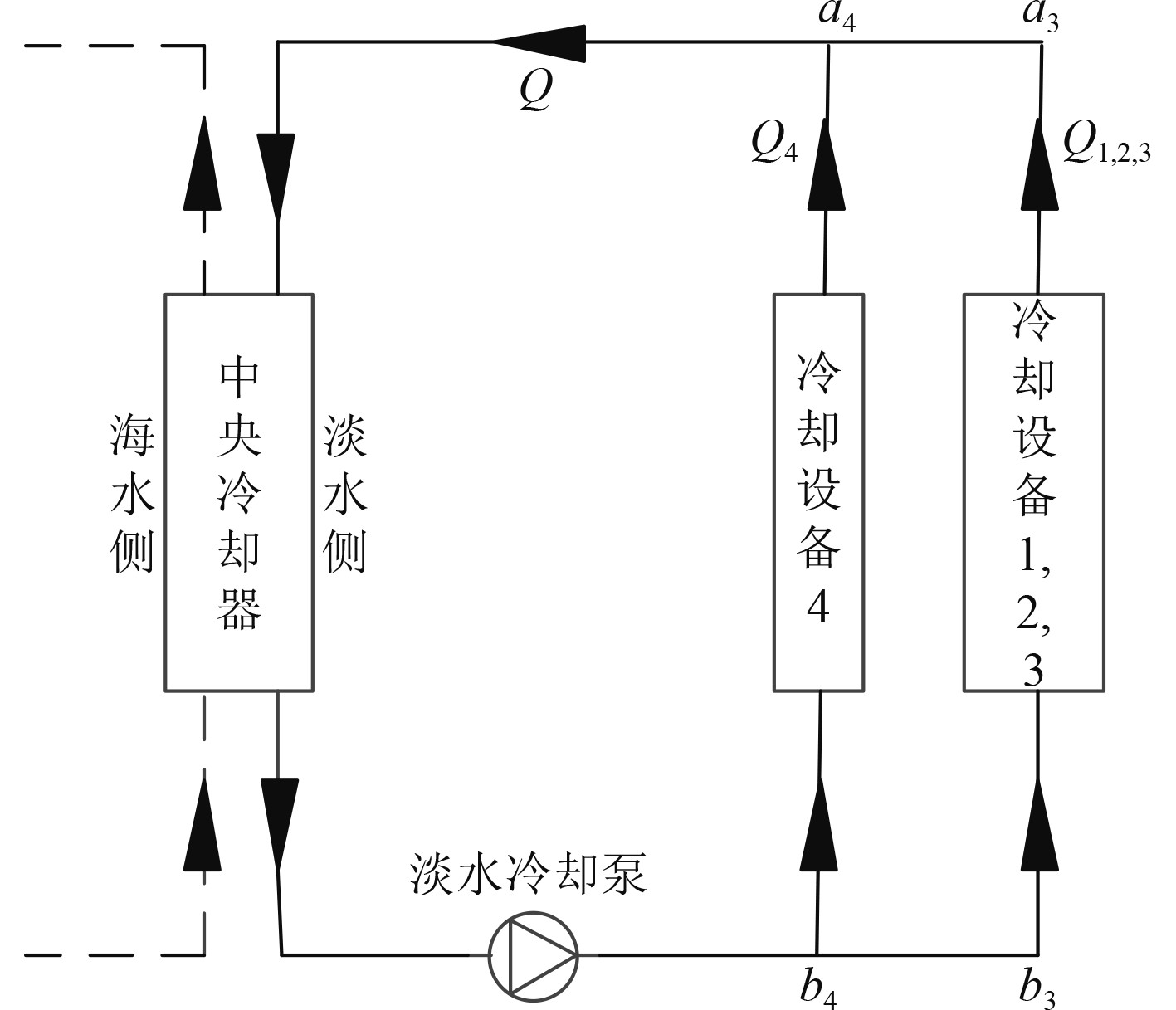
经过上述步骤后，冷却系统计算模型可简化为图6所示。

步骤6　参考图6，计算管段${b_4}{b_3}{a_3}{a_4}$阻抗，根据串联管路规律，可得：

${S_{{b_4}{b_3}{a_3}{a_4}}} = {S_{{b_4}{b_3}}} + {S_{1,2,3}} + {S_{{a_3}{a_4}}}。$

(15)

步骤7　再根据并联管路流量与阻抗分配关系，求解${Q_4}$与${Q_{1,2,3}}$：

$\left\{ \begin{gathered} {Q_4}:{Q_{1,2,3}} = \frac{1}{{\sqrt {{S_4}} }}:\frac{1}{{\sqrt {{S_{{b_4}{b_3}{a_3}{a_4}}}} }}，\\ {Q_4} + {Q_{1,2,3}} = Q。\end{gathered} \right.$

(16)

步骤8　参考图5，求解${Q_3}$与${Q_{1,2}}$：

$\left\{ \begin{gathered} {Q_3}:{Q_{1,2}} = \frac{1}{{\sqrt {{S_3}} }}:\frac{1}{{\sqrt {{S_{1,2}}} }}，\\ {Q_3} + {Q_{1,2}} = {Q_{1,2,3}}。\end{gathered} \right.$

(17)

步骤9　参考图2，求解${Q_2}$与${Q_1}$：

$\left\{ \begin{gathered} {Q_2}:{Q_1} = \frac{1}{{\sqrt {{S_2}} }}:\frac{1}{{\sqrt {{S_{{b_2}{b_1}{a_1}{a_2}}}} }} ，\\ {Q_2} + {Q_1} = {Q_{1,2}} 。\\ \end{gathered} \right.$

(18)

经过步骤1~步骤9，根据各管路阻抗，并结合简单管路串并联基本运算方法计算出各支路流量，利用式(7)可计算出各管段的压头损失。

2.3 算例分析

以图2为算例进行演示，在进行淡水侧冷却管路水力及流量计算前，依据各设备供应商提供的散热量及系统冷却水温升数据，可计算出设备所需的冷却水流量，进一步根据管路流速要求，计算出各支管管径，各管段基本参数如表1所示。

管路绝对粗糙度为0.2 mm，利用阻抗平衡法，计算出各管段流量、流速等数据如表2所示。

计算结果表明，各管段计算出的实际流量与实际流速均与设计阶段有较大差距，可通过各调节支管阀门开度达到预期目的。

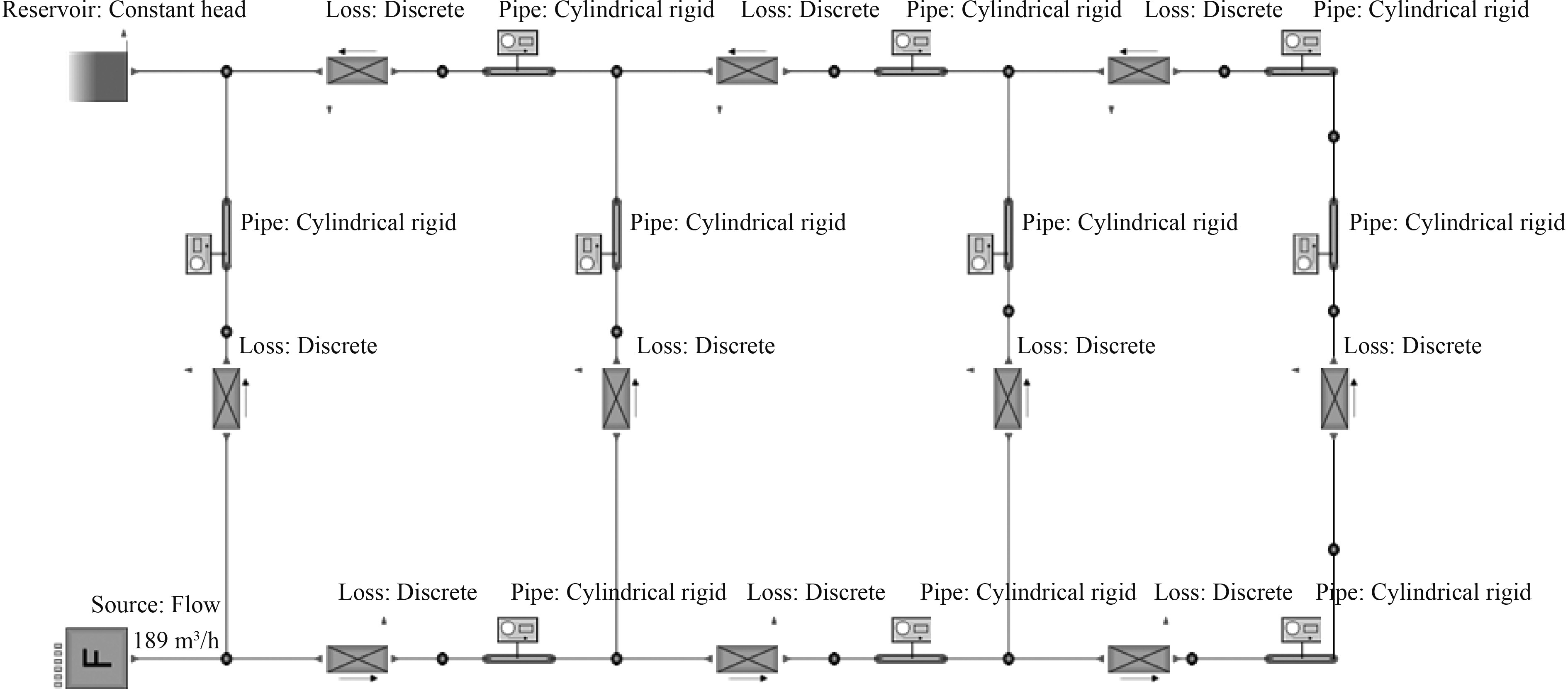
3 仿真验证

为验证阻抗平衡法计算的正确性，采用Flowmaster软件对上述算例进行仿真。建立淡水侧冷却水系统的仿真模型，如图7所示。利用恒流源Flow元件模拟淡水冷却泵，以一恒定流量持续输出冷却水；为提高计算效率，建模过程中忽略各管段的弯头，各管段中设备、阀门及其他管路附件均简化为Discrete Loss元件，其阻力系数等于各管段中所有设备及附件阻力系数之和；选用Cylindrical Rigid元件模拟各管段，输入表1中各管段的规格参数，采用稳态计算模式，对淡水侧水力特性进行仿真。仿真数据如表3所示。

分析可知，仿真流量与理论计算流量最大误差为1.23%，仿真流速与理论计算流速最大误差为1.31%，仿真得出的压头损失与理论计算压头损失最大误差为3.51%，验证了阻抗平衡法理论计算数据的正确性。

4 流量调节分析

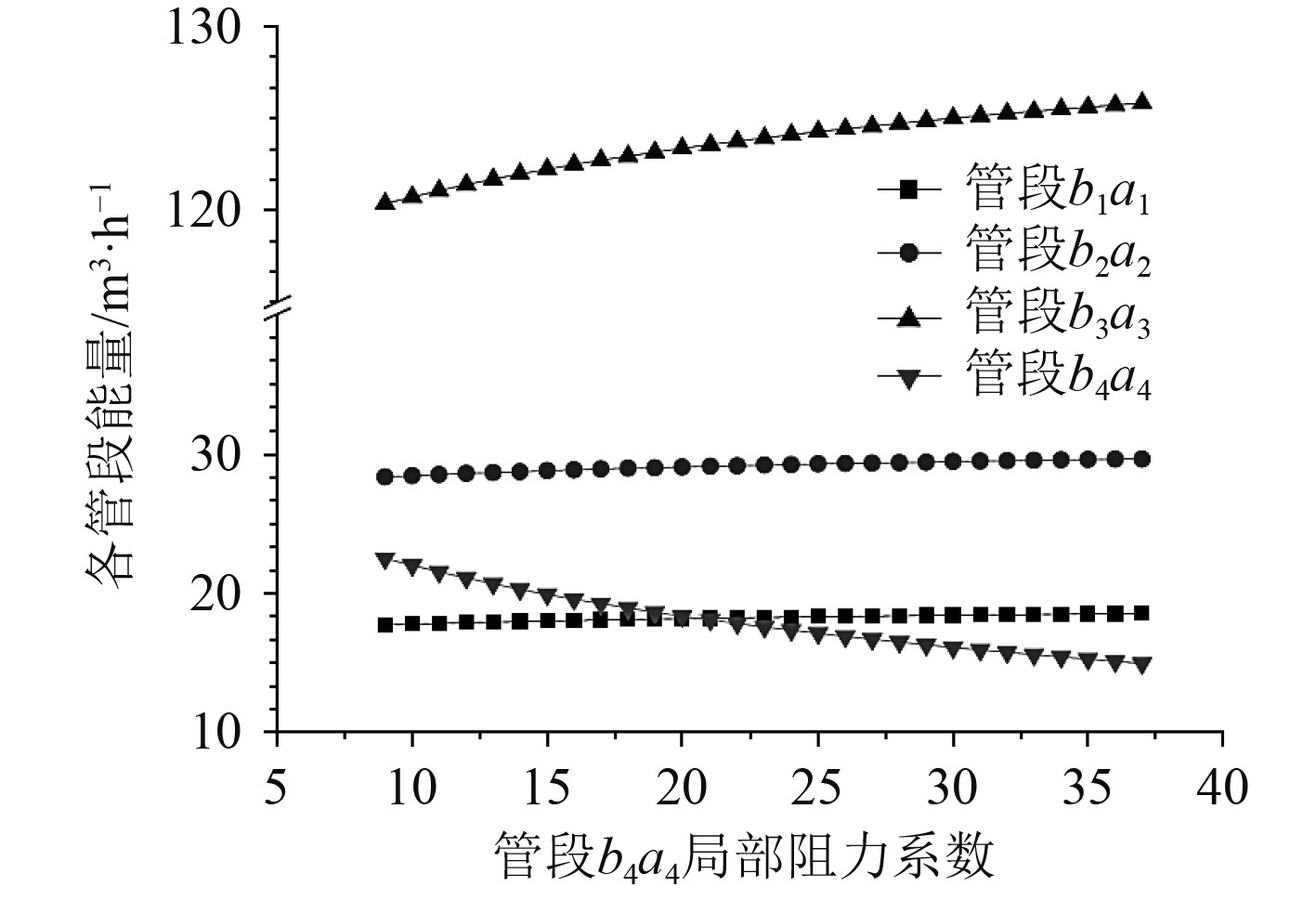
由计算结果可知，在各管路经过串并联组成管网的情况下，管段${b_1}{a_1}$内流量较设计阶段减小34.34%，管段${b_4}{a_4}$内流量较设计阶段增加50.12%，各冷却支管实际流量、流速等参数均会与设计阶段存在偏差，造成设备冷却不足或过冷却。在管路敷设完成的情况下，可通过调节各支管的阀门开度进行流量调节。

管段${b_4}{a_4}$内流量较设计阶段增加较多，首先考虑减小此管段上的阀门开度，增加局部阻力系数，调节结果如图8所示。随管段${b_4}{a_4}$局部阻力系数的增加，${b_4}{a_4}$段中的流量在逐渐减小，当其局部阻力系数为36时，流量为15.105 m³/h。但在调节过程中其余各管段流量均产生变化，尤其是管段${b_3}{a_3}$流量增加至125.719 m³/h，因此只调节单个管段阀门开度无法完成冷却流量的重新分配。

在流量调节过程中，为达到设计流量要求，可转变为已知各管段规格参数及流量，求解各管段局部阻力系数的问题，采用阻抗平衡法从反向进行计算，步骤如下：

$\frac{{{S_1} + {S_{{b_2}{b_1}}} + {S_{{a_1}{a_2}}}}}{{{S_2}}} = \frac{{Q_2^2}}{{Q_1^2}}，$

(19)

$\frac{1}{{\sqrt {{S_{1,2}}} }} = \frac{1}{{\sqrt {{S_2}} }} + \frac{1}{{\sqrt {{S_1} + {S_{{b_2}{b_1}}} + {S_{{a_1}{a_2}}}} }}，$

(20)

$\frac{{{S_{1,2}} + {S_{{b_3}{b_2}}} + {S_{{a_2}{a_3}}}}}{{{S_3}}} = \frac{{Q_3^2}}{{{{({Q_{^1}} + {Q_2})}^2}}}，$

(21)

$\frac{1}{{\sqrt {{S_{1,2,3}}} }} = \frac{1}{{\sqrt {{S_3}} }} + \frac{1}{{\sqrt {{S_{1,2}} + {S_{{b_3}{b_2}}} + {S_{{a_2}{a_3}}}} }} ，$

(22)

$\frac{{{S_{1,2,3}} + {S_{{b_4}{b_3}}} + {S_{{a_3}{a_4}}}}}{{{S_4}}} = \frac{{Q_4^2}}{{{{({Q_{^1}} + {Q_2} + {Q_3})}^2}}} 。$

(23)

通过式(19)~式(23)，无法直接求出各管段阻抗值，但可分析得出${S_1}$、${S_2}$、${S_3}$、${S_4}$呈一定比例关系，说明各管段阻抗有多组解可使系统达到设定流量。另外，在选解过程中须注意，在阀门全开状态下阻抗最小，调节过程中各管段阻抗只能在原基础上增大。以图2系统及表1数据为例，固定管段${b_1}{a_1}$的阻抗值${S_1}$不变，按照式(19)~式(23)可计算出${S_2}$、${S_3}$、${S_4}$，进而可由式(5)求解出各管段局部阻力系数，调节阀门使各管段局部阻力系数达到设定值，即可取得目标流量值。

利用上述方法，逐步求解出各管段阻抗以及局部阻力系数，如表4所示。

分析管段${b_1}{a_1}$以及${b_2}{a_2}$，可以看出，虽然初始状态两管段长度以及局部阻力系数均相同，但由于${b_2}{b_1}$以及${a_1}{a_2}$段阻抗的存在，两管段初始流量并不相同，需调节${b_2}{a_2}$段阀门以改变局部阻力系数使流量达到均衡。

5 结　语

1）阻抗计算法可根据管路基本特征，准确计算出在初始状态下各支管的流量、流速、压头损失等参数，利用Flowmaster软件对算例进行了仿真，仿真流量与理论计算流量最大误差为1.23%，仿真流速与理论计算流速最大误差为1.31%，仿真计算得出的压头损失与理论计算压头损失最大误差为3.51，二者吻合良好，验证了阻抗平衡法理论计算数据的正确性。

2）管路流量可采用改变阀门开度进行调节，可利用阻抗平衡法反向计算出在设定流量下的各支管阻抗以及局部阻力系数，精准进行流量控制。

3）阻抗平衡法在计算过程中，充分考虑到每一管段的影响因素，并且无需求解复杂方程，可作为中央冷却系统水力的计算工具。