2. 天津大学 天津市港口与海洋工程重点实验室,天津 300072
2. Tianjin Key Laboratory of port and Ocean Engineering, Tianjin University, Tianjin 300072, China
在邮轮众多特殊结构中,支柱结构可以起到承载和拓展空间的作用,是邮轮上层建筑中不可或缺的组成部分,了解该结构的特性十分必要。目前在支柱结构领域,学者们的研究主要集中在邮轮支柱的作用与布置方式[1-2]、偏心支柱在极限状态下的特性[3]、波浪力对支柱的影响[4]、支柱倾斜程度和船体运动之间的关系[5]。各大规范对支柱结构的关注点集中在单一支柱许用应力的计算[6-8]。对于由连续支柱及其附属结构构成的支柱连接节点结构,研究相对较少。
本文借助Workbench软件,通过建立不同尺寸下的支柱连接节点模型,探讨重要构件尺寸对结构失效模式和极限承载力的影响,并根据有限元计算结果,使用非线性回归分析推导出结构极限承载力计算公式。在此基础上,建立支柱连接节点极限状态函数,形成了结构可靠性分析流程。为验证该流程的适用性,通过算例对上述流程进行验证。本文研究结果可为邮轮支柱连接节点结构设计提供一定参考。
1 支柱连接节点模型的建立与验证本文研究的支柱连接节点位于豪华邮轮中央大厅。根据支柱截面的形状,支柱连接节点可分为圆钢-圆钢型、圆钢-H钢型和圆钢-方钢型3种,本文研究对象是圆钢-圆钢型,该结构各构件参数如表1所示[3]。
|
|
表 1 支柱连接节点各构件尺寸 Tab.1 Dimensions of each component of column connection node |
结构建模区域参考了《邮轮局部结构直接计算指南(2021)》[9]中的相关规定,即支柱连接节点模型需包括上下支柱和中间构件,与上下支柱连接的甲板其有限元模型应延伸至支撑该甲板的纵桁、强横梁或者舱壁处。建模方法采用壳单元与实体单元混合建模的方法,其中上支柱与下支柱采用壳单元建模,单元尺寸设为20 mm,剩余结构采用实体单元建模,单元尺寸50 mm,模型细节如图1所示。
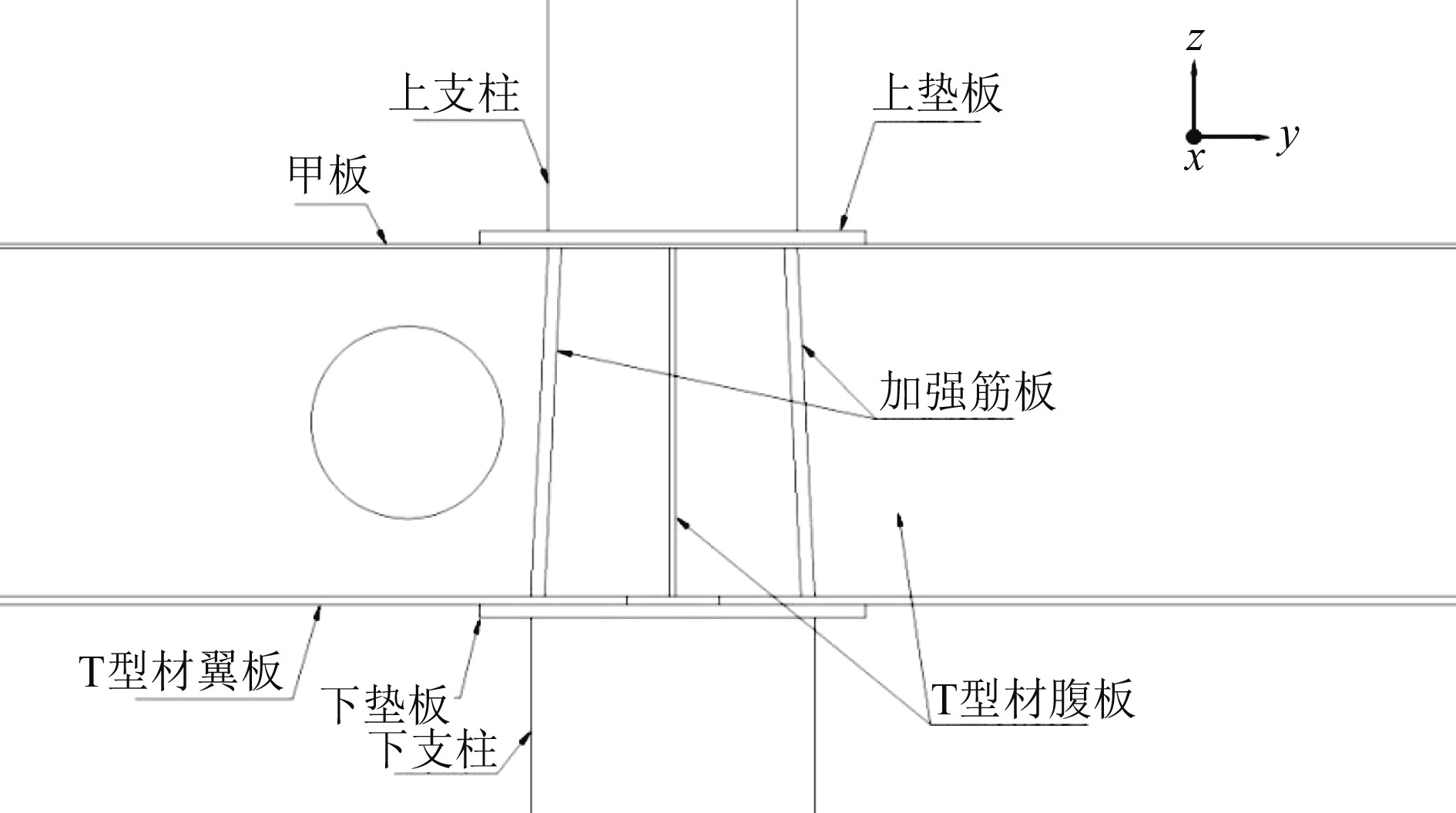
|
图 1 支柱连接节点模型细节 Fig. 1 Details of column connection node model |
模型分析采用Workbench中的static structural模块。模型材料为AH36钢,屈服强度σy为355 MPa,弹性模量E为206 GPa,泊松比μ为0.3,材料均为理想弹塑性材料。模型边界条件[9]和外载荷如表2所示,外载荷设置为垂直向下100 mm的位移载荷是为了保证结构达到极限状态。
|
|
表 2 支柱连接节点边界条件和外载荷 Tab.2 Boundary conditions and external loads of column connection nodes |
图2为T型材腹板厚度T对支柱连接节点失效模式的影响。可以看出,当T较小时,加强筋板和T型材腹板在极限状态下出现明显变形,随着T增加,支柱连接节点中间构件强度升高,加强筋板和T型材腹板在极限状态下变形逐渐减少,而上支柱柱脚处开始出现明显失效。

|
图 2 不同T型材腹板厚度下支柱连接节点极限应力云图 Fig. 2 Cloud chart of ultimate stress of column connection node under different T-section web thickness |
图3为上支柱直径D1与下支柱直径D2比λ对支柱连接节点失效模式的影响。可以看出,当λ=1.00时,结构在极限状态下主要于上支柱柱脚及周围甲板处失效。随着λ下降,结构的失效位置转移至下垫板、加强筋板及T型材腹板、翼板等构件处。

|
图 3 不同上支柱与下支柱直径比下支柱连接节点极限应力云图 Fig. 3 Cloud chart of ultimate stress of column connection node under different diameter ratios of upper and lower columns |
图4为甲板厚度t对支柱连接节点失效模式的影响。可以看出,当t较小时,上支柱柱脚周围的甲板会在极限状态下发生明显凹陷,且越靠近上支柱柱脚的甲板凹陷程度越高。随着t增加,支柱连接节点上部构件强度升高,T型材翼板和下支柱垫板由于承担的压力逐渐增加而成为结构的主要失效部位。

|
图 4 不同甲板厚度支柱连接节点极限应力云图 Fig. 4 Cloud chart of ultimate stress of column connection node with different deck thickness |
图5(a)为改变T型材腹板厚度T对支柱连接节点极限承载力R的影响。可以发现,将 T由4 mm提升至8 mm,R的增幅达到32%,但将T由8 mm提升至12 mm,R仅增加了8%,由此可以得出升高T对R的影响呈现出先大后小的趋势。实际设计中可通过增加T提升结构强度,但增幅不宜过大。
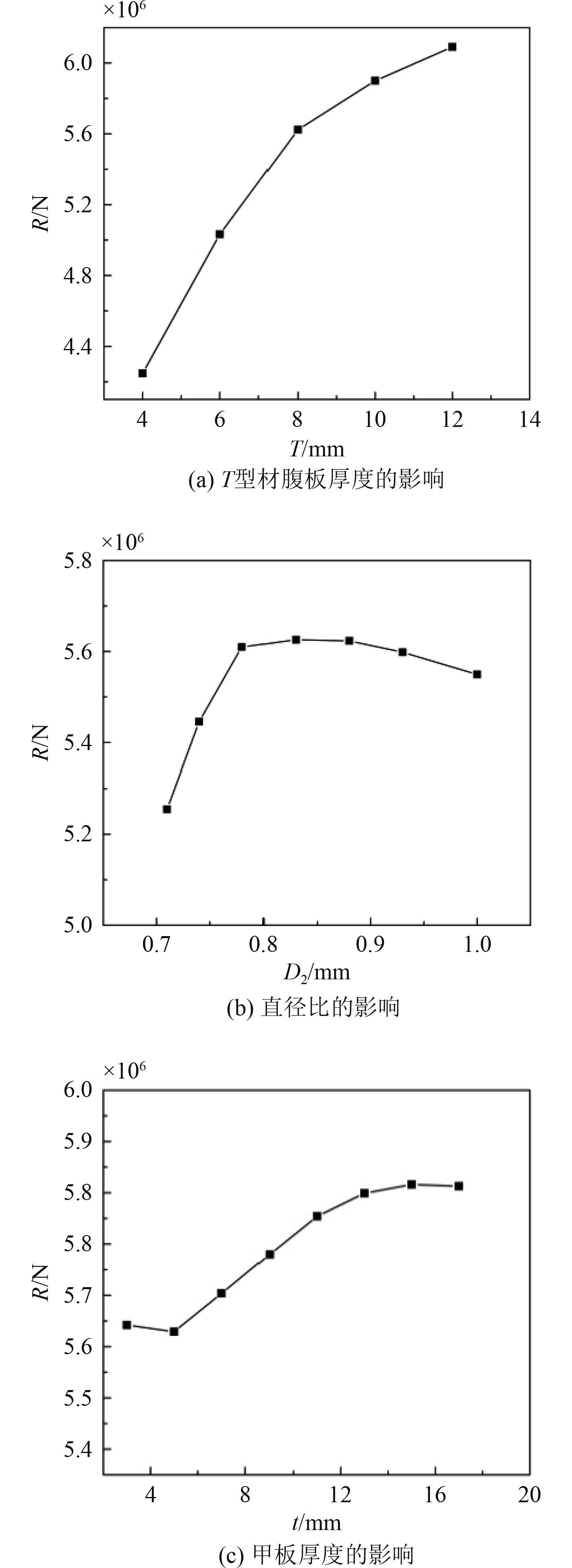
|
图 5 不同构件尺寸对支柱连接节点极限承载力的影响 Fig. 5 Effect of different member sizes on ultimate bearing capacity of column connection joints |
图5(b)为改变上支柱D1与下支柱直径D2之比λ对支柱连接节点极限承载力R的影响。可以发现,将λ从1减小至0.83,R出现少量增长;将λ从0.83减小至0.71,R出现明显下滑,下滑幅度达到6%。由此可以得出随着λ减小,R呈现出先少量增加后迅速下滑的趋势。实际设计中应谨慎选择λ值,避免λ过小削弱结构强度。
图5(c)为改变甲板厚度t对支柱连接节点极限承载力R的影响。可以发现,总体上增加t可以提升支柱连接节点的结构强度,这种提升作用在t位于5~11 mm时表现的尤为明显,提升幅度达到4%,其余厚度下增加t对结构强度影响有限。实际设计中可通过适当增加t提升结构强度。
3 支柱连接节点极限承载力预测支柱连接节点极限承载力预测公式主要考虑了T型材腹板、支柱、甲板3种重要构件尺寸带来的影响。
使用Workbench软件计算T型材腹板板厚位于4~12 mm,上支柱与下支柱直径比位于0.78~1 mm,甲板厚度位于3~17 mm,共计200个支柱连接节点模型的极限承载力,计算结果见表3。表中,R为支柱连接节点的极限承载力,MN;α为T型材腹板板厚T与T型材腹板高H的比值;λ为下支柱直径D1与上支柱直径D2之间的比值;β为甲板的柔度系数。
|
|
表 3 不同构件尺寸下支柱连接节点极限承载力有限元模型计算值与公式预测值 Tab.3 Finite element model calculation value and formula prediction value of ultimate bearing capacity of column connection node under different member sizes |
| $ \alpha = \frac{T}{H},$ | (1) |
| $ \lambda = \frac{{{D_1}}}{{{D_2}}} ,$ | (2) |
| $ \beta {\text{ = }}\left(\frac{l}{t}\right)\sqrt {\frac{{{\sigma _y}}}{E}}。$ | (3) |
式中:l为板材宽度,对于甲板来说是两条纵骨之间的距离;t为甲板板厚;σy为屈服强度;E为弹性模量。
通过非线性回归分析求解支柱连接节点的极限承载力公式。进行非线性回归分析需给定拟合函数模型,使用的拟合函数模型如下式:
| $ \frac{R}{{A{\sigma _{{y}}}}} = {b_1}\alpha _{}^{{b_1}}\lambda _{}^{{b_2}}{\beta ^{{b_3}}} 。$ | (4) |
式中:b1、b2、b3、b4均为无量纲常数;A为上支柱横截面积。
将表3中的R值代入非线性回归程序后可计算出拟合函数模型中b1、b2、b3、b4的数值分别为3.413,0.330,−0.043,−0.023。将式(4)中的变量A和σy移至等号右侧,并将4个无量纲常数计算值代入式(4),可以得出支柱连接节点极限承载力计算公式,如下式:
| $ R = 3.413A{\sigma _{{y}}}\alpha _{}^{0.33}\lambda _{}^{( - 0.043)}{\beta ^{\left( { - 0.023} \right)}} 。$ | (5) |
为验证式(5)的准确性,使用该式预测上述200个不同尺寸下支柱连接节点的极限承载力R0,结果如表3所示,R和R0的数值对比图如图6所示。可以发现,根据公式预测结果绘制的曲线和根据有限元模型计算结果绘制的曲线走势较为接近。由此可以判定,本文给出的支柱连接节点极限承载力预测公式较为可靠。
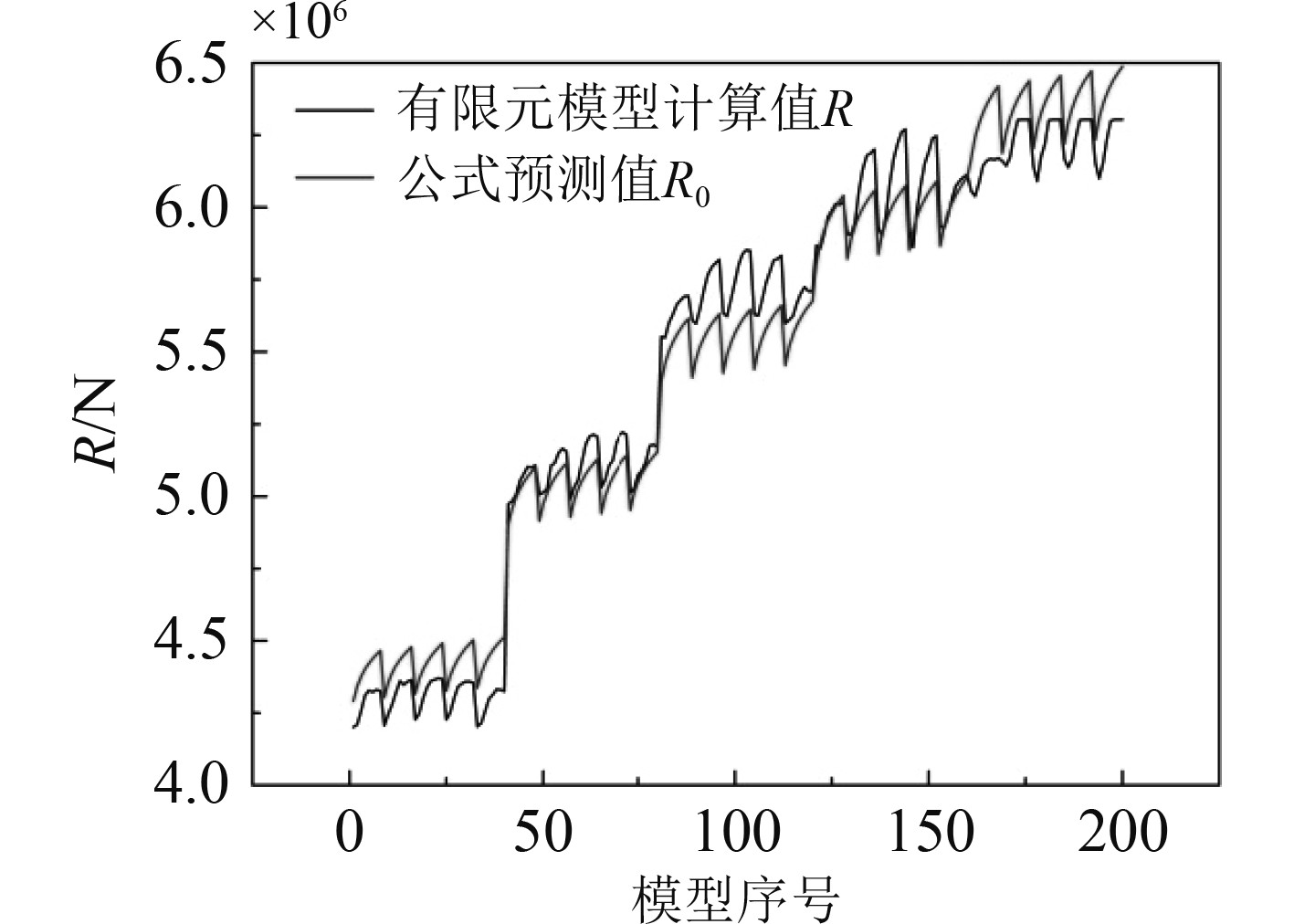
|
图 6 有限元模型计算结果曲线与公式预测结果曲线对比图 Fig. 6 Comparison between the calculated result curve of finite element model and the predicted result curve of formula |
进行结构可靠性分析首先要获得该结构的极限状态函数。一般情况下,极限状态函数可以写为如下形式:
| $ Z = g\left( {S,R} \right) = R - S。$ | (6) |
式中:Z代表极限状态函数,当
| $ S = 7.06{\text{ab}}h + P。$ | (7) |
式中:a为支柱所支持甲板面积的长度;b为支柱所支持甲板面积的平均宽度;h为支柱所支持甲板的计算压头;P为上支柱上方所传递的载荷。
联立式(1)~式(7)可得极限状态函数,如下式:
| $ \begin{split} Z=& R-S=3.413A{\sigma }_{\text{y}}{\left(\frac{T}{H}\right)}^{0.33}{\left(\frac{{D}_{1}}{{D}_{2}}\right)}^{(-0.043)}\times \\ & {\left(\text{(}\frac{\text{l}}{t})\sqrt{\frac{{\sigma }_{y}}{E}}\right)}^{\left(-0.023\right)}-7.06\text{ab}h-P 。\end{split} $ | (8) |
将式(8)及式(8)中重要变量的均值和方差输入可靠性分析程序,可计算出支柱连接节点的失效概率与可靠性指标。
4.2 支柱连接节点可靠性分析实例在计算实例中使用JC法进行可靠性分析。JC法作为一次二阶矩法的改进方法,可以处理非正态分布变量和非线性极限状态函数,是目前应用比较广泛的一种可靠性分析方法。
算例中的可靠性分析对象其构件参数参考表1,极限状态函数参考式(8)。为简化计算,式(8)中的一些变量可视为常量,这些变量包括:上支柱横截面积A,本文设为0.0178 m2;上支柱直径D1,本文设为323 mm;T型材腹板高度H,本文设为450 mm;甲板计算压头h,由CCS《邮轮规范》[11]中的规定可以确定为0.9 m;上方支柱传递载荷P,本文规定为3.5 MN。
式(8)中的其余变量均视为随机变量,根据赵晋[12]、严力宇[13]等的研究,这些随机变量的统计特性如表4所示。
|
|
表 4 支柱连接节点极限状态函数所涉及随机变量的统计特性 Tab.4 Statistical characteristics of random variables involved in limit state function of column connection node |
将上述数据代入JC法程序可得本算例中支柱连接节点的失效概率Pf为2.109×10−4,可靠性指标β为3.526,算例中的支柱连接节点较为可靠。
由上述计算过程可以判断,本文给出的可靠性分析流程可对支柱连接节点结构进行可靠性分析。
5 结 语本文通过研究邮轮支柱连接节点极限状态下的表现和探讨支柱连接节点可靠性分析流程,得出如下结论:
1)随着T型材腹板板厚、上支柱与下支柱直径比和甲板厚度等构件尺寸的变化,支柱连接节点的失效模式也会产生一定程度的变化,且每种构件尺寸的改变都会对结构失效模式产生不同的影响。
2)增加T型材腹板厚度、甲板厚度会提升支柱连接节点极限承载力;随着上支柱与下支柱直径比的减小,支柱连接节点的极限承载力呈现先少量增加后迅速减小的趋势。
3)本文根据有限元模型计算结果推导出的支柱连接节点极限承载力公式经检验较为可靠。
4)本文给出了从安全角度出发的支柱连接节点可靠性分析流程,并通过算例验证了其适用性。
| [1] |
朱波. 邮轮上层建筑参与总纵强度有效度研究[D]. 武汉: 武汉理工大学, 2018.
|
| [2] |
郭国虎. 大型邮轮上层建筑典型承载结构强度评估方法研究[D]. 武汉: 武汉理工大学, 2019.
|
| [3] |
甘进, 叶文强, 任鹏良, 等. 大型邮轮偏心支柱结构极限承载力研究[J]. 中国造船, 2021, 62(3): 28-39. GAN Jin, YE Wenqiang, REN Pengliang, et al. Research on the ultimate bearing capacity of large cruise ship eccentric strut structure [J]. Ship Building Of China 2021, 62 (3): 28-39. |
| [4] |
AGBOMERIE C O A, STEPHEN Q B, YE Jianqiao. Wave induced stress profile on a paired column semisubmersible hull[J]. Engineering Structures, 2017, 143: 77–90.
|
| [5] |
李冬琴, 刘存杰, 徐士友. 小水线面双体船支柱斜度对其耐波性能影响分析[J]. 舰船科学技术, 2016, 38(11): 20-23. LI Dongqin, LIU Cunjie, XU Shiyou. Analysis of the influence of the tilt of the pole of the SWATH catamaran on its seakeeping performance[J]. Ship Science and Technology, 2016, 38(11): 20-23. |
| [6] |
BV. Rule for the Classification of Steel Ships NR456-July2017[S]. 2017.
|
| [7] |
DNV. DNV GL Class Documents: Rules for Classification, Class Programmers, Class Guidelines, Offshore Standards and Statutory Interpretations[S]. 2018.
|
| [8] |
CCS. 钢质海船入级规范(2015)[S]. 2015.
|
| [9] |
CCS. 邮轮局部结构直接计算指南 (2021) [S]. 2021.
|
| [10] |
张俊, 凌芳芳. CCS规范中支柱载荷规定解析[J]. 船舶工程, 2018, 40(S1): 83-85. ZHANG Jun, LING Fangfang. Analysis of the provisions on pillar load in the CCS code[J]. Ship Engineering, 2018, 40(S1): 83-85. DOI:10.13788/j.cnki.cbgc.2018.S1.083 |
| [11] |
CCS. 邮轮规范(2015) [S]. 2015.
|
| [12] |
赵晋. 船舶极限强度可靠性分析中结构要素提取及计算方法研究[D]. 武汉: 华中科技大学, 2015.
|
| [13] |
严力宇. 考虑参数随机性的碰撞/搁浅受损船体结构极限强度研究[D]. 镇江: 江苏科技大学, 2020.
|
 2023, Vol. 45
2023, Vol. 45
