2. 江苏大学 机械工程学院,江苏 镇江 212013
2. School of Mechanical Engineering, Jiangsu Univercity, Zhenjiang 212013, China
豪华客滚船是一种货运与客运及休闲娱乐相结合的特殊功能性船舶,随着豪华客滚船对客户乘坐舒适性能的要求越来越高,噪声失控一系列损害人体健康[1-3]的问题在行业内也受到更高关注。国际海事组织[4-6]与2012年修订了《船上噪声等级规则》MSC.337(91)规范,对船舶内舱室的声压级有了明确严格的规定。
船舶噪声预报能有效提供理论上建成状态以及舾装后的船舶舱室噪声水平。船舶舱室噪声控制在船舶设计初阶段是最能降低成本及缩短建造周期的,传统的噪声预测方法以数值预测法为主,如有限元、有限元-统计能量混合法以及统计能量法[7]。
高处等[8]基于统计能量法对整船进行高频统计能量模型建立并进行传递路劲分析。汤伟民等[9]基于统计能量法对某客滚船进行舱室噪声预测,研究舱室噪声主要贡献量,进而有针对性进行降噪设计。由于统计能量法(SEA)需模态密度较高的先决条件[10],在中低频领域,模态密度较小,反而会造成预报的不精确。朱锡等[11]采用有限元的方法对基座结构噪声进行预测。代文强等[12-13]将能量有限元的方法运用到高速列车中,并施加多激励,对比实验,验证了准确性。但有限元法适用于低频噪声预测,对于船舶这种大体积模型,在中高频段进行分析存在计算量过大,现有计算水平跟不上的问题。张勇等[14]将FE-SEA法运用在特种车辆上,通过仿真与实验对比证明了该方法的可行性。罗文俊等[15-16]将FE-SEA运用在高速列车车内结构噪声的分析,并分析了不同吸声材料对车内降噪的影响。辛子豪等[17]将FE-SEA分析法运用在平台支持船上,通过对比SEA与FE-SEA这种方法得到的舱室声压级数据来证明混合模型的必要性。
以上研究多基于一种方法对舱室进行噪声预报,而忽略了其预报方法的适用性和不同频段的预报准确性。本文结合多种方法、分频段预测、基于统计能量法、有限元-统计能量混合法以及有限元法对客滚船进行全频段噪声预测。对舱室噪声频段基于模态密度进行高、中、低频划分,分别建立声学预报模型,数值计算重要参数及输入激励,进行舱室声压级预测,对不满足噪声规范部分进行降噪处理,满足规范要求。
1 船舶舱室布局及船体结构国际海事组织舱室标准MSC.337(91)根据船舶不同吨位,不同舱室制定了相应的舱室噪声限值,超过舱室噪声规范会被要求整改降噪。同时,对于降噪设计需考虑经济成本,建造修改周期等条件。以某客滚船为研究对象,该船总吨位5584 t,总长101 m,型宽18.04 t。总吃水量1427 t。图1为船舶总体模型及第3层平面图。
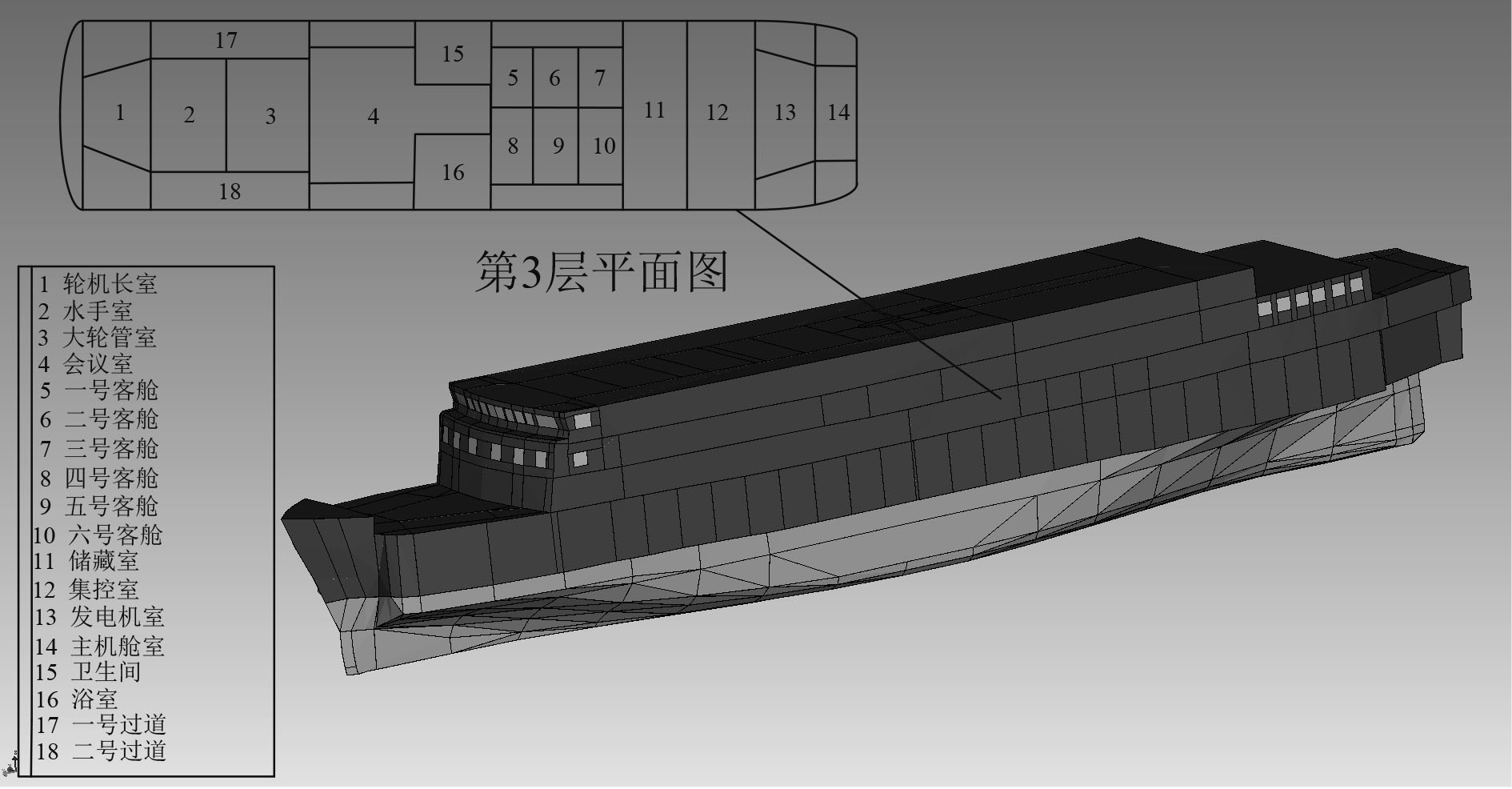
|
图 1 客滚船舱室布局 Fig. 1 Cabin layout of passenger rolling ship |
为对豪华客滚船进行噪声预测,使其满足噪声规范要求,提出基于统计能量法、有限元-统计能量混合法、有限元法开展豪华客滚船全频段噪声预测及降噪设计,参照船舶结构图、总布置图及舾装图建立客滚船全频段噪声预报模型。
1.1 高频SEA模型建立基于SEA法,以客滚船舱室结构布局为基础建立客滚船声振耦合模型,对模型进行相应简化,除去影响较小的部件。对船体各舱壁结构建立板子系统,对整船进行舱室划分,密封舱室为声腔子系统。整船共划分为1350个板子系统以及76个声腔子系统。其中,车辆舱所在甲板划分成27个声腔系统,车辆舱甲板上生活区部署了37个舱室。为更真实地模拟船体实际吃水工况,将满载工况时船体外壳水线以下的平板子系统设置为与海水接触的面,并设置半无限流体模拟噪声在海水中的传播。详细如图2所示,
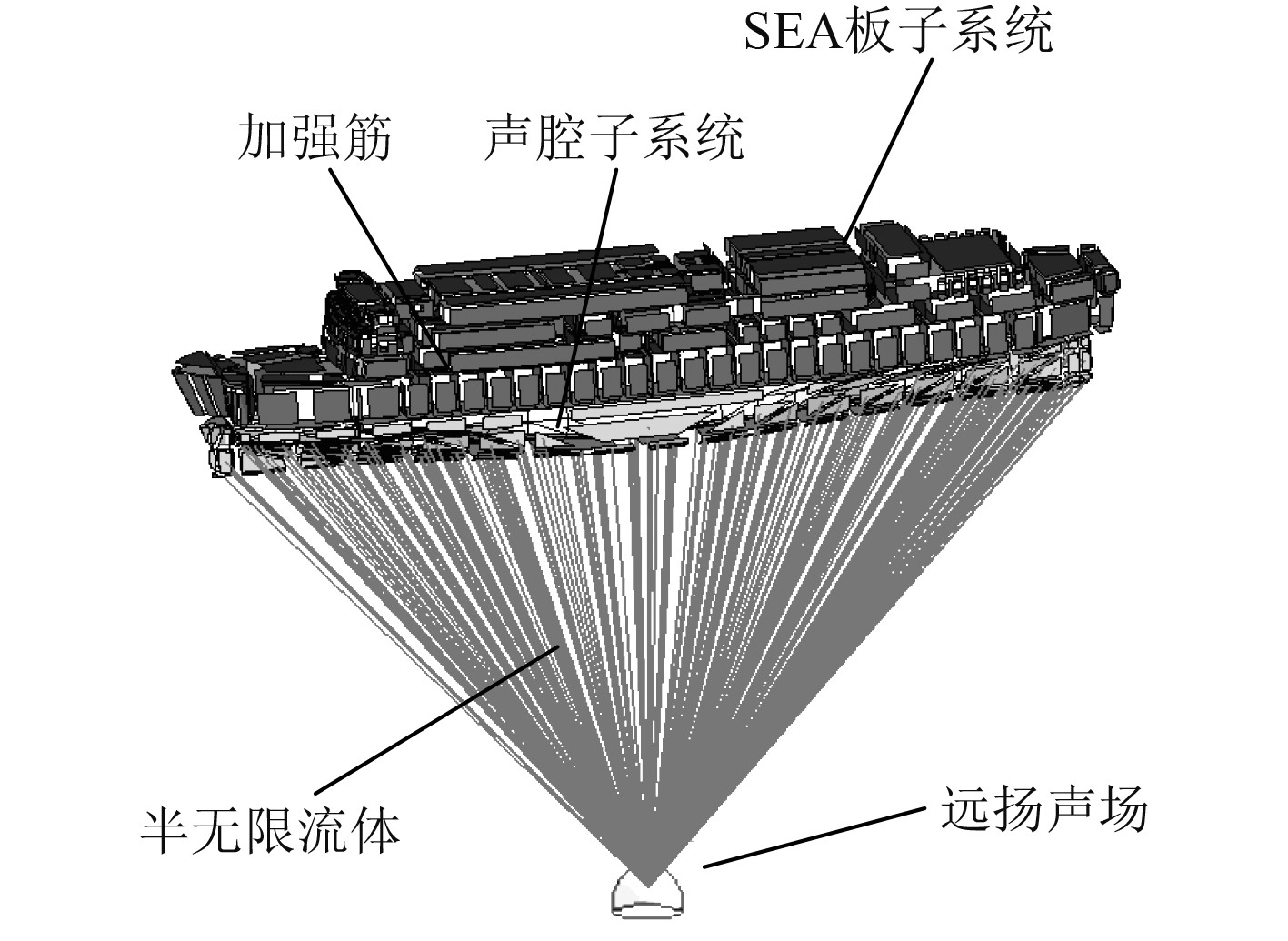
|
图 2 全船统计能量模型 Fig. 2 Full ship statistical energy model |
对建立的SEA子系统进行模态数计算,以主机舱室及发电机舱室为例,选取部分子系统进行模态计算。
根据频段内模态数值在1~5的区间划分3个频段:N>5,运用高频能量统计法;N<1,运用低频有限元法;1≤N≤5运用中频有限元-统计能量混合法。根据模态数划分为高频、中频以及低频分析频段,依次建立各频段声学模型。
1.2 中频FE-SEA混合模型建立经计算发现船舶底部板子系统模态数在200~500 Hz存在模态数较小的现象,使用统计能量法计算会存在较大误差,使用有限元法又存在计算量较大的问题。基于波动理论,运用FE-SEA混合法,建立中频混合模型,设置频段为200~500 Hz,将整个系统划分为确定子系统和不确定子系统。对客滚船船底模态数小于5的部件进行网格划分,网格大小为130 mm,根据有限元网格建立FE子系统,对上层建筑及周边满足模态数要求的板块建立SEA板子系统,2个部分系统进行混合连接,构建混合模型。
如图3所示,建立确定性子系统(FEA)与不确定子系统(SEA),进行混合连接。上层板子系统构建舱室声腔、过道声腔以及辅助声腔共73个声腔,构建了中频混合模型。
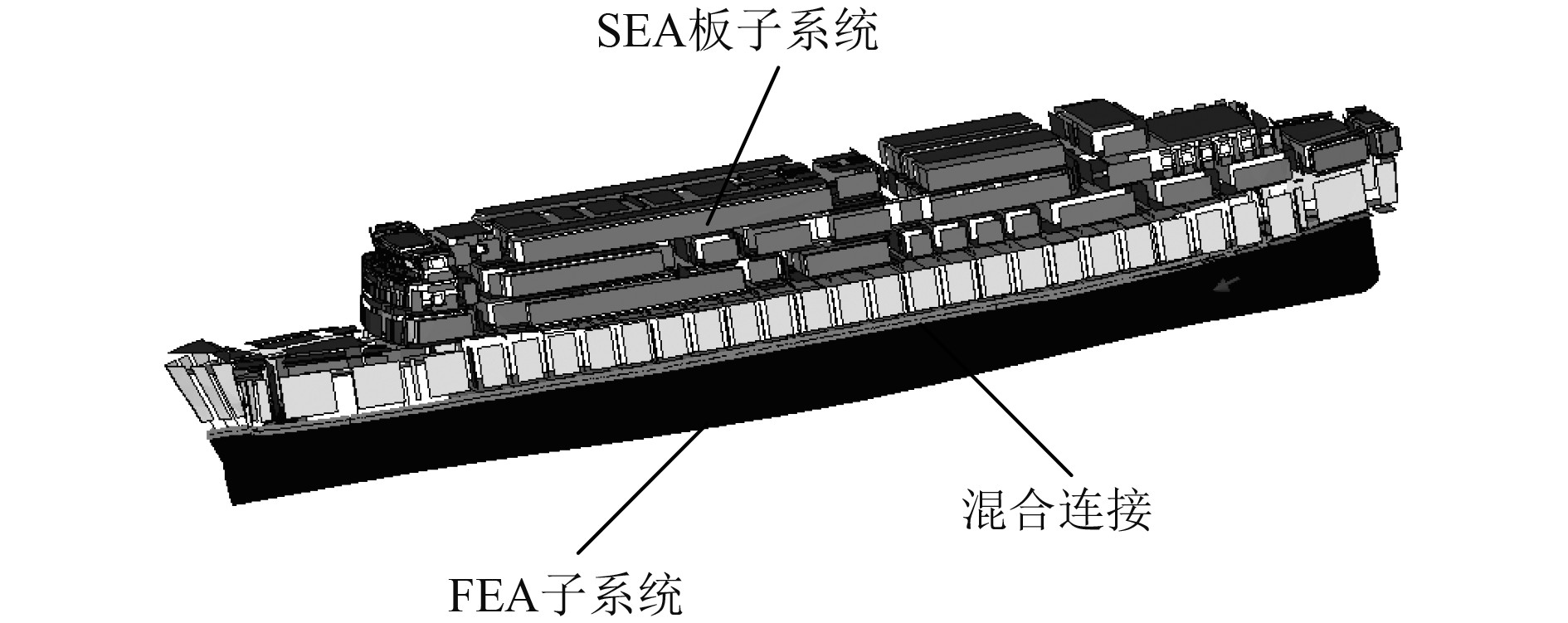
|
图 3 中频FE-SEA混合模型 Fig. 3 Medium frequency FE-SEA hybrid model |
200 Hz以下建立以有限元法进行噪声预测,设置63~200 Hz为低频段,基于有限元进行传播介质离散化处理,对客滚船全船进行网格划分,保留内部舱室布局结构及船舶外形主要特征。如图4(a)所示,整体船舶结构分为船底曲率板、上层甲板、内部舱壁以及窗户等区域。结构模型采用四边形网格进行离散处理,网格尺寸不超过波长的1/6,单元尺寸设定为2 000 mm,由355683个单元组成。建立有限元子系统如图4(b)所示。
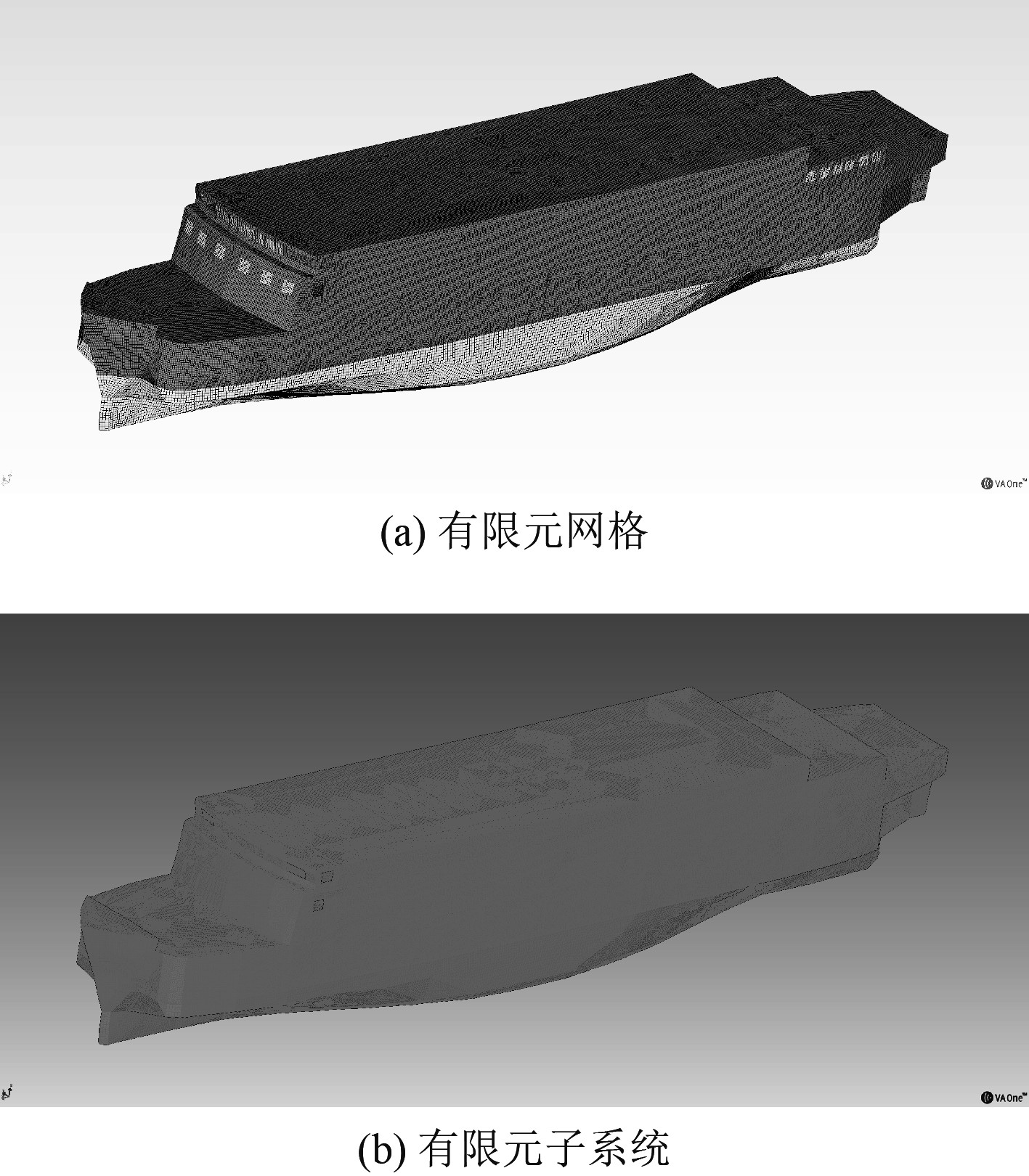
|
图 4 低频FEA模型 Fig. 4 Low frequency FEA model |
豪华客滚船整体结构复杂,为方便计算建模,对船体结构进行简化,主要设置为各类板材和加强筋的组合。船体、主甲板、驾驶甲板、龙骨板等均为加筋钢板。整个船舶船底及底层甲板设置板厚为10 mm钢板,上层甲板为8 mm厚钢板,窗户设置为玻璃,加强梁部分以铝合金为构建材料,材料参数如表1所示。
|
|
表 1 结构材料属性 Tab.1 Structural material properties |
内损耗因子是反映子系统能量传递损耗的物理量,本文内损耗因子中结构子系统内损耗因子和声腔子系统内损耗因子组成。

|
图 5 材料内损耗因子 Fig. 5 Loss factor within the material |
通过经验公式计算获得平均吸声系数作为声腔内损耗因子,计算公式为[9]:
| $ \eta =\frac{A{c}_{0}}{4V\omega }\alpha 。$ | (1) |
式中:
子系统间的耦合损耗因子根据能量子系统净功率流进行计算。对该模型进行耦合,初创建点、线、面3种耦合方式。经研究发现仅保留面连接耦合,噪声激励传播更加准确,对应理论计算方法,可具体参考文献[6]。
经过计算获得耦合损耗因子,以主机舱室为例进行分析。
舱室的内装结构可用舱室的折合吸声系数[18]表示,如表2所示。
|
|
表 2 舱室吸声系数 Tab.2 Cabin sound absorption coefficient |
根据分贝叠加原理,噪声激励较小声源可忽略不计,从而确定客滚船主要激励源:柴油机发电机、发电机组、螺旋桨及车辆舱通风噪声。根据提供的柴油机及发电机基本参数,通过经验公式计算获得。
1)柴油机激励计算
本文客滚船所用柴油机为6缸4冲程的中速机柴油机,质量为18 000 g,额定功率为2 000 kW,额定转速为750 r/min。
基座振动加速度级公式为[18]:
| $ {L}_{a}=-20{\rm{lg}}m+20{\rm{lg}}{P}_{e}+30\lg\frac{n}{{n}_{e}}+120+{C}_{a} 。$ | (2) |
式中:
|
|
表 3 柴油机噪声倍频程修正值 Tab.3 Diesel engine noise octave correction values |
柴油机辐射声功率级需考虑进气和排气2个方面。故将柴油机辐射声分为进气口辐射声功率级以及进气口辐射声功率级。
进气口辐射声功率级:
| $ {L}_{w,in}=10\lg{P}_{e}+57+{C}_{w,in}。$ | (3) |
排气口辐射声功率级:
| $ \begin{split} {L}_{w,out}=&v77+10\mathrm{lg}\left({P}_{e}\times {n}_{e}\right)+30\mathrm{lg}\left(\frac{n}{{n}_{e}}\right)+\\ & 10\lg\left\{\frac{1}{{\left\{\dfrac{{f}_{r}}{f}\right\}}^{3}+\left\{\dfrac{f}{{f}_{r}}\right\}}\right\}。\end{split} $ | (4) |
式中:
2)发电机噪声
客滚船发电机额定功率为300 kW,额定转速为1800 r/min。发电机的噪声同样由结构噪声以及辐射噪声组成。结构噪声以加速度级的方式添加,辐射噪声用声辐射功率级的方式添加。
电机的振动加速度级:
| $ {L}_{a}=10\lg{P}_{e}+7\lg{n}_{e}+62+{C}_{a}。$ | (5) |
电机辐射声功率级:
| $ {L}_{w}=10\lg{P}_{e}+57+{C}_{w}。$ | (6) |
式中:
|
|
表 4 发电机噪声倍频程修正值 Tab.4 Generator noise octave correction values |
3)空调通风系统噪声
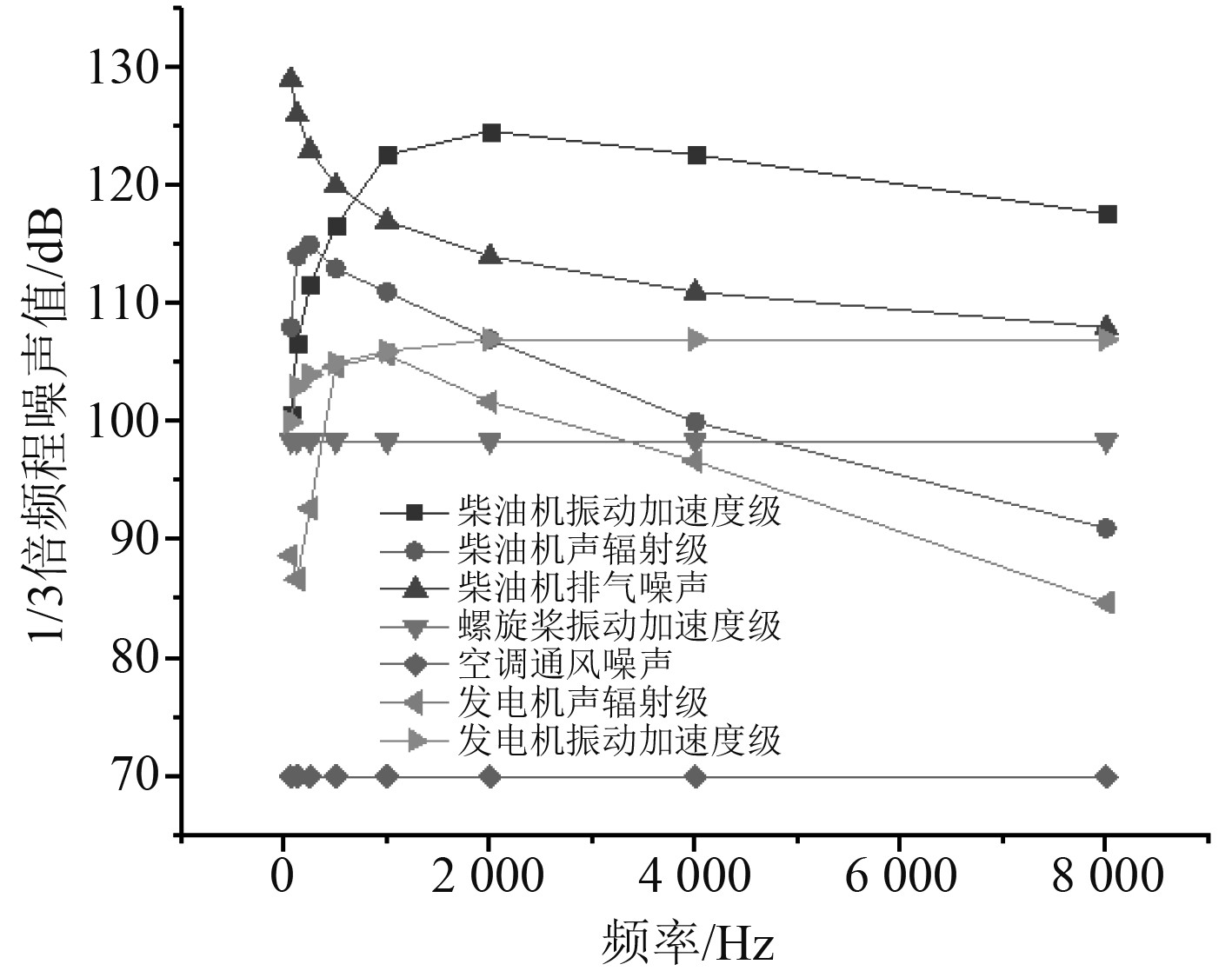
由于车辆舱内部载运车辆在行驶中会产生大量费气,故对于舱室内部通风排气的需求较高。该车辆舱顶部开设有8个空调通风管道。依照空调系统的主机参数,系统噪声预估值为70 dB。图6为各噪声估值及激励加载方式。
|
图 6 1/3倍频程噪声源估算 Fig. 6 1/3 octave noise source estimation |
将各项参数及激励数值输入声学模型,整船声学模型设置为1/3倍频程进行求解。对于中频FE-SEA混合模型及低频FEA模型计算前需进行模态计算,获得船体舱壁模态属性,导入进行噪声预报分析;根据SEA分析法,对500~8000 Hz频段内进行高频舱室噪声预测;根据有FE-SEA混合法,对200~500 Hz频段内进行中频段舱室噪声预测;根据有FEA分析法,对63~200 Hz频段内进行低频段舱室噪声预测;参考规范、舱室噪声等级采用A计权声压级。全速航行工况下,客滚船舱室噪声声压分布云图如图7所示。

|
图 7 舱室噪声分布云图 Fig. 7 Cabin noise distribution cloud map |
可以看出,全船舱室噪声主要集中在船尾主机舱、发电机舱位置附近。在低频范围内,振动加速度级对全船噪声贡献量占比更多。随着频率的提高,主机、辅机及空调通风系统等声辐射噪声的舱室噪声贡献量比重随之增加。对于车辆舱部分,这一现象更加明显,在空调通风口处,随着频率的提高,车辆舱内噪声分布云图更加明显。
3.2 预测值与标准值对比分析对不同频率下的声压级进行加权修正,采用A计权评价标准,与IMO舱室MSC.337(91)噪声规范进行对比。通过统计能量法和混合法进行计算分析,得出各自频段内的A计权声压值,通过计算公式[19]得出整体频段总声压级,即
| $ {L}_{A}=10{\rm{lg}}\left(\sum {10}^{{0.1L}_{Ai}}\right)。$ | (7) |
式中,
对比表5可知,在未经降噪处理前,存在舱室噪声不满足规范的情况,为了使其满足要求,设计降噪方案进行降噪处理。
|
|
表 5 部分重要舱室声压级预报结果 Tab.5 Forecast results of sound pressure level in some important compartments |
为了有效控制客滚船舱室超标噪声,对舱室噪声能量输入进行主要传递路径分析,研究超标舱室主要输入激励频域特征。由图8可知,由于主机舱位于船舶中后方,整体功率流遵循从后往前,从下往上的流动方向。

|
图 8 整船激励功率流 Fig. 8 Whole ship excitation power flow |
以集控室为例,分析该舱段传递路径中,各板子系统及声腔子系统能量输入占比,进一步分析主要激励贡献量,为舱室降噪设计提供指导。
由图9可知,16号车辆舱主要贡献由17号车辆舱声腔声辐射噪声引起,同时板子系统占比贡献为结构噪声,舱段位于船体后半部分,上方为储藏室,储藏室后方为集控室,集控室后方为发电机室和主机舱室,同时该舱段设置了通风口。分析可知16号车辆舱主要噪声来源于空调通风噪声、及主机、发电机引起的结构噪声。以相同方法对超标舱室进行贡献量分析,分析噪声贡献量。

|
图 9 16号车辆舱能量输入 Fig. 9 Vehicle cabin 16 energy input |
舱室噪声控制主要从噪声源控制、传播途径控制及人耳接受处控制3个方面出发。对于船舶噪声控制而言,传播途径控制是现阶段船舶舱室噪声控制较为高效也是最经济的控制措施。
根据噪声超标原因,选择在传递途径过程中,以敷设声学包的形式进行减振、吸声降噪处理。对超标舱室进行如下处理:
1) 主机舱室、发电机室舱壁位置敷设声学包,底部安装浮动地板,柴油机组安装隔振垫。
2) 集控室、车辆舱空调通风管路上安装消声器,舱壁位置敷设声学包。
车辆舱尾部舱壁靠近柴油机发电机组,根据材料的隔声性能,选择矿物棉作为板材的材料,铺设在尾部舱壁上。在顶部的空调通风口位置附近辐射吸声材料,选取泡沫塑料及泡沫金属作为吸声材料构建声学包。所用声学包用吸声隔声性能较好的泡沫、纤维材料。方案如下:20 mm的胶合板+25 mm的泡沫金属+20 mm的胶合板。设置声学包安装在舱室舱壁的四周和天花板内壁,地板不做处理,主机舱、发电机舱安装浮动地板。经降噪后,不达标舱室噪声得到下降,如表6所示。
|
|
表 6 舱室降噪前后对比 Tab.6 Cabin noise reduction before and after comparison |
计算得出超标舱室经降噪处理,满足MSC.337(91)限值规范。
5 结 语本文以某豪华客滚船为研究对象,针对舱室噪声预测与降噪设计,基于统计能量法、有限元-统计能量混合法、有限元法开展全频段噪声预测工作。结果表明,在不进行降噪措施下,该客滚船存在舱室声压级不满足规范的现象,验证了对大型船舶进行降噪设计的必要性。具体得出结果如下:
1) 本文进行船舶声振耦合模型建立,分别基于统计能量法、有限元-统计能量混合法、有限元法建立3个频段的声振耦合模型。
2) 通过理论方法,计算了模态密度、内损耗因子、耦合损耗因子以及主要输入激励,将参数加载在不同频段声学模型中。
3) 对舱室噪声进行预测,分析整船舱室声压级分布规律,对比了客滚船舱室不同区域声压级与舱室标准,发现存在不满足情况。
4) 对客滚船超标舱室进行传递路劲分析,及输入贡献量分析,为针对性的降噪设计提供指导,进行降噪设计使其满足舱室噪声规范。
| [1] |
NATHAN D. Underwater noise abatement: economic factorsand policy options[J]. Environmental Science&Policy, 2019, 92: 116-123. |
| [2] |
BADINO A, BORELLI D, GAGGERO T. Normativeframework for ship noise: present and situation and futuretrends[J]. Noise Control Engineering Journal, 2012, 60(6): 740-762. DOI:10.3397/1.3701045 |
| [3] |
BADINO A, BORELLI D, GAGGERO T. Noise emitted fromships: impact inside and outside the vessels[J]. Procedia-Social and Behavioral Sciences, 2012, 48: 868-879.
|
| [4] |
ZHANG Bo, XIANG Yang, HE Peng. Study on pred IMO. Code on Noise Levels on Board Ships[S]. 2012.
|
| [5] |
IHLENBURG F, BABUSKA I. Finite element solution of the Helmholtz equation with high wave number Part I: the hp-version of the FEM[J]. Computers and Mathematics with Application, 1995, 30: 9-37. |
| [6] |
姚德源, 王其政. 统计能量分析原理及其应用[M]. 北京: 北京工业大学出版, 1995
|
| [7] |
LYON R H, MAIDANIK G. Power flow between linearly coupled oscillators[J]. Journal of Acoustics Society of America, 1962, 34(5): 623-639. DOI:10.1121/1.1918177 |
| [8] |
高处, 杨德庆. 船舶舱室噪声传递路径分析的声振熵赋权图法[J]. 上海交通大学学报, 2014, 48(4): 469-474. DOI:10.16183/j.cnki.jsjtu.2014.04.005 |
| [9] |
汤伟民, 林嘉欢, 张俊. 基于统计能量法的客滚船舱室降噪设计[J]. 中国造船, 2020, 61(4): 209-222. DOI:10.3969/j.issn.1000-4882.2020.04.022 |
| [10] |
林天然, 李霞. 能量分析方法及应用综述[J]. 振动与冲击, 2021, 13(40): 222-238. |
| [11] |
朱锡, 胡忠平, 石勇. 预报基座结构噪声的有限元方法研究[J]. 海军工程大学学报, 2003, 15(6): 33-36. DOI:10.3969/j.issn.1009-3486.2003.06.008 |
| [12] |
代文强, 郑旭, 郝志勇, 等. 采用能量有限元分析的高速列车车内噪声预测[J]. 浙江大学学报(工学版), 2019, 53(12): 2396-2403. DOI:10.3785/j.issn.1008-973X.2019.12.018 |
| [13] |
LANGLEY R S, BREMNER P. A hybrid method for the vi-bration analysis of complex structural-acoustic systems[J]. The Journal of the Acoustical Society of America, 1999, 105(3): 1657-1671. DOI:10.1121/1.426705 |
| [14] |
张勇, 王坤祥, 盛陈, 等. 某特种车车内中频噪声的混合FE-SEA法分析[J]. 机械科学与技术, 2018, 37(11): 1698-1704. DOI:10.13433/j.cnki.1003-8728.20180118 |
| [15] |
罗文俊, 蒋峻楠, 雷晓燕, 等. 基于FE-SEA混合法的车内结构噪声预测分析[J]. 铁道学报, 2017, 39(12): 137-145. DOI:10.3969/j.issn.1001-8360.2017.12.019 |
| [16] |
罗文俊, 蒋峻楠, 刘全民, 等. 基于FE-SEA混合法的列车结构噪声降噪研究[J]. 铁道学报, 2020, 42(10): 113-117. DOI:10.3969/j.issn.1001-8360.2020.10.016 |
| [17] |
辛子豪, 樊红, 邹郁筱, 等. FE-SEA方法在平台支持船噪声预报中的应用[J]. 噪声与振动控制, 2021, 41(1): 21-26. DOI:10.3969/j.issn.1006-1355.2021.01.005 |
| [18] |
中国船级社 . 船舶及产品噪声控制与检测指南[S]. 2013.
|
| [19] |
贺启环. 环境噪声控制工程[M]. 北京: 清华大学出版社, 2011.
|
 2023, Vol. 45
2023, Vol. 45
