0 引　言

船舶在航行时承受着来自船舶自身和外部环境的各种外力，比如船舶波浪抨击力、船身自重和载重的重力等。船舶工作过程的力学特性分析是指进行船舶的运动学特性（如速度、加速度、姿态等）以及动力学特性（受力、扭矩、振动等）分析，基于运动学和动力学分析，实现船舶结构的稳定性评估。

有限元分析可以用于模拟船舶在不同工况下的受力情况，利用有限元分析方法对船舶结构进行力学、动力学、疲劳等方面的分析和计算，以评估船舶结构在不同工况下的性能和安全性，这种应用可以帮助设计师优化船舶结构设计，提高船舶的安全性、可靠性和性能，并且有助于降低成本和提高设计效率。

本文分别从船舶结构设计中的极限强度、疲劳强度等理论入手，基于有限元分析技术进行了船舶结构设计的优化和仿真。

1 船舶制造结构设计的极限强度和疲劳特性研究 1.1 船体结构的极限强度理论分析

在船舶舱室、甲板等区域，大风浪、碰撞或其他极端情况下的载荷较大，为了防止船体结构在扭矩、弯矩作用下发生破坏，往往在舱壁等位置设置多个筋板。本节针对船体结构的极限强度理论进行分析，主要考虑船体结构在短时间内受到的作用力。

船体结构以高强度钢材焊接件为主，包括船壳板焊接件，船壳板是船体结构的主要承载部位，其上的焊接件包括纵向缝、横向缝、甲板焊接件等；船舶框架焊接件，船舶框架是船体结构的骨架，其上的焊接件包括纵向框架、横向框架、斜框等^[1]。

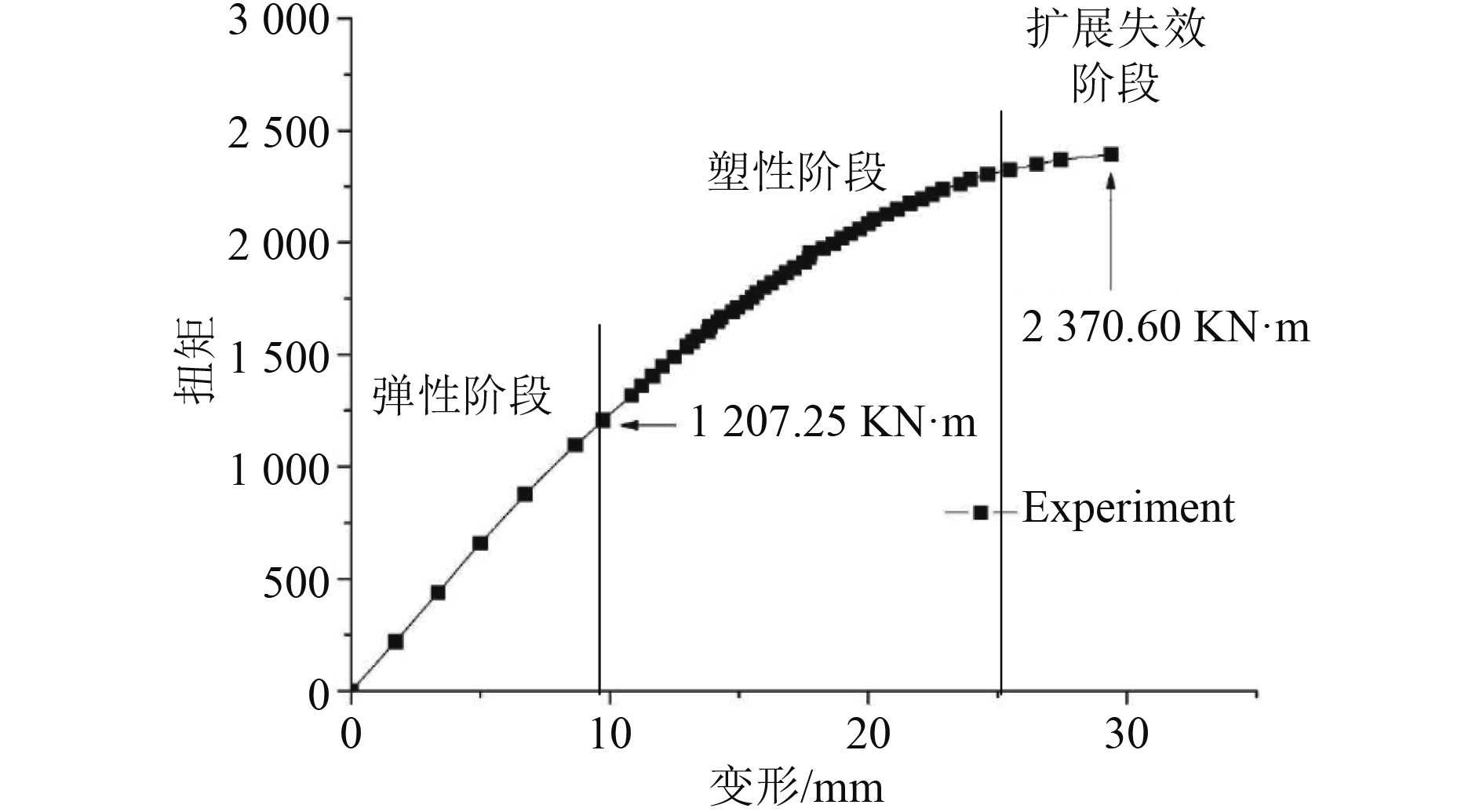
针对高强度钢Q420，本文研究该材料的结构应力-应变关系，如图1所示。

可知，高强度钢Q420的结构应力-应变可以分为弹性阶段、塑性阶段和扩展失效阶段，高强度钢Q420结构的应力表达式为：

$ {\sigma _x} = \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _x} \times E}\text{，} {{\varepsilon _x} \leqslant {\varepsilon _y}} \text{，} \\ {{\sigma _y}}\text{，} {{\varepsilon _x} > {\varepsilon _y}} \text{。} \end{array}} \right. $

式中：$ {\varepsilon _x} $为弹性应变；$ {\varepsilon _y} $为塑性应变；$ {\sigma _y} $为极限屈服应力；$ E $为弹性模量。

1）弹性阶段

当船体结构的应力-应变处于稳定阶段，结构发生弹性变形时，材料处于弹性阶段，外加作用力产生的应力撤除后，材料产生的变形就会恢复，此时，船体结构的应力-应变模型为：

$ \sigma = \left\{ {\begin{array}{*{20}{l}} {E{\varepsilon _x}}\text{，} {{\sigma _{}} \leqslant {\sigma _y}}\text{，} \\ {E{\varepsilon _x}\frac{{{A_r}}}{A}}\text{，}{\rm{else}} \text{。} \end{array}} \right. $

式中，$ {A_r} $为结构的应力横截面^[2]。

2）塑性阶段

随着外加载荷的不断提高，船体结构产生的应变和挠度不断增加，当达到材料的屈服极限时，材料会进入塑性阶段，产生不可恢复的变化。

材料挠度的增量为：

$ w = \frac{{2a}}{{\text{π}} }\sqrt {{\varepsilon _y} - {\varepsilon _x}} \text{。} $

此时船舶结构的应力表示为：

$ {\sigma _n} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{M_p} - (1/8)q{a^2}}}{{{A_r}{w_T}}}} \text{，} {{\sigma _x} \leqslant {\sigma _y}} \text{，} \\ {\dfrac{{{M_p} - (1/8)q{a^2}}}{{{A_r}{w_T}}}} \text{，} {\rm{else}} \text{。} \end{array}} \right. $

式中：$ {M_p} $为结构所受的最大弯矩；$ q $为作用力；$ a $为单位长度；$ {w_T} $为最大挠度变形量。

3）扩展失效阶段

船舶结构所受的极限载荷进一步增大，则材料在塑性变形的基础上快速失效，进入扩展失效阶段。

1.2 船舶结构的疲劳特性理论分析

疲劳破坏是船舶结构的主要破坏形式之一，特别是对于长期处于海上运行的船舶。疲劳破坏是由于结构在循环载荷作用下的应力集中和积累所致，导致材料的裂纹和最终的破坏。船舶在波浪、海风和船舶运行振动等环境载荷的作用下，结构会受到变化的疲劳应力，从而容易产生疲劳破坏。

为了减少疲劳破坏对船舶结构的影响，船舶设计和制造中需要考虑疲劳寿命的评估和控制，采用合适的材料、结构设计和工艺，以提高船舶结构的抗疲劳能力，特别对于大型船舶。

常用的材料疲劳分析方法包括疲劳裂纹扩展理论和线性累积损伤理论。

1）裂纹扩展理论

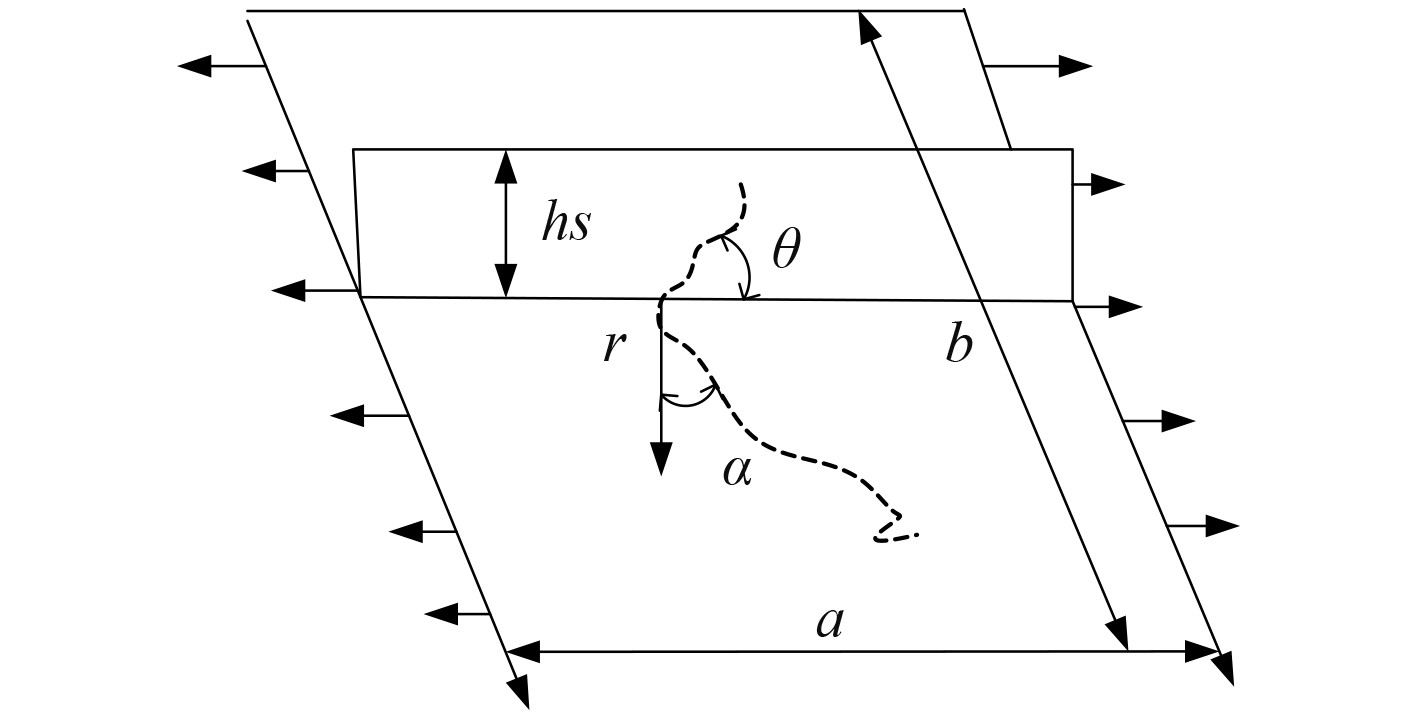
裂纹扩展理论是基于断裂力学基础上进行材料的疲劳寿命计算，图2为典型的筋板结构裂纹扩展示意图。

图中，筋板长度为a，宽度为b，裂纹扩展角度与长度方向的夹角为$ \theta $，裂纹尖端为r，筋板的应力场建模为：

$ {\sigma _{ij}} = \frac{{{K_c} \cdot {K_1}}}{{\sqrt {2{\text{π}} r} }}{\phi _i}(\theta ) \text{。} $

式中：$ {\sigma _{ij}} $为应力张量；$ {K_{\text{1}}} = \sigma \sqrt {{\text{π}} a} $，为材料的应力强度因子，也可记为${K_1} = \sigma \sqrt {{\text{π}} a} f(a,W, \cdots ) \text{。} $其中$ {K_c} $为材料的应力强度因子，表征材料的韧性，计算式为，$ f(a,W, \cdots ) $为尺寸修正函数；$ {K_c} $为材料的应力强度因子，表征材料的韧性。

$ {K_c} = \sigma \sqrt {{\text{π}} a} f(\frac{a}{W}, \cdots ) 。$

建立材料的断裂力学屈服应力和应变^[3]为：

$ \begin{gathered} {\sigma _p} = \frac{1}{{2{\text{π}} }}{\left( {\frac{{{K_1}}}{{{\sigma _w}}}} \right)^2}\text{，} \\ {\delta _p} = \frac{1}{{2{\text{π}} }}{\left( {\frac{{{K_1}}}{{{\sigma _{\text{w}}}}}} \right)^2}{(1 - 2v)^2}\text{。} \\ \end{gathered} $

式中：$ {\sigma _w} $为材料的断裂屈服应力；$ v $为泊松比。

2）线性累积损伤理论

线性累积损伤理论也是一种常见的疲劳评估方法，该算法基于材料的S-N曲线。

定义材料的应力为$ {S_i} $，该应力下的材料具有的循环次数为$ {N_i} $，实际工况下产生$ {n_i} $次循环，根据线性累积损伤理论可得损伤值为：

$ {D_i} = \frac{{{n_i}}}{{{N_i}}} \text{。} $

结构的总损伤为：

$ D = \sum\limits_{i = 1}^k {} \frac{{{n_i}}}{{{N_i}}} \text{。} $

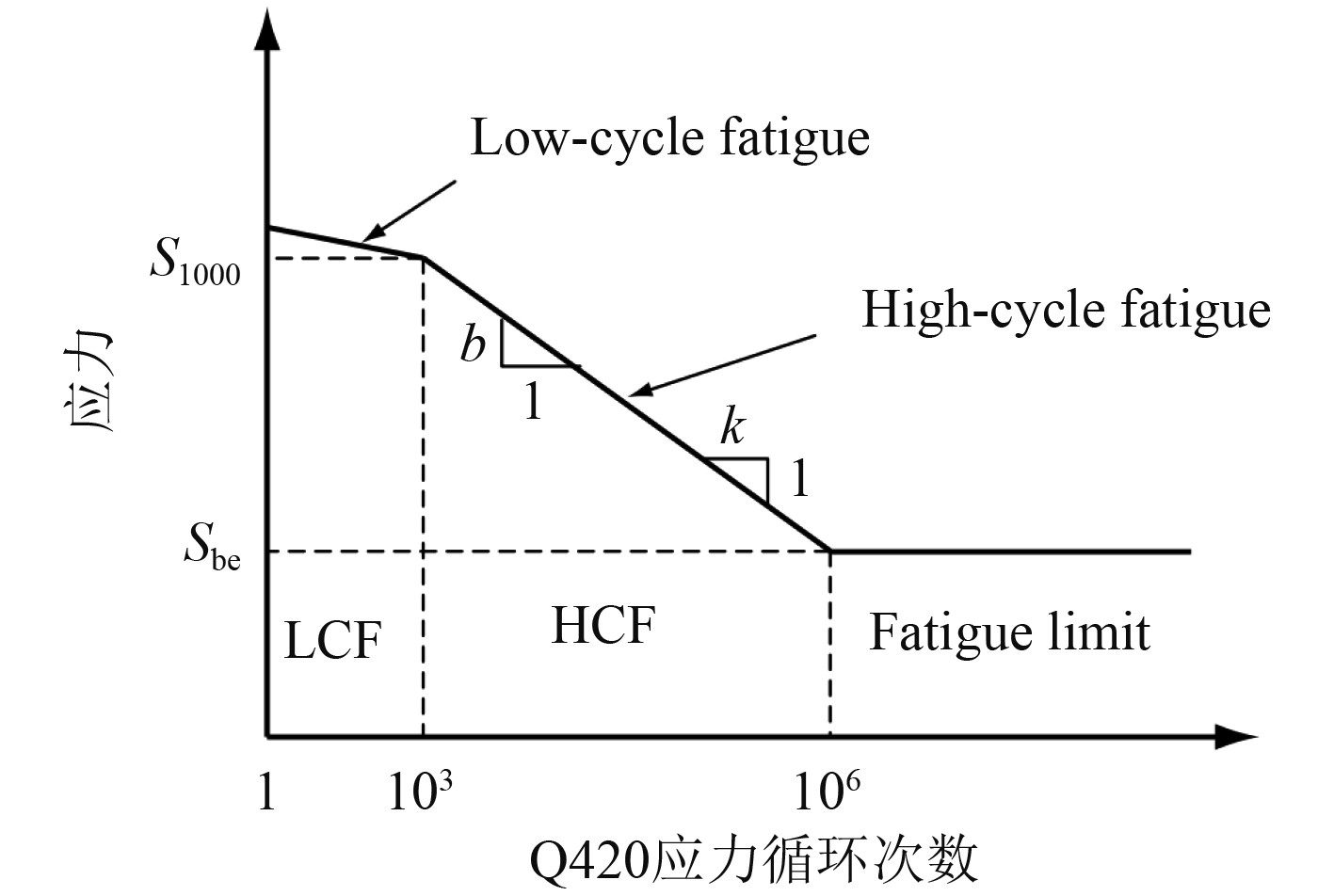
船舶结构高强钢Q420的材料S-N曲线如图3所示。

可知，Q420的疲劳分为低周疲劳low-cycle fatigue、高周疲劳high-cycle fatigue和无限循环寿命阶段。

2 基于有限元分析的船舶制造结构设计仿真

有限元分析基于变分原理可以得到结构的平衡方程和边界条件，将结构看作连续介质，应用弹性力学理论描述结构的变形和应力，基于胡克定律等材料本构方程进行建模，将结构分割为有限数量的单元，建立单元之间的相互作用关系，通过数值积分计算单元的刚度矩阵和质量矩阵，最终得到整个结构的刚度矩阵和质量矩阵。

有限元分析的基本流程如图4所示。

船舶结构的有限元分析是为了评估船舶结构在不同工况下的应力、变形和疲劳性能。船舶舱壁结构有限元分析的关键流程有：

1）几何建模

首先进行船舶结构的几何建模，包括舱壁的形状、尺寸、结构连接等，通常使用CAD软件进行建模，生成几何模型，比如Catia、Proe等。

2）网格划分和材料建模

将船舶结构离散化为有限元网格，划分为多个单元，通常采用三角形或四边形单元。网格划分需要考虑结构的几何形状和复杂度，以及分析的精度要求。材料建模是指确定船舶结构所用材料的力学性能参数，包括弹性模量、泊松比、屈服强度等，建立材料模型^[4]。

本文针对船舶的壳体结构进行有限元分析，主要材料包括18CrNiMo、Q345A、Q235b等，表1为船舶壳体结构的材料属性。

船舶壳体有限元模型如图5所示。

3）载荷和边界条件

确定船舶舱壁结构在不同工况下受到的载荷，包括静载荷、动载荷、海洋环境载荷等。同时需要设定结构的边界条件，包括支撑约束、外部约束等^[5]。

施加在船舶壳体的载荷谱函数为：

$ S\left( w \right) = \frac{{1.25{w_p}^4{H_s}{e^{1.25\frac{{{w_p}}}{w}}}}}{{4{w^5}}} \text{。} $

式中：$ w $为振动角频率；$ {w_p} $为波峰频率；$ {H_s} $为船体结构的载荷幅值。

4）求解和评估

通过有限元分析软件进行数值计算，求解船舶壳体结构在不同载荷下的应力、变形等响应。对有限元分析的结果进行评估，包括结构的安全性、疲劳寿命、应力集中区域等，评估结构的性能是否满足设计要求。

针对船舶壳体与甲板连接焊缝位置，进行不同载荷下的应力计算，载荷-应力和变形结果如表2所示。

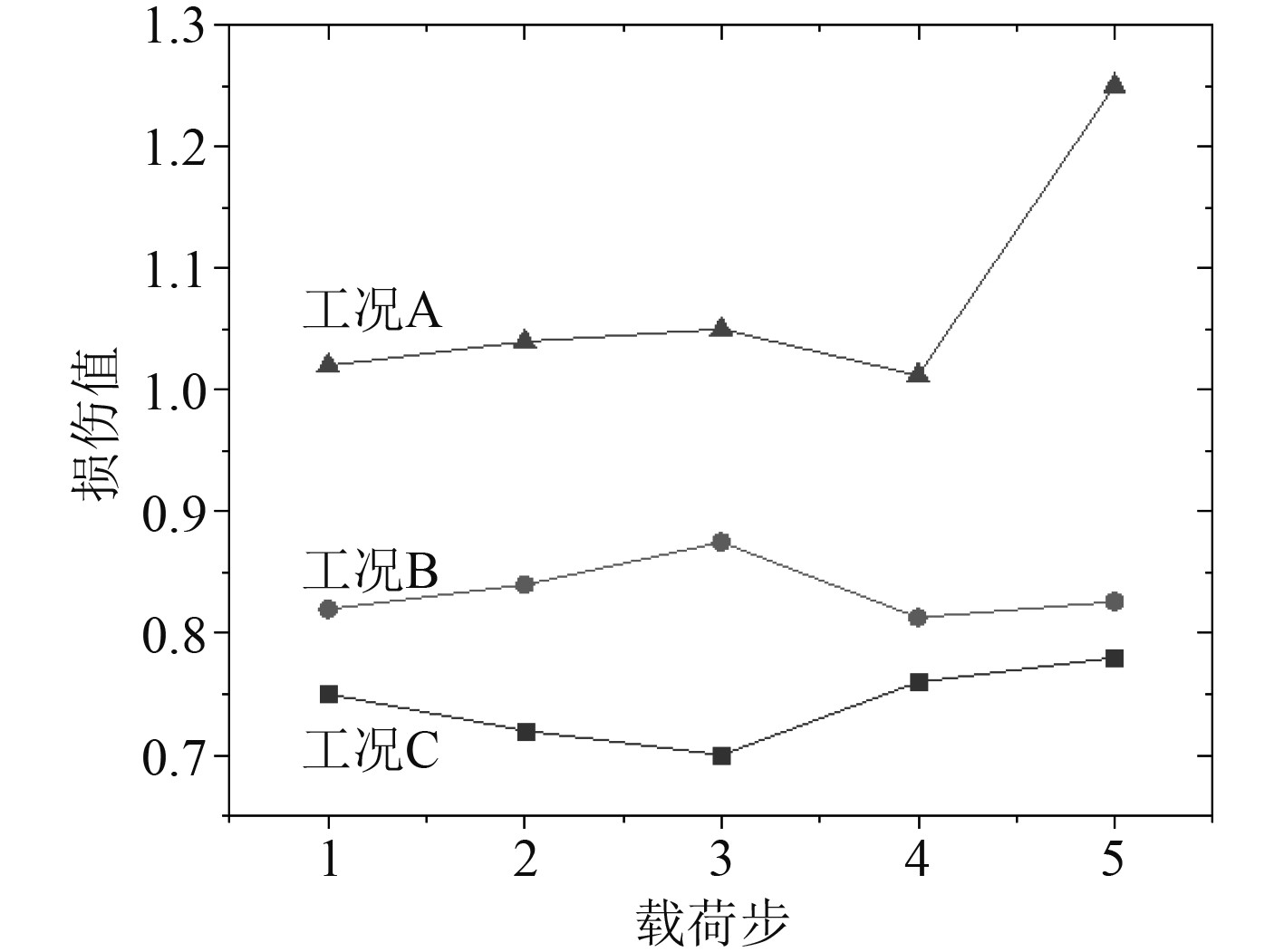
仿真得到3种工况（A：风速10 m/s；B：风速8 m/s；C：风速6 m/s）的结构损伤结果如图6所示。可以看出，随着平均风速的降低，结构的损伤值明显减小。

3 结　语

有限元分析技术在材料结构强度、疲劳计算中具有广泛的应用，本文针对船舶壳体结构分布进行极限强度理论分析和材料的疲劳强度理论分析，并结合有限元仿真软件和三维设计软件进行了船舶壳体的有限元仿真，对于改善船舶壳体结构的极限和疲劳强度设计有重要作用。