2. 江苏现代造船技术有限公司,江苏 镇江 212003
2. Jiangsu Modern Shipbuilding Technology Co., Ltd., Zhenjiang 212114, China
开体泥驳也称对开泥驳,配合挖泥船等疏浚船舶作业,用以装载、运输、抛投泥沙、石料等。开体泥驳兼有载重型船舶和布置地位型船舶的特点,在设计时要解决“装得下”和“抛得出”2个问题。有别于其他货船,开体泥驳的2个半体,通过布置在泥舱前后两端的甲板铰链连接,采用船体整体对开的形式,依靠货物重力卸货。泥舱满载时,产生倾向张开的力矩(即半体开合力矩),通过油缸拉力锁紧2个半体。卸除油缸拉力(或由液压阀换向,油缸产生推力)后,半体张开,实现快速排泥。随着泥舱的排空,半体开合力矩倾向关闭,半体自动关闭锁紧。
CCS、BV等船级社的规范[1-2]中规定,开体泥驳连接2个半体的甲板铰链构件尺寸由直接计算确定,作用其上的载荷应根据在各设计工况下预期的最大静、动载荷的适当组合来确定。开体泥驳的受力情况较为复杂,不同海况的波浪载荷对结构受力的影响难以直接评判,甲板铰链及其周边结构应力情况复杂,一旦设计不当,会导致半体无法正常开合,严重地还将导致结构的破坏,引发事故。在甲板铰链的设计实践中,一般采用增大甲板铰链尺寸的方法,以此提高甲板铰链的安全系数。但这种方法往往造成结构冗大,空船重量增加。
袁万洪[3]结合一艘500 m3开体泥驳,提出通过半体受力分析,并参照母型船进行结构设计的方法。闫桂荣[4]对从船级社规范的角度入手,对开体泥驳的力学原理、受力、结构形式和尺寸校核等作了详细说明。杨敬东等[5]对一艘60 m3开体泥驳的铰链臂和甲板铰链结构受力进行了理论分析并加以改进,并采用有限元方法对改进后的铰链臂结构进行强度校核。
本文以1800 m3沿海自航开体泥驳为研究对象,采用基于波浪载荷直接计算的方法对甲板铰链进行受力分析。本船的主要参数:船长72.80 m,型宽15.10 m,型深5.20 m,设计吃水4.00 m,泥舱长度42 m,单边最大开体角度15°,甲板铰链布置在泥舱前后的甲板面上,间距43.2m。
采用大型商业有限元分析软件MSC.Patran/Nastran建立船舶满载航行和开体15°两种工况下的全船结构有限元模型,借助CCS基于三维线性频域势流理论开发的水动力计算软件WALCS对船舶各工况下的波浪载荷进行直接计算,将波浪载荷计算结果导入到全船结构有限元模型中,得出甲板铰链载荷,分析不同浪向角的波浪载荷对开体状态下甲板铰链的影响,估算甲板铰链的疲劳寿命。
1 甲板铰链载荷计算的常规方法开体泥驳所受主要载荷有舷外水压力、船体自重(包含油、水等重量)和泥沙重力三大类,舷外水压力包含海水静压力和海水动压力。我国船级社《国内航行海船建造规范》(2022)(以下简称“《规范》”)中,将海水静压力、船体自重和泥沙重力所引起的甲板铰链载荷称为静载荷,由海水动压力引起的甲板铰链称载荷为动载荷。
利用《规范》中对甲板铰链静载荷的计算公式,得到本船甲板铰链的水平静力Fsh=937.08 kN。动载荷的计算目前尚无统一的公式,事实上,受波浪、浮态等因素的影响,动载荷的大小很难被准确的计算出来。在开体泥驳的设计实践中,常用的动载荷计算有3种方法:1)经验公式法,通过对大量数据的统计和回归分析后给出;2)经验系数法,文献[4]认为,在满载吃水状态下,在离岸15 n mile以内的区域,动力取静力的60%左右,超过15 n mile的区域取静力的70% 左右,同时根据实际情况,考虑是否增加一定比例的海况储备;3)母型船换算法,与船舶耐波性实验的相关理论相似,可近似认为,当母型船与设计船的傅汝德数和斯图罗哈数相等时,动载荷与排水量成正比。3种动载荷计算方法结果比对如表1所示。在求得动力后,可计算出甲板铰链所受到的合力,并以此校核轴销、中心眼板、两侧眼板以及各眼板与甲板连接处的剖面等处的取值是否满足相应规范要求。
|
|
表 1 3种动载荷计算方法结果比对 Tab.1 Comparison of the results of the three dynamic load calculation methods |
可以看出,基于甲板铰链的载荷计算进行设计存在以下问题:1)3种动载荷计算方法所求得的数据相差较大,取值方法存在较大的主观性;2)3种方法均未对海况因素进行量化;3)设计过程未按料力学中由强度理论建立的强度条件
利用MSC.Patran软件,建立本船满载航行(LC01工况)和开体15°(LC02工况)下的主船体有限元结构模型,如图1所示,各工况主要参数见表2。左、右半体的甲板铰链利用MPC-RJOINT进行约束[6]。主船体与甲板铰链连接处网格进行细化,甲板铰链采用精细网格,网格大小不大于50 mm×50 mm。
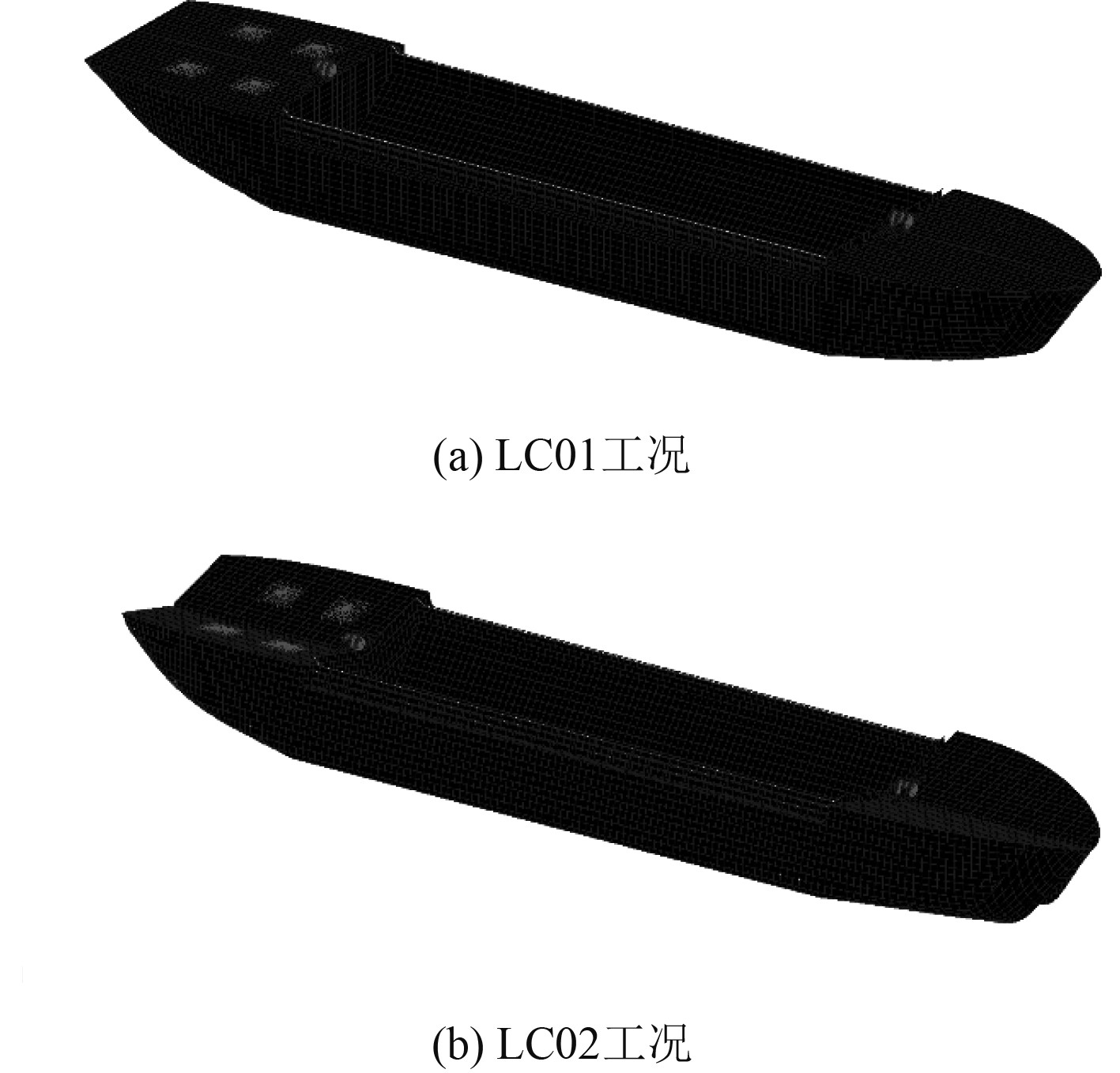
|
图 1 开体泥驳主船体部分有限元模型 Fig. 1 FEM of main hull of split hopper barge |
|
|
表 2 计算工况 Tab.2 Calculated working conditions |
将MSC.Patran/Nastran中建立的船体外壳模型导入到WALCS中,从稳性计算书中获得船体质量分布,软件自动调整浮态后生成湿表面模型,进而计算波浪载荷。
2.2.1 频率响应函数RAO的计算设计波的选取应以对所考察结构起决定性作用的波浪载荷分量作为依据,为简便分析,选取最大垂向波浪弯矩作为本船的主要载荷控制参量,根据《规范》中有关规定,波浪频率范围取0.2~3 rad/s,步长取0.1 rad/s,浪向角取 0º(顶浪)、30º、60º、90º(横浪)、120º、150º、180º(随浪),计算航速取0。设置15个载荷响应的计算剖面,其中剖面8为船中剖面。计算得到15个计算剖面中最大垂向波浪弯矩幅值所在剖面的波浪载荷响应值如图2所示。

|
图 2 第8剖面垂向波浪弯矩频率响应函数 Fig. 2 Frequency response function of vertical wave bending moment in profile 8 |
载荷控制参数达到最大值时对应最危险海况,通过对RAO的计算得知,各工况最大垂向波浪弯矩均出现在第8剖面,LC01工况下RAO在0°浪向下,频率0.8时达到幅值,LC02工况下RAO在180°浪向下,频率0.9时达到幅值。
2.2.2 波浪载荷的长期预报使用双参数波浪谱和中国近海波浪散布图进行长期预报统计,由于我国《规范》中并未规定甲板铰链动载荷长期预报的确定概率,本文借鉴BV船级社规范[2]的有关规定,取10−5,得到主要载荷控制参数的长期预报值,如表3所示。
|
|
表 3 载荷控制参数的长期预报极值 Tab.3 Long-term forecast extremes of load control parameters |
等效设计波包括浪向、波幅、频率以及相位角等4个主要参数,其中频率、浪向和相位角取频率响应函数RAO达到幅值时的频率、浪向和相位角,波幅确定公式为:
| $ {a}_{w}=\frac{{L}_{j}}{{A}_{j}}。$ | (1) |
式中:

|
图 3 波浪压力云图 Fig. 3 Wave pressure cloud |
海水静压力可直接通过下式加载:
| $ {P}_{sw}={\rho }_{w}g\left(d-{'}z\right)。$ | (2) |
式中:
船体自重包含为主船体重量、上层建筑重量、油水备品等重量。主船体重量通过设定重力加速度的方式施加,并调节模型重心与实船重心一致;在尾升高甲板上的甲板室铰链处施加集中载荷模拟上层建筑重量;根据油水装载情况,加载油水对船体结构的压力计算式为:
| $ P=\rho g\left({'}z-a+2.5{f}_{r}\right)。$ | (3) |
式中:
泥舱内泥沙的重力直接作用在泥舱斜板、舱口围板和泥舱端壁上。考虑我国《规范》中的对泥舱相关结构视为深舱结构,故同样通过式(3)加载泥沙压力。LC02工况下不加载泥沙压力。
2.4 边界条件有限元静力分析需要模型为全自由结构,即结构模型中没有机构,且没有刚体运动,否则会导致结构刚度矩阵奇异,求解失败。船舶在波浪中航行时拥有6个方向的自由度,加之结构载荷大多非平衡,对本船进行结构强度直接计算时,可以使用惯性释放法(inertia relief),通过结构的惯性(质量力)来平衡外力,使结构模型的刚度矩阵正定。在提交MSC.Nastran计算时,只需要对某一个节点进行6个自由度的约束(虚支座),假设模型处于一种“静态”的平衡状态,可进行有限元准静态结构分析[7-8]。
2.5 计算结果通过计算,LC01工况下甲板铰链最大相当应力65.5 MPa,LC02工况下甲板铰链最大相当应力109 MPa,均小于材料的屈服极限,相对于甲板铰链材料(Q235D)屈服强度的安全系数超过2。在各工况下,中心铰链眼板的相当应力水平高于两侧铰链眼板,每块铰链眼板的最大应力均出现在与轴承支座的过渡处,铰链眼板自由边的中间部分出现高应力区,如图4所示。
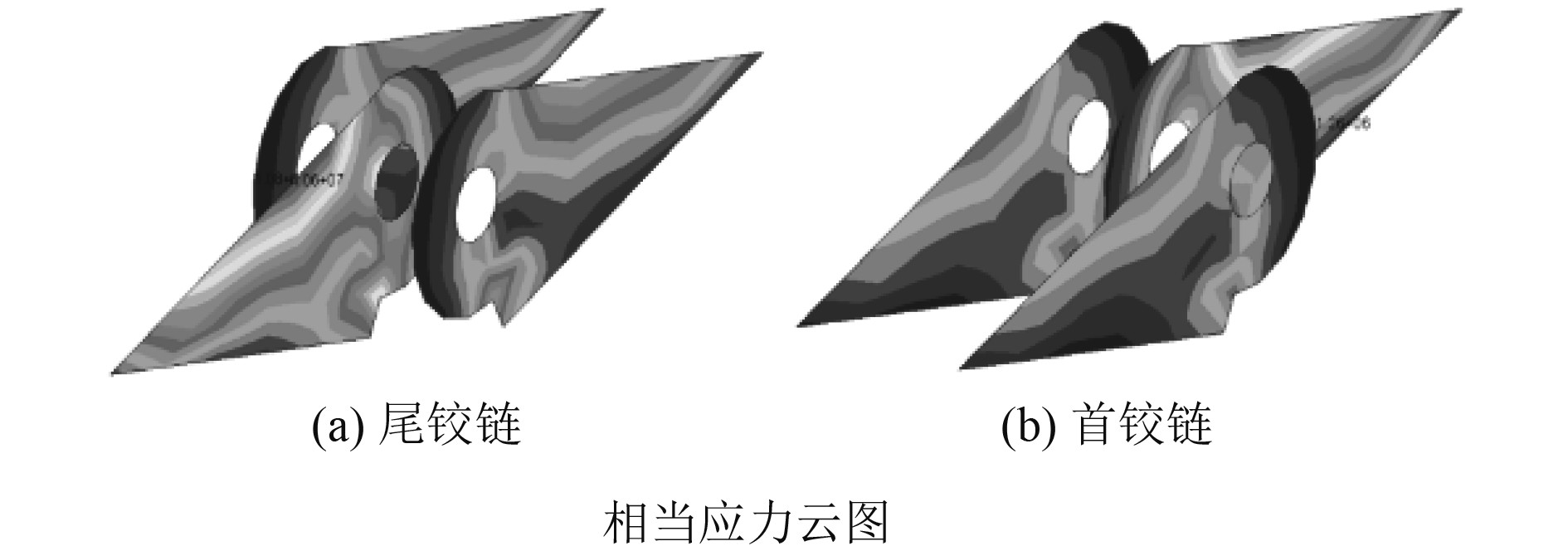
|
图 4 LC02工况首尾铰链相当应力云图 Fig. 4 Head and tail hinge von mises clouds under LC02 |
船舶在开体状态下,泥舱内的泥沙被排空,利用LC02工况下的有限元模型,分别加载相同波幅、频率、浪向角0°(顶浪)、30°、60°、90°(横浪)、120°、150°、180°(随浪)下的波浪载荷,海水静压力和船体自重加载方式同前。在MSC.PATRAN中计算得到各浪向角下甲板铰链的应力水平,如表4所示。
|
|
表 4 不同浪向角下的甲板铰链应力水平 Tab.4 Deck hinge von mises under different wave angles |
由计算结果可知,甲板铰链的整体应力水平,在斜浪状态下最大,随浪状态次之,顶浪状态小于随浪状态,横浪状态最小。在各浪向角下,受开体状态下船体尾倾的影响,尾铰链的应力水平和高于首铰链。眼板与轴承支座的过渡处,以及铰链眼板自由边的中间部分同样出现高应力区。
根据铰链机构的运动原理,横浪状态下的甲板铰链应力水平最小,与实际情况相同。但在横浪状态下进行排泥作业时需要考虑横浪作用对船舶稳性的影响[9]。
4 甲板铰链的疲劳寿命估算常规方法进行甲板铰链设计,无法对铰链的疲劳寿命进行评判。在甲板铰链的设计实践中,一般采用增大甲板铰链尺寸的方法,以此提高甲板铰链的安全系数,这种做法往往导致结构重量偏大。
通过前面的分析可知,甲板铰链开合时的最大工作应力小于材料的屈服应力,甲板铰链在此循环载荷作用下产生应力疲劳(高周疲劳)。甲板铰链连接开体泥驳的2个半体,对船舶安全起到至关重要的作用,对于此类经历大量循环的零部件,应采用无限寿命设计[10]。
由于船体载荷的随机性,很难准确地描绘出甲板铰链全生命周期中的载荷谱。为简便分析,可将甲板铰链在每次开合动作中的载荷视为变幅循环载荷,循环应力的峰谷值Smax、Smin可用上文中 LC01和LC02工况中的最大值和最小值,取Smax=109.8 MPa,Smin=2.92 MPa。利用Goodman公式将上述应力峰谷值转化为循环特性参数R=-1时的等效应力S-1。
| $ \frac{{S}_{a}}{{S}_{-1}}+\frac{{S}_{m}}{{S}_{u}}=1 。$ | (4) |
式中,Su为材料极限强度,取Su=310 MPa。
其中:
| $ {S}_{a}=\frac{1}{2}\left({S}_{\rm max}-{S}_{\rm min}\right),$ | (5) |
| $ {S}_{m}=\frac{1}{2}\left({S}_{\rm max}+{S}_{\rm min}\right) 。$ | (6) |
可得S-1=62.89 MPa,代入S-N曲线方程,选用文献[11]中所提供传统实验方法获得的Q235钢材的S-N曲线lgN=24.088−7.829lgS,可计算得甲板铰链的预估寿命为N=8.11×109,满足无限寿命设计的要求[12]。
5 结 语常规的甲板铰链设计,存在载荷取值主观性大、应力衡准困难、海况影响考虑不准确等问题。基于波浪载荷直接计算的开体泥驳甲板铰链设计方法可以很好地避免上述问题。采用该方法对1 800 m3沿海自航开体泥驳甲板铰链进行计算分析,可得出以下结论:
1)本船甲板铰链构件尺寸取值偏大,有一定的优化空间。
2)斜浪状态下甲板铰链的整体应力水平最大,随浪状态次之,顶浪状态再次之,横浪状态最小。
3)每块铰链眼板的最大应力出现在与轴承支座的过渡处,该处形状应做到平滑过渡,焊缝打磨光滑,防止出现应力集中。
4)铰链眼板自由边的中间部分存在高应力区,这与结构力学中机构形成破坏的一般规律相符,可以考虑在自由边增加面板,提高铰链眼板的承载能力。
5)中心铰链眼板应力水平均高于两侧铰链眼板。可考虑采用偶数眼板型(如“2+2”型)的甲板铰链,通过直接计算法进行设计,获得眼板的应力水平,配合疲劳寿命估算,减少结构重量。
| [1] |
中国船级社. 国内航行海船建造规范(2022) [S]. 北京: 人民交通出版社, 2022.
|
| [2] |
BV. Rules for the Classification of Steel Ships. PT D. Chapter 13. Ships for Dredging Activity [S]. 2022.6.
|
| [3] |
袁万洪. 500 m3开体泥驳总体设计简介[J]. 船海工程, 1996(6): 33-35. |
| [4] |
闫桂荣. 开体式挖泥船液压缸及甲板铰链的设计分析[J]. 船舶工程, 2013, 35(3): 16-18+58. DOI:10.13788/j.cnki.cbgc.2013.03.015 |
| [5] |
杨敬东, 黎扬武, 刘美山, 等. 60m3铰接式对开泥驳铰链系统受力分析及优化设计[J]. 重庆交通大学学报:自然科学版, 2020, 39(12): 130-134. |
| [6] |
冯立静, 张国友, 等. 基于Patran/Nastran的铰链模拟分析[J]. 机械设计与制造, 2009(10): 232-234. DOI:10.3969/j.issn.1001-3997.2009.10.092 |
| [7] |
刘健中, 管义锋. 大洋综合资源调查船全船结构强度有限元分析[C]// 船舶与海洋结构学术会议暨中国钢结构协会海洋钢结构分会成立三十周年纪念学术会议, 2015.
|
| [8] |
张少雄, 杨永谦. 船体结构强度直接计算中惯性释放的应用[J]. 中国舰船研究, 2006, 1(1): 58-61. |
| [9] |
盛振邦, 刘应中. 船舶原理[M]. 上海: 上海交通大学出版社, 2004.
|
| [10] |
C. B, 谢联先. 机械零件的承载能力和强度计算[M]. 机械工业出版社, 1984.
|
| [11] |
王晓钢, 郭杏林, 张小鹏. 利用热像法快速获取Q235钢的疲劳极限与S-N曲线[C]// 2010年海峡两岸材料破坏/断裂学术会议暨第十届破坏科学研讨会/第八届全国MTS材料试验学术会议论文集, 2010.
|
| [12] |
陈传尧. 疲劳与断裂[J]. 武汉: 华中科技大学出版社, 2002.
|
 2023, Vol. 45
2023, Vol. 45
