2. 中集海洋工程研究院有限公司,山东 烟台 264670
2. CIMC Offshore Engineering Research Institute, Yantai 264670, China
发射场地选择是火箭发射的一个重要考虑因素。目前,火箭发射的方式主要分为地面发射、海上发射和空中发射,各国最先研究的发射方式是地面发射,因为地面发射与海上发射、空中发射相比更为容易。受成本和技术的影响,目前各国空中发射的研究相对来说较少[1-2]。海上发射公司已经多次成功完成了海上火箭发射,掌握海上火箭发射技术对未来国家的经济发展和国防事业有着极为重要的影响。对于海上发射来说,要保证火箭高效安全的发射,发射船的性能极为重要[3-4]。为了提高船舶的性能,国内外学者进行单学科及多学科优化,主要包括耐波性、阻力和操纵性。Lawrenced[5]研究了不同参数对船舶阻力的影响。结论为最重要的参数是长细比,并且其越大阻力越小。Miao等[6]将NM理论与CFD技术结合,开发了一个水动力优化模型,大大降低了计算成本。Wang等[7]应用NURBS方法对船体曲面进行改造,通过兴波理论计算三体船的阻力,结合梯度下降法提出了一种高效的船体优化方法。刘畅等[8]创建了一个用于发射平台耐波性性能优化的系统,该系统由发射平台、耐波性优化设计、船体型线改造组成,可实现以集装箱船为代表的发射平台耐波性优化。钱建魁[9]将耐波性和阻力结合,以船体型线参数为变量,将船体水动力性能作为优化目标,通过遗传算法搜索遍历,得到一组最优解。王许浩[10]在单体船上增加了一对组合减摇装置,耐波性得到了大幅度提升,并且其阻力没有多大改变。冯佰威[11]把耐波性、阻力等水动力性能指标作为优化目标,以船体型线参数为变量,建立了多学科优化平台。Thiagajan[12]以船宽、船长和水线面面积为变量,分别以滑行艇的耐波性、稳性和操作性为优化目标,利用saea和idea算法求解,但没有给出三者共同优化的结果。Scamardella[13]以浮心纵向位置、棱形系数和方形系数为变量,应用参数化建模,将晕船率作为优化目标。然后,将得到的优化船型与母型船比较,其性能远优于母型船。Vernengo[14]通过全局收敛遗传算法对不同航速下,双体船的耐波性和阻力进行优化,在高速航行时,阻力降低15%,垂荡加速度降低30%。刘波等[15]采用二进制编码的遗传算法进行船体局部优化,并通过3个算例对算法进行验证。周凤杰[16]采用粒子群-遗传算法研究船舶避碰的路径优化,仿真结果表明该算法收敛速度较快。吴贝尼等[17]提出一种基于遗传算法的双向渐进结构理论,以解决传统算法中参数设置不当而无法求得全局最优解的问题。本文建立了火箭竖起时的弯矩模型,并以火箭所受弯矩为优化目标函数,以方形系数、船长和船宽为优化变量进行了全因子试验,应用BP神经网络模型对母型船完成了优化设计。
1 母型船参数根据火箭发射对场地的要求,船长范围为100≤L≤110,船宽范围为30≤B≤35,并且发射船应能够承受火箭发射瞬间对其造成的巨大冲击力,因此发射载体的吨位应在8000 t以上。油船纵向强度大、压载水量大、航行稳定性好,并且甲板面积足够大,能够确保发射过程的安全以及火箭发射配套设施的布置。因此,以油船作为火箭载体的母型船。其参数如表1所示。
|
|
表 1 母型船主要参数 Tab.1 Main parameters of mother ship |
在发射船的整个设计阶段,总布置设计有极为重要的地位。总布置设计工作会对船舶的性能有很大影响。考虑到用于发射火箭的特殊性,应保证船舶的首尾吃水深度一致。根据空船的重量重心,以及发射船在型线、结构布局和设备的布置,对火箭发射船进行重量重心估算,如表2所示。
|
|
表 2 重量重心估算 Tab.2 Weight center of gravity estimation |
发射船受到风和浪的作用会产生六自由度运动,火箭竖起之后,将随发射船的运动而运动,火箭的重心很高,转动惯量大。因此,火箭会产生巨大的弯矩,如果弯矩超过火箭材料所允许的弯矩值,会影响火箭的安全发射。建立火箭力学模型,推导火箭的弯矩函数,为优化目标函数和优化变量的确定奠定了基础。建立三维空间坐标系,Y轴沿船长方向,X轴向右,Z轴指向火箭方向[18],如图1所示。火箭基本参数见表3。

|
图 1 火箭模型图 Fig. 1 Rocket model |
|
|
表 3 火箭基本参数 Tab.3 Parameters of rocket |
对火箭承受弯矩影响最大的是发射船纵摇幅值、横摇幅值和垂荡加速度,忽略纵荡和横荡对火箭弯矩的影响,考虑到保证火箭竖起时的安全,火箭竖起时,应该调节发射船使其处于迎浪或者背浪状态。可将火箭固定于发射船的情形视为一端固定于刚性固定端、一端自由的非均匀弹性悬臂结构,以此来计算火箭的运动和受力情况。
| $ S = {{\theta z\sin\lambda t}} ,$ | (1) |
| $ a = \ddot S = {{\theta z}}{{\lambda}^{\text{2}}}\sin{\lambda{t}}, $ | (2) |
| $ f(x,t) = m(z)a = m(z)\ddot S = m(z){{\theta z}}{{\lambda}^{\text{2}}}\sin {{\lambda t}} 。$ | (3) |
式中:
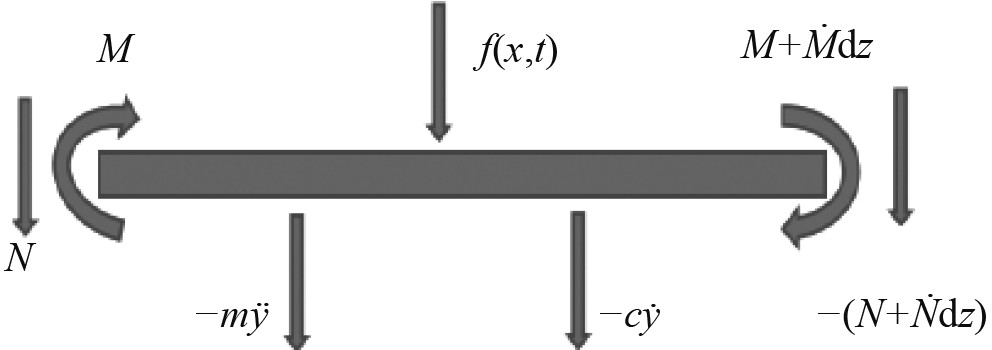
|
图 2 火箭微元受力分析图 Fig. 2 Force analysis diagram of micro element of rocket |
由力的平衡方程
| $ N + \dot Ndz - N + m\ddot y{\rm{d}}z - F{\rm{d}}z + c\dot y = 0 ,$ | (4) |
即
| $ \dot N{\rm{d}}z + m\ddot y{\rm{d}}z - F{\rm{d}}z + c\dot y = 0 。$ | (5) |
考虑火箭材料的非弹性阻尼,应力应变关系可表示为:
| $ \varepsilon = {{y}}\cdot \ddot{y} ,$ | (6) |
| $ {\sigma} = {{E }\varepsilon } + {{{c}}_{{s}}}{\dot \varepsilon } 。$ | (7) |
通过截面应力积分得到弯矩:
| $ M = \int\limits_A \sigma y{\rm{d}}A ,$ | (8) |
对火箭全长进行积分得到总弯矩:
| $ \begin{split} {{M}}{{{y}}_{\theta}} = {{\lambda}^{\text{2}}}{\theta\text{sin}\lambda t}\int_{\text{0}}^{{L}} {m(z)} \cdot {z^2}{\rm{d}}z + \frac{{\eta}}{{{{{m}}_{\eta}}}} \cdot \\ \int_0^L {f(z) \cdot m(z){\rm{d}}z\int_0^L {f(z)} } \cdot {z^2} \cdot m(z){\rm{d}}z,\end{split} $ | (9) |
| $ M{y_L} = (g + \ddot z)\sin {\alpha}\int_{\text{0}}^{{L}} {{\text{m(z)}} \cdot {{{z}}^{\text{2}}}} {\rm{d}}z ,$ | (10) |
| $ M = M{y_{\text{θ }}} + M{y_L},$ | (11) |
| $ \sin {\alpha} = \frac{{{{\theta}_{}}\int_0^L {f(z) \cdot z \cdot m(z){\rm{d}}z} }}{{{L}}} \cdot \frac{{\eta}}{{{{{m}}_{\eta}}}},$ | (12) |
| $ {\eta} = \frac{{{{{{(}}\frac{{\lambda}}{{{p}}}{\text{)}}}^{\text{2}}}}}{{\sqrt {{{{\text{(1 - }}\frac{{{{\lambda}^{\text{2}}}}}{{{{{p}}^{\text{2}}}}}{\text{)}}}^{\text{2}}} + 4{\varphi }\frac{{\lambda}}{{{p}}}{{\text{)}}^{\text{2}}}} }},$ | (13) |
| $ {m_{\eta}} = \int_0^L {{f^2}(z)} \cdot m(z){\rm{d}}z。$ | (14) |
根据文献[19],长征六号火箭参数积分得到的总弯矩函数表达式为:
| $ M = 2278322.838 \cdot {\theta_{}} + 103495.6558 \cdot {\theta_{}} \cdot \ddot z 。$ | (15) |
式中:
由优化目标函数可知,目标函数由纵摇幅值和垂荡加速度决定,取对发射船的纵摇幅值和垂荡加速度影响大的船长、船宽和方形系数为优化变量,同时保持型深和排水量等参数一致。根据火箭发射条件的要求,船长选取104 m、106 m、108 m、110 m,船宽选取30 m、31 m、32 m、33 m,方形系数选取0.6、0.64、0.68、0.72、0.76、0.8进行全因子试验,母型船及96个样本点参数如表4所示。
|
|
表 4 母型船和部分样本点参数 Tab.4 Parameters of mother ship and some sample points |
使用Maxsurf计算母型船及样本点的纵摇幅值和垂荡加速度,计算时选取JONSWAP谱,有义波高取为4 m,跨零周期为8 s,浪向角为0°,将纵摇幅值和垂荡加速度代入火箭弯矩公式,计算结果如表5所示。
|
|
表 5 运动响应和弯矩计算结果 Tab.5 Calculation results of motion response and bending moment |
通过对96个样本点计算可知,最小弯矩为90123.79 N·m,相比母型船109820.01 N·m减小了17.9%,该样本点的船长为110 m,船宽30 m,方形系数为0.8。在该样本点附近,等距划分船长109~110 m、船宽30~31 m、方形系数0.755~0.8 m各10份,得到1000个样本点,通过现代优化算法对1000个样本进行最小弯矩的搜索预测。目前常用到的现代搜索优化模型包括遗传算法、支持向量机和神经网络模型,遗传算法在搜索过程中有预测效率低和局部搜索能力差的缺点,支持向量机在处理小规模数据时效果比较好,因为其泛化能力相比其他算法优良,但当数据规模较大时效果则不佳。因此,选取神经网络模型作为该问题的优化算法。
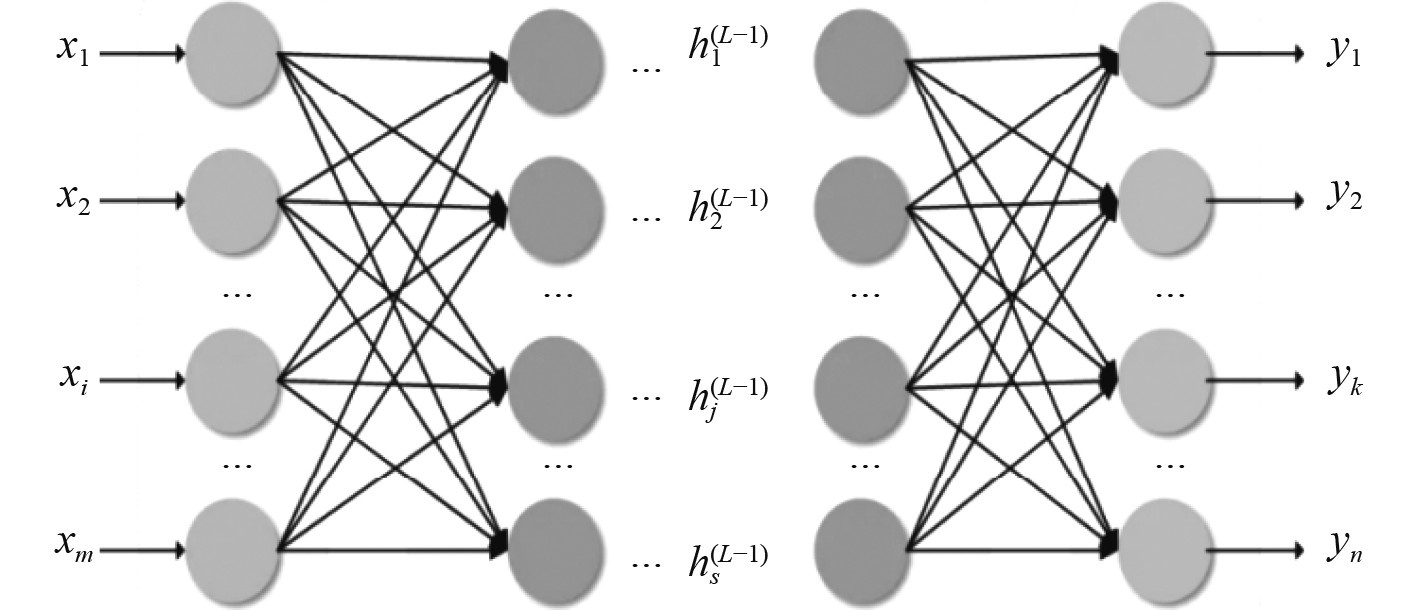
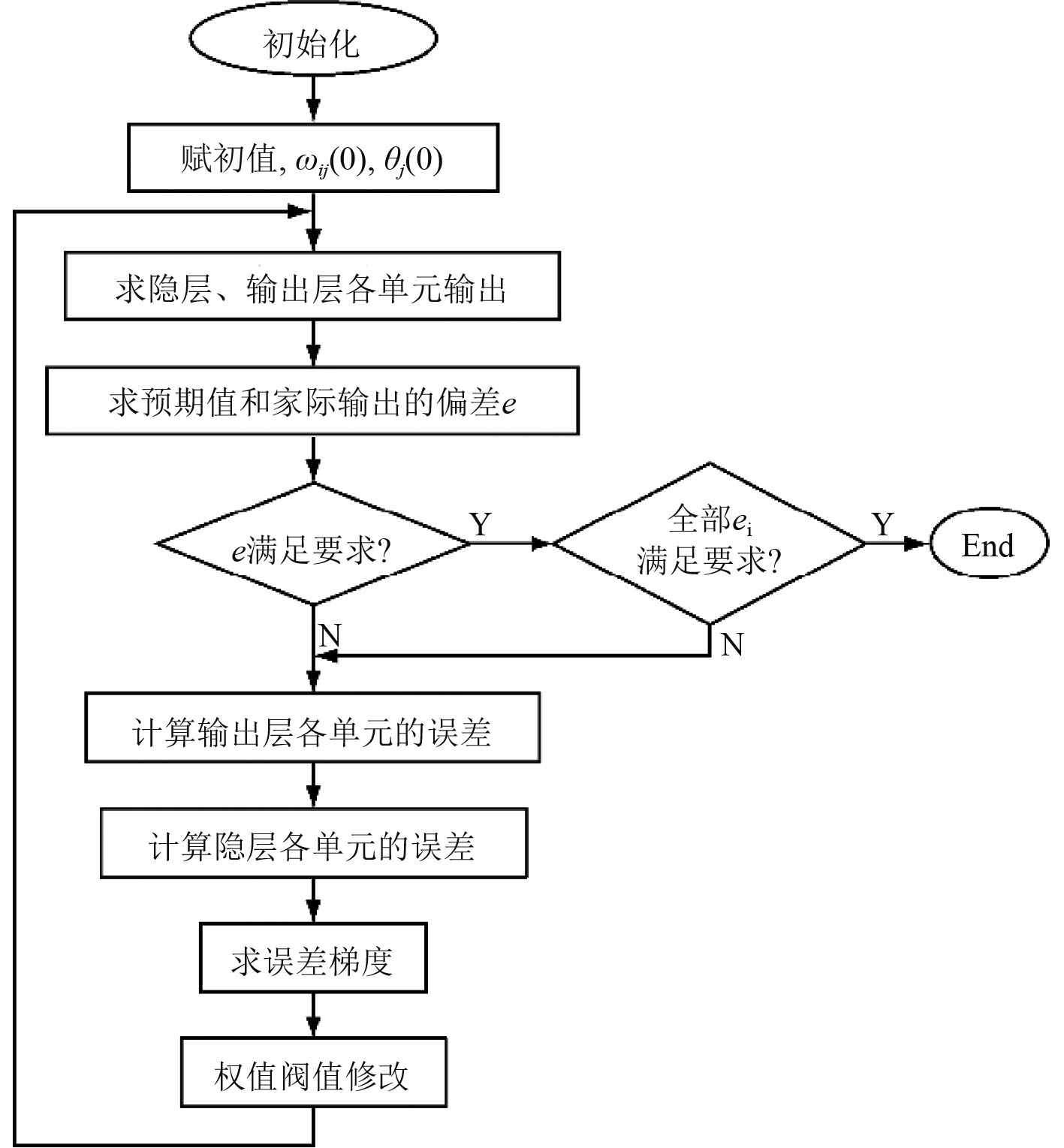
神经网络模型也被称为连接机模型,具有自组织、分布式处理、自学习等一系列优点,被广泛的应用在计算机视觉、图像识别等领域。BP神经网络是目前应用最多的一种神经网络形式,其原理如图3所示。它具备强大的处理非线性映射能力、自适应、自学习和容错能力等,BP神经网络算法流程图如图4所示。因此,选用BP神经网络模型依据96个样本点的计算结果,搜索预测1000个样本点,见表6。
|
图 3 BP神经网络原理 Fig. 3 Schematic diagram of BP neural network |
|
图 4 BP神经网络算法流程图 Fig. 4 Flow chart of BP neural network algorithm |
|
|
表 6 部分样本点参数 Tab.6 Parameters of some sample points |
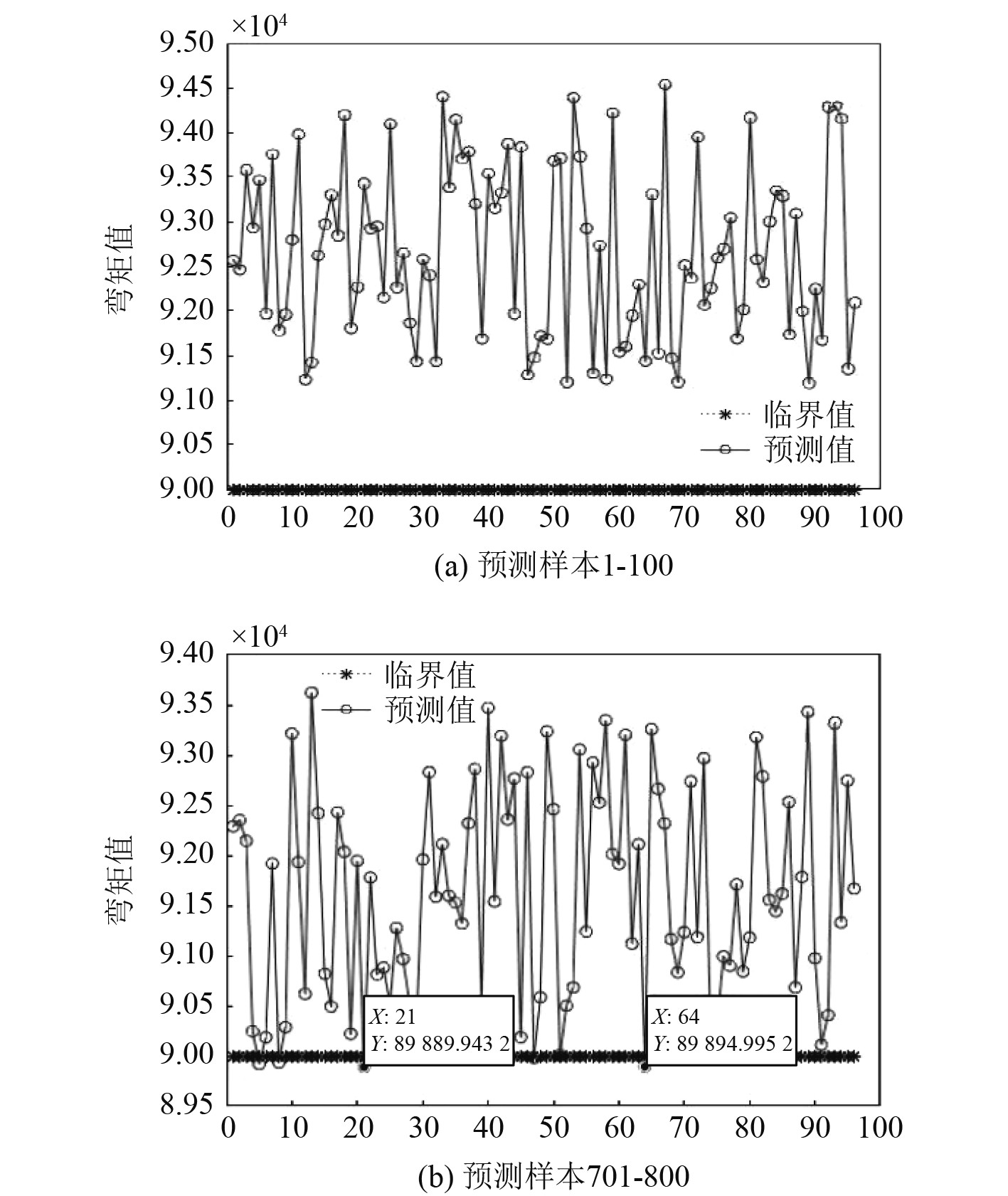
因数据量较大,将上述1000个样本点分10次通过BP神经网络进行预测,结果如图5所示。然后,筛选出预测结果中的部分优异样本,通过Maxsurf进行再计算。
|
图 5 BP神经网络部分搜索预测结果 Fig. 5 Partial search and prediction results of BP neural network |
由表7可知,BP神经网络预测结果与实际计算结果的平均误差不到1%,验证了模型的准确性。804号样本点弯矩值最小,为88500.61 N·m,船长为109.9 m,船宽30.1 m,方形系数0.77。相比母型109820.01 N·m,弯矩减少了19.41%。因此,火箭所受弯矩通过BP神经网络模型得到了进一步优化,BP神经网络能够很好地预测不同方形系数、船长和船宽下的火箭弯矩。
|
|
表 7 结果对比 Tab.7 Comparison of results |
本文对所选取的母型船按火箭发射要求进行总布置设计。以方形系数、船长和船宽为优化变量进行了全因子试验,通过Maxsurf计算母型船和96个样本点的六自由度运动,再计算弯矩得到最优样本点。采用BP神经网络模型,结合仿真计算结果,在方形系数、船长和船宽3个输入参数下,训练了火箭弯矩的BP神经网络预测模型,并通过该预测模型对扩大的样本群搜索遍历得到最优解。最后,将部分样本通过Maxsurf再计算,并与BP神经网络预测结果比较,得出如下结论:
1)最后优化得到的船型弯矩比母型船减少了19.41%,验证了该模型在火箭发射船设计优化方面的适用性。
2)BP神经网络预测值与实际计算结果的误差不到1%,为海上火箭发射是否存在风险提供了一种预知方法。
3)从优化结果来看,为了提高海上火箭发射的安全性,采用较大的长宽比和方形系数。
| [1] |
徐菁. 1996-2005年全球运载火箭发射概况[J]. 国际太空, 2006: 1−3
|
| [2] |
张健壮. 2007世界航天运载业分析[J]. 中国航天, 2008: 22−27
|
| [3] |
范永辉, 许焕武. 2009年各国航天发射回顾[J]. 中国航天, 2010: 33−37
|
| [4] |
徐映霞. 2014世界航天器发射统计[J]. 国际太空, 2015: 5−18
|
| [5] |
LAWRENCE J. Optimization of marine vessels on the basis of tests on model series[J]. Journal of Marine Science and Technology, 2020: 887–900.
|
| [6] |
MIAO Aiqin. WAN Decheng. Hull form optimization based on an NM+CFD integrated method for KCSm[J]. International Journal of Computational Method, 2020, 17(10): 2050008.
|
| [7] |
WANG S M. DUAN W Y. Study on fast interference wave resistance optimization method for trimaran outrigger layout. Ocean EngineeringVolume, 2021(232): 109104.
|
| [8] |
刘畅, 朱仁庆, 杨松林. 船舶耐波性模糊优化方法研究[J]. 华东船舶工业学院学报, 2002, 16(2): 12−17
|
| [9] |
钱建魁. 基于水动力性能的船型多学科优化设计[D]. 武汉: 武汉理工大学, 2011.
|
| [10] |
王许洁. 高耐波性单体复合船型构型及水动力性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [11] |
冯佰威. 基于多学科设计优化的船舶水动力综合优化研宄[D]. 武汉: 武汉理工大学: 2011
|
| [12] |
THIAGAJAN KP. Infulence of Blige keel Width on roll Damping of FPSO[J]. Journal of offshore Mechanics & Arctic Engineering, 2010: 397-408
|
| [13] |
SCAMARDELLA P. Experimental investigation of viscous ROll damping on DTMB model 5671 hull form[C]//ASME 2007, International Conference on Offshore Mechanics and Arctic Engeering: 2007: 221-570.
|
| [14] |
VERNENGO. Resistance and seakeeping optimization of a fast multihull passenger ferry[J]. International Journal of Offshore and Polar Engineering, 2015(1): 26-34. |
| [15] |
刘波, 林焰, 吕镇旺, 等. 基于量子行为遗传算法的船体局部结构优化[J]. 船舶力学, 2017, 21(4): 484−492.
|
| [16] |
周凤杰. 船舶避碰的粒子群-遗传算法混合优化研究[J]. 船舶力学, 2021, 25(7): 909−916.
|
| [17] |
吴贝尼, 夏丽娟. 基于遗传算法的双向渐进结构优化方法研究[J]. 船舶力学, 2021, 25(2): 193−210.
|
| [18] |
殷金龙. 海上火箭发射平台的设计与仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [19] |
白乐巍. 基于近似模型的火箭发射船耐波性优化[J]. 船舶工程, 2017.
|
 2023, Vol. 45
2023, Vol. 45
