2. 上海交通大学 海洋工程国家重点实验室,上海 200240
2. State Key Laboratory of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China
水下滑翔机是一种新型的水下潜器。其采用净浮力和姿态角调整来获得推进力,故能源消耗极小,只在需调整净浮力和姿态角时才会消耗少量的能量,而且有效率高、续航力大(可达上千千米)的特点[1]。尽管水下滑翔机的航行速度比较慢,但是其具有制造成本和维护费用低、可重复使用、并可大量投放等特点,满足了长期大范围海洋勘探的需要。
当水下滑翔机具有良好的操纵性时,在直线航行时能保持运动方向,需要转向时能迅速地改变航向,使滑翔机按照预定的航线航行,并且具有适当的停止性能。因此水下滑翔机的操纵性能影响着水下滑翔机的作业使命和航行性能,优良的水下滑翔机外型与合适的操纵面相结合能更好地体现其操纵性能。而在水下滑翔机设计阶段,预知操纵性能的关键一环是得到操纵性水动力系数[2]。
水动力系数的获取方法包括经验公式估算方法、约束模型实验法、自航模型试验方法。其中经验公式估算方法有很大的局限性,尤其是对于复杂的海况和构型,其精度得不到保障;约束模型试验周期长,成本高,船模与实船之间存在尺度效应,实用性受到限制。
随着CFD技术的快速发展,用数值模拟代替真实的模型试验,可大幅缩短试验周期,大大降低试验成本。刘帅等[3]用CFD方法基于UDF的添加动量源项法完成了潜艇旋臂实验的数值模拟,计算结果与实验误差在15%以内。高婷等[4]采用CFD方法模拟了SUBOFF艇体的纯横荡和纯首摇运动,计算结果与实验误差在15%以内。董苗苗等[5]详细地论述了潜体水动力系数的计算,并用PMM计算了某水下航行器的相关水动力系数。吴兴亚等[6]建立了不同振荡模式下的水动力导数求解方法,并对计算结果进行了验证。
为了分析和快速预报水下滑翔机的操纵性能,本文基于CFD方法,对水下滑翔机的操纵水动力导数进行计算。相关研究成果对水下滑翔机操纵性快速预报具有一定的指导意义。
1 水下潜器操纵模型选用固定坐标系

|
图 1 固定坐标系和运动坐标系 Fig. 1 Fixed coordinate system and moving coordinate system |
基于格特勒用于潜艇模拟研究的标准运动方程[7],当动系原点与质心不重合时,可得水下潜器六自由度操纵运动一般方程如下:
| $ \begin{split} & X=m\left[(\dot{u}-v r+w q)-x_{\theta}\left(q^{2}+r^{2}\right)+y_{\theta}(p q-\dot{r})+z_{\theta}(p r+\dot{q})\right] ,\\ & Y=m\left[(\dot{v}-v p+u r)-y_{G}\left(r^{2}+p^{2}\right)+z_{\theta}(q r-\dot{p})+x_{G}\left(g_{p}+\ddot{r}\right)\right] ,\\ & Z=m\left[(\dot{w}-u q+v p) - z_{G}\left(p^{2}+q^{2}\right) + x_{G}(r p-\dot{q})+q_{G}(r q+\dot{p})\right] ,\\ & \left.K=I_{x} \dot{p}+\left(I_{u}-I_{v}\right) q r + m\left[y_{G}(\dot{w}+p v-q u)-z_{G}(\dot{v} + r u - p w\rangle\right)\right] ,\\ & M=I_{y} \dot{q}+\left(I_{x}-I_{z}\right) r p+m\left[z_{G}(\dot{u}+q w-r v)-x_{g}(\dot{w}+p-p)\right],\\ & N=I_{s} \dot{r}+\left(I_{v}-I_{u}\right) p q+m\left[x_{G}(\dot{v}+r u-p w)-y_{G}(\dot{u}+q w-r v)\right] 。\end{split} $ | (1) |
式中:
若已知外力和外力矩,可通过求解操纵运动方程进行操纵性能分析。外力和外力矩主要包括水下潜器所受的流体动力和自身的浮力与重力,其中,流动动力是操纵性研究的基础,常通过泰勒展开方法分解为一系列的水动力导数进行表述。表1为与水平面运动相关的水动力导数,与垂直面运动相关的水动力导数描述与此类似。
|
|
表 1 与水平面运动相关的水动力导数 Tab.1 Hydrodynamic derivatives related to horizontal plane motion |
为了比较精确地确定水动力导数,目前常用的方法是进行约束模型试验。约束模型试验主要采用机械的拘束,强迫模型做规定的运动。试验时,在基准运动上叠加1个或者2个扰动,并定量地改变扰动量,测得作用于模型上的水动力,从而求得操纵水动力导数。当前的约束船模试验方法主要包括斜航试验、回转臂试验和平面运动机构试验(Planar Motion Mechanism,PMM)。本文采用斜航试验测量表1中的位置水动力导数,采用PMM中的纯横荡运动和纯首摇运动测量表1中的旋转和惯性水动力导数。对于与垂直面运动相关的水动力导数,可通过将模型旋转90°,采用相同方法测量。
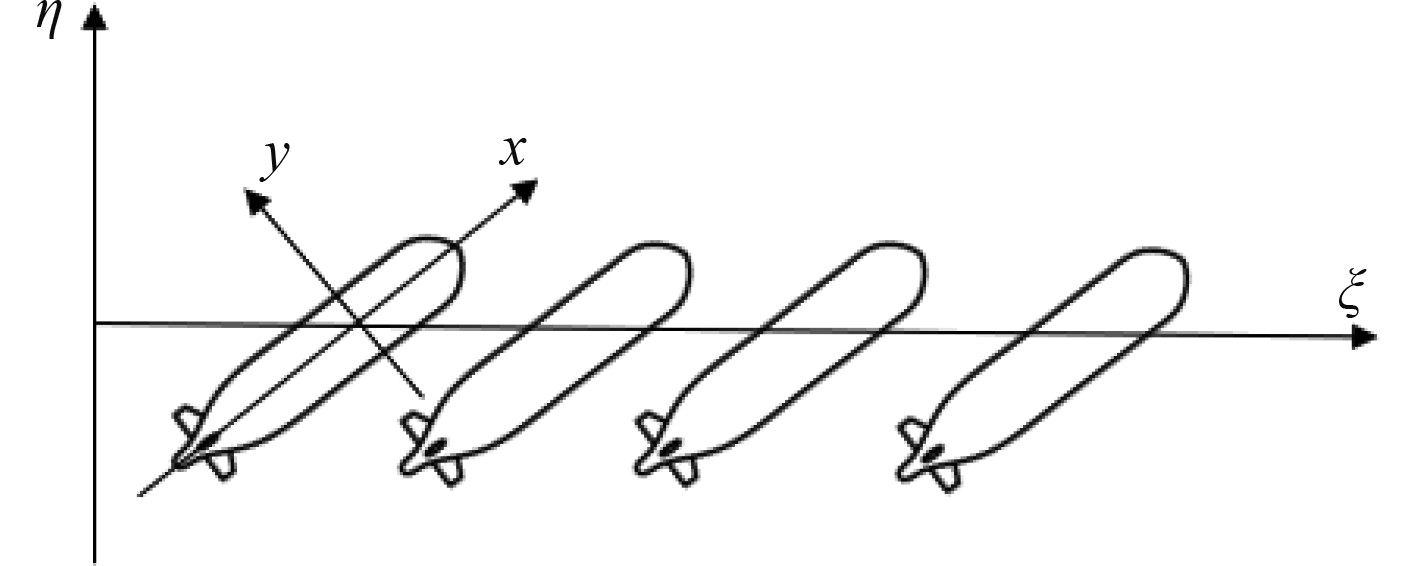
2.1 斜航试验水下潜器作斜航运动如图2所示。斜航运动时,取首摇角速度
|
图 2 水下潜器的斜航运动示意图 Fig. 2 Schematic diagram of the oblique motion of the underwater submersible |
| $ \left\{ \begin{split} & {r}=0 ,\\ & v=-v \sin \beta 。\end{split}\right. $ | (2) |
式中:
若外形左右对称,其水动力方程可表达为:
| $ \left\{\begin{split} {Y}=Y_{\mathrm{v}} v+Y_{\text {wav }} v^{3},\\ N=N_{v} v+N_{v v v} v^{8} 。\end{split} \right.$ | (3) |
采用最小二乘法对不同速度下的水动力和力矩分别进行拟合,可得水动力导数
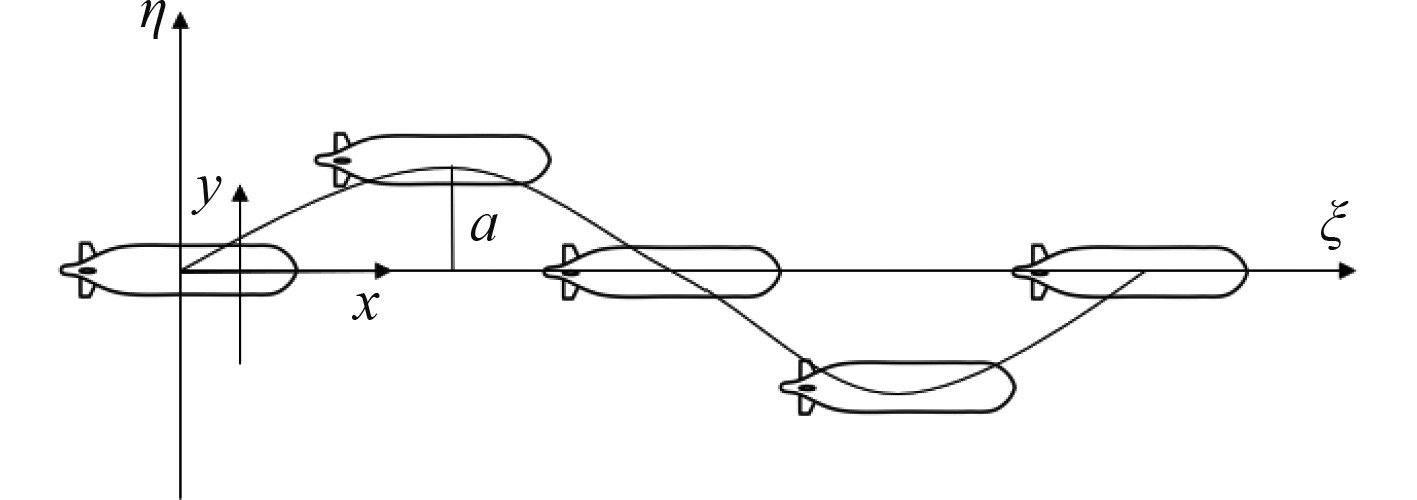
水下潜器的纯横荡运动如图3所示,潜器沿纵向匀速运动同时叠加一个横向低频振荡,运动过程中首向角不发生改变。其运动方程可描述为:
|
图 3 水下潜器的纯横荡运动示意图 Fig. 3 Schematic diagram of pure sway motion of underwater submersible |
| $ \left\{\begin{split} & \psi=r=0,\\ & y=a \sin \omega t,\\ & v=\dot{y}=a \omega \cos \omega t ,\\ & \dot{v}=\ddot{y}=-a \omega^{2} \sin \omega t 。\end{split} \right.$ | (4) |
式中:
水下潜器作纯横荡运动时,考虑其作小振幅振荡,在线性假设下,其在随体坐标系下水动力方程可表示为:
| $ \left\{\begin{split} &Y=Y_{\dot{v}}+Y_{v} v+Y_{0} ,\\ &N=N_{t} \dot{v}+N_{u} v+N_{0} 。\end{split} \right.$ | (5) |
将运动方程公式代入,可得:
| $ \left\{\begin{split}&Y=-a \omega^{2} Y_{i} \sin \omega t+a \omega Y_{v} \cos \omega t+Y_{0},\\ &N=-a \omega^{2} N_{i} \sin \omega t+a \omega N_{v} \cos \omega t+N_{0}。\end{split}\right. $ | (6) |
根据最小二乘法对式(6)中的水动力系数进行辨识,可得水动力导数
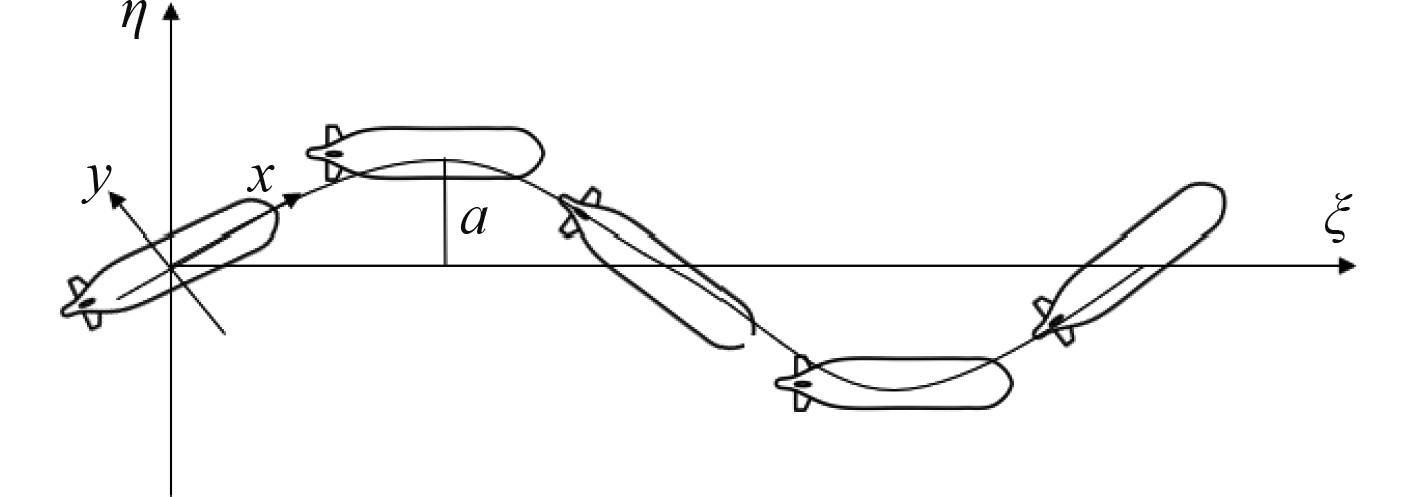
图4为水下潜器做纯首摇运动的示意图。潜器在沿纵向方向上匀速运动的同时叠加一个横向方向上低频振荡和首向角周期性的变动,合速度方向与潜器中纵剖面方向一致,其运动方程可表示为:
|
图 4 水下潜器的纯首摇运动示意图 Fig. 4 Schematic diagram of pure bow motion of underwater submersible |
| $\left\{ \begin{split} & v=\dot{v}=0 ,\\ & \psi=\psi_{0} \cos \omega t, \psi_{0}=\frac{-a \omega}{V},\\ & r=\dot{\psi}=-\psi_{0} \omega \sin \omega t,\\ & \dot{r}=\ddot{\psi}=-\psi_{0} \omega^{2} \cos \omega t 。\end{split}\right. $ | (7) |
水动力方程可表示为:
| $\left\{ \begin{split}& Y=Y_{\dot{r}} \dot{r}+Y_{\mathrm{r}} r+Y_{0},\\& N=N_{r} \dot{r}+N_{\mathrm{r}} r+N_{0} 。\end{split} \right.$ | (8) |
将运动方程公式代入,可得:
| $ \left\{\begin{split} &Y=-\psi_{0} \omega^{2} Y_+ \cos \omega t-\psi_{0} \omega Y_{\mathrm{r}} \sin \omega t+Y_{0} ,\\ &N=-\psi_{0} \omega^{2} N_{i} \cos \omega t-\psi_{0} \omega N_{\mathrm{r}} \sin \omega t+N_{0}。\end{split} \right.$ | (9) |
同样,根据最小二乘法对式(9)中的水动力系数进行辨识,可得水动力导数
在水下潜器流场的统计模拟中,水被认为是一种可压缩的粘性液体,在流动时遵循质量定律和运动定律,其张量形式下的连续性方程和描述湍流统计量的演化的系综平均N-S方程如下:
| $ \begin{split} & \frac{\partial \bar{u}_{i}}{\partial x_{i}}=0 ,\\ & \rho \frac{\partial \bar{u}_{i}}{\partial t}+\rho \bar{u}_{j} \frac{\partial u_{i}}{\partial x_{j}}=-\frac{\partial \bar{p}_{i}}{\partial x_{i}}+\frac{\partial}{\partial x_{j}}\left(\mu \frac{\partial u_{i}}{\partial x_{j}}-\rho \overline{u_{j}^{j} x_{j}^{j}}\right)。\end{split} $ | (10) |
式中:
考虑到自由剪切层对湍流粘度的影响、边界层边缘与自由剪切层的影响和近壁面区和远场的流体运动状态,因此本文采用了
| $ \begin{split} & \frac{\partial}{\partial t}(\rho k)+\frac{\partial}{\partial x_{i}}\left(\rho k u_{i}\right)=\frac{\partial}{\partial x_{j}}\left[\varGamma_{k} \frac{\partial k}{\partial x_{j}}\right]+\widetilde{G_{k}}-\boldsymbol{Y}_{k}+\boldsymbol{S}_{k} ,\\ & \frac{\partial}{\partial t}(\rho \omega)+\frac{\partial}{\partial x_{i}}\left(\rho \omega u_{i}\right)=\frac{\partial}{\partial x_{j}}\left[\varGamma_{\omega} \frac{\partial \omega}{\partial x_{j}}\right]+\widetilde{G_{\omega}}-Y_{\omega}+D_{\omega}+S_{\omega}。\end{split} $ | (11) |
式中:
STAR-CCM+中的DFBI模块是流体与刚体之间耦合的动态流体相互作用,根据六自由度刚体的运动移动整个流体网格。对于纯横荡和纯首摇运动可以采用DFBI中的平面运动机构来计算。
DFBI中的平面运动机构用正弦摆动运动的形式预先指定
| $ r=\left(\begin{array}{c} r_{x} \\ r_{y} \\ r_{x} \end{array}\right)=\left(\begin{array}{c} V_{0} \cdot t \\ y_{0} \cdot \sin (2 {\text{π}} f \cdot t) \\ z \end{array}\right) 。$ | (12) |
其中:
关于横摇角,纯横荡和纯首摇运动均设置
| $ \left\{\begin{split} & \psi=\psi_{0}+\cos (2 {\text{π}} f+t) ,\\ & \psi_{0}=\arctan \left(\frac{y_{0}+2 {\text{π}} f}{V_{0}}\right)。\end{split} \right.$ | (13) |
以SUBOFF模型对CFD数值模拟求解方法进行验证。SUBOFF几何外形如图5所示,主要由回转体壳体和尾端4个十字形舵组成。模型总长4.35611 m,直径0.50801 m,重量为701.7701 kg。

|
图 5 SUBOFF几何模型 Fig. 5 SUBOFF geometric model |
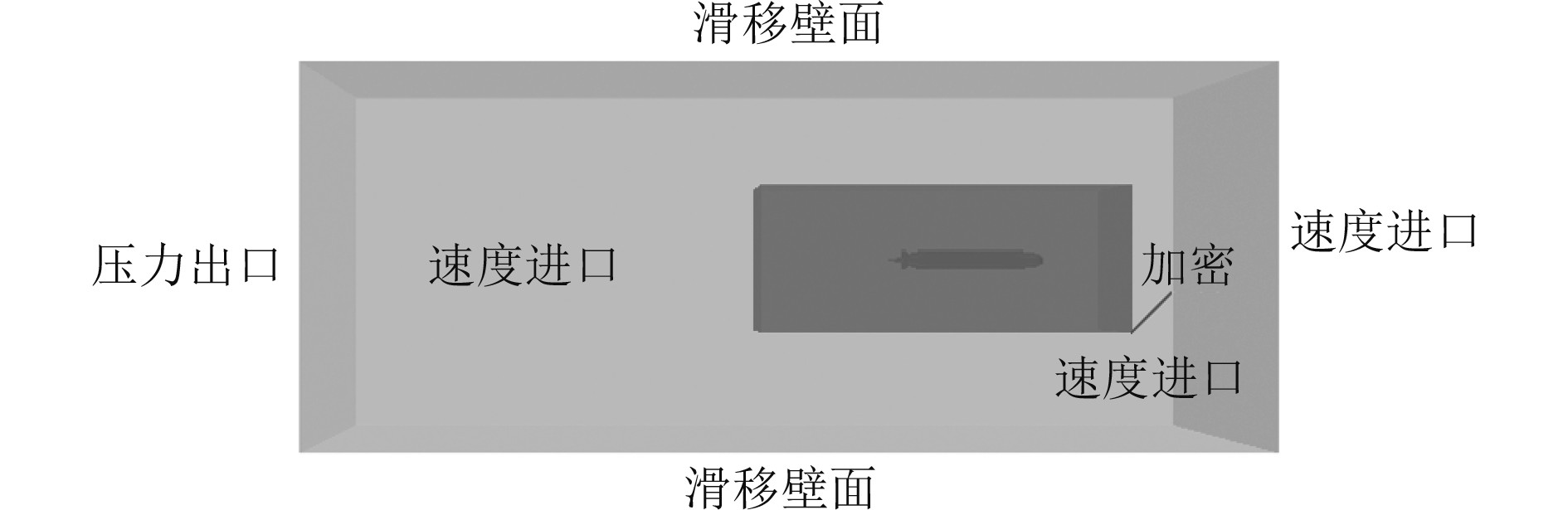
计算域的选取如图6所示。在艇体的周围建立一个长方体计算域,取艇首处为坐标原点,在其后方3L(L为艇长)处设置压力出口,在前方、上下左右方L处设置速度进口。
|
图 6 SUBOFF计算区域 Fig. 6 SUBOFF calculation area |
计算域的网格划分如图7所示。在划分网格时,对网格设置时在近艇区域设置较密的网格然后以一定的膨胀系数外推。

|
图 7 SUBOFF计算区域网格划分 Fig. 7 Meshing of SUBOFF calculation area |
选用隐式不定常和液体,利用分离流方法来处理边界层产生的流动分离现象,湍流模式采用
1)斜航试验
取水下潜器的漂角分别为

|
图 8
侧向力 |
|
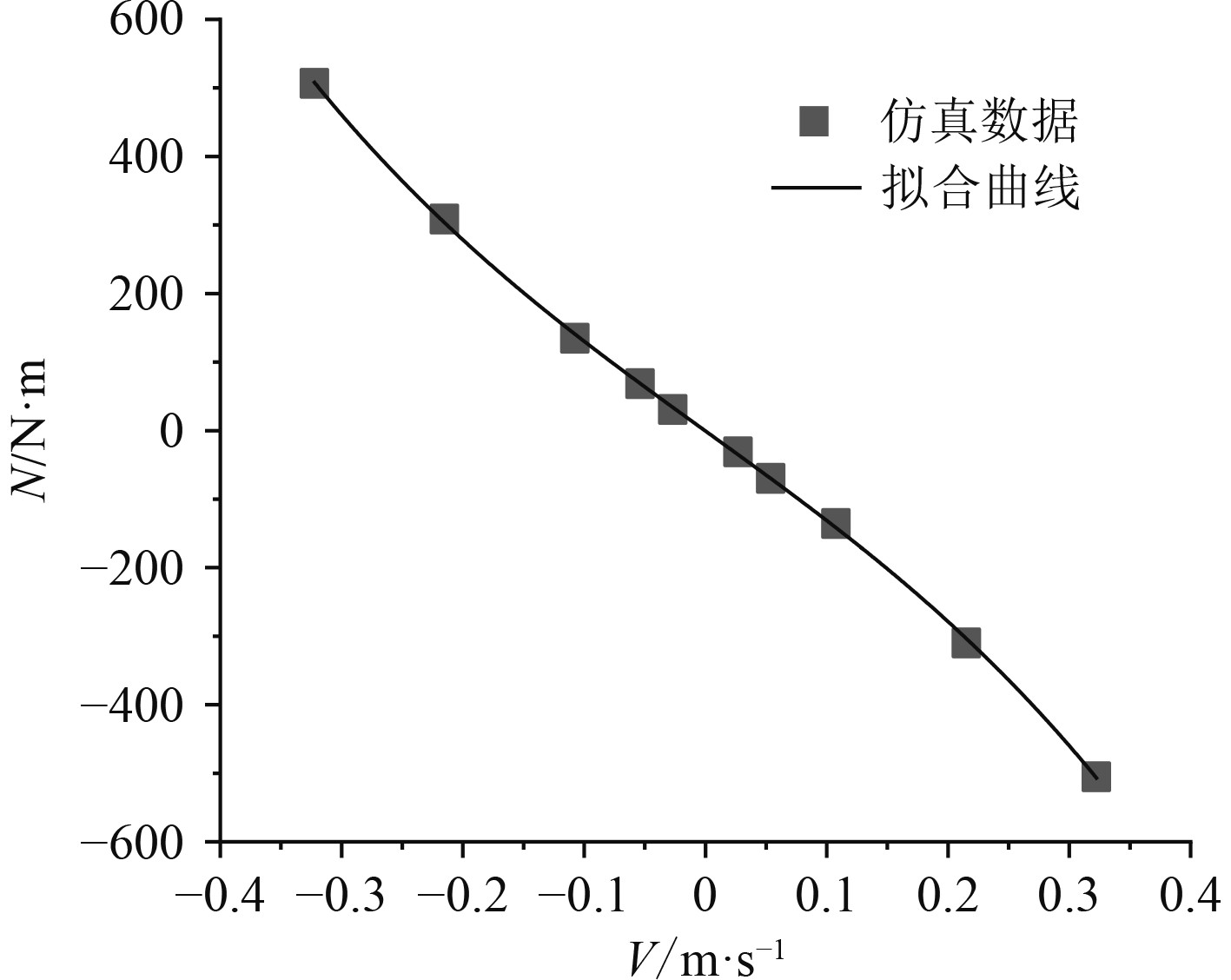
图 9
首摇力矩 |
采用最小二乘法分别对不同速度下的侧向力
|
|
表 2 基于斜航运动的水动力导数计算值与试验值对比 Tab.2 Comparison of calculated and experimental values of hydrodynamic derivatives based on oblique motion |
2)纯横荡运动
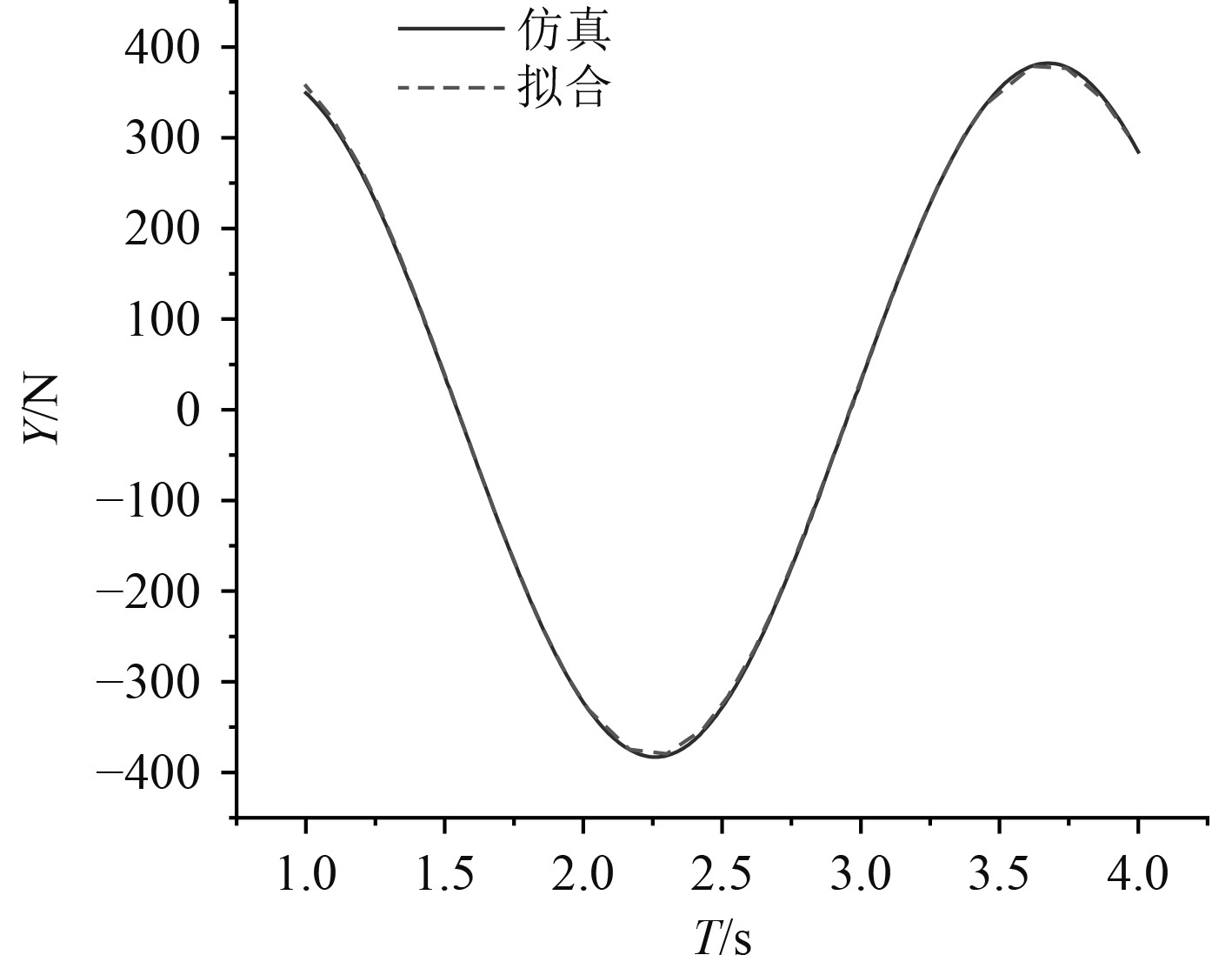
采用STAR-CCM+软件数值模拟SUBOFF模型的小振幅纯横荡运动。对于 DFBI模块的平面运动机构参数设置,设置振荡频率为0.353 3 Hz,振幅为0.1m,分别得到图10所示的侧向力

|
图 10
侧向力 |
|
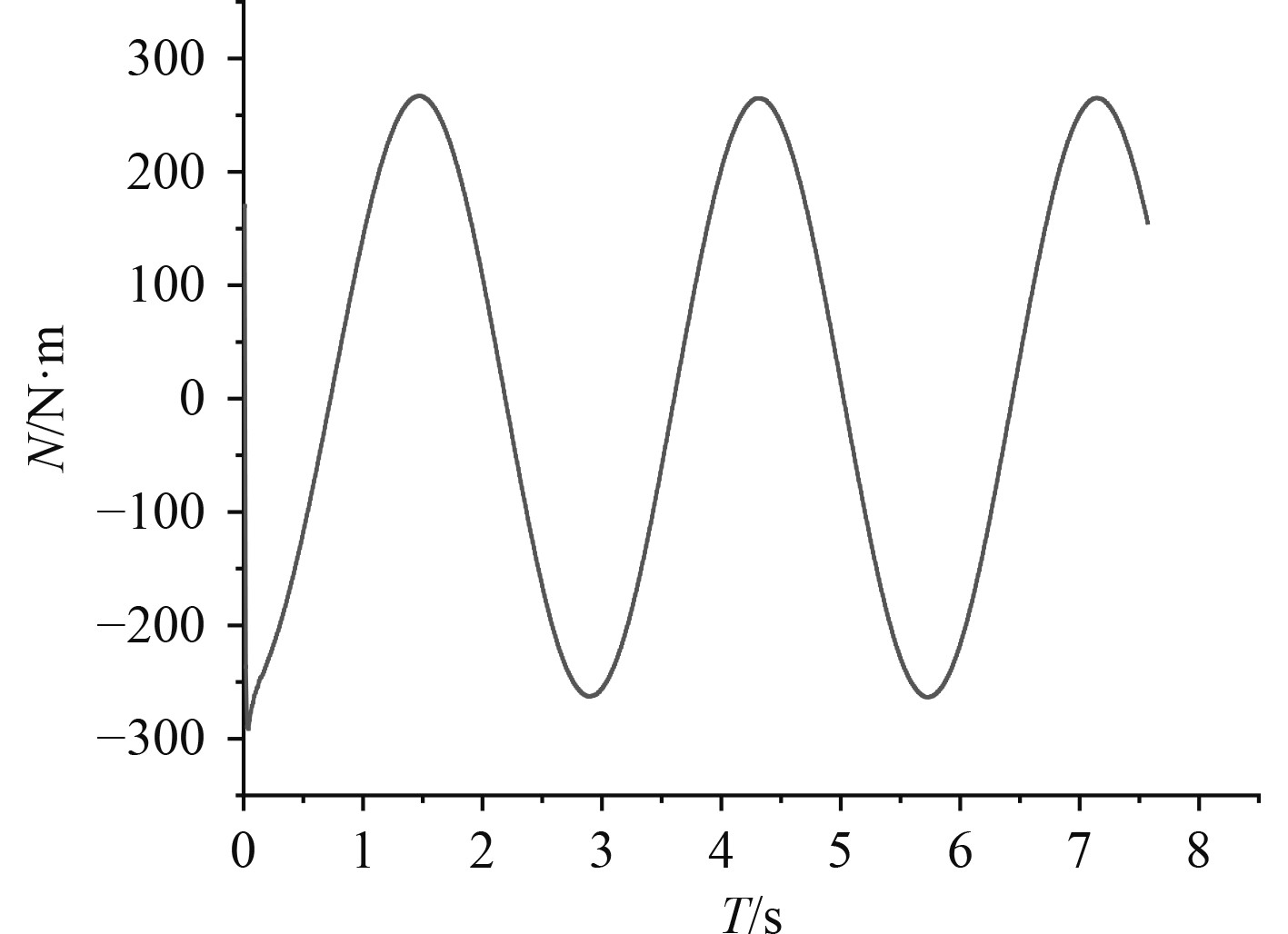
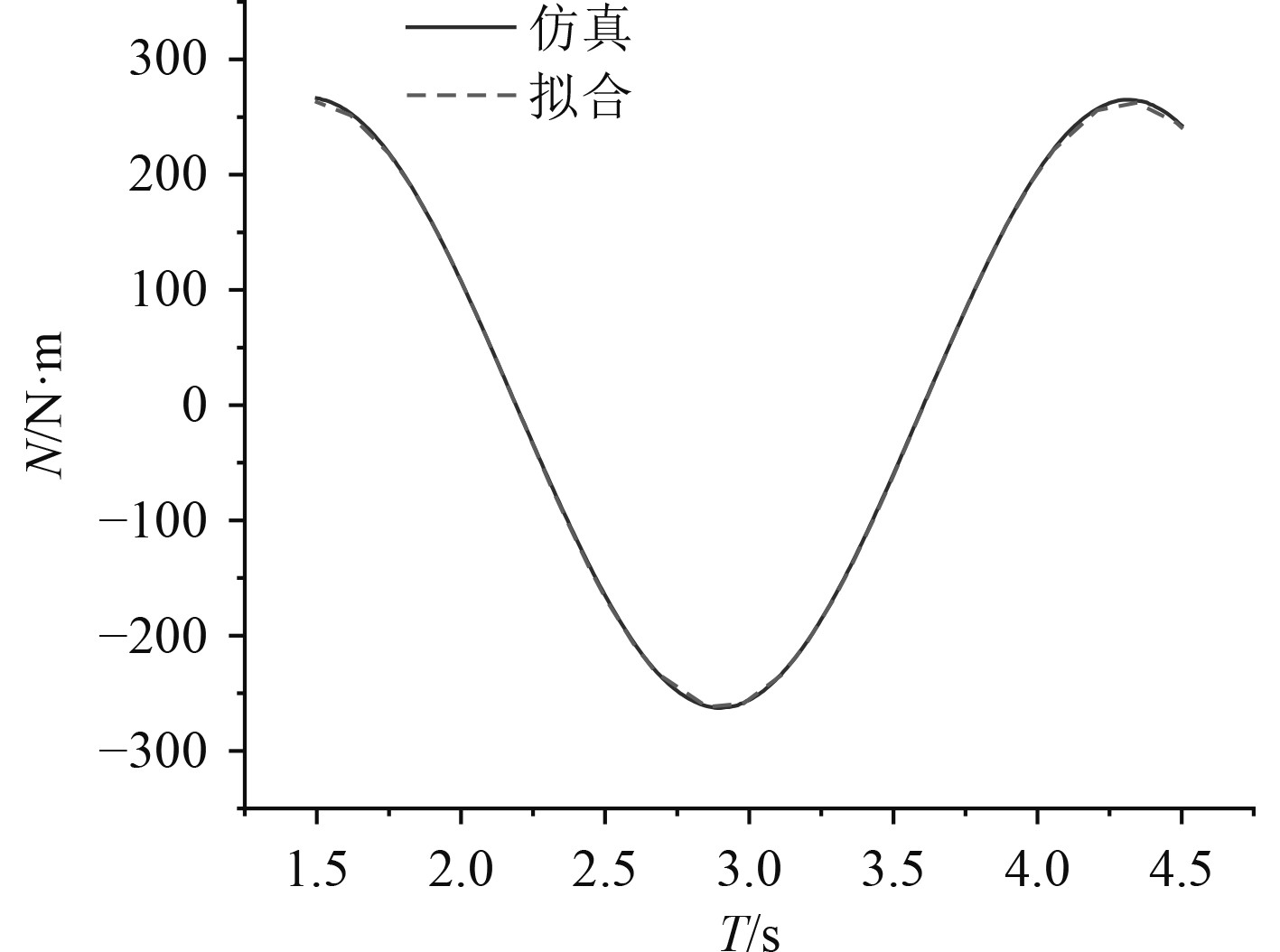
图 11
首摇力矩 |
选取图10中的一个稳定周期,基于式(6),采用最小二乘法对侧向力
|
图 12
水动力导数 |
|
图 13
水动力导数 |
|
|
表 3 基于纯横荡运动的水动力导数计算值与试验值对比 Tab.3 Comparison of calculated and experimental values of hydrodynamic derivatives based on pure sway motion |
3)纯首摇运动
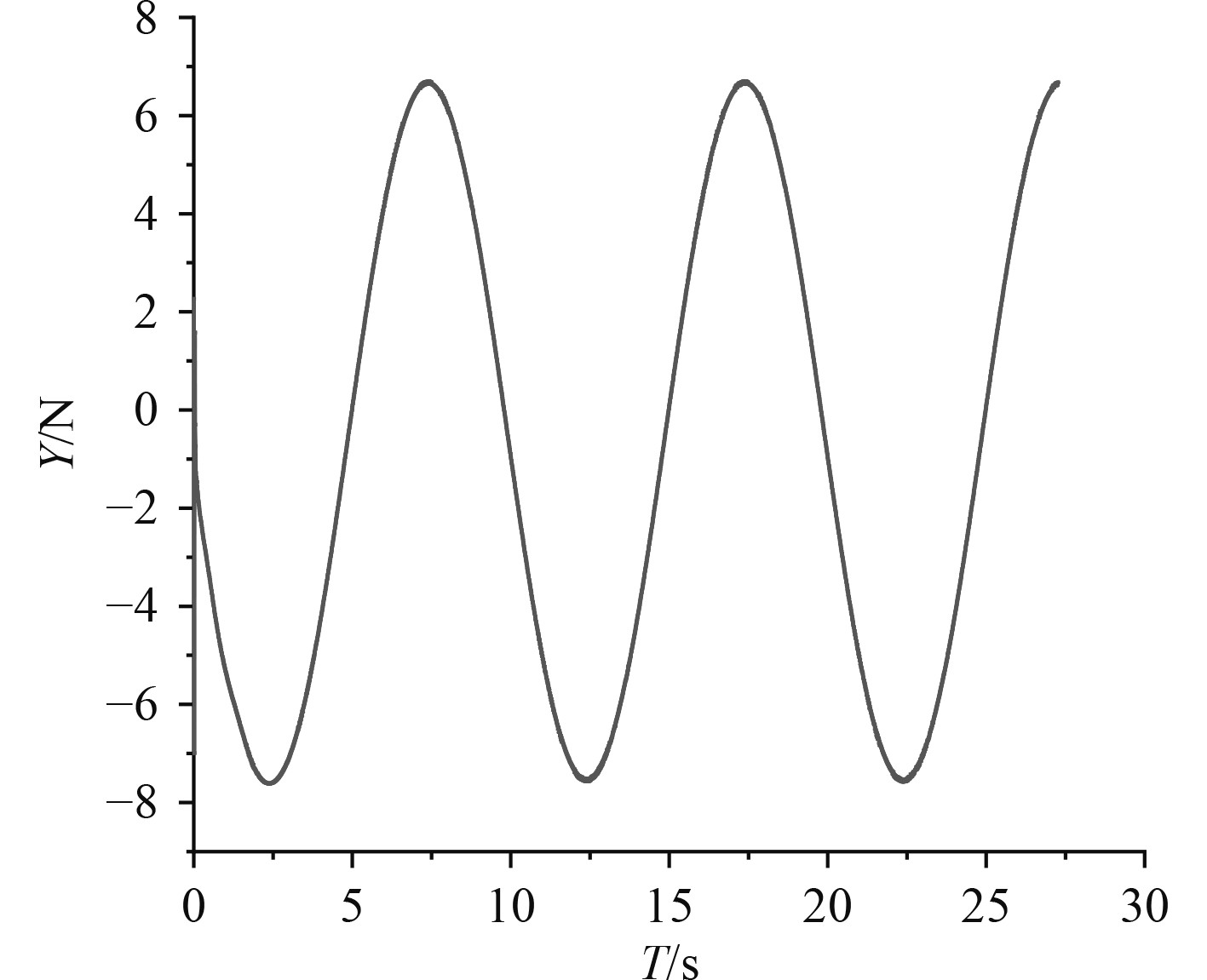
采用STAR-CCM+软件数值模拟SUBOFF模型的纯首摇运动。对于 DFBI模块的平面运动机构参数设置,设置振荡频率为0.1 Hz,振幅为0.1 m,分别得到图14所示的侧向力
|
图 14
侧向力 |
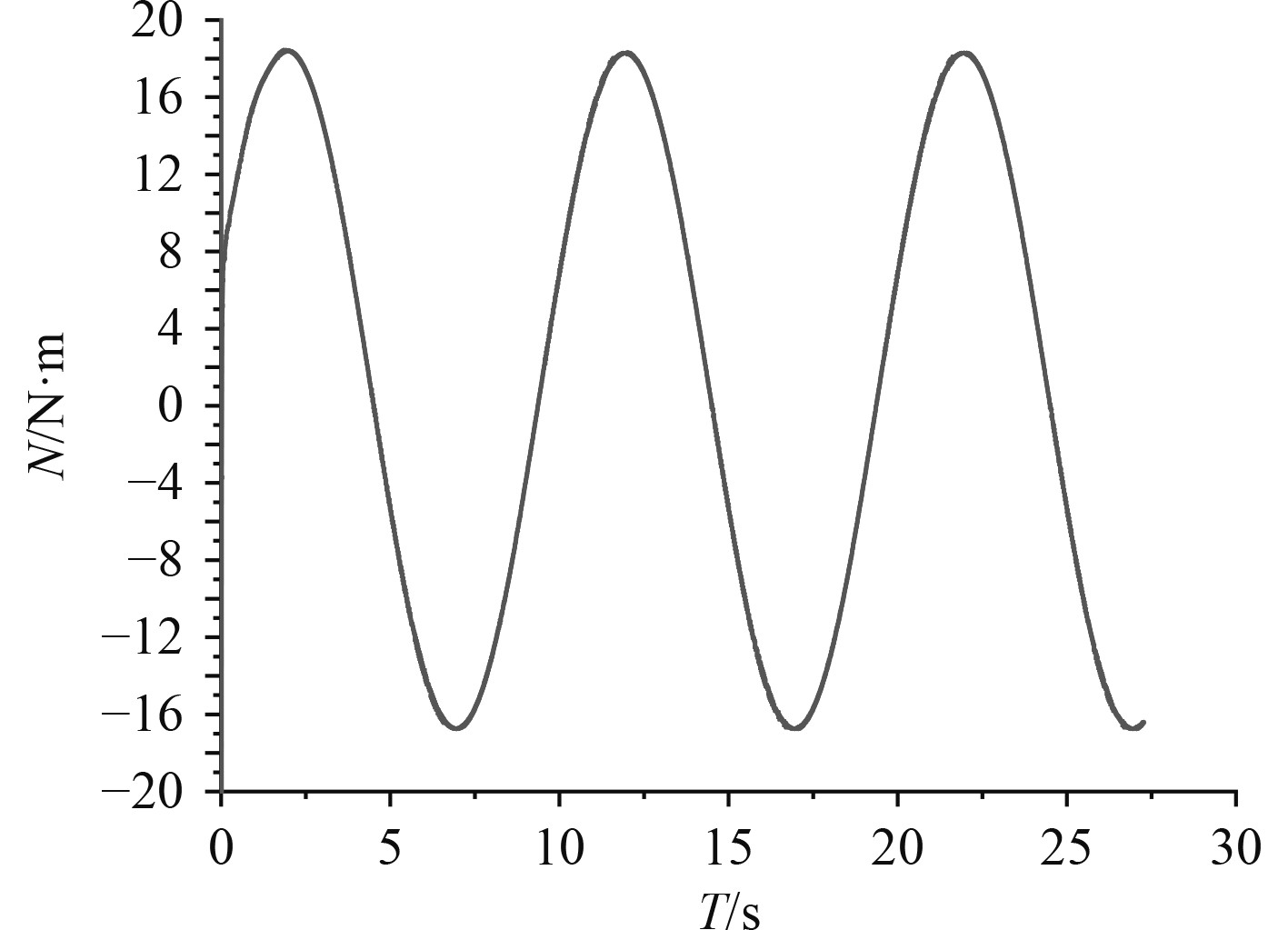
|
图 15
首摇力矩 |
选取图14中的一个稳定周期,基于式(9),采用最小二乘法对侧向力

|
图 16
水动力导数 |
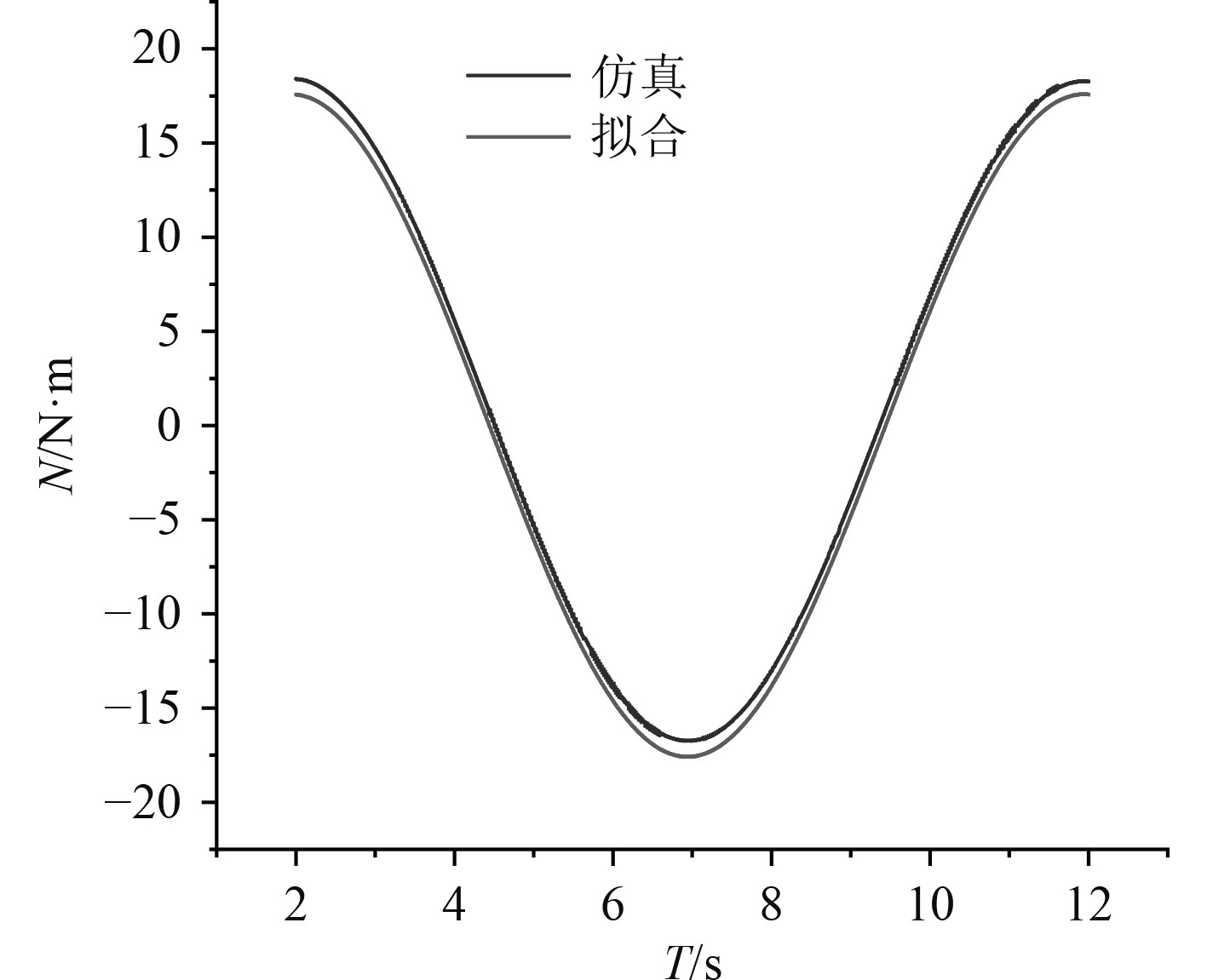
|
图 17
水动力导数 |
|
|
表 4 基于纯首摇运动的水动力导数计算值与试验值对比 Tab.4 Comparison of calculated and experimental values of hydrodynamic derivatives based on pure bow motion |
可以看出:通过斜航试验计算的
本文要计算的水下滑翔机几何外形如图18所示。水下滑翔机的模型长5.65 m,直径1.06 m,重量为1141.412 kg。

|
图 18 水下滑翔机几何模型 Fig. 18 Geometric model of underwater glider |
计算域的选取如图19所示。在艇体的周围建立一个长方体计算域,取艇首处为坐标原点,在其后方2L(L为艇长)处设置压力出口,在前方、上下左右方L处设置速度进口。
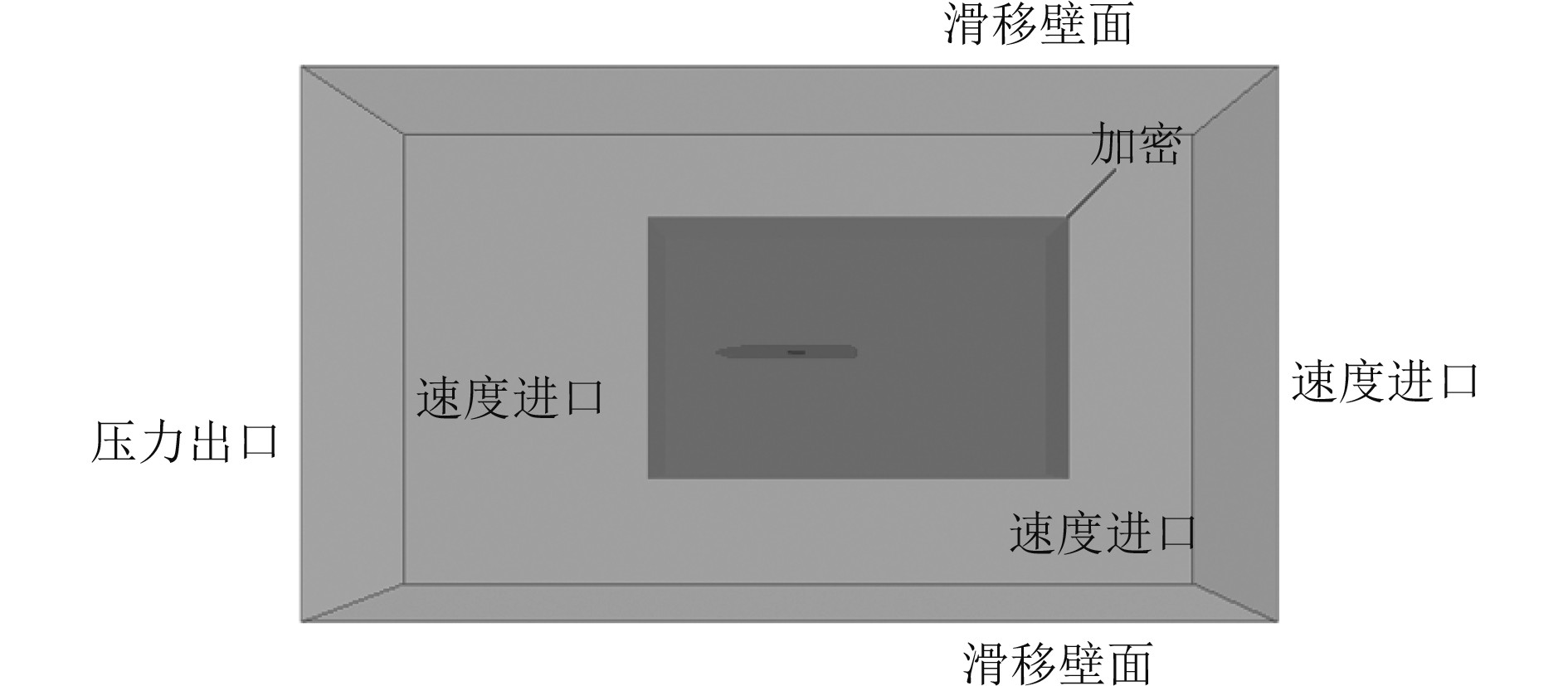
|
图 19 水下滑翔机计算区域 Fig. 19 Underwater glider computing area |
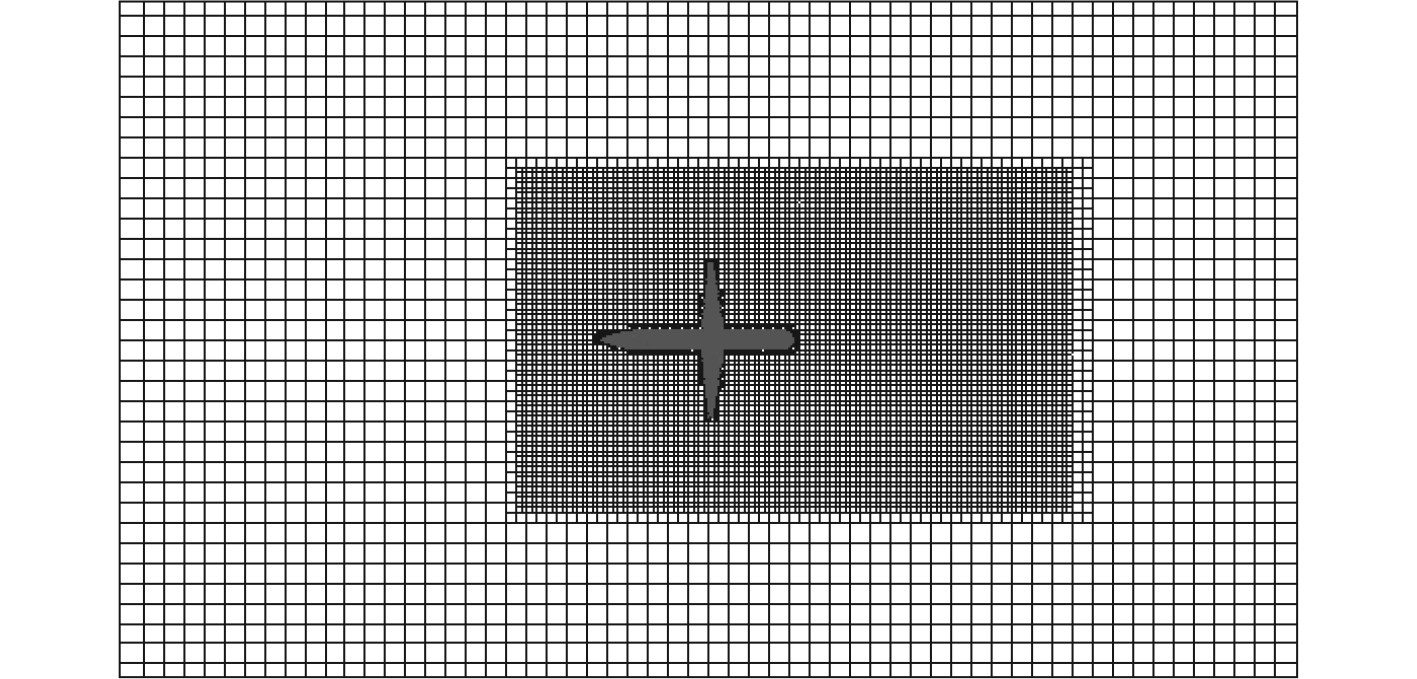
计算域的网格划分如图20所示。在划分网格时,对网格设置时在近艇区域设置较密的网格然后以一定的膨胀系数外推。
|
图 20 水下滑翔机计算区域网格划分 Fig. 20 Grid division of underwater glider calculation area |
取水下滑翔机的漂角分别为
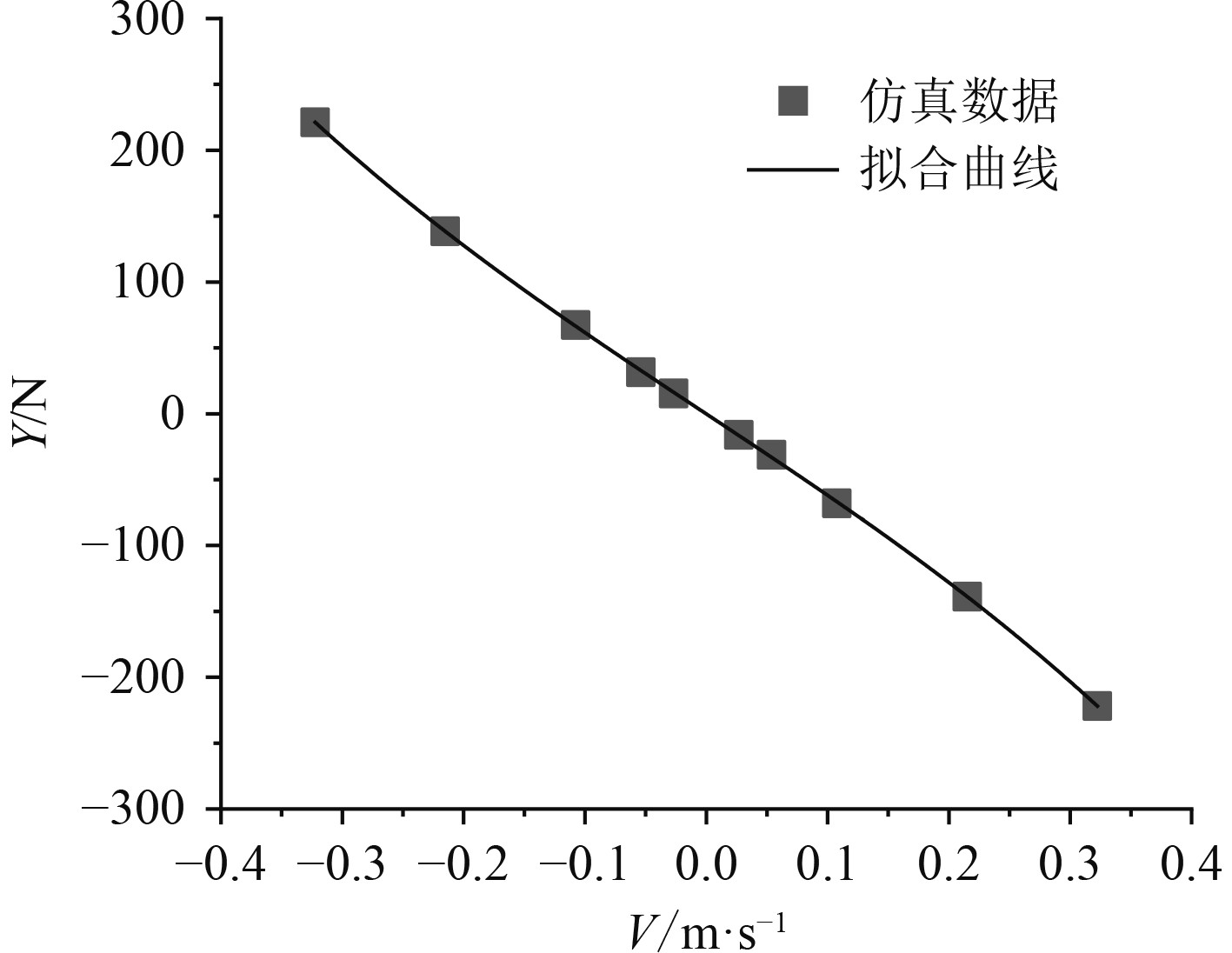
采用最小二乘法分别对不同速度下的侧向力
|
图 21
侧向力 |
|
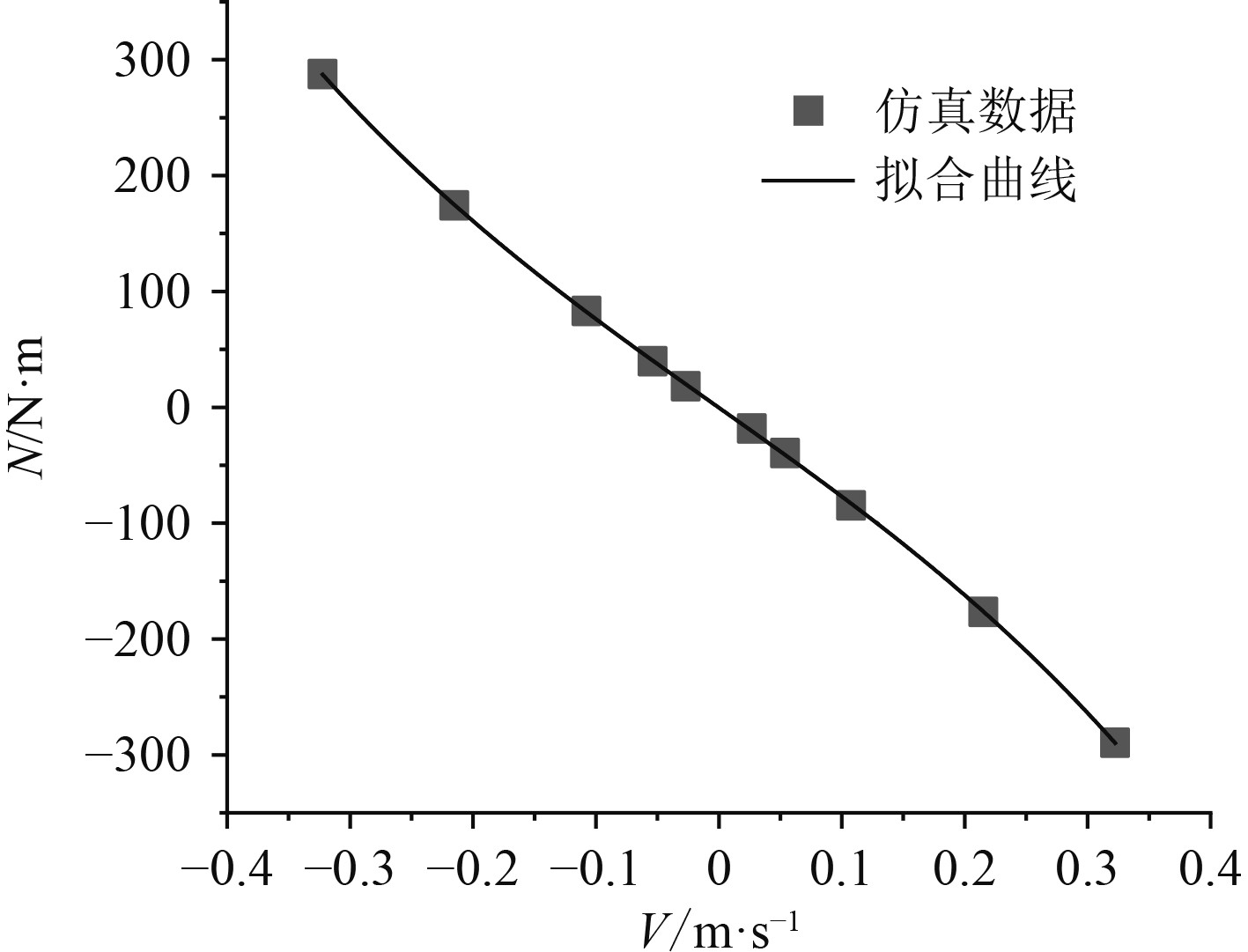
图 22
首摇力矩 |
|
|
表 5 基于斜航运动的水动力导数计算值 Tab.5 Calculated values of hydrodynamic derivatives based on oblique motion |
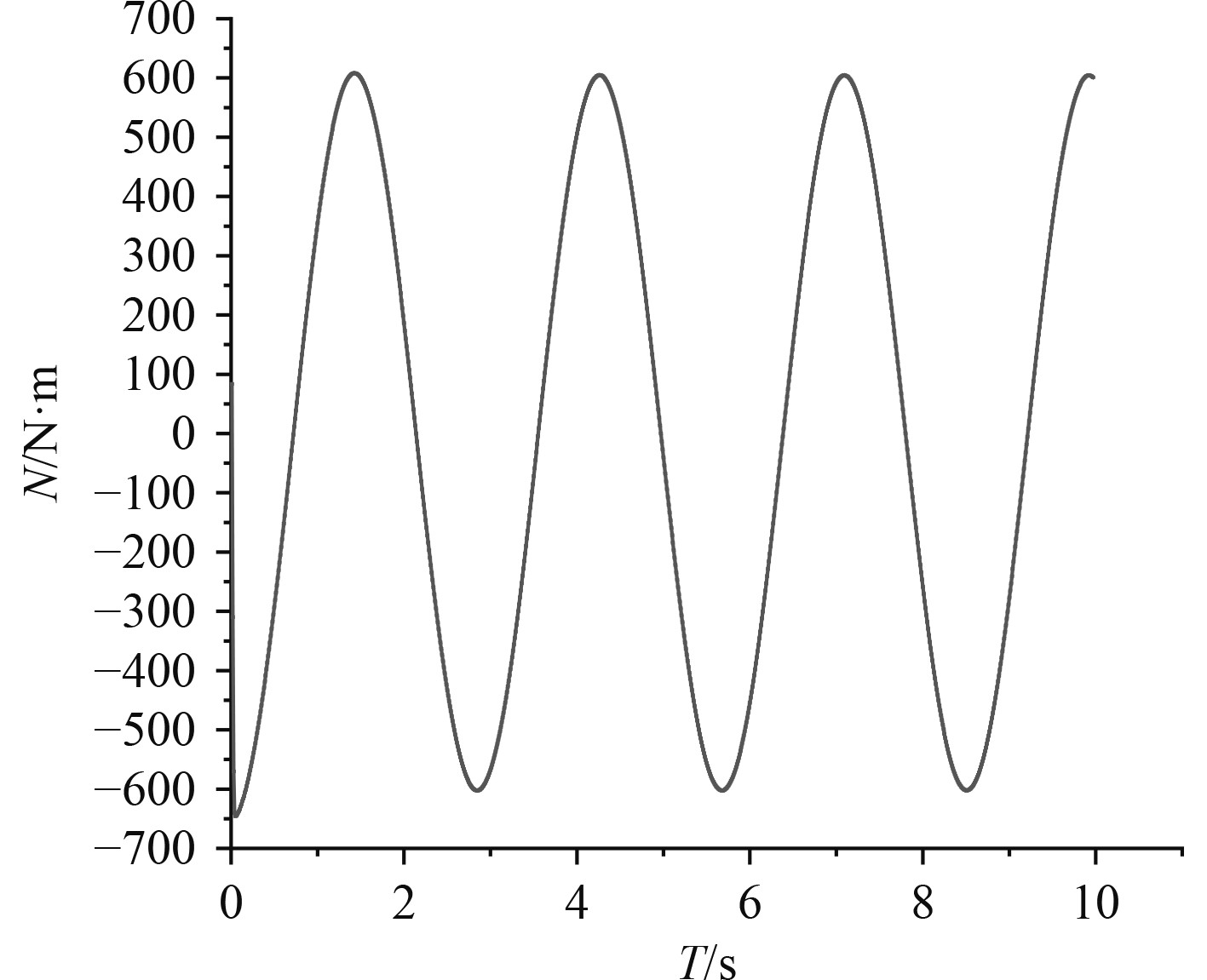
采用STAR-CCM+软件数值模拟水下滑翔机模型的小振幅纯横荡运动。对于 DFBI模块的平面运动机构参数设置,设置振荡频率为0.3533 Hz,振幅为0.1 m,分别得到图23所示的侧向力

|
图 23
侧向力 |
|
图 24
首摇力矩 |
选取图23中的一个稳定周期,基于式(6),采用最小二乘法对侧向力

|
图 25
水动力导数 |
|
图 26
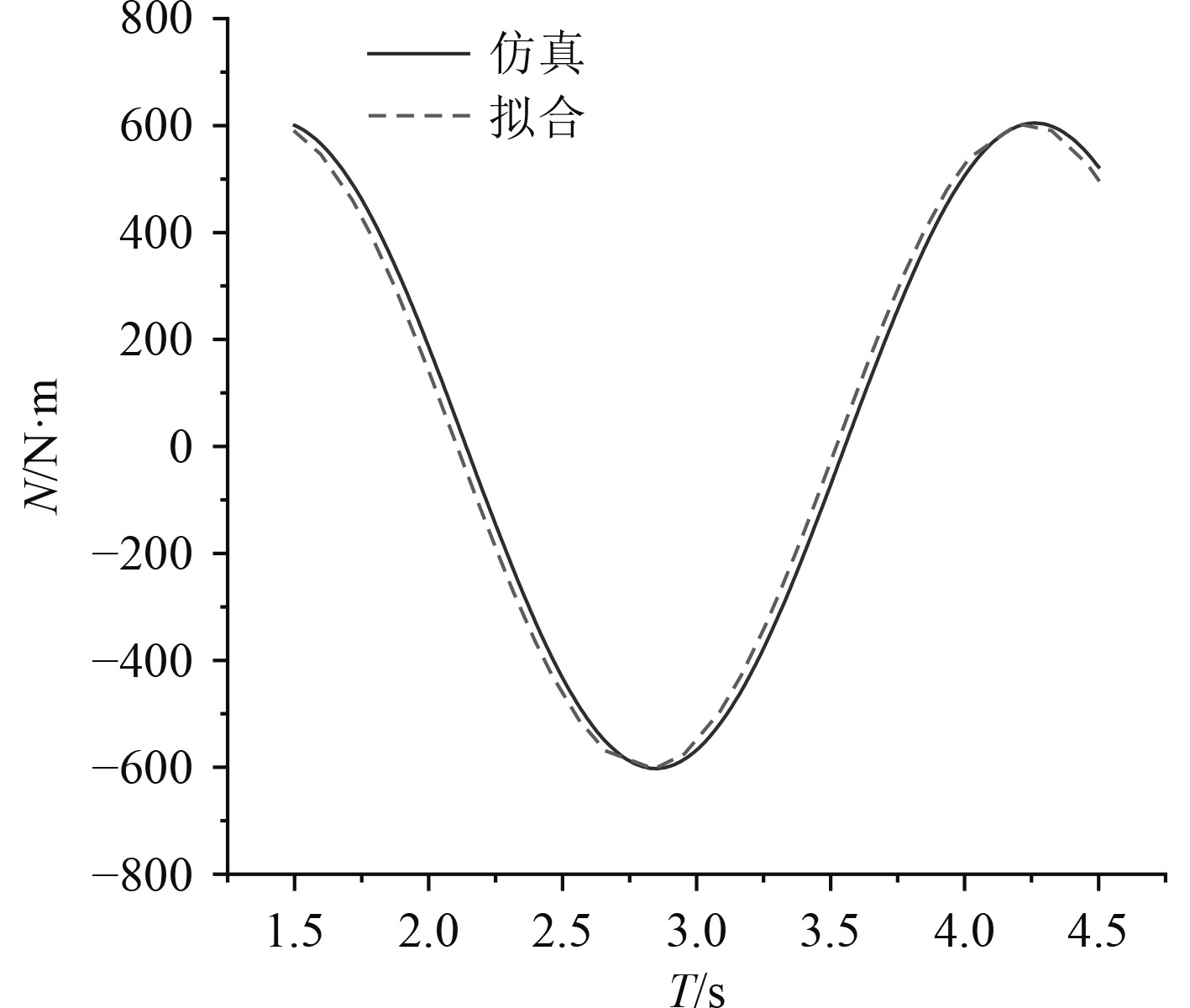
水动力导数 |
|
|
表 6 基于纯横荡运动的水动力导数计算值 Tab.6 Calculated values of hydrodynamic derivatives based on pure sway motion |
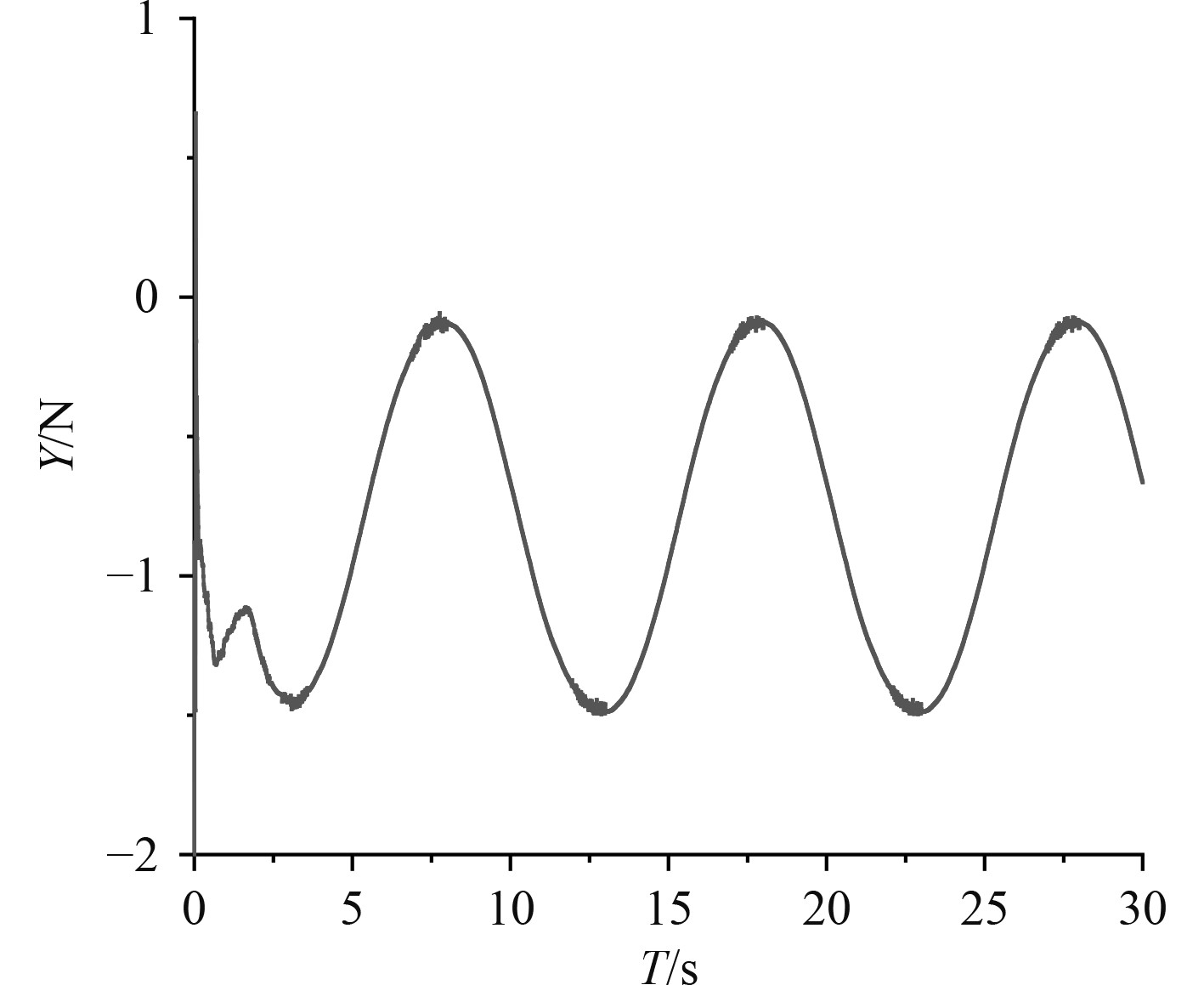
采用STAR-CCM+软件数值模拟水下滑翔机模型的纯首摇运动。对于 DFBI模块的平面运动机构参数设置,设置振荡频率为0.1 Hz,振幅为0.1 m,分别得到图27所示的侧向力
|
图 27
侧向力 |
|
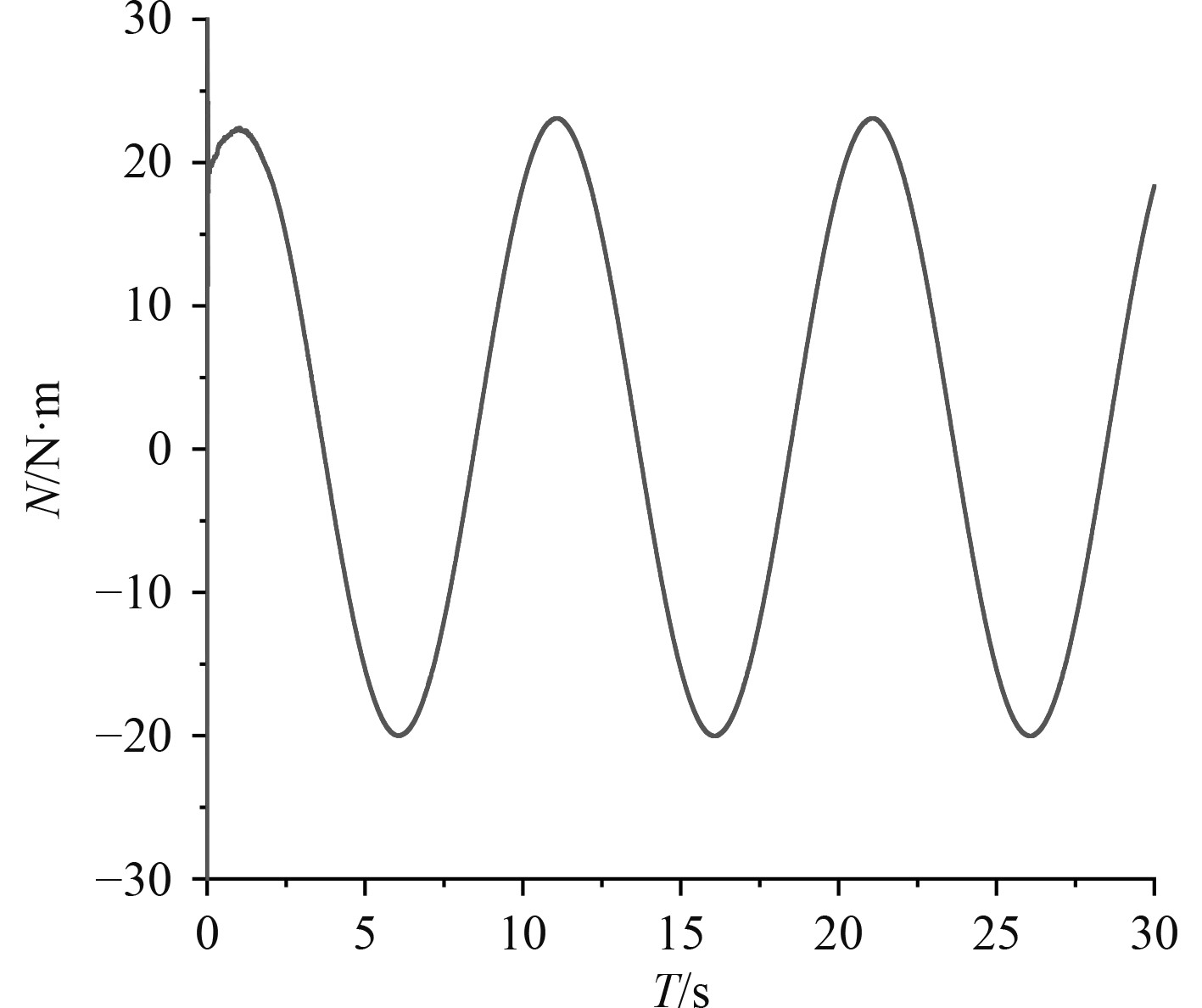
图 28
首摇力矩 |
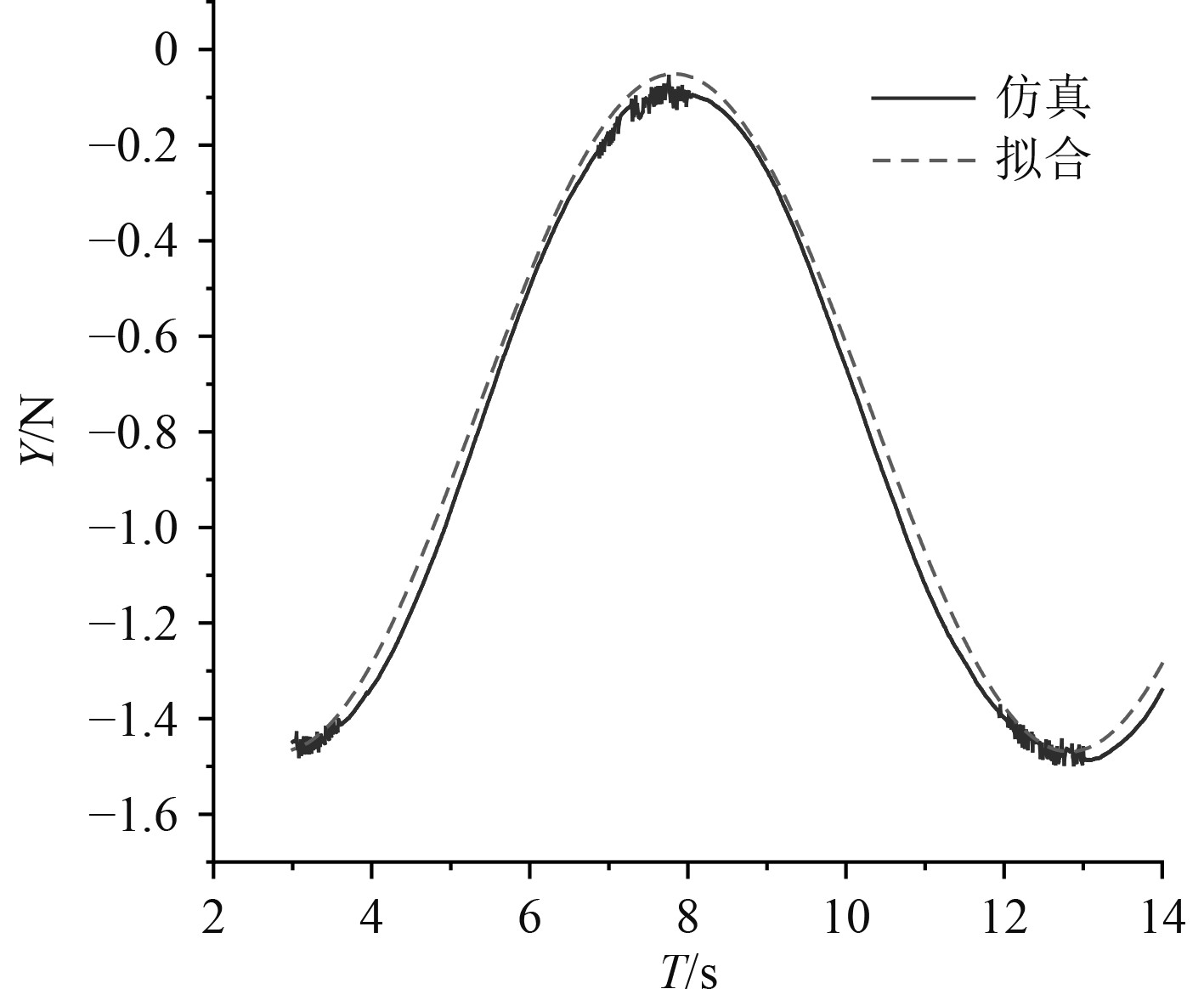
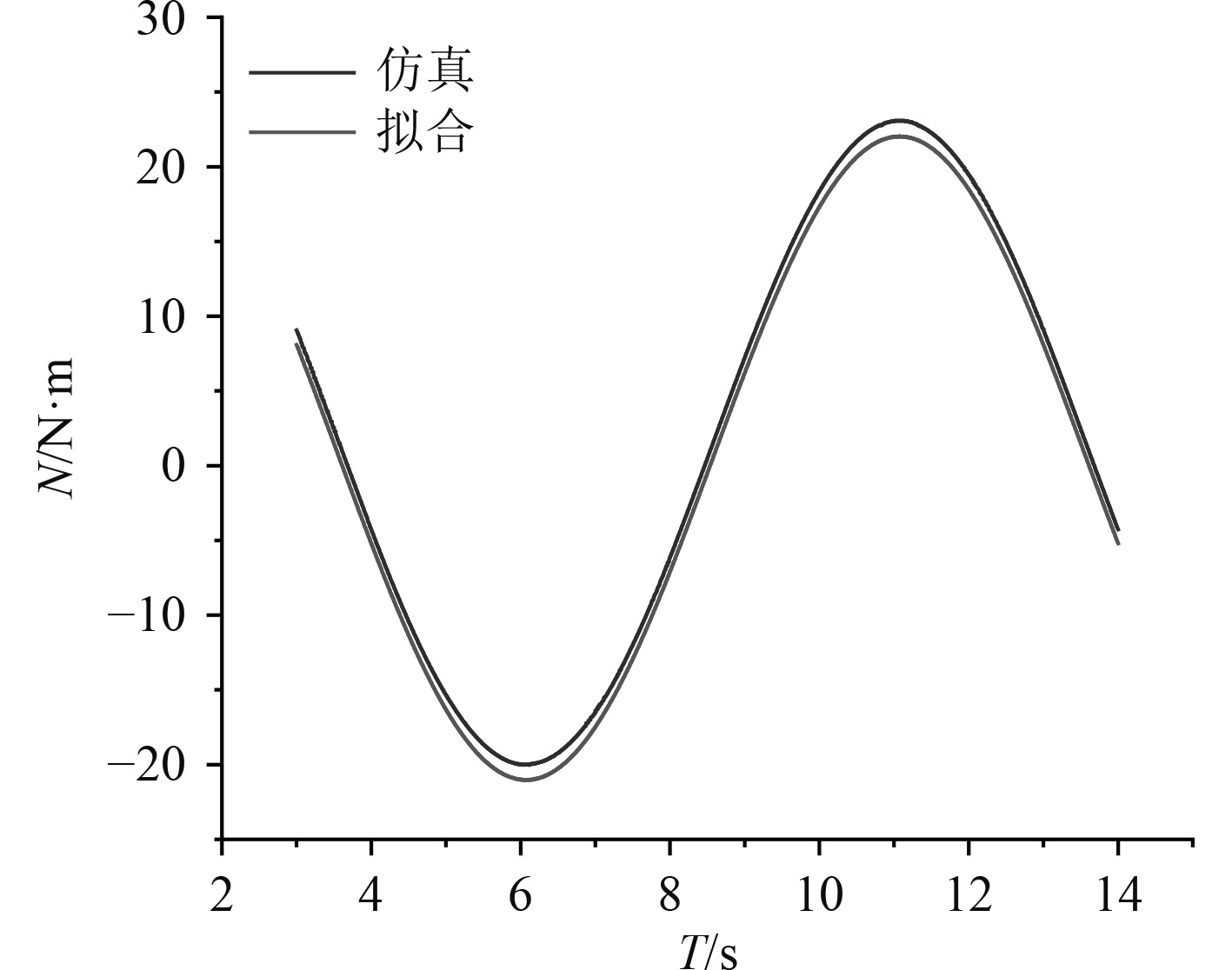
选取图27中的一个稳定周期,基于式(9),采用最小二乘法对侧向力
|
图 29
水动力导数 |
|
图 30
水动力导数 |
|
|
表 7 基于纯首摇运动的水动力导数计算值 Tab.7 Calculated values of hydrodynamic derivatives based on pure yaw motion |
本文采用CFD方法,通过对水下潜器的斜航运动、纯横荡和纯首摇运动进行数值模拟,拟合计算出SBUOFF潜艇模型和水下滑翔机的水动力导数,结果表明:
1)SUBOFF潜艇模型的水动力导数计算值与试验值满足误差要求,证明了采用CFD方法数值模拟约束模型试验,可用于水下潜器的水动力导数计算。
2)基于CFD方法和约束模型试验可快速准确估算水下滑翔机的水动力导数,具有一定的工程实用价值,可为下一步水下滑翔机的操纵性仿真预报工作奠定基础。
| [1] |
严升, 张润锋, 杨绍琼, 等. 水下滑翔机纵垂面变浮力过程建模与控制优化[J]. 中国机械工程, 2022, 33(1): 109-117. DOI:10.3969/j.issn.1004-132X.2022.01.012 |
| [2] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995: 225-229.
|
| [3] |
刘帅, 葛彤, 赵敏. 基于源项法的潜艇旋臂试验模拟[J]. 大连海事大学学报, 2011, 37(2): 1-4. DOI:10.16411/j.cnki.issn1006-7736.2011.02.020 |
| [4] |
高婷. 基于空间拘束运动模拟的AUV动力学建模与操纵性优化设计[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [5] |
董苗苗, 张喜秋, 于昌利, 等. 潜体水动力系数计算研究综述[J]. 舰船科学技术, 2019, 41(1): 1-6. DONG Miaomiao, ZHANG Xiqiu, YU Chuangli, et al. A review of research on the calculation of hydrodynamic coefficients for submerged bodies[J]. Ship Science and Technology, 2019, 41(1): 1-6. DOI:10.3404/j.issn.1672-7649.2019.01.001 |
| [6] |
吴兴亚, 高霄鹏. 基于操纵运动方程的水动力导数计算方法研究[J]. 舰船科学技术, 2017, 39(1): 26-31. WU Xingya, GAO Xiaopeng. Research on the calculation method of hydrodynamic derivatives based on manipulation motion equations[J]. Ship Science and Technology, 2017, 39(1): 26-31. DOI:10.3404/j.issn.1672-7619.2017.01.006 |
| [7] |
Simcenter STAR-CCM+ Documentation[M]. Siemens Digital Industries Software, 2020.
|
| [8] |
LIN Yu-Hsien, TSENG Shao-Huang, CHEN Yen-Hung. The experimental study on maneuvering derivatives of a submerged body SUBOFF by implementing the Planar Motion Mechanism tests[J]. Ocean Engineering, 2018(170).
|
 2023, Vol. 45
2023, Vol. 45
