在船体构件几何形状不连续的地方,会出现应力集中现象。特别是对一些几何形状突变的地方,例如散货船槽形横舱壁底凳的上下折角点,油船底边舱内底处的折角点,应力集中现象十分严重,在设计和建造过程中需重点关注[1],并采取一定措施来控制这些地方的应力峰值。相对来说,既能节省结构重量又能兼顾建造工艺的方法是通过在这些高应力集中区域设置应力释放孔[2],来降低应力峰值。但能将应力峰值降低到何种程度,取决于应力释放孔的形状、尺寸和位置等参数。如果这些参数设计合理,可最大程度地降低高应力区域应力峰值,反之,设置应力释放孔则起不到应有的作用,甚至可能恶化关注区域结构的应力水平。因此,建立合适的优化模型和求解流程,对应力释放孔的形状、尺寸和位置等参数进行优化,对于应力释放孔的设计十分必要。
应力释放孔附近结构型式比较复杂,求解校核区域结构的应力分布需采用有限元法。本文选取Isight多学科优化软件作为计算平台,集成基于PCL语言编写的应力释放孔参数化建模程序,调用Nastran进行应力计算,并采用遗传算法进行优化求解,可得最优的应力释放孔形状和尺寸,为降低应力集中区域结构的应力水平和峰值提供一种新解决思路。
1 优化模型应力释放孔一般设置在由于应力集中引起的船体结构局部高应力区域,如结构折角点处。它的作用效果与其形状、尺寸和位置等参数紧密相关。为了控制关注和校核区域结构的应力峰值,可构建以优化区域结构屈服利用因子为目标函数的船体应力释放孔形状优化和尺寸优化数学模型。
本文以某散货船槽形横舱壁底凳的上折角点处结构作为数值算例,对船体应力释放孔的优化模型和优化流程进行阐述。
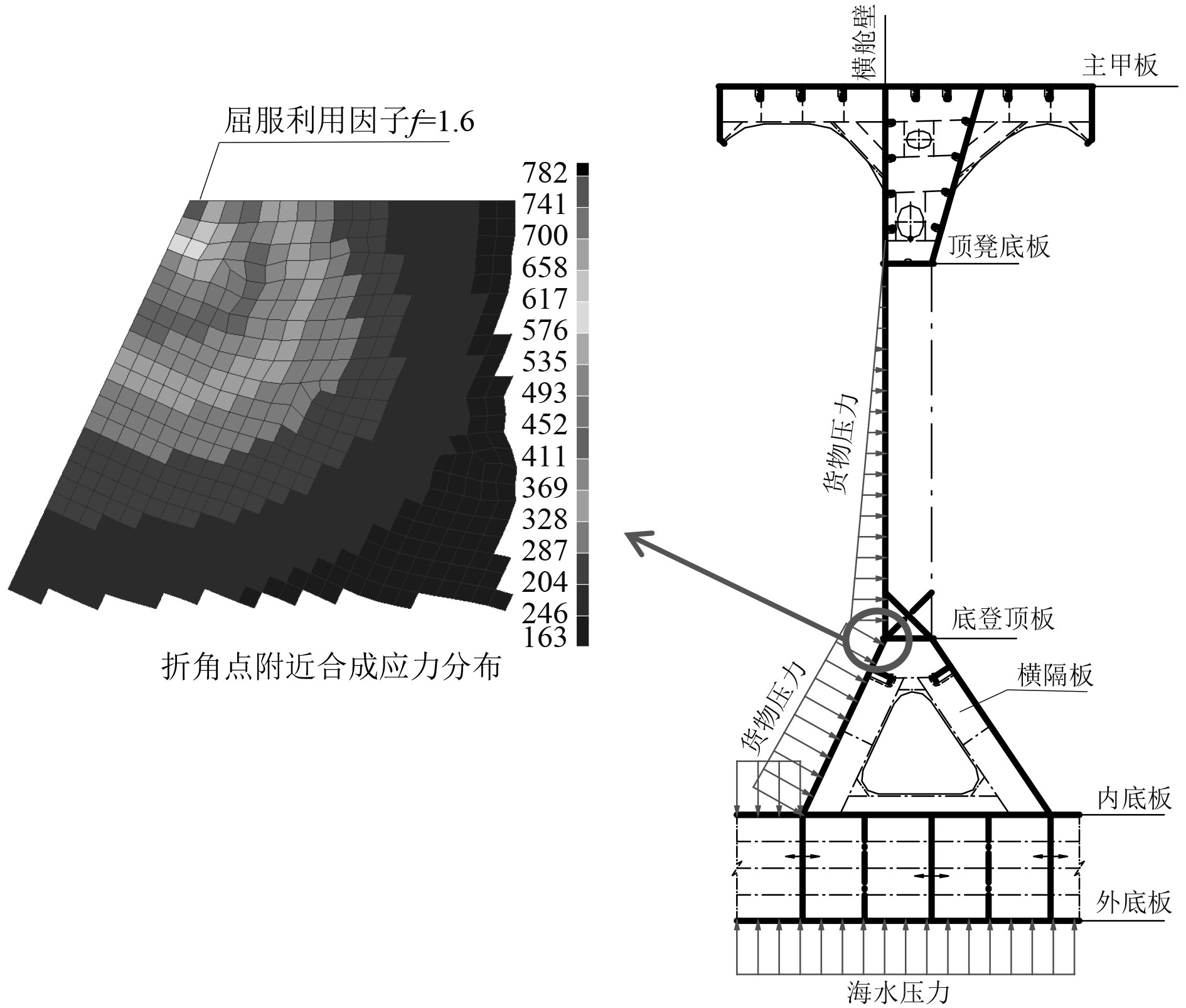
1.1 数值算例图1为某散货船槽形横舱壁的典型纵剖面结构,由于底凳上折角点附近结构形式复杂,无法用解析法求得该处的应力分布,本文采用有限元细网格数值分析法进行求解。在三舱段有限元模型中,对底凳上折角点处的网格进行细化(该处结构净板厚25 mm,但为了准确模拟应力释放孔的几何形状,细化网格尺寸取为10 mm×10 mm),以便求解该处的详细应力分布。
|
图 1 某散货船槽形横舱壁纵剖面结构及折角点处应力水平 Fig. 1 The longitudinal section structure and stress level at the bending point of the trough shaped transverse bulkhead of a bulk carrier |
为节省优化计算时间,本文计算校核区域应力分布时,仅考虑众多工况中取决定作用的工况。根据舱段有限元分析结果,对于底凳上折角附近结构的构件尺寸,其决定工况为隔舱装载工况,即在重货舱一侧受到货物压力,船底及舷侧受到海水压力,同时整个横剖面承受一定的船体梁载荷。
舱段有限元分析细网格计算结果显示,底凳横隔板在上折角点附近结构的应力集中现象十分严重,最大应力峰值出现在折角点处,在未设置应力释放孔时,优化区域结构最大屈服利用因子f =1.6(见图1)。
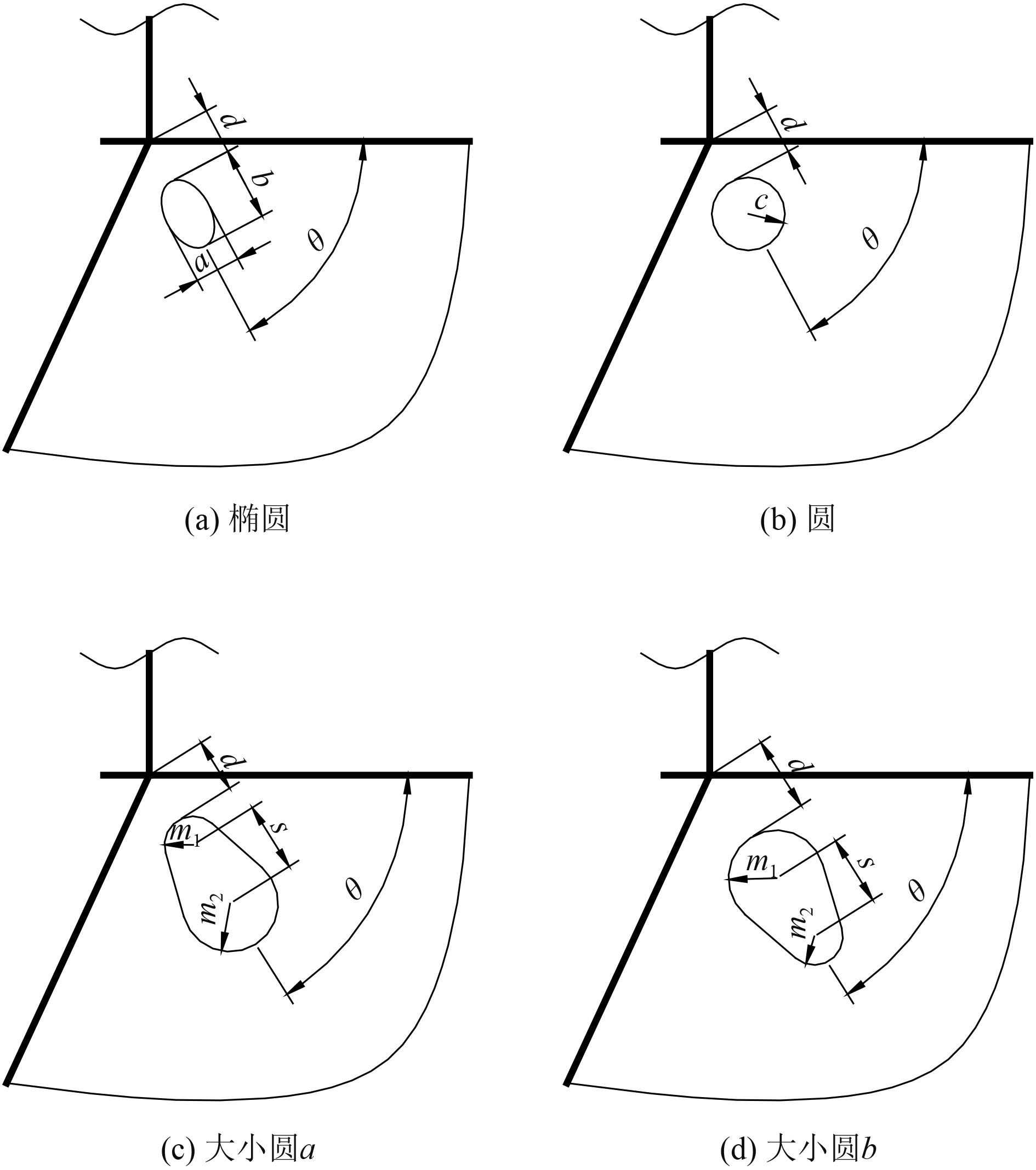
船体结构设计中,常见的应力释放孔有3种形式,分别是椭圆应力释放孔、圆形应力释放孔和大小圆应力释放孔,其中大小圆应力释放孔还可细分为小圆接大圆和大圆接小圆2种形式。各应力释放孔的形状、尺寸和位置等优化设计参数如图2所示。
|
图 2 应力释放孔的形状、尺寸及位置等优化设计参数 Fig. 2 Optimization design parameters for the shape, size, and position of stress relief holes |
以应力释放孔的形状,尺寸和位置等参数作为优化设计变量,以优化区域结构的归一化屈服利用因子为优化目标函数,以应力释放孔的位置边界、施工工艺和非优化区域结构的应力水平为约束条件,建立船体应力释放孔的形状优化和尺寸优化数学模型。
式(1)~式(3)分别为椭圆、圆形和大小圆应力释放孔优化模型的数学表达式。
| $\left\{ \begin{array}{l} {\rm{Find}}\quad X = {[a,b,d,\theta ]^{\rm T}},\\ {\rm{Min}}\quad f(X) = \max({f_{{\rm{weld}}}}(x),{f_{{\rm{nonweld}}}}(X)),\\ {\rm{s.t}}.\left\{ \begin{array}{l} 30 \leqslant a \leqslant140,\\ 40 \leqslant b \leqslant160,\\ 35 \leqslant d \leqslant100,\\ 15{\rm{^\circ }} \leqslant\theta \leqslant100^\circ,\\ {{b}} > a + 10,\\ \theta - a\tan \left( {\dfrac{{\dfrac{a}{2} + 20}}{{d + \dfrac{b}{2}}}} \right) \geqslant 10{\rm{^\circ }},\\ \theta + a\tan \left( {\dfrac{{\dfrac{a}{2} + 20}}{{d + \dfrac{b}{2}}}} \right) \leqslant105{\rm{^\circ }},\\ {{k}_{{\rm{nopt}}}}(X) \leqslant1。\end{array} \right. \end{array} \right. $ | (1) |
| $\left\{ \begin{array}{l} {\rm{Find}}\quad X = {[c,d,\theta ]^{{\rm{T}}}},\\ {\rm{Min}}\quad f(X) = \max({f_{{\rm{weld}}}}({\rm{X}}),{f_{{\rm{nonweld}}}}(X)),\\ {\rm{s.t}}.\left\{ \begin{array}{l} 30 \leqslant c \leqslant90,\\ 35 \leqslant d \leqslant100,\\ 15{\rm{^\circ }} \leqslant\theta \leqslant100{\rm{^\circ }},\\ (d + c)\cdot\sin(\theta ) - c > 25,\\ (d + c)\cdot\sin(115{\rm{^\circ }} - \theta ) - c > 25,\\ {{k}_{{\rm{nopt}}}}(X) \leqslant1。\end{array} \right. \end{array} \right. $ | (2) |
| $ \left\{ \begin{array}{l} {\rm{Find}}\quad X = [{{\rm{m}}_{\rm{1}}}{\rm{,}}{{\rm{m}}_{\rm{2}}}{\rm{,s,d,}}\theta {{\rm{]}}^{\rm{T}}},\\ {\rm{Min}}\quad f(X) = \max({f_{{\rm{weld}}}}(X),{f_{{\rm{nonweld}}}}(X)),\\ {\rm{s.t}}.\left\{ \begin{array}{l} 30 \leqslant{m_1} \leqslant80,\\ 30 \leqslant{m_c} \leqslant80,\\ 10 \leqslant s \leqslant100,\\ 35 \leqslant d \leqslant100,\\ 15{\rm{^\circ }} \leqslant\theta \leqslant100{\rm{^\circ }},\\ (d + {m_1})\cdot\sin(\theta ) - {m_1} > 25,\\ (d + {m_1})\cdot\sin(115{\rm{^\circ }} - \theta ) - {m_1} > 25,\\ (d + {m_1} + {\rm{s}})\cdot\sin(\theta ) - {m_2} > 25,\\ (d + {m_1} + {\rm{s}})\cdot\sin(115{\rm{^\circ }} - \theta ) - {m_2} > 25,\\ {{k}_{{\rm{nopt}}}}{{(X)}} \leqslant1。\end{array} \right. \end{array} \right. $ | (3) |
式中:f(X)为归一化屈服利用因子;fweld(X) =σweld(X)/ [σ]weld,为优化区域内,邻近焊缝单元的最大屈服利用因子;fnonweld(X) =σnonweld(X)/ [σ]nonweld,为优化区域内,非邻近焊缝单元的最大屈服利用因子;σweld(X)、σnonweld(X),为优化区域内,邻近焊缝和非邻近焊缝单元的最大合成应力;[σ]weld、[σ]nonweld分别为邻近焊缝和非邻近焊缝单元的许用合成应力,对于本文算例,分别为489 MPa和554 MPa;knopt(X)=σnopt(X)/1012,为对于非优化区域结构,设置应力释放孔后与设置前的最大合成应力之比值。约束该参数值不大于1,表示设置应力释放孔后不能增加非优化区域结构的应力水平。
为了减小计算规模,并考虑到实际加工精度的限制,优化过程中所有变量均取整数,变化步长取为1。
2 优化求解以Isight软件作为计算平台,集成基于Patran软件的应力释放孔参数化建模程序,调用Nastran软件进行应力计算,并利用Isight自带的多岛遗传算法进行优化求解[3~5]。
2.1 模型参数化基于有限元前处理软件Patran,采用PCL(Patran自带的编译语言)语言,编写应力释放孔关于优化变量的参数化建模程序。对于任意优化变量,该程序可快速生成满足计算要求的有限元模型[6,7]。为使参数化建模程序具备一定通用性,在程序编写过程中可采用模块化的编程思路。
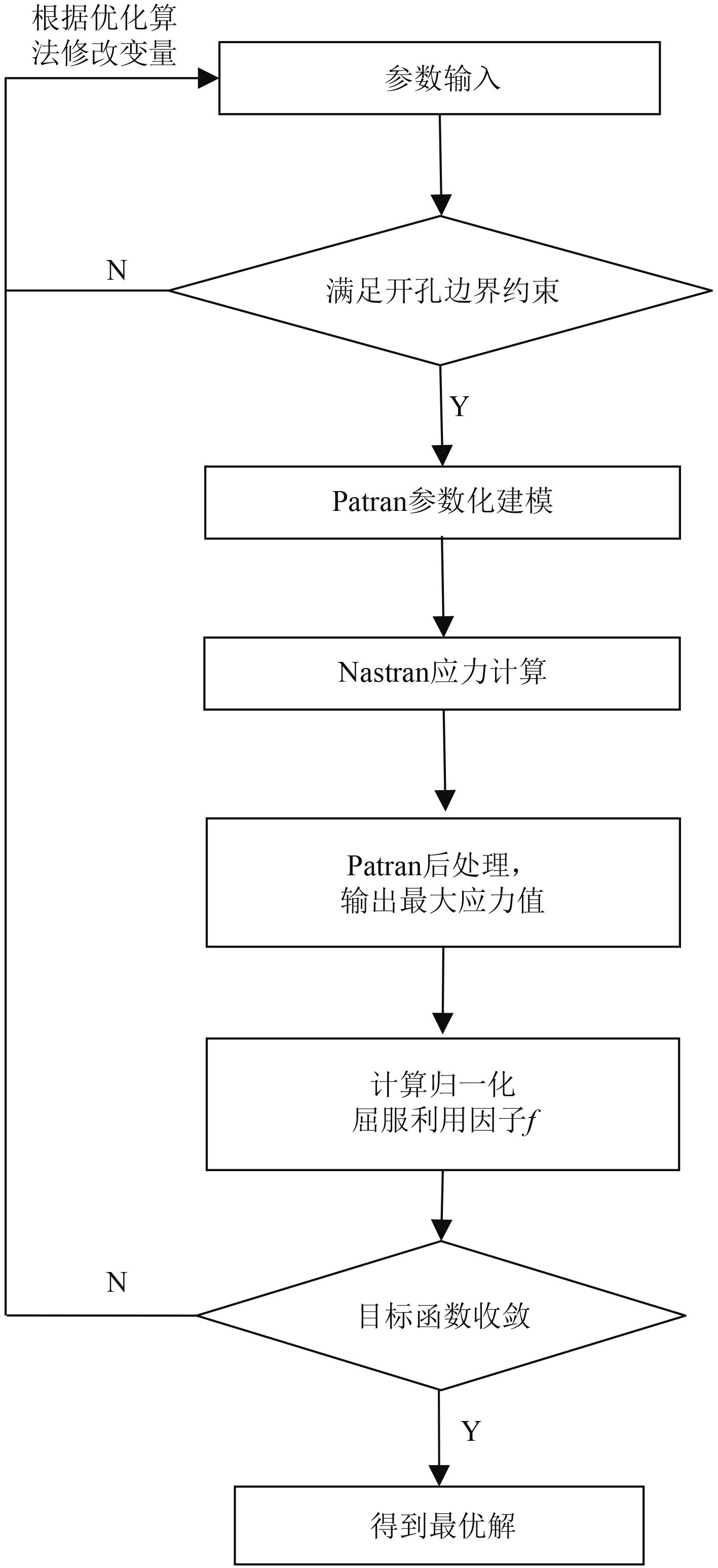
2.2 Isight集成以Isight作为优化计算平台,本文应力释放孔优化模型的计算流程如图3所示[8]。由于应力释放孔各优化参数之间需满足一定约束条件,应力释放孔的几何形状方能构建成功,因此调用参数化建模程序之前,需进行开孔边界约束判断,对于不满足该约束的输入,需根据优化算法进行调整。在优化计算的初始迭代阶段,会有大量输入参数不满足该约束,随着优化算法的智能化筛选,不满足该约束的输入快速减少。
|
图 3 Isight关于应力释放孔优化模型的计算流程 Fig. 3 The calculation process of Isight's optimization model for stress release holes |
由于应力释放孔优化模型中优化变量为离散变量,且考虑到遗传算法具有强大的全局寻优能力,本文采用Isight自带的多岛遗传算法求解。为了控制优化计算时间,并兼顾一定计算精度,根据本文优化模型中的实际变量个数,将软件中默认的子种群数、岛数和进化代数均由10改为8,其他参数设置保持不变。
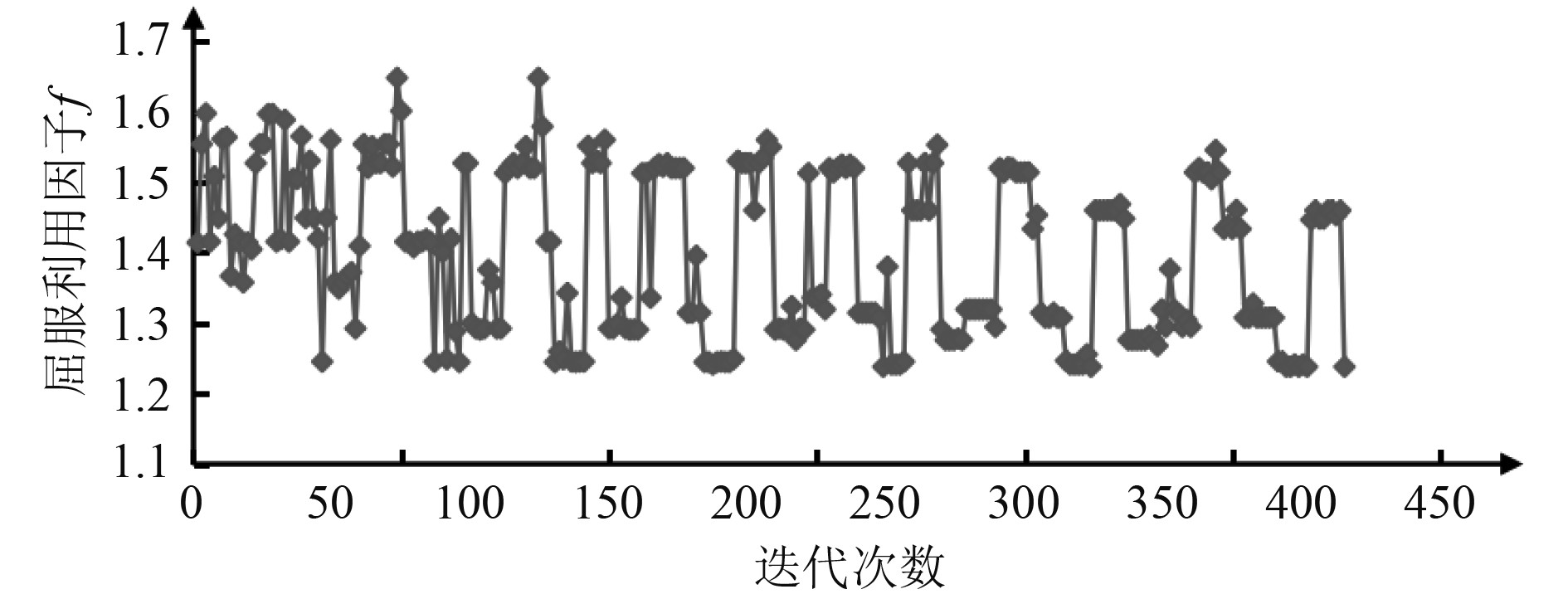
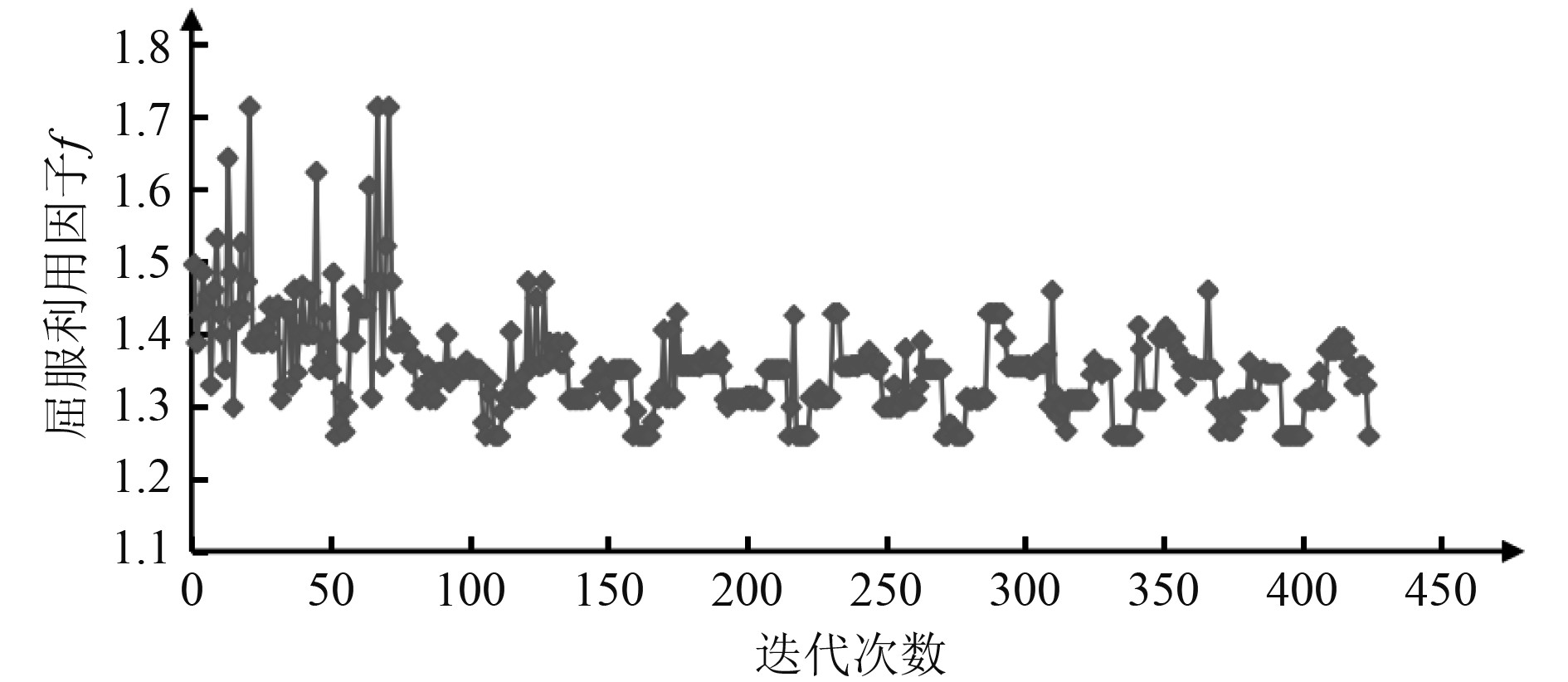
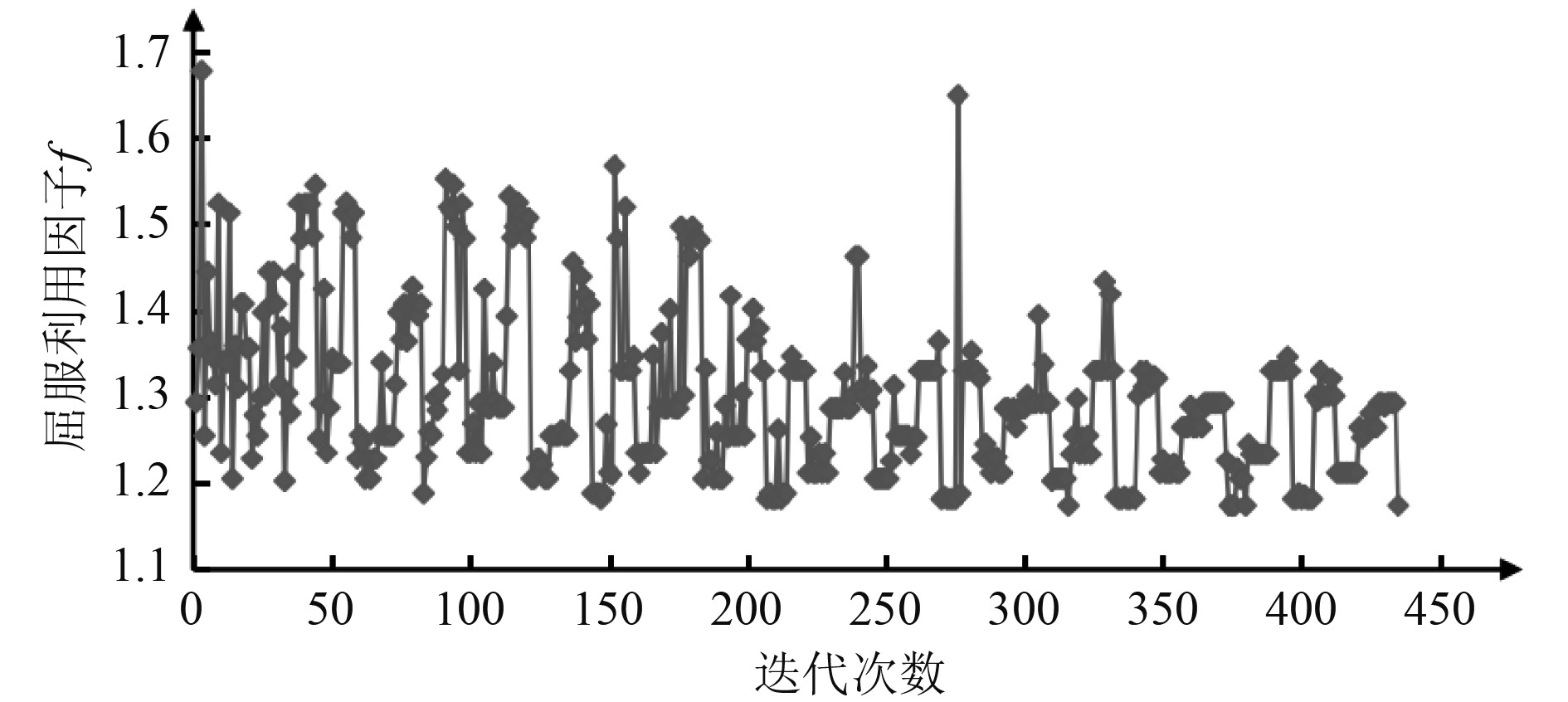
3 优化结果及分析 3.1 计算结果对于本文的3种应力释放孔优化模型,根据优化算法的设置,均需经过512次迭代,得到各自的最优解。图4~图6分别为各优化模型满足约束条件的目标函数变化曲线。
|
图 4 椭圆应力释放孔优化模型目标函数变化曲线 Fig. 4 Objective function variation curve of optimization model for elliptic stress release hole |
|
图 5 圆形应力释放孔优化模型目标函数变化曲线 Fig. 5 Objective function curve of optimization model for circular stress release hole |
|
图 6 大小圆应力释放孔优化模型目标函数变化曲线 Fig. 6 Objective function variation curve of optimization model for large & small circular stress release hole |
为了便于对各优化模型的计算结果进行比较和分析,将椭圆、圆形和大小圆应力释放孔优化模型的初始值和最优值分别列于表1~表3。
|
|
表 1 椭圆应力释放孔优化结果比较 Tab.1 Result for elliptic stress release hole |
|
|
表 2 圆形应力释放孔优化结果比较 Tab.2 Result for circular stress release hole |
|
|
表 3 大小圆应力释放孔优化结果比较 Tab.3 Result for large and small circular stress release hole |
可以得出:
1)对于3个应力释放孔优化模型,经过优化求解后,目标函数值即优化区域结构的归一化屈服利用因子,相对初始值均有一定程度的下降,相对于无应力释放孔时下降程度更大,同时非优化区域结构的应力水平也有一定程度的下降;
2)对于椭圆应力释放孔优化模型,初始设计虽然可以降低优化区域结构的应力峰值,但非优化区域结构的应力水平略有增加,不满足约束条件,经优化求解后,优化区域和非优化区域结构的应力水平均有降低;
3)对于圆形应力释放孔优化模型,初始设计下优化区域结构的屈服利用因子比无应力释放孔时更大,说明初始设计值不尽合理,经优化求解后,屈服利用因子下降明显;
4)3种应力释放孔优化模型相比较而言,大小圆应力释放孔优化模型的最优解降低应力峰值的效果最为明显,相比不设置应力释放孔而言,显著降低了优化区域的屈服利用因子,在不增加重量的前提下,结构安全性大幅提升。
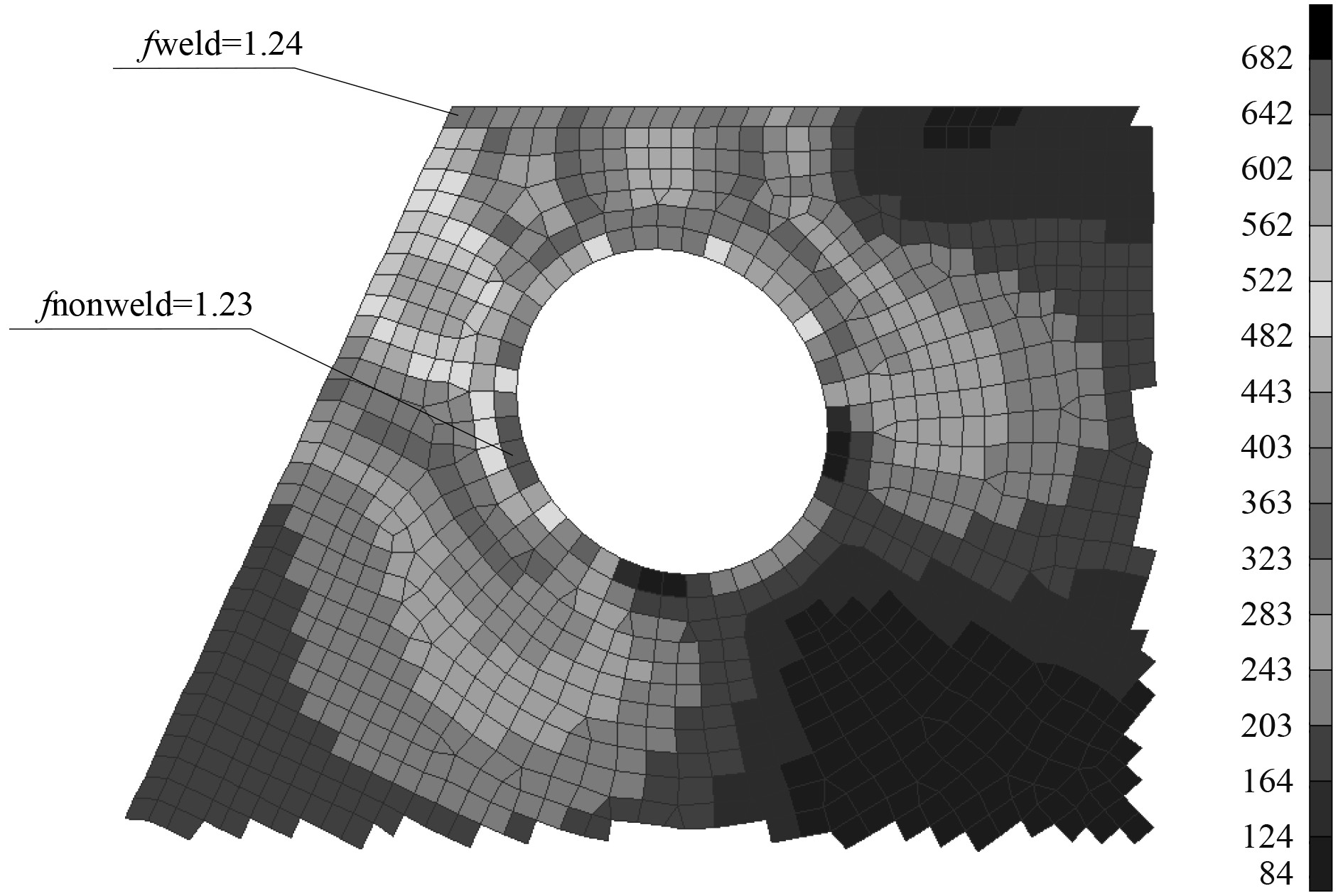
为了展示优化区域结构的应力水平,图7~图9给出了3种应力释放孔优化模型对应最优解的详细应力分布云图。
|
图 7 最优椭圆应力释放孔的应力 Fig. 7 Best result for elliptic stress release hole |

|
图 8 最优圆形应力释放孔的应力 Fig. 8 Best result for circular stress release hole |

|
图 9 最优大小圆应力释放孔的应力 Fig. 9 Best result for large & small circular stress release hole |
综合以上分析,可以得出如下结论:
1)对于应力释放孔的设计,在各设计参数未经优化前,一方面,可能使得优化区域结构的屈服利用因子比无应力释放孔时更大,起到负面作用;另一方面,也可能导致虽然降低了优化区域结构的应力峰值,但会提高非优化区域结构的应力水平,顾此失彼。因此,对应力释放孔进行形状优化和尺寸优化十分必要。
2)本文构建的船体应力释放孔优化模型可行,通过优化求解可得到最优的应力释放孔开孔形式,大幅降低关注区域结构的应力峰值和水平,在不增加结构重量的情况下,提高结构的安全性。本文提出的3种应力释放孔优化模型具备一定通用性,只需对部分模型参数稍作修改,可应用于其他船体结构部位。
3)3种应力释放孔优化模型相比较而言,大小圆应力释放孔优化模型的最优解降低应力峰值的效果最为明显,特别是相比不设置应力释放孔而言,显著降低了优化区域结构的屈服利用因子,同时非优化区域结构的应力水平也相应降低。
| [1] |
IACS. Common structural rules for bulk carriers and oil tankers[S]. 2017.
|
| [2] |
谢小龙, 罗仁杰, 次洪恩, 等. 船体应力释放孔的设计[J]. 船海工程, 2019, 48(4): 51-54. XIE X L, LUO R J, CI H E, et al. Design of stress relief holes for ship hulls[J]. Marine Engineering, 2019, 48(4): 51-54. DOI:10.3963/j.issn.1671-7953.2019.04.012 |
| [3] |
罗仁杰, 邱伟强, 蔡诗剑, 等. 船体纵骨上附连挺筋软踵形状参数优化[J]. 船舶与海洋工程, 2016, 32(6): 39-48. LUO R J, QIU W Q. CAI S J, et al. Optimization of shape parameters for soft heels attached to longitudinal ribs of ship hull[J]. Marine Engineering, 2016, 32(6): 39-48. DOI:10.14056/j.cnki.naoe.2016.06.007 |
| [4] |
何祖平, 王德禹. 基于MSC. Patran二次开发的结构参数化建模及其集成开发环境[J]. 船海工程, 2005(2): 17-20. HE Z P, WANG D Y. Based on MSC structural parameterized modeling and integrated development environment for Patran's secondary development[J]. Marine Engineering, 2005(2): 17-20. DOI:10.3963/j.issn.1671-7953.2005.02.007 |
| [5] |
马静敏, 沈友徽, 李华. 基于iSIGHT的油船槽形横舱壁优化设计[J]. 船海工程, 2005(1): 35-37. MA J M, SHEN Y Z, LI H. Optimization design of tank shaped transverse bulkheads for oil tankers based on iSIGHT[J]. Marine Engineering, 2005(1): 35-37. DOI:10.3963/j.issn.1671-7953.2005.01.014 |
| [6] |
陈哲超, 李文华, 罗仁杰. 散货船重压载舱横舱壁底凳与内底连接处结构加强方案研究[J]. 船舶, 2018(5): 23-32. CHEN Z C, LI W H, LUO R J. Research on structural reinforcement scheme for the connection between the bottom bench and inner bottom of the horizontal bulkhead in heavy ballast tanks of bulk carriers[J]. Shipping, 2018(5): 23-32. DOI:10.19423/j.cnki.31-1561/u.2018.05.023 |
| [7] |
MSC. Patran2012 PCL reference manual [M]. Software corporation, 2012.
|
| [8] |
MSC. Patran2012 PCL and customization [M]. Software Corporation, 2012.
|
| [9] |
SIMULIA. Isight 5.7 user’s guide [M]. 2012.
|
 2023, Vol. 45
2023, Vol. 45
