2. 船舶振动噪声重点实验室,湖北 武汉 430064
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430064, China
舰船结构的轻量化、高性能化设计是未来海军装备的发展趋势,研究开发新材料、新结构形式的需求日益增长。负泊松比(NPR)材料作为一种超材料,其在受到单轴拉伸时横向会发生膨胀,受压后横向同时收缩。这种独特的拉胀现象使其具备优越的抗拉压性能[1-2]、振动噪声吸收性能[3-4]、能量吸收性能[5-6]。众多优异的力学性能使负泊松比材料满足更苛刻的工程要求,得以应用在舰船防护、航天航空和军事工程等领域[7]。
自Gibson等[8]首次提出自主设计的负泊松比蜂窝形状(内凹六边形胞元构型)以来,根据各类应用场合而设计的负泊松比胞元形状不断更新。学者们主要针对二维负泊松比结构进行研究,最常见的二维负泊松比蜂窝结构的微观构型包括内凹角六边形[8-9]、手性蜂窝[10-11]、星形[12-13]、箭型[14-15]等形式。该类结构通常由二维几何形式的胞元沿面外方向延展一段距离形成,其仅在其面内呈现负泊松比效应,由胞元的平面上的内凹或旋转特性获得,而结构在第三维度上不具备负泊松比效应,存在一定的局限性。
近年来,工业技术的蓬勃发展促进了三维负泊松比材料的设计与制备。Evans等[16]设计出了第一个各向正交三维的负泊松比构型。随后,Yang[17]、Wang[18]等针对三维内凹六边形蜂窝结构力学性能进行深入研究。Gao[19]等基于二维箭型蜂窝构型,设计出了三维箭型负泊松比结构。周冠等[20]将非线性变形理论与铁木辛柯梁理论相结合,推导出箭形负泊松比结构的简化力学性能。相较二维负泊松比结构,三维负泊松比结构具备更佳的各向同性,能够在各个轴向上均呈现出负泊松比的特性,突破了二维形式的局限性,具有更广阔的应用前景。
然而当前,对三维负泊松比结构的研究还处于相对初步的阶段,仍有大量新构型的设计亟待挖掘,对其力学性能的研究也尚显不足[21]。由于三维负泊松比蜂窝材料的构型通常非常复杂,结合试验的分析论证更为有限。
本文提出一种新型三维负泊松比蜂窝(Three-dimensional Negative Poisson ratio Honeycomb,3D-NPH)结构,基于单胞分析法构建了该结构在准静态载荷作用下的等效力学模型,分析了胞元各几何参数对结构整体性能的影响。同时,将理论解与有限元结果及试验结果对比分析,验证了本文所建立的新型3D-NPH结构力学模型的合理性,为后续该型结构的动力学研究及实际应用提供参考。
1 三维负泊松比蜂窝结构设计二维内凹负泊松比结构首先由Almgren[22]提出,如图1(a)所示。在此二维构型基础上,通过与初始结构所在平面相垂直的平面上设置一个与其共用直杆MN的相同结构,可将负泊松比效应拓展到该维度上,并依据结构本身的对称性,构造出了如图1(b)所示的三维负泊松比胞元。

|
图 1 二维与三维负泊松比结构 Fig. 1 2D and 3D negative poisson's ratio structure |
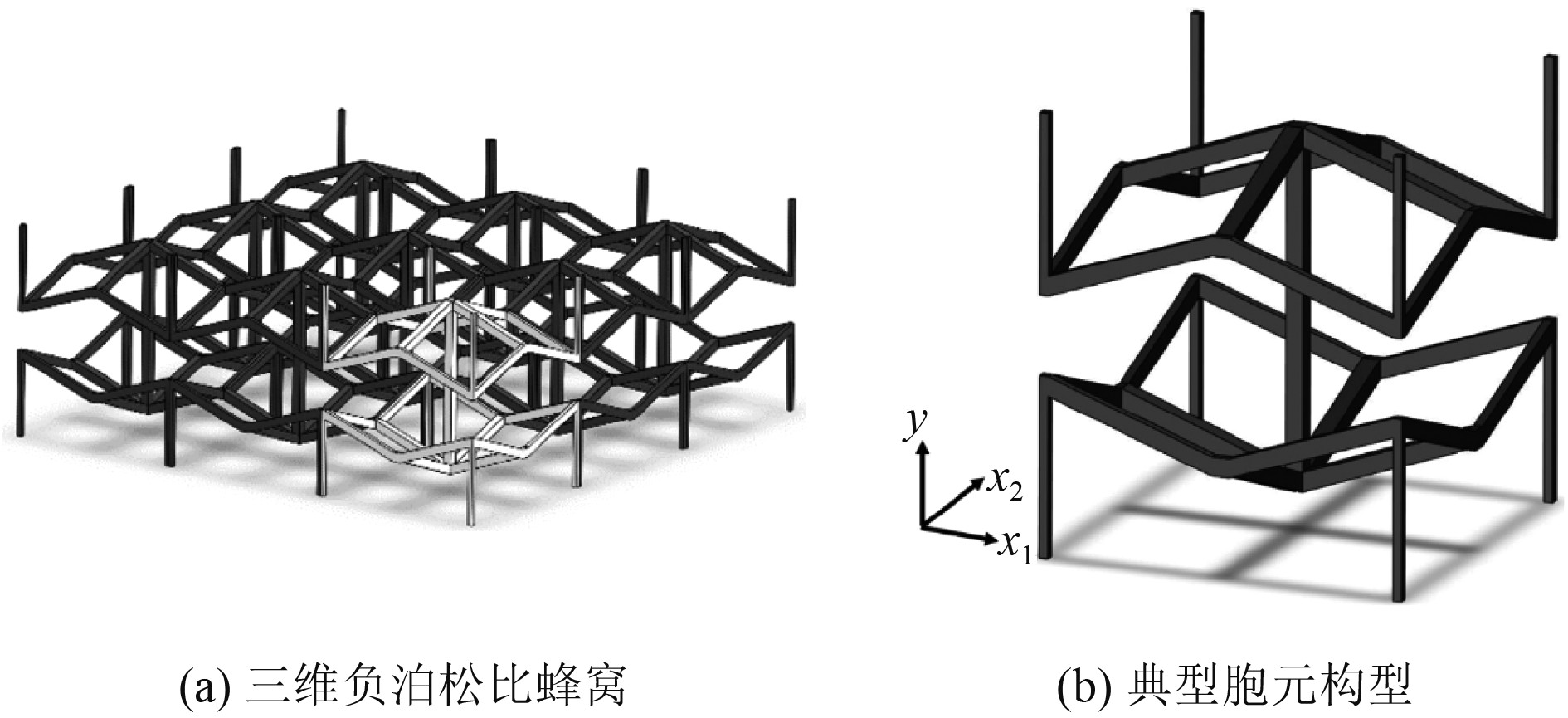
将胞元在3个轴向上重复排列组成整个蜂窝结构,如图2(a)所示,这种结构在三轴向上都可呈现出负泊松比效应。便于后续的受力分析,选取如图2(b)所示形式代表整体的蜂窝结构,作为典型的单位胞元。
|
图 2 三维负泊松比蜂窝结构及其典型胞元 Fig. 2 3D Negative poisson's ratio honeycomb and its typical cells |
对于二维负泊松比结构,当受到轴向压缩载荷的时候,内凹方向上的胞壁会发生弯曲变形,且水平方向的胞壁与内凹方向的胞壁之间夹角和内凹胞壁与轴线之间的夹角会同时缩小。因此,在垂直于载荷方向上,元胞会产生压缩应变,产生水平面上的收缩现象,如图3 (a)所示。由于三维负泊松比元胞由2个二维胞元正交组成,所以维元胞能够在横截面内的3个轴向上同时产生收缩现象,表现出更为显著的负泊松比效应,如图3 (b)所示。

|
图 3 二维与三维负泊松比结构变形特征对比 Fig. 3 Deformation characteristics of 2D-NPR ctructure and 3D-NPR structure |
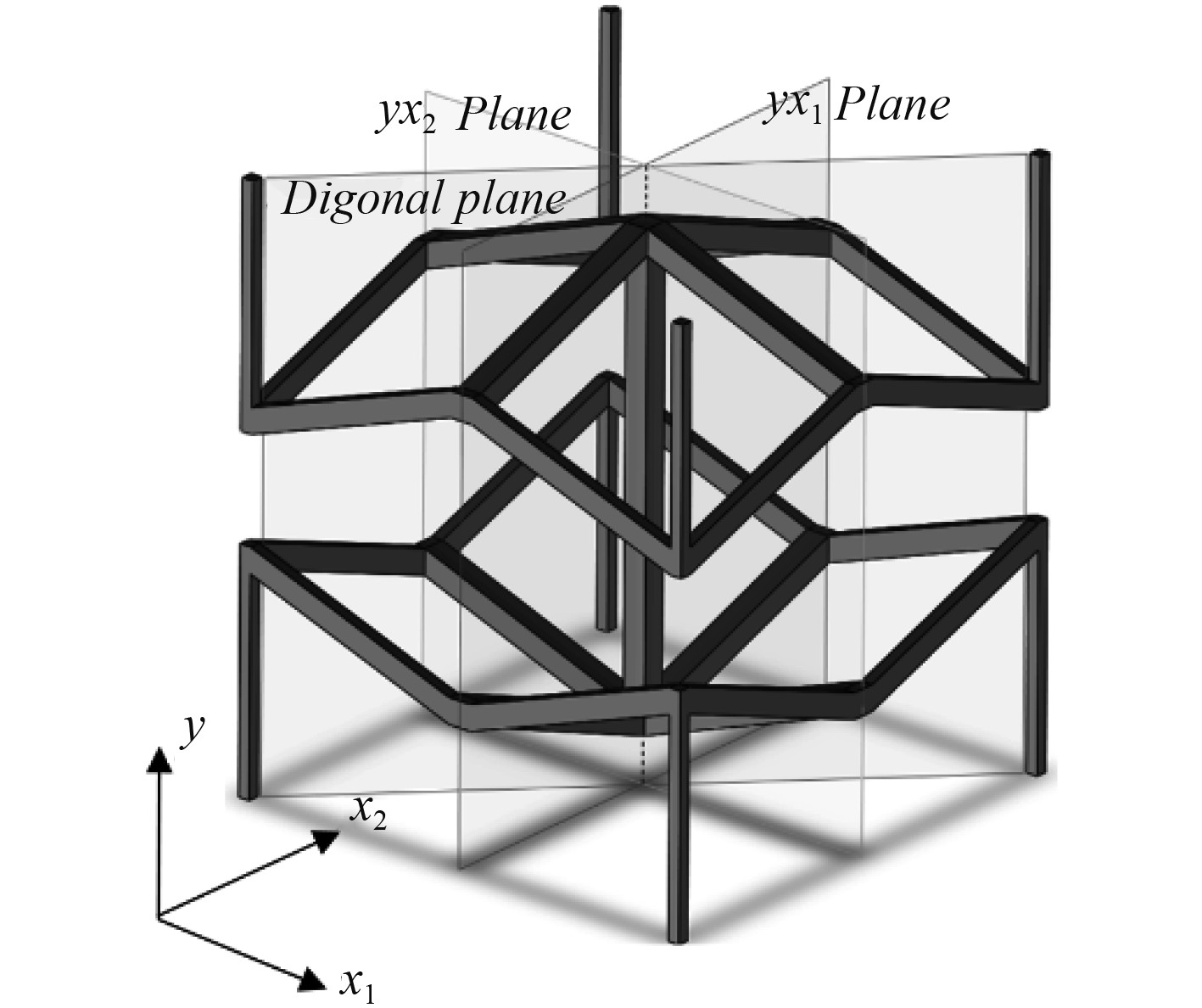
结构在准静态载荷作用下的力学表征是描述其性能重要参数,是结构动力学性能研究及工程应用的基础。本文所提出的新型三维负泊松比蜂窝结构,具备高度的对称性。如图4所示,胞元结构关于竖直平面,水平平面和对角平面对称。因此,该结构在轴
|
图 4 胞元对称性示意图 Fig. 4 The symmetry of unit cell |
为了简化受力分析过程而又不损失结果的可靠性,在进行胞元受力分析前作如下假设:
1)蜂窝结构的力学性能对边界条件的设置较为敏感,蜂窝中所包含的胞元数量会影响结构整体呈现的力学性能。为了消除边界效应带来的影响,假定3D-NPH中的胞元数量无限,以模拟其高度对称的特性,因此可以将3D-NPH结构中任意竖直方向的直杆和内凹方向的斜杆视为等效构件,极大简化了分析过程。
2)3D-NPH胞元中直杆与斜杆的重叠处假定为与杆件构成整体,在受到轴向压载时不发生旋转弯曲变形。因此,胞元中的所有杆件链接处都被认为是刚性的。
3)将胞元中的杆件视为梁单元,为提高计算结果的准确性,采用铁木辛柯梁理论进行分析,同时考虑了胞元在受力产生的弯曲变形、剪切变形及杆件的轴向拉伸或压缩变形。
4)忽略扭转的影响,因为当结构承受对称载荷时,杆件产生的扭转力矩可以被抵消。
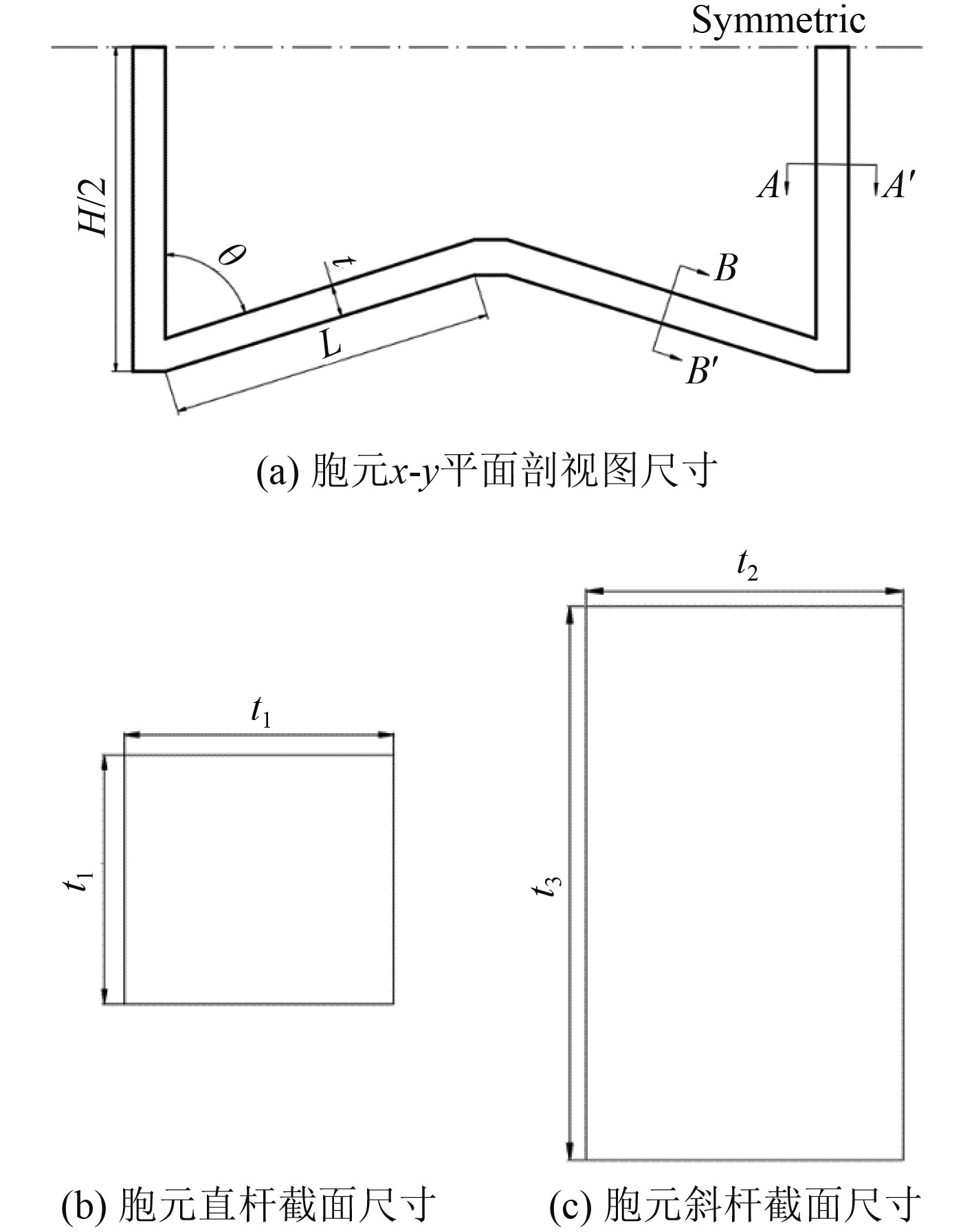
5)假定蜂窝中的所有杆件的截面均为正方形,由于在周期性的阵列过程中,竖直方向的直杆会与4个相邻的胞元所共用,而内凹方向的斜杆会有2个相邻胞元所共享。因此,假定蜂窝中杆件的横截面的边长为t时,则胞元直杆的截面为
|
图 5 胞元几何参数 Fig. 5 Geometry parameters of unit cell |
单胞法是从无限大的多胞结构中取一基本胞元来研究其等效力学性能[23],从而表征整体结构的性能。
当3D-NPH胞元受到y轴向上的单轴压缩时,由于结构本身的对称性,其在

|
图 6 y轴压缩时胞元受力情况 Fig. 6 Loading condition of the unit cell in y direction |
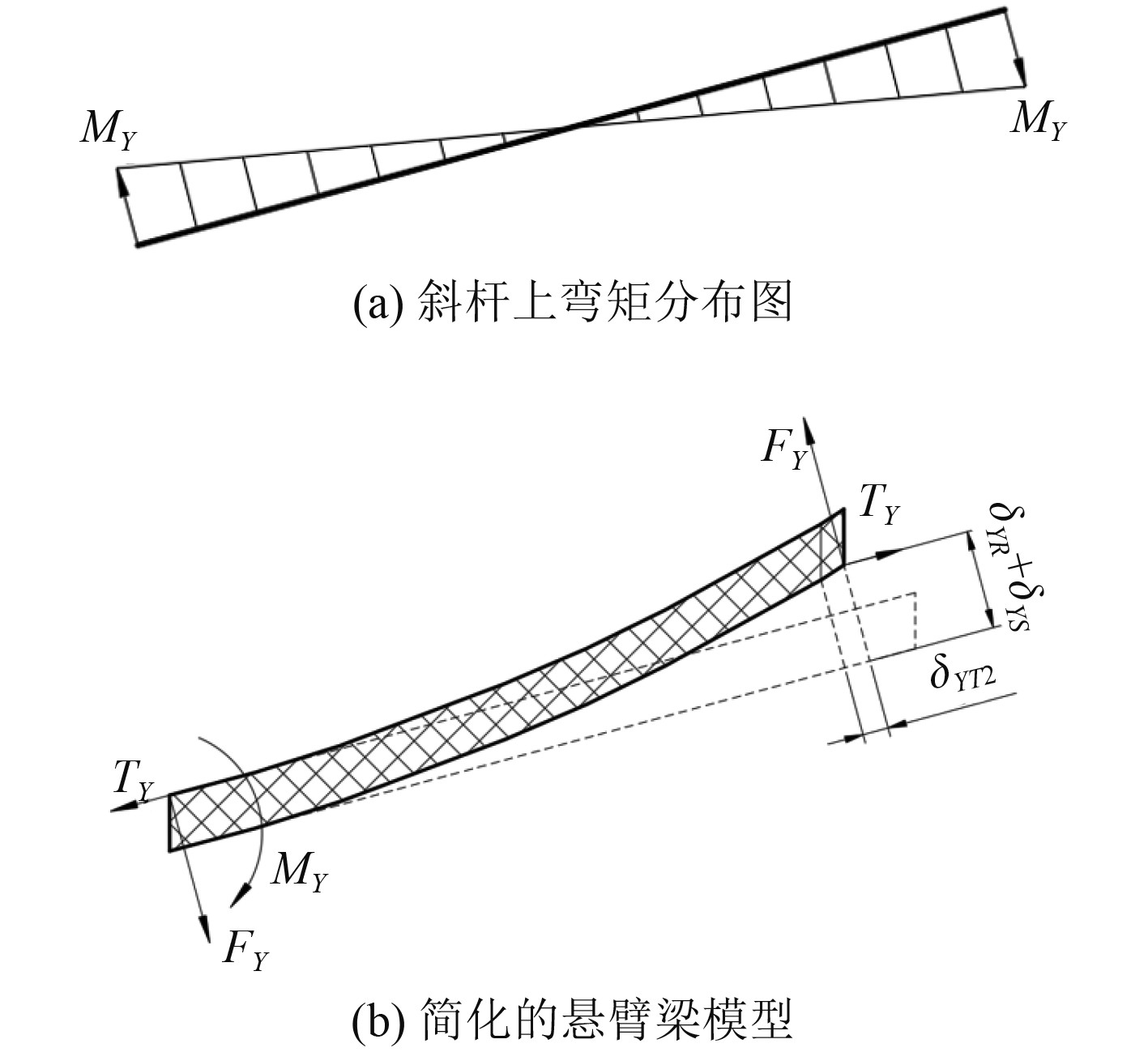
将杆件视为两端固支的梁。如图7(a)所示,竖直方向的直杆在承受载荷时仅产生y轴向上的压缩变形。对于胞元中斜杆而言,杆件中点处的有效力矩为0,杆件受力情况如图7(b)所示。因此,在进一步分析中,可以将斜杆的一半视为悬臂梁,如图8所示。

|
图 7 胞元中杆件受力情况 Fig. 7 Loading condition of the rods in the cell |
|
图 8 斜杆简化力学模型 Fig. 8 Simplified mechanical model of oblique rod |
假设3D-NPH胞元结构受到的为无穷远处应力
| $ \begin{split} {\delta _{YR}} & = \frac{{\partial {U_{YR}}}}{{\partial {F_Y}}} = \frac{\partial }{{\partial {F_Y}}}\mathop \int \nolimits_0^{\frac{L}{2}} \frac{{{M_Y}{{\left( x \right)}^2}}}{{2EI}}{\rm{d}}x =\\ & \mathop \int \nolimits_0^{\frac{L}{2}} \frac{{{M_Y}\left( x \right)}}{{{E_s}I}}\frac{{\partial {M_Y}\left( x \right)}}{{\partial {F_Y}}}{\rm{d}}x = \frac{{{P_Y}{L^3}\sin \theta }}{{4{E_s}{t^4}}}。\end{split} $ | (1) |
式中:
压力
| $ {{\text{δ }}_{YT2}} = \frac{{{\sigma _{Y\infty }}}}{{{E_s}}}\frac{L}{2} = \frac{{{T_Y}L}}{{2{E_s}{t_2}{t_3}}} = \frac{{{P_Y}\cos \theta L}}{{4{E_s}{t^2}}}。$ | (2) |
在斜杆长度与厚度之比较小的情况下,需要考虑剪切力对变形的影响。基于Timoshenko梁理论,杆件由于剪切力产生的位移可以表示为:
| $ {\delta _{YS}} = \frac{{\partial {U_{YS}}}}{{\partial {Q_Y}}} = \frac{{3{Q_Y}L}}{{5AG}} = \frac{{3{P_Y}\sin \theta L}}{{20{t_2}{t_3}\left( {\dfrac{{{E_s}}}{{2\left( {1 + \upsilon } \right)}}} \right)}} = \frac{{3{P_Y}\sin \theta L}}{{10{t^2}\left( {\dfrac{{{E_s}}}{{2\left( {1 + \upsilon } \right)}}} \right)}}。$ | (3) |
式中:
对于胞元中垂直结方向上的直杆,其在受到轴向压缩载荷时,产生的压缩变形为:
| $ {{\text{δ }}_{YT1}} = \frac{{{\sigma _{Y\infty }}}}{{{E_s}}}\frac{H}{2} = \frac{{{P_Y}H}}{{32{E_s}{t^2}}} 。$ | (4) |
总结上述计算结果,胞元分别在x轴和y轴向上的位移为:
| $ \left\{ \begin{aligned} & {{\delta _{Yx}} = [2({\delta _{YR}} + {\delta _{YS}})]{\text{cos}}\theta - 2{{\text{δ }}_{YT2}}\sin \theta } ,\\ & {{\delta _{Yy}} = [2({\delta _{YR}} + {\delta _{YS}})]{\text{sin}}\theta + 2{{\text{δ }}_{YT2}}\cos \theta - {{\text{δ }}_{YT1}}} 。\end{aligned} \right. $ | (5) |
将接触面的作用力和蜂窝胞元的截面积的比值定为等效应力,通过等效应力和等效应变的比值求出等效弹性模量。因此,胞元在y方向的等效弹性模量为:
| $ {E}_{y}=\frac{{\sigma }_{y}}{{\varepsilon }_{y}}=\frac{{\sigma }_{Y\infty }}{\dfrac{[2({\delta }_{YR}+{\delta }_{YS})]\text{sin}\theta +2{\text{δ}}_{YT2}\mathrm{cos}\theta -{\text{δ}}_{YT1}}{\dfrac{H}{2}-L\sin\text{ }\theta }} 。$ | (6) |
胞元等效泊松比可表示为:
| $ \begin{split} {\upsilon }_{yx}& =-\frac{{\varepsilon }_{x}}{{\varepsilon }_{y}}={\upsilon }_{y{x}_{1}}={\upsilon }_{y{x}_{2}}=\\ & -\frac{[2({\delta }_{YR}+{\delta }_{YS})]\text{sin}\theta +2{\text{δ}}_{YT2}\mathrm{cos}\theta -{\text{δ}}_{YT1}}{[2({\delta }_{YR}+{\delta }_{YS})]\text{cos}\theta -2{\text{δ}}_{YT2}\mathrm{sin}\theta }\left(\frac{\dfrac{H}{2}-L{\rm{sin}}\text{ }\theta }{L{\rm{cos}}\theta }\right) \end{split}。$ | (7) |
将无穷远处的压应力
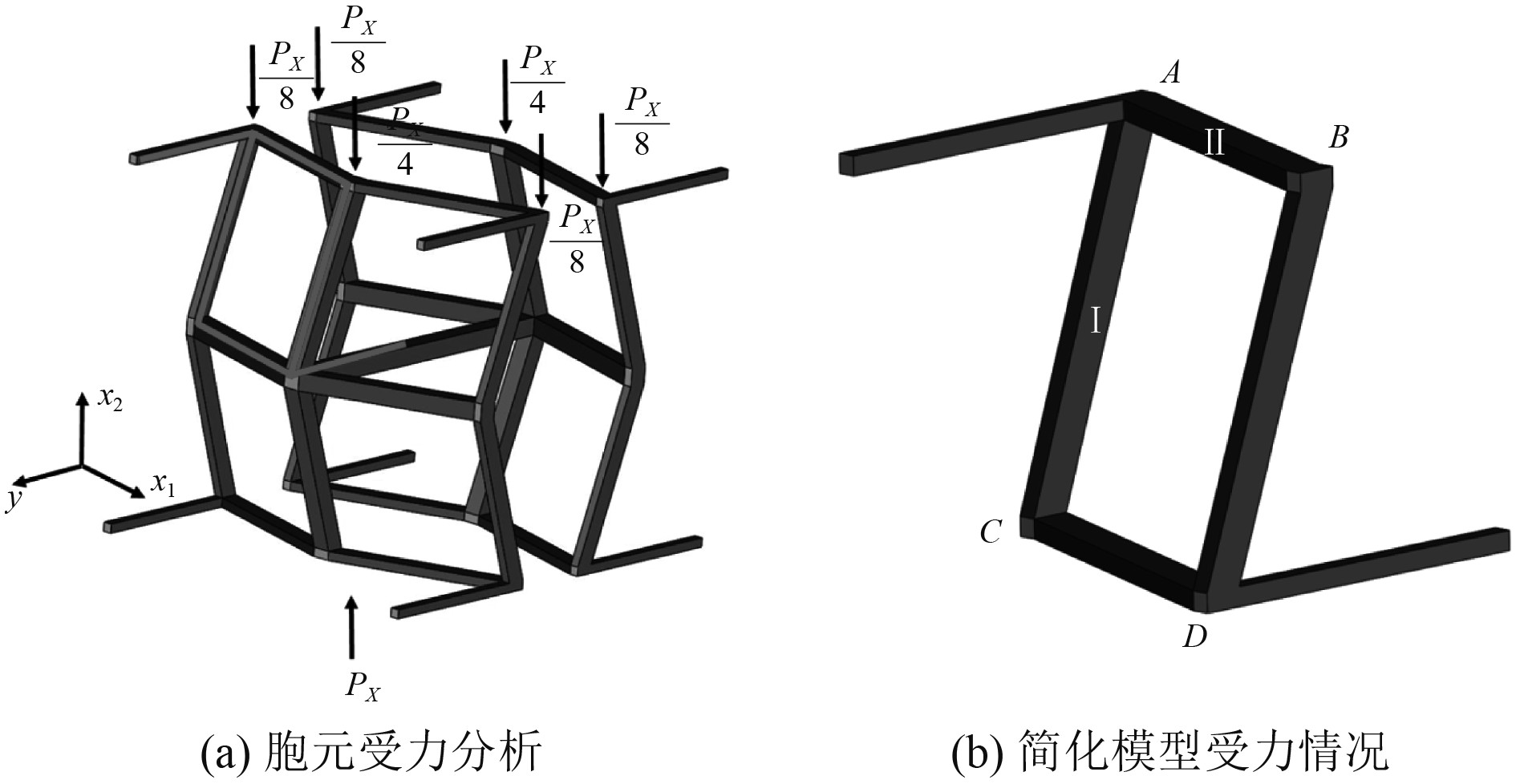
|
图 9 x轴压缩时胞元受力情况 Fig. 9 Loading condition of the unit cell in x direction |
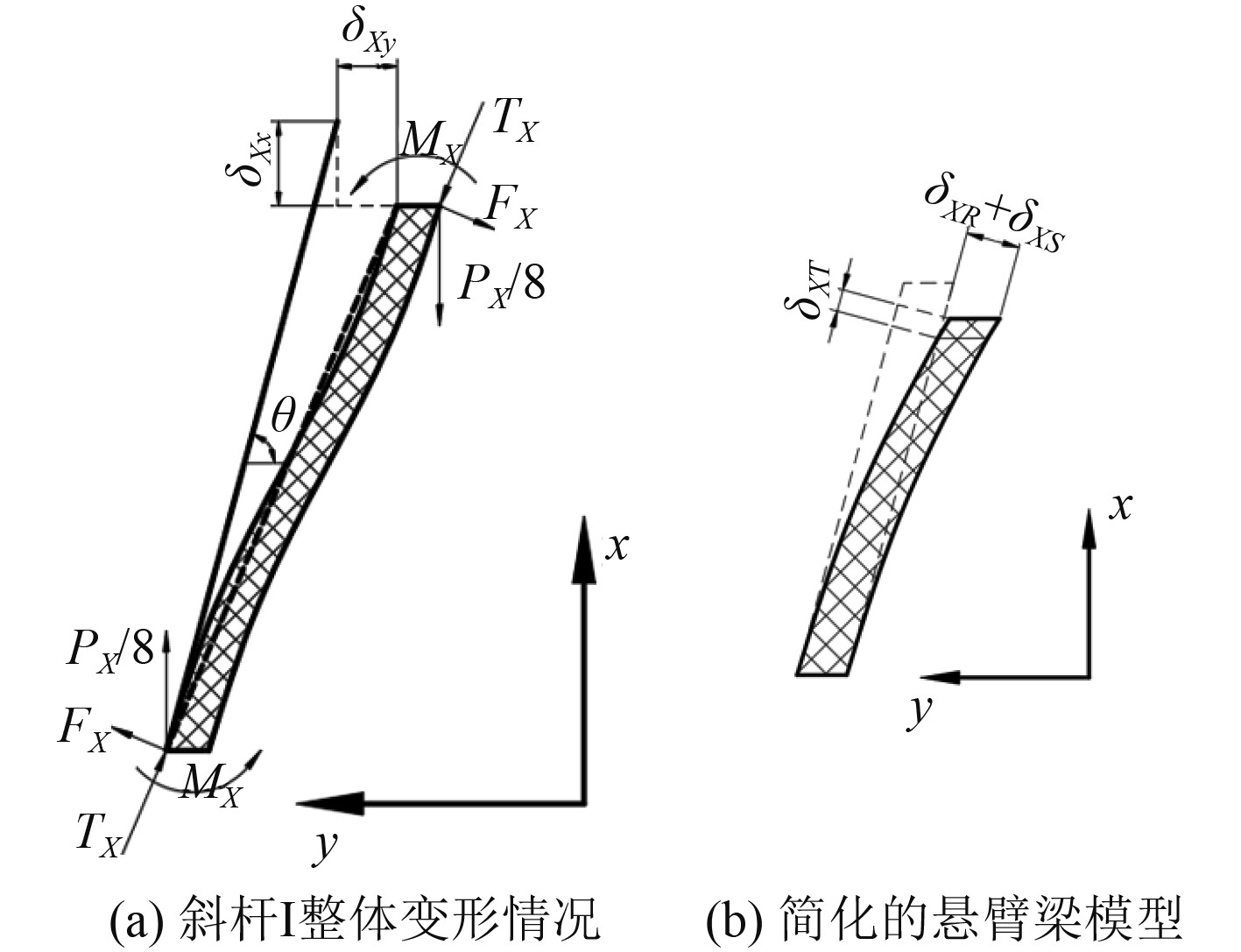
|
图 10 斜杆I受力分析; Fig. 10 Loading condition of oblique rod |
斜杆结构I的整体变形可以分为:压缩变形,剪切变形和弯曲变形,各表达式如下:
弯曲变形
| $ {\delta _{XR}} = \frac{{({P_X}\cos \theta ){L^3}}}{{16E{t_2}t_3^3}} = \frac{{({P_X}\cos \theta ){L^3}}}{{8{E_s}{t^4}}} 。$ | (8) |
式中:
压缩变形
| $ {{\text{δ }}_{XT}} = \frac{{{\sigma _T}}}{{{E_s}}}\frac{L}{2} = \frac{{{T_X}L}}{{2{E_s}{t_2}{t_3}}} = \frac{{{P_X}L\sin \theta }}{{8{E_s}{t^2}}} 。$ | (9) |
式中:
剪切变形
| $ {\delta _{XS}} = \frac{{3{P_X}L\cos \theta }}{{40{t_2}{t_3}\left( {\dfrac{{{E_s}}}{{2\left( {1 + \upsilon } \right)}}} \right)}} = \frac{{3{P_X}L\cos \theta }}{{20{t^2}\left( {\dfrac{{{E_s}}}{{2\left( {1 + \upsilon } \right)}}} \right)}}。$ | (10) |
式中:
因此,胞元在x轴上的等效弹性模量及胞元的等效泊松比可表达为:
| $ {E}_{x}=\frac{{\sigma }_{x}}{{\varepsilon }_{x}}=\frac{{\sigma }_{X\infty }}{\dfrac{[2({\delta }_{XR}+{\delta }_{XS})]\mathrm{cos}\theta +2{\text{δ}}_{XS}\mathrm{sin}\theta }{L{\rm{sin}}\text{ }\theta }},$ | (11) |
| $ {\upsilon }_{xy}=-\frac{{\varepsilon }_{y}}{{\varepsilon }_{x}}={\upsilon }_{{x}_{1}y}={\upsilon }_{{x}_{2}y}=-\frac{{\delta }_{x}}{{\delta }_{y}}\left(\frac{\dfrac{H}{2}-L{\rm{cos}}\text{ }\theta }{L{\rm{sin}}\text{ }\theta }\right) 。$ | (12) |
设计3D-NPH结构压缩试验以验证其力学性能解析公式的合理性。利用快速成型技术(3D 打印),选用韧性加强的光敏树脂材料Somos® EvoLVe 128来制作构件,该种材料更加接近于金属的材料特性,能很好地体现负泊松比材料的拉胀特性。
3D-NPH在x轴与y轴向呈现的力学性能不相同,对于同一胞元形状的芯层均设计了2种试件,每种试件各由内凹角θ=65°、70°和75°的胞元组成。图11为内凹角θ=65°的试件模型。

|
图 11 3D-NPH结构试件 Fig. 11 3D-NPH structure specimen |
所设计试件在长度与宽度方向上均包含4个完整胞元,满足规范GB1453-2005《夹层结构或芯子平压性能试验方法》的要求。为了便于试验设备进行加载,在各个试件受载的两端设计了一个40 mm宽的平板段。各试件中胞元的直杆长度均为H=20 mm,斜杆长L=10 mm,杆件厚度t=2 mm。通过MTS(Mechanical Testing & Simulation)电子万能试验机对3D打印方法制备的3D-NPH试件施加轴向压缩载荷。试验过程中采用位移加载的形式,柱头的移动速度恒定在1 mm/min,模拟出结构在准静态下的受力状态。
提取MTS试验机压头得到的力-位移曲线中的数据可得到各个3D-NPH试件的等效弹性模量。根据经典的弹性模量公式,试件的等效弹性模量可通过下式求得:
| $ {E^{exp}} = \frac{{{\sigma ^{exp}}}}{{{\varepsilon ^{exp}}}} ,$ | (13) |
| $ {\sigma ^{exp}} = \frac{{{F^{exp}}}}{{{S^{exp}}}},$ | (14) |
| $ {\varepsilon ^{exp}} = \frac{{{\delta ^{exp}}}}{{H_V^{exp}}}。$ | (15) |
其中:
为消除边界效应对试验数据的影响,选取如图12所示的试件中心区域的胞元作为位移采集对象。

|
图 12 3D-NPH试件标定点 Fig. 12 Calibration points of 3D-NPH specimen |
选取区域内胞元上的9个节点作为标定点,分别按行标记为A1~3、B1~3及C1~3。假定变形后的标定点记为A′1~3,B′1~3及C′1~3,则变形前后竖直方向和水平方向的位移可表示为:
| $ \Delta {{{y}}_{exp}} = \frac{{\displaystyle\sum \nolimits_1^3 \left( {{A_i}{C_i} - {{A'}_i}{{C'}_i}} \right)}}{3},$ | (16) |
| $ \Delta {{{x}}_{exp}} = \frac{{\displaystyle \sum \nolimits_1^3 \left( {{A_i}{B_i} - {{A'}_i}{{B'}_i}} \right)}}{3} 。$ | (17) |
而3D-NPH试件的等效泊松比值计算下公式为:
| $ {\upsilon _{xexp}} = \frac{{{\varepsilon _{yexp}}}}{{{\varepsilon _{xexp}}}} = \frac{{\dfrac{{\Delta {{{y}}_{exp}}}}{{{y_o}}}}}{{\dfrac{{\Delta {{{x}}_{exp}}}}{{{x_o}}}}},$ | (18) |
| $ {\upsilon _{yexp}} = \frac{{{\varepsilon _{xexp}}}}{{{\varepsilon _{yexp}}}} = \frac{{\dfrac{{\Delta {{{x}}_{exp}}}}{{{x_o}}}}}{{\dfrac{{\Delta {{{y}}_{exp}}}}{{{y_o}}}}} 。$ | (19) |
式中,
提取MTS试验机压头得到的力-位移曲线中的数据代入式(11)中可得到各个3D-NPH试件的等效弹性模量。利用试件x、y 方向上选取节点的位移的数据结果代入式(18)与式(19)即可计算的得到相应试件的等效泊松比值。
利用有限元软件对3D-NPH胞元进行模拟仿真。基体材料采用Somos® EvoLVe 128,设置为理想弹塑性模型,具体数据如表1所示。
|
|
表 1 Somos® EvoLVe 128材料属性 Tab.1 Material properties of Somos® EvoLVe 128 |
有限元模型与各试件中的胞元尺寸保持一致。采用8节点实体单元、缩减积分方程和沙漏控制方法建立有限元模型,如图13所示。在综合考虑模型的复杂度、仿真精度和效率的基础上,选择网格大小为1 mm网格对模型进行划分。分别在胞元的上表面和侧表面上(左面)施加沿y方向和x方向的1 mm/min的强制位移,以研究结构在相应方向上的力学性能。

|
图 13 胞元有限元模型 Fig. 13 FEA model of unit cell |
提取试验结果、有限元仿真结果、理论解,进行对比验证。图14及图15分别为3D-NPH结构在y轴和x轴向上受压时,胞元泊松比值、等效弹性模量(
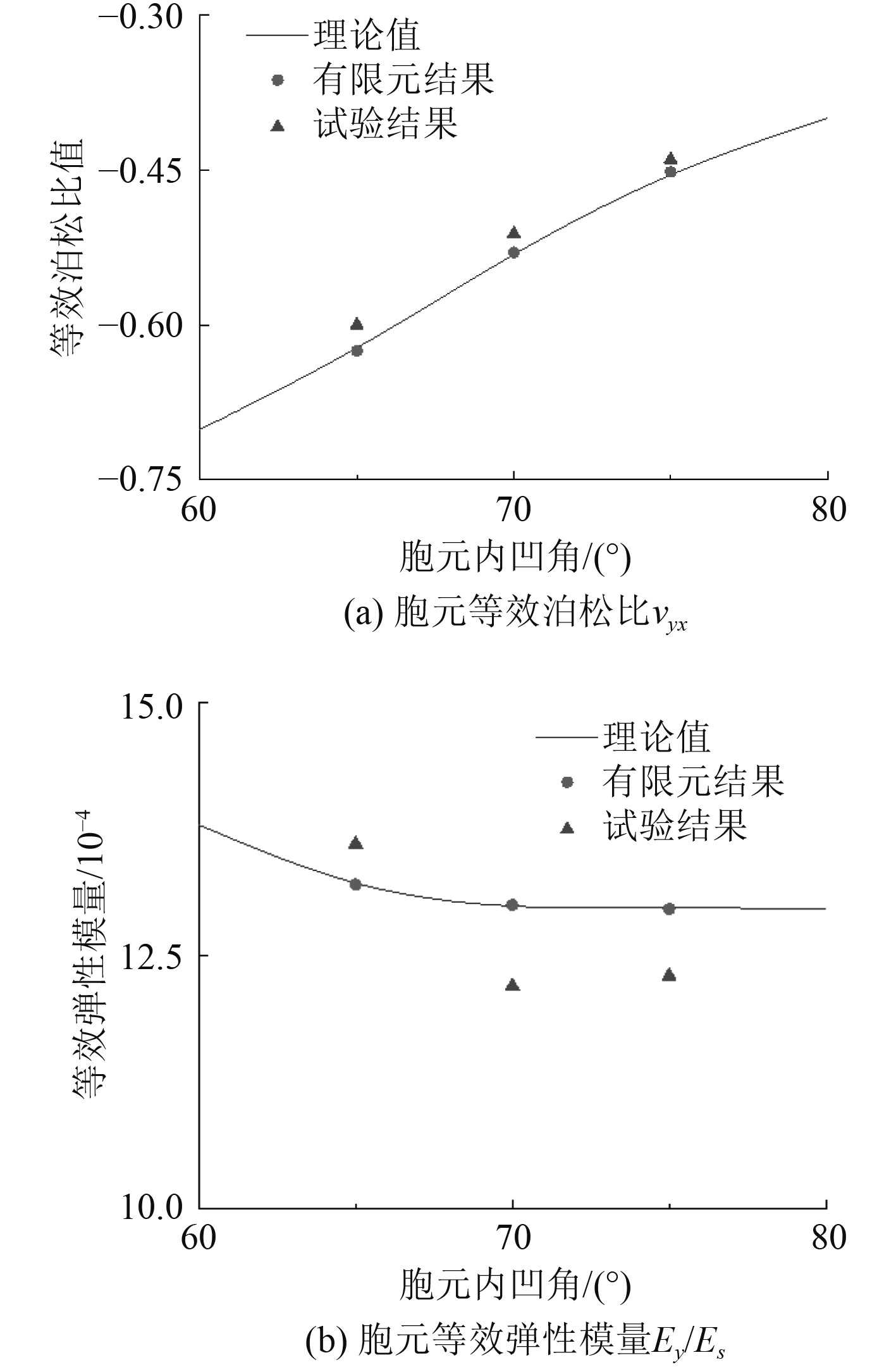
|
图 14 理论解、有限元及试验结果对比(y轴压缩) Fig. 14 Comparison of analytical and FEA Results under compression in y direction |
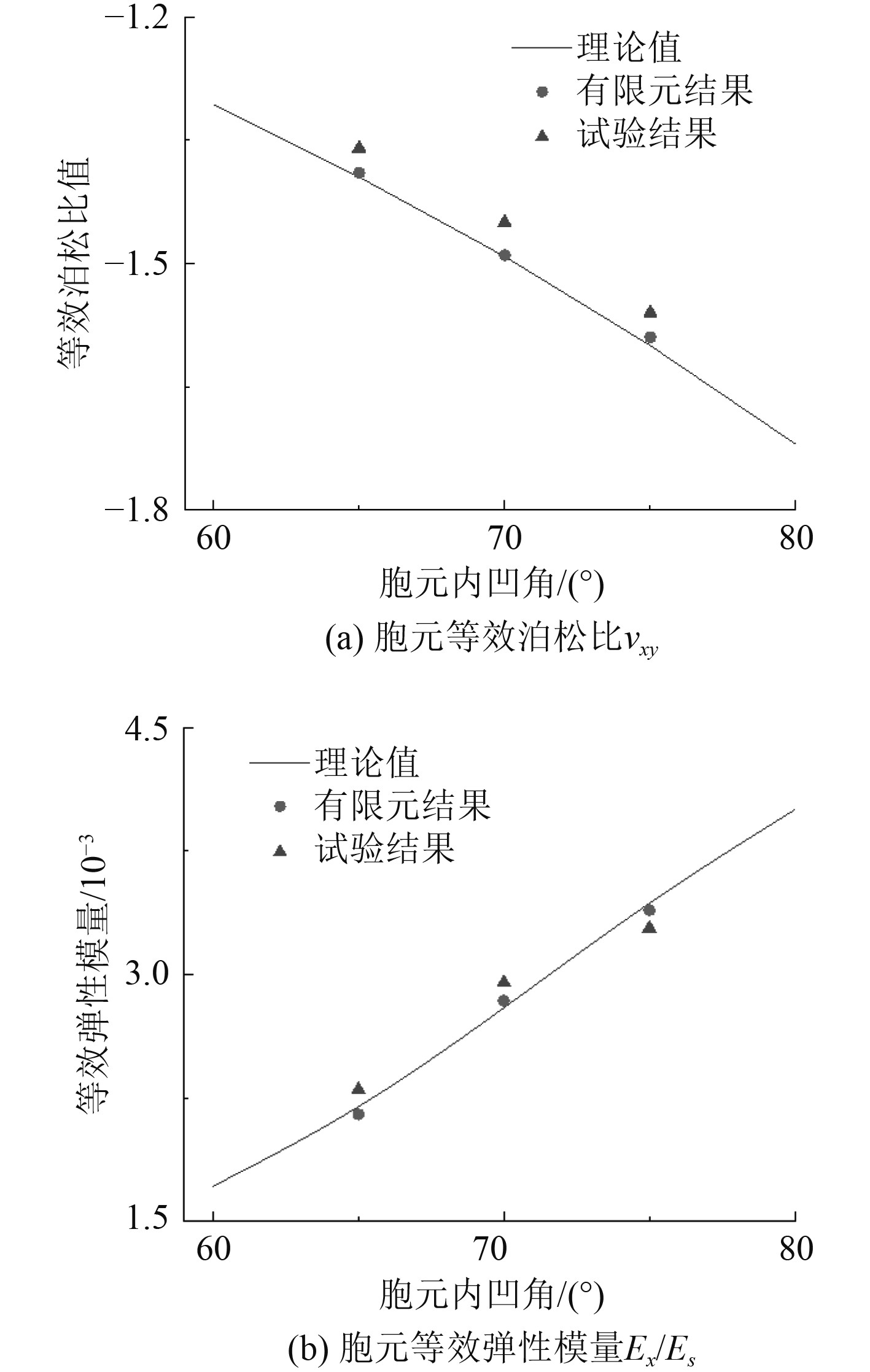
|
图 15 理论解、有限元及试验结果对比(x轴压缩) Fig. 15 Comparison of analytical and FEA Results under compression in x direction |
可以看出,解析解结果与有限元仿真结果基本一致,产生误差原因可能是由理论分析过程中的蜂窝边界条件简化假设所致。试验结果与理论解之间的误差也在合理的范围之内,在2.4%~5.9%,试件本身可能存在的缺陷,以及试件在持续受压的过程中可能产生的轻微面外位移将导致误差产生。总体来看,有限元结果与试验结果均与理论值之间的存在良好一致性,验证了本文所建立3D-NPH结构力学性模型的有效性。
4 胞元参数对力学性能的影响分析选取
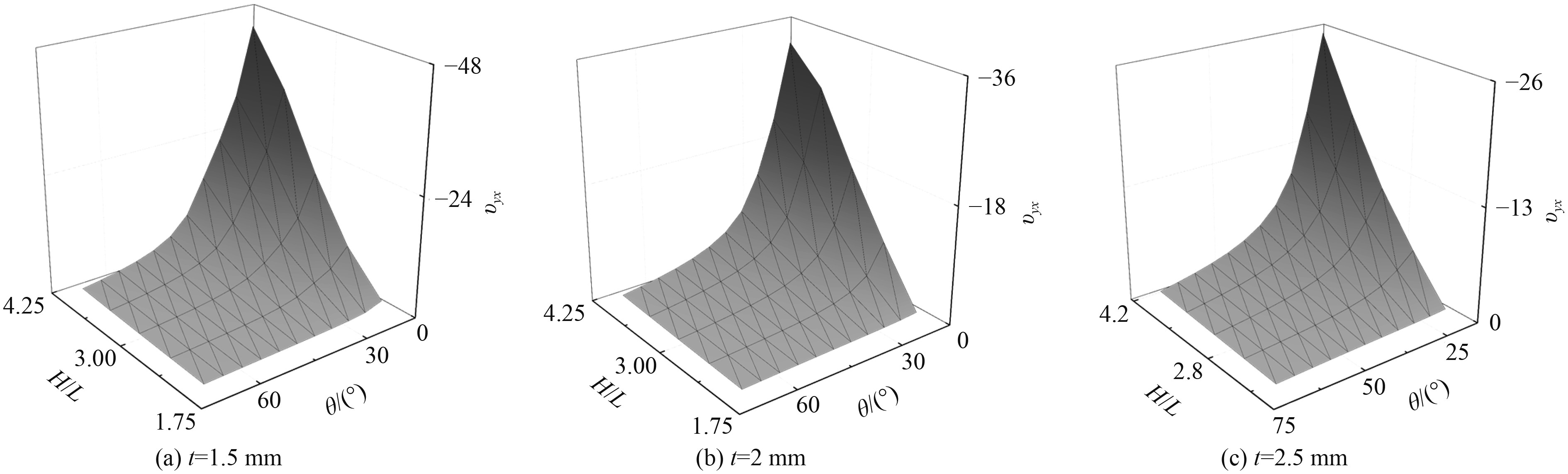
3D-NPH结构在y轴向上的等效泊松比变化规律如图16所示。可以看出,胞元等效泊松比的绝对值随着H/L的增大而增大。在L固定的情况下,H/L的增加意味着胞元在y方向上尺寸的增加,而x方向尺寸保持不变,结构的拉胀效应(auxetic)会更加明显。同时,当θ减小时,结构负泊松比效应愈加明显。横向对比,杆件的增厚会使得胞元的泊松比效应下降,且杆件厚度越大,泊松比值对几何参数H/L和θ的敏感度越低。其原因可能是由于杆件厚度的增加,胞元占据空间的密度越大,留给胞元发生收缩变形的空间被压缩,致使其负泊松比效应被削弱。
|
图 16 y轴胞元的泊松比随几何参数H/L、θ和t的变化趋势 Fig. 16 Variation of poisson's ratio of cells in y-axis with geometric parameters H/L、θ and t |
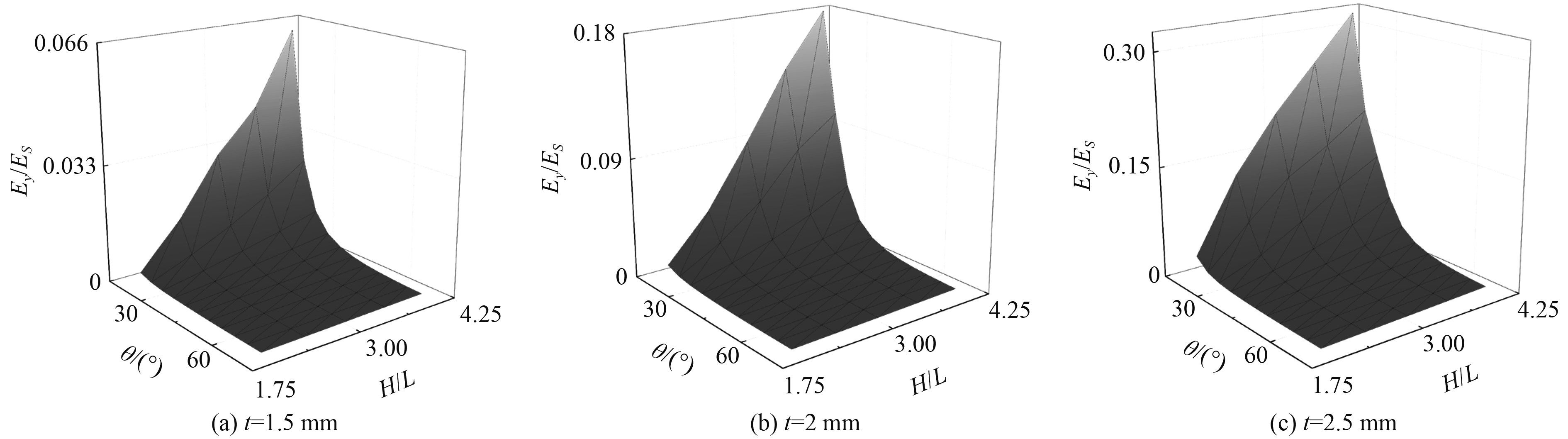
θ、H/L和t对3D-NPH结构等效弹性模量
|
图 17 y轴的等效弹性模量随几何参数H/L、θ和t的变化趋势 Fig. 17 Variation of normalized effective modulus of cells in y-axis with geometric parameters H/L,θ and t |
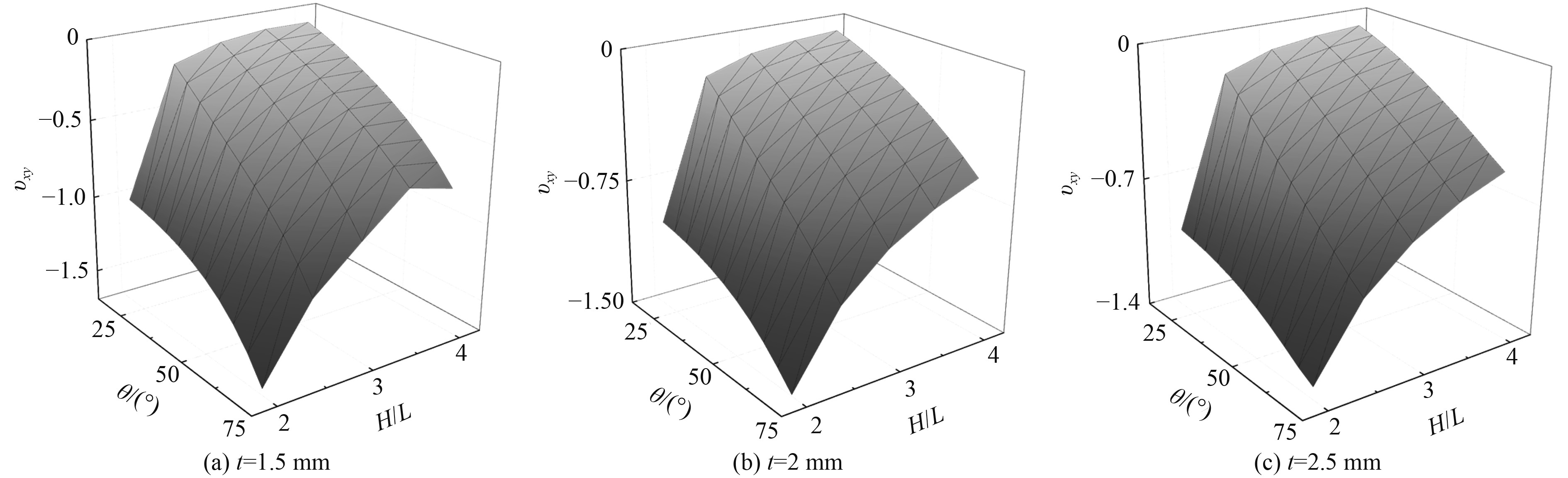
3D-NPH在x轴向上的等效泊松比随θ、t和H/L的变化规律如图18所示。可以看出,结构在x轴向等效泊松比的绝对值随着H/L的增加而减小。当L固定,H/L的增加意味着胞元在y方向尺寸的增加,胞元在各方向上产生的位移保持不变,则y向应变
|
图 18 x轴胞元的泊松比随几何参数H/L、θ和t的变化趋势 Fig. 18 Variation of poisson's ratio of cells in x-axis with geometric parameters H/L,θ and t |
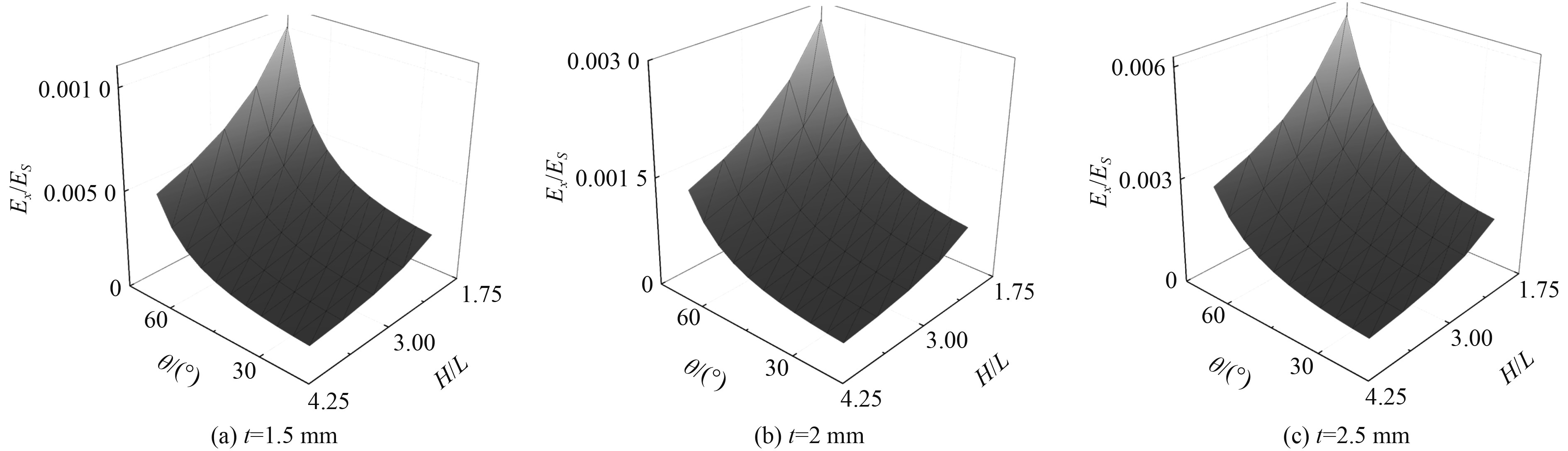
3D-NPH等效弹性模量
|
图 19 x轴的等效弹性模量随几何参数H/L、θ和t的变化趋势 Fig. 19 Variation of normalized effective modulus of cells in x-axis with geometric parameters H/L,θ and t |
本文基于典型二维内凹六边形提出一种新型三维负泊松比蜂窝(3D-NPH)结构,建立了该种3D-NPH结构的等效力学模型,并开展轴向压缩试验对理论结果进行验证。通过研究可得到以下结论:
1)本文设计的3D-NPH在3个维度上均呈现负泊松比效应,其构型具有高度对称性,在轴
2)基于Timoshenko梁理论建立的胞元等效力学模型考虑了弯曲、拉压以及剪切变形,通过试验验证表明,该力学模型具有较高准确度。
3)胞元内凹角θ、杆厚t和胞元直杆与斜杆长度之H/L是影响3D-NPH结构力学表征的重要参数。杆厚t的增加对于3D-NPH胞元的x及y轴向的弹性模量均有提升作用,但会抑制负泊松比效应;而H/L与凹角θ对力学性能的影响与胞元受力方向息息相关。
分析提供了3D-NPH结构负泊松比效应及承载能力对各项几何参数的敏感程度,可作为其在不同运用场景下参数优选的依据,为3D-NPH在舰船结构轻量化、高性能化设计领域中的运用提供理论依据。
| [1] |
ARGATOV II, Guinovart-Díaz R, SABINA F J. On local indentation and impact compliance of isotropic auxetic materials from the continuum mechanics viewpoint[J]. International Journal of Engineering Science, 2012, 54(5): 42-57. |
| [2] |
LAKES R S, ELMS K. Indentability of conventional and negative Poisson's ratio foams[J]. Journal of Composite Materials, 1992, 27(12): 1193-1202. |
| [3] |
CHEN C P, LAKES R S. Micromechanical analysis of dynamic behavior of conventional and negative Poisson’s ratio foams[J]. Journal of Engineering Materials and Technology, 1996, 118(3): 285-288. DOI:10.1115/1.2806807 |
| [4] |
MA Y, SCARPA F, ZHANG D, et al. A nonlinear auxetic structural vibration damper with metal rubber particles[J]. Smart Materials and Structures, 2013, 22(8), Article ID 084012.
|
| [5] |
IMBALZANO G, TRAN J P, NGO T, et al. Three-dimensional modelling of auxetic sandwich panels for localised impact resistance[M]. Journal of Sandwich Structures and Materials. 2015, 19(3): 291−216.
|
| [6] |
HOU S, LIU T, ZHANG Z, et al. How does negative Poisson’s ratio of foam filler affect crashworthiness?[J]. Materials & Design, 2015, 82: 247-259. |
| [7] |
XIN R, DAS R, TRAN P, et al. Auxetic metamaterials and structures: a review[J]. Smart Materials & Structures, 2018, 27(2).
|
| [8] |
GIBSON L J, ASHBY M F, SCHAJER G S. The mechanics of two-dimensional cellular materials[J]. Proceedings of the Royal Society of London. 1982, 382(1782): 43−59.
|
| [9] |
CHOI J B, LAKES R S. Analysis of elastic modulus of conventional foams and of re-entrant foam materials with a negative Poisson's ratio[J]. International Journal of Mechanical Sciences. 1995, 37(1): 51−59.
|
| [10] |
PRALL D, LAKES R S. Properties of a chiral honeycomb with a Poisson's ratio of-1[J]. International Journal of Mechanical Sciences. 1997, 39(3): 305−307.
|
| [11] |
ALDERSON A, ALDERSON K L, ATTARD D, et al. Elastic constants of 3-, 4- and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading[J]. Composites Science and Technology. 2010, 70(7): 1042−1048.
|
| [12] |
THEOCARIS P S, STAVROULAKIS G E, PANAGIOTOPOULOS P D. Negative Poisson's ratios in composites with star-shaped inclusions: a numerical homogenization approach[J]. Archive of Applied Mechanics. 1997, 67(4): 274−286.
|
| [13] |
JOSEPH N. G, RUBEN G, BRIAN E, et al. Auxetic behaviour in non-crystalline materials having star or triangular shaped perforations[J]. Journal of Non-Crystalline Solids. 2010, 356(37): 1980−1987.
|
| [14] |
LARSEN U, SIGNUND O, BOUWSTA S. Design and fabrication of compliant micromechanisms and structures with negative Poisson's ratio[J]. Journal of Microelectromechanical Systems. 1997, 6(2): 99−106.
|
| [15] |
李谱, 乐京霞, 李晓彬, 等. 厚度梯度型箭形负泊松比蜂窝基座抗冲击性能[J]. 爆炸与冲击, 2020, 40(7): 27-37. DOI:10.11883/bzycj-2019-0414 |
| [16] |
EVANS K E, NKANSAH M A, HUTCHINSON I J. Auxetic foams: modelling negative Poisson's ratios[J]. Acta Metallurgica Et Materialia. 1994, 42(4): 1294.
|
| [17] |
YANG L, HARRYSSON O, WEST H, et al. Mechanical properties of 3D re-entrant honeycomb auxetic structures realized via additive manufacturing[J]. International Journal of Solids and Structures. 2015, 69-70: 475-490.
|
| [18] |
WANG X T, WANG B, LI X W, et al. Mechanical properties of 3D re-entrant auxetic cellular structures[J]. International Journal of Mechanical Sciences. 2017, 131−132: 396−407.
|
| [19] |
GAO Q, GE C Q, ZHUANG W C, et al. Crashworthiness analysis of double-arrowed auxetic structure under axial impact loading[J]. Materials & Design. 2019, 161: 22−34.
|
| [20] |
周冠. 新型负泊松比结构关键技术研究及其在车身设计中的应用[D]. 长沙: 湖南大学, 2015.
|
| [21] |
YANG L. Structural design, optimization and application of 3d re-entrant auxetic structures [J]. Dissertations & Theses Gradworks, 2011: 3497326.
|
| [22] |
ALMGREN R F. An isotropic three-dimensional structure with Poisson's ratio=−1[J]. Journal of Elasticity. 1985, 15(4): 427−430.
|
| [23] |
GIBSON L J, ASHBY M F. Cellular solids: structure and properties[J]. Cellular Solids, 1988(9): 499-521.
|
 2023, Vol. 45
2023, Vol. 45

