环肋圆柱耐压壳结构因其具备优异的结构性能,在潜艇或深潜器的结构设计中具有广泛应用,但随着现代潜器不断朝着大深度水下作业的发展,耐压壳结构的重要性和要求与日俱增,首先一方面耐压壳既能承受巨大静水压力,保证舱室内部人员及设备的安全性,同时又组成一个水密空间,是浮力的主要提供者;另一方面,在设计过程中,其结构型式尽量合理,在满足强度和稳定性的前提下尽可能使耐压壳结构轻量化,这样不仅节省建造材料,同时能将省下的重量转化为有效装载[1]。因此,耐压壳结构的优化设计是一项极其重要的工作,具备实际的工程价值。
针对环肋圆柱壳结构优化设计,国内外学者做了大量研究。Bagheri等[2]采用遗传算法对加筋圆柱壳进行结构优化,以最小结构重量作为目标函数,研究了不同目标加权系数和边界条件下对最优解的影响。Sadeghifar等[3]采用遗传算法以最小结构重量和最大轴向屈曲应力为目标函数进行优化,研究了不同截面形状筋材加筋下对优化结果的影响。Rao等[4]引入非线性约束优化技术,对静水压力下加筋柱壳最小质量问题进行研究。王燕[5]采用分段优化的思想,将耐压壳分成若干特征段分别进行优化设计,对环肋圆柱壳进行强度和稳性有限元分析的基础上又构建了二阶响应面和Kriging近似模型,使用混合整型优化方法得到最低结构重量。余俊等[6]针对深海高强度钢,以单位体积重量最轻为目标,采用多岛遗传算法和二次规划法对环肋圆柱壳进行整体和局部寻优,提出了适用于该高强度钢优化结果的拟合公式。黄加强[7]提出一种适用于超长舱段环肋圆柱壳的变刚度设计方法,结果表明,使用该方法相较于等刚度可获得更轻的结构重量。Gang H等[8]探索了几种不同加筋形式的圆柱壳,并分别给出了强度和稳定性的分析方法,得出其中最佳的加筋形式,可为实际工程提供参考。
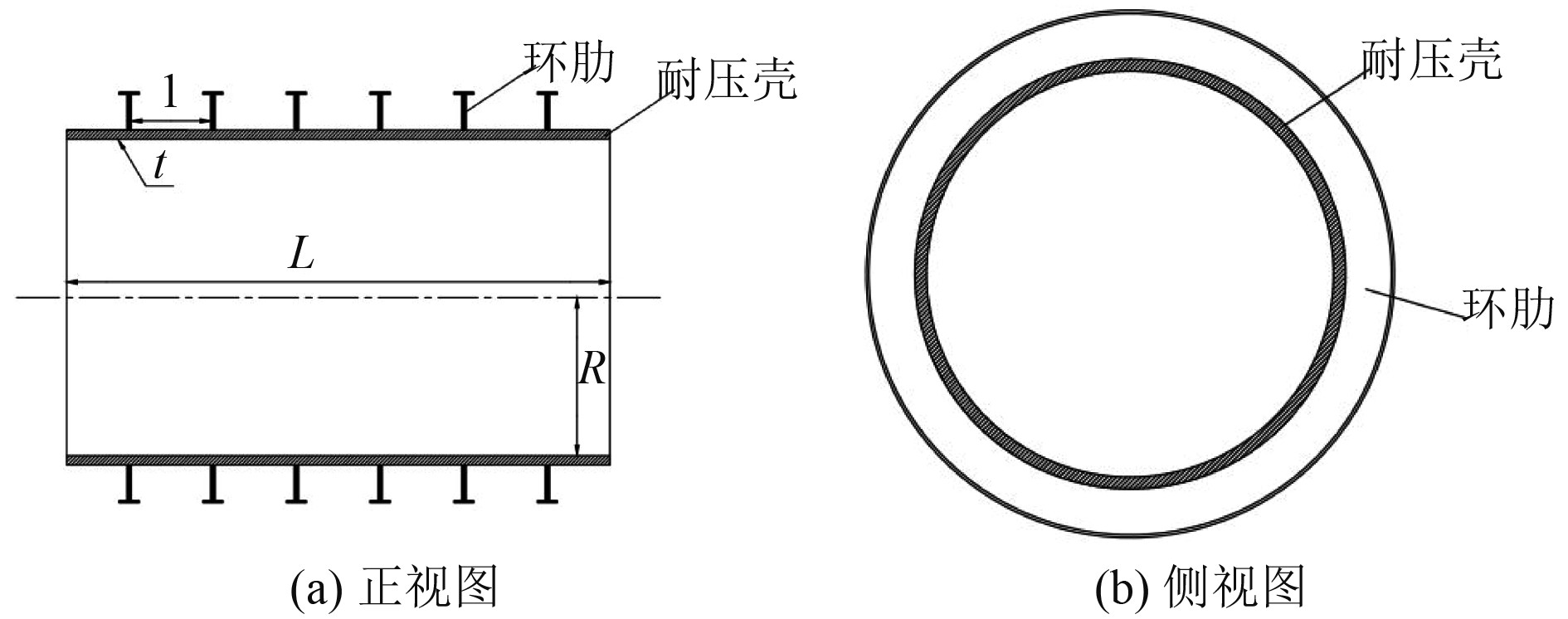
1 环肋圆柱壳结构模型及计算分析 1.1 环肋圆柱壳模型环肋圆柱耐压壳结构如图1所示。选用某潜器方案设计下的环肋圆柱耐压壳作为示例,对其进行优化,该方案下结构尺寸为:环肋圆柱壳长度L=7 m,半径R=3 m,肋距l=600 mm,板厚t=28 mm,肋骨T型材面板长度b=80 mm,腹板高度h=224 mm,面板宽度
|
图 1 环肋圆柱壳结构示意图 Fig. 1 The diagrammatic drawing of ring-stiffened cylindrical shell |
|
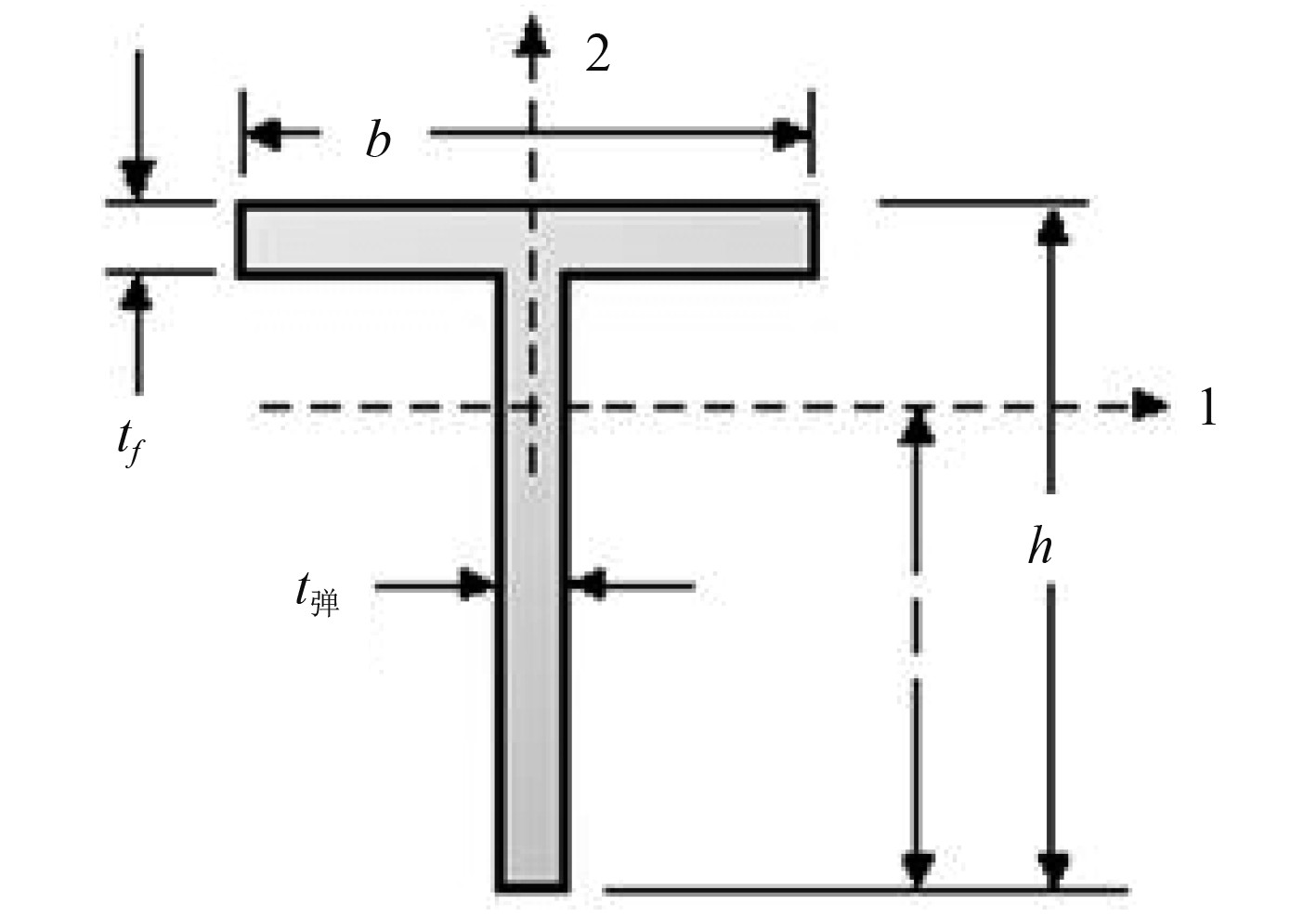
图 2 T型材尺寸参数示意图 Fig. 2 Schematic diagram of T profile size parameters |
|
|
表 1 高强度钢材料属性 Tab.1 High strength steel material properties |
计算环肋圆柱壳强度可采用理论解析法或有限元分析法。理论解析法即按照规范中提供的经验公式计算结构应力及稳定性,而有限元法即借用计算机中的有限元软件进行结构分析,本文使用Abaqus软件建立该结构模型,其中圆柱壳采用壳单元S4R模拟,肋骨采用梁单元B31模拟,网格边长为0.1 m,圆柱壳两端采取刚性固定边界条件,在壳体外表面施加6.4 MPa的载荷模拟极限潜深下的静水压强,接着通过静力分析可得到结构的应力分布。
1.2 环肋圆柱壳结构计算规范中提供了环肋圆柱壳结构强度及稳定性需要校核的部位和计算方法,其中必须作校核的是:相邻肋骨跨中处的壳板中面周向应力,肋骨跨端的壳板内表面纵向应力、肋骨应力,相邻肋骨间壳板失稳临界压力以及舱段总体稳性,具体计算公式如下:
| $ \left\{ \begin{gathered} {u_1} = u\sqrt {1 - \gamma },\;\;\;\;\;\;\;\;\;\;\;\;\;\;{u_2} = u\sqrt {1 + \gamma },\;\;\;\;\;\; \\ u = \frac{{\sqrt[4]{{3(1 - {\mu ^2})}}}}{2}\frac{l}{{\sqrt {Rt} }},\;\;\;\gamma = \frac{{\sqrt {3(1 - {\mu ^2})} }}{2}\frac{{{P_j}{R^2}}}{{E{t^2}}} 。\\ \end{gathered} \right.\; $ | (1) |
式中:
| $ \left\{ \begin{aligned} & {F_1}({u_1},{u_2}) = \frac{{\sqrt {1 - {\gamma ^2}} ({\rm{ch}}2{u_1} - \cos 2{u_2})}}{{{F_5}({u_1},{u_2})}},\\ & {F_2}({u_1},{u_2}) = \frac{{3(1 - 0.5\mu )({u_2}{\rm{sh}}2{u_1} - {u_1}\sin 2{u_2})}}{{\sqrt {3(1 - {\mu ^2})} {F_5}({u_1},{u_2})}} ,\\ & {F_3}({u_1},{u_2}) = \frac{{6(1 - 0.5\mu )({u_1}{\rm{ch}}{u_1}\sin {u_2} - {u_2}{\rm{sh}}{u_1}\cos {u_2})}}{{\sqrt {3(1 - {\mu ^2})} {F_5}({u_1},{u_2})}},\\ & {F_4}({u_1},{u_2}) = \frac{{2(1 - 0.5\mu )({u_1}{\rm{ch}}{u_1}\sin {u_2} + {u_2}{\rm{sh}}{u_1}\cos {u_2})}}{{{F_5}({u_1},{u_2})}} ,\\ & {F_5}({u_1},{u_2}) = {u_2}{\rm{sh}}2{u_1} + {u_1}\sin 2{u_2} ,\\ & \beta = \frac{{lt}}{F} 。\end{aligned} \right. $ | (2) |
式中:
1)相邻肋骨跨中处的壳板中面轴向应力
| $ \left\{ \begin{gathered} {K_1} = 1 - \frac{{{F_4}({u_1},{u_2})}}{{1 + \beta {F_1}({u_1},{u_2})}} ,\\ \sigma _2^0 = {K_1}\frac{{{P_j}R}}{t} 。\\ \end{gathered} \right. $ | (3) |
2)肋骨跨端的壳板内表面纵向应力
| $ \left\{ \begin{gathered} {K_2} = 0.5 + \frac{{{F_2}({u_1},{u_2})}}{{1 + \beta {F_1}({u_1},{u_2})}} ,\\ {\sigma _1} = {K_2}\frac{{{P_j}R}}{t} 。\\ \end{gathered} \right. $ | (4) |
3)肋骨应力
| $ \left\{\begin{gathered} {K_f} = (1 - \frac{\mu }{2})\frac{{\beta {F_1}({u_1},{u_2})}}{{1 + \beta {F_1}({u_1},{u_2})}},\\ {\sigma _f} = {K_f}\frac{{{P_j}R}}{t} 。\\ \end{gathered} \right.$ | (5) |
4)相邻肋骨间壳板失稳临界压力
| $ \left\{ \begin{gathered} {P_e} = E{(\frac{t}{R})^2}\frac{{0.6}}{{u - 0.37}} ,\\ {\sigma _e} = \frac{{{P_e}R}}{t},\\ {P_{cr}} = 0.75{C_s}{P_e} 。\\ \end{gathered} \right. $ | (6) |
其中,Cs为修正系数,
式中:
5)舱段总体稳性
| $ \left\{ \begin{gathered} \alpha = {\text{π}} R/L ,\\ {P_{e2}} = \frac{E}{{1 + \dfrac{{{\alpha ^2}}}{{2({n^2} - 1)}}}}\left[\frac{t}{R}\frac{{{\alpha ^4}}}{{{{({\alpha ^2} + {n^2})}^2}({n^2} - 1)}} + \frac{I}{{{R^3}l}}({n^2} - 1)\right] 。\end{gathered} \right. $ | (7) |
式中,
| $ {P}_{{}_{cr}}^{'}=0.83{C}_{s}{P}_{e2} 。$ | (8) |
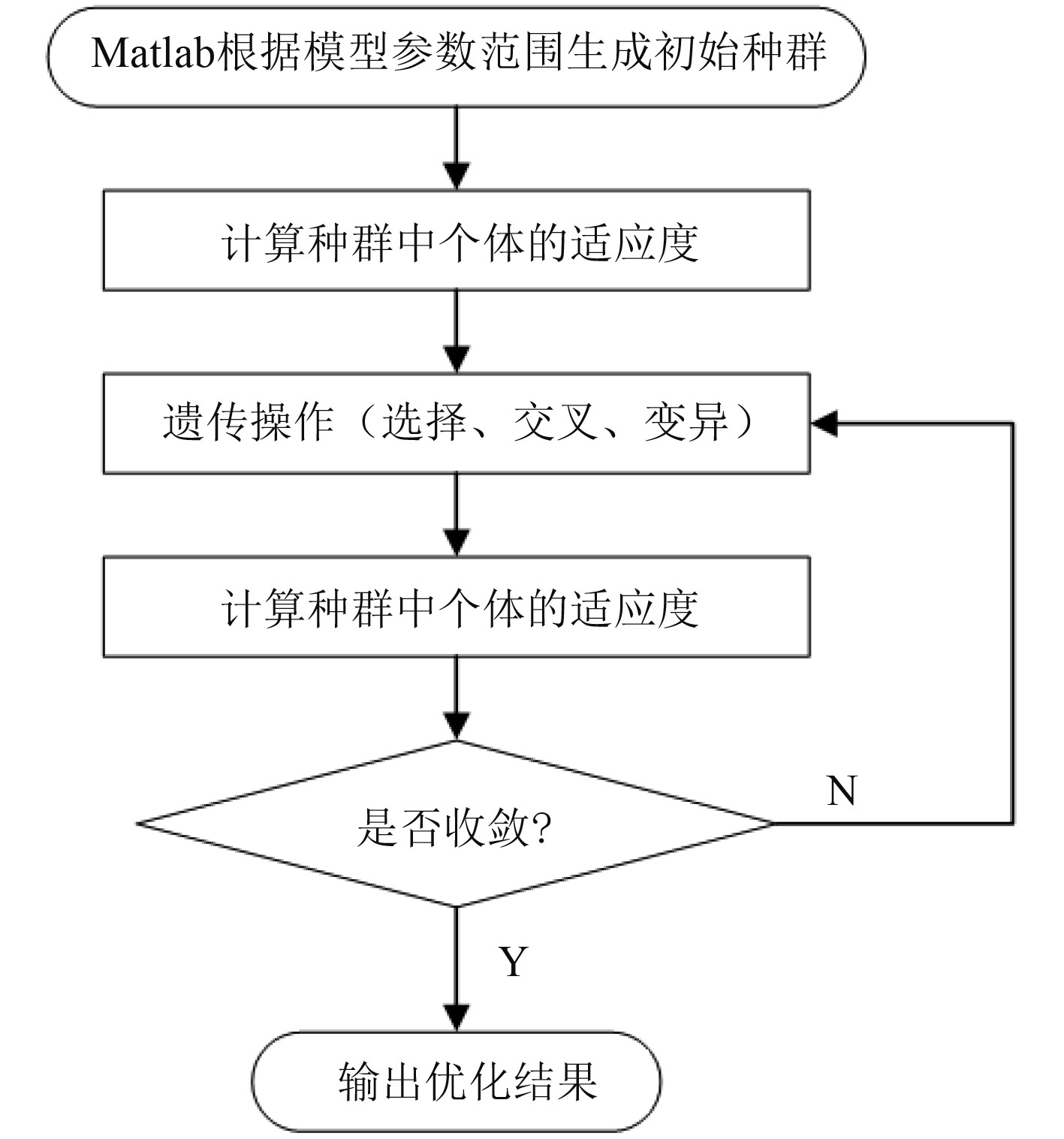
采用Matlab的遗传算法进行求解,遗传算法通过一定数量的候选解种群迭代的执行选择、交叉、变异、评价等操作使得种群不断朝向更好的解进化,整个求解流程如图3所示。
|
图 3 遗传算法优化流程图 Fig. 3 Genetic algorithm optimization flow chart |
结构优化设计之前需建立优化设计数学模型,该模型的好坏直接影响优化结果,模型中必须要明确设计变量、约束条件及目标函数。
1)设计变量
在本次优化设计中共有6个设计变量,分别为圆柱壳厚度t、肋距l、肋骨尺寸中的面板长度b、面板厚度
|
|
表 2 优化前环肋圆柱壳参数 Tab.2 Optimization of parameters of front ring stiffened cylindrical shell |
|
|
表 3 设计变量取值范围 Tab.3 Range of design variables |
2)约束变量
对于环肋圆柱壳应力所需要满足的约束条件为:
| $ 127{\sigma }_{1}\leqslant 1.15{\sigma }_{s} \text{,} {\sigma }_{2}^{0}\leqslant 0.85{\sigma }_{s} \text{,} {\sigma }_{f}\leqslant0.6{\sigma }_{s} ,$ | (9) |
对于环肋圆柱壳稳定性所需要满足的约束条件为:
| $ {P}_{cr}\geqslant {P}_{j}^{'},\;\;{P}_{cr}^{'}\geqslant {1.2P}_{j},$ | (10) |
对于环肋尺寸参数需满足的约束条件为:
| $ 131b/{t}_{f}\leqslant 8 \text{,} h/{t}_{w}\leqslant 20 \text{,} {t}_{w}\leqslant 2t \text{,} {t}_{w}\leqslant {t}_{f} \text{,} 0.3\leqslant \frac{b\cdot {t}_{f}}{h\cdot {t}_{w}}。$ | (11) |
3)目标函数
以环肋圆柱壳结构重量最低为目标函数:
| $ W={W}_{shell}+{W}_{ring}=2{\text{π}} RtL+2{\text{π}} nRA。$ | (12) |
式中:
将设计变量、约束条件、目标函数编译进Matlab遗传算法程序模块中,同时设置初始种群规模为50、交叉概论为0.9、变异概论为0.2、进化迭代次数为100进行多次优化计算,得出优化后设计变量的取值及环肋圆柱壳力学性能优化前后对比表分别如表4和表5所示。
|
|
表 4 设计变量优化结果 Tab.4 Optimization results of design variables |
|
|
表 5 环肋圆柱壳各性能优化结果 Tab.5 Performance optimization results of ring stiffened cylindrical shell |
环肋圆柱壳设计最理想的状态是,强度与稳定性计算值在不超过许用值的前提下尽量相接近,此时,材料运用最充分,重量最节省。由表4和表5的结果可看出,优化后的环肋圆柱壳壳板中面周向应力
建立优化后设计变量建立环肋圆柱壳模型,使用Abaqus软件对该模型的强度及稳定性进行计算,结果如图4所示。可知,环肋圆柱壳结构周向应力为581 MPa,轴向应力为573 MPa,肋骨应力为478 MPa。经校核均满足要求,验证上述优化设计后方案的有效性。

|
图 4 优化后计算结果 Fig. 4 Calculation results after optimization |
本文对某潜器环肋圆柱壳结构建立了优化设计数学模型,采用遗传优化算法对其结构进行优化设计,得出优化后的方案,之后根据优化结果使用有限元方法对其强度和稳定性进行校核验证,结果表明该方案满足要求。同时,优化后的环肋圆柱壳结构重量相较于优化前降低7%左右。优化后的强度和稳定性更接近许用值,材料得到充分运用,优化效果较理想。另外,该优化设计模式(初步设计-校核-算法优化-优化方案)相较于传统设计模式(初步设计-校核-反复迭代设计-反复校核-优化方案)具备优化求解效率高、效果好的特点,该研究方法可为今后类似结构物优化设计提供参考。
| [1] |
朱绍文. 大直径应急逃生舱强度与冲击环境研究[D]. 哈尔滨: 哈尔滨工程大学, 2020.
|
| [2] |
BAGHERI M, JAFARI A A, SADEGHIFAR M. Multi-objective optimization of ring stiffened cylindrical shells using a genetic algorithm[J]. Journal of Sound and Vibration, 2011, 330(3): 374-384. DOI:10.1016/j.jsv.2010.08.019 |
| [3] |
SADEGHIFAR M, BAGHERI M, JAFARI A A. Multiobjective optimization of orthogonally stiffened cylindrical shells for minimum weight and maximum axial buckling load[J]. Thin-Walled Structures, 2010, 48(12): 979-988. DOI:10.1016/j.tws.2010.07.006 |
| [4] |
RAO S S, REDDY E S. Optimum design of stiffened cylindrical shells with natural frequency constraints[J]. Computers & Structures, 1980, 12(2): 211-219. |
| [5] |
王燕. 潜艇结构的优化设计方法研究[D].哈尔滨: 哈尔滨工程大学, 2010.
|
| [6] |
余俊, 欧阳吕伟, 李艳青, 等. 深海高强度钢环肋圆柱壳单位容积重量优化设计[J]. 舰船科学技术, 2018, 40(13): 11-16. DOI:10.3404/j.issn.1672-7649.2018.07.003 |
| [7] |
黄加强. 超长舱段加筋圆柱壳结构优化设计[J]. 船舶力学, 2016, 20(Z1): 137-141. |
| [8] |
GANG H , GUANGWU Z . Analtsis and optimization of stiffened cylindrical shells under external pressure[J]. International Shipbuilding Progress, 1994.
|
| [9] |
李学斌, 朱学康. 潜艇耐压圆柱壳的多目标优化设计[J]. 中国造船, 2009, 50(1): 10-18. DOI:10.3969/j.issn.1000-4882.2009.01.002 |
 2023, Vol. 45
2023, Vol. 45
