随着国际上对燃料排放要求的法律法规越来越严格,天然气在满足法规要求的前提上,其低于柴油的运输购买价格可直观地为船东节省运营成本,因此将LNG 作为燃料应用到船舶领域已成为必然趋势[1]。与此同时,LNG燃料的某些特性,也使得其使用过程中安全问题越发得到重视。
在标准大气压下,液化天然气存储所需温度大约为零下162℃,液化后的密度为450~470 kg/m3,体积约为气体状态下的1/600。LNG的燃点为650℃,在空气中的爆炸极限为5.3%~14.0%,与其他化学品相比,LNG 具有更加易爆、易燃的危险性。尤其是在船舱中泄漏的LNG,会在空间有限的舱室内形成比液态状态下体积大数百倍的天然气蒸汽云,此时小于1 mJ(任何明火、电火花、来自低压电源以及人体摩擦所产生的静电,其能量均超过了1 mJ)的能量通常就足以点燃混合气云,产生燃烧爆炸等风险后果[2]。通过研究大量的船舶及海洋结构物事故统计[3],可发现海洋结构物发生重大事故的直接致因主要是火灾爆炸事件。不仅会造成大面积的人员伤亡和结构损伤,而且会产生各种污染物,对海洋环境造成严重破坏。由此可看出,对于船舶、油气平台等大型海洋结构物而言,其在爆炸作用下产生的结构响应对于结构的安全性分析研究有着极大的意义。
目前,国内外相关研究一般是针对在爆炸产生的冲击载荷作用下,对结构的力学性能及损伤响应进行分析。Yin等[4] 通过数值模拟手段,对不同形式爆炸载荷作用下,舱壁结构在爆炸冲击载荷下的损伤情况及毁伤特性进行了研究,提出一种新型箱型梁防护结构。于文静[5]基于有限元软件 Ansys/Ls-dyna,在选用材料本构模型时,将应变率效应纳入考量,针对导管架海洋平台结构材料在高温下性能的变化规律开展研究。Liu等[6]通过非线性耦合的数值模拟方法,建立能够模拟流体与固体之间相互接触作用的FSI 模型,并由此开展在水下发生爆炸时,舰艇结构的动态响应研究。
为了研究天然气泄漏所形成的蒸气云爆炸后,对舱室的损害情况,本文采用有限元软件MSC.Dytran对LNG船舶的舱室结构在承受爆炸冲击作用下的结构瞬态过程进行数值模拟,为LNG船舶的设计建造提供参考依据。
1 计算理论 1.1 空中爆炸理论爆炸是通过点燃爆炸物,迫使其能量在一瞬间快速释放的过程。当爆炸产生时,起爆点附近产生爆炸产物并迅速向周围膨胀,周遭介质会受到压缩,在爆炸物与介质的交界面处,爆炸产物会以球形波阵面的形式快速向四周扩散,同时不断挤压与其相邻的介质,使其压力骤然上升,也就形成了最初始的冲击波。
当冲击波形成后,最初的压力值较高,由于与外界压力差的存在,其开始自发地由压力中心向外界进行扩散,并在这一过程中不断消耗能量,压力值也不断衰减,当扩散到一定范围时,它的压力会降至与初始压力持平。由于惯性作用,爆炸冲击波并不会立刻停止扩散,而是以不断降低的扩张速度继续扩散,当速度降为0时,达到最大范围。此时爆炸产物内部由于过度扩张,其压力值反而会低于外界大气压,即整个区域出现负压的情况,此时在内外压力差的作用下,会使得过度扩张后的爆炸产物向着压力中心开始反向坍缩。同理,由于惯性作用亦会出现压力又再次高于外界压力的情况。该过程如图1所示。经过若干次扩张-坍缩的脉动过程后,爆炸区域的压力值会不断趋于平衡状态,最终停止。

|
图 1 空中爆炸冲击波传播原理示意图 Fig. 1 Schematic diagram of the propagation principle of the shock wave of an aerial explosion |
空中爆炸冲击波
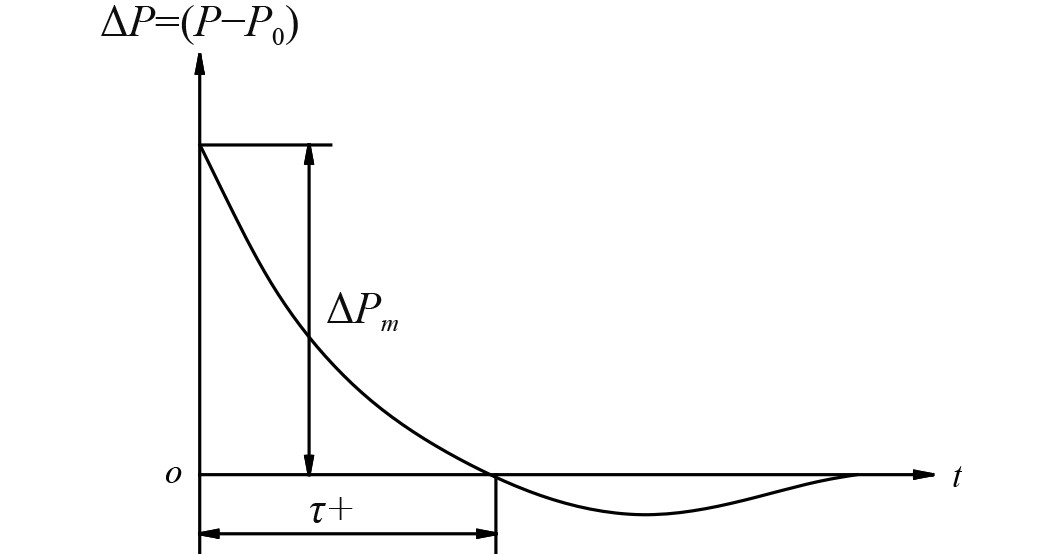
|
图 2 空气冲击波超压峰值曲线 Fig. 2 Air shock wave overpressure peak curve |
Henrych等[7]针对空中爆炸冲击波载荷的传播规律,提出了经验公式。以TNT球形炸药为例,冲击波瞬时压力
| $ \begin{aligned}[b] &\Delta p = \frac{{1.40717}}{{\bar r}} + \frac{{0.5597}}{{{{\bar r}^2}}} - \frac{{0.03572}}{{{{\bar r}^3}}} + \\ &\frac{{0.000625}}{{{{\bar r}^4}}} ( 0.05 \leqslant \bar r \leqslant 0.3 ),\end{aligned}$ | (1) |
| $ \Delta p = \frac{{0.61938}}{{\bar r}} - \frac{{0.03262}}{{{{\bar r}^2}}} + \frac{{0.21324}}{{{{\bar r}^3}}} ( 0.3 \leqslant \bar r \leqslant 1 ) ,$ | (2) |
| $ \Delta p = \frac{{0.0662}}{{\bar r}} + \frac{{0.405}}{{{{\bar r}^2}}} + \frac{{0.3288}}{{{{\bar r}^3}}} ( 1 \leqslant \bar r \leqslant 10 ) 。$ | (3) |
式中:
对于蒸气云爆炸计算来说,常用的计算模型有数值模型、物理模型以及其他相关模型3类。其中,数值模型虽然能够准确模拟出蒸气云爆炸的情况,但有对计算设备要求高、计算时间长等缺点,不易使用。而物理模型属于一种对爆炸过程进行简单化处理的模型,模型精度以及计算准确度都较差。相关模型也被称作缩放比例模型,这当中最为典型的是日本学者惠美洋彦提出的TNT当量法。TNT当量法是将蒸气云爆炸时产生的破坏作用等效替换为TNT炸药爆炸的破坏作用,从而将复杂的蒸气云模型转化为当量的TNT炸药模型。TNT当量法的准确性相比于物理模型而言更高,同时其对设备精度的要求比数值模型低,被国内外许多学者广泛应用于蒸气云爆炸模拟[8-9]。
因此,对于船舱内天然气泄漏后形成的天然气云,可通过TNT当量法对气云的爆炸能量进行估测计算,计算公式如下:
| $ {W_{{\rm{TNT}}}} = A{W_i}\frac{{{Q_i}}}{{{Q_{{\rm{TNT}}}}}}。$ | (4) |
式中:
选取某典型船舶舱室结构,利用有限元分析软件MSC.Patran建立舱室的有限元模型,泄漏天然气的爆源位置被设置在舱室中心处位置。由于需模拟真实爆炸冲击波与舱室钢结构之间的相互作用,因此在模拟中采用流固耦合算法。用欧拉网格来模拟爆炸介质,即空气域,并将舱室的上下甲板、横舱壁以及舷侧外板设置为耦合面。建立具体舱室模型如图3所示。
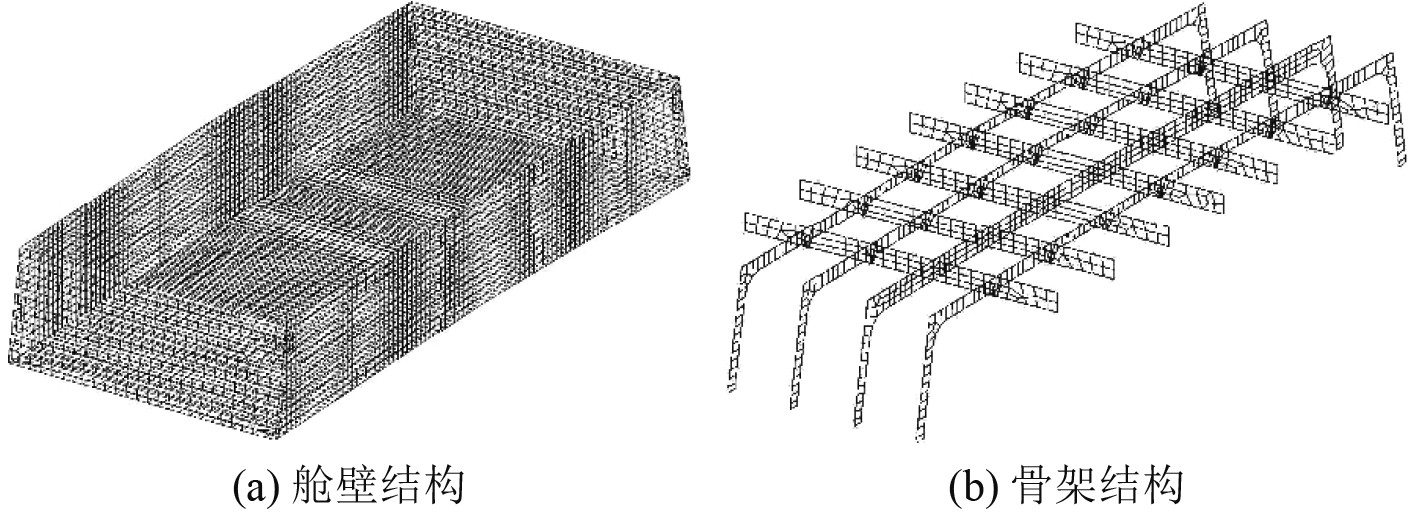
|
图 3 舱室结构有限元模型示意图 Fig. 3 Schematic diagram of the finite element model of the cabin structure |
对于天然气泄漏爆炸而言,参与爆炸反应的天然气总质量越多,爆炸能量就越高。因此,选取最为危险的情况作为计算工况,即舱室中充满泄漏的天然气,其泄漏总量计算式为:
| $ {W}_{i}\text={\rho }_{0}{V}_{舱} 。$ | (5) |
式中:
因此,根据式(5)可得泄漏天然气总质量
| $ {r_{{\rm{TNT}}}}{\text{ = }}\sqrt[3]{{\frac{{3{W_{{\rm{TNT}}}}}}{{4\text{π} {\rho _{{\rm{TNT}}}}}}}}。$ | (6) |
式中:
根据式(4),可得舱室中泄漏LNG的当量TNT高能气体球半径
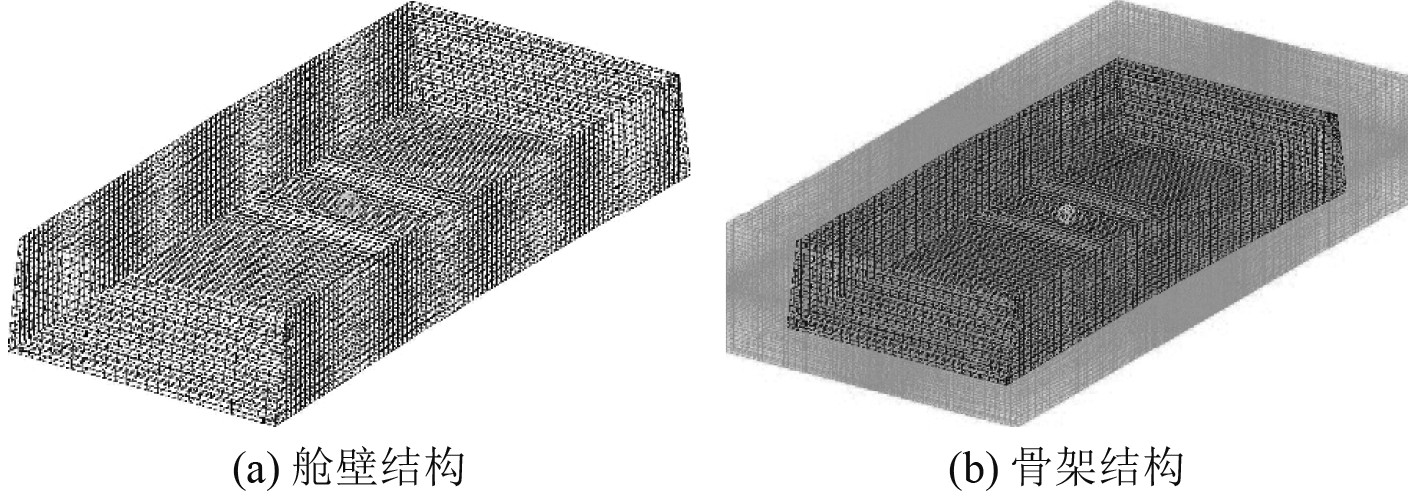
|
图 4 欧拉网格有限元模型示意图 Fig. 4 Schematic diagram of the finite element model of Euler mesh |
在数值模拟过程中,所设置的材料参数会对计算结果产生很大影响。在天然气泄漏爆炸作用下,舱室结构受到空中爆炸冲击波载荷是一个瞬态响应过程,换言之材料发生应变的速率很快,舱室结构应着重考虑应变率。因此,参考实验数据的拟合情况,本文选用拟合较好的Cowper-Symonds[10]本构模型作为计算模型。Cowper-Symonds模型中动态屈服应力
| $ {\sigma _{{y}}}{\text{ = [1 + (}}\frac{{{\varepsilon _0}}}{D}{{\text{)}}^{1/q}}{\text{](}}{\sigma _0}{\text{ + }}\beta {E_p}\varepsilon _p^{eff}{\text{)}}。$ | (7) |
式中:
| $ RPN{\text{ = }}S \times O \times D。$ | (8) |
货舱舱室结构采用一般强度船用钢材料(Q235钢),采用弹塑性的材料类型,屈服模型选用Von-mises屈服模型。具体的结构尺寸及材料各项参数如表1和表2所示[11]。
|
|
表 1 结构尺寸 Tab.1 Structural dimensions |
|
|
表 2 材料参数 Tab.2 Material parameters |
以可燃气云充斥整个舱室,并且天然气达到完全反应为模拟条件,计算最差情况下爆炸对舱室结构的毁伤影响。根据上文,可得此时参与爆炸的LNG质量为327.78 kg,结合式(4)取等效TNT质量为135 kg。
3.1 冲击波压力分析经过计算模拟,得到爆炸发生后,冲击波压力载荷的传播过程以及空间分布。由于所选舱室整体呈扁平形状,上下甲板距离爆源最近,最快受到冲击波压力载荷作用,因此选择以上下甲板为例展现冲击波在接触到舱壁结构后的变化情况,如图5所示。

|
图 5 冲击波压力分布云图 Fig. 5 Shock wave pressure distribution cloud |
可以看出,爆炸发生后,能量以冲击波的形式迅速向外扩散传递。冲击波载荷在0.0004 s时,接触到炸点处的上下甲板,此时压力峰值高达13.3 MPa聚集于上下甲板结构内表面上,并随后沿着上下甲板向四周继续扩散。此时舱壁结构承受到剧烈冲击,极易发生毁伤变形。
由图5(c)~5(e)可看出,波阵面在上下甲板相撞后发生反射效应,冲击波载荷逐渐离开上下甲板内表面,并且两股反射波逐渐于舱室爆源区域两侧的中部区域相撞。此时,冲击波压力峰值已降至3.02 MPa,已不足最初峰值的1/4,证明绝大部分的爆炸能量及冲击载荷由爆源附近的上下甲板结构承受、吸收,说明密闭空间中,可燃气体的爆炸具有较强的局部效应。
两股反射波于图5(f)中,即0.0020 s时完成交汇,再次形成一股高压冲击波,此时压力峰值再次回升至5.47 MPa,并继续向爆源的左右方向进行扩散,如图5(g)~5(h)所示。说明在密闭舱室内不仅需要考虑最先接触冲击波的爆源附近结构,由于舱壁反射形成的汇聚波会形成二次冲击载荷高峰,其对结构产生的破坏效果同样不容忽视。
最终,冲击波经过与上下甲板、横舱壁及舷侧外板等结构的多次反射、汇聚后,如图5(i)所示在舱室的下方两角隅处产生压力汇集,压力峰值回升至10.0 MPa,甚至与最初上下甲板所承受的压力峰值接近。由此可见,容易发生汇集现象的舱室角落处在爆炸事故中也存在较大损伤风险。
3.2 结构损伤分析船舶舱室结构在承受爆炸后所产生的塑性形变以及应力、应变是评价舱室结构毁伤程度的重要依据,能够非常直观且真实地反映出舱室结构的损伤变形程度,同时也有助于对容易发生损坏的区域进行识别。t=0.0078 s时,舱室结构(舱壁、骨架)的损伤响应图如图6、图7所示。

|
图 6 舱壁结构损伤响应图 Fig. 6 Bulkhead structural damage response diagram |

|
图 7 骨架结构损伤响应图 Fig. 7 Skeleton structure damage response diagram |
由于发生爆炸的舱室属于相对密闭空间,爆炸所产生的能量大部分由舱室结构吸收。其中,爆点附近的结构出现较为集中的塑性变形,表明密闭空间内的爆炸具有局部效应。此外,发现除爆点附近处的结构外,由于冲击波具有在角隅处汇集这一特性的缘故,出现位移以及应力最多的是横舱壁与甲板以及骨架交接缝处,且出现了较多裂口。这可能导致冲击波、高温火焰以及未燃烧的可燃气体外溢至外围舱室,造成连锁反应,产生更广范围的损伤,因此这一区域结构的抗爆性能需着重加强。
为了更深入地研究舱室结构中的抗爆薄弱点,分别在甲板、横舱壁、舷侧外板以及骨架结构上选取最后时刻发生损伤位移最大的节点作为测点,可更好地反映出爆炸冲击波对不同结构的直接损伤程度。图8为不同结构测点在每一个时刻点所受位移、应力、应变的时间历程曲线。

|
图 8 不同结构测点时间历程曲线图 Fig. 8 Time history curves of measurement points of different structures |
对比舱室不同结构对爆炸的响应结果,可发现:
1)甲板测点在爆炸发生初期,应力、应变均在非常短的时间内迅速攀升,并且峰值均是所有结构中最高的,是3种部件中受损伤最大,风险最高的部件;
2)横舱壁在爆炸发生一段时间之后,其各项数值也以较快的速度开始攀升,应力值峰值稍低于甲板,应变值甚至略高于甲板,在3种部件中是受损仅次于甲板的部件;
3)较为特殊的是,舷侧外板由于距离炸点较远,因此在爆炸初期受到的损伤最小,位移与应变攀升较缓慢,但当结构趋于稳定时,甲板与横舱壁应力值均有所回落,而舷侧外板却成为应力值最高的结构并保持在较高数值,因此舷侧外板虽然直接受到的首次冲击损伤较轻,却是受到后续反射波冲击损伤响应最久的结构;
4)骨架结构则是四者中受损最轻的结构。
3.3 结构吸能分析对于船舶舱室结构而言,塑性变形能是衡量舱室结构损伤程度的重要参考数据之一,可准确地反映出结构承受爆炸冲击载荷的损伤变形情况。选取上甲板、下甲板、横舱壁、舷侧外板、骨架结构6种不同结构,其所吸收塑性形变能随时间的变化曲线如图9所示,各个结构吸收塑性形变能的最大值及占总吸能的比值如表3所示。

|
图 9 不同结构吸能时间历程曲线图 Fig. 9 Curves of energy absorption time history of different structures |
|
|
表 3 不同结构吸能最大值 Tab.3 Maximum energy absorption of different structures |
可以看出,在爆炸发生前期,上甲板以最快的速度吸收变形能,并持续稳定提高,但最终吸能总量在所有构件中最低,占总能量的13.79%;而横舱壁结构的吸能开始时间虽较晚,却以非常快的速度迅速蹿升并且不断增高,最终吸收了最多的塑性变形能,占总能量的29.20%。可知,这二者依然是舱室结构中承受爆炸损伤最为严重的构件。此外,对于骨架结构而言,由于起到支撑、连接舱室其他结构的作用,在吸能过程中会分摊其他结构的变形能,因此总吸能量排在第二位,但由于其栅格式的结构特性导致其所受损伤最轻。
4 结 语本文基于显式非线性有限元软件MSC.Dytran,采用欧拉-拉格朗日流固耦合的方法,对船舶舱室结构在LNG泄漏爆炸冲击作用下的毁伤过程及其动态响应进行数值仿真研究,得到了冲击波压力分布、舱室结构损伤及吸能的变化规律,通过对比分析得出以下结论:
1)爆炸发生初期的瞬间,绝大部分的爆炸能量及冲击载荷由爆源附近的上下甲板结构所承受,密闭空间中可燃气体的爆炸具有较强局部效应。
2)在密闭舱室内,由于舱壁反射形成的汇聚波会形成二次冲击载荷高峰,并于舱室的下方角隅处产生压力汇集,压力值甚至接近爆炸发生瞬间压力最大值的75%,导致舱壁与骨架交接处出现较多裂口,存在较大风险。
3)爆炸发生后,甲板结构的应力应变值攀升速度最快,峰值最高;横舱壁结构所吸收的塑性变形能在所有结构中最大,占总吸能的29.20%。而骨架作为支撑结构也吸收了23.40%的能量,但由于其栅格式的结构设计导致其抗爆性能优秀,受损伤最轻。综合而言,甲板与横舱壁是舱室中受损伤最严重,损伤响应最大的结构,在后续研究中应予以重视。
| [1] |
蒋玮, 朱新礼. 液化天然气作为船用燃料的可行性研究[J]. 船舶与海洋工程, 2013(3): 74-78. DOI:10.3969/j.issn.2095-4069.2013.03.016 |
| [2] |
郑国鹏. LNG船舶泄漏的危害性及防范措施[J]. 水运管理, 2009, 31(9): 34-35. DOI:10.3969/j.issn.1000-8799.2009.09.013 |
| [3] |
HALIM S Z, JANARDANAN S, FLECHAS T, et al. In search of causes behind offshore incidents: Fire in offshore oil and gas facilities[J]. Journal of Loss Prevention in the Process Industries, 2018, 54: 254-265. DOI:10.1016/j.jlp.2018.04.006 |
| [4] |
YIN Q, CAO G, XIE R, et al. Research on a ship bulkhead structure under the combined load [M]. Hydraulic Engineering V. CRC Press, 2017: 201-211.
|
| [5] |
于文静. 导管架海洋平台钢结构在爆炸和火灾作用下的力学性能研究[D]. 上海: 上海交通大学. 2012.
|
| [6] |
LIU Y L, ZHANG A M, TIAN Z L, et al. Numerical investigation on global responses of surface ship subjected to underwater explosion in waves[J]. Ocean Engineering, 2018, 161: 277-290. DOI:10.1016/j.oceaneng.2018.05.013 |
| [7] |
HENRYCH J, ABRAHAMSON G R. The dynamics of explosion and its use [M]. Amsterdam Elsevier Scientifi Pub, 1979.
|
| [8] |
张玉若. 液化石油气事故机理及模拟评价方法[J]. 工业安全与环保, 2006, 32(3): 56-58. |
| [9] |
白丽萍, 刘江涛, 刘丽珍, 等. 管廊中天然气管道舱泄漏爆炸当量计算及简析[J]. 城市燃气, 2017(9): 7-11. DOI:10.3969/j.issn.1671-5152.2017.09.002 |
| [10] |
COWPER G R , SYMONDS P S . Strain-hardening and strain-rate effects in the impact loading of cantilever beams [J]. Small Business Economics, 1957.
|
| [11] |
赵世超. 压缩天然气 (CNG) 运输船货舱结构抗爆性能研究[D]. 镇江: 江苏科技大学, 2017.
|
 2023, Vol. 45
2023, Vol. 45
