2. 华中科技大学 船舶与海洋工程学院,湖北 武汉 430074
2. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
舰船在执行海上作战任务时,易遭受各类武器的打击,打击形式包括接触式的直接冲击形式和非接触式的爆炸冲击形式。接触式的冲击形式包括导弹等直接碰撞冲击形式,在弹体的速度不足够快时,这种接触式的冲击形式容易被导弹防御系统拦截。而非接触的爆炸冲击形式主要包括空中爆炸和水下爆炸冲击,由于水较于空气有更大的密度,爆炸产生的冲量也会更大。此外,水下炸药一旦引爆就无法被拦截。因此,研究水下爆炸载荷特性对于研究舰船抗水下爆炸性能具有前瞻性意义。
对于水下爆炸冲击载荷的研究最早可追溯到1941年Taylor[1]对于平板水下爆炸载荷入射、反射压力的理论研究。对于水下爆炸冲击载荷的计算,Cole[2]在1948年全面总结了包括水下爆炸研究的试验及理论成果、水下爆炸现象、载荷传播分布特点、试验研究方法和载荷测试方法。通过总结相关资料,给出了水下爆炸的相关经验公式。中远场水下爆炸冲击作用过程中,冲击波压力冲击与气泡脉冲击作用在结构上的时间相差大约数十、数百毫秒不等,往往可分开研究。在水下爆炸的数值仿真的方法上,有限元软件AUTODYN[3-4]、LS-DYNA[5-7]以及MSC/DYTRAN[8]等都可以很好地模拟水下爆炸冲击波和气泡脉动过程。
本文使用AUTODYN一维方法建立炸药与水域的多物质组有限元模型,模拟水下炸药爆炸形成的爆炸冲击波和气泡脉动过程。在数值仿真计算的基础上,使用经验公式计算几种验证工况下的冲击波压力历程以及气泡脉动半径变化过程,校核数值仿真计算的可靠性。
1 水下爆炸计算方法 1.1 水下爆炸冲击波计算方法Geer等[9]在实验基础上总结相关数据,将水下爆炸压力分为几个阶段。其中,指数衰减阶段描绘了水下爆炸冲击波指数式衰减的主要特征。冲击波峰值Pm以及冲击波冲量I可由下述经验公式估算得出:
| $ {P_m} = \left\{ \begin{gathered} 44.1{\left( {\frac{{{W^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}}}{R}} \right)^{1.5}},6 \leqslant \frac{R}{{{R_0}}} < 12 ,\\ 52.4{\left( {\frac{{{W^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}}}{R}} \right)^{1.13}},12 \leqslant \frac{R}{{{R_0}}} < 240 。\\ \end{gathered} \right. $ | (1) |
| $ I = 5768 \times \sqrt[3]{W}{(\frac{{\sqrt[3]{W}}}{R})^{0.89}} 。$ | (2) |
式中:W为炸药当量,kg;R0为炸药药包半径,m;R为爆炸源点距离结构的最近距离,即爆距,m。
1.2 水下爆炸气泡计算方法1960年,Cole给出了TNT球形装药水下爆炸气泡最大膨胀半径与气泡脉动周期经验公式。1973年,Zamyshlyayev[10]在Cole研究成果基础上进一步发展,总结水下爆炸气泡最大膨胀半径与气泡脉动周期经验公式如下:
| $ T = {K_T}\frac{{{W^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}}}{{{{\left( {1 + 0.1h} \right)}^{{5 \mathord{\left/ {\vphantom {5 6}} \right. } 6}}}}},$ | (3) |
| $ {R_{\max }} = \frac{{{K_R}}}{{{{\left( {1 + 0.1h} \right)}^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}}}{R_0} 。$ | (4) |
式中:T为气泡脉动周期,s;Rmax为气泡最大膨胀半径,m;KR、KT均为炸药参数。对于TNT炸药,
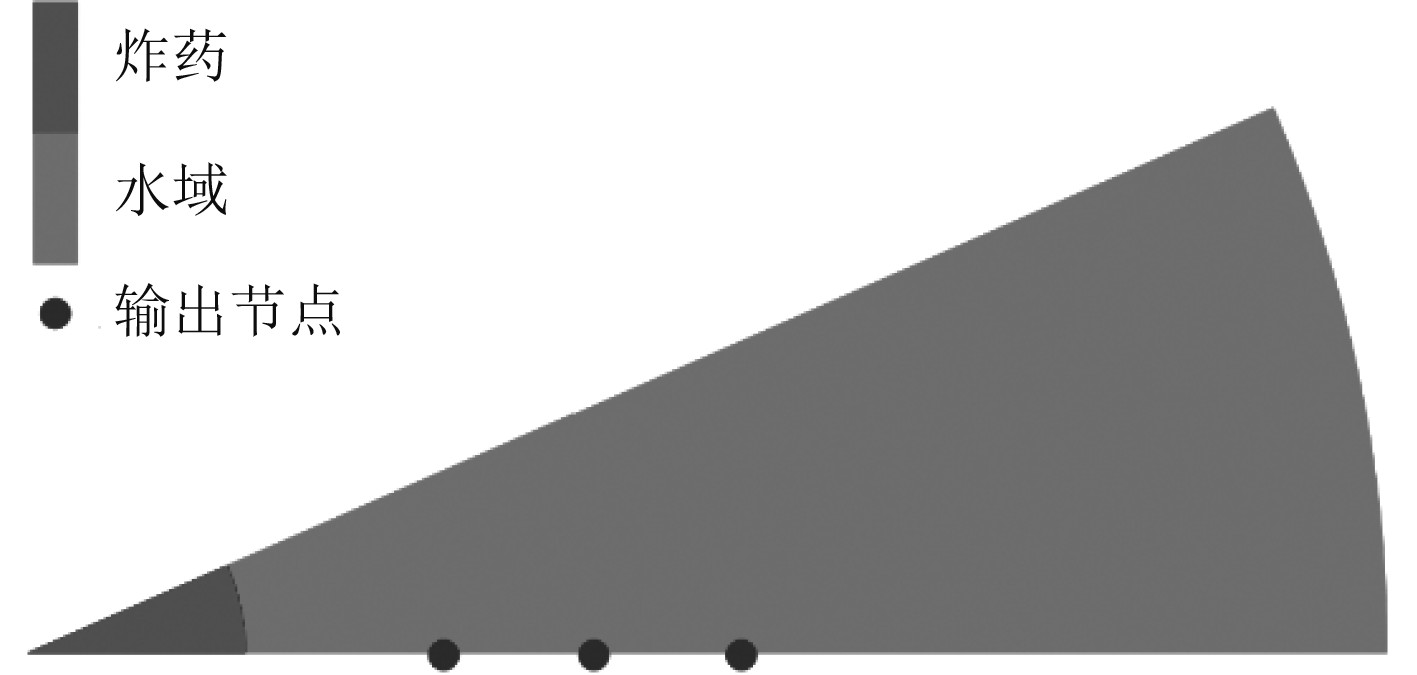
基于AUTODYN中多物质流固耦合算法,对水下爆炸过程进行数值仿真。本文只研究水下爆炸冲击的载荷特性,不涉及爆炸冲击波和气泡脉动载荷引起的结构响应,故数值仿真模型仅包括炸药和水域。对于球形炸药在无限水域中的爆炸问题,可简化成球对称问题,在AUTODYN中只需建立一维圆弧楔形水域,并在水域中填充炸药。为了对比水下爆炸时,冲击波压力和比冲量与经验公式之间的差距,通过提取水域一定位置上数个结点的冲击波压力值,结点示意图如图1所示。AUTODYN输出的压力值包括静水压力值与冲击波提取时,需去除静水压力。冲击波的超压曲线对时间的积分即可得到冲击波压力的比冲量曲线。
|
图 1 输出爆炸超压的结点示意图 Fig. 1 Diagram of nodes of output explosion overpressure |
考虑炸药当量与有限元尺寸效应之间的关系,给出了爆距Z、网格尺寸之比
| $ Z = \frac{R}{{{W^{1/3}}}},$ | (5) |
| $ \lambda = \frac{{{R_0}}}{{{L_e}}}。$ | (6) |
式中:R为爆心到输出节点的距离;W为炸药当量;R0为炸药药包半径,可根据炸药当量和炸药密度求得;Le为有限元模型网格尺寸。考虑到有限元模型的网格尺寸与计算精度和计算效率之间的关系,当
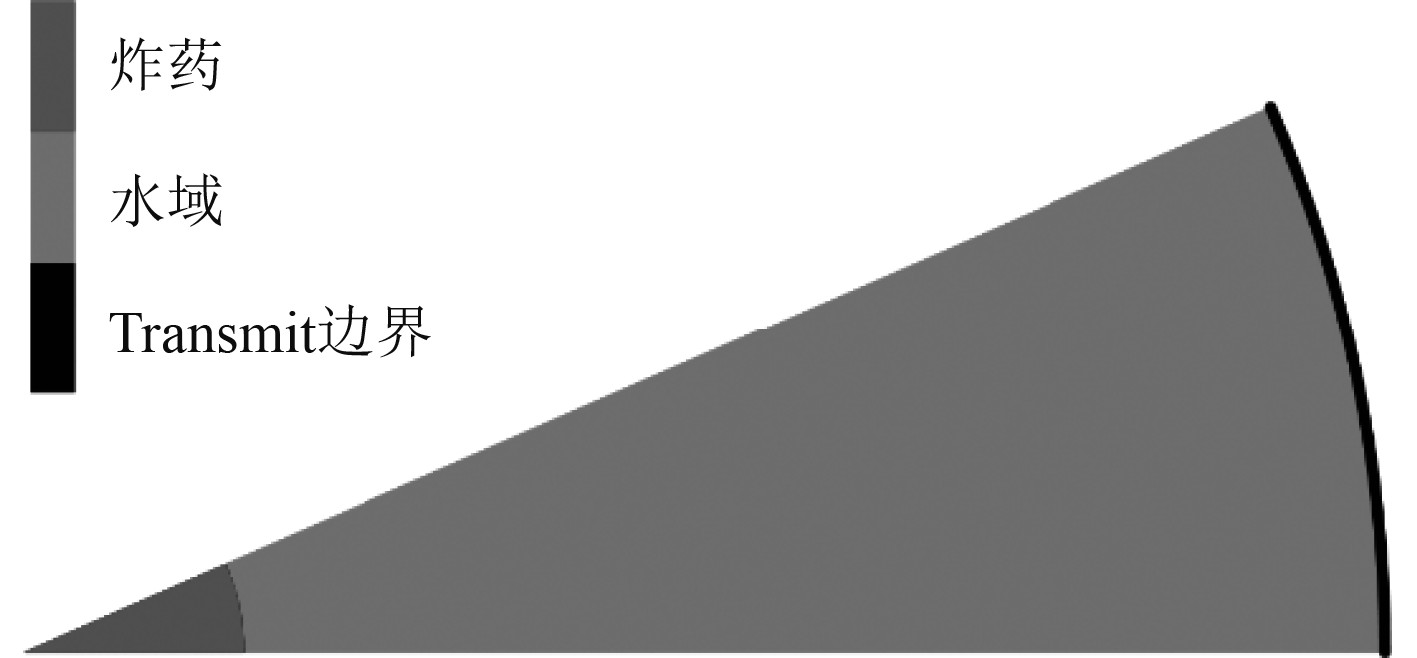
考虑到远场的爆炸加载条件,需要是冲击波作用到水域边界时不产生反射波,故在水域模型边界处设置无反射边界条件(Transmit边界),如图2所示。
|
图 2 边界条件示意图 Fig. 2 Diagram of boundary conditions |
在AUTODYN材料库中,采用JWL状态方程模拟炸药的本构关系:
| $ {P_2} = A(1 - \frac{\omega }{{{R_1}\nu }}){e^{ - {R_1}\nu }} + B(1 - \frac{\omega }{{{R_2}\nu }}){e^{ - {R_2}\nu }} + \frac{{\omega {e_2}}}{\nu }。$ | (7) |
式中:e2为单位体积炸药初始内能;ν为炸药的相对体积;A、B均为材料参数;R1、R2和ω均为常数。
本文用到了2种炸药TNT和HBX-1,HBX-1炸药的材料参数可在AUTODYN中定义,其JWL状态方程相关参数如表1所示。
|
|
表 1 HBX-1炸药的JWL状态方程参数 Tab.1 JWL equation of state parameters for HBX-1 explosive |
对于水域,采用多项式状态方程,当水处于压缩状态时(
| $ {P_1} = {A_1}\mu + {A_2}{\mu ^2} + {A_3}{\mu ^3} + \left( {{B_0} + {B_1}\mu } \right){\rho _0}{e_1} 。$ | (8) |
当水处于膨胀状态时(
| $ {P_1} = {T_1}\mu + {T_2}{\mu ^2} + {B_0}{\rho _0}{e_1}。$ | (9) |
当水既不膨胀也不压缩时(
| $ {P_1} = {B_0}{\rho _0}{e_1}。$ | (10) |
式中:
不同水深下静水压力可定义为:
| $ {P_1} = {P_0} + {\rho _0}gh 。$ | (11) |
式中:P0为水-空气界面处的大气压力;g为重力加速度;h为炸药的爆炸深度。
联立式(10)和式(11),可计算得出不同水深下水的内能。
3 结果分析 3.1 冲击波压力结果分析 3.1.1 有效性验证为了验证水下爆炸冲击波数值模拟的有效性,设置4种工况分别验证炸药当量W、爆距R以及爆炸深度H对于有限元计算有效性的影响。具体计算工况如表2所示。
|
|
表 2 水下爆炸冲击波验证工况 Tab.2 Verifying case for underwater blast shock wave |
根据式(5)和式(6),按照给定的炸药当量W和爆距R可计算得出爆炸距离Z和炸药半径R0。通过控制炸药半径与网格尺寸之比大于3,即可保证有限元计算结果的准确性,各工况下的炸药、水域网格数量等参数如表3所示。
|
|
表 3 有限元模型及网格尺寸 Tab.3 Finite element model and mesh size |
汇总冲击波超压压力峰值与比冲量峰值,并计算仿真结果与经验公式结果之间的相对误差,如表4所示。结果表明,超压峰值与比冲量峰值的相对误差都控制在15%以内,验证了有限元计算结果的准确性。
|
|
表 4 验证工况冲击波压力峰值与比冲量峰值计算结果汇总 Tab.4 Summary of peak shock wave and specific impulse of verifying case |
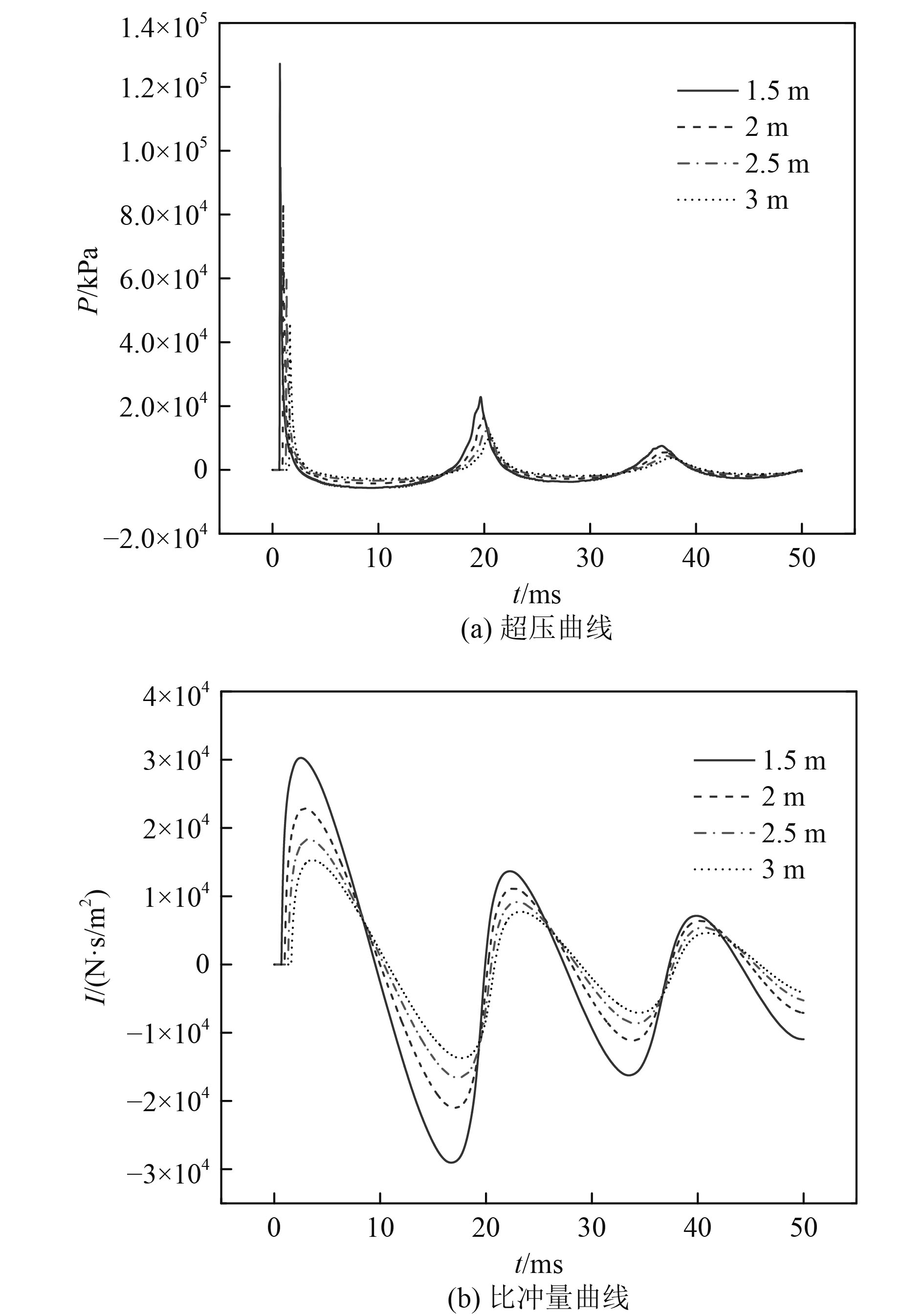
在保证爆炸炸药当量相当和爆炸深度相同的情况下,通过调整爆距计算4种不同爆距下,水下爆炸冲击波的峰值压力与比冲量历程曲线及变化趋势。不同爆距下,除去静水压力的超压曲线以及比冲量曲线如图3所示。
|
图 3 不同爆距计算结果 Fig. 3 Numerical results under different detonation distance |
可以看出,爆炸压力在爆炸初期呈现陡增然后呈现极速衰减的变化形式,后续出现负压以及二次压力峰值。随着爆距的变小,负压呈现增大趋势,且二次峰值呈现增加趋势。比较一次峰值与二次峰值,二次压力峰值明显远低于一次峰值且二次峰值持续时间较长。对于比冲量而言,压力使比冲量曲线迅速上升,随着负压的出现,比冲量又迅速减为0并达到负值,因此水下爆炸冲击波比冲量曲线呈现往复振荡的特点。相关计算结果如表5所示。
|
|
表 5 不同爆距冲击波压力峰值与比冲量结果 Tab.5 Peak shock wave and specific impulse under different detonation distance |
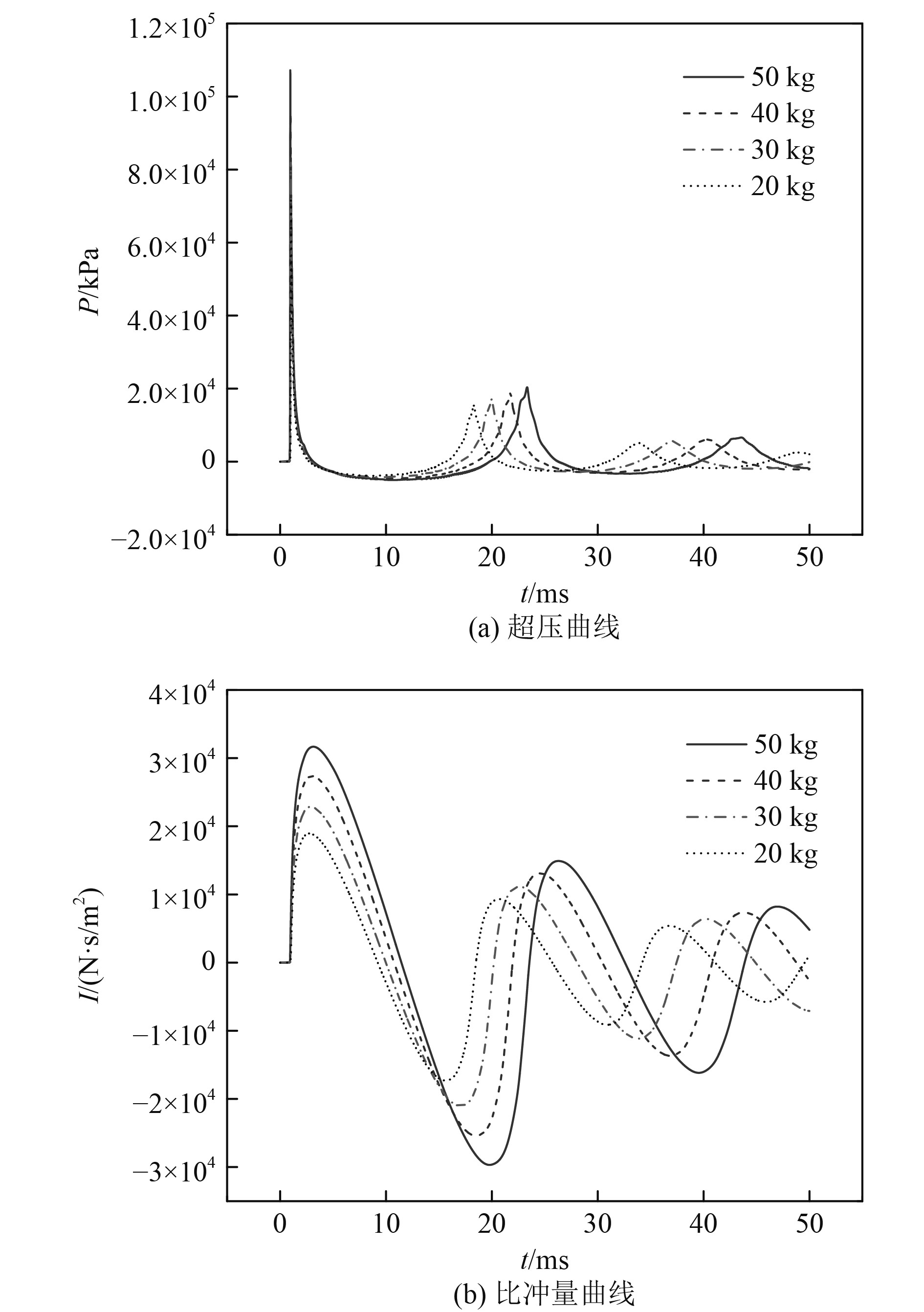
考虑相同爆距以及相同水深条件下,研究不同炸药当量对于不同结点处冲击波压力超压以及比冲量的影响,故设计4种不同的炸药当量20 kg、30 kg、40 kg、50 kg工况。计算得到的超压曲线以及比冲量历程曲线,如图4所示。
|
图 4 不同炸药当量计算结果 Fig. 4 Numerical results under different equivalent of explosive |
可以看出,在炸药当量增加的情况下,冲击波压力呈现增加趋势,负压也越大,二次压力的峰值也呈现增加趋势。同时随着炸药当量的增加二次压力峰值出现更晚。而对于比冲量曲线,比冲量峰值随炸药当量增加而增加,其数值在正负幅值间振荡。随着爆炸当量的增加,振荡的周期呈现增长趋势。不同炸药当量的冲击波压力峰值及比冲量值见表6。
|
|
表 6 不同炸药当量冲击波压力峰值与比冲量结果 Tab.6 Peak shock wave and specific impulse under different equivalent of explosive |
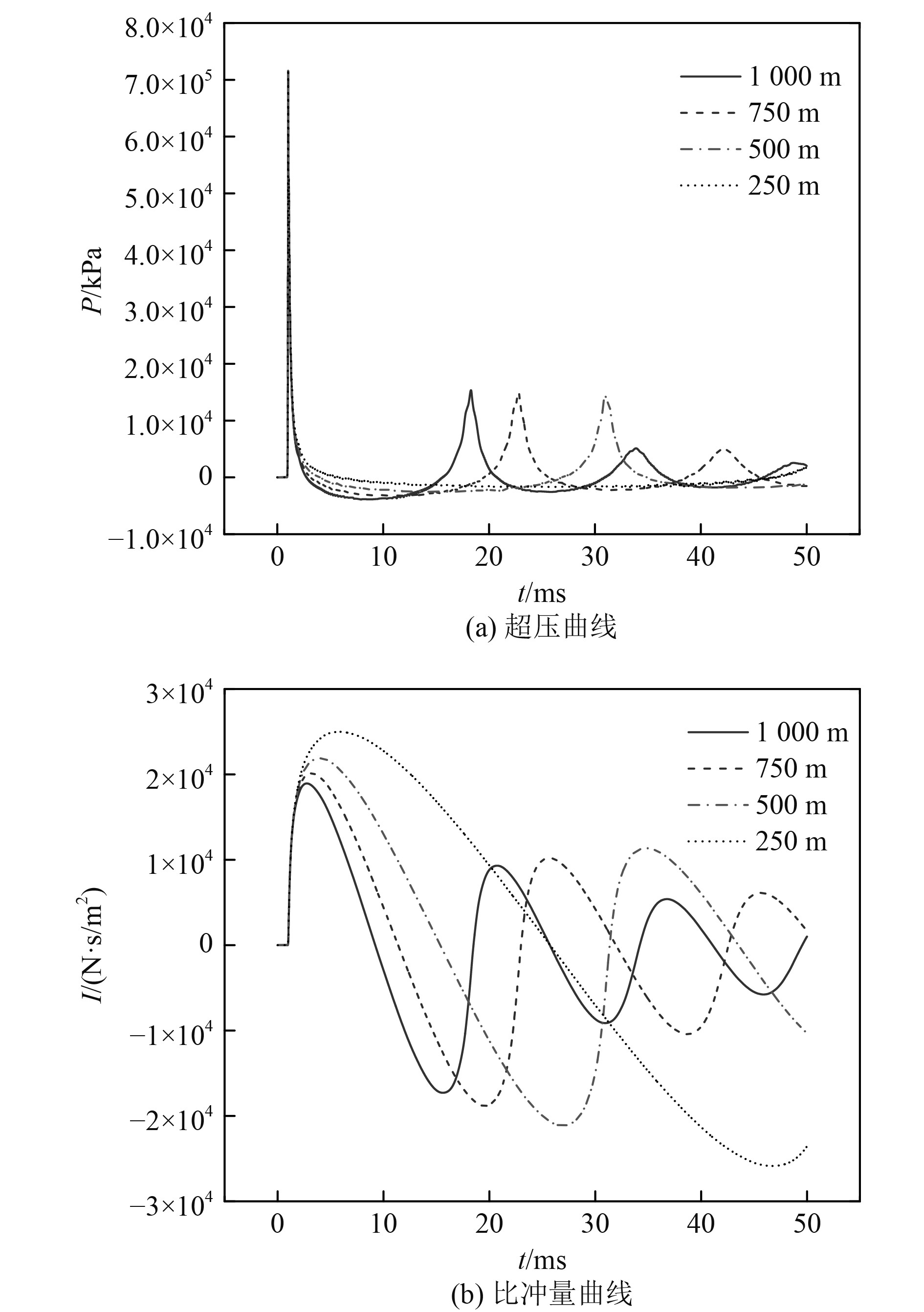
在控制爆距与炸药当量相同的情况下,研究不同水深工况下,冲击波压力与比吸能的变化情况。共设置250 m、500 m、750 m和1000 等4种工况,这4种工况下的超压曲线与比冲量历程曲线见图5。
|
图 5 不同水深计算结果 Fig. 5 Numerical results under different depth of water |
可知,随着水深的增加,一次压力峰值与二次压力峰值基本变化不明显。不同水深负压的峰值以及持续时间仍然存在一定区别,随着水深增加,负压增大,持续时间越短。从比冲量曲线上看,水深的变化对于比冲量的影响较为明显,主要体现在一次压力峰值衰减之后。随着水深的增大,比冲量曲线的振荡时间变短,原因在于静水压力的增加会使爆炸气泡的膨胀收缩变快,从而导致2次压力峰值的时间间隔更短。不同水深冲击波压力峰值与比冲量峰值结果如表7所示。
|
|
表 7 不同水深冲击波压力峰值与比冲量峰值结果 Tab.7 Peak shock wave and specific impulse under different depth of water |
为了验证气泡脉动数值仿真的有效性,考虑炸药当量与爆炸深度对于气泡脉动所产生气泡半径以及脉动周期的影响,设置如表8所示工况。
|
|
表 8 气泡脉动数值模拟验证工况 Tab.8 Verifying case for the numerical simulation of the bubble pulsation |
图6给出了3种验证工况下的气泡脉动过程中气泡半径的变化曲线。一方面,在炸药当量相同时,随着爆炸深度的增加,气泡第一次脉动的直径减小且脉动周期变小。另一方面,在爆炸深度相同时,随着炸药当量的增加,第一次气泡脉动的气泡半径明显增大,脉动周期有较少的增长。表9列出了仿真计算与经验公式计算得到的最大膨胀半径与气泡脉动周期,相对误差均不超过15%,由此验证了有限元计算的准确性。
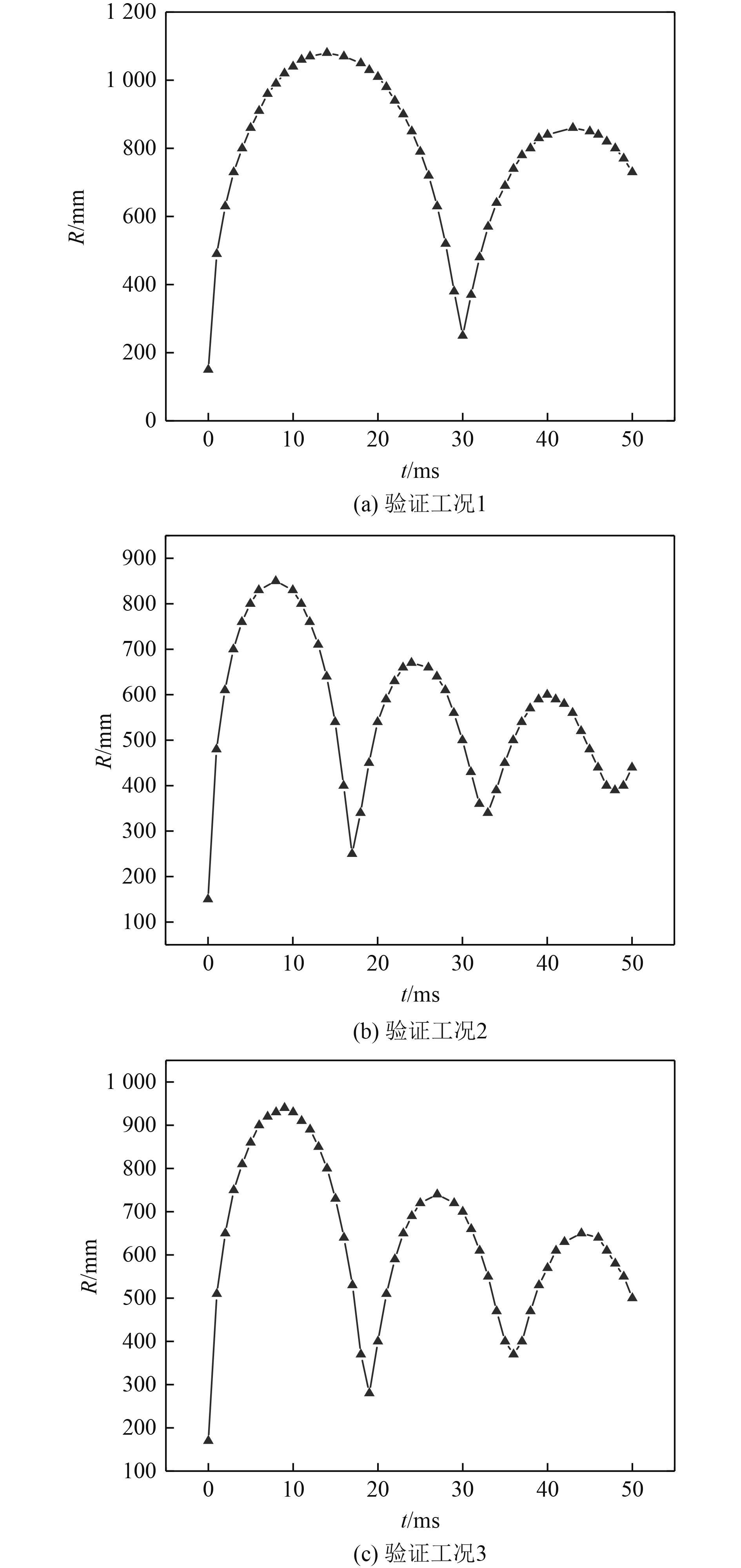
|
图 6 验证工况气泡脉动过程中气泡半径的变化 Fig. 6 The change of bubble radius during bubble pulsation in verifying case |
|
|
表 9 气泡最大膨胀半径及气泡脉动周期计算结果汇总 Tab.9 Summary of the maximal bubble expansion radius and bubble pulsation period in verifying case |
考虑在水深同为1000 m条件下,设置4种炸药当量,分别为20 kg、30 kg、40 kg和50 kg,通过有限元计算得到在不同炸药当量下,气泡脉动过程中气泡半径的变化过程,如图7所示。
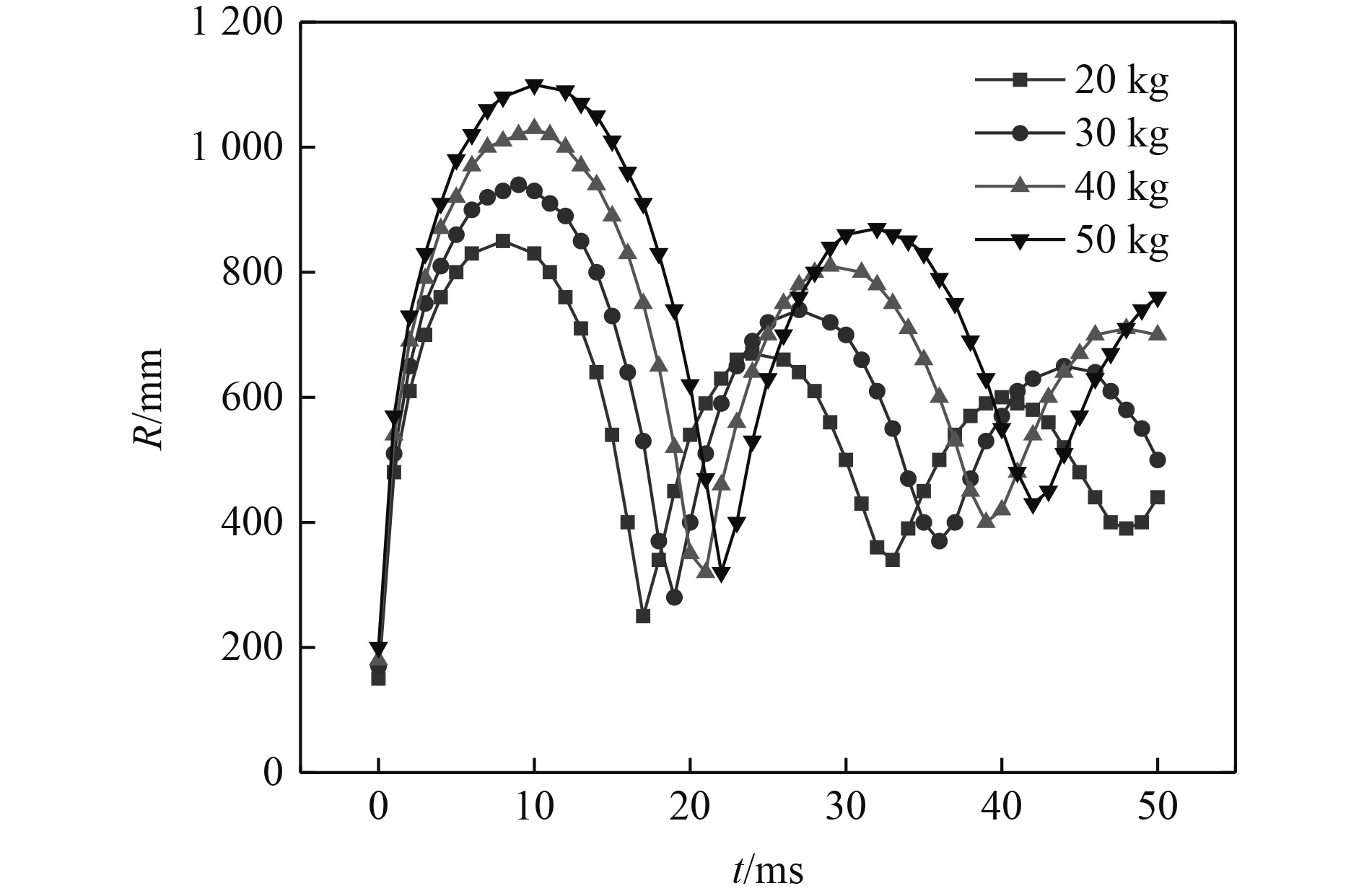
|
图 7 不同炸药当量气泡脉动过程中气泡半径的变化 Fig. 7 The change of bubble radius during the process of the bubble pulsation under different equivalent of explosive |
可知,随着炸药当量的增加,气泡半径也呈现增加趋势,且气泡脉动的周期也呈现增加趋势。当炸药当量为50 kg时,最大气泡半径达到1100 mm,相较于炸药当量20 kg时,约增加了29.4%。炸药当量50 kg时,气泡最大脉动周期为22 ms,较炸药当量20 kg时,约增加了29.4%。表10为不同炸药当量气泡最大膨胀半径及气泡脉动周期计算结果。
|
|
表 10 不同炸药当量气泡最大膨胀半径及气泡脉动周期计算结果 Tab.10 The maximal bubble expansion radius and bubble pulsation period under different equivalent of explosive |
在保持炸药当量相同情况下,研究水深对于气泡脉动的气泡半径以及脉动周期的影响,因此设置400 m、600 m、800 m和1000 m这4种不同的水深,气泡脉动过程中,气泡半径的变化历程如图8所示。
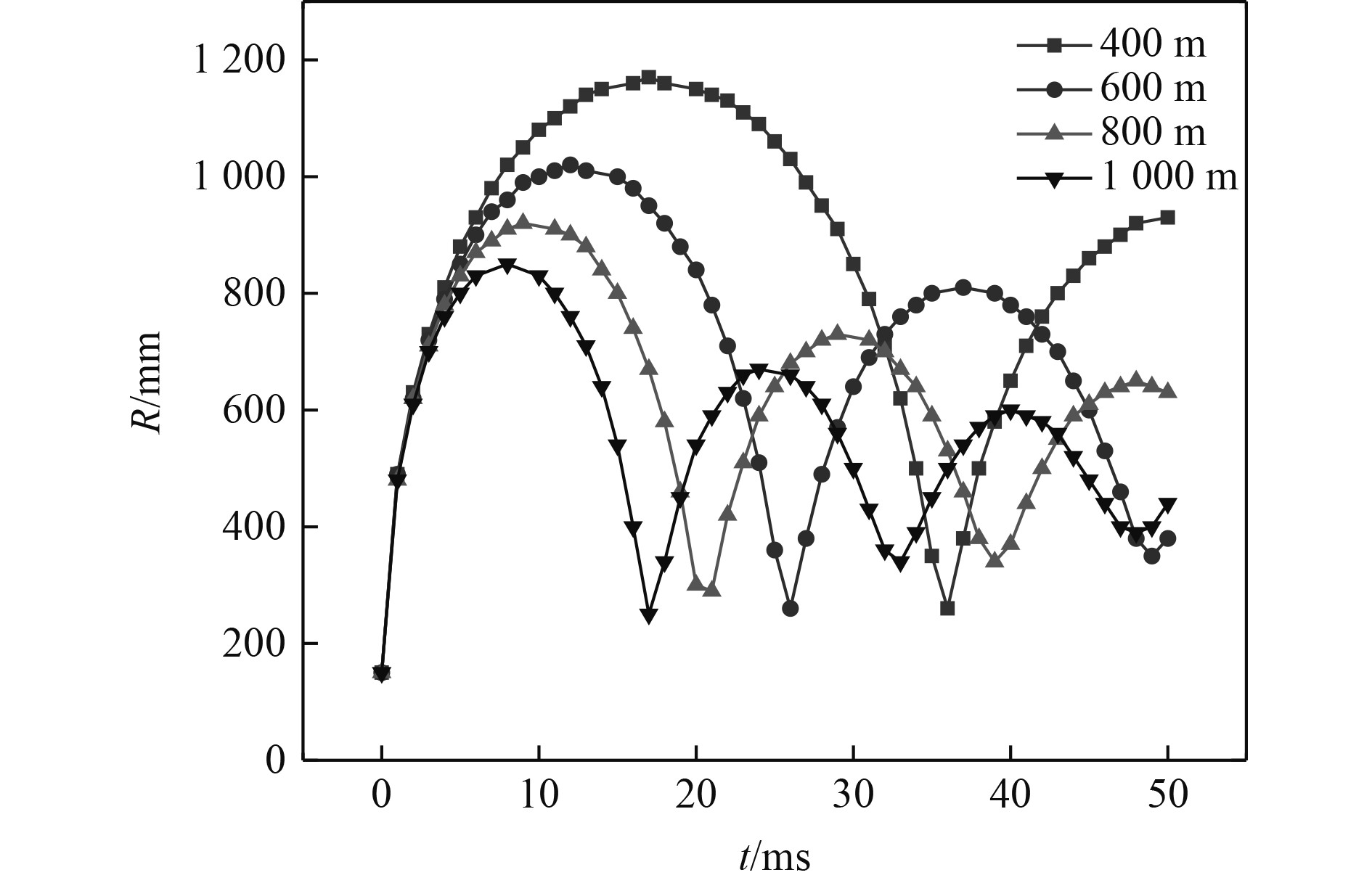
|
图 8 不同水深气泡脉动过程中气泡半径的变化 Fig. 8 The change of bubble radius during the process of the bubble pulsation under different depth of water |
由图8可知,随着水深的增加,气泡最大半径呈现减小的趋势,气泡脉动周期同样也呈现缩短趋势。结果表明,静水压力的增加会使气泡脉动受到更多抑制。不同水深,下第一次气泡脉动的结果如表11所示。爆炸深度为1000 m时,气泡脉动半径为850 mm,相较于400 m爆炸水深时,减小了27.4%。爆炸深度为1000 m时,气泡脉动周期为17 ms,相较于爆炸水深400 m时,减小了52.8%。表11为不同水深气泡最大膨胀半径及气泡脉动周期计算结果。
|
|
表 11 不同水深气泡最大膨胀半径及气泡脉动周期计算结果 Tab.11 The maximal bubble expansion radius and bubble pulsation period under different depth of water |
本文通过AUTODYN一维楔形体模型模拟了水下爆炸过程,数值计算得到的爆炸冲击波超压幅值、比冲量、气泡半径和脉动周期与经验公式计算结果相比,误差均在15%以内,验证了有限元计算模型的有效性。研究结果表明:
1)水下爆炸冲击波的超压峰值、二次压力峰值以及比冲量峰值均随着爆距的增加呈减小趋势,减小的速度随着爆距的增加而减缓。冲击波压力峰值、二次压力波峰值、冲击波比冲量峰值随着炸药当量的增加呈增大趋势,从冲击波压力峰值到二次压力波峰值之间相隔的时间也会随着炸药当量的增加而增加。
2)不同爆深工况下,超压曲线的压力峰值及二次压力波峰值基本相等,但爆深越大时,超压曲线负压区压力越大,两次压力峰值之间的时长越短,冲击波比冲量峰值随着水深的增加呈减小趋势。
3)水下爆炸气泡最大膨胀半径随炸药当量的增大而增大,水下爆炸气泡脉动周期随炸药当量的增大而增大,水下爆炸气泡二次脉动最大半径及二次脉动周期同样随炸药当量的增加而增大,但气泡二次脉动最大半径与第一次脉动最大半径相比较小。
4)水下爆炸气泡最大膨胀半径随爆深的增大而减小,水下爆炸气泡脉动周期随爆深的增大而减小,水下爆炸气泡最大膨胀半径和气泡脉动周期减小的速度随着爆深的增加而减缓。水下爆炸二次脉动最大半径及二次脉动周期同样随爆深的增加而减小。
| [1] |
TAYLOR G I. The pressure and impulse of submarine explosion waves on plates[J]. The scientific papers of GI Taylor, vol. 3. Cambridge, UK: Cambridge University Press. 1963: 287–303.
|
| [2] |
库尔. 水下爆炸[M]. 罗耀杰, 韩润泽, 官信译. 北京: 国防工业出版社, 1960
|
| [3] |
ZHAO Z T, RONG J L, ZHANG S X. A numerical study of underwater explosions based on the ghost fluid method[J]. Ocean Engineering, 2022, 247: 109796.
|
| [4] |
S TANAKA, I BATAEV, M NISHI, et al. Micropunching large-area metal sheets using underwater shock wave: experimental study and numerical simulation[J]. International Journal of Machine Tools and Manufacture, 2019, 147: 103457.
|
| [5] |
LI G L, SHI D Y, CHEN Y Y, et al. A study on damage characteristics of double-layer cylindrical shells subjected to underwater contact explosion[J]. International Journal of Impact Engineering. 2023, 172: 104428.
|
| [6] |
L J REN, H H MA, Z W SHEN, et al. Blast response of water-backed metallic sandwich panels subject to underwater explosion – Experimental and numerical investigations[J]. Composite Structures. 2019, 209: 79–92.
|
| [7] |
LEBLANC J, SHUKLA A. Dynamic response of curved composite panels to underwater explosive loading: Experimental and computational comparisons[J]. Composite Structures, 2011, 93: 3072–3081.
|
| [8] |
HONG Y J, XI Z. Dynamic response of a ring-stiffened cylindrical shell subjected to underwater explosive loading[J]. Applied Mechanics and Materials, 931(6): 105−107.
|
| [9] |
GEERS T L, HUNTER K S. An integrated wave-effects model for an underwater explosive bubble[J]. The Junmal of the Acoustical Society of America, 2022, 111(4): 1584–1601.
|
| [10] |
ZAMYSHLYAIEV B V. Dynamic loads in underwater explosion, AD-757183.
|
| [11] |
张社荣, 李宏璧, 王高辉, 等. 水下爆炸冲击波数值模拟的网格尺寸确定方法[J]. 振动与冲击, 2015, 34(8): 93–100.
|
 2023, Vol. 45
2023, Vol. 45
