2. 湖北省磁悬浮工程技术研究中心,湖北 武汉 430070
2. Hubei Maglev Engineering Technology Research Center, Wuhan 430070, China
阻尼减振技术是一种常见的减振手段,工程实际中将阻尼材料附加到机械设备上,通过阻尼耗散系统能量来降低系统振动的方法被大量使用,如摩擦阻尼、橡胶阻尼和粘弹性阻尼等[1]。但由于常见的阻尼减振方法对温度和工作环境等较敏感,因而在高温高压等恶劣环境下使用会受到限制[2]。
颗粒阻尼技术利用碰撞和摩擦作用来消耗振动能量,将振动能量转变为热等能量,产生阻尼效应实现减振目标[3]。为研究其工作原理,学者们先后采用了多相流体法、恢复力曲面法和离散单元法等方法进行研究[4-5]。其中,离散单元法是目前应用最为广泛的理论方法,是针对颗粒运动分析复杂性而提出的一种求解散体力学的数值方法,可较方便地计算颗粒特征属性及耗散能量[6]。
颗粒阻尼器对原系统结构改变较少,增加的附加质量也不多,且具有结构简单、可靠度高、耐温性优异、易用于恶劣环境等优点[7]。杨俊等[8]将其用于抑制轴系纵振,研究了转速对减振效果的影响。叶林昌等[9]分别将其应用到电子设备的电路板、动力装置基座减振优化等场合,大大扩宽了颗粒阻尼的工程应用,促进了颗粒阻尼器的发展。
颗粒阻尼器由于其优越的减振性能,已在土木、建筑等领域得到应用,但在舰船浮筏隔振系统中的应用研究较少。浮筏隔振系统是将若干待隔振的振源设备独立地安装在同一个充当中间质量的平台上,再对该平台进行减振[10]。筏架作为舰船上安装振源设备的公用平台,在设计时有较强灵活性,可对其贴附阻尼材料来提高减振性能。因此,本文将颗粒阻尼器应用到隔振系统筏架上,对其减振性能进行研究和探索,分析各种参数对减振性能的影响,为将其有效应用于隔振系统提供参考。
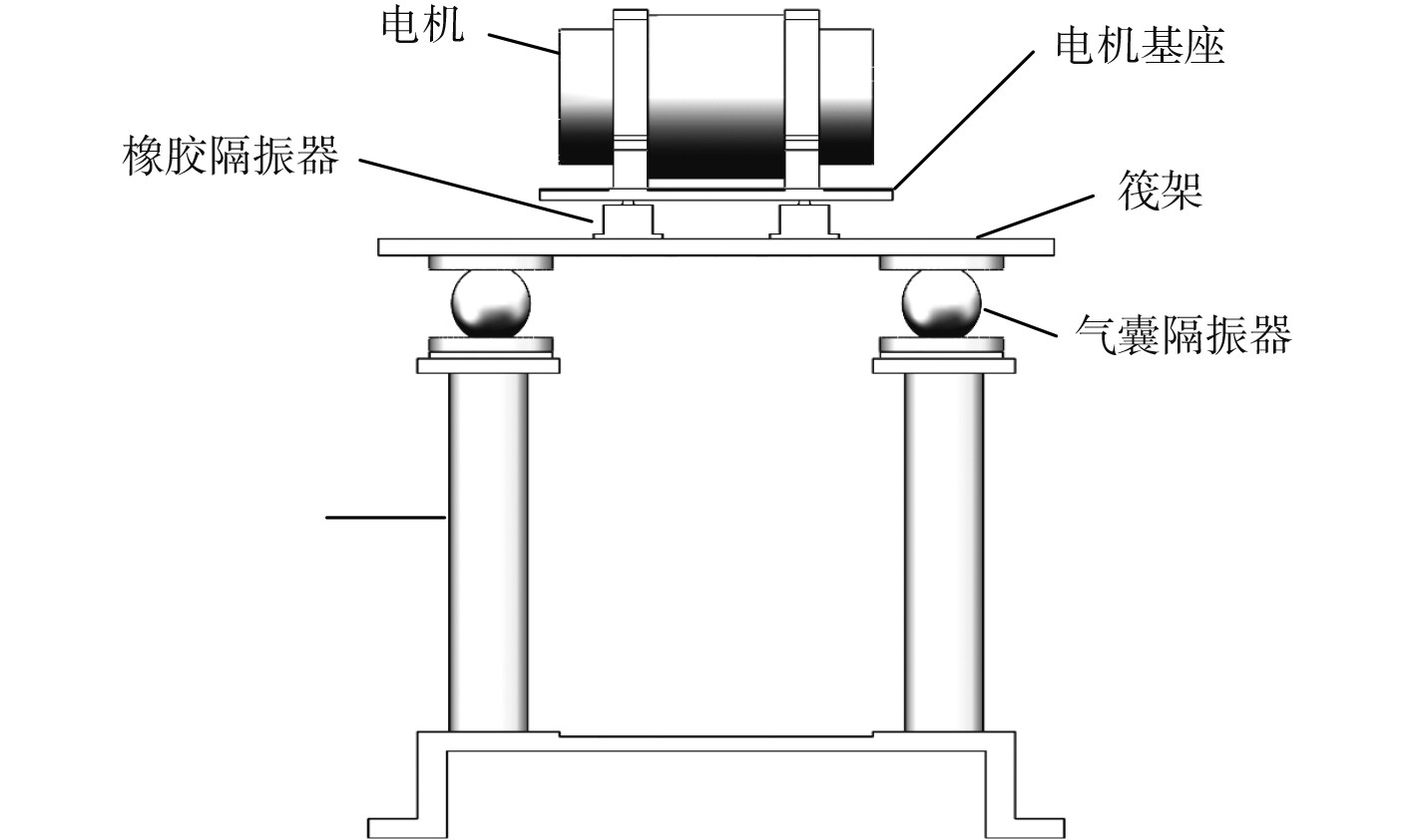
1 隔振系统分析 1.1 隔振系统结构本文隔振系统的结构如图1所示。其中,电机作为振动输入源可输出0~50 Hz,最大5 kN的激励,使用螺栓将其固连在电机基座上,电机基座与筏架通过橡胶阻尼器相连,筏架与刚性机座之间通过气囊隔振器连接。
|
图 1 隔振系统结构示意图 Fig. 1 The structure of vibration isolation platform |
设定气囊隔振器的充气压力为0.3 MPa,此时4个气囊总刚度为K=501.76 kN/m,以此状态下的系统为本次研究对象。
1.2 隔振系统振动特性分析本文针对隔振系统设计颗粒阻尼器,为了进行合理的阻尼器参数设计,需了解该隔振系统的振动特性。采用模态叠加法对隔振平台进行谐响应分析,得到该系统在电机激励下的加速度响应,以此来预估隔振平台的振动特性,仿真模型如图2所示。

|
图 2 隔振系统仿真模型 Fig. 2 Simulation model of vibration isolation system |
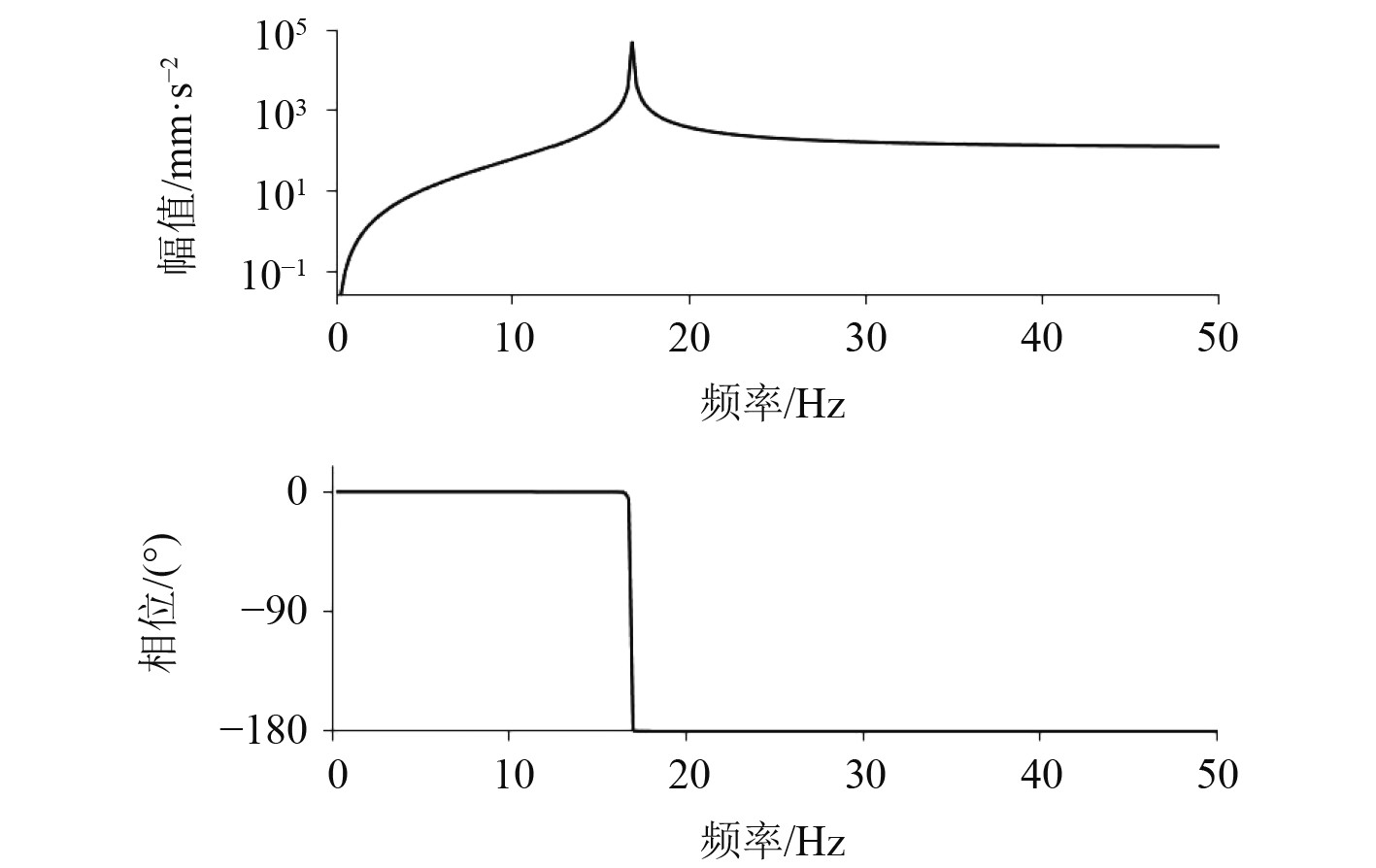
在仿真模型中,将作用点放在电机基座上,施加频率范围为0~50 Hz的激振力,监测筏架加速度响应,结果如图3所示。
|
图 3 筏架加速度响应曲线 Fig. 3 Acceleration response curve of raft frame |
可以看出,当激励频率为17 Hz时,加速度响应曲线出现峰值。因此,将隔振系统在17 Hz处的响应为基础进行颗粒阻尼器的参数设计。
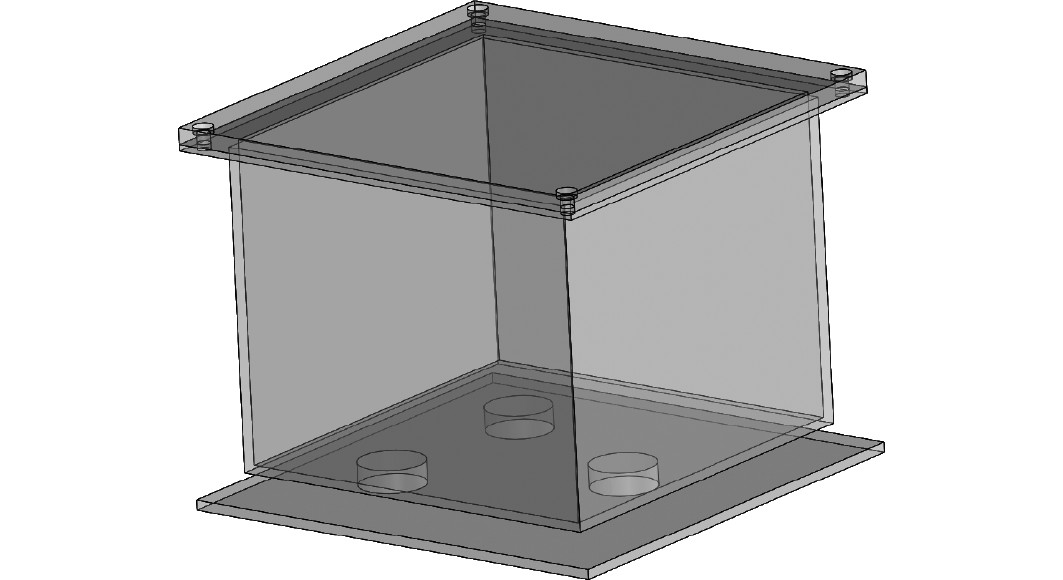
2 颗粒阻尼器模型建立 2.1 颗粒阻尼器外形设计颗粒阻尼器结构分为内嵌式和外置式。根据隔振平台的结构特征,本次采用外置式,通过夹具将其固定在筏架上适当位置,具体结构如图4所示。腔体尺寸为120 mm×120 mm×100 mm,壁厚为2 mm,材料采用有机玻璃。
|
图 4 颗粒阻尼器外形 Fig. 4 Shape of particle damper |
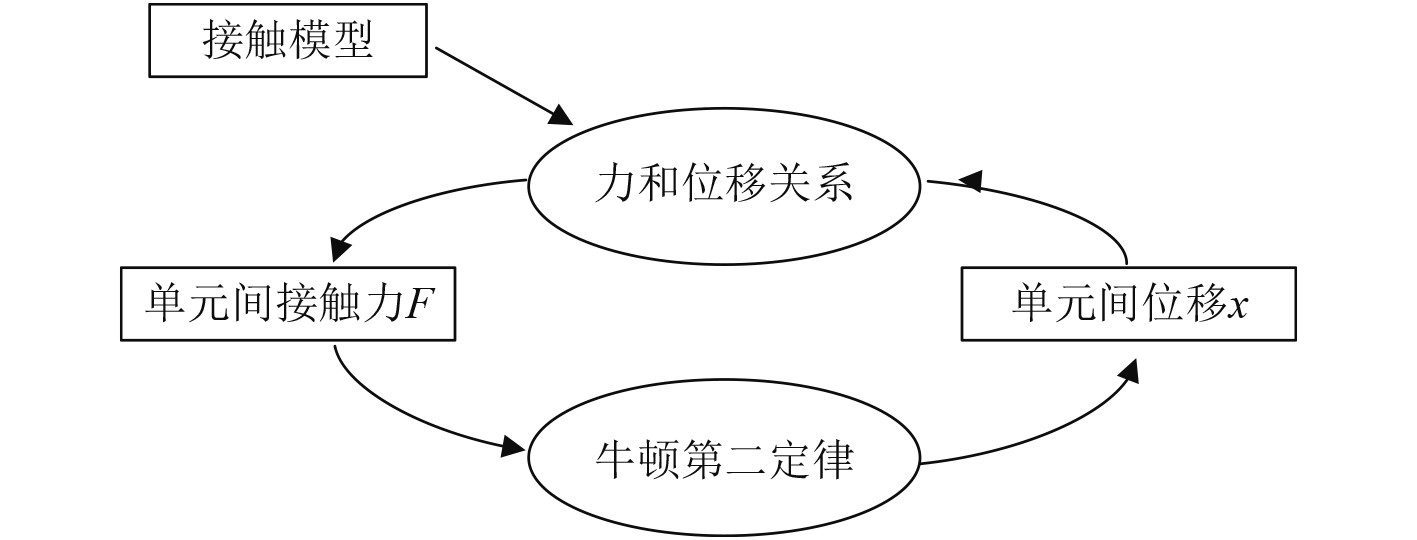
离散单元法是求解颗粒散体力学的数值理论方法,将系统看成由独立单元构成,各单元之间通过点线面进行接触,在外力作用下,单元间产生力的作用,利用牛顿第二定律计算单元加速度,然后通过积分求对应的速度与位移,同时得到单元变形量。根据结果更新单元状态,又会产生新一步的单元间作用力,通过时间步迭代方法,形成循环并一直计算下去,直至达到终止条件,循环过程如图5所示。
|
图 5 计算循环示意图 Fig. 5 Schematic of the calculation cycle |
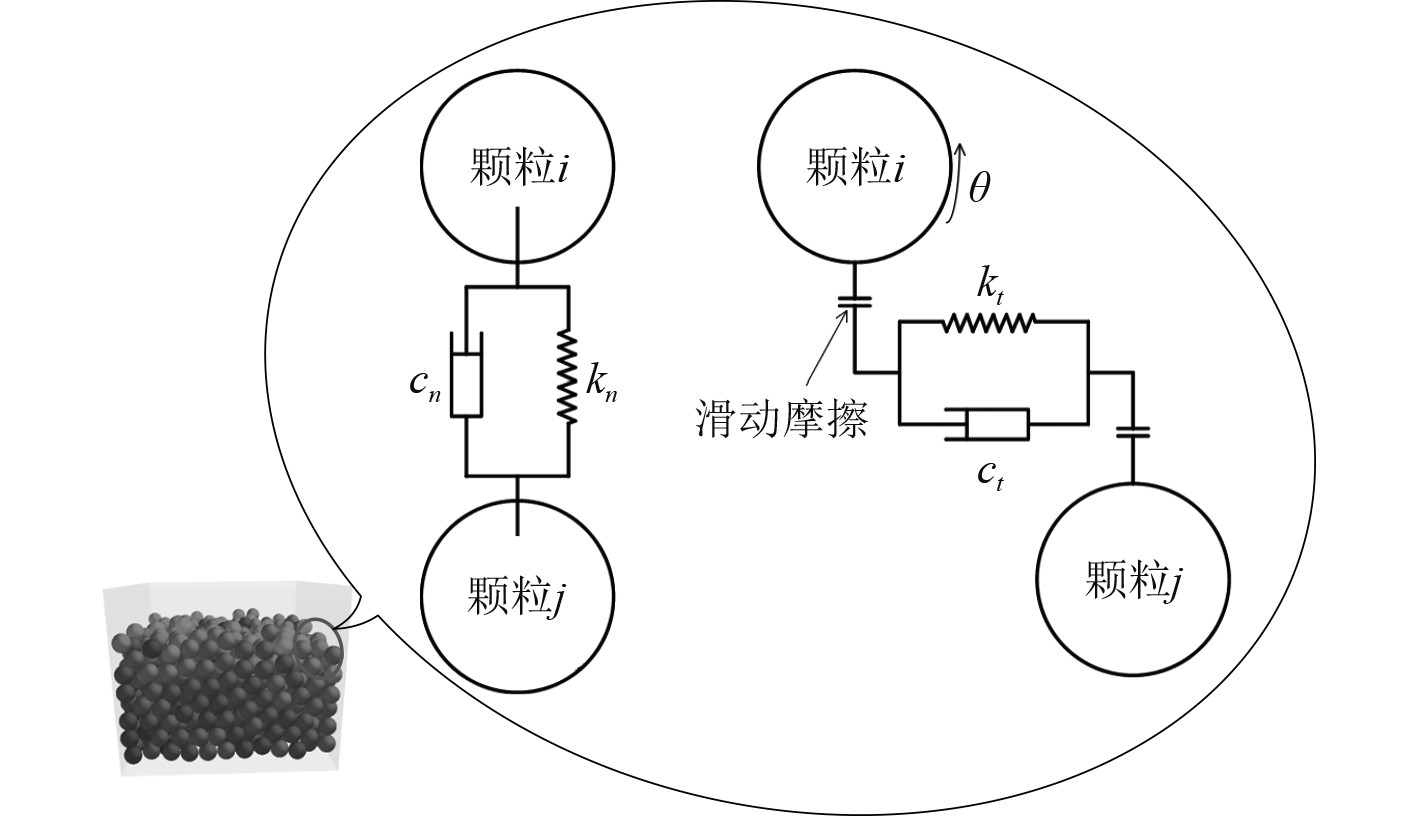
运动过程中,各单元间相互碰撞和摩擦产生接触力,接触模型作为离散单元法的核心,决定了颗粒碰撞和摩擦过程中所受力和力矩的大小。本文采用Hertz-Mindlin接触模型进行仿真计算,颗粒简化模型将颗粒间受到的力简化为法向和切向力,以弹簧、阻尼器和滑动器来表示,如图6所示。
|
图 6 接触模型简化示意图 Fig. 6 Simplified representation of the contact model |
颗粒接触过程的法向接触力可表示为:
| $ {F_{nij}} = {m^*}\frac{{{{\rm{d}}^2}{x_n}}}{{{\rm{d}}{t^2}}} + {c_n}\frac{{{\rm{d}}{x_n}}}{{{\rm{d}}t}} + {k_n}{x_n}。$ | (1) |
颗粒接触过程的切向接触力和力矩可表示为:
| $ {F_{tij}} = {m^*}\frac{{{{\rm{d}}^2}{x_t}}}{{{\rm{d}}{t^2}}} + {c_s}\frac{{{\rm{d}}{x_t}}}{{{\rm{d}}t}} + {k_t}{x_t} ,$ | (2) |
| $ {T_{ij}} = {J_{ij}}\frac{{{{\rm{d}}^2}\vartheta }}{{{\rm{d}}{t^2}}} + s({c_t}\frac{{{\rm{d}}{x_t}}}{{{\rm{d}}t}} + {k_t}{x_t})。$ | (3) |
式中:m*为颗粒的等效质量;xn和xt为颗粒间的法向和切向相对位移;cn和ct为法向和切向阻尼系数;kn和kt为法向和切向弹性系数;Jij为2个颗粒的等效转动惯量;θ为颗粒的旋转角度;s为旋转半径。
2.3 颗粒阻尼器耗能模型通过对力学模型进行数学计算,即可得到各个时刻的力和位移信息,进而可计算出不同时刻的能量。碰撞过程引起的能量损失通常由碰撞前后的动能损失作为计算依据。
| $ \Delta {E_e} = \frac{1}{2}\frac{{{m_i}{m_j}}}{{{m_i} + {m_j}}}(1 - {e^2}){v_{ij}}。$ | (4) |
摩擦过程所消耗的能量可表示为:
| $ \Delta {E_f} = {\mu _s}\left| {{F_n}{x_t}} \right| 。$ | (5) |
综上,可求出颗粒进行一次碰撞和摩擦所消耗的能量,系统消耗的总能量为所有颗粒之间以及颗粒与阻尼器壁之间的碰撞和摩擦耗能总和:
| $ \Delta E = \sum {\Delta {E_e}} + \sum {\Delta {E_f}} 。$ | (6) |
可以看出,耗能与颗粒质量、恢复系数、摩擦系数、颗粒数量等参数密切相关。
2.4 颗粒阻尼器等效阻尼模型颗粒阻尼器通过阻尼耗能的方式进行减振,可通过理论计算得到其等效质量和阻尼系数,将其附加于振动结构上,模拟颗粒阻尼器产生的实际减振效果。
通过离散元仿真可得到颗粒阻尼器的耗能数据,参照式(7)~式(9)即可得颗粒阻尼器的耗散功率效率e和等效动态质量Me,进而求得等效阻尼系数c[11]。
| $ e = \frac{{{E_T}}}{{{\text{π}} m|V{|^2}}},$ | (7) |
| $ {M_e} = \frac{{2{E_k}}}{{|V{|^2}}} ,$ | (8) |
| $ c = e \cdot \omega \cdot m 。$ | (9) |
式中:ET为单个周期的耗能;Ek为所有颗粒动能的平均值;m为颗粒总质量;|V|为阻尼器速度;ω为激励频率。
得到其等效阻尼和等效质量后,即可通过有限元软件将其等效施加在筏架正确位置,来代替颗粒阻尼器完成整个隔振系统的仿真,得到不同参数影响下的加速度响应,进而分析减振效果。
3 颗粒阻尼器参数影响分析为使颗粒阻尼器具有更优的减振性能,针对各个参数进行分析,得到合理参数。同时通过理论计算得到颗粒阻尼器的等效质量和阻尼,利用有限元仿真来分析减振效果。
3.1 不同材料颗粒影响分析颗粒材料属性会直接影响到阻尼器的耗能,不同材料具有各异的性能。为研究不同材料颗粒对耗能的影响,选用了45钢、玻璃和铅3种常用材料进行研究,其主要性能参数如表1所示。
|
|
表 1 颗粒材料参数 Tab.1 Material parameters of particles |
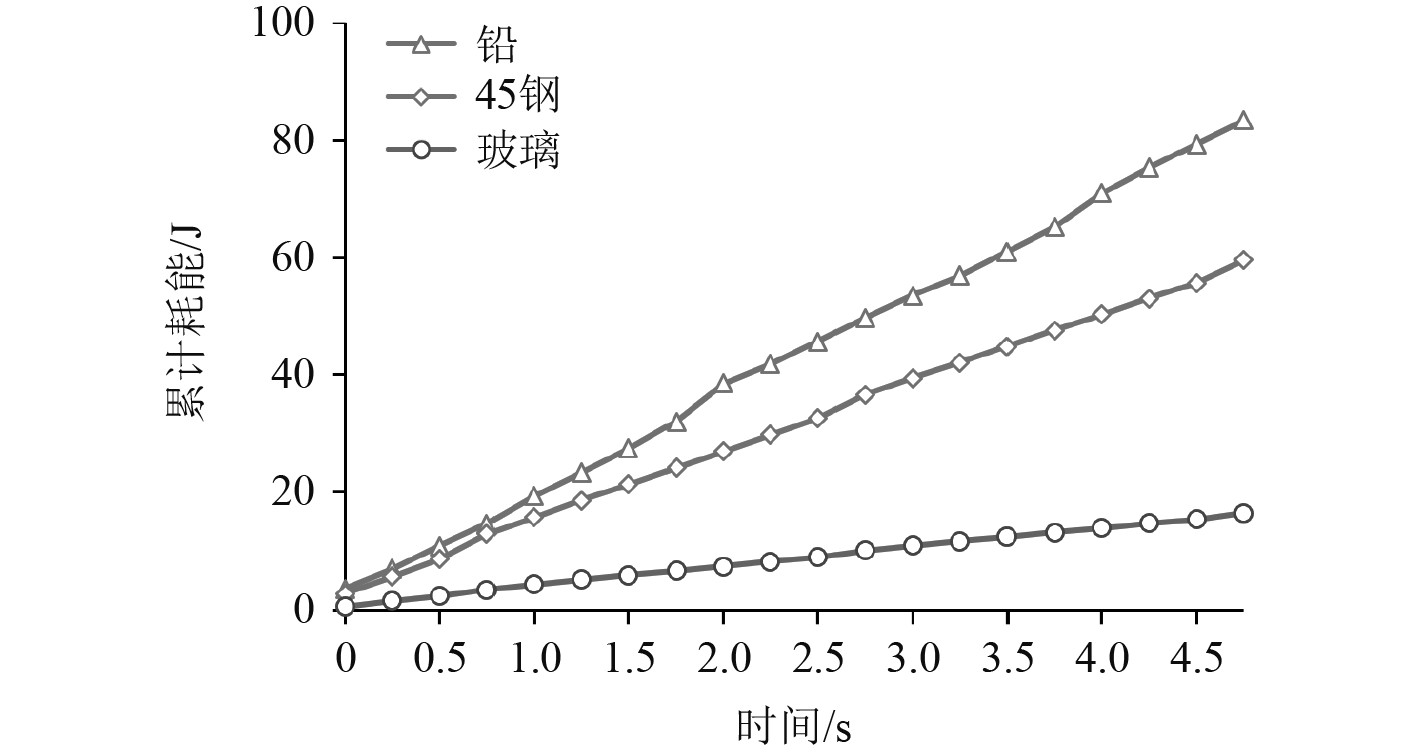
根据仿真结果,统计3种材料的耗能数据,如图7所示。可以看出,铅颗粒耗能最大,45钢次之,玻璃最小。
|
图 7 不同材料下耗能情况 Fig. 7 Energy consumption of different materials |
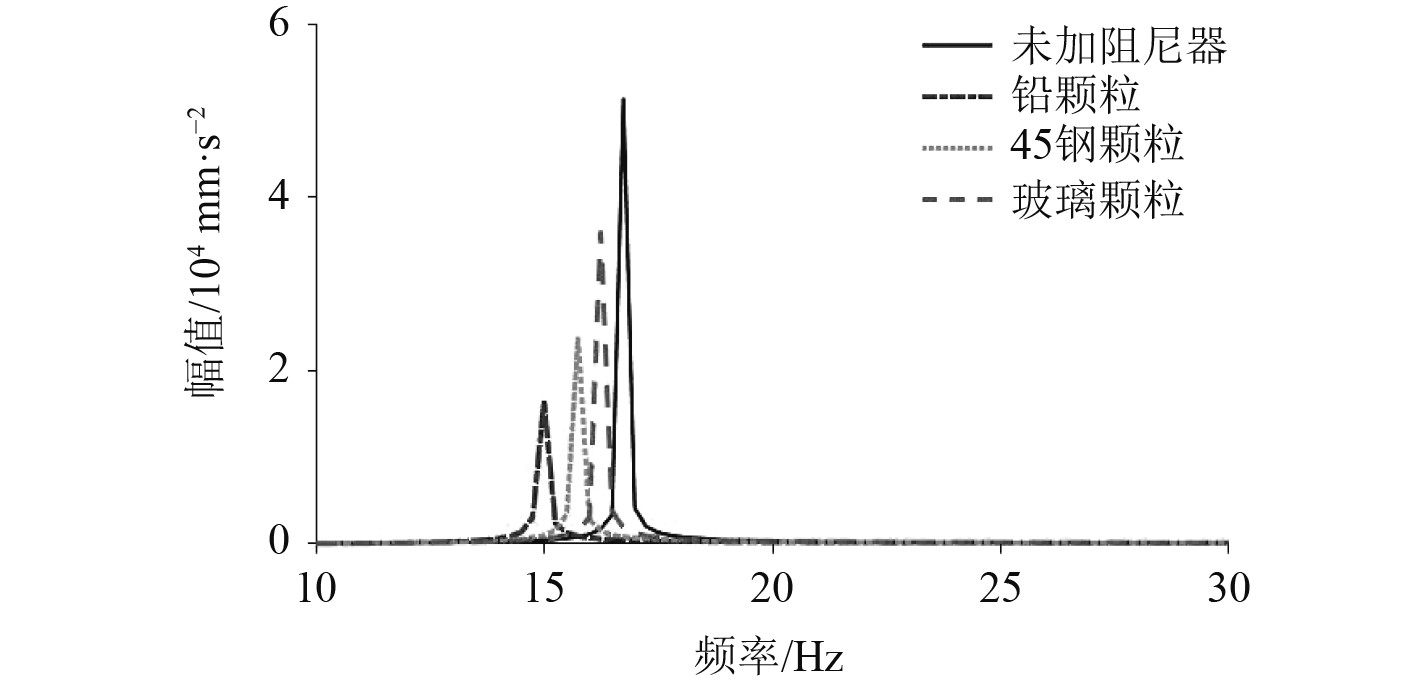
根据耗能仿真结果,计算不同材料参数下的等效质量和阻尼,通过有限元仿真得到在不同材料颗粒阻尼器下的减振效果,结果如图8所示。可以看出,阻尼器填充颗粒为铅、45钢和玻璃时,相比未加阻尼器时,最大减振效果为66%、54%和29%,表明颗粒阻尼器具有良好的减振效果。
|
图 8 不同颗粒材料下筏架加速度响应 Fig. 8 Acceleration response of raft frame under different particles materials |
根据材料性能分析,密度对于耗能影响较大,即比重越大,颗粒之间碰撞和摩擦会消耗更多的能量,因此在选用材料时优先选用密度较大的材料,但密度大会带来附加质量变大的问题,在一些工程场合中对于附加质量的大小较敏感,因此要结合实际情况进行合理选择。
3.2 阻尼器填充率影响分析填充率代表填充到容器的颗粒所占体积与容器体积的比值,计算式为:
| $ \alpha = \frac{{n{d^3}}}{V} 。$ | (10) |
式中:α为填充率;d为颗粒直径;n为填充颗粒数量;V为颗粒阻尼器的体积。
表2为不同填充率下颗粒数目。
|
|
表 2 不同填充率下颗粒数目 Tab.2 Number of particles under different filling rates |
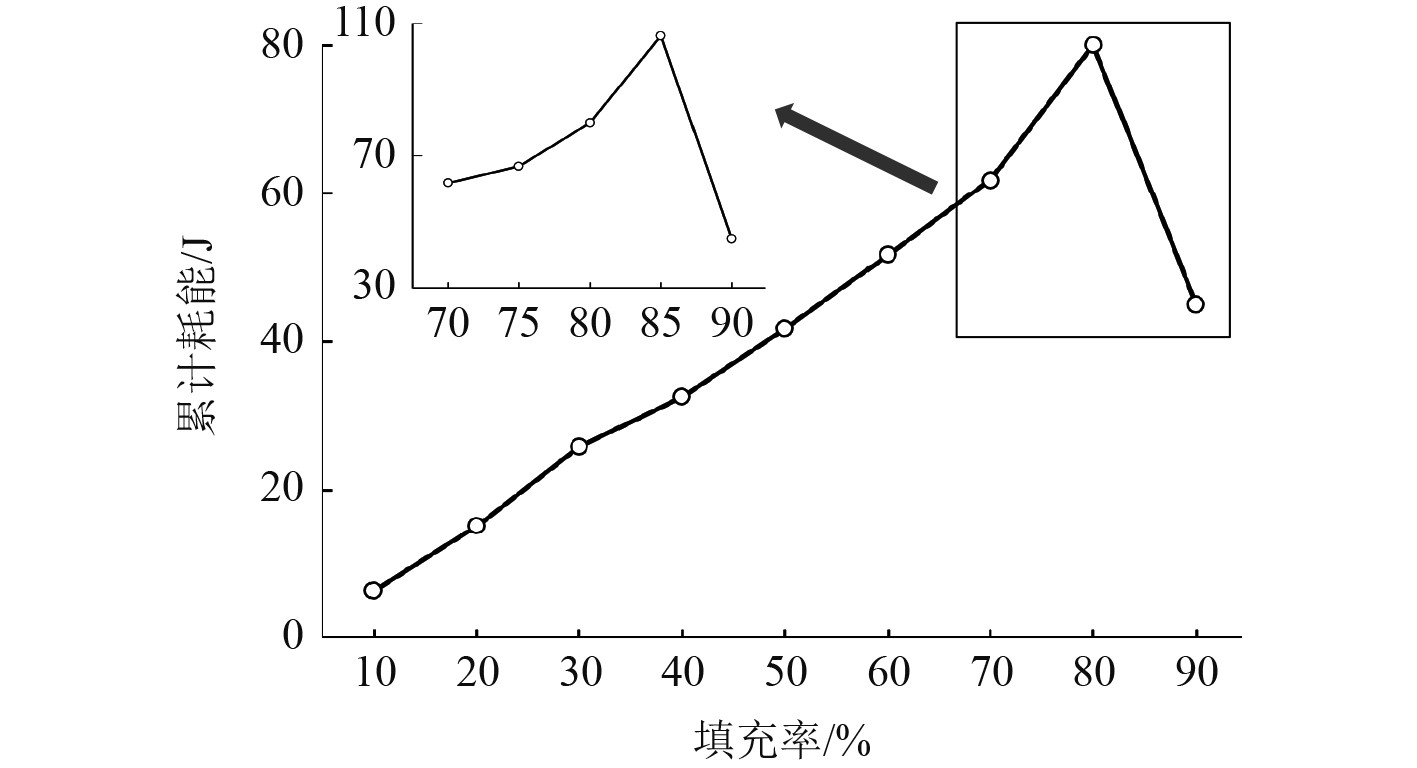
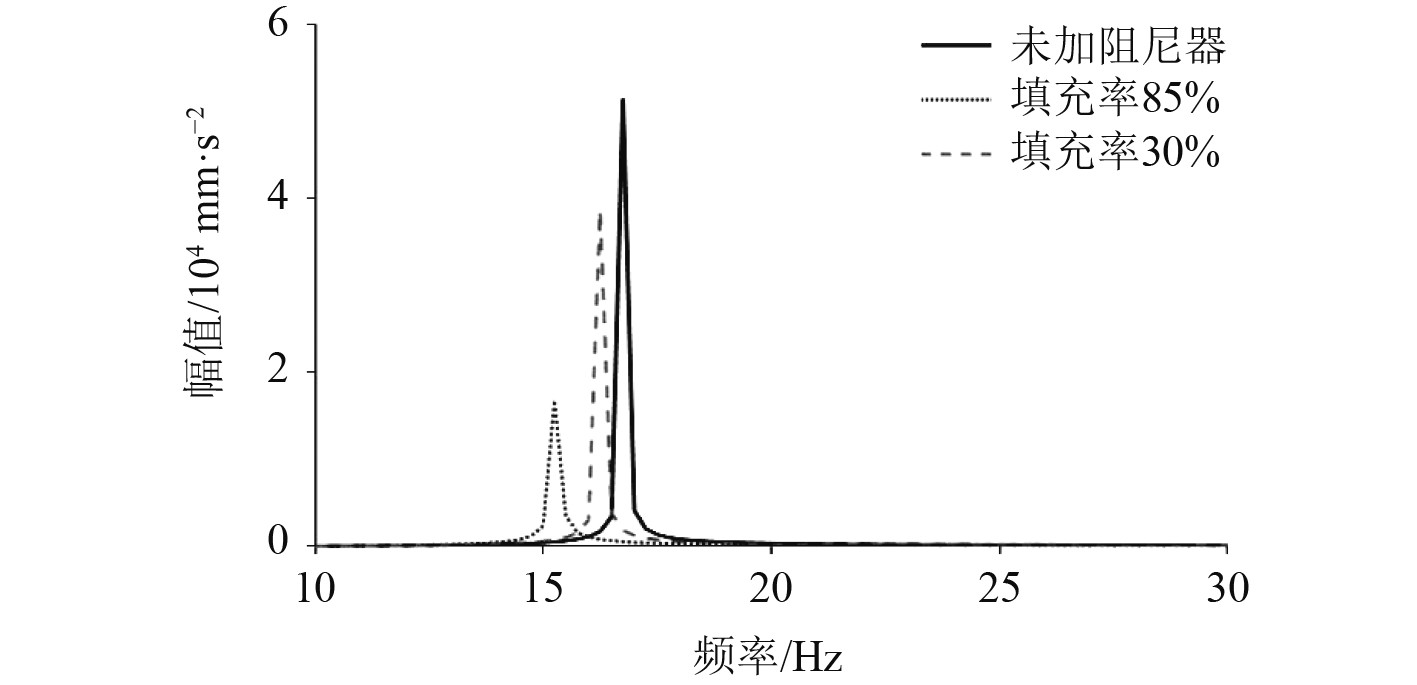
由图9和图10可知,填充率为85%时耗能最大,此时最大减振效果达到68%,而填充率为30%时减振效果仅为25%。当填充率较低时,颗粒少导致颗粒间的碰撞和摩擦次数减少,因此耗能较低;当填充率大于85%后,颗粒数目过多,导致颗粒在容器内的运动空间受限,则碰撞和摩擦次数都会相应减少,因此耗能降低,削弱了减振效果。
|
图 9 不同填充率下耗能情况 Fig. 9 Energy consumption under different fill rates |
|
图 10 不同填充率下筏架加速度响应 Fig. 10 Acceleration response of raft under different fill rates |
图11为不同填充率下的颗粒运动矢量图。可以看出,当颗粒填充率低时,颗粒有较大活动空间,颗粒表现为自由运动,颗粒活性高;当填充率较高时,颗粒活动空间严重受限,颗粒团聚在一起进行运动,颗粒活性较低,导致耗能减小。

|
图 11 不同填充率下颗粒运动情况 Fig. 11 The movement of particles under different filling rates |
同一填充率下,填充不同直径的颗粒时,颗粒数目不同,从而对耗能产生影响。粒径的选择与阻尼器的形状尺寸及外部激励有关,对于不同的外部条件会存在最优粒径。
因此,为研究粒径变化对耗能会产生何种影响,在保证填充颗粒总质量相同下,分别取直径为6~16 mm的颗粒进行仿真,间隔为2 mm,颗粒填充情况如图12所示,颗粒数目如表3所示。

|
图 12 3种粒径下颗粒填充情况 Fig. 12 Filling status of particles under the three particle sizes |
|
|
表 3 不同颗粒直径下颗粒数目 Tab.3 Number of particles at different particle diameters |
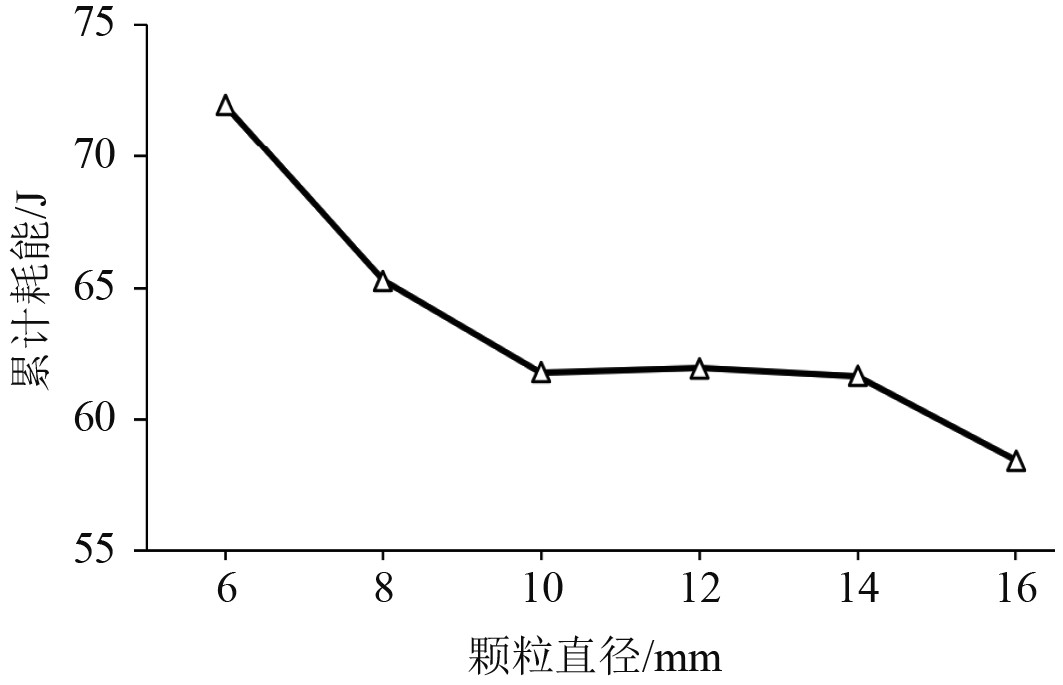
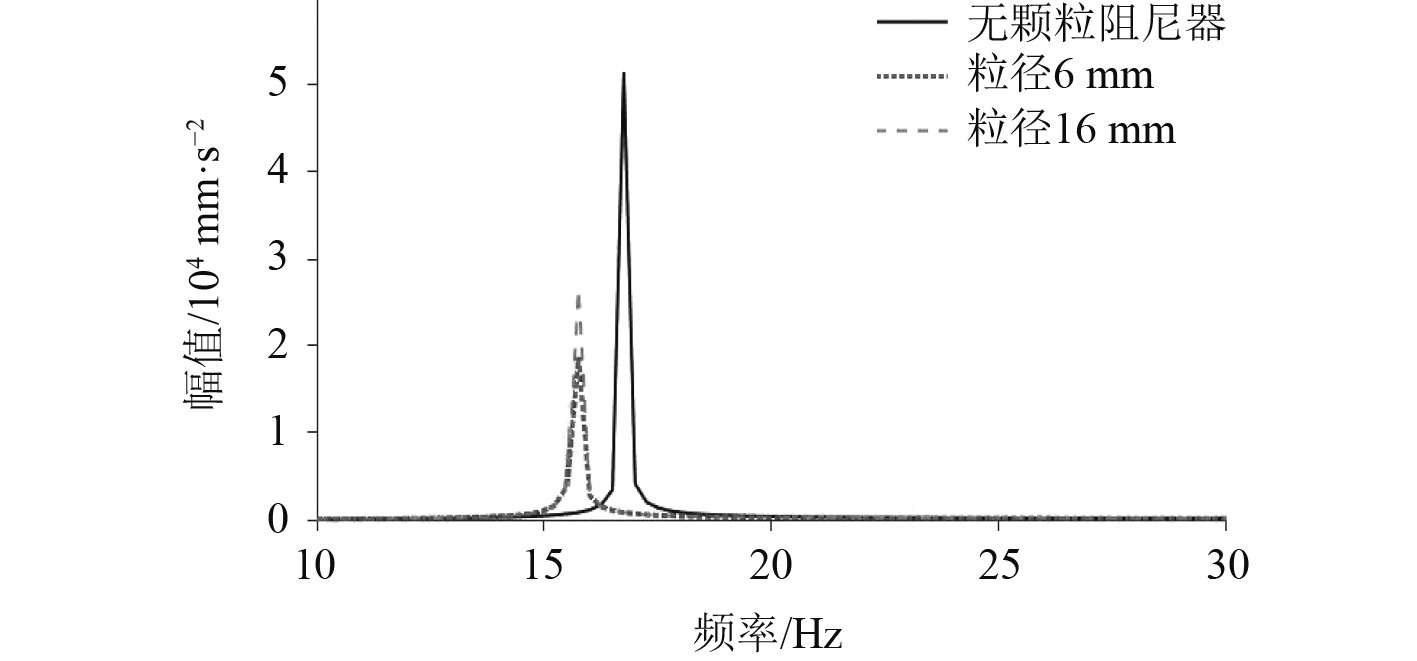
从图13和图14可看出,不同粒径产生的耗能不同,粒径为6 mm时耗能最大,此时最大减振效果为70%。随着粒径增大,单个颗粒质量增大,单次碰撞和摩擦产生的耗能也随之变大。但在相同质量下,粒径增大引起颗粒数目减少,碰撞次数会大幅减少,故耗能也随之减少,减振效果变差。
|
图 13 不同粒径下耗能情况 Fig. 13 Energy consumption under different particle diameters |
|
图 14 不同粒径下筏架加速度响应 Fig. 14 Acceleration response of raft frame under different particle diameters |
高填充率下颗粒堆积情况严重,下层颗粒受到上层颗粒的压力较大,使得颗粒运动性降低,因此通过对阻尼器内部进行纵向分隔,提高底层颗粒运动性,进而提高颗粒阻尼器耗能。针对颗粒阻尼器在不同分层数下,对耗能的影响进行仿真分析,分层方案如表4所示。
|
|
表 4 分层数及单层颗粒数目 Tab.4 Number of layers and number of particles per layer |
图15为3种分层方案在同一时刻的颗粒运动状态。可以看出,随着分层数增加,底层颗粒的速度在明显增大,说明增加分层数可减小底层颗粒受到的压力,缓解底层颗粒大量堆积造成的碰撞效果不明显状况,故而提高颗粒的运动性,增加耗能。

|
图 15 不同层数下颗粒的运动状况 Fig. 15 The movement of particles under different layers |
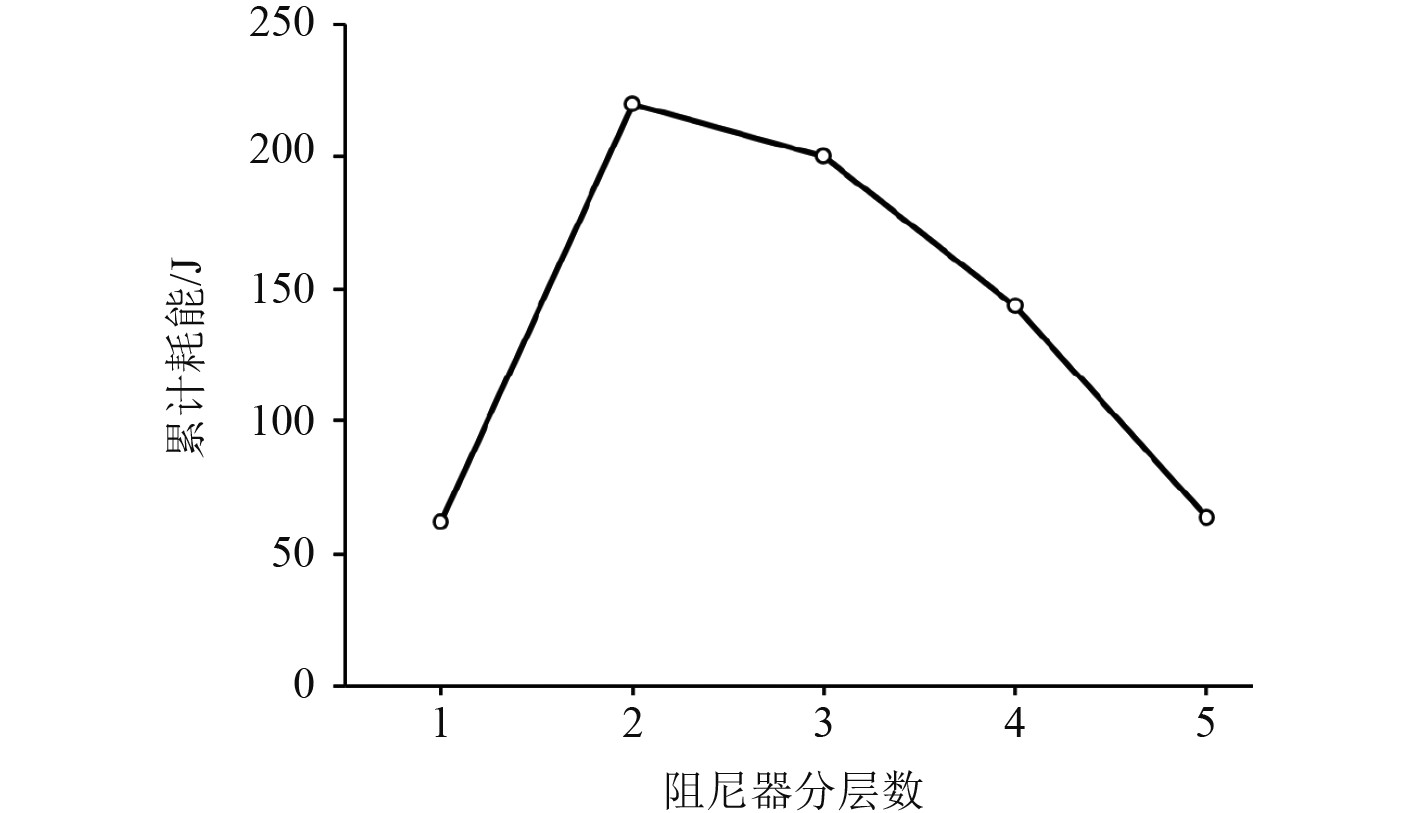
图16为不同分层方案所对应的颗粒阻尼器耗能情况。可以看出,耗能并未出现一直增大的现象。当分层数为2时耗能最大,此时最大减振效果达到75%。分层数为3和4时,耗能要低于2层,但仍比单层耗能要高。通过分层可提高底层颗粒的运动性,增加颗粒与容器的碰撞次数,但分层数过多引起每层颗粒数目减少,颗粒碰撞次数减少,综合下来反而降低了整体耗能。因此,选择合适的分层数可大幅优化颗粒阻尼耗能,实现更好减振效果。
|
图 16 不同分层数下耗能 Fig. 16 Energy consumption under different layer numbers |
本文将颗粒阻尼器应用于舰船浮筏隔振系统上,通过谐响应分析得到该系统振动特性,然后采用离散单元法研究了不同颗粒阻尼器参数对耗能的影响。同时根据耗能结果,最后采用有限元法分析了颗粒阻尼器产生的减振效果。本文主要结论如下:
1)颗粒阻尼器能够对隔振系统产生良好的减振效果,通过合理的颗粒阻尼器参数设计可大幅提高系统减振性能。
2)在选用颗粒材料时,优先使用密度大的材料,能够取得较优减振性能;填充率并非越大越好,最优填充率一般处于85%附近。同等条件下,使用小尺寸颗粒能够增大能耗,提高减振性能。
3)条件允许下,应对阻尼器进行合理分层,能够大幅提升其减振性能,但分层数不宜过多,建议分2~3层为最佳。
| [1] |
古龙, 闵捷. 船舶振动噪声控制技术的现状与发展[J]. 舰船科学技术, 2019, 41(23): 1-5. GU L, MIN J. Review of vibration and noise control technology for submarines[J]. Ship Science and Technology, 2019, 41(23): 1-5. |
| [2] |
夏兆旺, 茅凯杰, 薛 程, 等. 基于颗粒阻尼技术的海洋平台桁架结构振动特性研究[J]. 江苏科技大学学报(自然科学版), 2018, 32(1): 46-50. |
| [3] |
闫维明, 王宝顺, 黄绪宏. 颗粒阻尼器的研究进展及其在土木工程中的应用展望[J]. 土木工程学报, 2020, 53(5): 32-41. |
| [4] |
SAEKI M. Analytical study of multi-particle damping[J]. Journal of Sound and Vibration, 2005, 281(3-5): 1133-1144. DOI:10.1016/j.jsv.2004.02.034 |
| [5] |
NIKLAS M, ROBERT S. Damping prediction of particle dampers for structures under forced vibration using effective fields[J]. Granular Matter, 2021, 23(64): 1-13. |
| [6] |
ALLAH R, YASUSHI I, YUHIRO I, et al. Experimental and numerical analysis of torque properties of rotary elastomer particle damper considering the effect of gap and no gap between rotor and body of the damper[J]. Shock and Vibration, 2021: 7724156.
|
| [7] |
鲁正, 吕西林, 闫维明. 颗粒阻尼技术研究综述[J]. 振动与冲击, 2013, 32(7): 1-7. |
| [8] |
杨俊, 刘正林, 刘杰, 等. 颗粒阻尼抑制水下航行器轴系纵振模拟试验[J]. 交通运输工程学报, 2021, 21(5): 161-176. |
| [9] |
叶林昌, 肖望强, 沈建平, 等. 基于粒子阻尼的动力装置基座减振优化设计研究[J]. 振动与冲击, 2021, 40(3): 40-47. |
| [10] |
胡泽超, 何琳, 李彦. 隔振器分布对浮筏隔振系统隔振性能的影响[J]. 舰船科学技术, 2016, 38(21): 48-52. HU Z C, HE L, LI Y. The influence of the isolator’s distribution on floating raft isolation system′s performance[J]. Ship Science and Technology, 2016, 38(21): 48-52. |
| [11] |
武宏程, 耿建强, 李 勇, 等. 颗粒碰撞阻尼器特性仿真分析与试验验证[J]. 噪声与振动控制, 2020, 40(2): 221-225. |
 2023, Vol. 45
2023, Vol. 45
