目前,海军装备的防空反导导弹、干扰弹和反潜火箭深弹等小口径弹药多采用倾斜发射方式,存在贮弹密度小、空间利用率低等问题。而舰载导弹垂直发射装置具备载弹密度高、弹药配置灵活的优势,选取其作为装载方式能提高整体发射系统的性能,已引起国内外广泛关注[1−2]。
国内外对垂直发射装置的燃气排导系统进行了大量的仿真和试验研究。邴笑寒等[3]深入分析了垂直发射系统内部燃气流场的压强特性,结果表明当导弹发射时初始冲击波在整个燃气排导系统中会产生较高压力峰值。杨志宏等[4]给出了排气管直径、收缩段高度和排气弯管半径等不同因素对排导效率的影响程度;刘方等[5]研究分析了公共燃气排导对一种共架发射装置的影响,并从配套设备选择和系统布局等多个方面进行优化设计。赵贤超[6]对导弹发生意外点火时,垂发装置的排导系统内部流场压强分布情况进行了数值仿真研究,最终得到流场内部不同位置的压强分布规律。赵若男[7]研究了不同结构的导流型面对燃气排导和发射箱内部流场的影响,研究结果表明相比较斜平面结构的导流器,圆弧结构的导流器更有利于降低流场压强和温度,从而达到改善发射箱内部流场环境的效果。王俊敏等[8]建立实际发射工况下的导弹垂直发射燃气排导系统气固两相流模型,并给出了发射高度和燃烧室压强对两相流场参数分布的影响。
本文基于某型高密度垂直发射系统的结构形式,以其内部燃气排导流场为研究对象,建立相应的三维燃气流场模型,对比分析了不同导流结构对燃气排导性能的影响,仿真结果对燃气排导系统的优化设计及高密度垂直发射系统的工程应用等具有重要意义。
1 数值模拟方法 1.1 基本假设发动机喷管喷出的燃气流不仅含有大量凝相,而且含有多种成分,并伴随着剧烈的化学反应。因此为简化计算,在分析计算过程中,对燃气流场做如下假设:
1)假设燃气流为理想气体,是性质单一稳定,满足理想气体状态方程;
2)忽略燃气凝相带来的影响以及凝相与燃气两相间的动量和能量交换;
3)忽略导弹运动带来的发射初始流场变化,认为发射初始阶段导弹静止不动。
1.2 控制方程采用流体力学计算软件求解非定常N-S方程的方法对发射系统内部燃气流场进行数值仿真,其基本方程组的具体形式如下:
1)质量守恒方程
| $ \frac{\partial \rho}{\partial t}+\frac{\partial \rho u}{\partial x}+\frac{\partial \rho v}{\partial y}+\frac{\partial \rho \omega}{\partial z}=0 。$ | (1) |
式中:u、ν、ω分别为在x、y、z方向上的速度分量,m/s;t为时间,s;ρ为密度,kg/m3[9]。
2)动量守恒方程:
| $ \begin{split} \frac{\partial(\rho u)}{\partial t}+&\frac{\partial(\rho u u)}{\partial x}+\frac{\partial(\rho u v)}{\partial y}+\frac{\partial(\rho u \omega)}{\partial z}= \\ &\mu_{\mathrm{off}}\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}+\frac{\partial^{2} u}{\partial z^{2}}\right)-\frac{\partial p}{\partial x},\end{split} $ | (2) |
| $ \begin{split} \frac{\partial(\rho v)}{\partial t}+&\frac{\partial(\rho v u)}{\partial x}+\frac{\partial(\rho v v)}{\partial y}+\frac{\partial(\rho v \omega)}{\partial z}= \\ &\mu_{\mathrm{eff}}\left(\frac{\partial^{2} v}{\partial x^{2}}+\frac{\partial^{2} v}{\partial y^{2}}+\frac{\partial^{2} v}{\partial z^{2}}\right)-\frac{\partial p}{\partial y},\end{split} $ | (3) |
| $ \begin{split} \frac{\partial(\rho w)}{\partial t}+&\frac{\partial(\rho w u)}{\partial x}+\frac{\partial(\rho w)}{\partial y}+\frac{\partial(\rho w w)}{\partial z}= \\ &\mu\;_{\mathrm{ef}}\left(\frac{\partial^{2} w}{\partial x^{2}}+\frac{\partial^{2} w}{\partial y^{2}}+\frac{\partial^{2} w}{\partial z^{2}}\right)-\frac{\partial p}{\partial z}-\rho g \beta\left(T-T_{\mathrm{ref}}\right)。\end{split} $ | (4) |
式中:μeff为有效粘度,μeff=μ1+μt,μ1为流体动力粘度,μt为湍动粘度;β为气体膨胀系数;g为重力加速度;T为温度;Tref为参考温度[9]。
3)能量守恒方程:
| $ \begin{split} \frac{\partial(\rho T)}{\partial t}+&\frac{\partial(\rho u T)}{\partial x}+\frac{\partial(\rho v T)}{\partial y}+\frac{\partial(\rho w T)}{\partial z}= \\ &\frac{\lambda_{\mathrm{df}}}{C_{\mathrm{p}}}\left(\frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}+\frac{\partial^{2} T}{\partial z^{2}}\right)+S_{\mathrm{T}}。\end{split} $ | (5) |
式中:λeff为有效导热系数;Cp为比热容;ST为自定义源项[9]。
1.3 湍流模型湍流模型采用标准k-ε双方程湍流模型。具体方程组如下:
1)湍流动能方程:
| $ \begin{split} \frac{{\partial (\rho k)}}{{\partial t}} + &\frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[\left(\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}\right)\frac{{\partial k}}{{\partial {x_j}}}\right] +\\ & {G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k} 。\end{split} $ | (6) |
2)湍流动能耗散率方程:
| $ \begin{split} \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + &\frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}[(\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}})\frac{{\partial \varepsilon }}{{\partial {x_j}}}] + \\ & {G_{1\varepsilon }}\frac{\varepsilon }{k}({G_k} + {G_{3\varepsilon }}{G_b}) - {G_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon } 。\end{split} $ | (7) |
式中:k为湍动能;ε为湍流耗散率;Sk、Sε为自定义源项;Gk与Gb为湍动能产生项,G1ε、G2ε、G3ε是经验常数[9]。
2 计算模型 2.1 几何模型和网格划分为满足小口径弹药的装填密度需求,基于某型高密度垂直热发射系统开展仿真研究。其中,装置主体结构分为上下2层,中间利用隔离装置分开,下层的燃气流直接从发射筒底部排导至压力室。考虑到安装空间的限制,上层采用公共的中心排气通道来满足上层燃气的排导。发射系统几何模型具体组成如图1所示。
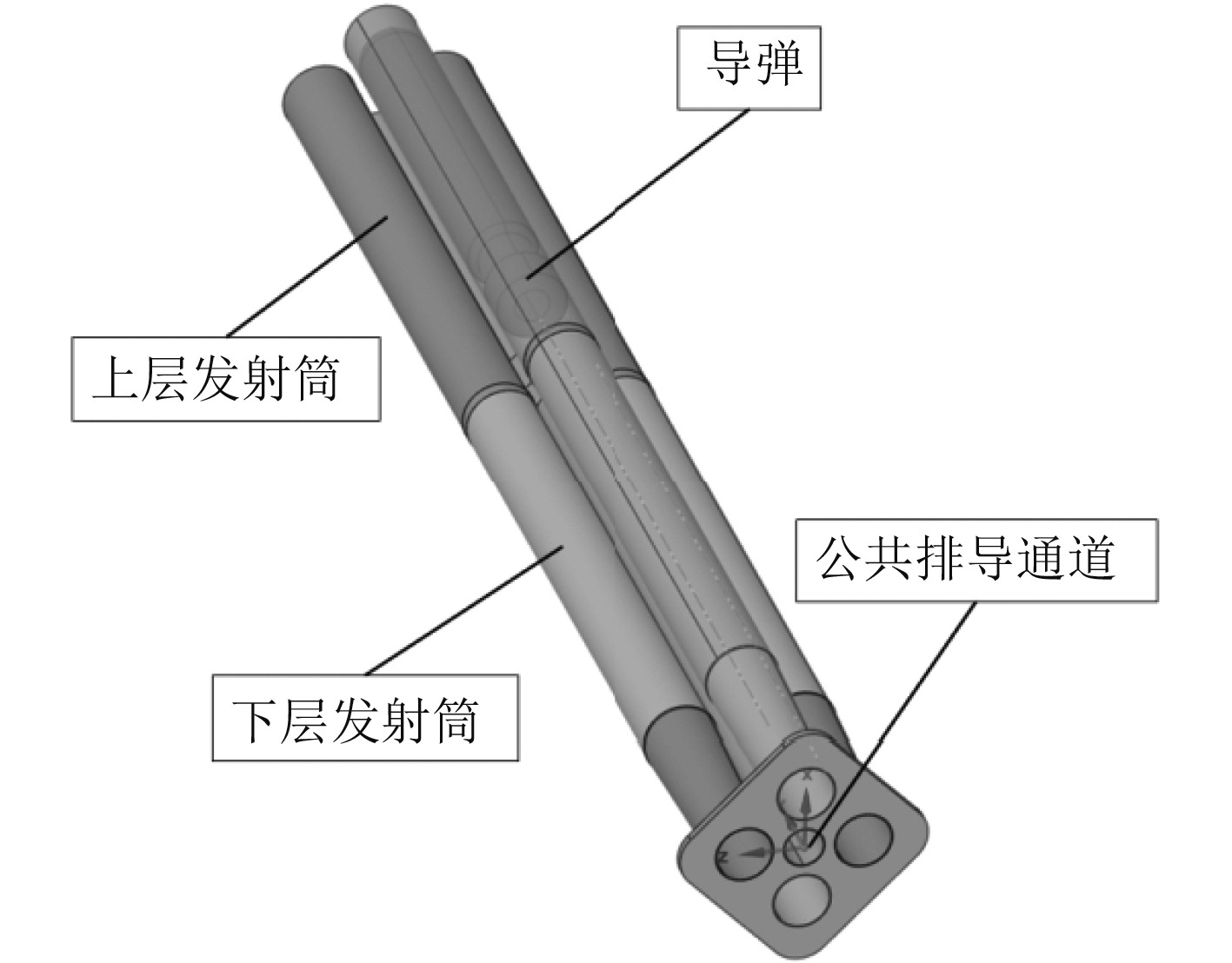
|
图 1 高密度垂直热发射装置基本组成和结构示意图 Fig. 1 The composition and structure diagram of high density vertical launch emitter |
高密度垂直发射系统燃气排导的难点在于公共排气管路的设计,同时单个发射筒排出燃气时相邻筒通过阀门防止燃气流进其他筒段。因此,流场计算域可简化为上层单筒发射工况,计算域全部采用非结构化网格划分,并对燃气射流区域网格进行局部加密。具体网格如图2所示。

|
图 2 计算域网格模型 Fig. 2 The grid model of computing domain |
计算区域边界条件设置如下:
1)入口边界条件
喷管入口设置为压力入口条件,总温T=3 082 K,总压随时间变化的曲线如图3所示。
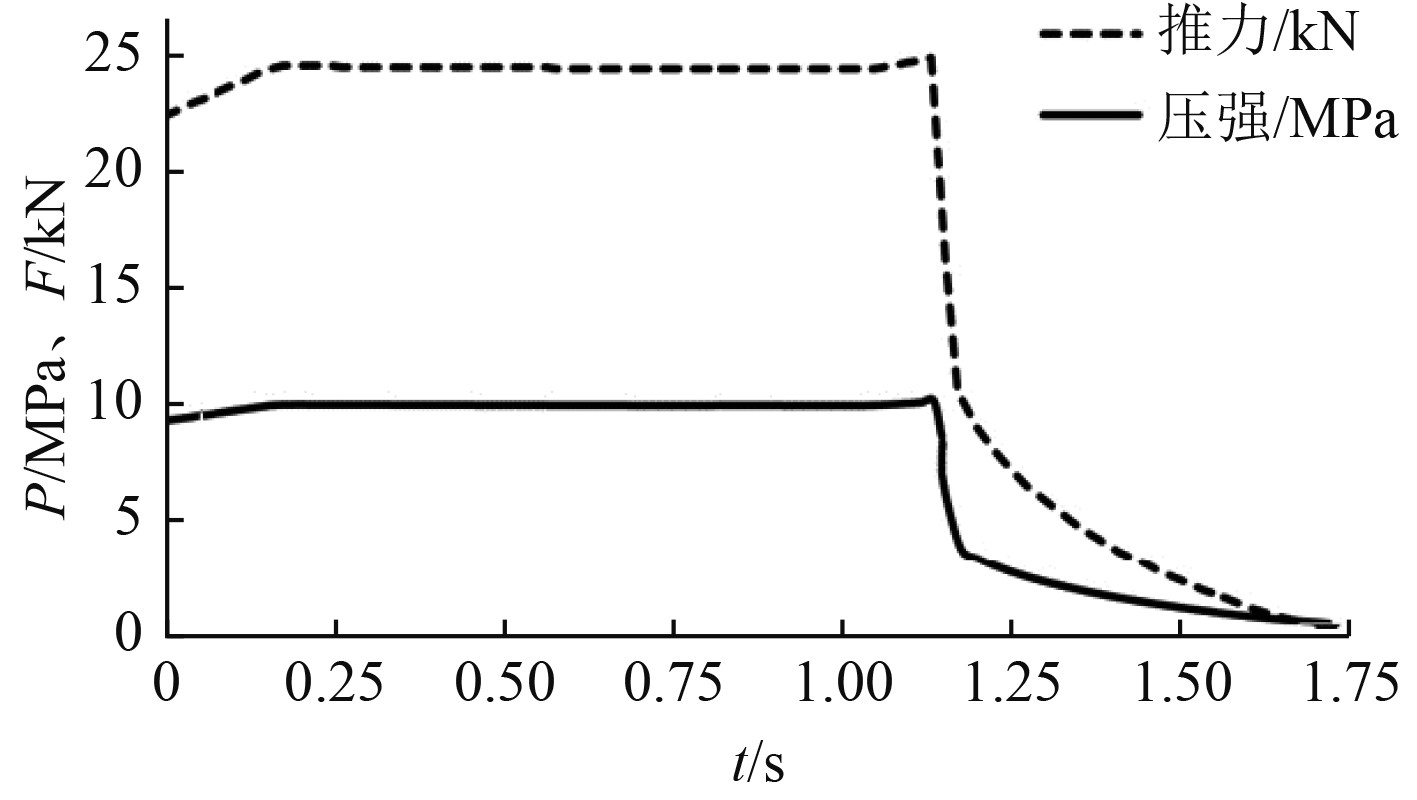
|
图 3 发动机推力和压强随时间变化曲线 Fig. 3 Curve of engine thrust and pressure over time |
2)出口边界条件
压力出口环境条件设置为P0=101 325 Pa;T0=300 K。
其余边界均设为绝热无滑移壁面。
2.3 工况设置导流型面的结构是影响发射筒内部燃气排导的重要因素之一。因此设置不同导流型面与水平面的夹角作为计算工况,对整个发射筒内部流场的分布影响情况进行研究。具体计算工况设置如表1所示。
|
|
表 1 计算工况 Tab.1 Calculation conditions |
按燃气流的流动方向,流场主要可分为如图4所示的3个区域。其中,A区包括弹体发动机喷管入口到发射筒底部导流面,燃气流从发动机喷管喷出,射流核心区的高速燃气流撞击筒底导流面;B区包括从导流面到公共排导通道,燃气流冲击导流面,部分燃气沿导流面流向公共排导通道;C区包括从导流面到发射筒内,由高速燃气流冲击发射筒底部形成的反喷流进而流入弹筒间隙。
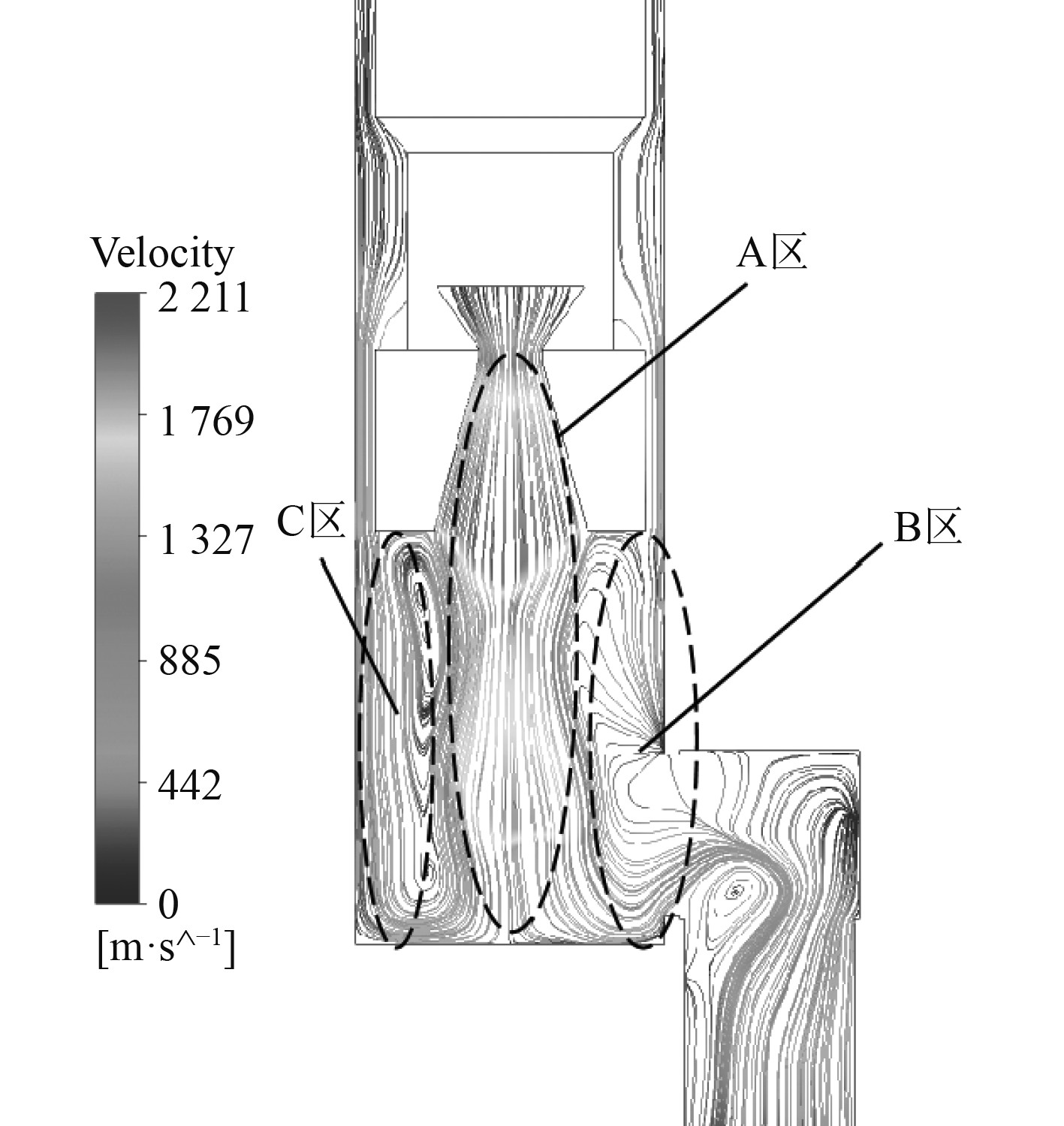
|
图 4 发射筒燃气流场区域示意图 Fig. 4 The diagram of gas flow field in the launcher |
图5给出了发射筒发射初始燃气流场的温度云图,流场温度最高约3 300 K。根据温度分布变化可看出,发动机喷管喷出的燃气流直接撞击导流型面,在发射筒底部形成高温区域,随后受两处区域影响,逐渐向发射筒其他地方流动,一部分沿弹筒间隙向上流动,一部分沿公共排导通道排出。

|
图 5 发射初始燃气流场温度云图 Fig. 5 Temperature nephogram of gas flow field at the initial launch |
根据上述分析可知,导流面对流场B区和C区的影响较大,从而影响发射筒的排导效果。假设中心燃气流冲击导流型面,速度垂直向下。经导流面撞击后发生偏折,其中α和β分别为燃气流向上偏折角和向下偏折角,θ为导流型面和水平面的夹角。示意图如图6所示。
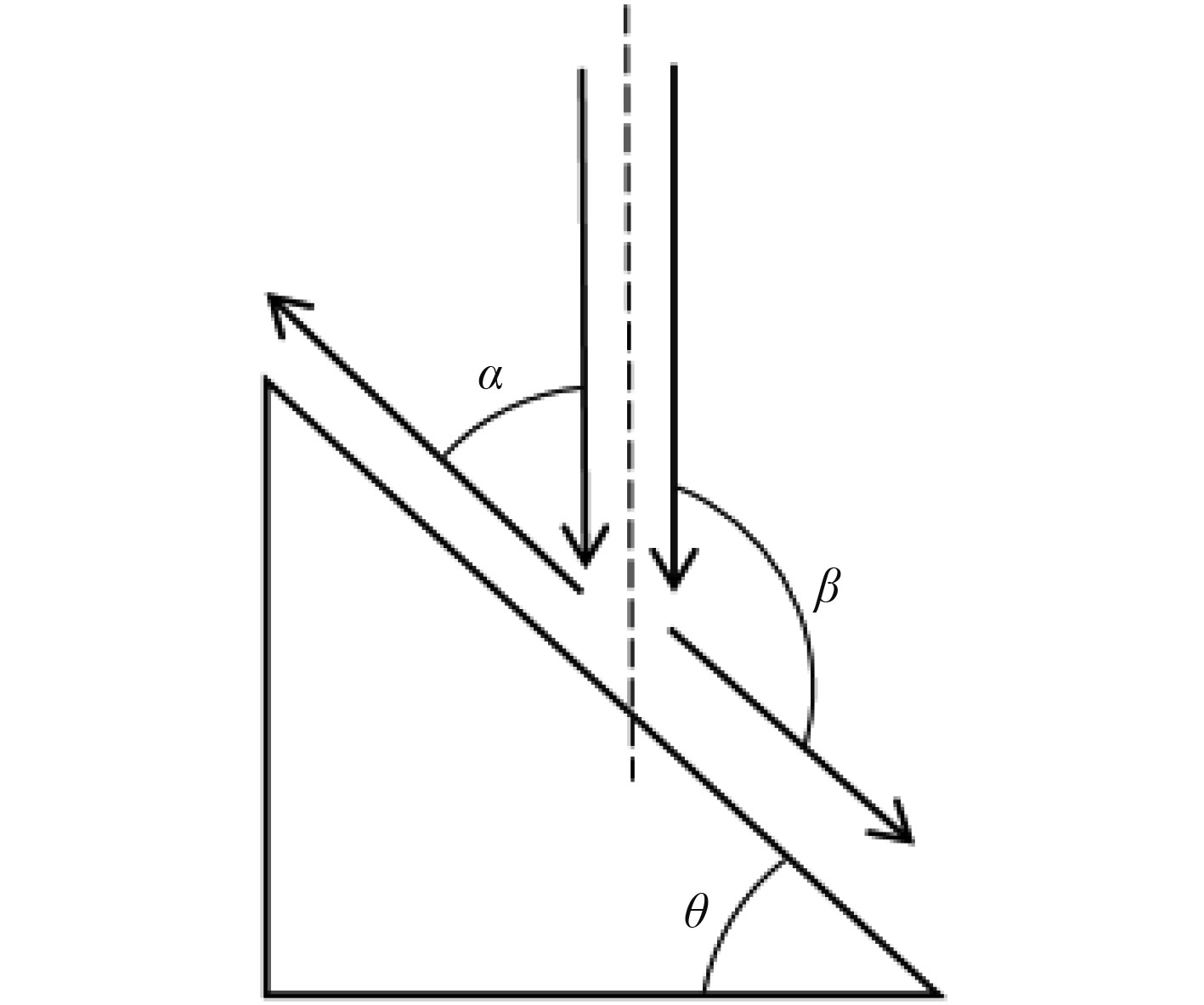
|
图 6 燃气撞击导流面示意图 Fig. 6 The diagram of gas impacting diversion surface |
图7分别给出了t=5 ms和t=20 ms时的速度流线图。当t=5 ms时,经导流面作用一部分向上流动的燃气速度普遍较高,并且和燃气主流相互作用最终形成图中的涡流区。随着时间推移,流场中的燃气流流动情况有所变化,大部分燃气流向公共排导通道流动,进入回流区的燃气流量明显减少。
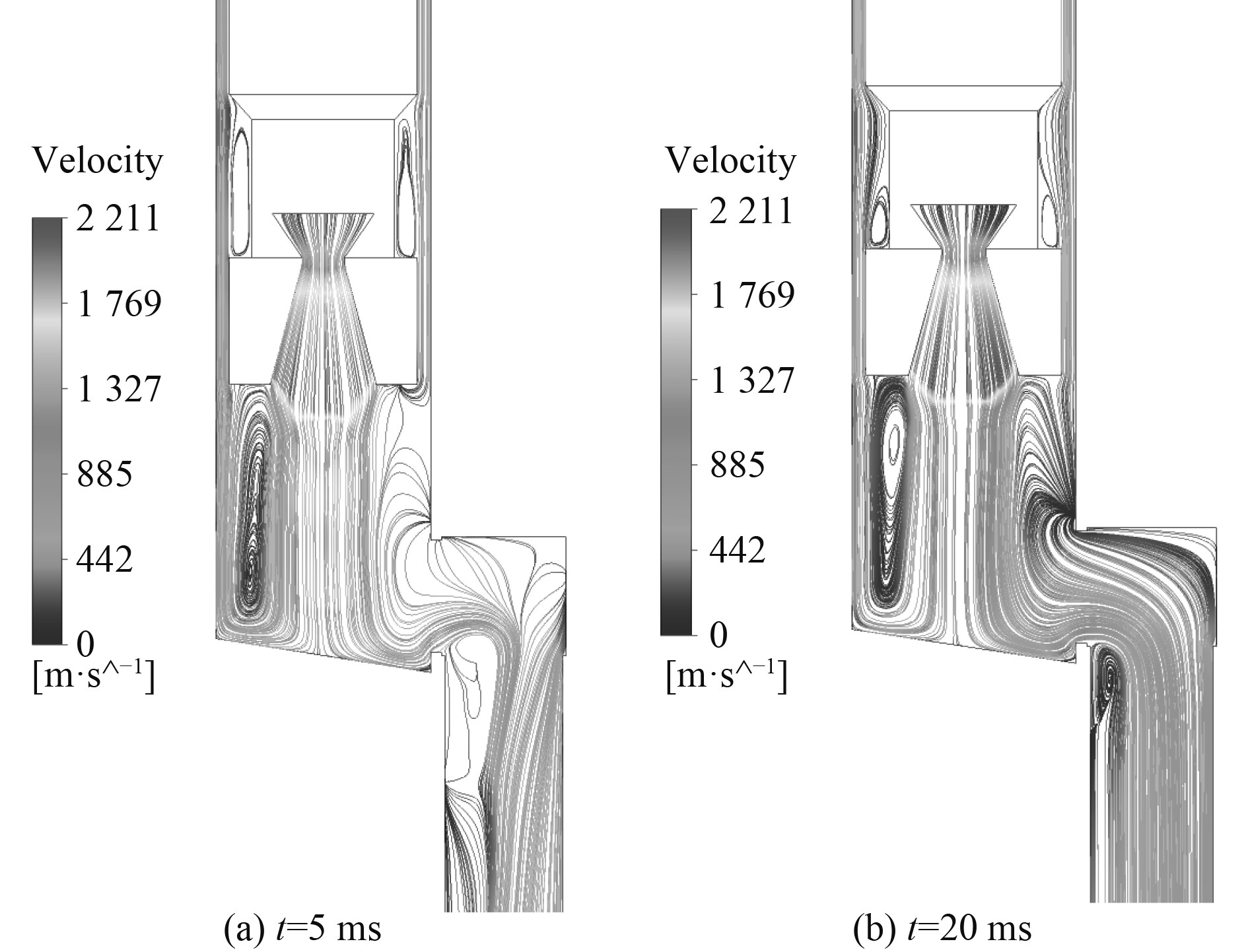
|
图 7 不同时刻下XY平面速度流线示意图 Fig. 7 The diagram of XY plane velocity streamline at different times |
图8分别给出了t=20 ms时,导流面和水平面呈不同夹角下的速度流线图。可看出,随着导流面夹角的增大,引起燃气流偏折角随之增大,远离导流流动的燃气流受到压缩,导致流动速度随之降低;另外,和燃气主流相互影响,在导流面附近部分燃气流形成了涡流区。
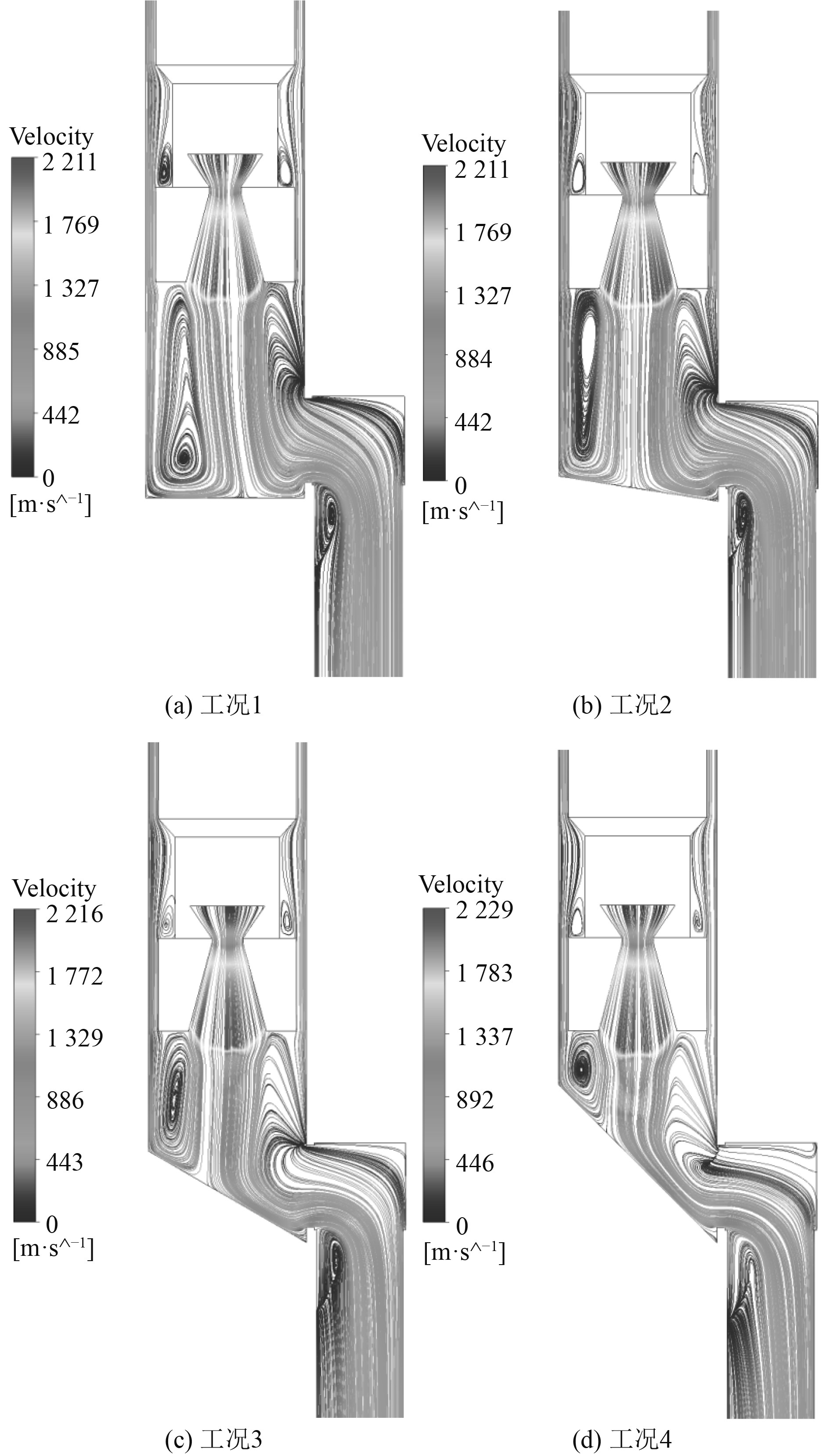
|
图 8 t=20 ms时不同工况下XY平面速度流线示意图 Fig. 8 The diagram of XY plane velocity streamline under different working conditions when t=20 ms |
图9给出了不同导流结构下的承压情况。图中纵坐标轴表示的无量纲压力值表达式为:
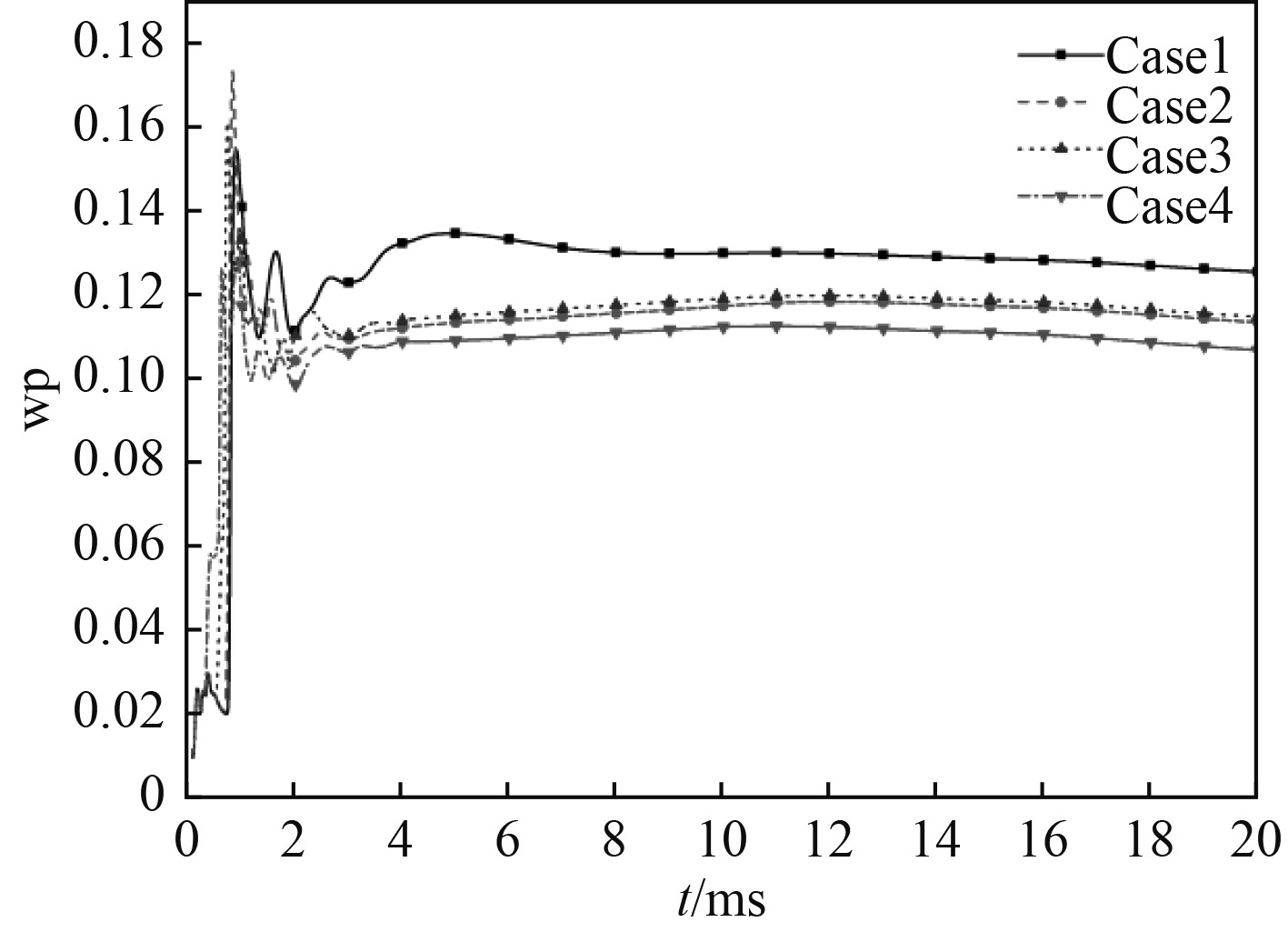
|
图 9 导流面无量纲压力对比 Fig. 9 Comparison of dimensionless pressure at the diversion surface |
| $ {W_P} = \frac{{{p_m}}}{{{p_{in}}}}。$ | (8) |
式中:
由图9可看出,随着导流型面夹角的增大,导流型面表面压力明显降低,表明受燃气主流冲击作用也较小。
3.3 排导性能影响| $ \eta = \displaystyle\frac{{{{\dot m}_0}}}{{{{\dot m}_i}}} = \frac{{\displaystyle\sum\limits_{k = 1}^n {{\rho _k}{A_k}{{\overline v }_k}} }}{{\displaystyle\sum\limits_{i = 1}^m {{\rho _i}{A_i}{{\overline v }_i}} }} 。$ | (9) |
式中:
最终得到各工况下的数据如表2所示。可看出,当导流型面夹角为45°时,排导效果较优,效率可达79.98%。此时导流面承受压力也相对较低,为1.07 MPa,相较于夹角为0时的工况降低了15%左右。因此综合来看,改变导流型面夹角的确对发射筒内部流场环境有所改善,减弱了导流型面受到燃气流冲击的影响,并提高了垂直热发射系统的排导性能。
|
|
表 2 仿真结果对比 Tab.2 Comparison of simulation results |
1)为满足小口径弹药装载密度的需求,基于某型高密度垂直发射系统建立内部三维流场模型,通过数值仿真揭示了导弹发射初始过程燃气流场流动规律,验证了其合理性;
2)通过改变不同导流型面的夹角,对比分析后得到性能更优的燃气排导结构,燃气排导效率达到79.98%,承受压力降低至1.07 MPa,减弱了燃气流冲击带来的影响。
本文的仿真计算仍存在不足,一方面由于计算精度限制,另一方面实际发射过程中燃气的多组分、多相流都会对排导性能产生干扰,而本文在计算过程中假设燃气流为理想气体。后续可考虑提高仿真模型的精度以及优化导流结构设计方面来提高整个系统的排导性能。
| [1] |
徐悦, 张振鹏, 陈小庆. 舰载导弹垂直发射装置进展研究[J]. 导弹与航天运载技术, 2007(3): 22−25
|
| [2] |
谷荣亮, 杜江, 时继庆. 战术导弹垂直发射系统的现状及发展趋势[J]. 上海航天, 2003, 20(3): 28-32. |
| [3] |
邴笑寒, 刘林密. 导弹垂直发射燃气排导系统流场数值分析[J]. 兵器装备工程学报, 2016, 37(1): 52-54. BING Xiao-han, LIU Lin-mi. Numerical calculation of flow field in vertical launching gas exhaust system[J]. Journal of Ordnance Equipment Engineering, 2016, 37(1): 52-54. |
| [4] |
杨志宏, 刘俊州. 垂直发射装置燃气排导效率研究[J]. 舰船科学技术, 2018, 40(6): 139-142. YANG Zhi-hong, LIU Jun-zhou. Research on the gas exhaust efficiency of a vertical launcher[J]. Ship Science and Technology, 2018, 40(6): 139-142. |
| [5] |
刘方, 辜健, 邱志明, 等. 基于公共燃气排导结构的共架发射系统武器选择与布局方法[J]. 海军航空工程学院学报, 2012, 24(2): 53-56. |
| [6] |
赵贤超. 意外点火时燃气排导系统流场仿真分析[J]. 实验流体力学, 2012, 26(4): 60-62,78. ZHAO Xian-chao. Simulation for jet flow of gas exhaust on thunderbolt ignition[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(4): 60-62,78. |
| [7] |
赵若男, 姜毅, 李静, 等. 不同导流型面对燃气流场的影响研究[J]. 固体火箭技术, 2020, 43(5): 671-678. |
| [8] |
王俊敏, 邴笑寒, 田琼, 等. 导弹垂直发射燃气排导系统两相流场数值分析[J]. 海军航空工程学院学报, 2020, 35(4): 324-334. |
| [9] |
潘树国, 台经华, 李翔宇, 等. 导流格栅对发射箱内流场环境影响研究[J]. 舰船科学技术, 2022, 44(20): 71-77. PAN Shu-guo, TAI Jing-hua, LI Xiang-yu, et al. Research on influence of diversion grille structure on flow field environment in a launch canister[J]. Ship Science and Technology, 2022, 44(20): 71-77. |
| [10] |
张程, 金玲, 张木, 等. 一种异型同心筒发射装置的排导性能仿真研究[J]. 航空动力学报, 2019, 34(1): 248-256. ZHANG Cheng, JIN Ling, ZHANG Mu, et al. Numerical simulation on the drainage performance of a special shaped concentric cylinder launcher[J]. Journal of Aerospace Power, 2019, 34(1): 248-256. |
 2023, Vol. 45
2023, Vol. 45
