0 引　言

船舶安全航行是航运领域的重要问题，如何确保船舶在复杂海况下的安全航行是当前研究的热点^[1]。航行路径规划是当前解决船舶航行安全问题的主要方式之一^[2]。刘晨霞等^[3]针对复杂的洋流环境，利用生物启发神经网络进行传播航行路径规划。该方法路径搜索过程缺乏灵活性，在出现移动障碍物条件下无法及时进行避障。潘伟等^[4]针对船舶航行路径规划问题，利用Delaunay三角剖分算法构建海洋环境模型，研究环境影响力条件下的船舶安全航行路径。该方法路径规划效率较差。杨琪森等^[5]针对船舶路径规划问题，基于海洋环境与国家相关避碰标准，构建马尔可夫决策模型，获取安全航行路径。该方法所规划出的航行路径虽然能够确保安全性，但无法保障航程最短。针对上述问题，本文研究虚拟环境下船舶安全航行路径智能规划仿真方法，从三维空间角度出发对船舶航行路径进行智能规划，在保障船舶航行安全性的同时确保航程最短。

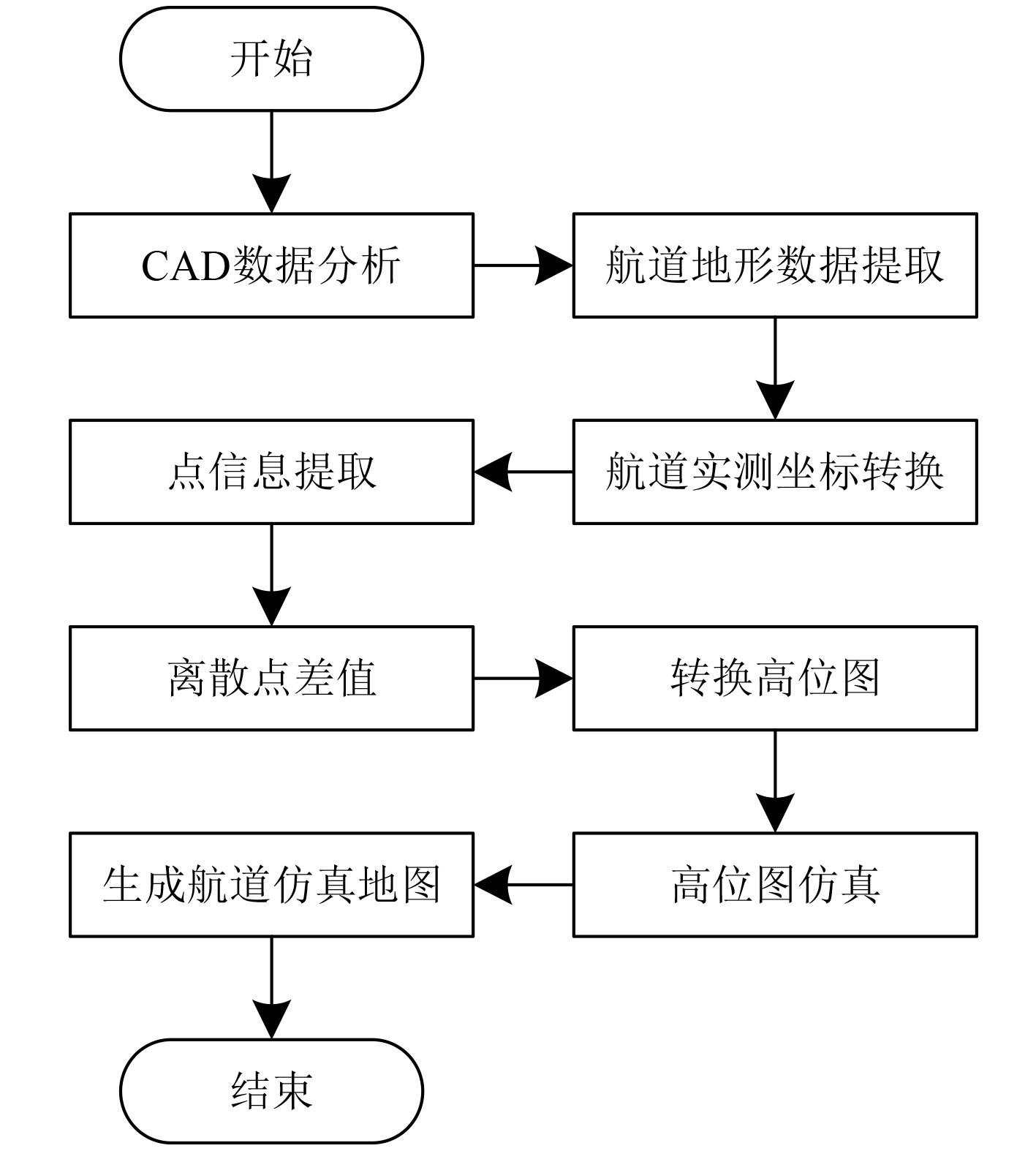
1 船舶安全航行路径智能规划仿真方法 1.1 虚拟环境下航道地形建模

在虚拟环境下，航道地形构建是船舶航道三维场景构建的基础，高精度的航道地形不仅是船舶安全航行过程中航标布设的关键，同时也是后续航行路径智能规划仿真精度的关键。当前航道测量数据主要通过Auto CAD 图形数据形式保存，大部分GIS软件无法直接读取图形数据格式，所以在航道地形模型构建过程中，需先针对前航道测量数据实施采集与转换后才能应用在后续的可视化处理过程中。图1为船舶航行航道虚拟环境下的数据处理流程。

转换后的船舶航行航道高程信息为具有离散性特征的点，在此基础上进行差值处理，同时针对网格点生成等值线，利用连续极小泛函序列方法获取船舶航行航道等距网格数据，具体过程如下：依照船舶航行航道高程信息的真实性实施类别划分，生成泛函系列 $ {\phi _1}\left( {{u_1}, \cdots ,{u_N}} \right),{\phi _2}\left( {{u_2}, \cdots ,{u_N}} \right), \cdots ,{\phi _k}\left( {{u_k}, \cdots ,{u_N}} \right) $ 。

计算等距网格内不同单元的权重是利用连续极小泛函序列方法获取船舶航行航道等距网格数据的核心，公式描述如下：

$ u\left( {x,y} \right) = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {{u_{ij}}} } {\emptyset _{ij}}\left( {x,y} \right) ，$

(1)

式中， $ {u_{ij}} $ 和 $ {\emptyset _{ij}} $ 分别为 $ i,j $ 位置单元的值和设置距离。 $ {\emptyset _{ij}} $ 的计算过程如下：

$ \begin{split} &{\emptyset _i}\left( x \right) = \left\{ {1,x \in \left[ {ih + a - \frac{h}{2}} \right]} \right.，\\ & 0,x \in \left[ {ih + a - \frac{h}{2},\left( {i + 1} \right)h + a - \frac{h}{2}} \right]。\end{split} $

(2)

利用对象图像渲染引擎对航道网格数据进行处理即可得到航道地形模型。

1.2 船舶三维模型构建

图2为利用Solid Works软件构建船舶三维模型的流程。可知，船舶三维模型构建主要分为6个环节。船舶三维模型构建过程中，型线模型的构建极为重要。选取三次B样条曲线绘制船舶船体横剖线。在Solid Works软件内输出船舶船体横剖线图，通过拟合获取不同横剖线上的控制点信息。采集各点坐标信息，构建船舶船体箱线图，同时在相应表内存储不同控制点坐标信息。通过一根B样曲线描述船舶船尾的横剖线，其中包含若干段指点与B样条曲线交叉。在B样条曲线与直线一起存在于横剖线内时，不仅将直线与样条曲线分别进行作图，同时还要保障不同模型图均处于相同草图内，令2种图处于相切的几何相关性内。

船舶三维模型构建过程中，利用分析与处理模块处理型值表内的控制点坐标信息，确定读到的控制点是属于B样条曲线，还是属于直线段。若是属于前者，则确定当前段曲线中所包含的控制点数量。在遍历任意横剖线中全部控制点后，利用循环控制画线函数在对应的基准面内绘制B样条曲线，并将其引入直线段所处的草图内，在B样条曲线同直线相交区域引入相切的几何约束。对全部型线进行处理后，即可实现船舶船体型线图的绘制。

1.3 船舶安全航行路径智能规划模型

根据生成的航道地形模型与船体模型进行航行路径规划。在船舶安全航行路径智能规划过程中，设定 $ S\left( {{x_s},{y_s},{z_s}} \right) $ 和 $ E\left( {{x_e},{y_e},{z_e}} \right) $ 分别为船舶所需规划路径的起点坐标和终点坐标。依照两者间线段最短的标准，在 $ S\left( {{x_s},{y_s},{z_s}} \right) $ 和 $ E\left( {{x_e},{y_e},{z_e}} \right) $ 之间进行连接，获取向量 $ SE $ ，设定船舶航行路径的搜索方向，以 $ P = ( p_1^0,p_2^0,p_3^0, \cdots , p_n^0 ) $ 表示 $ SE $ 同各切面产生的交集点集合。在搜索路径点过程中，以 $ p_1^0 $ 为初始，确定 $ p_2^0 $ 是否处于平面(YOZ)₂的可行区域内，若是，则通过向量 $ p_1^0p_2^0 $ 表示(YOZ)₁与(YOZ)₂间的路径；若不是，则以 $ {\left( {YOZ} \right)_1} $ 表示路径在(YOZ)_i-1平面上的点，将其投影至(YOZ)_i上，得到点 $ {p'_{i - 1}} $ ，将其作为基准点获取(YOZ)_i内的可行点，设定搜索步长为一个网格单元长度。确定搜索所得路径点同障碍物的边缘是都小于连个单元格长度，是则用1表示，不是则用0表示，存储0和1块矩阵，获取(YOZ)_i可行点集合 $ \left( {{x_i},{y_1},{z_1}} \right),\left( {{x_i},{y_1},{z_2}} \right), \cdots ,\left( {{x_i},{y_i},{z_i}} \right), \cdots , \left( {{x_i},{y_a},{z_b}} \right) $ 。其中， $ a $ ， $ b $ 表示 $ {\left( {YOZ} \right)_i} $ 内横纵坐标面编号。

设定(YOZ)_i的一个可行点为 $ {p_i}\left( {{x_i},{y_1},{z_2}} \right) $ ，则利用式（3）确定点与点间的距离L_j和点与 $ p_i^0 $ 间的距离L_k：

$ \left\{ \begin{gathered} {L_j} = \sqrt {{{\left( {{y_i} - {y_{i - 1}}} \right)}^2} + {{\left( {{z_i} - {z_{i - 1}}} \right)}^2}}，\\ {L_k} = \sqrt {{{\left( {{y_i} - y_{i - 1}^0} \right)}^2} + {{\left( {{z_i} - z_{i - 1}^0} \right)}^2}}。\\ \end{gathered} \right. $

(3)

由此可通过L_i描述L_j与L_k的和。考虑可行点数量较多，因此L_i值具有多样性，仅在其值为最小值的条件下才能够作为下一个路径点。

在L_i值最小的条件下，L_j与L_k也最小。L_j值最小即为所选路径点同前一路径点间的距离最小，满足船舶路径规划内整体距离最小的标准，而L_k最小就是(YOZ)_i-1与(YOZ)_i间的路径向量p_i-1p_i在整体方向上同 $ SE $ 一致，满足船舶路径规划过程中路程最短标准。在此条件下可通过式（4）描述p_i-1p_i的绝对值：

$ \left| {{p_{i - 1}}{p_i}} \right| = \sqrt {{{\left( {{x_i} - {x_{i - 1}}} \right)}^2} + {{\left( {{y_i} - {y_{i - 1}}} \right)}^2} + {{\left( {{z_i} - {z_{i - 1}}} \right)}^2}}。$

(4)

在确定(YOX)_i内的路径点后，将其连接到E上，获取新的向量p_iE ，利用其与能够获取一系列新的点，将作为选取后续路径点的参考值，循环上述过程即可获取舰船航行时最短的安全路径。依次连接每段最短的安全路径即可由 $ S\left( {{x_s},{y_s},{z_s}} \right) $ 至 $ E\left( {{x_e},{y_e},{z_e}} \right) $ 的船舶安全航行路径规划结果。

2 仿真结果与分析

为验证本文方法的实际应用性能，以某海域为仿真海域，采用本文方法对船舶与海域进行虚拟仿真。

2.1 航道地图模型与船舶模型构建结果

航道地图模型与船舶模型的构建是船舶安全航行路径规划的基础，其对于最终船舶安全航行路径规划结果的准确性产生直接影响。图3为本文方法的航道地图模型与船舶模型构建结果。分析可知，采用本文方法能够有效构建出虚拟的航道地图模型与船体仿真模型。所构建出的航道地图模型能够整体展示航道三维场景，而船体仿真模型能可直观展示船舶的不同水线角，所构建的模型均较为完善。

2.2 路径规划结果

图4为本文方法对仿真船舶在仿真海域中的路径安全航行路径智能规划的仿真结果。其中左下角圆点为船舶航行的始点，右上角圆点为船舶航行的终点。分析图4得到，无论船舶航行海域中是固定障碍物还是具有移动障碍物，采用本文方法均能够有效规划出船舶航行路径，且所规划出的船舶航行路径均能够躲避全部障碍物，保障船舶航行过程中的安全性。

2.3 航行路径规划结果分析

为验证本文方法所规划出的安全航行路径是否满足始点与终点间距离最短的要求，将本文方法在不同障碍物条件下的航行路径规划结果与实际最短航行路径进行对比，所得结果如表1所示。

分析表1得到，在固定障碍物条件下，采用本文方法仿真所得的安全航行路径规划距离与实际最短航行距离差异0.4 km。在移动障碍物条件下，采用本文方法仿真所得的安全航行路径规划距离与实际最短航行距离差异0.5 km。这些差异可能是由于航道地图生成的偏差所导致的。以上数据说明采用本文方法进行航行路径规划，不仅能够保障船舶航行的安全性，同时也能够满足航程最短的要求。

3 结　语

本文研究虚拟环境下船舶安全航行路径智能规划仿真方法，仿真结果显示本文方法能够有效规划出船舶安全航行路径。但规划结果与实际最短航行距离存在微弱差异，这种差异主要是由航道地图生成偏差所造成的。因此在本文方法后续优化过程中将主要针对航道地图生成方面进行深度优化，由此提升本文方法的准确性。