舰船舱室人因可靠性评估是驾驶员胜任力分析、绩效考核的重要内容。考虑舰船航行环境条件的多变性,驾驶员要在长时间内保持高度的警觉和专注,需要具备良好的生理和心理状况、专业的驾驶技能和知识,包括船舶操作、导航、天气预测、应急处理等方面的知识[1]。除此之外,驾驶员需要与船员、指挥员和其他相关人员进行有效的沟通和协作,才能保证航行状态不出现意外情况[2]。由此可知,舰船舱室驾驶员的可靠性评估是一个重要的议题,涉及多个因素,包括生理和心理状况、技能和知识水平等。张爱琳等[3]使用贝叶斯网络技术,分析船舶引航员认知可靠性与引航失误问题,实现了船舶引航人因可靠性定量评估。但贝叶斯网络需要先验知识,如果先验知识错误或不完备,可能会导致评估结果有误。龚恒宇等[4]利用模糊综合评价方法与相似度系数,针对舰船舱内协作能力进行评估,此方法主要侧重于定性评估舰船舱内组织协作能力,评估内容单一,普适性有待优化。
综上所述,舰船舱室人因可靠性评估问题,属于驾驶员综合操舵能力的多因素评估,多因素评估评估常用方法中,灰色关联分析方法是一种比较简单、可靠的分析方法。为此本文设计基于灰色关联分析的舰船舱室人因可靠性评估方法,用于驾驶员人因可靠性定量与定性相结合的综合评估。
1 舰船舱室人因可靠性评估 1.1 舰船舱室人因可靠性评估标准分析方法认知可靠性模型(HCR)是一种用于评估人类在特定任务中表现可靠性的方法[5]。在本文研究问题中,不同舰船舱室驾驶员,其操舵认知行为存在差异,主要分为技能型、规则型、知识型。技能型操舵认知行为表示舱室驾驶员可在恶劣天气、航道信号显示异常等复杂工况中,根据自己的视觉感知、听觉感知信息,快速调整舵令完成舰船控制。规则型操舵认知行为下,驾驶员需要多次分析自己在舰船舱室的操舵行为,是否满足标准规定,此类操舵认知过程消耗驾驶员的时间与精力较多。在HCR模型中,常用人因错误率作为行为可靠性的定性分析指标。为此,将人因错误率作为舰船舱室人因可靠性参考标准的制定指标。考虑舰船舱室人因可靠性评估时,驾驶员操舵存在动态认知过程,此过程行为数据规模较大,因此,本文先以定量分析的角度,制定评估参照的参考标准。基于此标准,利用灰色关联分析方法,快速完成舱室驾驶员人因可靠性的定性评估。人因可靠性参考标准如表1所示。
|
|
表 1 人因可靠性参考标准 Tab.1 Human reliability reference standards |
表1中,舰船舱室人因错误率的分析方法为:
| $ g = {\rho ^{ - \left( {\frac{{\frac{t}{{D \cdot {T_{0.5}}}} - \varepsilon }}{\phi }} \right)\varphi }} 。$ | (1) |
其中:
基于式(1)与表1的参考标准,便可设定舰船舱室人因可靠性评估所用参考样本,用于后续人因可靠性评估。
1.2 基于余弦定理的人因可靠性评估指标筛选方法以舰船舱室操舵事故作为指标筛选源,从个体
| $ \cos \left[ {\alpha \left( {e,o} \right)} \right] = \frac{{\left\langle {{{\left( {{{\bar W}_e}} \right)}_{1*n}},{{\left( {{{\bar W}_o}} \right)}_{1*n}}} \right\rangle }}{{\left| {{{\left( {{{\bar W}_e}} \right)}_{1*n}}} \right| \times \left| {{{\left( {{{\bar W}_o}} \right)}_{1*n}}} \right|}}。$ | (2) |
当余弦值
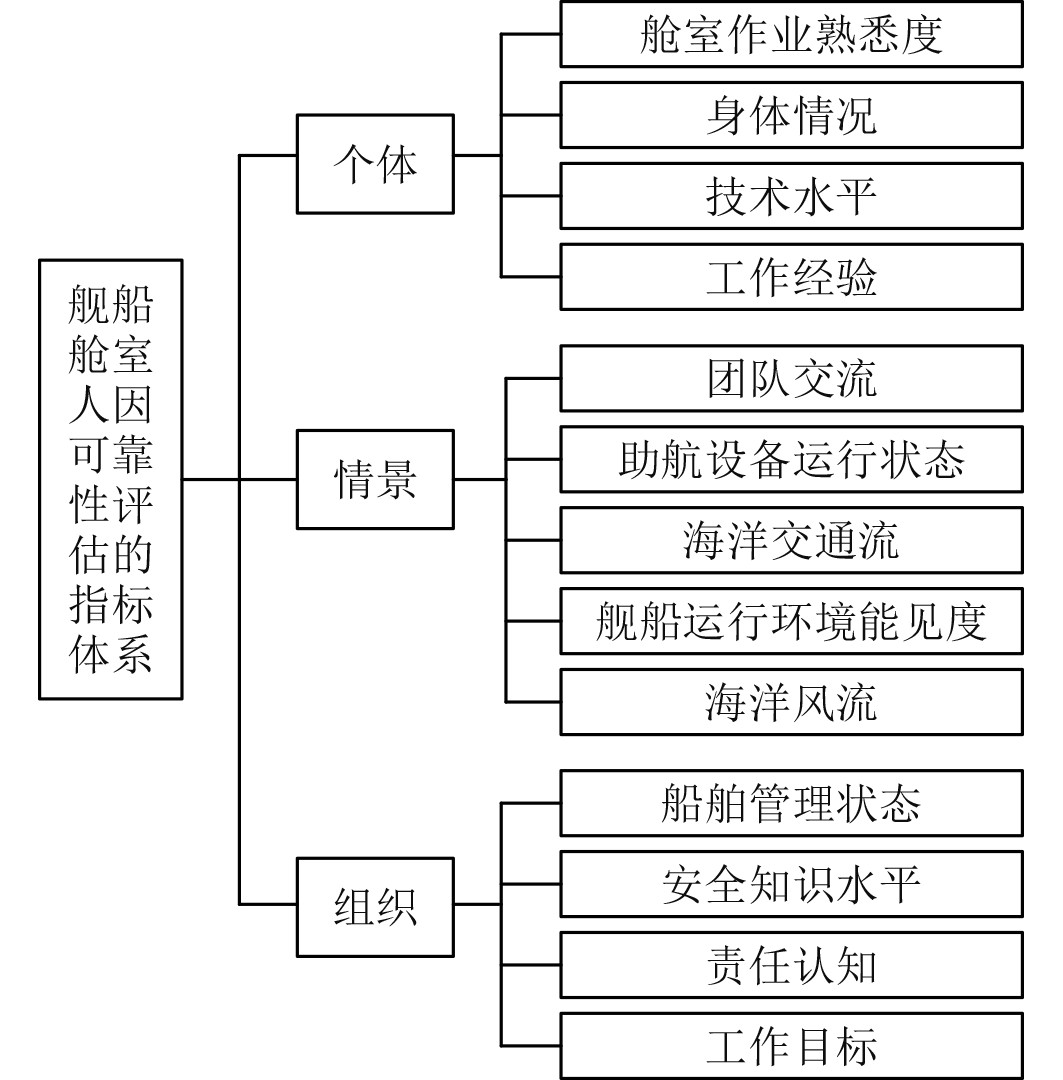
|
图 1 舰船舱室人因可靠性评估指标 Fig. 1 Human reliability evaluation indicators for ship cabins |
设置舰船舱室人因可靠性参考标准为因变量因素,设置的评价指标因素为自变量因素,则舰船舱室人因可靠性评估时,因变量为参考序列
为便于分析,把图1每个舱室人因可靠性评估序列均值化处理,并组建无量纲序列,则
| $ \left( {{Y_1},{Y_2},...,{Y_m}} \right) = \left[ {\begin{array}{*{20}{c}} {{y_{01}}}&{{y_{02}}}& \cdots &{{y_{0m}}} \\ {{y_{11}}}&{{y_{12}}}& \cdots &{{y_{1m}}} \\ \vdots & \vdots &{}& \vdots \\ {{y_{m1}}}&{{y_{m2}}}& \cdots &{{y_{mm}}} \end{array}} \right]。$ | (3) |
式(3)中列与列之间的距离即为其相似度,若距离较小,则2组序列变化状态存在一致性,表示所评估的驾驶员某评估指标与参考标准相同。运算式(3)中首行参考序列(满足人因错误率标准的驾驶员的指标数据)和剩下对比序列(被测驾驶员的评估指标数据)的绝对差值,其绝对差值矩阵为
一般情况下,舰船舱室人因可靠性评估时,绝对值序列数据之间,数量级会存在明显不同,需规范化处理才可合并运算。设置绝对差值矩阵最大数
| $ 0 \leqslant \frac{{\Delta \left( {\min } \right)}}{{\Delta \left( {\max } \right)}} \leqslant \frac{{{\Delta _{0j}}\left( t \right)}}{{\Delta \left( {\max } \right)}} \leqslant 1。$ | (4) |
其中,
| $ {\delta _{0j}}\left( t \right) = \frac{{\Delta \left( {\min } \right) + \Delta \left( {\max } \right)}}{{{\Delta _{0j}}\left( t \right) + \Delta \left( {\max } \right)}} 。$ | (5) |
其中,
将绝对差值矩阵中数据使用式(5)转换,获取的关联系数矩阵为:
| $ {\delta _{0j}} = \left[ {\begin{array}{*{20}{c}} {{\delta _{11}}}& \cdots &{{\delta _{1m}}} \\ \vdots &{}& \vdots \\ {{\delta _{m1}}}& \cdots &{{\delta _{mm}}} \end{array}} \right] 。$ | (6) |
关联系数数值大于1,此数值可表示对比序列和参考序列在某指标上的关联水平。
1.3.5 基于灰色关联度的人因可靠性评估结果判断被测驾驶员人因可靠性评估所用对比序列样本,和参考序列样本的关联度,需由
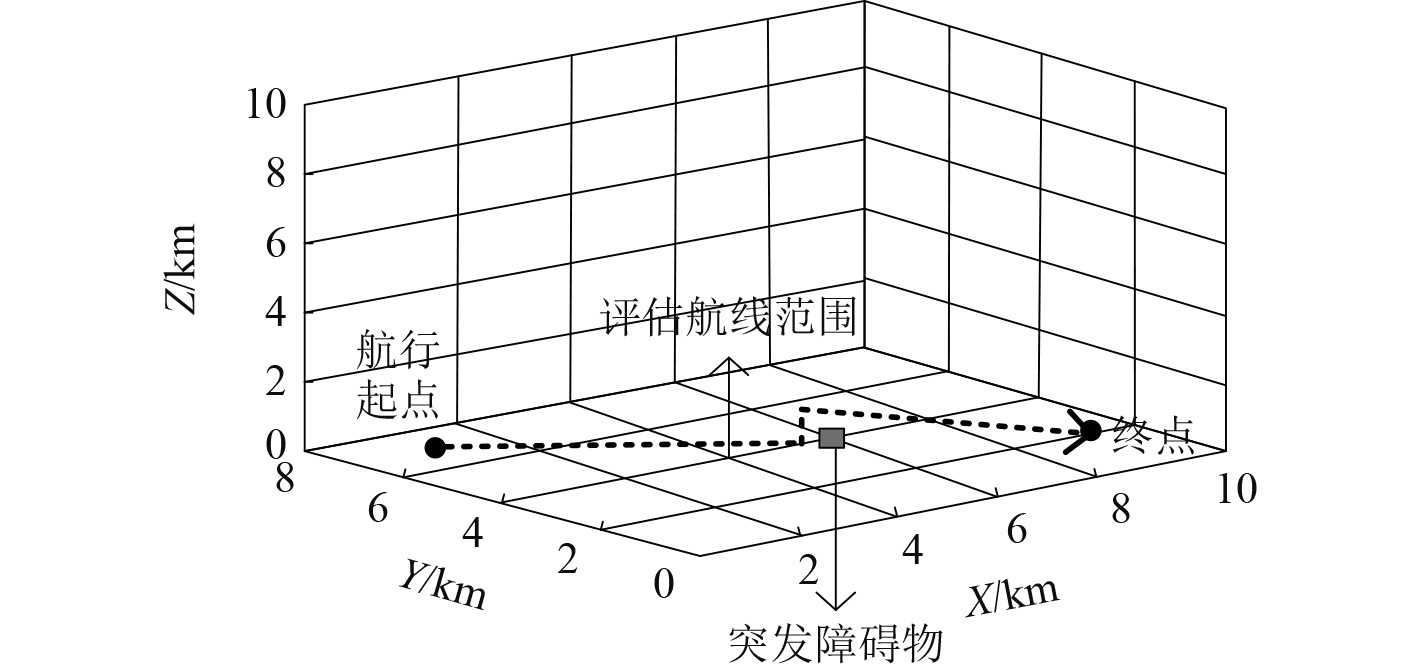
为测试本文方法使用效果,以舰船避碰问题为例,使用本文方法评估舰船舱室驾驶员的人因可靠性。舰船航行环境如图2所示。舰船自航行地点航行至终点时,因出现突发障碍物,舱内驾驶员需要合理操舵,控制舰船快速改变航线躲避障碍物。为此,以躲避障碍物的航线段为评估区间,使用本文方法评估驾驶员的舱室人因可靠性。
|
图 2 舰船航行环境 Fig. 2 Ship navigation environment |
表2为4位驾驶员的驾驶技能考核实况数据,4位驾驶员的应激动作输出模式分为混乱式、机会式、战术式、战略式。将表2数据结合表1标准进行对比分析,4位驾驶员中,只有1#驾驶员的人因错误率超出标准范围,剩下3位驾驶员的人因错误率均处于标准范围之内,但4#驾驶员和障碍物碰撞次数为0次,且单位路程增加量最少,仅有81.34 m,不存在超出边界问题、终点位置与方向都不存在偏差,说明该驾驶员的舱室操舵技能最可靠。
|
|
表 2 4位驾驶员的驾驶技能考核实况数据 Tab.2 Actual data of driving skills assessment for four drivers |
使用本文方法对表2中4#驾驶员进行人因可靠性评估,基于表1所示参考标准,以及所构建的人因可靠性评估指标,通过灰色关联度判断驾驶员的人因可靠性,并将可靠性评估结果与表2实况数据进行比较,从而判断本文方法评估结果的准确性。本文方法对舰船舱室人因可靠性评估结果如图3所示。本文方法对表2中4#驾驶员进行人因可靠性评估后,4#驾驶员对突发障碍物时,人因可靠性评估所用序列,与参考序列的灰色关联度始终接近于1,所以可认定该驾驶员人因可靠性优。此评估结果结合表2实况数据可证实,本文方法可准确评估舰船舱室人因可靠性。
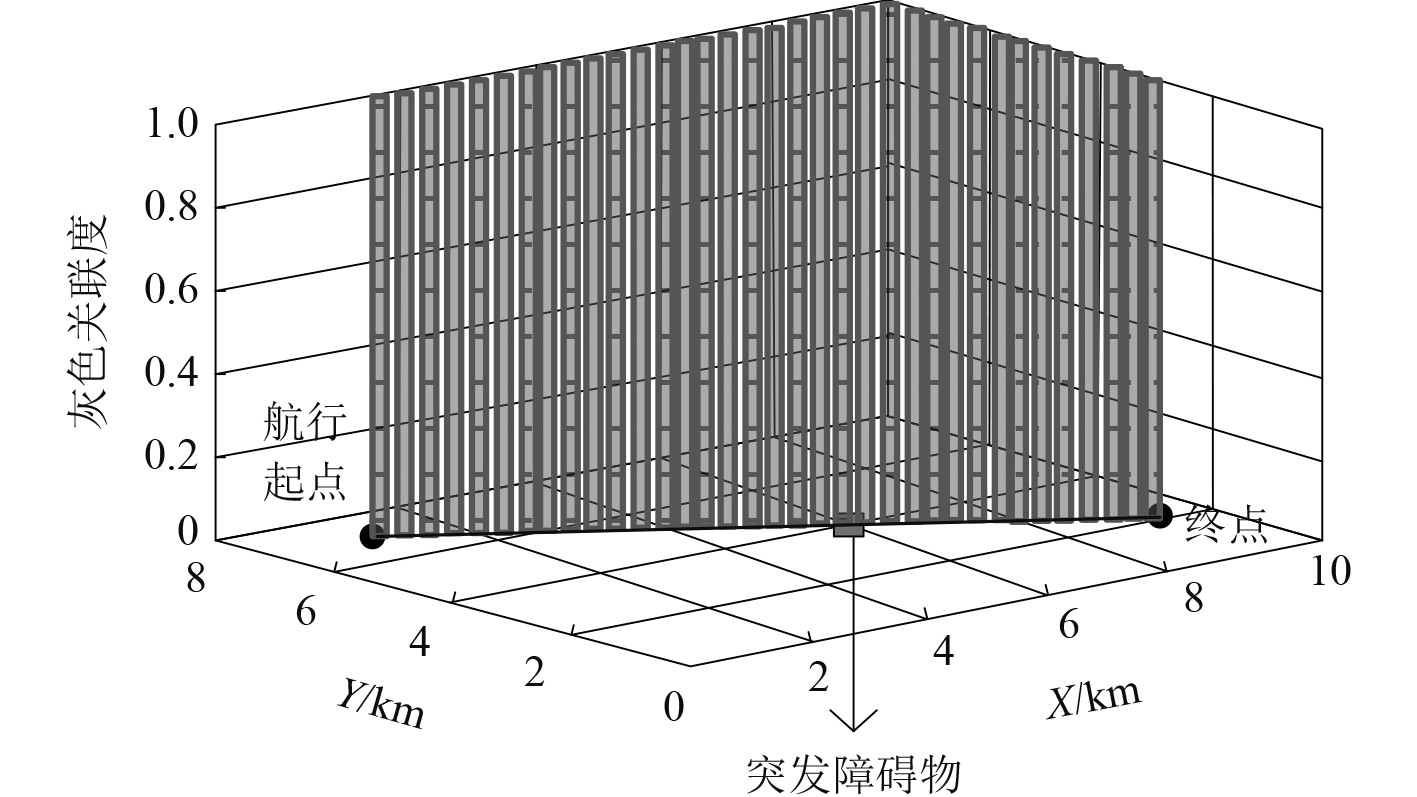
|
图 3 4#驾驶员人因可靠性评估的灰色关联度详情 Fig. 3 Details of grey correlation degree for human reliability assessment of 4 # drivers |
在舰船舱室人因可靠性评估中,灰色关联分析可以用于分析多种因素下人员行为可靠性,实现人因可靠性的综合判断。本文提出基于灰色关联分析的舰船舱室人因可靠性评估方法,该方法在实验中被验证具备可用性,能够定量、定性评估舱室驾驶员的操舵行为,以及对舰船航行状态的影响。
| [1] |
郝勇, 时间, 吴昊旻. 基于冰山模型的长江危险品船船员素质评价指标体系构建[J]. 安全与环境学报, 2020, 20(4): 1376-1383. HAO Yong, SHI Jian, WU Hao-min. Building up quality evaluation index piles of crew members in charge of dangerous goods processing along the Yangtze River based on the iceberg model[J]. Journal of Safety and Environment, 2020, 20(4): 1376-1383. |
| [2] |
岑康, 张翌东, 黄夏雨, 等. 考虑人因可靠性的安全仪表功能SIL验证方法研究[J]. 中国安全生产科学技术, 2020, 16(3): 31-36. CEN Kang, ZHANG Yi-dong, HUANG Xia-yu, et al. Study on verification method of safety integrity level (SIL) for safety instrumented function considering human reliability[J]. Journal of Safety Science and Technology, 2020, 16(3): 31-36. |
| [3] |
张爱琳, 刘晓佳. 改进CREAM模型的船舶引航员人因可靠性预测[J]. 中国航海, 2021, 44(1): 32-37+43. ZHANG Ai-lin, LIU Xiao-jia. Improved CREAM model for prediction of human reliability concerning harbor pilots[J]. Navigation of China, 2021, 44(1): 32-37+43. |
| [4] |
龚恒宇, 曹辉. 船舶机舱协作式模拟训练评估方法[J]. 船海工程, 2020, 49(1): 111-114+119. GONG Heng-yu, CAO Hui. Evaluation method for collaborative simulation training of marine engine room[J]. Ship & Ocean Engineering, 2020, 49(1): 111-114+119. |
| [5] |
李星, 谭麟, 高凌云, 等. 系统安全领域人因错误理论研究进展[J]. 中国电子科学研究院学报, 2020, 15(7): 612-619+628. LI Xing, TAN Lin, GAO Ling-yun, et al. Research progress of human error theory in industry safety engineering[J]. Journal of China Academy of Electronics and Information Technology, 2020, 15(7): 612-619+628. |
 2023, Vol. 45
2023, Vol. 45
