随着船舶结构设计规范的逐步提升,船舶结构的振动问题成为船体结构设计的重要技术问题之一[1]。船舶在海面上航行过程中,如果船体出现持续性的剧烈震荡,船体的结构则会产生疲劳损伤,从而对船舶的安全航行产生一定的影响[2]。船舶螺旋桨产生的压力和船舶主机产生的压力之间的不平衡是船舶振动的主要原因[3]。螺旋桨和主机在工作的过程中,其内部出现的不平衡力会通过船舶上的机械连接结构传输到船体各个部位,因此对船体上连接结构的动力学特性进行研究十分重要。由于船体结构上设备的连接形式多样性,这极大的增加了研究的难度,使得相关的研究文献比较少[4]。船体上的连接部位需要承受并且传递动静载荷,因此会造成相应的振动以及碰撞。如果不能适当处理这些连接部位,则会加剧这种震荡,甚至会扩大连接界面的间隙从而造成整体结构的失效。因此船体上机械连接结构形式对连接结合面的动力学特性有很大的影响。本文对船舶机械设备连接结构损耗进行研究,有助于船舶连接结构技术的发展。
1 船舶连接结构结合面阻尼分析 1.1 阻尼耗能的数学模型在船体结构的设计制造过程中,船体结构通常都会存在振动以及噪声问题,这些振动及噪声会对船体的结构产生十分严重的破坏[5]。为了能够对船体结构的振动、冲击以及噪声等问题进行抑制,则需要将这些异常的能量消耗掉,消耗这些能量最常用的方法是增大阻尼。通常来讲,建造材料、结构粘性流体介质等材料的耗能作用共同产生了阻尼[6]。一般可以使用滞迟回线的方法对船体连接结构的阻尼耗能进行定量分析。由于存在阻尼作用的影响,动态激励的相位要超前于位移响应的相位,如下式:
| $ F = {F_0}\sin \omega t = {F_0}{e^{j\omega t}}\text{,} $ | (1) |
| $ \Delta = {\Delta _0}\sin \left( {\omega t - \alpha } \right) = {\Delta _0}{e^{j\left( {\omega t - \alpha } \right)}}\text{。} $ | (2) |
阻尼的动态刚度属于复数,其计算方法是激励力和位移之间的比值,如下式:
| $ {k^*} = \frac{F}{\Delta } = \frac{{{F_0}}}{{{\Delta _0}}}{e^{i\alpha }} = k{e^{j\alpha }}\text{,} $ | (3) |
将式(1)和式(2)中的ωt消去,则可以获得动态力和位移之间的数学关系,其表示的是一个封闭的椭圆形回线。该封闭回线的内部面积就是该动态力在一个周期内的做功,如下式:
| $ \delta W = \int {F{\mathrm{d}}\Delta = \text{π} {F_0}{\Delta _0}\sin \alpha } \text{,} $ | (4) |
此时,船体连接结构的弹性性能表达式如下:
| $ W = \frac{1}{2}{F_0}\left( {{\Delta _0}\cos \alpha } \right)\text{。} $ | (5) |
假设采用单位弧度做的功来表示损耗的能量,则可以使得式(4)中的δW和式(5)中的W具备一样的量纲,其单位弧度做的功可以使用式(6)来表示。
| $ \Delta W = \frac{{\delta W}}{{\alpha \pi }} = \frac{1}{2}{F_0}{\Delta _0}\sin \alpha \text{。} $ | (6) |
损耗能量和弹性性能之间的比值是船体连接结构阻尼的物理本质,假设将这个比值定义成连接结构阻尼的损耗因子,则根据式(4)和式(6)可以得到该损耗因子的计算方法,如下式:
| $ \eta = \frac{{\Delta W}}{W} = \tan \alpha \text{。} $ | (7) |
可以看出,船体连接结构的阻尼损耗因子和滞后角之间存在紧密联系,并且船体连接结构的阻尼损耗因子会随着滞后角的增大而增大,根据式(7)则可以将式(3)改为下式:
| $ K' = K\left( {\cos \alpha + j\sin \alpha } \right)\text{,} $ | (8) |
式中,K′为复刚度。阻尼损耗因子可以使用复刚度的虚部和实部之间的比值来表示,如下式:
| $ \eta ' = \frac{{{Im} \left[ {{K^*}} \right]}}{{{Re} \left[ {{K^*}} \right]}}\text{。} $ | (9) |
对比式(7)和式(9)两种不同的船体连接结构阻尼损耗因子的不同数学模型可以看出,船体连接结构的损耗因子不但可以表示出能量的损耗量,即位移相位滞后于力相位,同样可以表示损耗因子是复刚度虚部和实部之间的比值。
1.2 阻尼的测量方法以牛顿定律以及达朗贝尔原理为基础,阻尼震荡系统的微分方程可以表示为:
| $ {\boldsymbol{M}}\dot x + {\boldsymbol{C}}\dot x + {\boldsymbol{K}}x = f\left( x \right)\text{。} $ | (10) |
如果阻尼形式为比例形式,则其微分方程如下式:
| $ {\boldsymbol{M}}\dot x + \left( {{\boldsymbol{K}} + jG} \right)x = F{e^{j\omega t}}\text{。} $ | (11) |
式中,G为比例阻尼。
内阻尼和外阻尼是阻尼的2种类型,在一个自由振动的阻尼系统中,其外力等于0,则可以得到下式:
| $ {s^2} + 2\xi {\omega _n}s + \omega _n^2 = 0\text{,} $ | (12) |
| $ {s_{1,2}} = \left( { - \xi \pm \sqrt {{\xi ^2} - 1} } \right){\omega _n}\text{。} $ | (13) |
式中,阻尼比ξ大于1时,则整个阻尼系统在强阻尼状态下,此时阻尼系统无法产生振动。当阻尼比ξ等于1的时候,此时整个阻尼系统处于临界状态,因此这个时候的系统振动会衰减很快;当阻尼比ξ小于1的时候,则整个阻尼系统处于弱阻尼状态,此时存在一对共轭复根,其固有频率的计算方法如下式:
| $ {\omega _d} = {\omega _n}\sqrt {1 - {\xi ^2}} \text{,} $ | (14) |
对数衰减率的计算方法如下式:
| $ \delta = \xi {\omega _n}T\text{,} $ | (15) |
频率响应函数的动态放大系数的计算方法如下式:
| $ \alpha = \frac{1}{{\sqrt {{{\left( {1 - \lambda } \right)}^2} + {{\left( {2\xi \lambda } \right)}^2}} }}\text{。} $ | (16) |
当激励频率比较小的时候,α的值趋近于1;当激励频率比较大的时候,α的值趋近于0。这表明,在高频的情况下,系统的响应幅值比较小,并且相位值接近于180°,同时激励力的相位和响应的相位相反。振动系统的阻尼测试方法主要有峰值法,其计算方法如下式:
| $ {\eta _q} = \frac{1}{{{{\left| Q \right|}_{\max }}}}\text{。} $ | (17) |
船舶连接结构可以使用直簧振子系统来描述,直簧振子系统中包含一个直簧以及一个质量物体,直簧的下端和结构相连,上端和质量物体互联。根据牛顿第二定律,直簧对质量物体的作用力可以用表示为:
| $ {F_r} = {\omega ^2}{m_r}{\bar w_r}\text{,} $ | (18) |
直簧对结构的作用力可以表示为:
| $ {F'_r} = {k_r}\left( {{{\bar w}_r} - {w_r}\left( {{x_r},{y_r}} \right)} \right)\text{。} $ | (19) |
式中:wr为直簧和结构连接处的位移;kr为直簧的刚度。
| $ {k_r} = {\bar k_r}\left( {1 + j\eta } \right)\text{。} $ | (20) |
根据位移阻抗,直簧振子的阻抗公式如下:
| $ {Z_{Fr}} = \frac{{{\omega ^2}{m_r}{k_r}}}{{{k_r} - {\omega ^2}{m_r}}}\text{。} $ | (21) |
为了研究动力吸振对船舶连接结构振动系统的影响,以钢板为例,在其中心处施加单位力激励,并且添加直簧振子动力吸振器,该直簧振子动力吸振器的阻抗曲线如图1所示。可以看出,直簧振子的阻抗值随着频率的增大先增大,然后在600 Hz处达到最大值,达到最大值之后,该阻抗值随着频率的增大而降低,并且最终趋于一个常数,该常数称为弹簧的刚度。

|
图 1 直簧振子阻抗值随频率的变化 Fig. 1 The impedance value of a straight spring oscillator changes with frequency |
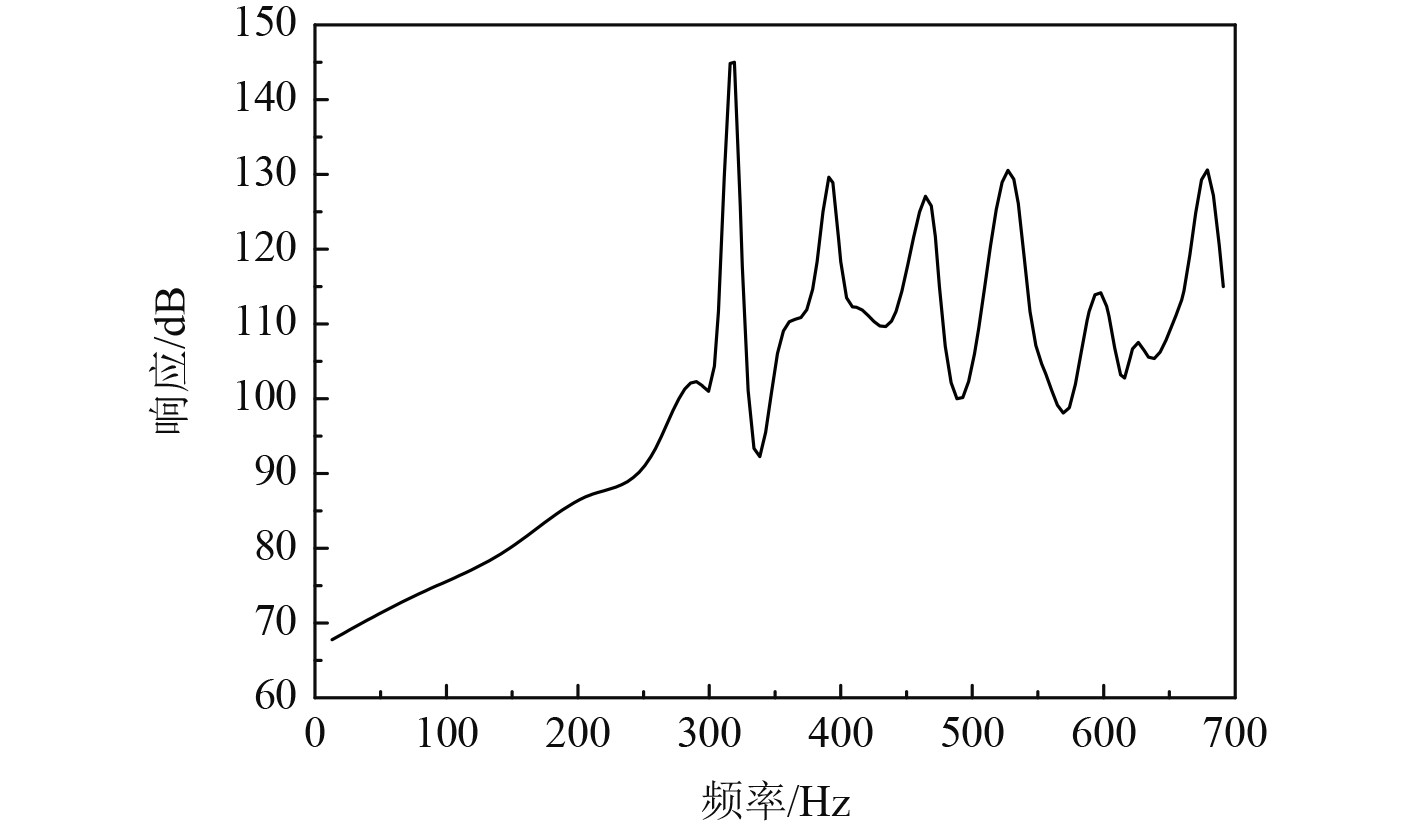
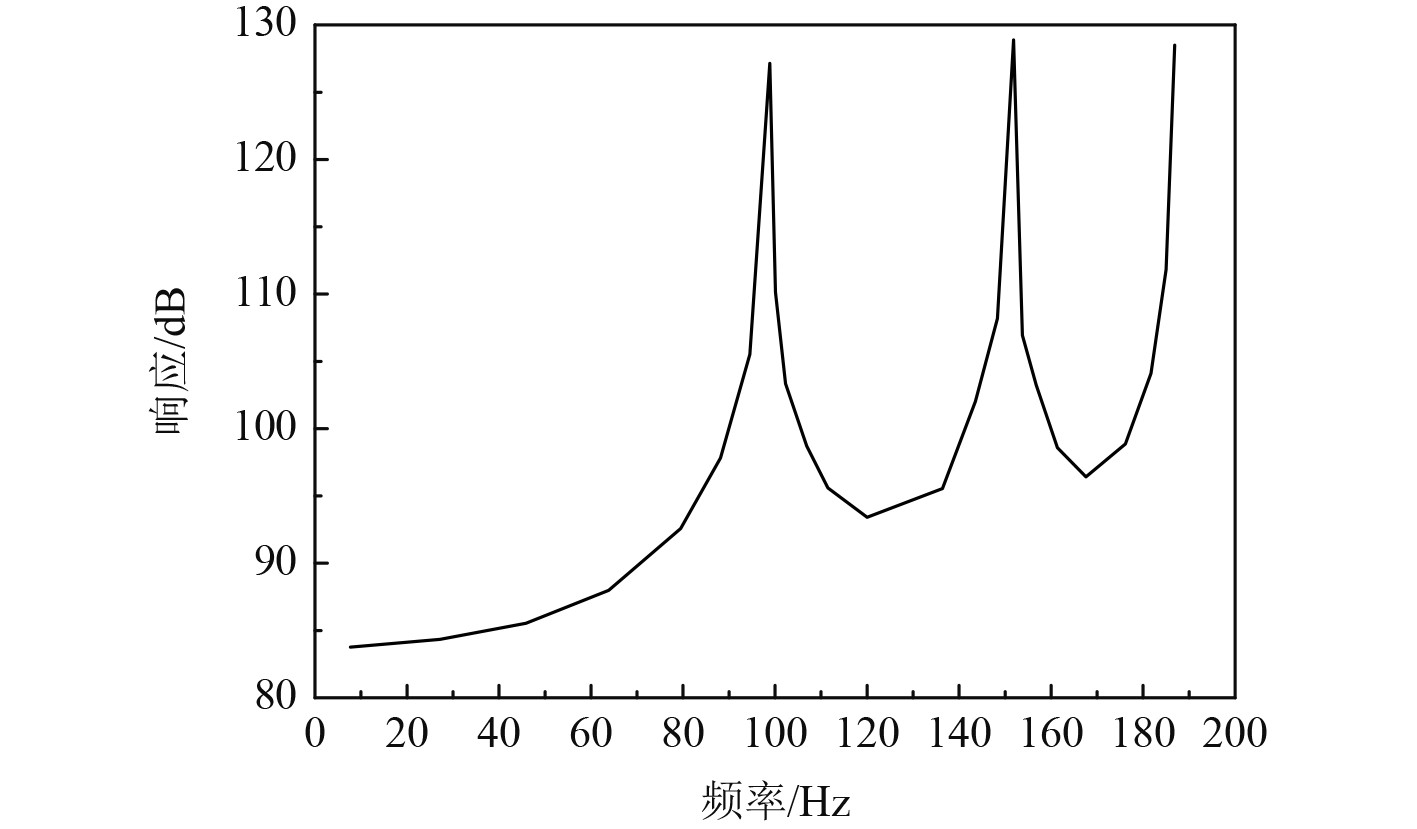
图2给出了不同频率下振动响应变化情况。可以看出,振动响应频率在300 Hz处存在一个明显的峰值。为了可以对船体连接结构局部阻尼的振动特性进行分析,以自由弯曲的振动梁为基础。该结构的基底材料为刚结构,在船体连接结构局部阻尼梁的其中一段添加0.01 N的激励,采用有限元数值法进行求解,则得到的局部约束激励端响应曲线以及局部约束非激励端响应曲线分别如图3和图4所示。图3和图4体现了动刚度理论对船体连接结构阻尼振动解算的可靠性。对局部阻尼模型进行模态分析,得到模态频率,然后利用式(22)得到固有频率。
|
图 2 不同频率下振动响应变化情况 Fig. 2 Changes in vibration response at different frequencies |

|
图 3 局部约束激励端响应 Fig. 3 Local constraint excitation end response |
|
图 4 局部约束非激励端响应 Fig. 4 Local constraint non excitation end response |
| $ \omega = \sqrt {{Re} \left( {{\varOmega ^2}} \right)} \text{。} $ | (22) |
本文以带有螺旋结构的悬臂梁来模拟船体机械设备连接结构,作为一种非保守的系统,螺旋连接结构的结合面比较复杂,因此使用统计能量法对螺旋连接结构进行非保守损耗因子研究。
对含有一对振子的非保守耦合系统,可以使用阻尼损耗能量来等效损耗因子,功率平衡数学模型如下式:
| $ \left\{ {\begin{array}{*{20}{c}} {{p_1} = \omega {\eta _1}{E_1} + \omega {{\eta '}_{12}}{E_1} - \omega {{\eta '}_{12}}{E_2}} ,\\ {{p_2} = \omega {\eta _2}{E_2} + \omega {{\eta '}_{21}}{E_2} - \omega {{\eta '}_{21}}{E_1}} 。\end{array}} \right. $ | (23) |
如果只对振子1添加激励,则可以得到其数学模型,如下式:
| $ \left\{ {\begin{array}{*{20}{c}} {{\eta _{s1}} = {\eta _1} + {{\eta '}_{12}} - {{\eta '}_{21}}E_{21}^{\left( 1 \right)}},\\ {0 = {\eta _2} + {{\eta '}_{21}} - {{\eta '}_{12}}E_{12}^{\left( 1 \right)}} 。\end{array}} \right.$ | (24) |
如果只对振子2添加激励,则可以得到等效耦合损耗因子的数学模型,如下式:
| $ \left\{ {\begin{array}{*{20}{c}} {{{\eta '}_{21}} = \dfrac{{E_{12}^{\left( 2 \right)}}}{{1 - E_{12}^{\left( 2 \right)}E_{21}^{\left( 1 \right)}}}{\eta _{s1}}} ,\\ {{{\eta '}_{12}} = \dfrac{{E_{21}^{\left( 1 \right)}}}{{1 - E_{12}^{\left( 2 \right)}E_{21}^{\left( 1 \right)}}}{\eta _{s2}}} 。\end{array}} \right. $ | (25) |
式中包含了连接结构的总损耗因子,在稳态情况下,假设只对振子i施加激励,则对于一个存在N个振子的保守系统而言,使用统计能量法进行分析的时候,振子i的总损耗因子如下式:
| $ {\eta _{si}} = {\eta _i} + \sum\limits_{j = 1,j \ne i}^N {{\eta _{ij}}} \text{,} $ | (26) |
振子的平均振动能量的数学模型如下式:
| $ {E_i} = \frac{1}{2}M{\bar v^2} = \frac{1}{2}M{\omega ^2}{\bar \mu ^2}\text{。} $ | (27) |
式中:Ei为平均振动能量;
将所有振子的平均振动能量进行叠加,则可以得到振动能量的比值如下式:
| $ \frac{{{E_2}}}{{{E_1}}} = \frac{{\displaystyle\sum\limits_{i = 1}^n {{m_{2i}}{{\left| {{v_{2i}}} \right|}^2}} }}{{\displaystyle\sum\limits_{j = 1}^n {{m_{1j}}{{\left| {{v_{1j}}} \right|}^2}} }}\text{。} $ | (28) |
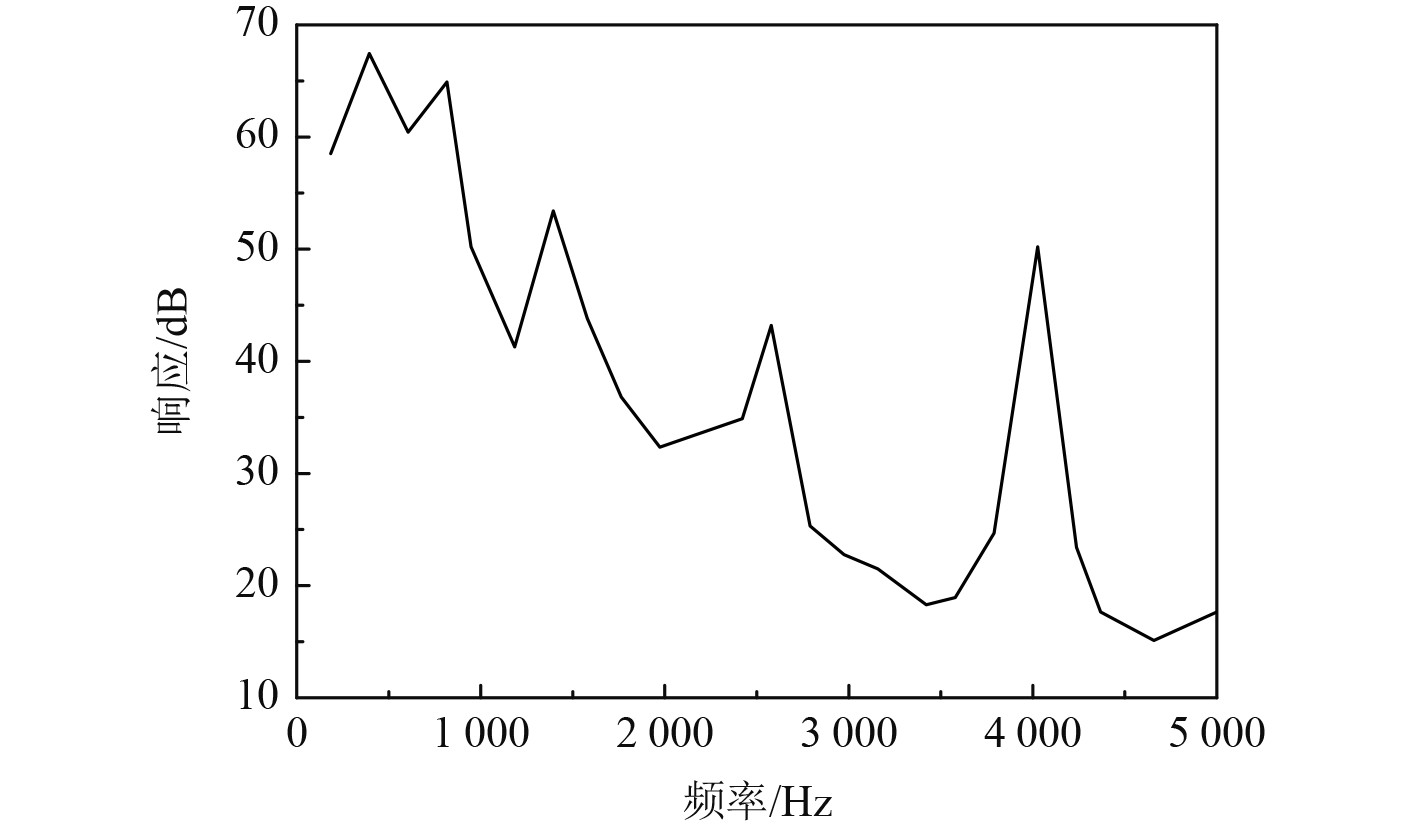
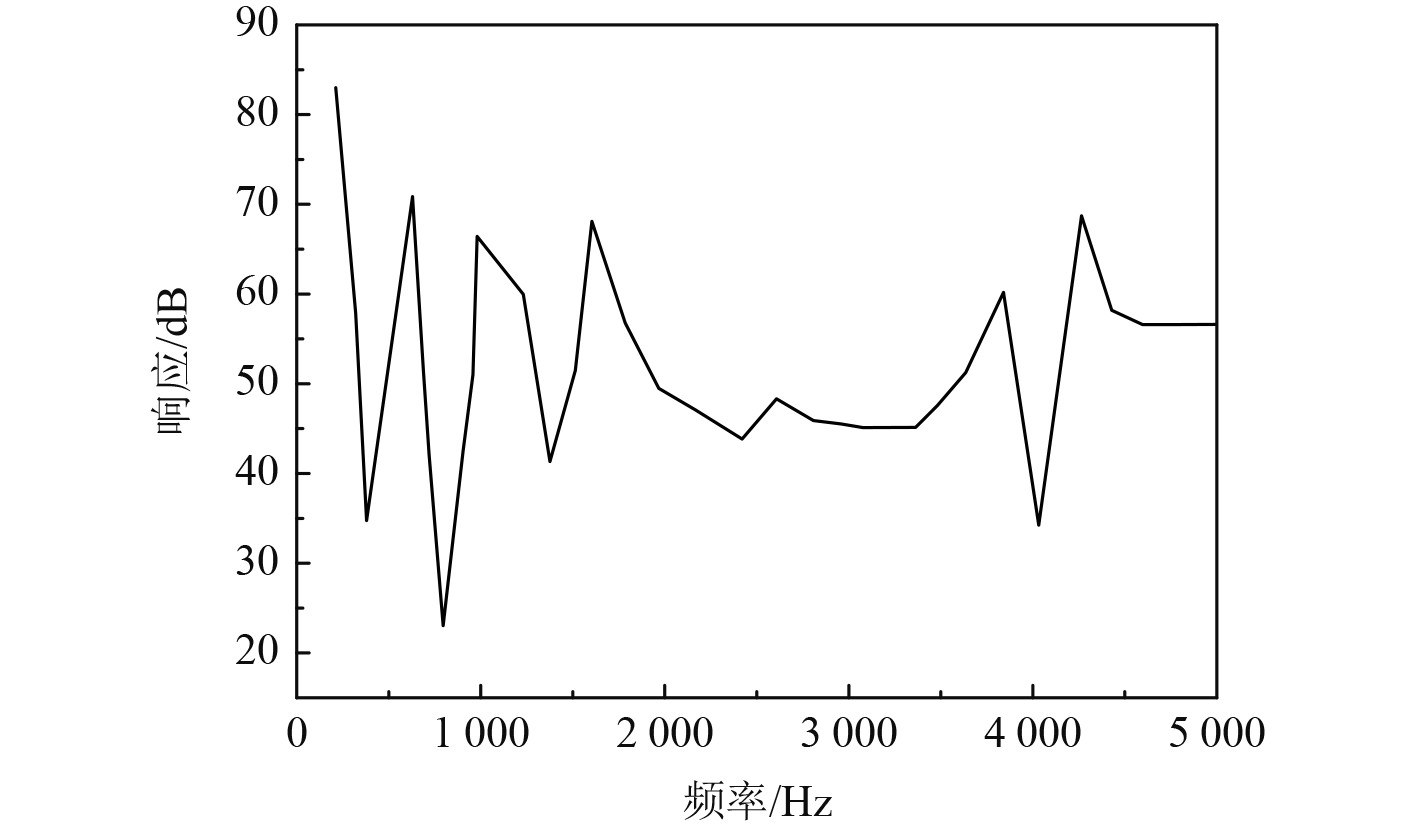
振子1受激励的响应情况如图5所示。可以看出,振子1的响应随着频率的增加,整体上处于下降趋势。振子2受激励的响应曲线如图6所示。可以看出,振子2的响应随着频率的增加,响应逐渐趋于稳定。
|
图 5 振子1受激励的响应 Fig. 5 Response of oscillator 1 under excitation |
|
图 6 振子2受激的响应 Fig. 6 Response of oscillator2 under excitation |
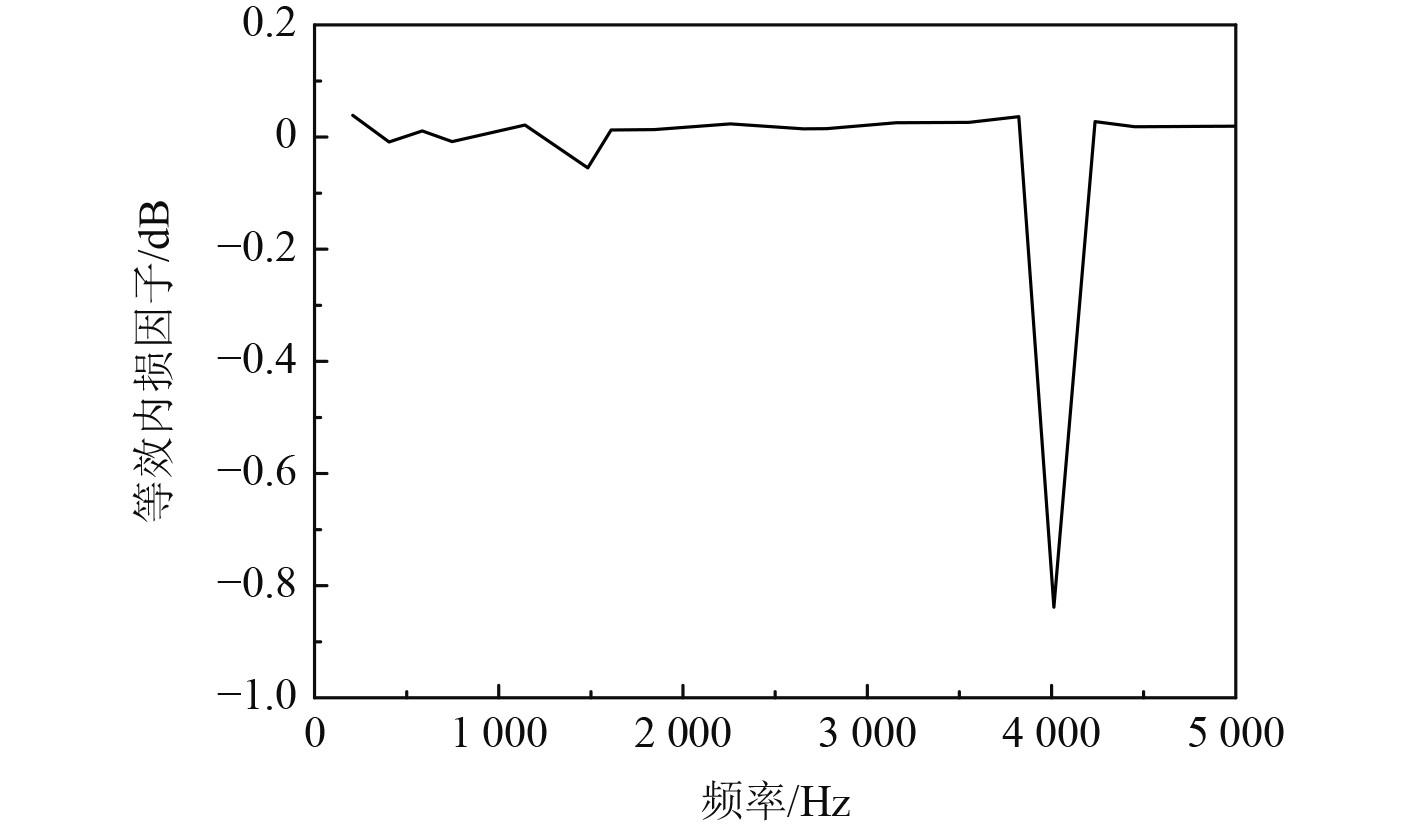
图7给出了等效内损因子变化曲线,由图可知,在频率为4 000 Hz的时候,等效内损因子存在突然降低的现象。
|
图 7 等效内损因子变化曲线 Fig. 7 Equivalent internal loss factor change curve |
在船舶振动试验中,常常会出现局部连接结构振动现象,则此时需要对结合面进行动力学分析。阻尼的耗能是船体连接结构结合面的能量损耗最主要的来源,结合面的阻尼是连接结构结合面的主要参数之一,因此阻尼的计算十分重要。在统计能量分析技术中,连接结构本身的耗能能力可以使用内损因子来表示,因此,对强耦合系统中的损耗因子的解算也十分重要。
| [1] |
王晋鹏, 常山, 刘更, 等. 船舶齿轮传动装置箱体振动噪声分析与控制研究进展[J]. 船舶力学, 2019(23): 1007-1019. |
| [2] |
赵钰. 船舶机械设备连接结构损耗分析研究[J]. 舰船科学技术, 2019(41): 64-66. |
| [3] |
徐小飞, 刘虎, 叶仁传. 大型船舶体振动与舱室噪声预报[J]. 船舶与海洋工程, 2023(39): 23-29+77. |
| [4] |
唐宇航, 陈志坚, 孙建连. 敷设阻尼及阻抗失配连接下管母线振动特性分析[J]. 船舶力学, 2018(22): 224-234. |
| [5] |
伍先俊, 朱石坚. 统计能量法及其在船舶声振预测中的应用综述[J]. 武汉理工大学学报, 2004(28): 212-215. |
| [6] |
程广利, 朱石坚, 伍先俊. 统计能量分析法及其损耗因子确定方法综述[J]. 船舶工程, 2004(26): 10-15. DOI:10.3969/j.issn.1000-6982.2004.04.003 |
 2023, Vol. 45
2023, Vol. 45
