2. 南京大全电气研究院有限公司,江苏 南京 211000;
3. 东南大学电气工程学院,江苏 南京 211000
2. Nanjing Daqo Electric Research Institute Co., Ltd., Nanjing 211000, China;
3. School of Electrical Engineering, Southeast University, Nanjing 211000, China
由于船舶的空间相对狭小且电气设备数量庞大,在进行电气设备信号采集时无法避免信号受到噪声干扰[1],尤其是在进行船舶的精细控制,如故障检测、电气设备控制、舰船航向和推理的控制等,若信号中存在噪声则无法顺利完成上述任务[2],可能会造成舰船严重事故。因此需要保证舰船的电气设备信号的纯净,去除信号中的噪声干扰。
针对信号的噪声干扰问题,许多学者进行了信号去噪研究。胡正伟等[3]提出了通信信号去噪方法,使用神经网络作为主要去噪手段,在网络中使用Noise2Noise算法作为核心,达到消除通信信号噪声的目的。赵寿生等[4]提出了振动信号去噪方法,结合经验模态分解和统计特征,首先检验噪声随机性,使用经验模态分解振动信号,将分解的信号进行重构,得到去噪后的振动信号。胡璞等[5]研究的角位移传感器采集信号去噪,先计算传感器的串扰电压,使用经验模态分解对信号分解,得到信号分量,重复分解新的信号分量并使用阈值函数消除噪声。上述方法虽然能够完成对信号噪声的去除,但是也存在一定的缺点。最主要的去噪效果不佳,去噪后的信号仍然存在较大的噪声干扰;算法的复杂度较高,很难保证信号的快速降噪,可能影响舰船的控制效果;使用传感器容易造成误报或漏报,使信号去噪效果完全丧失。
小波变换的时频性好、应用范围广泛且简单,为此提出基于小波变换技术的舰船电气设备信号去噪抑制方法,并分析其性能。
1 舰船电气设备信号去噪抑制 1.1 舰船电气设备噪声分析舰船电气设备数量庞大,其中包含动力设备、发电设备、通信设备、控制设备、照明、仪表等,在海面上电气设备若发生故障严重会导致沉船。因此,对于舰船电气设备监控和控制十分重要。对电器设备的监控,一般是通过传感器采集电气设备信号,根据信号分析设备的状态,而在舰船中,由于环境狭小,设备众多难免会在收集信号时产生噪声干扰,对电气设备信号产生干扰最多也是最严重的便是电磁干扰。虽然舰船电气设备信号噪声主要是电磁干扰产生的,但是其他类型的噪声干扰叠加也十分严重,因此需要对电气设备内的各种噪声进行去噪和抑制之后才能保证舰船的电气设备控制、故障检测等工作运行稳定。
1.2 基于小波变换的舰船电气设备信号去噪抑制 1.2.1 小波分解利用小波分解舰船电气设备信号,完成对噪声信号的去除便是小波变换去噪,使用小波变换去噪能够实现信号噪声的抑制,得到接近无噪声的舰船电气设备信号。小波分解结构如图1所示。
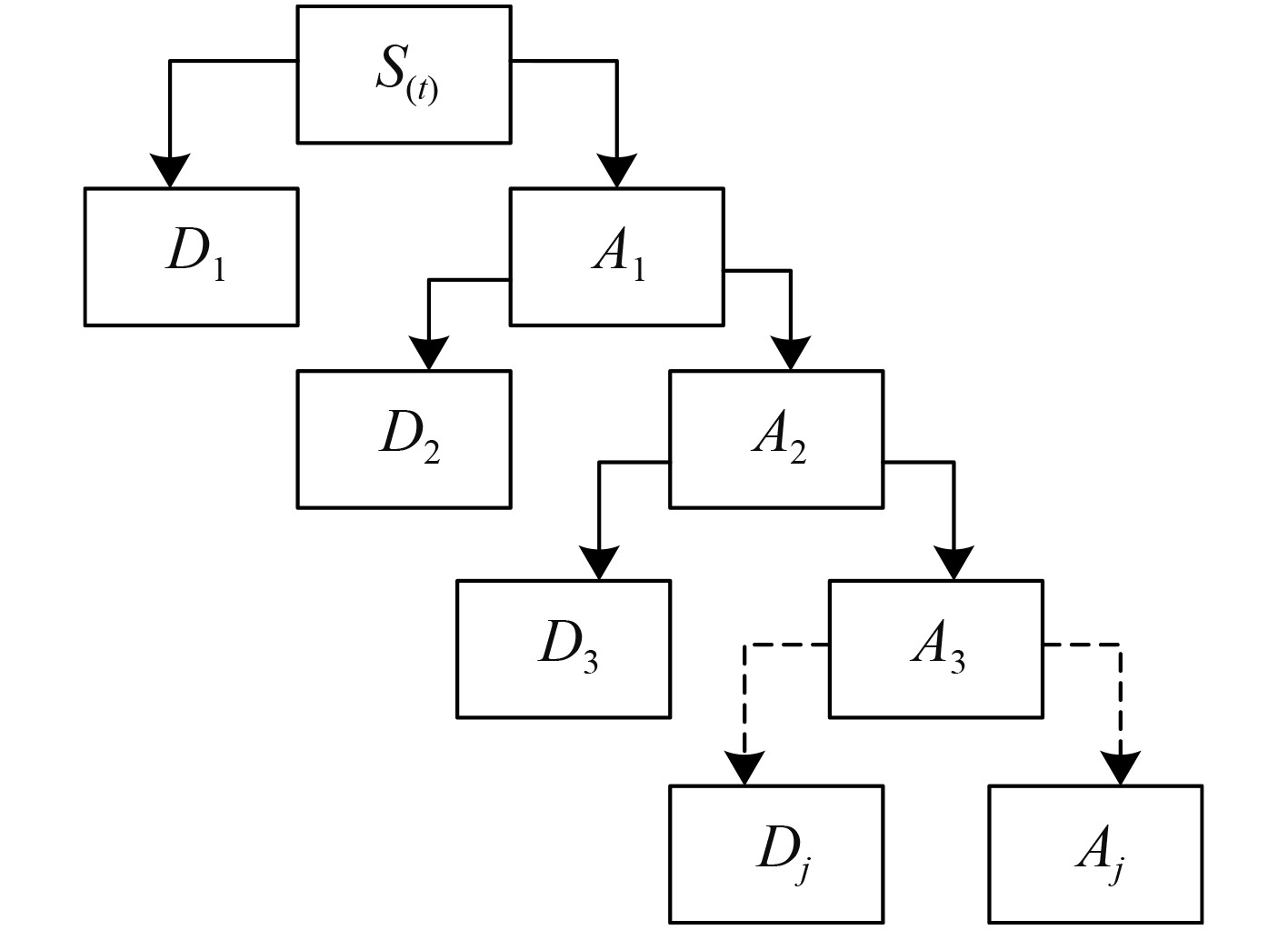
|
图 1 小波分解结构 Fig. 1 Wavelet decomposition structure |
图1中,Aj、Dj分别为
| $ S\left(t\right)=x\left(t\right)+\sigma e\left(t\right)。$ | (1) |
式中:x(t)为无噪声信号;e(t)为噪声;
对舰船电气设备信号分解后信号的可用信息基本处于低频,因此不对高频分解。
对信号的分解公式为:
| $ s\left( t \right) = \sum\limits_j {{c_{j,k}}H} + \sum\limits_j {{d_{j,k}}G} 。$ | (2) |
式中:
将分解到第
小波系数的阈值通常分为“硬”阈值函数与“软”阈值函数,在经过信号分解后由于噪声主要在高频部分因此对高频部分进行阈值量化。以高频部分的小波系数为输入,通过阈值函数计算降噪后的高频部分,小波降噪的阈值函数分为硬阈值函数和软阈值函数。硬阈值函数为:
| $ {w_\lambda } = \left\{ \begin{split} w ,\quad & | w | > \lambda ,\\ 0 ,\quad & | w | < \lambda。\\ \end{split} \right. $ | (3) |
式中:
软阈值函数,公式表达为:
| $ {w_\lambda } = \left\{ \begin{split} & {{\mathrm{sgn}}} \left( w \right)\max \left( {\left| w \right| - \lambda ,0} \right),& \left| w \right| > \lambda ,\\ & 0,& \left| w \right| \leqslant \lambda。\\ \end{split} \right. $ | (4) |
一般软硬阈值的选择需要依据含噪舰船电气设备信号的分解层数和噪声强度判断。
1.3 基于双树复小波和通用阈值的小波变换改进小波变换存在着如能量泄漏大、频带混叠大等问题,使用传统小波变换无法得到最佳舰船电气设备去噪抑制信号,需要对小波变换进行改进。
1.3.1 双树复小波改进在小波分解时利用实部树和虚部树对舰船电气信号进行分解,能够有效实现信号平移不变的特性,避免了小波变换的缺点,既能够保留小波变换的解析性好又可以达到舰船电气设备信号的完全重构,这是双树复小波的优点,双树复小波进行舰船电气设备信号分解如图2所示。图中h0和h1为实部树的低、高通滤波器,g0和g1为虚部树的低、高通滤波器,2虚表示抽点采样其间隔为2。通过实部树和虚部树进行舰船电气设备信号分解,在第1层中,两树拥有相同的采样周期间隔,保证虚部树能够采样实部树错过的数据。当分解层数变高,利用Q-Shift实现实部和虚部滤波器的采样周期延迟。
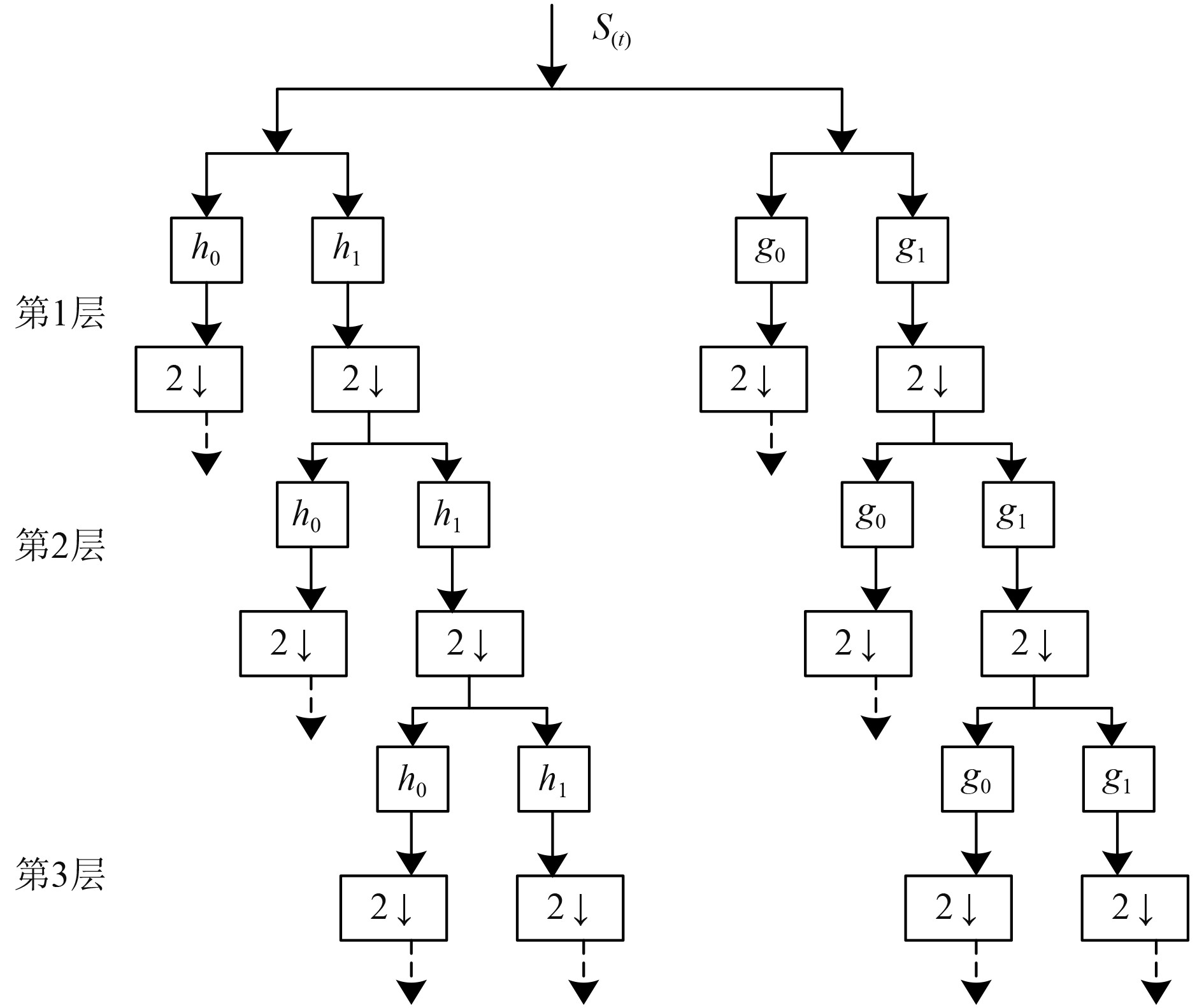
|
图 2 双树复小波信号分解 Fig. 2 Two-tree complex wavelet signal decomposition |
由于仅选择硬阈值或软阈值会产生伪吉布斯现象和边缘模糊失真等问题,因此对阈值函数进行改进。通过结合硬阈值函数和软阈值函数的优点,对阈值函数进行改进,新的阈值函数为:
| $ {w'_\lambda } = \left\{ \begin{split} & {\mathrm{sign}}\left( w \right)\left( {\left| w \right| - \frac{\lambda }{{\exp \left( {\dfrac{{\left| w \right| - \lambda }}{c}} \right)}}} \right),& \left| w \right| \geqslant \lambda ,\\ & 0, & \left| w \right| \leqslant \lambda 。\\ \end{split} \right. $ | (5) |
式中:
改进后的双树复小波变换去除舰船电气设备信号,具体流程为:
1)采集舰船电气设备原始信号,确定需要分解的层数;
2)使用改进后的小波阈值函数进行计算,构造尺度函数;
3)根据分解层数以及构造的尺度函数,利用实部树和虚部树分解舰船电气设备信号;
4)设定需要过滤的高频系数,通常该系数为0,利用通用阈值函数对高频系数进行去噪抑制处理,得出去噪抑制后的小波系数矩阵估值;
5)判断是否去噪完成,若未完成转至步骤2,若完成则输出去噪抑制后的舰船电气设备信号。
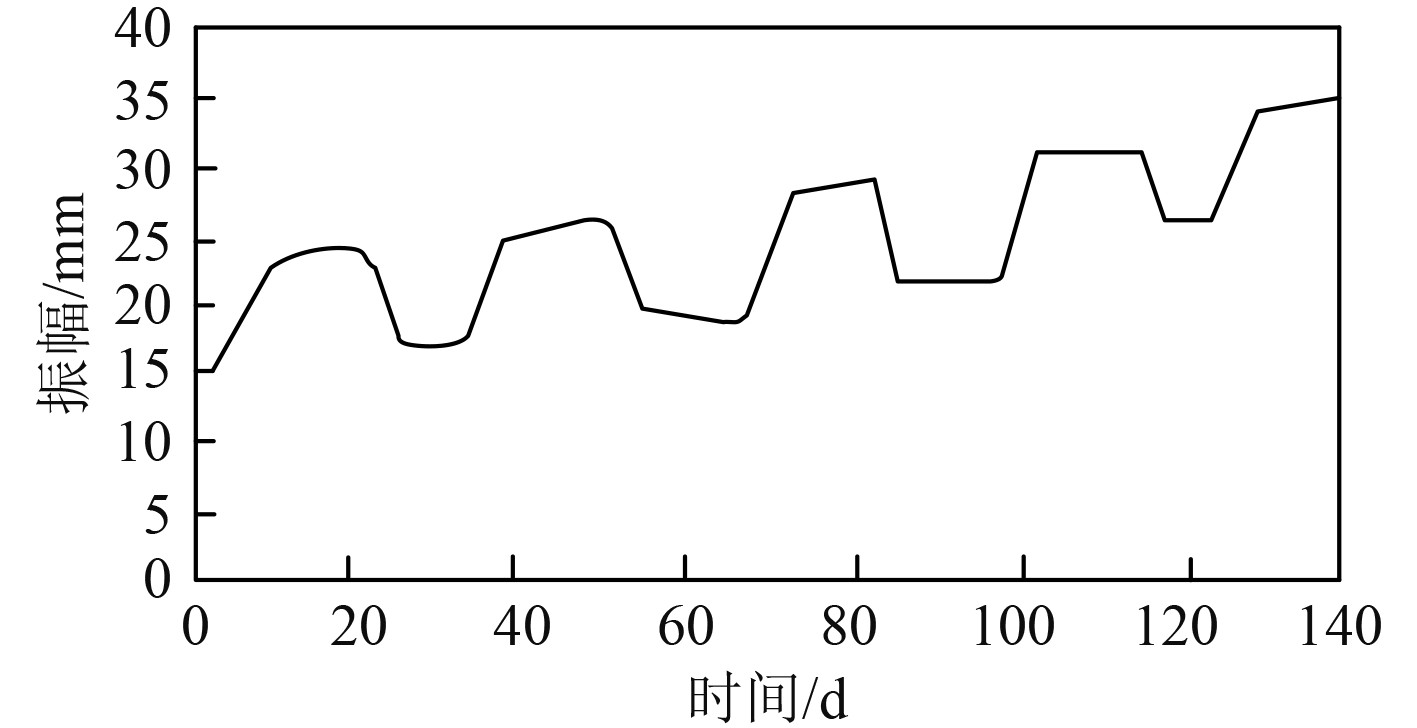
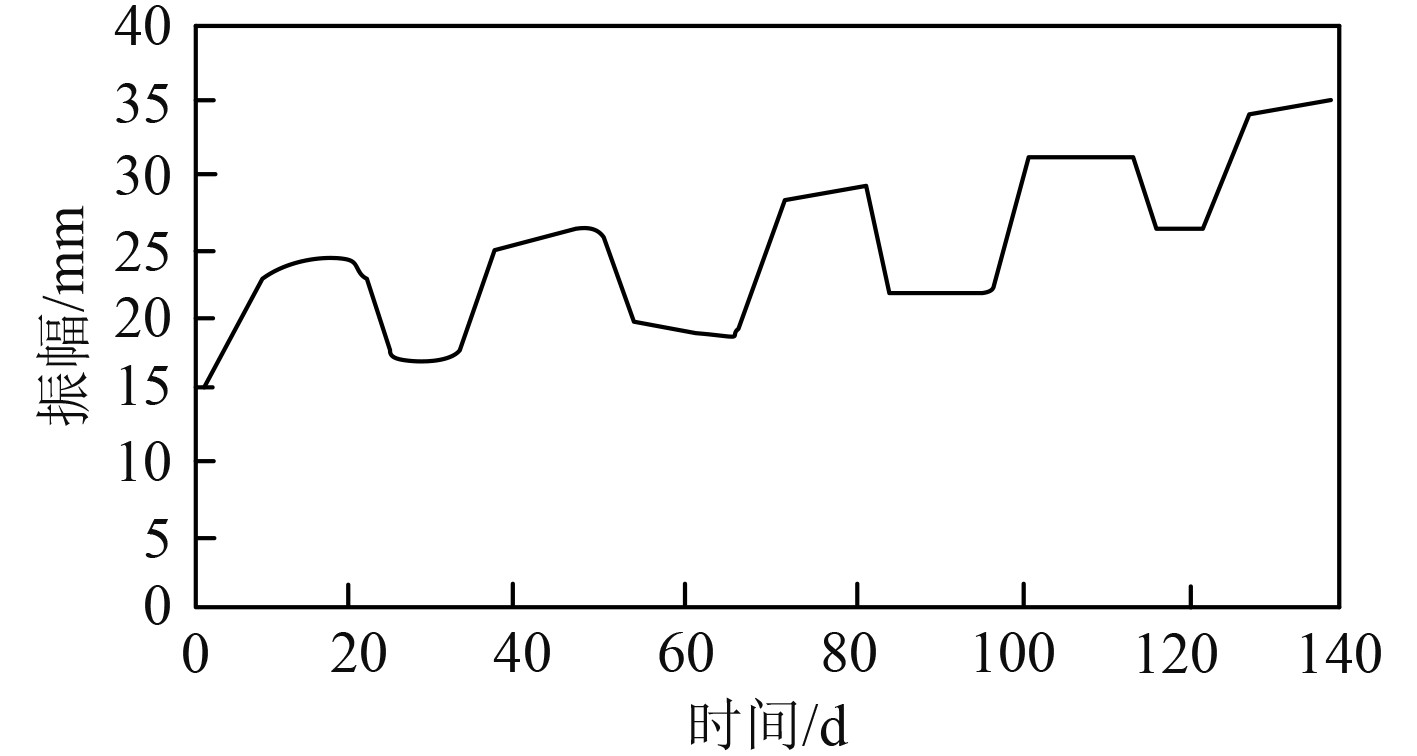
2 实验结果分析为验证本文方法的去噪效果,模拟一组无噪声的电气设备信号(见图3),对该信号增添噪声(见图4),采用选择硬阈值函数的小波变换降噪和改进后的小波变换降噪结果如图5和图6所示。通过图3~图6可以看出,使用硬阈值函数进行小波变换降噪信号中的曲线被校正称为直线,在添加噪声区域降噪后的信号与原始信号有相对明显的差别,使用本文改进后的小波变换降噪方法能够保证未添加噪声区域的信号保持基本不变,存在噪声的区域经过降噪后基本与原始信号一致,证明本文方法在船舶电气设备信号降噪抑制中具有明显的优势,可以进行实际应用。
|
图 3 无噪声信号 Fig. 3 Noiseless signal |

|
图 4 添加噪声信号 Fig. 4 Add noise signal |
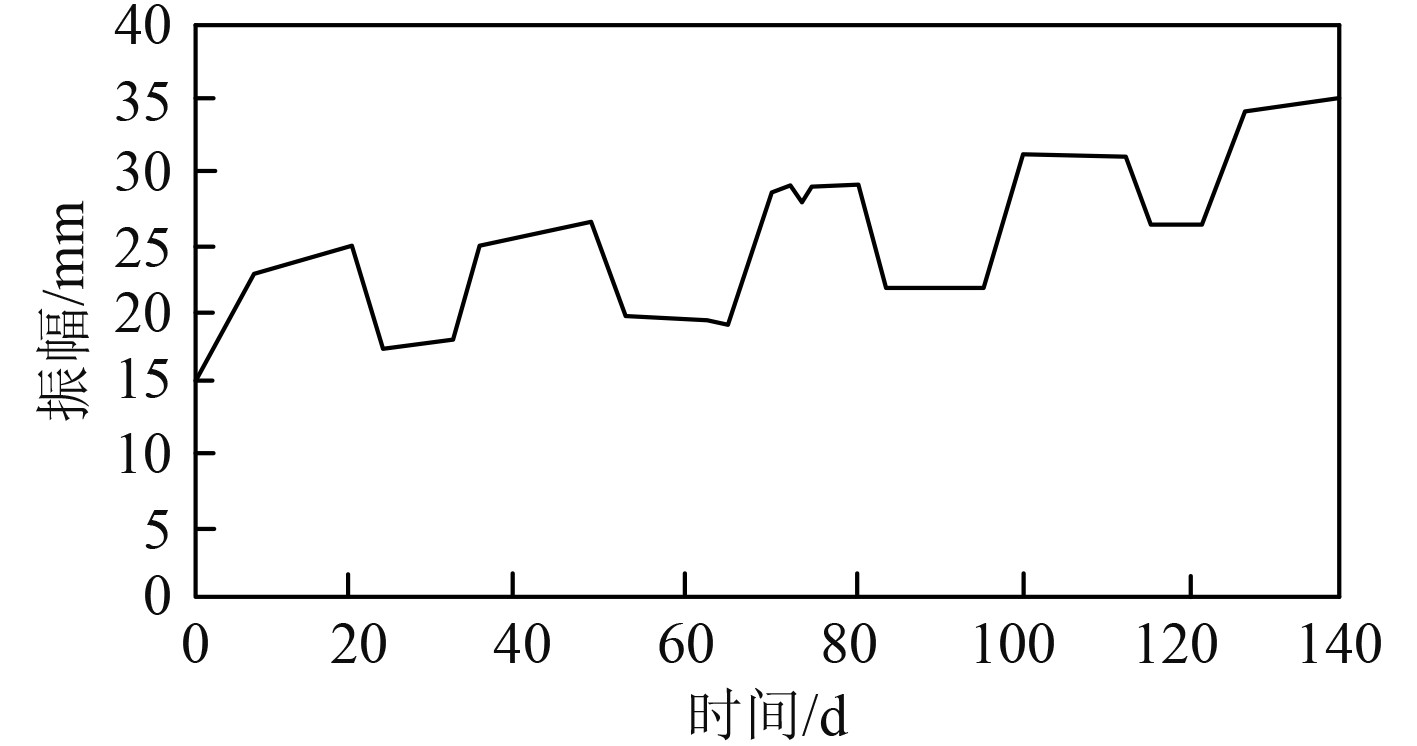
|
图 5 硬阈值小波变换降噪 Fig. 5 Hard threshold wavelet transform denoising |
|
图 6 改进后小波变换降噪 Fig. 6 Improved wavelet transform noise reduction |
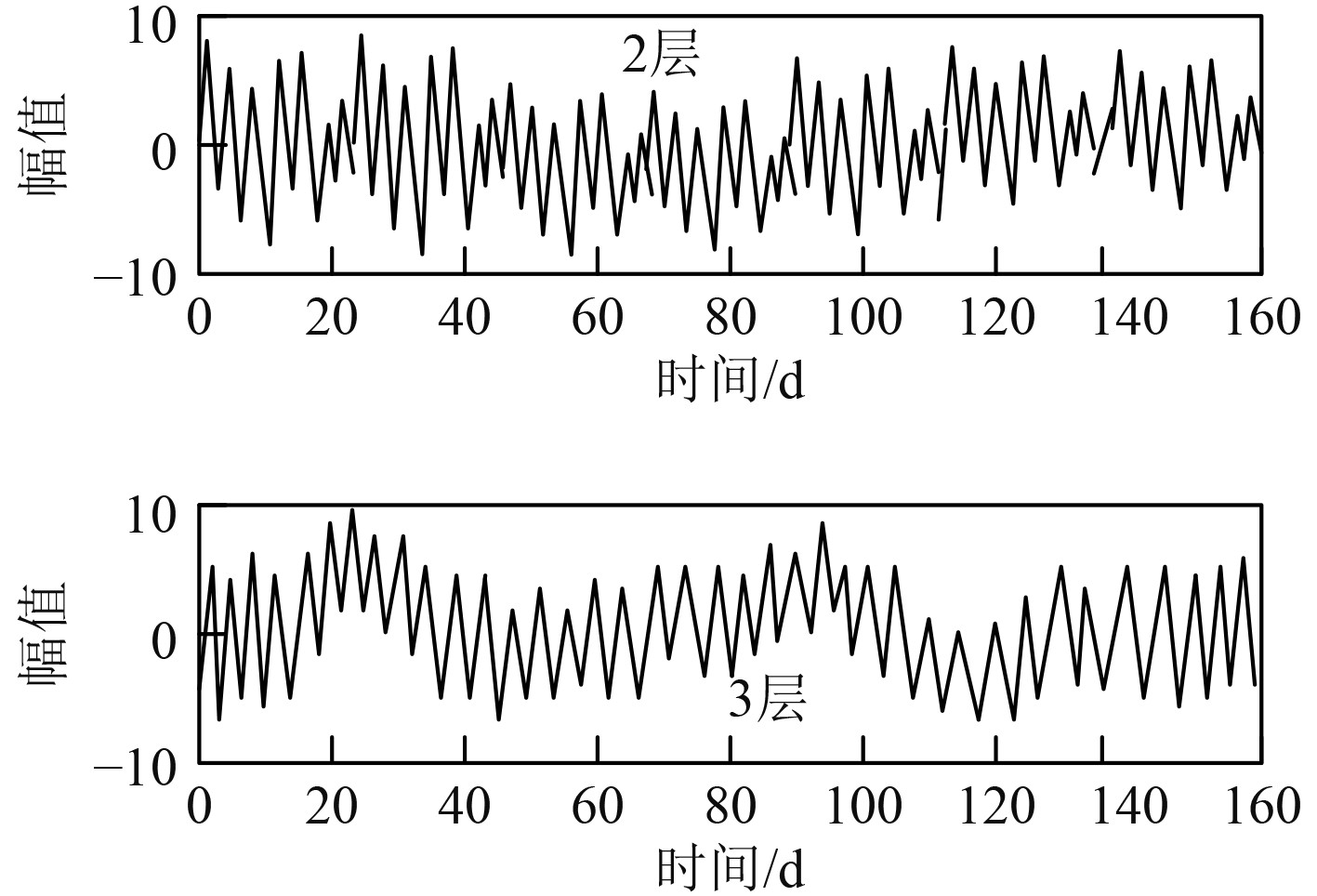
进行降噪抑制时对电气设备信号进行分解,分解之后发现在分解的电气设备信号中2层和3层的高频部分噪声最大,其中2层和3层高频部分的小波变换系数如图7所示,降噪后2层、3层高频部分的小波变换系数如图8所示。通过图7和图8可以看出,使用本文改进后的小波变换去噪抑制方式,在分解后的小波系数中表现明显。在噪声最大的高频部分2层、3层的电气设备信号杂乱,幅值波动大,使用本文方法进行降噪抑制后,虽然信号仍然有波动,但是信号波动已经被压缩到了一个极小的值,整体呈现一个十分平稳的信号,可显著提升信号质量。
|
图 7 降噪前信号高频部分2层、3层小波系数 Fig. 7 2-3 layer wavelet coefficients of the high frequency part of the signal before noise reduction |

|
图 8 降噪后信号高频部分2层和3层小波系数 Fig. 8 2-3 layer wavelet coefficients of the high frequency part of the signal after noise reduction |
为了获得更好的舰船电气设备信号,本文设计了基于小波变换技术的舰船电气设备信号去噪抑制方法。实验结果表明,本文方法对舰船电气设备信号进行降噪时,既能够保证准确地消除噪声,又能够保证原始的电气设备信号波形不受干扰,是一种理想的舰船电气设备信号去噪方法。
| [1] |
付国红, 张前丰, 程辉. 基于STM32和LabVIEW的双频激电信号采集系统设计[J]. 地球物理学进展, 2020, 35(1): 287-293. FU Guo-hong, ZHANG Qian-feng, CHANG Hui. Design of dual-frequency IP signal acquisition system based on STM32 and LabVIEW[J]. Progress in Geophysics, 2020, 35(1): 287-293. |
| [2] |
张文远, 李天昊. 电力线传输特性和噪声干扰对通信性能的相对影响[J]. 电力系统保护与控制, 2022, 50(7): 145-152. |
| [3] |
胡正伟, 王志红, 畅瑞鑫, 等. 基于改进Noise2Noise算法的电力线信号去噪[J]. 电力系统保护与控制, 2023, 51(9): 32-45. |
| [4] |
赵寿生, 汪卫国, 王丰华, 等. 基于统计特征与EMD算法的有载分接开关振动信号去噪[J]. 电工电能新技术, 2020, 39(1): 51-58. Zhao Shou-sheng, WANG Wei-guo, WANG Feng-hua, et al. Denoising method of vibration signal of on-load tap changer based on statistical feature and EMD algorithm[J]. Advanced Technology of Electrical Engineering and Energy, 2020, 39(1): 51-58. |
| [5] |
胡璞, 刘利民. 经验模态分解算法在角位移传感器信号去噪中的应用[J]. 传感技术学报, 2023, 36(1): 113-117. |
 2023, Vol. 45
2023, Vol. 45
