船舶机械设备的主动减振技术前景非常广阔。一方面,随着船舶规模越来越大,航速越来越快,船舶在航行中所受到的环境因素的影响也越来越大,因此采用主动减振技术可以有效提高船舶的稳定性和航行舒适度,减少船舶的疲劳损伤和维修费用。另一方面,随着科技的不断发展,主动减振技术的应用范围也在不断扩大。例如,利用智能化控制技术和传感器技术,可以实现对船舶机械设备的实时监测和控制,从而更加精准地进行减振操作,提高减振效果。此外,随着人工智能和大数据技术的应用,可以对船舶机械设备的运行状态进行智能化分析和预测,从而更好地预防故障和提高设备的可靠性。
本文介绍一种船舶动力系统的主动减振系统,从系统的硬件组成、减振控制原理等方面进行研究,并针对减振系统的减振性能进行了测试。
1 船舶动力系统主动减振系统基本原理 1.1 动力系统主动减振系统的硬件组成船舶主动减振系统可以帮助船舶在恶劣海况下减小振动和冲击,减少柴油主机等动力设备的机械磨损,提高船舶的航行性能。
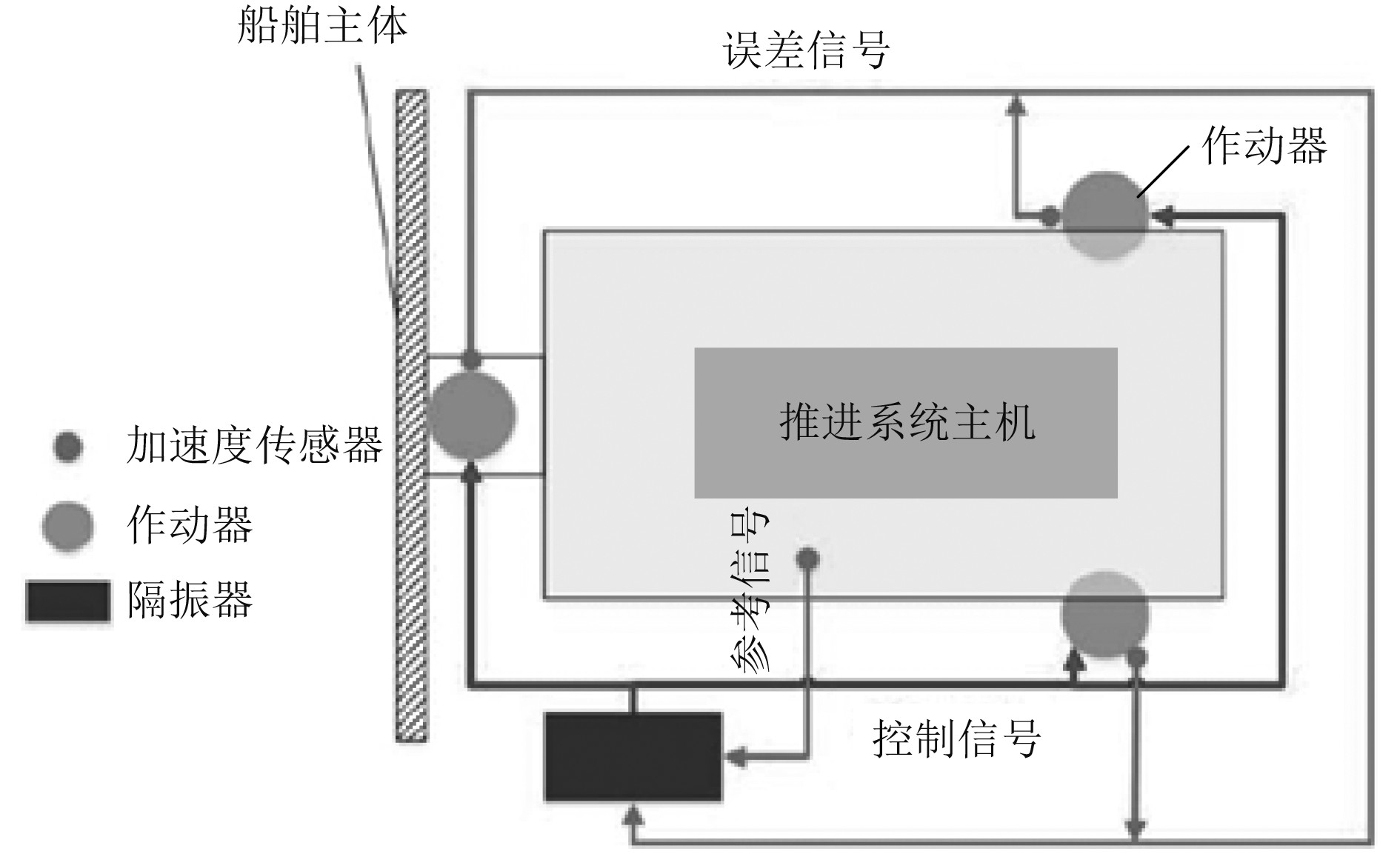
图1为船舶动力系统主动减振系统原理图。船舶动力系统主动减振系统包括主机、作动器号等。
|
图 1 船舶动力系统主动减振系统原理图 Fig. 1 Schematic diagram of active vibration reduction system for ship power system |
1)作动器
作动器是一种能够将电能、气压、水力等能量转换成机械运动的装置,作动器常用于机械系统、自动化控制系统、航空航天、机器人等领域。作动器根据其能量来源和动力传递方式可以分为多种类型,如电动作动器、气动作动器、液压作动器等。
电动作动器:通过电能转换为机械能,驱动机械系统的运动。常见的电动作动器包括电机、电磁铁、电液伺服阀等。
气动作动器:通过气压转换为机械能,驱动机械系统的运动,常见的气动作动器包括气缸、气动马达等。
液压作动器:通过液压能转换为机械能,驱动机械系统的运动,常见的液压作动器包括液压缸、液压马达、液压泵等[1]。
2)隔振器
隔振器是一种用于隔离和减少系统(如发动机、变速箱等)产生的振动和噪音传递到船舶主体结构的装置,通常被安装在发动机和船舶机舱甲板之间,起到减震和隔振的作用。动力系统隔振器通常由弹簧、减震器、橡胶减震元件等组成,其设计和选择需要考虑到动力系统产生的振动频率、振幅以及车辆结构的特性。
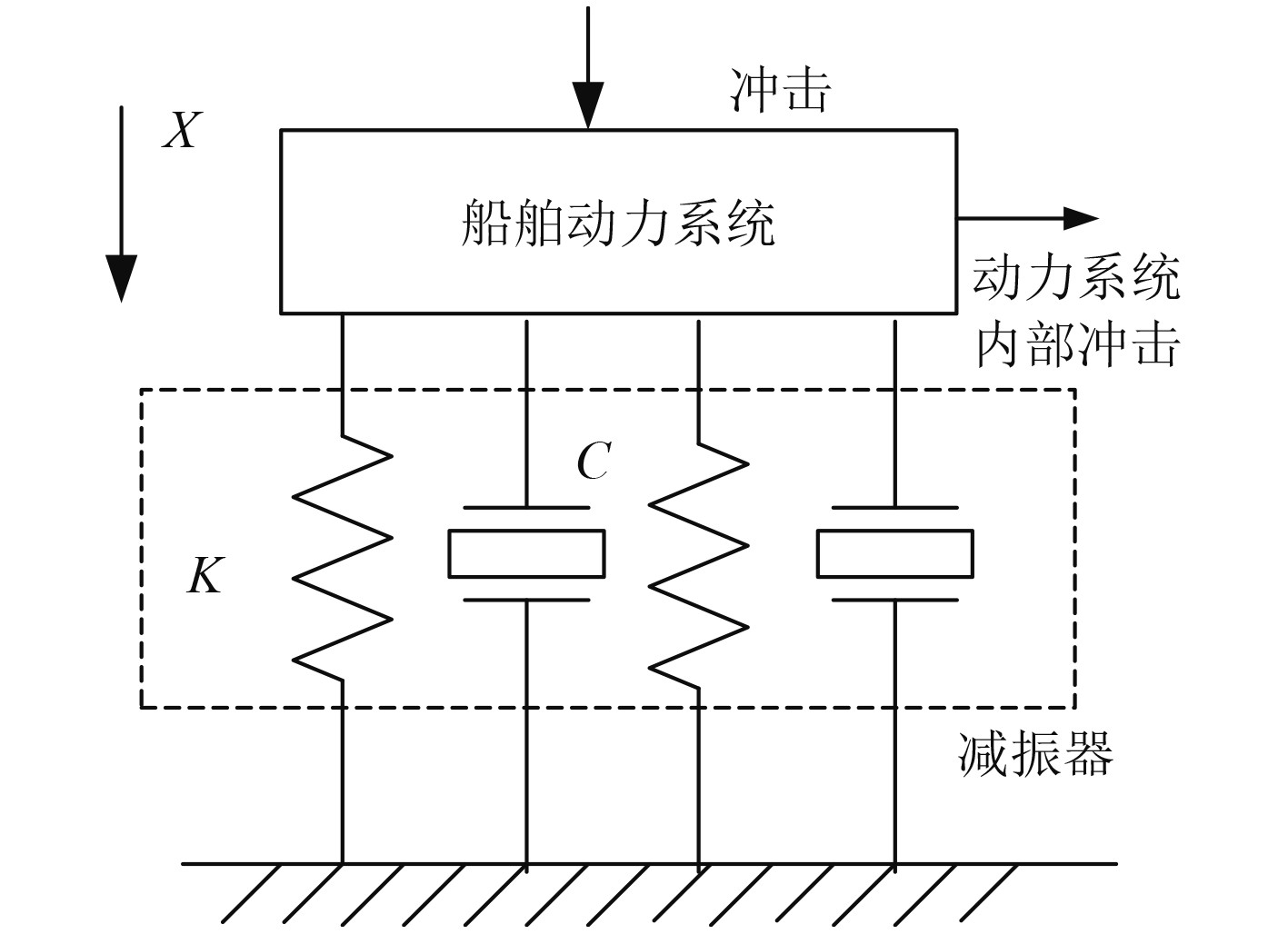
本文采用一种变阻尼元件进行船舶动力系统的隔振,图2为该隔振器的数学模型。
|
图 2 动力系统隔振器的数学模型 Fig. 2 Mathematical model of power system vibration isolator |
如图,振动冲击包含外部振动冲击和系统内部冲击,隔振器由阻尼器和弹性元件构成。
隔振器的数学模型为:
| $ F\cdot\sin\omega t\text{ = }\frac{1}{2}m\frac{\mathrm{d^2}x}{\mathrm{d}t^2}+c\frac{\mathrm{d}x}{\mathrm{d}t^{ }}+k。$ |
其中:
隔振器的幅频、相频特性如下:
| $ \left\{ {\begin{array}{*{20}{c}} {A(s) = \dfrac{1}{{\sqrt {{{\left( {1 - {s^2}} \right)}^2} + {\zeta _0}^2} }}},\\ {\varphi (s) = \dfrac{1}{{\tan ({\raise0.7ex\hbox{${2{\zeta _0}}$} \mathord{\left/ {\vphantom {{2{\zeta _0}} {1 - {s^2}}}}\right.} \lower0.7ex\hbox{${1 - {s^2}}$}})}}} 。\end{array}} \right. $ |
当隔振器处于运动状态时合力为:
| $ F_{A0}=F\sqrt{\frac{1+\left(2\zeta_0\omega/\omega_0\right)^2}{\left[1-\left(\omega/\omega_0\right)^2\right]^2+\left(2\zeta_0\omega/\omega_0\right)^2}}\text{。} $ |
建立船舶主动减振系统的多体动力学模型,假设船舶减振系统的刚体个数为m个,刚体质量为mm,冲击力为Fm,刚度为Km,阻尼为Cm,建立多体动力学模型如下式:
| $ \left\{\begin{array}{*{20}{l}}m_1\ddot{x}_1+C_1(\dot{x}_1-x)+K_1(x_1-x)=F_{1,} \\ ... \\ m_m\ddot{x}_m+C_m(\dot{x}_m-x)+K_m(x_m-x)=F_m ,\\ ... \\ m_0C_0\dot{x}+K_0x=\overline{F}。\end{array}\right. $ |
船舶动力系统主动减振系统的控制系统是其核心模块,系统通常包括传感器、控制器和执行器等组件,能够感知船舶动力系统产生的振动,并采取相应的控制措施来减少或抑制这些振动。
1)传感器
用于监测船舶动力系统的振动情况,通常包括加速度传感器、振动传感器等,这些传感器能够实时地获取振动数据,并将其发送给控制器进行处理。
2)控制器
控制器负责接收传感器传来的振动数据,进行数据处理和分析,并根据预设的控制算法,制定相应的控制策略。控制器还可以根据振动情况调节执行器的工作状态,以实现减振效果[2]。
3)执行器
执行器是根据控制器的指令,实施相应的控制动作。在船舶动力系统主动减振系统中,执行器可能包括液压缸、电动马达等,用于调节船舶动力系统的工作状态,以减少振动。
本文设计的主动控制系统采用X-LMS算法,其原理框图如图3所示。

|
图 3 船舶减振系统的控制器原理图 Fig. 3 Controller schematic diagram of ship vibration reduction system |
建立X-LMS控制器的数学模型为:
| $ \left\{ {\begin{array}{*{20}{l}} {{y_i}(n) = \displaystyle\sum\limits_{i = 0}^{L - 1} {{w_{i,l}}} x(n - l)} ,\\ {{e_j}(n) = {d_j}(n) - \displaystyle\sum\limits_{i = 1}^m {{s_{ij}}} (n)*{y_i}(n)} ,\\ {{W_i}(n + 1) = {W_i}(n) + {\mu _i}\displaystyle\sum\limits_{j = 1}^m {X_{ij}^\prime } (n){e_j}(n)} ,\\ {X_{ij}^\prime (n) = \left[ {x_{ij}^\prime (n),x_{ij}^\prime (n - 1), \cdots ,x_{ij}^\prime (n - L + 1)\left. {} \right]} \right.} ,\\ {x_{ij}^\prime (n) = \displaystyle\sum\limits_{h = 1}^{H - 1} {{{\hat s}_{ij}}} x(n - h)} 。\end{array}} \right. $ |
模型中,作动器的编号为i,传感器的编号为j,作动器产生的响应信号为
船舶减振系统的随机激励是指在海上航行过程中,船舶受到的各种随机波浪、风浪等外界环境因素的影响,导致船舶产生的各种随机振动。这些随机振动具有非常复杂的特性,包括频率、振幅、相位等方面的随机性,因此对船舶减振系统的设计和控制提出了很高的要求。
船舶主动减振系统在处理随机激励和突变信号时,控制器需要具备宽带特性,能够适应不同频率范围内的随机振动,同时,减振系统需要具备自适应特性,能够根据实际情况调整控制策略,以适应不同的随机激励[3]。
在研究主动减振系统的随机激励时,以加速度半正弦波模拟振动信号,定义为:
| $ \frac{{{{\mathrm{d}}^2}y}}{{{\mathrm{d}}{t^2}}} = \left\{ \begin{gathered} 60\sin \left( {\frac{\text{π} }{{0.01}}t} \right),1 < t < 1.01,\\ 0,\;\;\;{\mathrm{else }}。\\ \end{gathered} \right. $ |
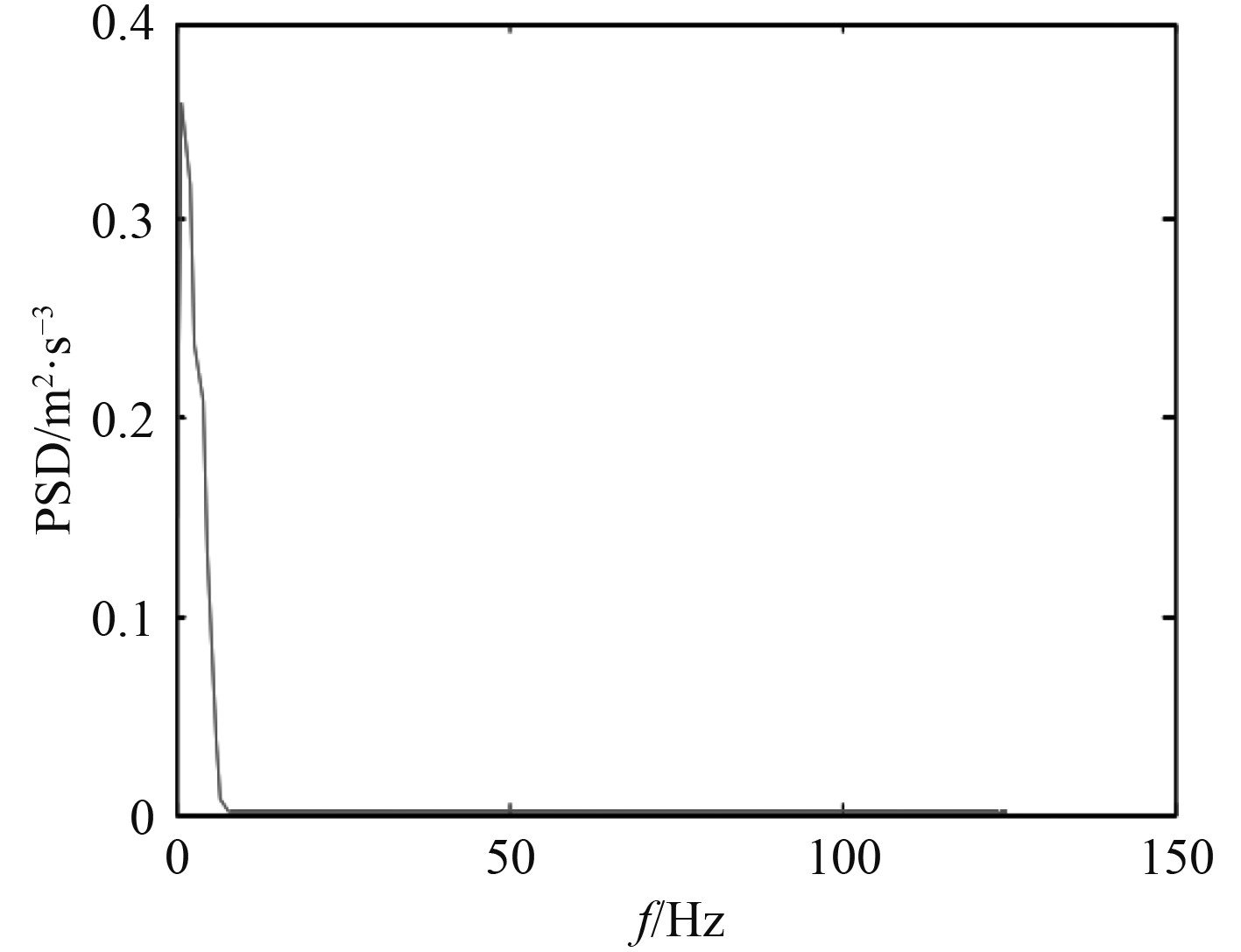
随机激励的频谱曲线如图4所示。
|
图 4 随机激励的频谱曲线 Fig. 4 Spectral curve of random excitation |
可以看出,随机激励在频率10 Hz附近的幅值最高,其余频率下的幅值相对较低。
船舶的振动固有频率按下式计算:
| $ f_1\text{ = }C_V\sqrt{\frac{j_V}{\Delta_mL_{ }^3}}\times0.016\text{。} $ |
其中:
| $ \Delta_m=\left(1.3+\frac{1}{3}\frac{s}{B}\right)M_o\text{。} $ |
其中:
用简谐振动模型来表征减振系统受到的随机激励,如下:
| $ \rho {\text{ = }}\frac{1}{2}{\rho _0}\cos wt \text{,} $ |
式中,
| $ \begin{gathered}\left(m_1+m_2\right)\ddot{x}_1+m_2\ddot{x}_2+R_1\left(x_1,x_2\right)=\frac{1}{2}\rho_0\cos wt-f_1,\\ \left(m_2\right)\dot{x}_1+m_2\ddot{x}_2+R_2\left(x_1,x_2\right)=-\frac{1}{2}\rho_0\cos wt-f_1。\\ \end{gathered} $ |
式中,
针对主动减振系统的随机激励和突变信号进行信号检测的仿真和测试,测试过程采用缩比试验台完成,表1为减振系统突变信号测试的设备物料表。
|
|
表 1 减振系统突变信号测试的设备物料表 Tab.1 Equipment and material list for vibration reduction system mutation signal testing |
测试过程的加速度计用来采集系统的振动,其中船体采集的振动信号为误差信号,动力系统推进主机的振动信号作为参考信号,信号采集后经过低通滤波器处理,进入控制器进行分析和检测[5]。
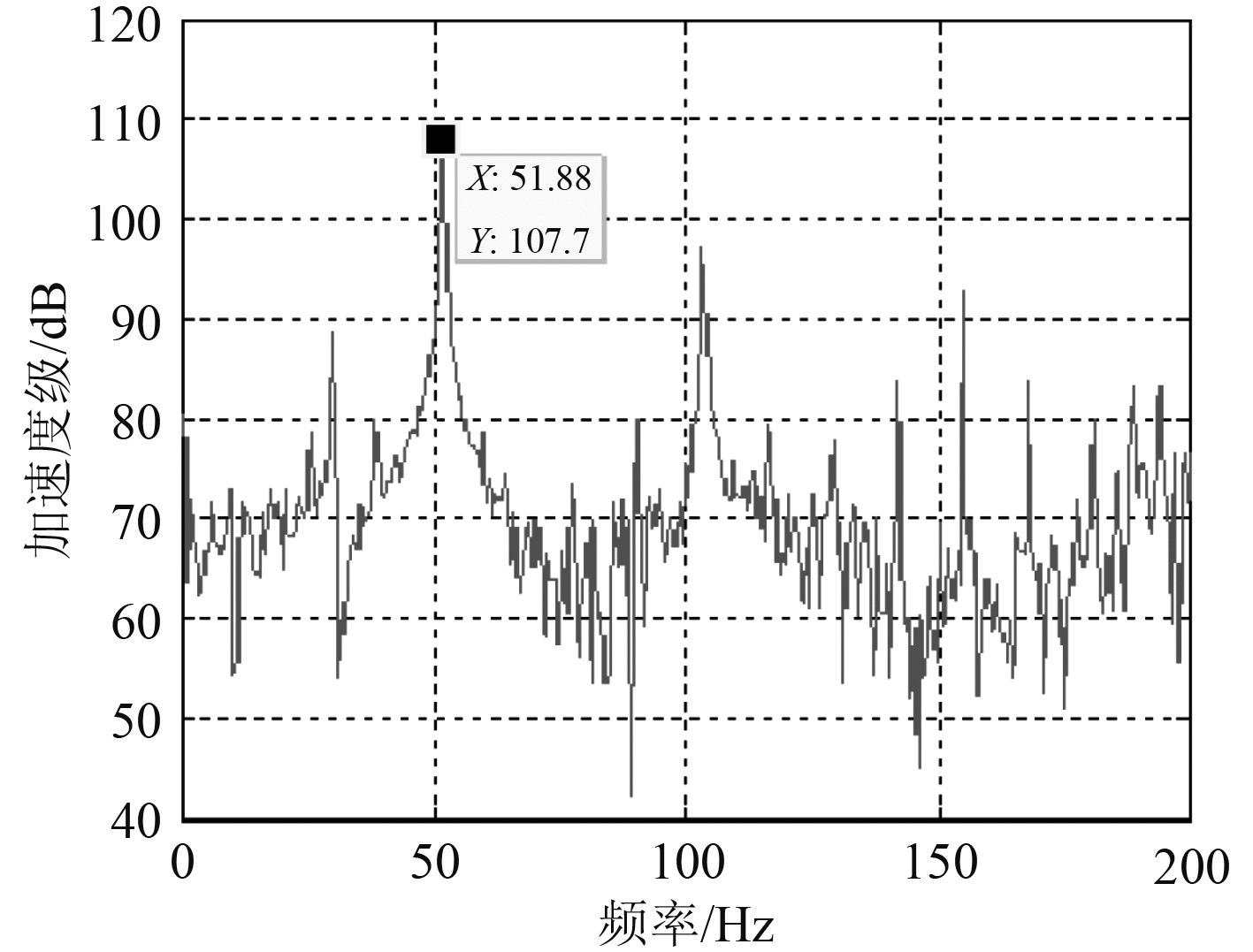
本文进行船舶柴油推进主机转速600 r/min下的船舶动力主机的振动情况测试,系统的激励频率为w=50 Hz,图5为随机激励下船舶动力主机的振动特性曲线,
|
图 5 随机激励下船舶动力主机的振动特性曲线 Fig. 5 Vibration characteristic curve of ship power main engine under random excitation |
可知,随机激励的一阶频率(50 Hz)以及倍频(100 Hz)时,船舶主机的振动最大。
3 结 语船舶动力系统主动减振技术对于改善船体的振动特性,提高船舶结构强度和可靠性有重要意义。本文针对船舶主动减振系统在突变激励下的特性进行研究,建立船舶主动减振系统的数学模型,结合X-LMS算法搭建了系统的控制器,并进行了随机激励下的系统振动测试。
| [1] |
周益品, 翁凌霄. 船舶减速器的振动监测和减振技术[J]. 舰船科学技术, 2020, 42(4): 25−27. ZHOU Yi-pin, WENG Ling-xiao. Ship Science and Technology, 2020, 42(04): 25−27. |
| [2] |
刘伟, 王磊, 俞强等. 船舶推力轴承纵向液压减振技术研究[J]. 舰船科学技术, 2016, 38(5): 59-62. LIU Wei, WANG Lei, YU Qiang, et al. Research on longitudinal hydraulic vibration damping technology of ship thrust bearing[J]. Ship Science and Technology, 2016, 38(5): 59-62. |
| [3] |
廖飞红, 李小平, 陈学东等. 精密主动减振器技术研究现状与进展[J]. 机械科学与技术, 2012, 31(9): 1411-1419. LIAO Fei-hong, LI Xiao-ping, CHEN Xue-dong, et al. Research status and progress of precision active shock absorber technology[J]. Mechanical Science and Technology, 2012, 31(9): 1411-1419. |
| [4] |
李品敏. 船舶振动及减振技术的应用分析[J]. 广东造船, 2008(4): 40-42. LI Pin-min. Application analysis of ship vibration and vibration reduction technology[J]. Guangdong Shipbuilding, 2008(4): 40-42. |
| [5] |
王国治, 孙培林, 方开翔. 阻尼减振技术在传动齿轮装置上的应用研究[J]. 华东船舶工业学院学报, 1994(3): 14-20. WANG Guo-zhi, SUN Pei-lin, FANG Kai-xiang. Research on the application of damping and damping technology in transmission gear device[J]. Journal of East China Institute of Shipbuilding Industry, 1994(3): 14-20. |
 2023, Vol. 45
2023, Vol. 45
