涡旋是波动中一种普遍存在的现象。波在空域的演变是由其相位波前的拓扑电荷所决定的,称一个具有螺旋状相位波前的波为涡旋波。波束绕着涡旋的中心转一整圈,相位以
由于声涡旋波是声波绕着声传播中心旋转,相位以
目前,考虑到水声信道的复杂性,为提升水声通信速率,通常采用时分、码分、频分等方式,实现同时发射不同水声信号,但这些方法会对通信性能产生一定影响。利用声涡旋波的正交特性,使得对于多模态的声涡旋复用系统成立,理论上在接收端可通过一组滤波器对不同模态的声涡旋进行完美分离和检测,从而实现水声通信速率的提升。
1 研究进展1999年,Hefner[2]完成了关于水下超声校准系统的声涡旋理论以及实验的研究,并根据声压和相位得到了声压和角动量的关系。2007年,Thide等首次进行了产生轨道角动量电磁波的仿真研究,开始了轨道角动量应用于无线通信的研究热潮。2008年,Karen Volke[3]解释了自由空间场的声涡旋,理论计算和实验结果表明,声涡旋的角动量能够传递到物质中。2009年,Karen[4]提出了一种螺旋波产生的方法,并对多声源的声波方承诺进行了简化,将其化为含有拓扑电荷的形式。根据两列正交驻波的叠加原理,定性测量出螺旋波的角动量、声压振幅以及声场相位。2011年,张黎坤[5]指出远场散射产生的力矩可以表示为角动量时间平均的积分。2012年,Andreas等[6]对在粘滞液体中的声涡旋进行了研究与实验,得到声压以及声相位的变化曲线。同年,Christine等[7]运用机械的方法,对涡旋声束所含轨道角动量的能量比进行了证明,对变化的拓扑电荷条件下的涡旋传播进行分析,结果表明轨道角动量同线性动量的比值与理论预期值一致。2017年,张翔等[8]利用64元相控阵列,在空气中完成了声轨道角动量复用的通信实验。在只有轨道角动量复用的情况下,实现了8.0±0.4 bit/s/Hz的频谱效率,并且可通过增加复用阶数,实现更高的频谱效率。
2 基于相控阵的声涡旋技术 2.1 相控阵原理等间距圆周相控阵如图1所示,
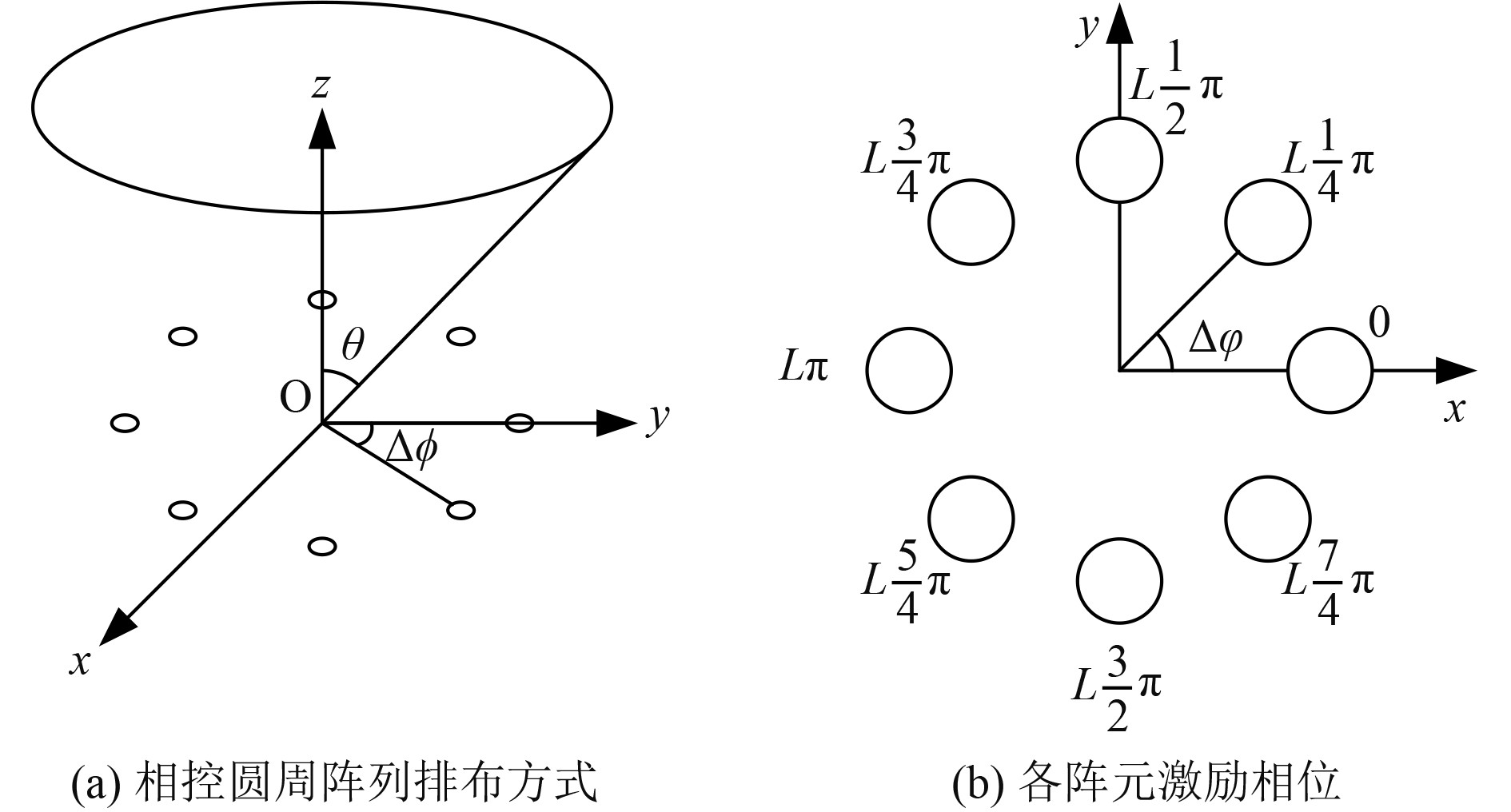
|
图 1 相控阵列示意图 Fig. 1 Schematic diagram of phased array |
| $ \begin{split}\overrightarrow{{r}_{n}} =&\overrightarrow{i}R\mathrm{cos}{\varphi }_{n}\mathrm{sin}\dfrac{\text{π} }{2}+\overrightarrow{j}R\mathrm{sin}{\varphi }_{n}\mathrm{sin}\dfrac{\text{π} }{2}+\overrightarrow{k}\mathrm{cos}\dfrac{\text{π} }{2} =\\&\overrightarrow{i}R\mathrm{cos}{\varphi }_{n}+\overrightarrow{j}R\mathrm{sin}{\varphi }_{n},\end{split} $ | (1) |
任意方向声线的单位矢量为:
| $ \overrightarrow{e}=\overrightarrow{i}\mathrm{sin}\theta \mathrm{cos}\beta +\overrightarrow{j}\mathrm{sin}\theta \mathrm{sin}\beta +\overrightarrow{k}\mathrm{cos}\beta,$ | (2) |
任意方向声线使发射阵第
| $ \begin{split}\mathrm{\xi }\left(n\right) =&\overrightarrow{{r}_{n}}\cdot \overrightarrow{e}=R\mathrm{cos}{\varphi }_{n}\mathrm{sin}\theta \mathrm{cos}\mathrm{\beta }+R\mathrm{sin}{\varphi }_{n}\mathrm{sin}\beta =\\ &R\mathrm{sin}\theta \mathrm{cos}\left({\varphi }_{n}-\beta \right),\end{split} $ | (3) |
在远场各点源声压同幅不同相,因此远场声压可表示为:
| $ {V}_{\varSigma }\left(\beta ,\theta \right)={\sum }_{n=1}^{N}{e}^{-jk\mathrm{\xi }\left(n\right)}={\sum }_{n=1}^{N}{e}^{-j\tfrac{2 \text{π} }{\lambda }R\mathrm{sin}\theta \mathrm{cos}\left({\varphi }_{n}-\beta \right)} 。$ | (4) |
利用轨道角动量可以获得声涡旋波,其工作原理是通过在正常声波上添加一个与空间方位角
| $ U\left(r,\theta \right)=A\left(r\right)\times {e}^{jL\theta } 。$ | (5) |
式中:
在发送端,将携带数据信息的声波,按方位角的变化添加相应的相位旋转,使原本在一个平面上同相发送的声波发生扭曲就形成声涡旋波。在接收端,通过对接收到的声涡旋波按方位角进行反向相位旋转,就可以把扭曲的声涡旋波恢复为正常声波。
图2为声涡旋波的发送和接收过程。

|
图 2 声涡旋波的发送和接收过程 Fig. 2 Transmission and reception process of acoustic vortex wave |
值得注意的是,具有不同模态的声涡旋波相互正交,如模态分别为
轨道角动量的正交性使得对于多模态的声涡旋复用系统成立,理论上在接收端可以通过一组滤波器对不同模态的声涡旋进行完美分离和检测。
2.3 基于相控阵的声涡旋原理发射模态
| $ {V}_{\varSigma }\left(\beta ,\theta \right)={\sum }_{n=1}^{N}{e}^{-j\tfrac{2 \text{π}}{\lambda }R\mathrm{sin}\theta \mathrm{cos}\left({\varphi }_{n}-\beta \right)}{e}^{-j{L\varphi }_{n}} ,$ | (6) |
引入传播距离
| $ {V}_{\sum }\left(\rho ,\alpha ,\theta \right)={\sum }_{n=1}^{N}{e}^{-j\tfrac{2\text{π} }{\lambda }\rho }{e}^{-j\tfrac{2\text{π} }{\lambda }R\mathrm{sin}\theta \mathrm{cos}\left({\varphi }_{n}-\beta \right)}{e}^{-j{L\varphi }_{n}},$ | (7) |
仿真不同发射模态下,声涡旋波的等波阵面旋转形态图,如图3所示。

|
图 3 不同模态的声涡旋波 Fig. 3 Acoustic vortex waves of different modes |
通过公式可看出,声场与传播的直线距离间为线性关系,即公式可改写为:
| $ {V}_{\sum }\left(\rho ,\alpha ,\theta \right)={e}^{-j\tfrac{2\text{π} }{\lambda }\rho }\cdot {V}_{\sum }\left(\alpha ,\theta ,0\right)。$ | (8) |
使用球坐标系,绘制等传播距离下,不同模态的归一化的声场分布图,此时传播距离为接收位置点与发射阵元中心间的直线距离。

|
图 4 球坐标系下等传播距离(ρ)的声场分布图 Fig. 4 Distribution of sound field with equal distance in spherical coordinate system (ρ) |
相控阵列是产生声涡旋波束的典型方法。阵列单元发射相同的信号,但是各阵元之间有相继连续的相位延迟,使得声涡旋波束围绕轴线旋转一周后,相位增加
声涡旋波束可以通过N个阵元的相控圆形阵来产生,使用简单水听器作为阵元,阵元相互之间等间隔均匀分布排列在圆周上,阵列单元被馈送相同的信号,相邻2个阵元的相位差表示为
目前,水声通信所使用的大部分阵列为全向发射接收,而声涡旋通信要求的则是定向发射接收,即只能在固定方向上接收到声涡旋信号,因此对换能器的布放方式有一定要求。相控阵列布放示意图如图5所示。
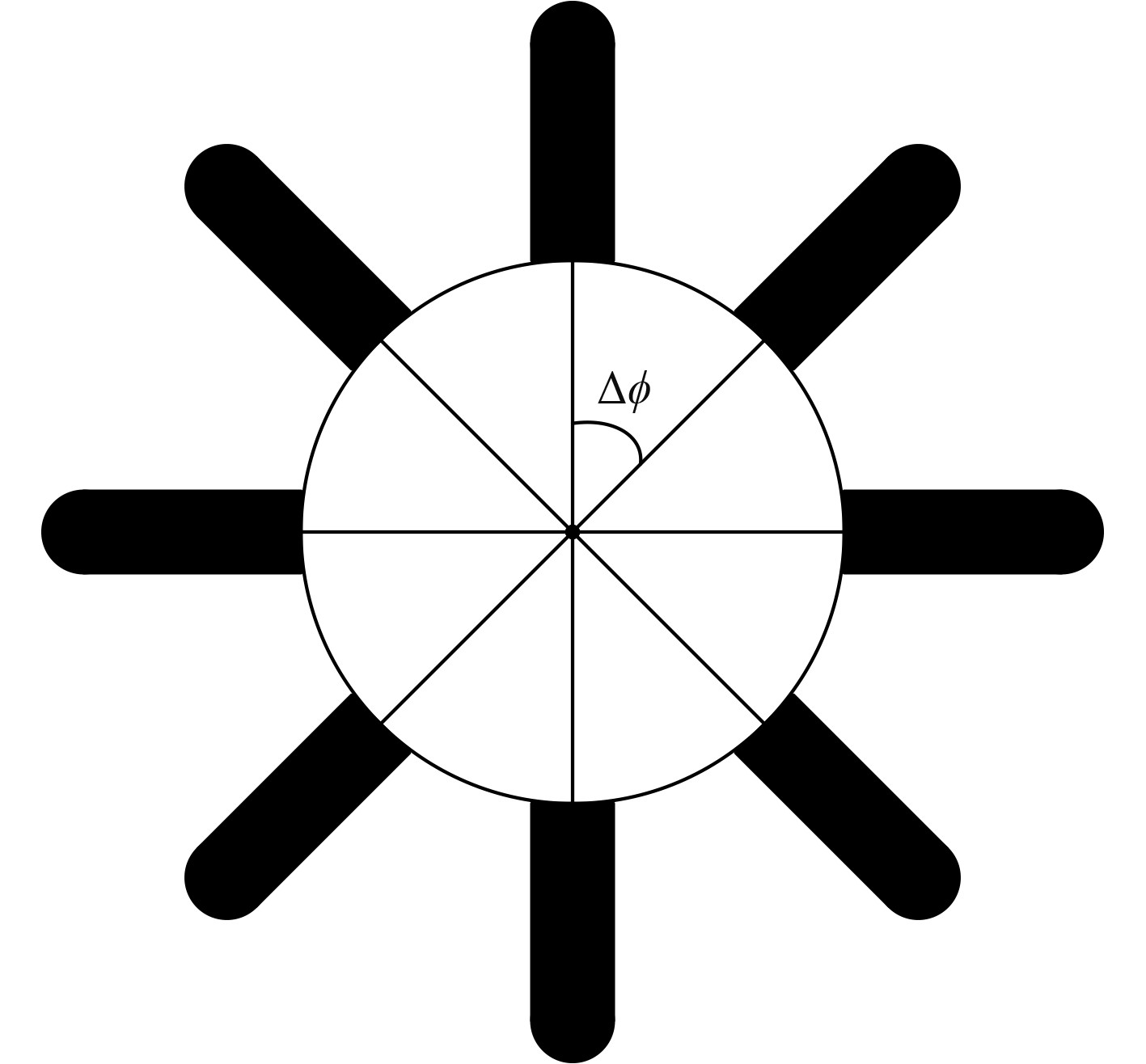
|
图 5 相控阵列示意图 Fig. 5 Schematic diagram of phased array |
根据式(4)可知,声涡旋通信的接收距离与阵列布放半径有关,具体分析如下:
假定发射阵和接收阵间的距离为
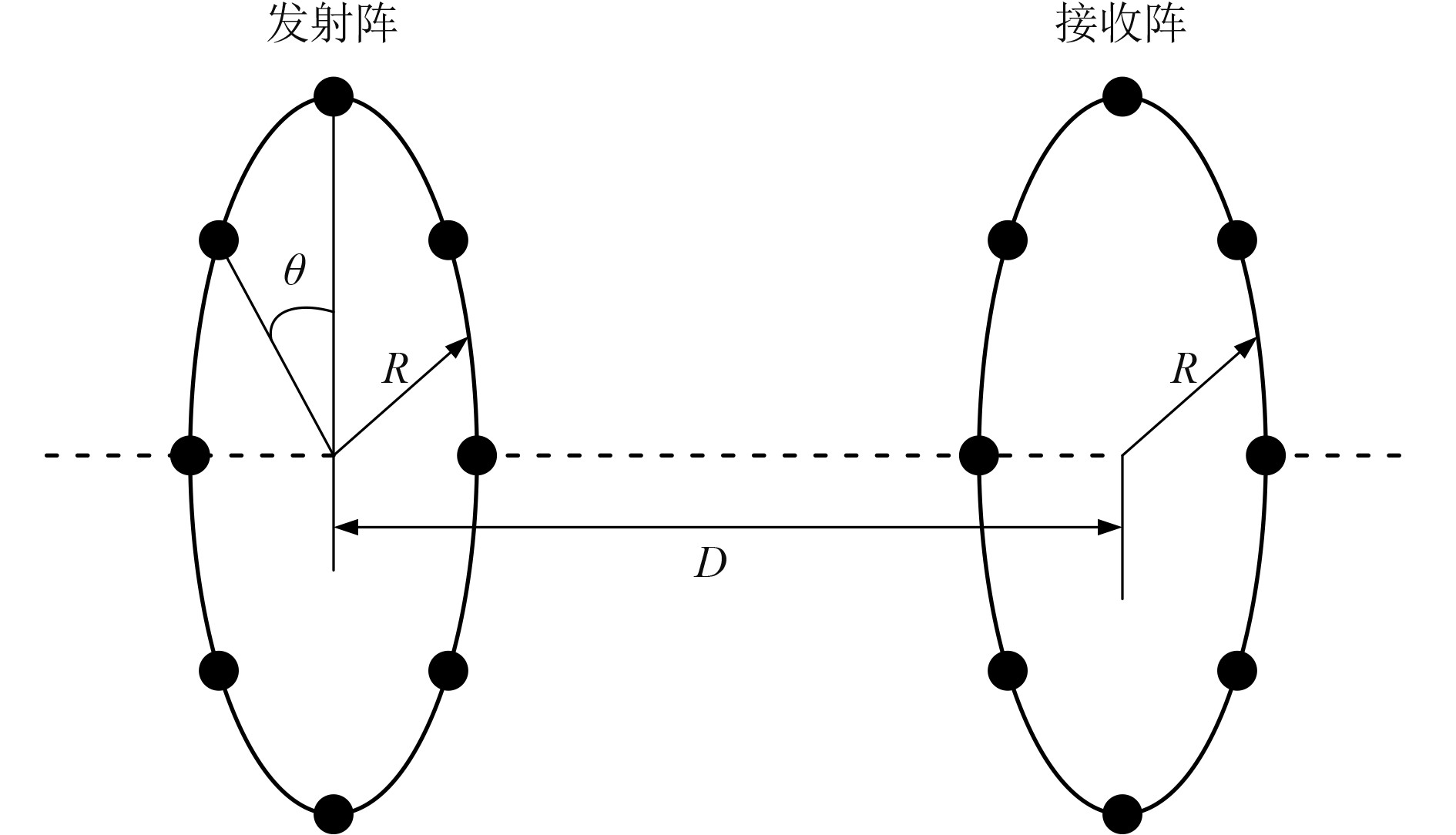
|
图 6 发射阵和接收阵布放示意图 Fig. 6 Layout of transmitting array and receiving array |
计算两阵元间传播距离时延:
| $ \begin{split}c\cdot t=& \sqrt{{\left(R{\cos}{\varphi }_{n}-R{\cos}{\varphi }_{m}\right)}^{2}+{\left(R{\sin}{\varphi }_{n}-R{\sin}{\varphi }_{m}\right)}^{2}+{D}^{2}}=\\& \sqrt{{4R}^{2}{{\sin}}^{2}\left(\frac{\left(n-m\right)\text{π} }{N}\right)+{D}^{2}}。\\[-15pt]\end{split} $ | (9) |
可知,相邻2个阵元的相位差:
| $ \Delta {\varphi }=\dfrac{2\text{π }{L}}{{N}},$ | (10) |
当发射模态
| $ \Delta \tau =\frac{\sqrt{{3R}^{2}+{D}^{2}}-D}{c} 。$ | (11) |
由于声信号采集处理时会被转换为数字信号,则要求时间间隔
同理,计算当发射模态
可知,采样频率、阵元半径不变,随着发射模态绝对值的增大,传播距离减小。经计算得到布放距离与发射模态绝对值间的对应关系,如表1所示。
|
|
表 1 布放距离与发射模态绝对值间的对应关系 Tab.1 Corresponding relationship between distance and absolute value of mode |
仿真柱坐标系下等传播距离(坐标轴z值不变)的声场幅度和相位的分布图,分别如图7和图8所示。其中,横纵坐标表示该接收平面上的位置,颜色标尺从上到下表示声压幅值或相位的大小,仿真三维图时,不同模态值都使用了同一颜色标尺,使得同一图片对比。
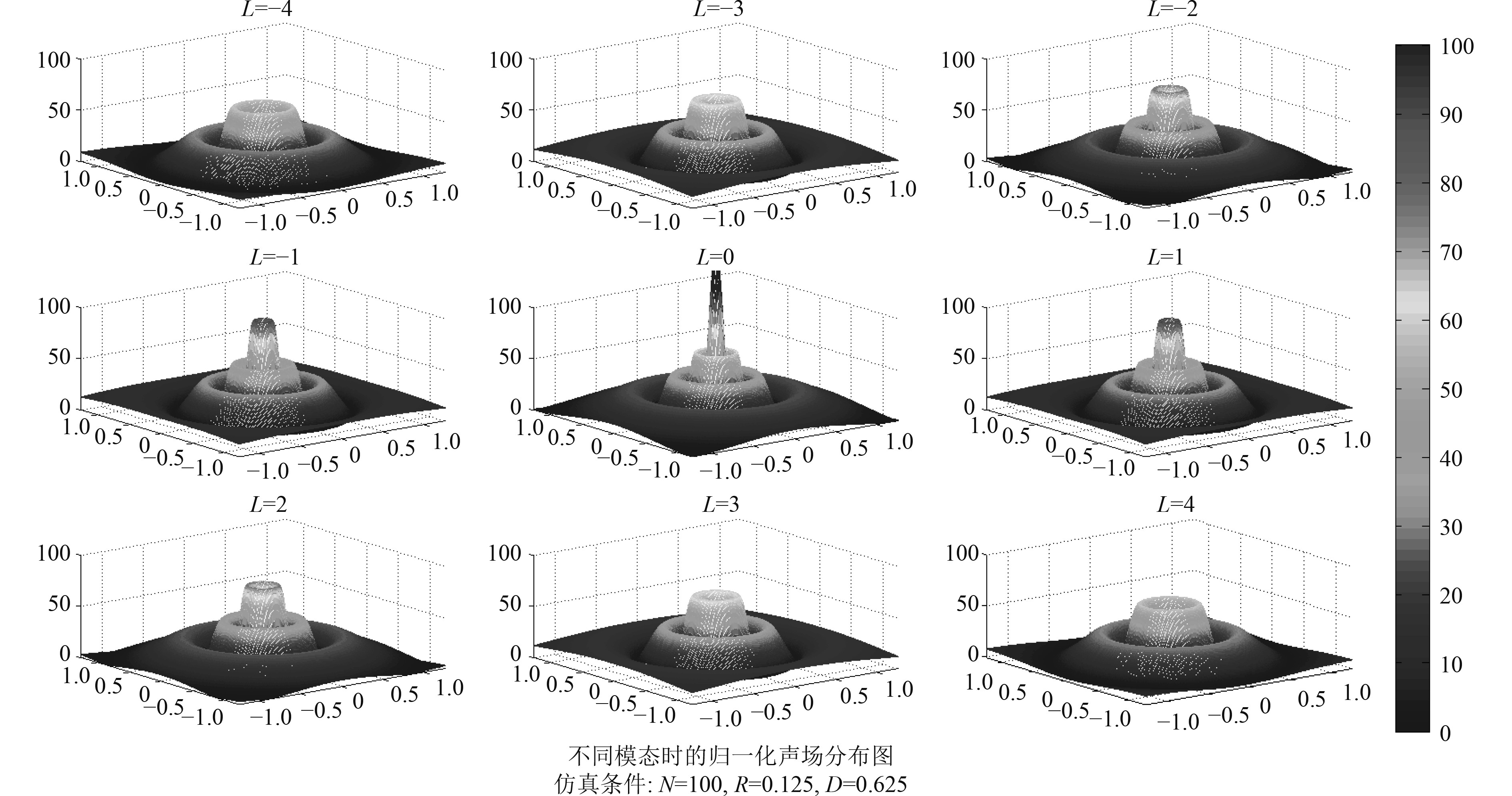
|
图 7 柱坐标系下等传播距离的声场幅度分布图 Fig. 7 Distribution of sound field amplitude with equal distance in cylindrical coordinate system |

|
图 8 柱坐标系下等传播距离的声场相位分布图 Fig. 8 Distribution of sound field phase with equal distance in cylindrical coordinate system |
由声涡旋波声场幅值和相位的分布图可看出:
1)中心位置的幅值非常小,即存在相位奇点;
2)模态数绝对值相同时,声涡旋波的幅值分布相同,相位涡旋方向相反;
3)随着模态数的增加,主瓣波束宽度变化。
仿真声涡旋波的波束宽度和方向图,如图9所示。
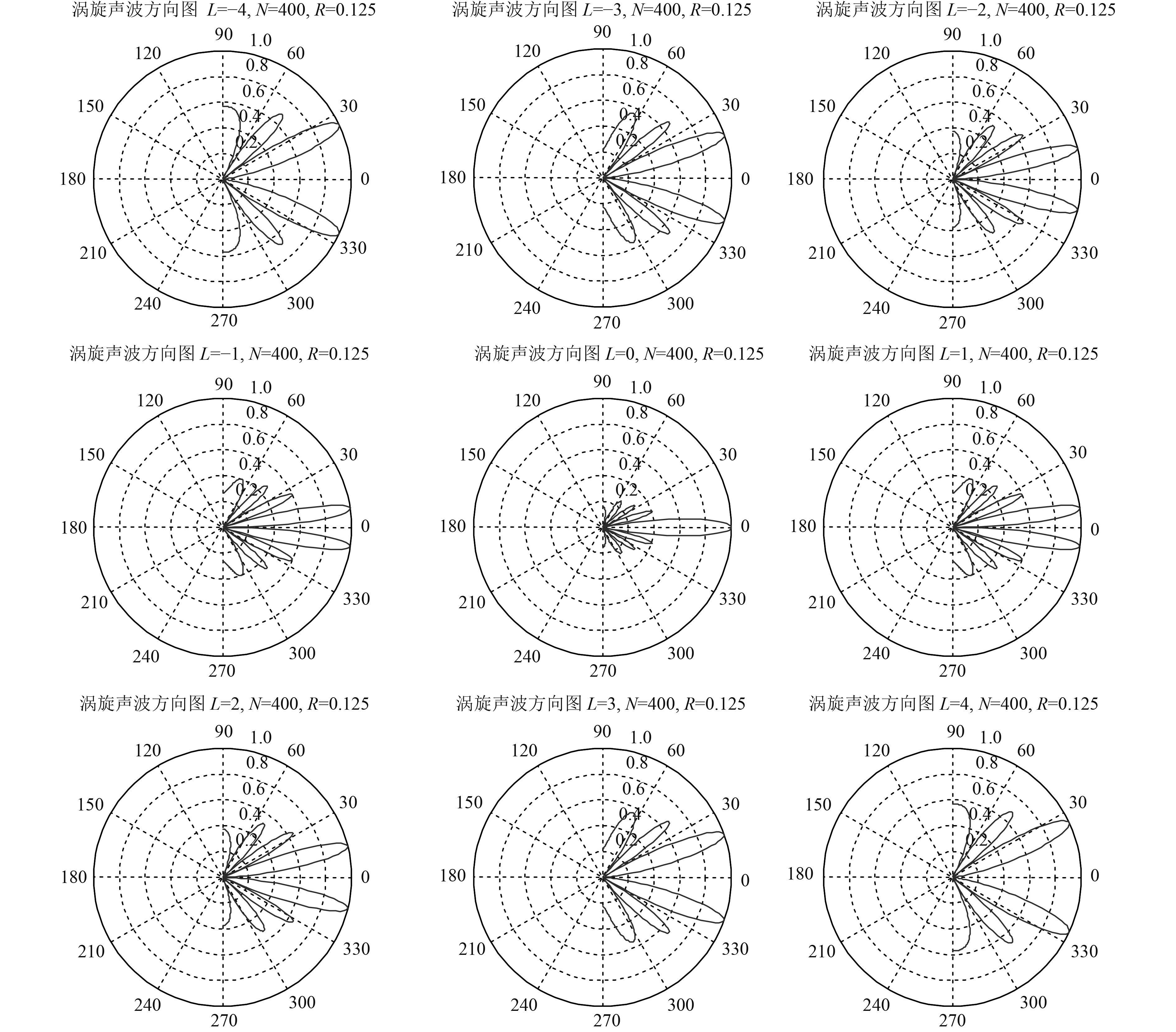
|
图 9 方向图和主瓣波束角 Fig. 9 Directional pattern and main lobe beam angle |
计算得到不同模态数时,其主瓣方向角和峰值如表2所示。
|
|
表 2 不同模态下的主瓣峰值和波束角 Tab.2 Main lobe peak and beam angle under different modes |
由仿真结果可看出:随着模态数的增大,产生的声涡旋波主瓣波束角增大,主瓣峰值减小。
4.1.2 声涡旋高速测试需注意的是,当前仿真条件下,收发阵列间距没有远大于阵元半径,因此仿真不能直接进行远场分析,需分别计算当前阵元与所有发射阵元的传播距离,得到时延差,在附加到发射阵各阵元信号上。
1)单独发射一个模态
生成发射信号,发射阵分别发射单个模态L=−1、0、+1时的声涡旋信号,对接收阵接收到的信号进行处理,得到相应的接收信号,进行解码验证。解码接收信号,均可得到正确的编码信息。
调整不同接收距离,并在仿真信号从发射阵到接收阵的传输过程中,叠加不同信噪比的白噪声,得到不同发射模态通信信号。仿真结果表明,使用声涡旋方式,单独发射一个模态时,通信性能没有损失。
2)同时发射2个模态
将2种模态的发射信号直接时域叠加,作为发射阵的发射信号。分别对接收阵接收到的信号进行
调整不同的接收距离,并在仿真信号从发射阵到接收阵的传输过程中,叠加不同信噪比的白噪声,得到不同发射模态通信信号。仿真结果表明,使用声涡旋方式,单独发射一个模态时,通信性能没有损失。
可得结论:2个不同模态信号同时发射时,相互间没有干扰,即验证了不同发射模态的2个信号完全正交。
4.2 实验室验证在实验室环境,分别在空气中和水桶中对声涡旋阵列进行实际测试。由于实验室环境空气中存在噪声,换能器的性能在空气中和在水中效果不同,设定空气中收发阵列布放间距为0.5 m,水桶中的阵列布放间距为0.5 m。
4.2.1 空气测试按照试验条件的要求摆放水声高速声涡旋收发阵,连接录音机后,发射阵分别发射试验模态L=−1、0、+1时的水声高速声涡旋信号,对接收阵接收到的信号进行处理,得到相应的接收信号,进行解码验证。
发射L=−1的水声高速声涡旋信号时,接收到的水声高速声涡旋信号信噪比为9.43 dB,解码信息完全正确。发射
按照要求摆放声涡旋收发阵,连接录音机后,发射阵分别发射试验模态L=−1、0、+1时的水声高速声涡旋信号,对接收阵接收到的信号进行处理,得到相应的接收信号,进行解码验证。
发射L=−1的水声高速声涡旋信号时,接收到的水声高速声涡旋信号信噪比为21.29 dB,解码信息完全正确。发射
本文结合轨道角动量原理,研究基于相控阵列的水声高速声涡旋波基本原理,仿真了其声场分布,研究分析了幅值和相位随模态变化的变化趋势。对水声高速声涡旋信号进行计算机仿真,从理论层面验证了不同模态的水声高速声涡旋波的正交特性,测试了多模态的水声高速声涡旋复用系统的通信性能,保证通信性能不变的前提下,实现了通信速率的提高。在空气中和水中分别试验验证同步发射2种不同模态时的水声高速声涡旋信号,试验结果显示通信性能不变时,通信速率提高1倍。后续项目研究可在此基础上,进一步增加多模态水声高速声涡旋复用系统所同步发射的模态数量,实现通信速率的进一步提升。
| [1] |
ALLEN L, BEIJERSBERGEN M W, SPREEUW R J C, et a1. Orbital angular momentum of light and the transformation of Leaguered-Gaussian laser modes[J]. Physical Review A, 1992, 45(11): 8185-8189. DOI:10.1103/PhysRevA.45.8185 |
| [2] |
HEFNER B T, MARSTON P L. An acoustical helicoidal wave transducer with applications for the alignment of ultrasonic and underwater systems[J]. The Journal of the Acoustical Society of America, 1999, 106: 3313. DOI:10.1121/1.428184 |
| [3] |
VOLKE-SEPULVEDA K, SANTILLAN A O, BOULLOSA R R. Transfer of angular momentum to matter from acoustical vortices in free space[J]. Physical Review Letters, 2008, 100(2): 24302. DOI:10.1103/PhysRevLett.100.024302 |
| [4] |
SANTILLAN A O, VOLKE-SEPULVEDA K. A demonstration of rotating sound waves in free space and the transfer of their angular momentum to matter[J]. American Journal of Physics, 2009, 77: 209. DOI:10.1119/1.3056580 |
| [5] |
ZHANG L, MARSTON P L. Angular momentum flux of no paraxial acoustic vortex beams and torques on axisymmetric objects[J]. Physical Review E, 2011, 84(6): 65601. DOI:10.1103/PhysRevE.84.065601 |
| [6] |
ANHAUSER A, WUNENBURGER R, BRASSELET E. Acoustic rotational manipulation using orbital angular momentum transfer[J]. Physical Review Letters, 2012, 109(3): 34301. DOI:10.1103/PhysRevLett.109.034301 |
| [7] |
DEMOTE C E M, YANG Z, VOLOVICK A, et a1. Mechanical evidence of the orbital angular momentum to energy ratio of vortex beams[J]. Physical Review Letters, 2012, 108(19): 194301. DOI:10.1103/PhysRevLett.108.194301 |
| [8] |
CHENG Zhi Shi, XIANG Zhang. High-speed acoustic communication by multiplexing orbital angular momentum.[J]. PNAS, 2017, 114(28): 7250-7253. DOI:10.1073/pnas.1704450114 |
 2023, Vol. 45
2023, Vol. 45
