0 引　言

波束形成作为声呐在水下探测中用以提高阵列输出信号增益的基本方法，一直是研究的重点方向。传统波束形成算法归纳起来主要包括经典常规波束形成方法、分裂阵波束形成方法、自适应波束形成方法三类^[1]。常规波束形成基于全阵列，优点是稳健性好、计算量小，缺点是其空间分辨力受限于瑞利限，且动态响应受旁瓣影响大^[2]；分裂阵波束形成是将线列阵分为若干个子阵，通过子阵间互相关等处理，实现测向^[3]；自适应波束形成是近年来的研究热点，典型的自适应波束形成算法有MVDR算法^[4-5]、MUSIC算法^[6-7]、ESPRIT算法^[8]等，但这些算法对接收信号信噪比和阵列形态要求较高。综上，现有的波束形成算法的稳健性、高分辨力往往不可同时兼顾。

本文针对传统波束形成算法中旁瓣抑制问题，对均匀线阵的波束指向性特点进行分析，将常规波束形成作为一个线性系统，以常规波束形成输出结果作为反卷积算法的输入，利用Richardson-Lucy迭代^[9]求解点声源散射函数，对常规波束形成输出结果与声源点散射函数进行卷积运算，实现水下目标方位估计。仿真对比常规波束形成和反卷积波束形成目标角度分辨力和目标噪声包络谱输出信噪比，并对湖试数据进行处理对比，验证了反卷积波束形成算法的弱目标检测和多目标分辨能力。

1 理论基础 1.1 均匀线阵指向性

均匀线阵自然指向性可以用公式表示为^[10]：

$ R(\theta ) = \left| {\frac{{\sin \left( {\displaystyle\frac{{N{\text π} d}}{\lambda }\sin \theta } \right)}}{{N\sin \left( {\displaystyle\frac{{{\text π} d}}{\lambda }\sin \theta } \right)}}} \right| 。$

(1)

其中： $ N $ 为阵元个数； $ d $ 为阵元间距； $ \lambda $ 为信号的波长。可以看出，线阵输出的幅度与信号入射角度 $ \theta $ 有关。当 $({{{\text π} d} \mathord{\left/ {\vphantom {{{\text π} d} \lambda }} \right. } \lambda })\sin \theta = \pm m{\text π} (m = 0,1,2, \cdots )$ ，线阵自然指向性对应极大值，其在 $ \sin \theta $ 轴上的坐标为：

$ \sin \theta = \pm m\frac{\lambda }{d} ，$

(2)

自然指向性函数的零点为：

$ \sin (\displaystyle\frac{{N{\text π} d\sin \theta }}{\lambda }) = 0 \text{，} \sin \theta = \pm m\frac{\lambda }{{Nd}}，m = 1,2,... ，$

(3)

则第一个零点的位置为 $ \displaystyle\frac{\lambda }{{Nd}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} $ ，且

$ \Delta \sin \theta = 2\frac{\lambda }{{Nd}}{\kern 1pt} 。$

(4)

$ \Delta \sin \theta $ 即为主波束宽度（两相邻第一零点的距离），又被称为瑞利限，可以表征基阵的多目标分辨能力。阵元个数 $ N $ 、阵元间距 $ d $ 和接收信号波长 $ \lambda $ 对波束形成算法有很大影响。

1.2 反卷积波束形成算法

当信号的入射角度不为 $ {0^ \circ } $ 时，即相邻阵元间存在相移 $ \beta $ 或时延 $ \tau $ 时，线阵的指向性可以用公式表示为：

$ R(\theta ) = \left| {\frac{{\sin \left( {\displaystyle\frac{{N(\varphi - \beta )}}{2}} \right)}}{{N\sin \left( {\displaystyle\frac{{(\varphi - \beta )}}{2}} \right)}}} \right| ，$

(5)

指向性函数的零点变为：

$ \frac{N}{2}(\varphi - \beta ) = \pm m{\text π} ，m = 1,2,... ，$

(6)

即

$\frac{N}{2}\left( {\frac{{2{\rm{ }}{\text π} d}}{\lambda }\sin \theta - \beta } \right) = \pm m{\text π} ，m = 1,2,... ，$

(7)

此时的 $ \theta $ 记为 $ {\theta _0} $ ，则

$ \sin {\theta _0} = \beta \frac{\lambda }{{2{\text π} d}} \pm m\frac{\lambda }{{Nd}} ，m = 1,2, \cdots 。$

(8)

从式（3）和式（8）的对比可知，当相邻阵元间存在相移或时延时，线阵指向性函数的零点与主极大位置在 $ \sin \theta $ 轴上位移相同数值，即常规波束形成具有线性，可以将其看做是一个线性系统，若声信号以角度 $ {\theta _0} $ 入射，该线性系统的输出则可相当于线阵自然指向性函数在 $ \sin \theta $ 轴上产生了 $ \sin {\theta _0} $ 的位移。

在常规波束形成为一个线性系统的设定条件下，其输出结果可以表示为声源的点散射函数与阵列指向性的线性卷积运算，如下式：

$ r(\sin \theta ) = s(\sin \theta ) * R(\sin \theta )。$

(9)

式中： $ \theta $ 为入射角度；*表示卷积运算； $ r(\sin \theta ) $ 为常规波束形成的输出； $ s(\sin \theta ) $ 为声源的点散射函数； $ R(\sin \theta ) $ 为基阵的指向性函数。在已知 $ r(\sin \theta ) $ 和 $ R(\sin \theta ) $ 的前提条件下，将两者反卷积，即可去除阵列指向性函数 $ R(\sin \theta ) $ 的影响，近似得到声源的点散射函数，获取更窄的主瓣和更低的旁瓣。

采用Richardson-Lucy公式对声源点散射函数进行求解可得：

$ \begin{aligned} & {s^{(n + 1)}}(\sin \theta ) = {s^n}(\sin \theta )\int_{ - \infty }^\infty \times\\ & {\frac{{R(\sin \alpha - \sin \theta )}}{{\displaystyle\int_{ - \infty }^\infty {R(\sin \alpha - \sin \theta ) \cdot } {s^n}(\sin \theta ){\rm{d}}\sin \theta }}} r(\sin \alpha ){\rm{d}}\sin \alpha 。\end{aligned} $

(10)

式中： $ \mathop {\lim }\limits_{n \to \infty } {s^n}(\sin \theta ) = \arg {\min _s}L(r(\sin \theta ),{r^n}(\sin \theta )) $ ； $ n $ 为迭代的次数； $ r(\sin \alpha ) $ 为 $ {s^n}(\sin \theta ) $ 和 $ R(\sin \theta ) $ 相卷积的运算结果。从式（10）分析可看出，迭代次数 $ n $ 对声源点散射函数有影响，当迭代次数越大，声源点散射函数越趋近于真实的声源分布。

均匀直线阵中第 $n$ 个阵元接收到的舰船辐射噪声可以用公式表示为：

$ {x_n}(t) = \sum\limits_{i = 1}^K {{s_i}(t)} {e^{ - j\omega {\tau _{ni}}}} + {\rm nois}{e_n}(t), i = 1,2,...,K，$

(11)

式中， ${\rm nois}{e_n}(t)$ 为背景噪声。第 $n$ 个阵元接收的第i个信号相对参考阵元的时延 ${\tau _{ni}}$ 如下式：

$ {\tau _{ni}} = \frac{{d(n - 1)\sin {\theta _i}}}{\lambda } 。$

(12)

式中， ${\theta _i}$ 为第i个信号的波达角度。

由式（12）可以看出，均匀线阵各阵元接收到的信号时延随信号入射角度的变化而变化。

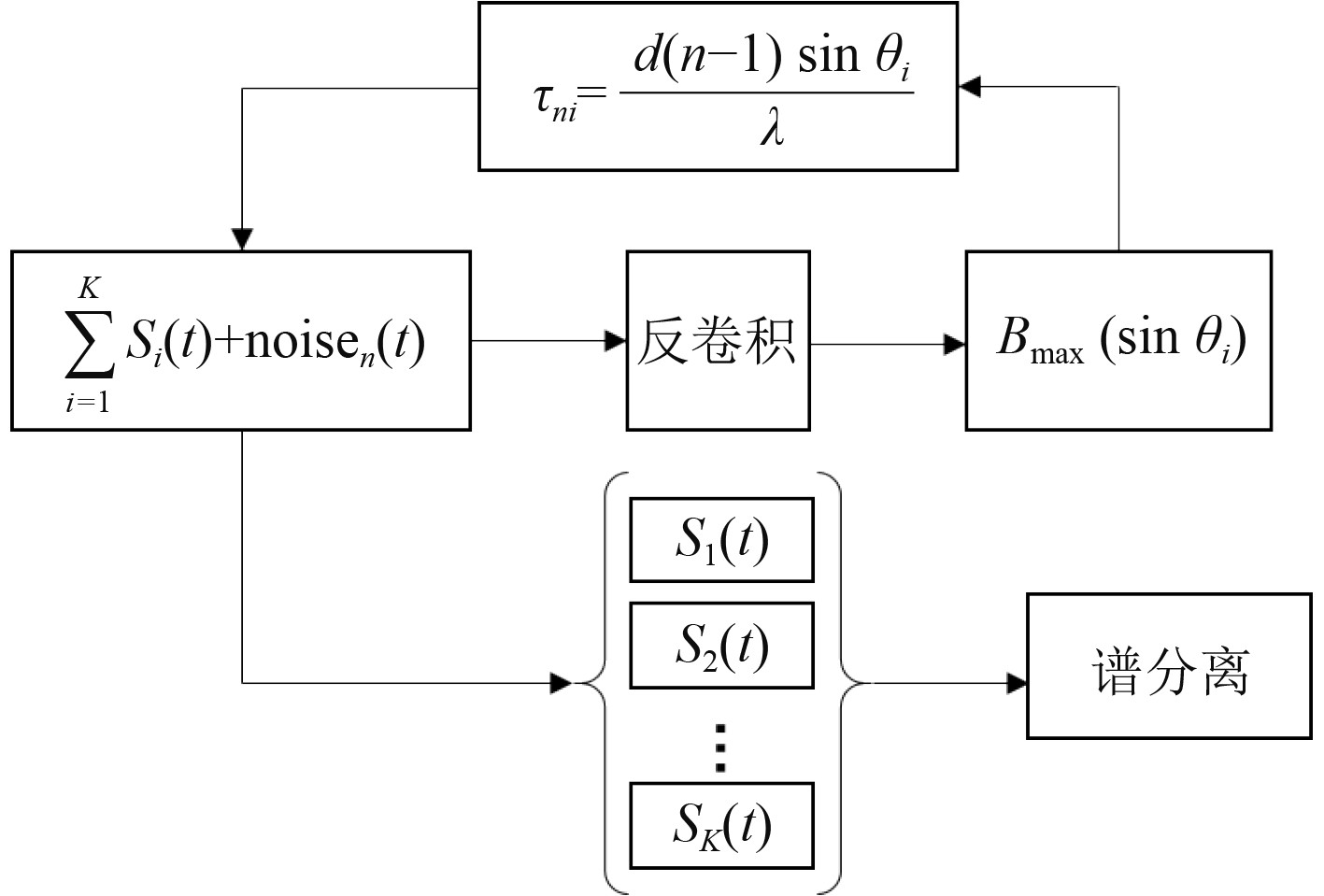
当空间中存在多个目标时，利用反卷积波束形成的高分辨特性，估计各个目标的波达角度，然后根据声波入射角度与时延的对应关系，对各个阵元接收的舰船辐射噪声进行时延补偿，补偿后的信号滤除了背景噪声和其他干扰信号的影响，各阵元时延补偿后的信号相位对其、累加，即可得到纯净的目标辐射信号。最后计算该信号的调制谱，实现多目标的调制谱分离，提高目标检测性能，具体算法流程如图1所示。

2 反卷积波束形成高分辨仿真分析 2.1 角度分辨力仿真对比

仿真条件：采用48阵元的均匀直线水听器阵，相邻阵元间距0.5 m，入射信号为舰船辐射噪声，假定信噪比为10 dB，反卷积瑞利迭代次数为200次。图2给出了2种方法角度分辨力的比较图，其中横轴为角度，纵轴为归一化波束形成输出幅度。

从图2可知，反卷积波束形成的主瓣宽度比常规波束形成更窄，当阵元个数相同时，反卷积波束形成相比常规波束形成拥有更优的角度分辨能力。

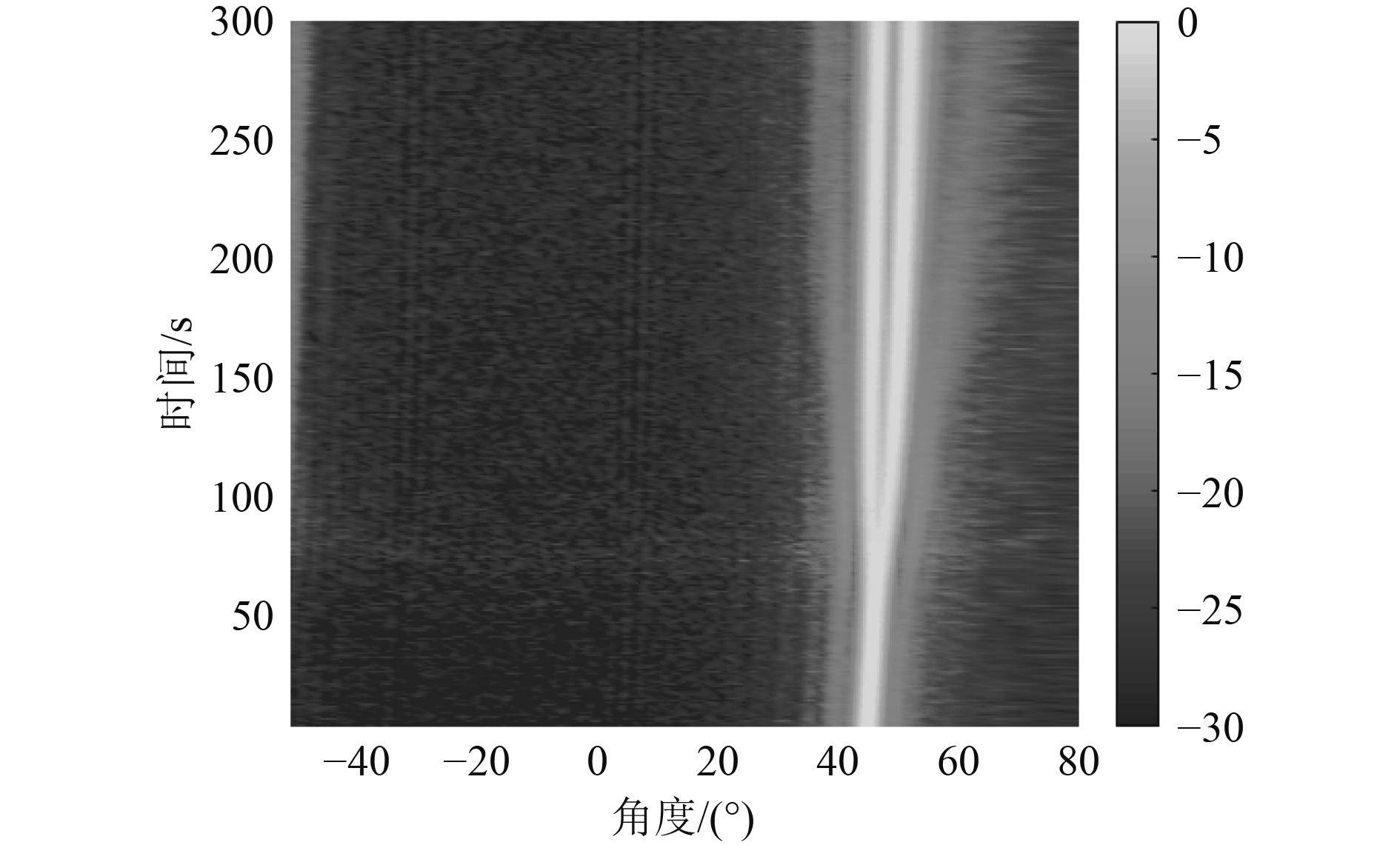
图3和图4仿真分析了反卷积波束形成和常规波束形成算法的多目标角度分辨力。0～76 s时，2个目标相距很近，无论是反卷积还是常规算法都无法将二者分开，随着目标的运动，角度差别越来越大，反卷积方法的分辨能力增强，从图3清晰可看到2个目标的运动角度，而图4中，2个波束对应的主瓣较宽且叠加在一起，无法准确分辨2个目标的到达角度。反卷积波束形成角度分辨力虽然具有一定局限性，但是整体计算效果优于常规波束形成。

2.2 包络谱分离仿真对比

考虑2个等强度入射的舰船辐射噪声信号，信号1的波达角度为2.3°，基频为17 Hz，信号2的波达角度为4.6°，基频为47 Hz，阵元个数为48，间距为0.5 m，分析的信号带宽为1～2 kHz，信噪比为0 dB，进行200次反卷积波束形成瑞利迭代。

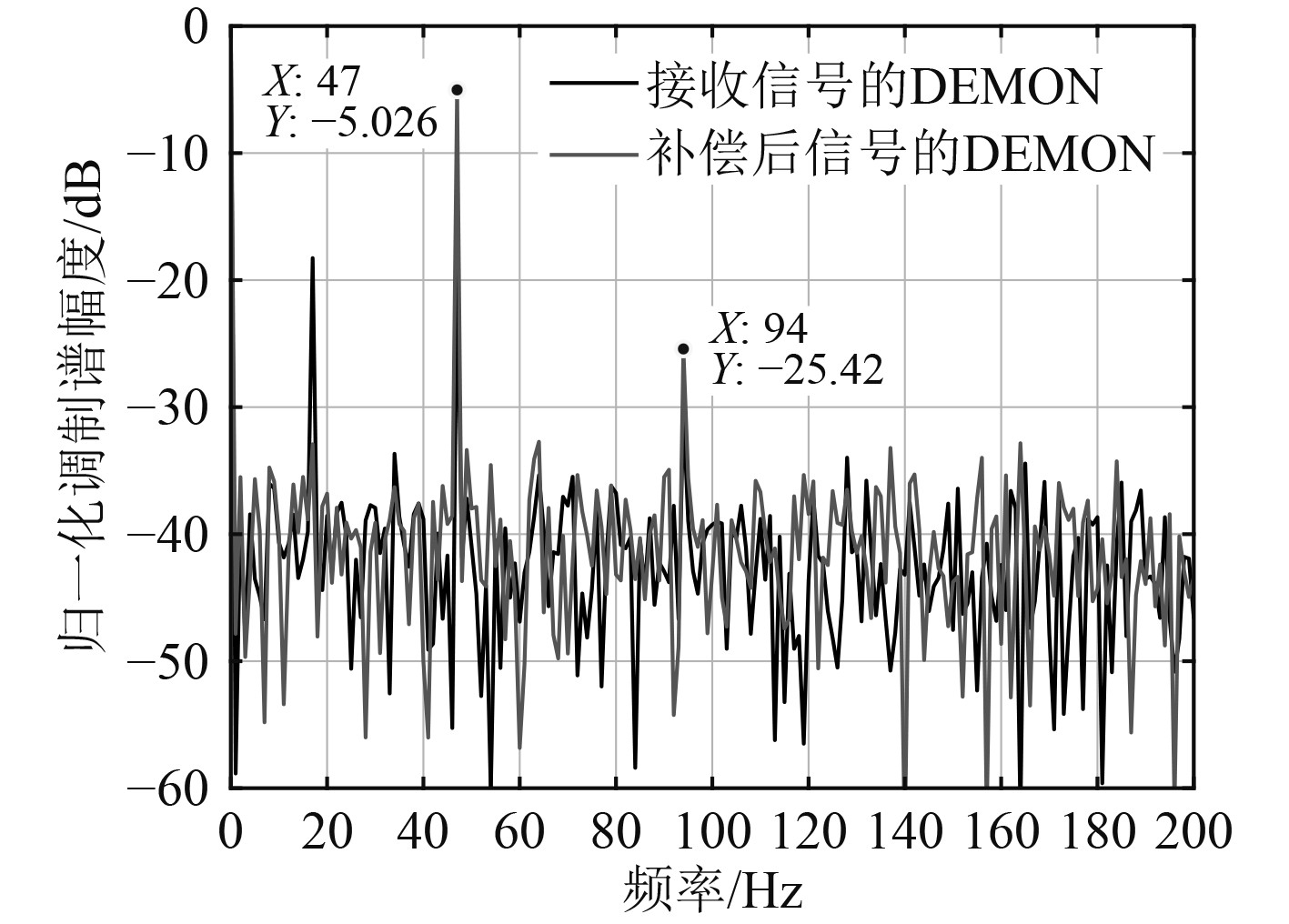
利用补偿后的信号提取得到的信号1和信号2的DEMON谱如图5和图6所示。从图中可以清晰地看到，阵元接收到的混合信号的包络谱被准确地分离开来，而且由于阵列处理的优势，分离后的包络谱的基频幅度增加，包络谱的输出信噪比较混合信号获得了约14 dB的增益。

3 反卷积波束形成高分辨湖试验证

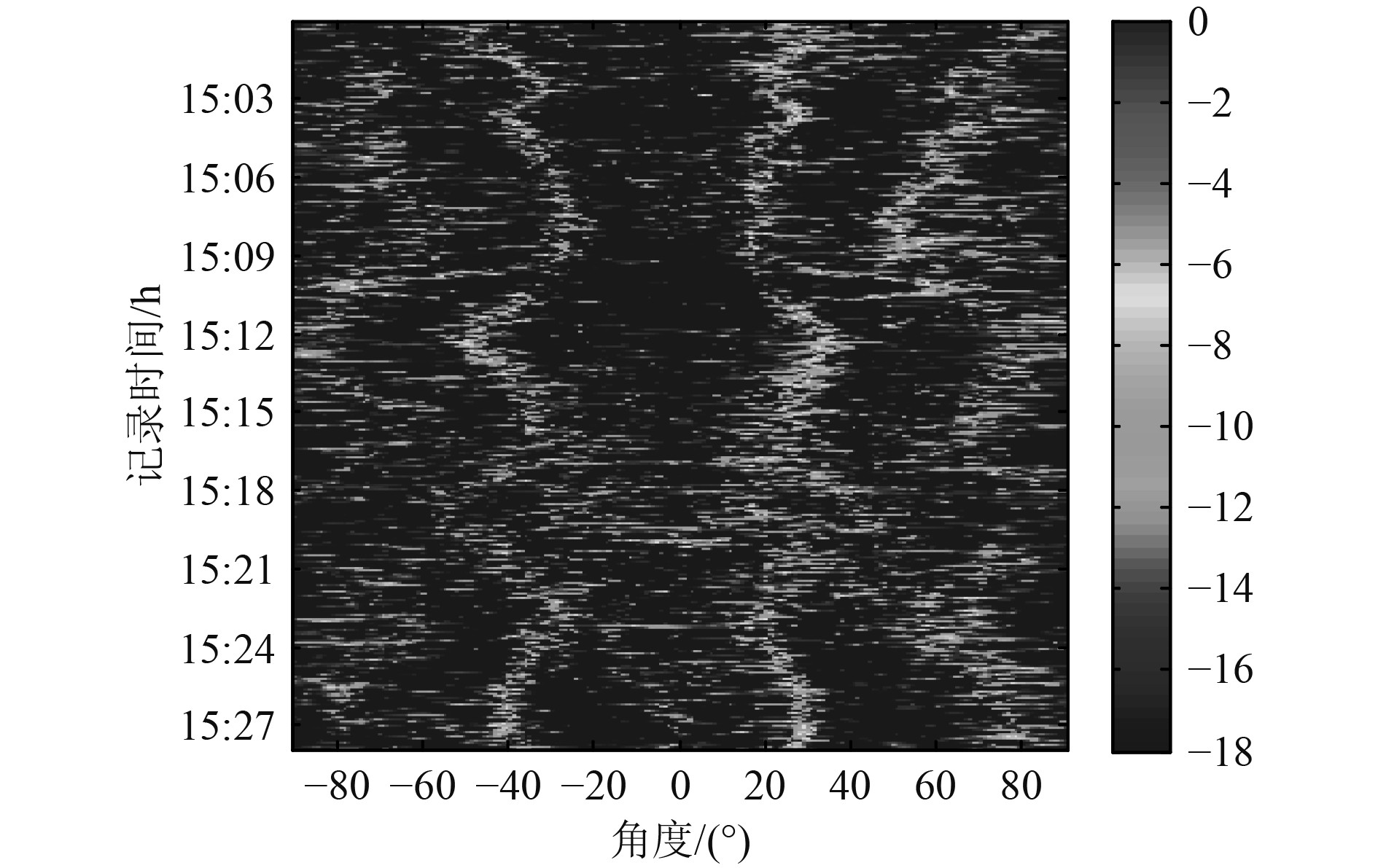
利用反卷积波束形成和常规波束形成处理湖试数据，对比结果如图7和图8所示。从图7可以看到，3条明显的亮线，由左至右分别代表船辐射噪声的海底反射波、直达波和海面反射波。图8中虽然可以看到3条路径的时间历程，但明显信噪比不高，主瓣较宽。对比图7和图8可以看出，反卷积波束形成得到的船辐射噪声多途反射波具有更窄的主瓣宽度，多途角度更容易分辨。

4 结　语

针对波束形成中旁瓣抑制问题，提出一种反卷积波束形成高分辨算法。将常规波束形成作为一个线性系统，由均匀线阵的波束指向性出发，利用Richardson-Lucy对点声源散射函数进行迭代求解，以常规波束形成输出结果作为输入，与声源点散射函数相卷积，抑制阵列指向性函数的影响，获取更窄的主瓣和更低的旁瓣，精确估计多目标波达角度，延时补偿各阵元收到的舰船辐射噪声，补偿后的信号相位对齐并累加，即可得到纯净的目标辐射噪声信号。仿真对比了常规波束形成和反卷积波束形成单目标角度分辨力，湖试数据处理对比了常规波束形成和反卷积波束形成多目标角度分辨力，验证了算法的高分辨特性；仿真对比了2个等强度目标不同波达角下，利用反卷积波束形成与常规波束形成获取的目标噪声包络谱输出信噪比，验证了反卷积波束形成算法的性能。结果表明，反卷积波束形成算法具有更优的多目标角度分辨力，能够实现多目标的调制谱分离，有效提高目标检测性能。