为了对水下实测信号进行建模,充分提取信号声学特性十分必要,这对水下信号处理、水下攻防、水下探测与识别等研究领域具有重要意义。时间和频率是描述信号的2个重要物理量,时频特征是声信号的重要特性,因此从时域、频域2个角度进行信号处理是提取信号声学特性研究中较常见的方法。
时域分析是在时间的维度对信号进行分析与处理,但实际中采集到的声信号一般较为复杂,存在信息相互叠加的现象,仅仅时域分析很难从中提取到有效信息。傅里叶变换解决了这个问题,使很多在时域中难以看到的信号特征在频域下很好的体现出来[1-5]。但傅里叶变换存在一定局限性:它是一种整体的、全局的积分变换,要么完全在时域,要么完全在频域,无法得出信号的时频局部特性。也就是说,通过单独的时域分析与频域分析,并不能知道信号在某一特定时间点的对应频谱,想要完成水声信号的建模,仅靠时域图与频域图得出的声特性信息还远远不够,需更清楚的了解水声信号的时频特性,这就要对信号进行时频分析。
短时傅里叶变换[5-12]时频分析理论是由Gabor在20世纪40年代提出的,是在傅里叶变换基础上的推广改进,其原理简单、功能强大,在今天仍然是信号分析与处理的有力工具。但针对某一特定信号进行短时傅里叶变换时频分析时,选择何种宽度、何种类型的时间窗使信号分析效果更好,这是不能确定的,也就是说,时间分辨率与频率分辨率之间是相互矛盾的。为解决这个问题,Norden. Huang提出了一种全新的信号处理时频分析方法——希尔伯特黄变换方法(HHT),它由EMD分解和Hilbert变换两部分构成,非常适用于处理水下冲击信号等这类非平稳信号[13-16]。
本文采用希尔伯特黄变换(HHT)时频分析方法,首先将信号进行HHT时频分析,得到信号声学特性;然后进行数学建模,构造函数表达式表示原始声信号。最后,比对模拟信号与原始信号的HHT分析结果,验证建模效果。
1 希尔伯特黄变换时频分析希尔伯特黄变换方法(HHT)是基于经验模态分解与希尔伯特谱技术,将复杂水声信号分解为有限数目个固有模态函数,赋予了信号瞬时频率合理的意义[17-20]。该方法分析信号的基本过程由两部分组成:首先,信号经过经验模态分解(EMD)后,自适应的按序排列为一系列有限数目的固有模态函数(IMF);然后,将固有模态函数经过希尔伯特变换得出时频谱图。
1.1 EMD原理在希尔伯特黄变换分析信号的2个步骤中,经验模态分解(EMD)是其中的核心部分,是将待分析信号分解为一系列固有模态函数(IMF)。EMD分解方法体现了“筛分”思想,基于上述假设,对信号
1)求出信号
2)对极大值、极小值包络曲线求平均,记为
| $ {a_{1,1}}(t) = \frac{{{x_{\max }}(t) + {x_{\min }}(t)}}{2} 。$ | (1) |
3)将原始信号与
| $ {h_{1,1}}(t) = x(t) - {a_{1,1}}(t)。$ | (2) |
判断差值
| $ {h_{1,k}}(t) = {h_{1,k - 1}}(t) - {a_{1,k}}(t)。$ | (3) |
直至
| $ {c_1}(t) = {h_{1,k}}(t) 。$ | (4) |
4)将第1个IMF分量
| $ {r_1}(t) = x(t) - {c_1}(t) 。$ | (5) |
5)将剩余序列看做一个新的原始信号,进行步骤1~步骤4,重复
| $ \begin{gathered} {r_1} - {c_2} = {r_2} ,\\ \cdots \\ {r_{n - 1}} - {c_n} = {r_n}。\\ \end{gathered} $ | (6) |
6)直到剩余序列
| $ x(t) = \sum\limits_{i = 1}^n {{c_i}(t) + {r_n}(t)} 。$ | (7) |
分析EMD分解的整个过程,可看出此分解是一种具有经验性、自适应性与滤波性的过程[21]。也就是说,整个分解过程可看做是一种自适应的“筛选”过程[22],且得到的一系列IMF分量是按照频率成分从高到低排列的。经过EMD分解得出的IMF分量非常适合进行希尔伯特变换,并且通过IMF的2个限定条件,可有效保证EMD分解得到的每一阶IMF分量经过希尔伯特变换求得的瞬时频率具有合理的物理意义。
1.2 希尔伯特谱分析EMD分解方法是基于信号局部特征的时间尺度,将信号“自适应”地分解为有限数目个IMF分量,给信号“瞬时频率”的概念赋予了实际意义。希尔伯特谱分析是希尔伯特黄变换理论中的第2步骤,是在EMD分解基础上进行的。根据式(7),得知EMD方法将原始信号分解为一系列IMF分量与一个剩余分量,对每个IMF分量
| $ \bar {{c_i}} (t) = \frac{1}{\text{π} }\int_{ - \infty }^\infty {\frac{{{c_i}(t)}}{{t - \tau }}} {\rm{d}}\tau 。$ | (8) |
结合原始IMF分量,可构造出解析信号表达式:
| $ {z_i}(t) = {c_i}(t) + j\bar {{c_i}} (t) = {a_i}(t){e^{j{\phi _i}(t)}} 。$ | (9) |
根据解析信号表达式,可进一步得出幅值函数与相位函数:
| $ \left\{ \begin{gathered} {a_i}(t) = \sqrt {{c_i}^2(t) + {{\bar {{c_i}} }^2}(t)} ,\\ {\phi _i}(t) = \arctan \frac{{{c_i}(t)}}{{\bar {{c_i}} (t)}}。\\ \end{gathered} \right. $ | (10) |
根据式(10),进而求得瞬时频率:
| $ {f_i}(t) = \frac{1}{{2\text{π} }}{\omega _i}(t) = \frac{1}{{2\text{π} }} \times \frac{{{\rm{d}}{\phi _i}(t)}}{{{\rm{d}}t}} 。$ | (11) |
至此,可用一种新的形式表示原始信号:
| $ x(t) = {{\rm{Re}}} \sum\limits_{i = 1}^n {{a_i}(t){e^{j\int {{\omega _i}(t){\rm{d}}t} }}} 。$ | (12) |
式中,
| $ x(t) = {{\rm{Re}}} \sum\limits_{i = 1}^n {{a_i}(t){e^{j{\omega _i}t}}} 。$ | (13) |
式中,
| $ H(\omega ,t) = {{\rm{Re}}} \sum\limits_{i = 1}^n {{a_i}(t){e^{j\int {{\omega _i}(t){\rm{d}}t} }}} 。$ | (14) |
对
| $ h(\omega ) = \int_0^T {H(\omega ,t)} {\rm{d}}t 。$ | (15) |
在室外较大水池布设声传感器,采用向水中抛重物方式产生水下冲击声信号,以该实测信号为研究对象,依次进行时域分析、频域分析与时频分析。单独的时域与频域分析结果如图1所示。

|
图 1 实测信号时域图与功率谱图 Fig. 1 Time domain diagram and power spectrum diagram of measured signal |
分析图1,发现单独对信号的时域与频域进行分析时,能抓取的信号特征很少。观察时域图,得出该信号为冲击信号,是非平稳信号,重物落水瞬间的信号能量较高。观察频域图,发现该信号是一个频带较宽的宽带信号,信号各频带对应的能量不同。对发现在2~7 kHz频带内能量较强,但找不出更多信息和更好规律来模拟该信号,
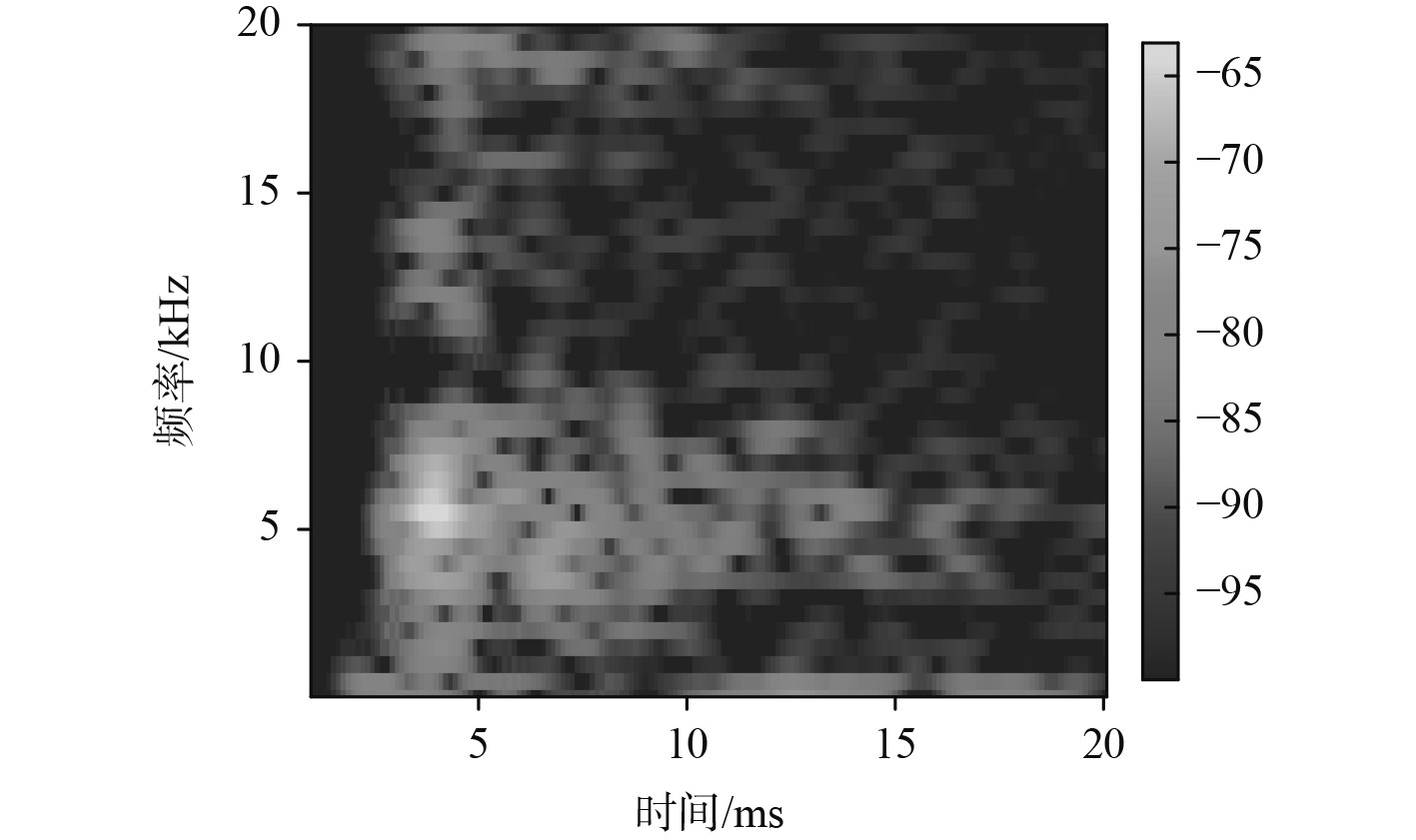
对信号进行短时傅里叶变换时频分析,结果如图2所示。分析时频图,可得知该信号的大部分能量集中在100 Hz~10 kHz范围内,进行滤波处理,去除频率小于100 Hz和大于10 kHz的部分,得出的时频图如图3所示。
|
图 2 短时傅里叶变换时频图 Fig. 2 Short time Fourier transform time-frequency diagram |
分析可知:在4 ms处有持续1.5 ms左右的从3~7 kHz的能量强区。从时频图可看到信号时频平面上的整体图,但仅可拿到较少的信号时间-频率的分布信息,无法给出时间-频率的函数关系,因此想要建立数学模型,拿到的这些信息还远远不够。
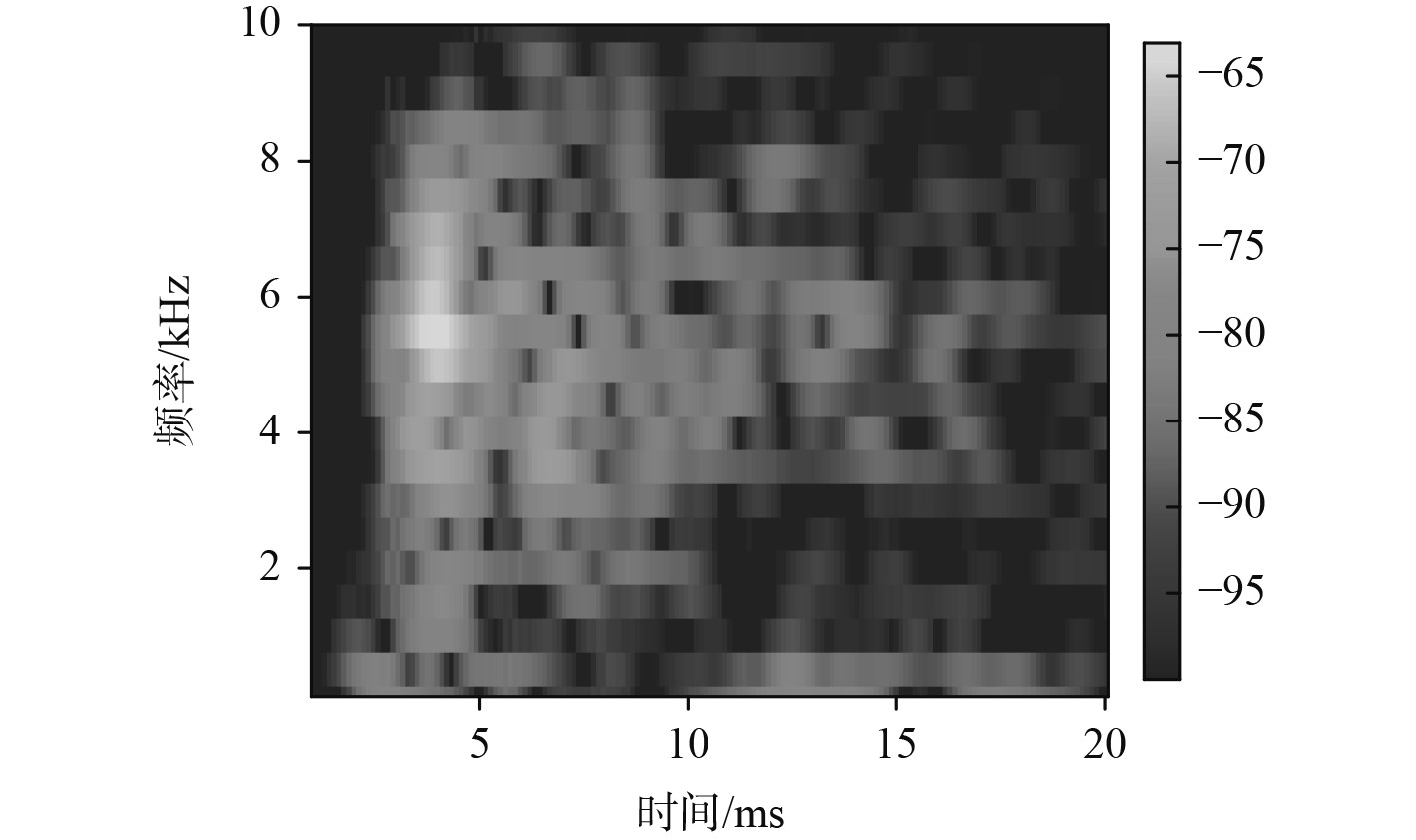
|
图 3 滤波处理的短时傅里叶变换时频图 Fig. 3 Short time Fourier transform time-frequency diagram of filtering processing |
对100 Hz~10 kHz滤波处理后的实测信号进行HHT时频分析,结果如图4所示。
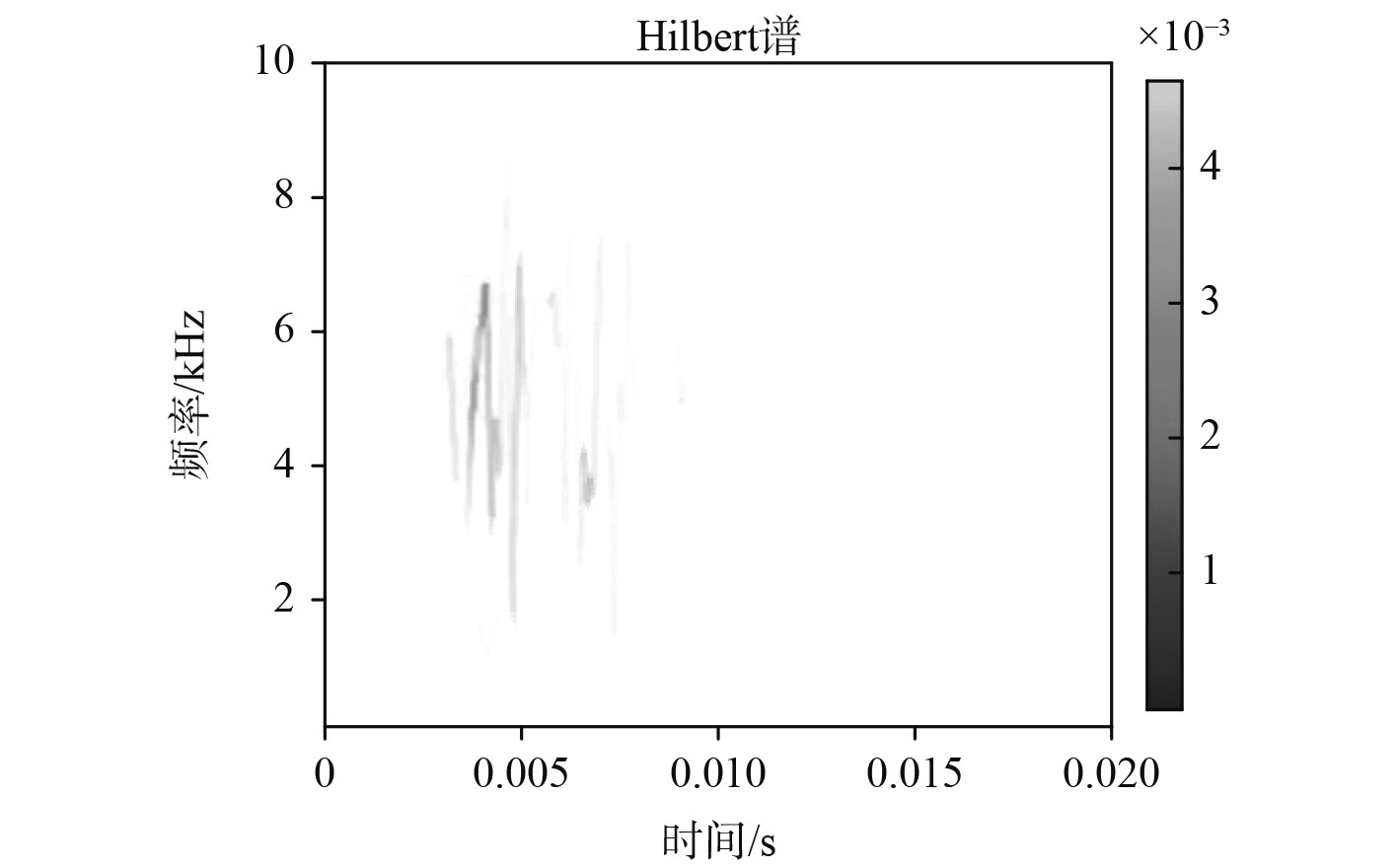
|
图 4 HHT时频分析图 Fig. 4 HHT time-frequency analysis diagram |
分析HHT时频谱图可发现:对于该信号某一频率成分出现的时刻,希尔伯特黄变换给出了精确结果。也就是说,可以给出瞬时频率与能量的分布情况,即非常清晰的时间、频率分布信息。在这些时频信息的基础上,可进行信号的建模研究。
对时频图设置一个阈值,去除能量较低的部分,这样使得时频图中时间与频率的关系更加明显。设置阈值限制后,选取其中能量强的部分,100 Hz~10 kHz滤波与阈值处理后该信号的HHT时频图如图5所示。观察图5可得:时间与频率基本满足线性关系,可将频率看做是一个自变量为时间的分段函数,因此该信号等同于一系列线性调频信号的“加和”。
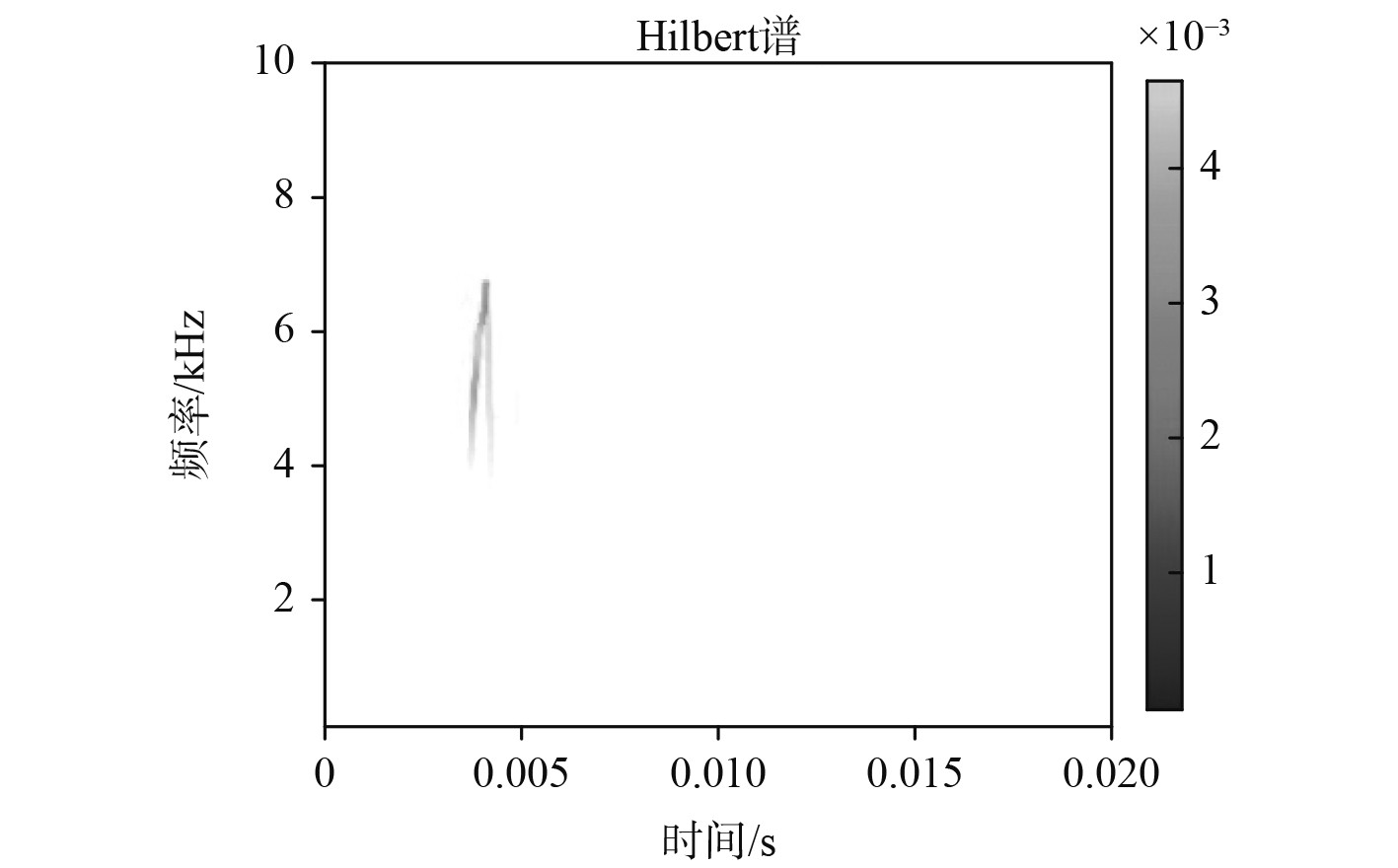
|
图 5 滤波与阈值处理后信号的HHT时频图 Fig. 5 HHT time-frequency diagram of filtered and threshold processed signals |
将HHT谱图放大并标示坐标,如图6所示。
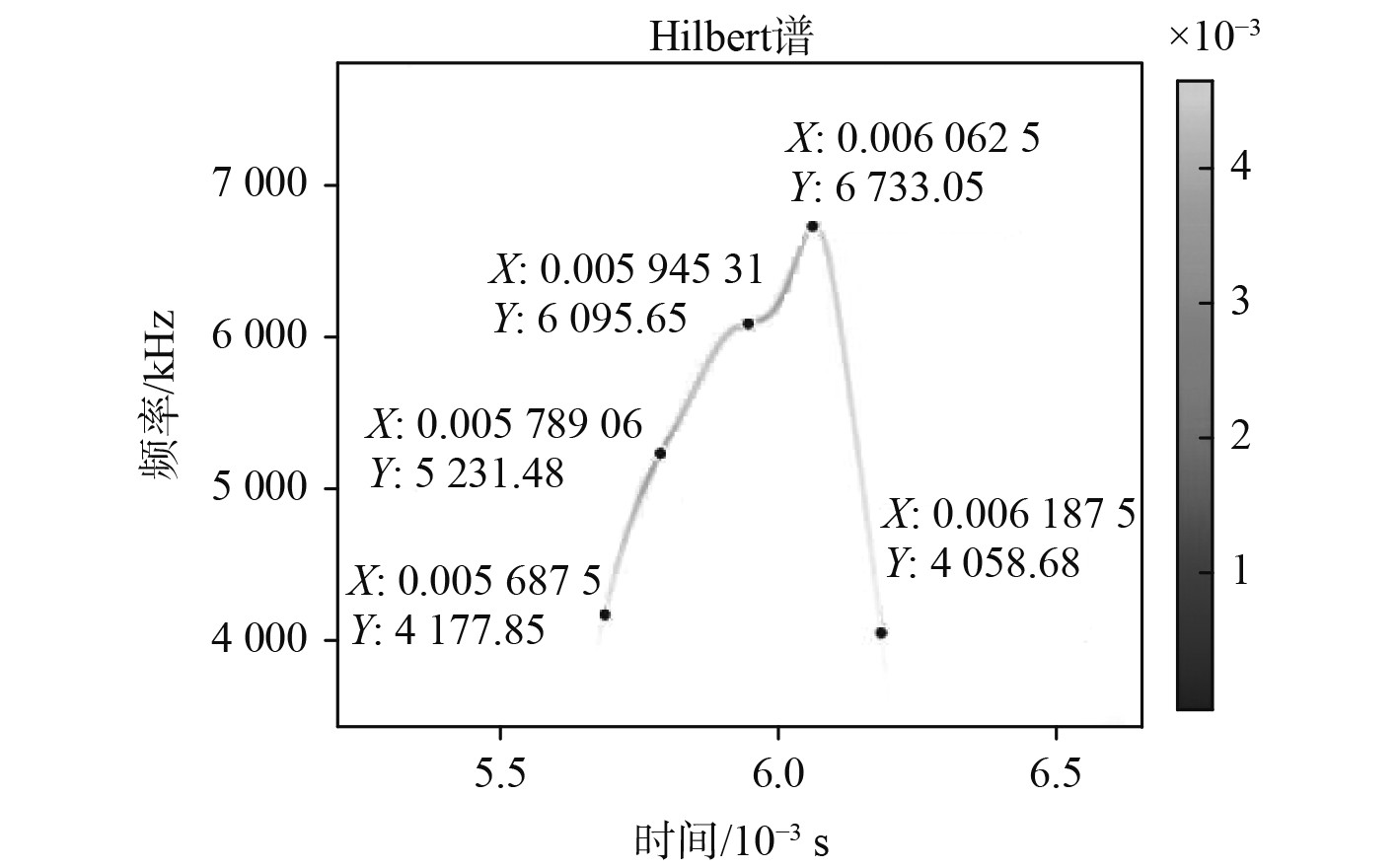
|
图 6 滤波与阈值处理后信号的放大HHT时频图 Fig. 6 Amplified HHT time-frequency diagram of filtered and threshold processed signals |
该信号的时间-频率分段函数可看做由4部分线性成分构成,因此可使用线性调频(LFM)信号模拟该信号。由图可知,该信号冲击时间大概持续10 ms,因此构造如下函数表达式:在0~0.02 s时间段内,包含10 ms的线性调频信号,其他时间段进行补零处理。构造信号的采样率与原始实测信号采样率保持一致,均为128 kHz。LFM信号的实数形式表达式如下式:
| $ x(t) = A\cos \left(2\text{π} *\left({f_0}t + \frac{\mu }{2}{t^2}\right) + \varphi \right)。$ | (16) |
式中:
| $ {s_1} = \left\{ \begin{gathered} 0,t \in [0,1{\rm{ms}}) \\ A = 0.05,{f_0} = 4\;000\;{\rm{Hz}},\mu = 4.8 \times {10^5},\varphi = {90^ \circ },\\ t \in [1\;{\rm{ms}},3.5\;{\rm{ms}}) \\ A = 0.06,{f_0} = 5\;200\;{\rm{Hz}},\mu = \frac{2}{7} \times {10^6},\varphi = {72^ \circ },\\t \in [3.5\;{\rm{ms}},7\;{\rm{ms}}) \\ A = 0.05,{f_0} = 6\;200\;{\rm{Hz}},\mu = 4 \times {10^5},\varphi = - {18^ \circ },\\ t \in [7\;{\rm{ms}},8.5\;{\rm{ms}}) \\ A = 0.025,{f_0} = 6\;800\;{\rm{Hz}},\mu = - 1.12 \times {10^6},\varphi =\\ {162^ \circ },t \in [8.5\;{\rm{ms}},11\;{\rm{ms}}] \\ 0,t \in (11\;{\rm{ms}},20\;{\rm{ms}}]。\\ \end{gathered} \right. $ | (17) |
对上述构建好的信号模型进行希尔伯特黄变换时频分析,结果如图7所示。
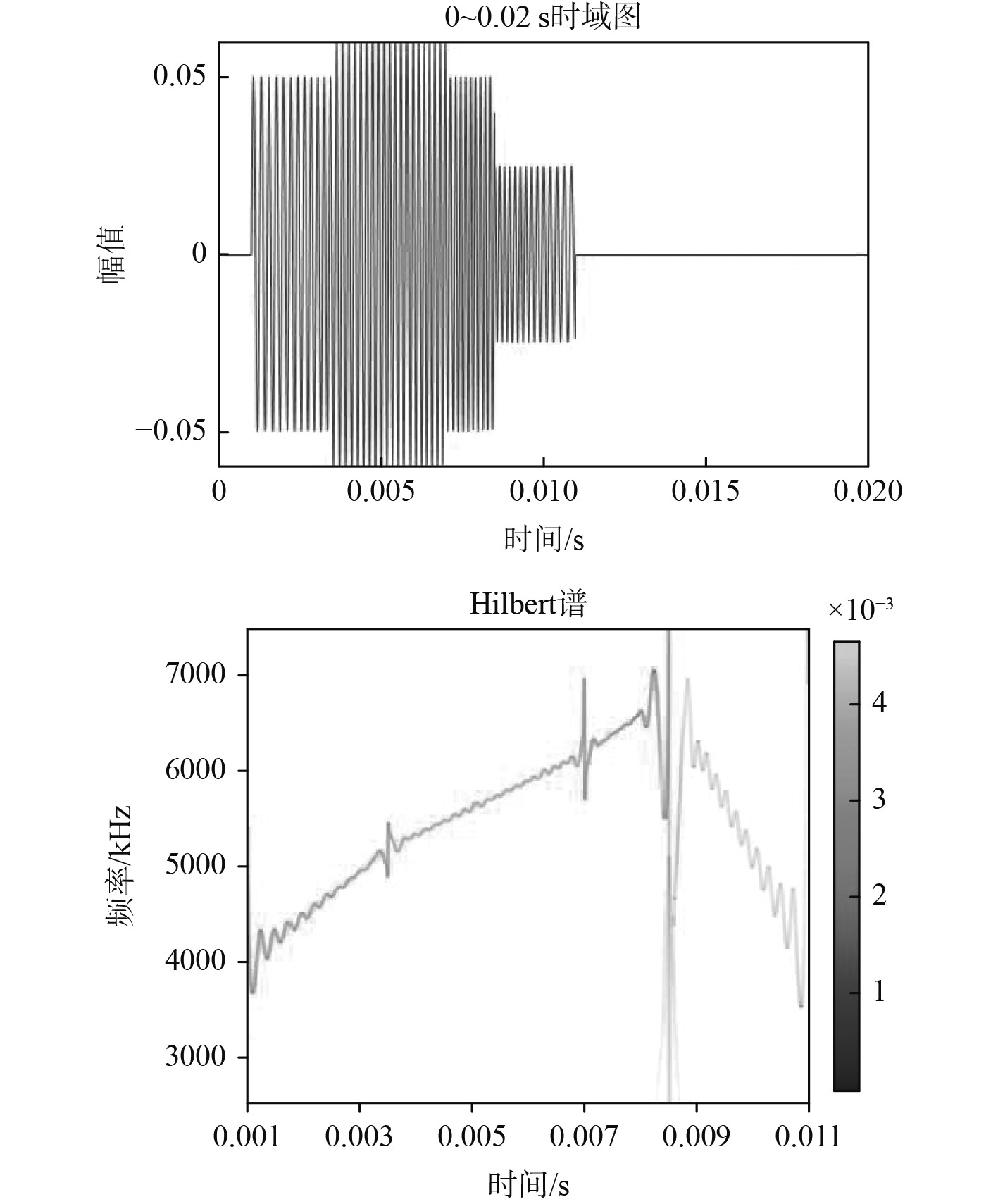
|
图 7 信号模拟函数的时域图与HHT时频图 Fig. 7 Time domain diagram and HHT time-frequency diagram of signal analog function |
通过分析以上HHT谱图可知,模拟函数较好体现了时频变化规律,建模信号的频谱走势与实测信号相同,具有与实测信号非常相似的时频特性。在各段信号接头处出现异常现象,是因为接头处并未完全光滑,频率发生了瞬间跳变与振荡。
3 结 语本文以实测水下冲击信号为研究对象,从时域与频域2个角度出发,对信号进行分析处理以提取声学特性。最终发现,希尔伯特黄变换时频分析方法可得到非常清晰的时间、频率分布信息,可以完成实测信号的数学建模。比较实测信号与模拟信号的HHT时频分析结果可知:用分段线性调频信号来模拟实测信号,可以得到相同的频谱走势与相似的时频特性,验证了HHT时频分析的优势与建模的可靠性。
| [1] |
陈博涛. EMD分解联合时频分析在阵列声波信号中的应用[D]. 长春: 吉林大学, 2010.
|
| [2] |
肖祺. 低信噪比信号调制识别中的时频分析与应用[D]. 杭州: 杭州电子科技大学, 2021.
|
| [3] |
黄会婷. 基于时频分析的超声信号处理方法研究[D]. 荆州: 长江大学, 2020.
|
| [4] |
曹晓勇. 基于时频分析的砼脱空声频信号特征研究[D]. 西安: 长安大学, 2014.
|
| [5] |
马妍. 基于时频分析的地震信号瞬时参数提取方法研究[D]. 大庆: 东北石油大学, 2013.
|
| [6] |
BABA T. Time-frequency analysis using short time Fourier transform[J]. The Open Acoustics Journal, 2012, 5(1): 245–253.
|
| [7] |
DJEBBARI A, REGUIG F B. Short-time Fourier transform analysis of the phonocardiogram signal[C]. Proceedings of ICECS, IEEE, 2000, 2: 844–847.
|
| [8] |
ZHONG J, HUANG Y. Time-frequency representation based on an adaptive short-time Fourier transform[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 5118-5128. DOI:10.1109/TSP.2010.2053028 |
| [9] |
MATEO C, TALAVERA J A. Short-time Fourier transform with the window size fixed in the frequency domain[J]. Digital Signal Processing, 2018, 77: 13-21. DOI:10.1016/j.dsp.2017.11.003 |
| [10] |
PORTNOFF M. Time-frequency representation of digital signals and systems based on short-time Fourier analysis[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1980, 28(1): 55-69. DOI:10.1109/TASSP.1980.1163359 |
| [11] |
王红萍. 非平稳信号时频分析方法性能研究[D]. 南京: 南京航空航天大学, 2008.
|
| [12] |
张旗. 非平稳信号的改进时频分析方法研究[D]. 西安: 西安电子科技大学, 2020.
|
| [13] |
AALAM M K,. Shubhanga k n. emd based detrending of non-linear and non-stationary power system signals[C]//Proceedings of INDICON, IEEE, 2021: 1–6.
|
| [14] |
HUANG N E, CHERN C C, HUAng K, et al. A new spectral representation of earthquake data: Hilbert spectral analysis of station TCU129, Chi-Chi, Taiwan, 21 September 1999[J]. Bulletin of the Seismological Society of America, 2001, 91(5): 1310-1338. |
| [15] |
HUANG N E, SHEN Z, LONG S R. A new view of nonlinear water waves: the Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31: 417-457. DOI:10.1146/annurev.fluid.31.1.417 |
| [16] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A:mathematical, physical and engineering sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [17] |
王黎黎. 基于希尔伯特—黄变换的时频分析算法研究[D]. 西安: 西安电子科技大学, 2009.
|
| [18] |
宋倩倩. 基于Hilbert-Huang变换的语音信号时频分析[D]. 无锡: 江南大学, 2009.
|
| [19] |
孙涛, 刘晶璟, 孔凡, 等. 小波变换和希尔伯特—黄变换在时频分析中的应用[J]. 中国水运(理论版), 2006(11): 111-113. |
| [20] |
杨培杰, 印兴耀, 张广智. 希尔伯特-黄变换地震信号时频分析与属性提取[J]. 地球物理学进展, 2007(5): 1585-1590. DOI:10.3969/j.issn.1004-2903.2007.05.037 |
| [21] |
HUANG N E. Review of empirical mode decomposition[J]. Proceedings of SPIE - The International Society for Optical Engineering, 2001, 4391: 71-80. |
| [22] |
HUANG N E. New method for nonlinear and nonstationary time series analysis: empirical mode decomposition and Hilbert spectral analysis[J]. Proceedings of SPIE - The International Society for Optical Engineering, 2000, 4056: 197-209. |
 2023, Vol. 45
2023, Vol. 45
