2. 崖州湾深海科技研究院,海南 三亚 572000
2. SJTU-Sanya Yazhou Bay Institute of Deepsea Science and Technology, Sanya 572000, China
随着人类对海洋探索的推进,深海定位技术变得越发重要,其中动力定位系统(Dynamic Positioning System,DP)就是深海定位技术的重要组成部分,且因其能在复杂的海况及超深水领域发挥作用,重要性日益提升。动力定位系统是指通过自身推进器之间的相互配合,来抵消外界风浪流干扰的系统,主要由位置测量系统,控制系统和推力系统等子系统组成[1],其中,控制系统和推力系统是整个动力定位系统的核心。Fossen[2]对动力定位的众多算法进行了详细介绍,并给出了众多算例。近年来随着智能化发展,众多学者致力于先进控制算法的研究,如非线性反步法[3]、动态面控制方法[4]、模糊自适应控制[5]、神经网络与鲁棒控制相结合的方法[6]、基于深度强化学习的方法[7]等,都展现了各自的控制特点。动力定位船舶在控制过程中有众多物理限制,如推进器角度的变化、推力的变化,这些变化都是有界的,且非瞬时的。模型预测控制(Model Predictive Control,MPC)因其在提前处理约束方面的优越性能,以及其在线滚动优化的特点[8],越来越多的学者研究将其应用到动力定位船舶上。
最初康斯伯格公司提出将MPC技术用于动力定位系统,主要因为其对目标函数的设计有利于降低能源的消耗,其研究结果表明该策略可使每年的燃料使用量降低近20%[9]。随后又因MPC可处理约束系统及在线滚动优化等优点,与动力定位技术所面临的问题相适应,MPC开始成为动力定位领域研究的一大热点。Fannemel[10]为解决线性化模型难以准确描述动力定位船舶,提出将非线性模型预测控制(The Nonlinear Model Predictive Control,NMPC)应用到动力定位上,并对其应用于动力定位系统的实际价值进行评估。Sotnikova和Veremey[11]则对变化缓慢的非线性模型进行了研究,在可预测时域内进行线性化,并假设线性模型和非线性模型的误差是定值,以此将复杂的动力定位船数学模型进行了线性化处理。
但目前大部分学者专注于对非线性模型预测的研究,却很少有学者关注模型预测控制的参数自整定问题,大部分还依赖于专家经验和以往数据里进行调参。而MPC的参数整定,是MPC控制策略至关重要的问题,通常在不同工况下,对参数的要求不同,在环境干扰多变的工况下,MPC的参数能够随船舶状态自动调整,对提高定位性能具有重要意义。本文提出一种策略,使用模糊算法对模型预测控制中的参数进行实时参数调整,在DP船状态发生改变时,模型预测参数也会发生相应的变化,以此来提高模型预测控制的精度。在此基础上设计一款非线性干扰观测器(Nonlinear disturbance observer,NDO)用于估计未知的环境力,实现对环境力的补偿,进一步提升系统的鲁棒性。
1 DP船数学模型 1.1 动力学模型和运动学模型通常对于水面动力定位船舶只需考虑水平面三自由度运动,即横荡,纵荡和首摇。在大地坐标系中船舶位置和欧拉角描述为
| $ \dot \eta = {\boldsymbol{R}}(\psi )\nu ,$ | (1) |
| $ {\boldsymbol{M}}\dot \nu + {\boldsymbol{C}}(\nu )\nu + {\boldsymbol{D}}(\nu )v = {\tau _{env}} + {\tau _c}。$ | (2) |
式中:
| $ {\boldsymbol{R}}(\psi ) = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0 \\ {\sin \psi }&{\cos \psi }&0 \\ 0&0&1 \end{array}} \right]。$ | (3) |
动力定位船舶会受到风浪流等多种环境力干扰,考虑这些环境干扰将导致动力定位产生较大误差,而面对时变未知环境干扰时,控制器很难实时获得精确环境干扰力。目前常用的解决方法是为控制系统设计干扰观测器,本文设计一款非线性干扰观测器,并对其稳定性进行证明。观测器设计如下:
| $ \left\{ \begin{gathered} {{\hat \tau }_{env}} = Z + K{\boldsymbol{M}}v ,\\ \dot Z = - KZ - K( - {\boldsymbol{C}}(\nu )\nu - {\boldsymbol{D}}(\nu )v + {\tau _c} + K{\boldsymbol{M}}v。\end{gathered} \right. $ | (4) |
其中,Z为辅助函数,
| $ {\boldsymbol{M}}\dot v = - {\boldsymbol{C}}(\nu )\nu - {\boldsymbol{D}}(\nu )v + {\tau _c} + {\tau _{env}},$ | (5) |
于是有:
| $ \begin{split} {{\dot {\hat \tau} }_{env}} =& - KZ - K( - {\boldsymbol{C}}(v)v - {\boldsymbol{D}}(v )v + {\tau _c} + KMv) + K{\boldsymbol{M}}\dot v = \\ &- K(Z + K{\boldsymbol{M}}v) + K{\tau _{env}} = K({\tau _{env}} - {{\hat \tau }_{env}}) = K{{\tilde \tau }_{env}} ,\end{split} $ | (6) |
因此:
| $ {\dot {\hat {\tau} }_{env}} = {\dot \tau_{env}} - {{\hat \tau }_{env}} = {\dot \tau _{env}} - K{{\tilde \tau }_{env}}。$ | (7) |
设计李雅普诺夫函数如下:
| $ {V_0} = \frac{1}{2}{\tilde \tau ^{\rm{T}}}_{env}{\tilde \tau _{env}} ,$ | (8) |
则
| $ \begin{split} {{\dot V}_0} =& {{\tilde \tau }^{\rm{T}}}_{env}{{\dot {\tilde \tau }}_{env}} = {{\tilde \tau }^{\rm{T}}}_{env}{{\dot \tau }_{env}} - {{\tilde \tau }^{\rm{T}}}_{env}K{{\tilde \tau }_{env}} \leqslant\\ &- {\lambda _{\min }}(K){{\tilde \tau }^{\rm{T}}}_{env}{{\tilde \tau }_{env}} + \varepsilon {{\tilde \tau }^{\rm{T}}}_{env}{{\tilde \tau }_{env}} +\\ &\frac{1}{{4\varepsilon }}{{\dot \tau }^{\rm{T}}}_{env}{{\dot \tau }_{env}} \leqslant - {k_0}{V_0} + \frac{1}{{4\varepsilon }}k_1^2 。\end{split} $ | (9) |
其中,
解不等式可得:
| $ 0 \leqslant {V_0} \leqslant \frac{{k_1^2}}{{4\varepsilon {k_0}}} + \left({V_0}(0) - \frac{{k_1^2}}{{4\varepsilon {k_0}}}\right){e^{ - {k_0}t}}。$ | (10) |
即有:
| $ ||{\tilde \tau _{env}}|| \leqslant \sqrt {\frac{{k_1^2}}{{2\varepsilon {k_0}}} + 2*\left({V_0}(0) - \frac{{k_1^2}}{{4\varepsilon {k_0}}}\right){e^{ - {k_0}t}}}。$ | (11) |
可知,
为将模糊算法应用于模型预测控制,选择如下非线性集中控制模型:
| $ \begin{split} & \dot X(t) = f(X(t),U(t),\\ &{\tau _{env}}(t)) = A(t)X(t) + B(t)U(t) + G(t){\tau _{env}}(t),\\ & Y(t) = C(t)X(t) 。\end{split} $ | (12) |
其中:
| $ A(t) = \left[ \begin{array}{cc} {0_{3 \times 3}}& R(\psi (t)) \\ {0_{3 \times 3}}& {M^{ - 1}}( - C(\nu (t)) + D) \end{array} \right],$ | (13) |
| $ B(t) = \left[ \begin{gathered} {0_{3 \times 3}} \\ {M^{ - 1}} \\ \end{gathered} \right]T(\alpha (t)) ,$ | (14) |
| $ G(t) = \left[ \begin{gathered} {0_{3 \times 3}} \\ {M^{ - 1}} \\ \end{gathered} \right],$ | (15) |
| $ C = \left[ {{I_{3 \times 3}}\quad{{\text{0}}_{3 \times 3}}} \right] 。$ | (16) |
其中,
| $ {T_i}({\alpha _i}(t)) = \left[ \begin{gathered} {\text{ }}\cos {\alpha _i}(t) \\ {\text{ }}\sin {\alpha _i}(t) \\ l{x_i}\sin {\alpha _i}(t) - l{y_i}\cos {\alpha _i}(t) \\ \end{gathered} \right] 。$ | (17) |
基于采样时间
| $ \begin{split} & X(k + 1) = X(k) + \int\nolimits_{k{T_s}}^{(k + 1){T_s}} {f(X(t),U(t),{\tau _{env}}(t)){\rm{d}}t} ,\\ & Y(k) = CX(k) 。\end{split} $ | (18) |
其中,
| $ \begin{split} \min J(U) = & \sum\limits_{j = 1}^{{N_P} - 1} {(||Y(k + j|k) - r(k + j)||_{{Q_{err}}}^2) + } \\ &||Y(k + {N_P}|k) - r(k + {N_P})||_{{q_{ter}}{Q_{err}}}^2 \times\\ &\sum\limits_{j = 0}^{{N_C} - 1} {||U(k + j|k)||_{{Q_{in}}}^2 + } \sum\limits_{j = 0}^{{N_C} - 1} {||\Delta U(k + j|k)||_{{Q_{din}}}^2} 。\end{split} $ | (19) |
| $ \begin{split} & {U_{\min }} \leqslant U(k + j|k) \leqslant {U_{\max }} ,\\ &\Delta {U_{\min }} \leqslant \Delta U(k + j|k)\leqslant\Delta {U_{\max}} 。\end{split} $ | (20) |
其中:
本文采用的模糊化方法是将模糊化规则和控制表对应,正常来说,需对输入输出给出模糊集和论域,并在此基础上确定隶属函数。参考Zhao[12]对角度偏差
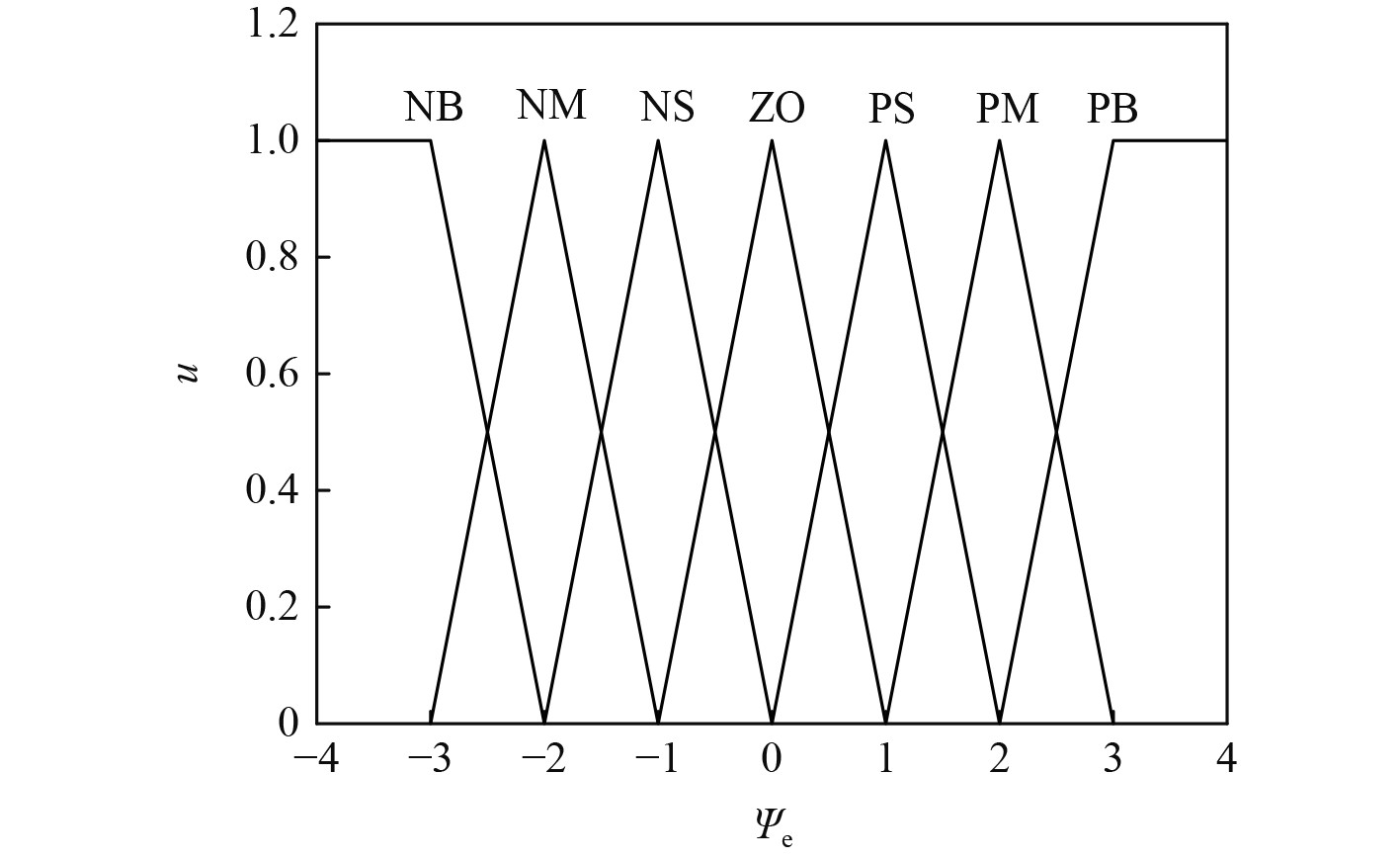
|
图 1
输入变量
|
| $ {u_{rP}} = \left\{ \begin{aligned} &{\text{0}},r < 0 ,\\ &{\text{1}} r \geqslant 0。\end{aligned} \right. $ | (21) |
| $ {u_{rN}} = \left\{ \begin{aligned} & 1,r < 0 ,\\ & 0,r \geqslant 0 。\end{aligned} \right. $ | (22) |
| $ {q_{3x}} = \frac{{{q_3} - {q_{3\min }}}}{{{q_{3\max }} - {q_{3\min }}}}。$ | (23) |
此时,对
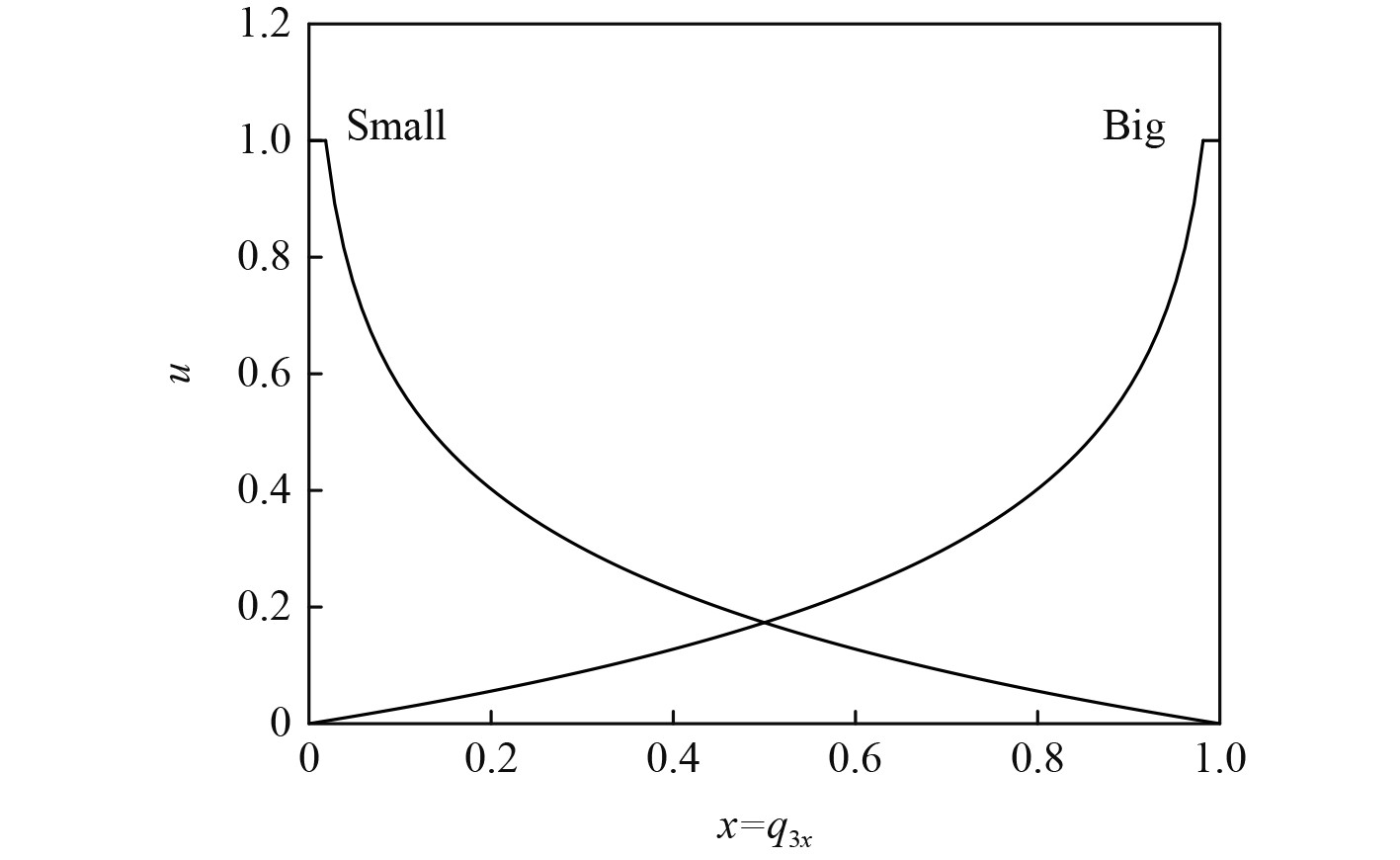
|
图 2
|
| $ \left\{ \begin{aligned} & {u_{Small}} = - \frac{1}{4}\ln x,\\ & {u_{Big}} = - \frac{1}{4}\ln (1 - x) 。\end{aligned} \right. $ | (24) |
需注意,
模糊规则本质上是一系列从专家和实际经验中获得的if-then语句,例如当
|
|
表 1 模糊规则表 Tab.1 Fuzzy rule base |
本文采用的是单值模糊器和乘积推理机,因此表1的14条规则所对应的具体值都可如下式表示:
| $ {u_i} = {u_{\psi ei}}*{u_{ri}}。$ | (25) |
同时:
| $ \sum\limits_{i = 1}^{14} {{u_i} = 1} 。$ | (26) |
其中,
| $ {q_{3x}} = \sum\limits_{i = 1}^{14} {{q_{3xi}}*{u_i}} 。$ | (27) |
当得出
| $ {q_3} = ({q_{\max }} - {q_{\min }})*{q_{3x}} + {q_{\min }}。$ | (28) |
需要说明的是,该方法同样适用于横荡和纵荡。
2 仿真DP船参数和环境载荷DP模型船主要参数如表2所示[13],螺旋桨布置如图3所示。
|
|
表 2 数值模拟参数设置 Tab.2 Parameter setting |
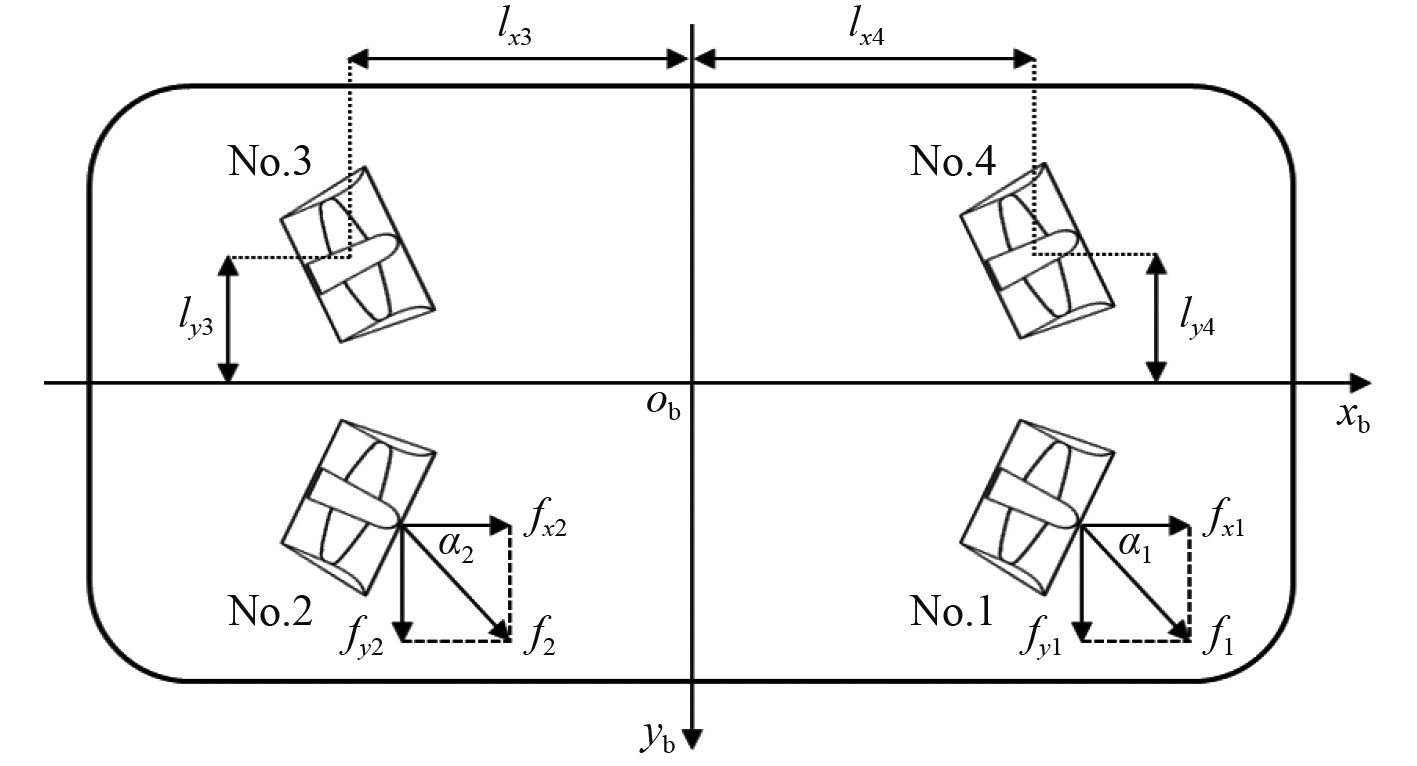
|
图 3 DP船推进器布置 Fig. 3 Thruster configuration of the DP ship |
环境干扰参照Fossen[14]选择如下:
| $ {\tau _{env}} = {R^{\rm{T}}}(\psi )b 。$ | (29) |
基于一阶马尔科夫模型构建低频环境力:
| $ \dot b = - {\boldsymbol{T}}_{env}^{ - 1}b + \varGamma \varpi 。$ | (30) |
其中,
对设计的非线性观测器进行仿真模拟,设计参数
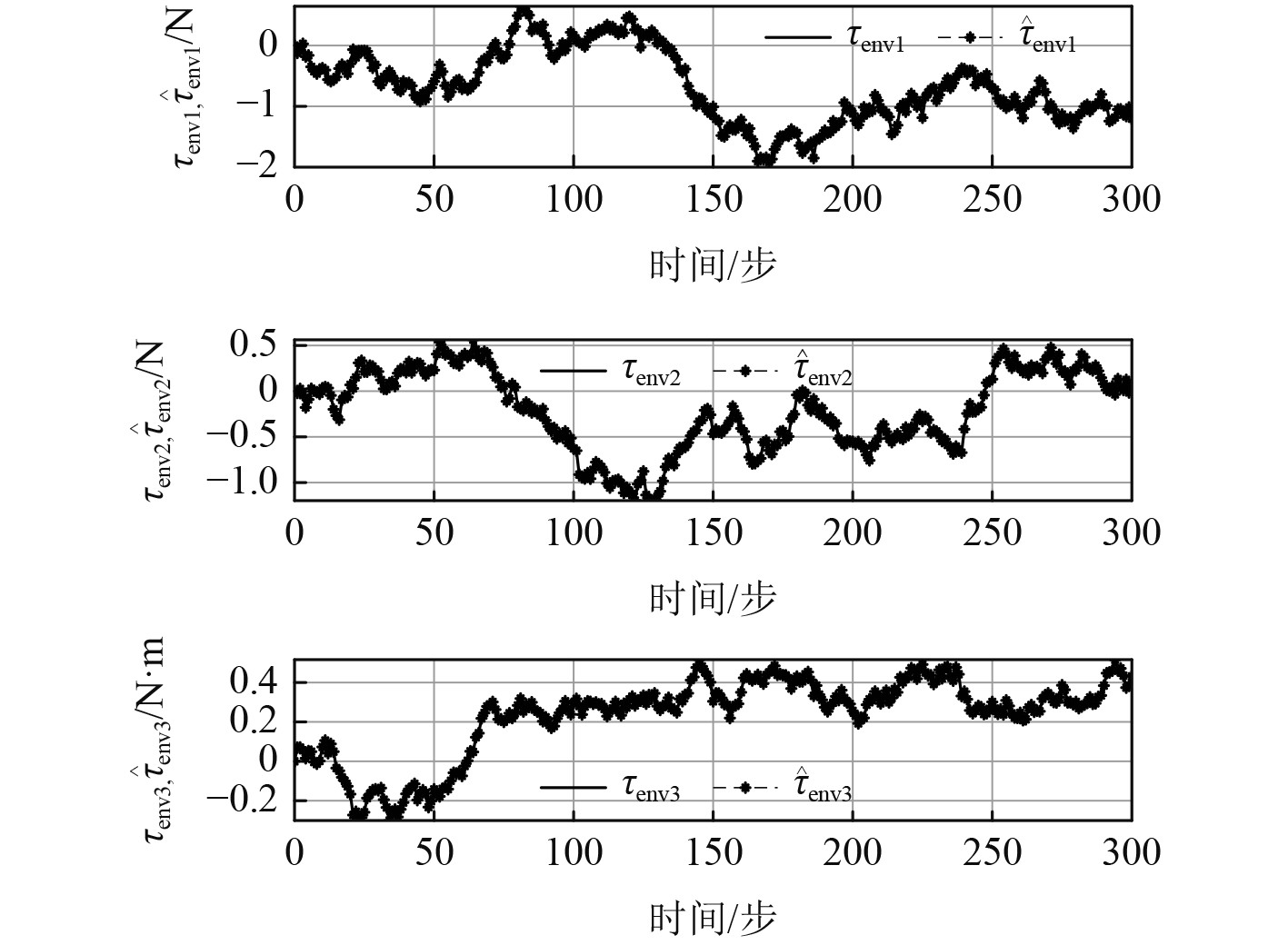
|
图 4 DP船所受环境干扰及观测值 Fig. 4 The environmental disturbances to the DP ship and the data of observer |
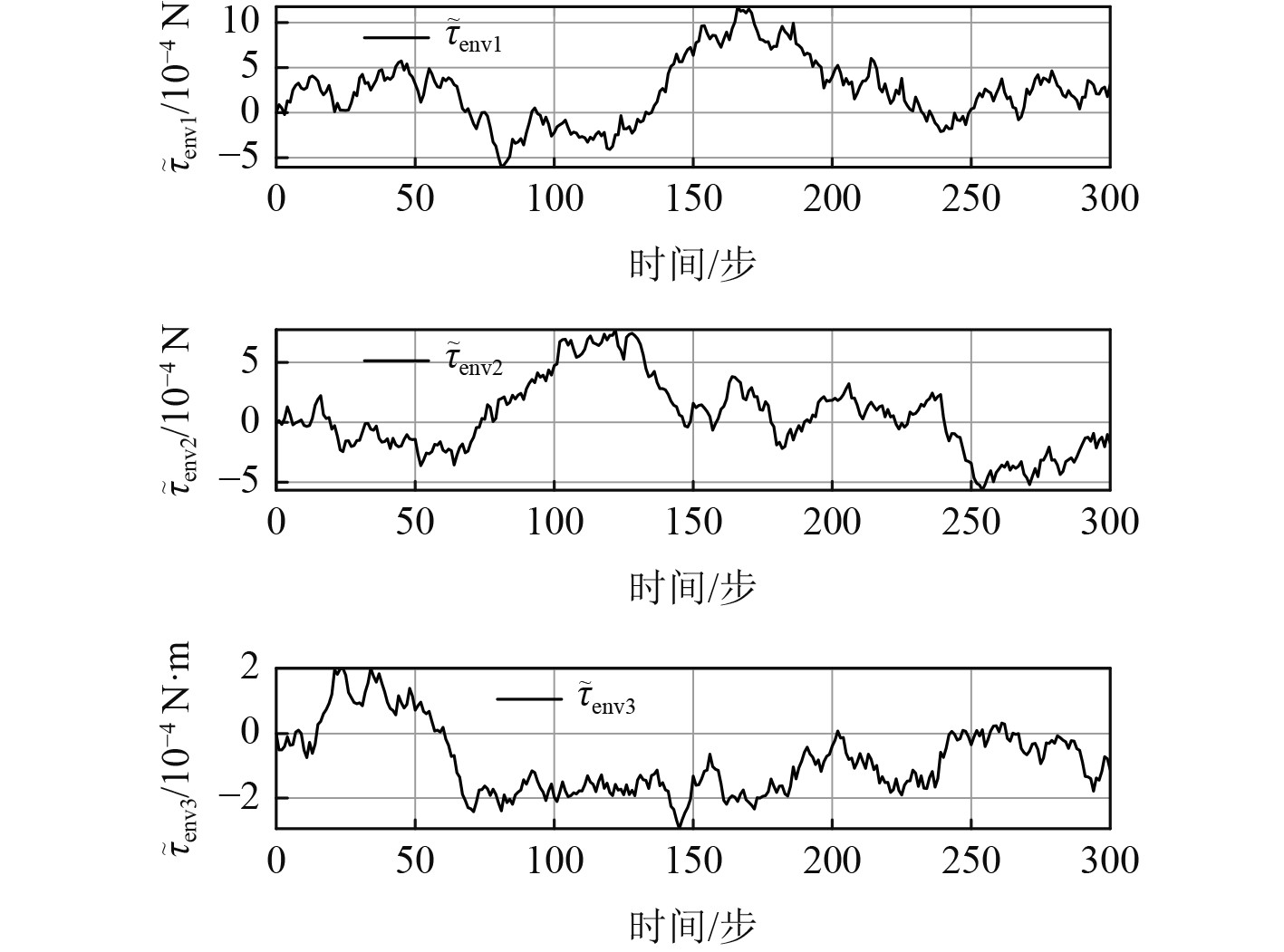
为了进一步验证观测器的性能,图5给出了
|
图 5 观测值误差 Fig. 5 observer errors |
将对参数固定的非线性模型预测策略(Nonlinear Model Predictive Control,NMPC)和模糊自适应模型预测控制策略(Fuzzy MPC)进行比较,这2种策略的区别仅在于Fuzzy策略对NMPC策略中的部分固定参数,进行了模糊化处理,在控制器中增加模糊化模块,其他各个参数设计保持一致,故可选取各参数如下:
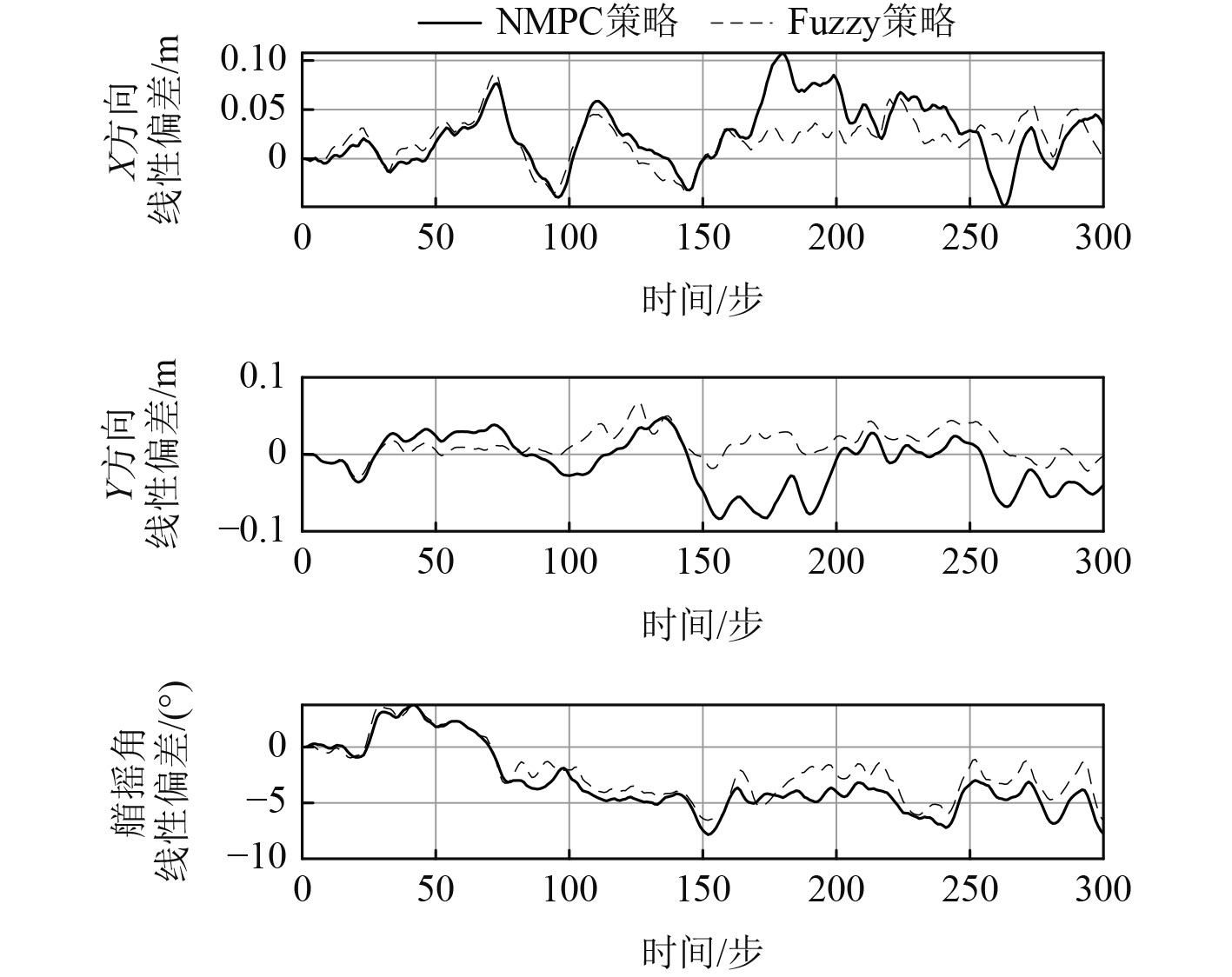
从图6可明显看出,Fuzzy策略的定位精度更高,波动幅度也小很多,在时间步长150步之前,2种策略控制精度趋势较为一致,Fuzzy策略精度稍高,而150步之后,开始出现较为不同的趋势。从环境干扰可看出,在150步左右时
|
图 6 两种策略下位置误差比较 Fig. 6 The comparison of the position errors using two strategies |
|
|
表 3 两种策略位置状态 Tab.3 The position state of the two strategies |
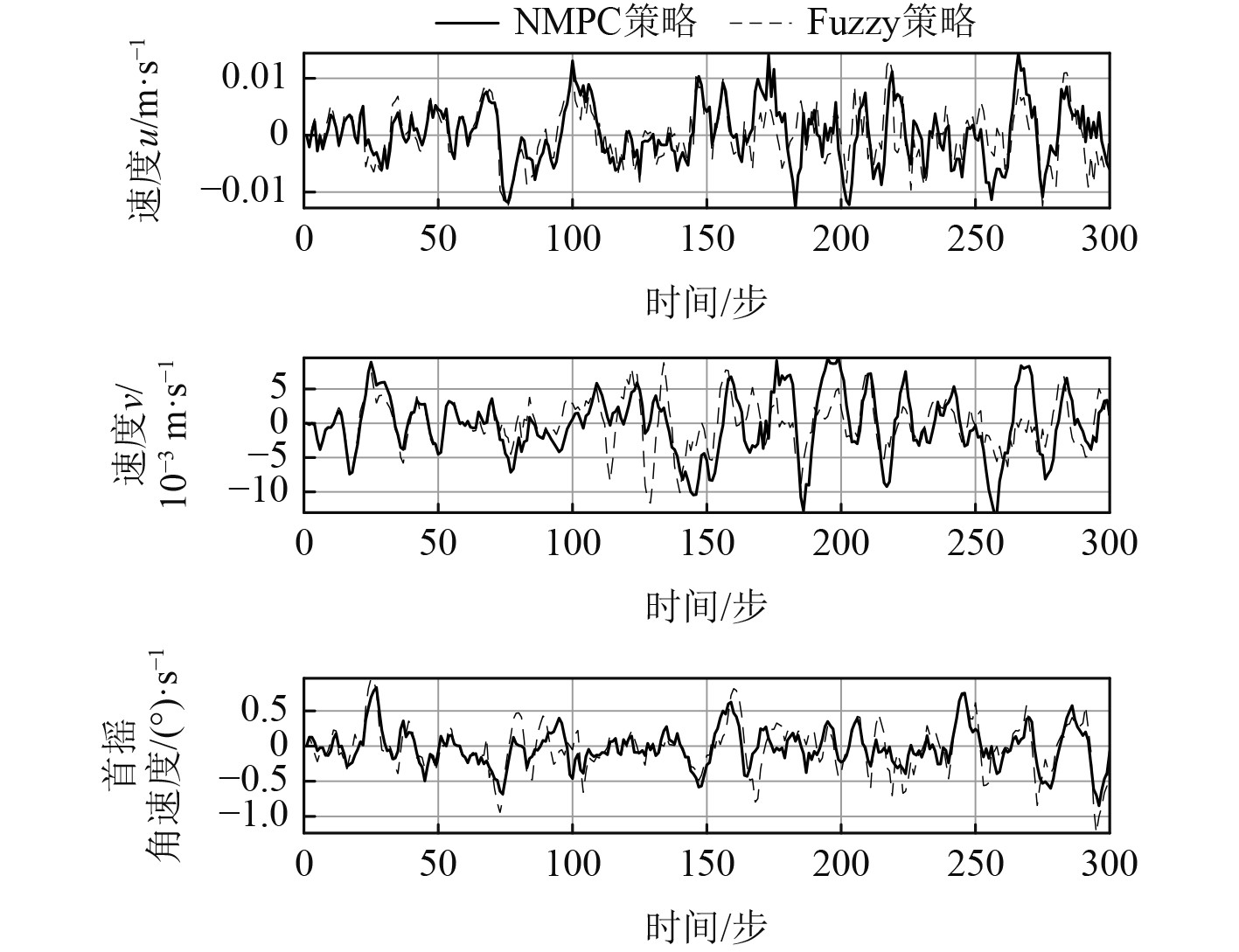
从图(7)可看出2种策略的速度变化,NMPC策略的速度标准差,分别为0.0052 m/s、0.0046 m/s和0.2747°/s,Fuzzy策略的速度标准差为0.0053 m/s、0.0040 m/s,0.3889°/s,这2种策略在速度的平稳性上是近似的,而Fuzzy策略却能获得更好的定位精度,说明对参数的模糊化调控能更及时应对外界干扰。
|
图 7 两种策略下速度比较 Fig. 7 The comparison of the velocities using two strategies |
为更进一步衡量动力定位的精度,引入参数,积分绝对误差(Integral Absolute Error,IAE)[15]。
| $ IAE(t) = \sum\limits_{k = 0}^{k = t} {\sqrt {{e^T}(k)e(k)} }。$ | (31) |
式中:

|
图 8 两种策略的IEA值 Fig. 8 IEA of two strategies |
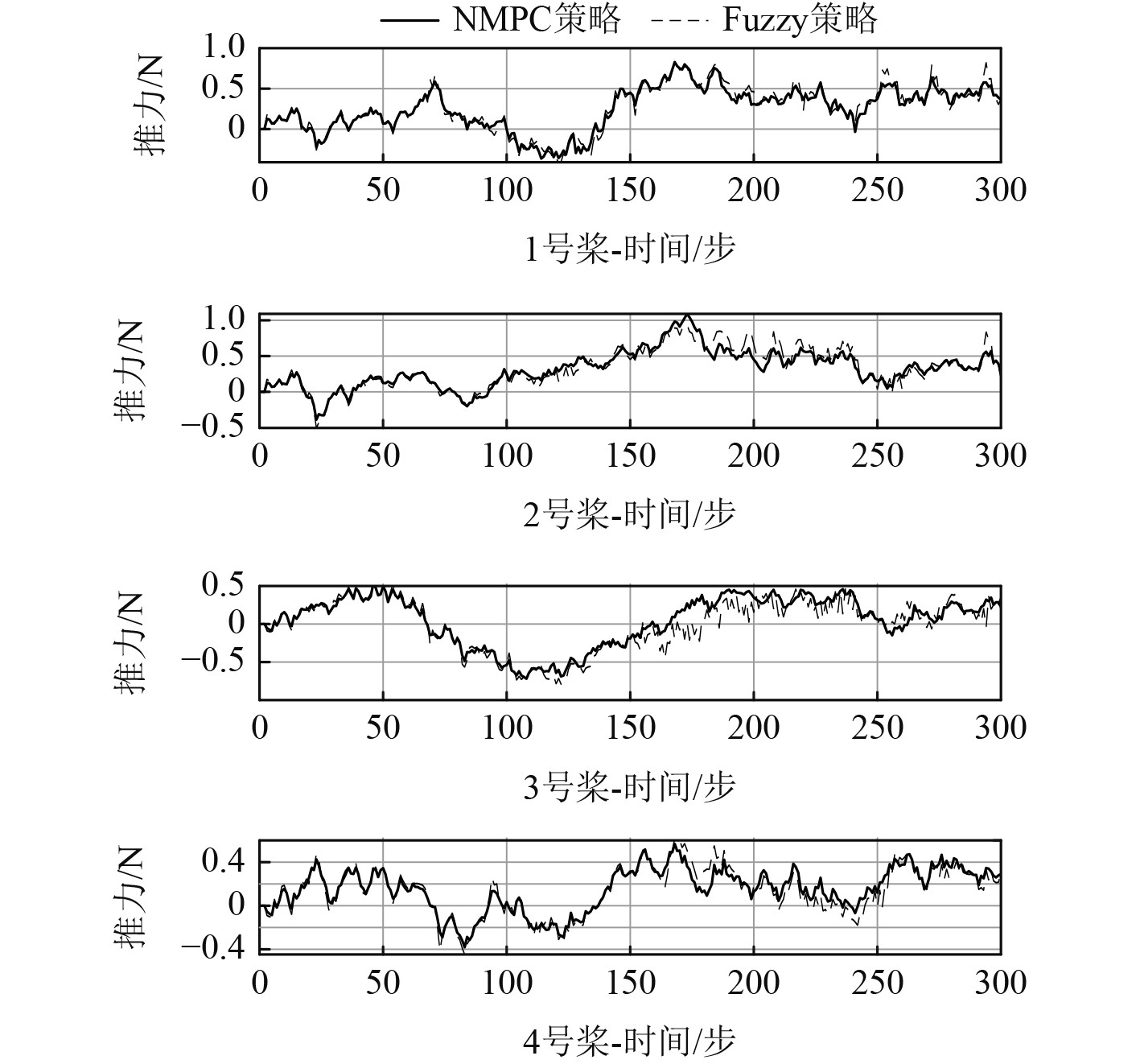
从图9可看出,2种策略在推力及推力变化上是相似的,由此可推断,在获得更好推力效果的同时,螺旋桨的功率变化并不大。为了能更进一步看出功率消耗的情况,现假定这里使用的螺旋桨均为定螺距桨,则功率和推力有如下关系:
|
图 9 两种策略下推进器推力比较 Fig. 9 The comparison of the thrusts using two strategies |
| $ P = \frac{{2\text{π} {K_Q}}}{{K_T^{3/2}{\rho ^{1/2}}D}}{T^{\frac{3}{2}}} = \zeta {T^{\frac{3}{2}}} 。$ | (32) |
其中:KT为推进器的推力系数;KQ为螺旋桨的扭矩系数;η为推进器的敞水效率;ρ为流体的密度;D为螺旋桨的直径;
本文针对MPC应用于DP船时的参数整定困难问题,设计了模糊自适应模型预测控制策略,引入模糊算法来实现模型预测控制的参数自整定。在此基础上为进一步提升控制系统鲁棒性,设计了一种非线性干扰观测器用于估计未知时变环境力,从而实现对环境力的补偿。通过理论和模拟仿真验证,在相同的环境干扰和模拟时域内,Fuzzy策略精度提升显著。通过IEA值可看出,在模拟结束时,精度提升26.6%。同时反映定位平稳性的标准差也小于NMPC策略,说明新的控制策略控制的更加平稳,定位精度更高,所消耗功率仅提升4.25%,验证了该策略的有效性,为解决模型预测控制的参数整定问题提供了一定参考性。
| [1] |
赵志高, 杨建民, 王磊, 等. 动力定位系统发展状况及研究方法[J]. 海洋工程, 2002(1): 91-97. ZHAO Zhigao, YANG Jianming, WANG Lei, et al. The development and research method of dynamic positioning system[J]. The Ocean Engineering, 2002(1): 91-97. DOI:10.16483/j.issn.1005-9865.2002.01.017 |
| [2] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. John Wiley & Sons, 2011.
|
| [3] |
ALMEIDA J, SILVESTRE C, PASCOAL A. Cooperative control of multiple surface vessels in the presence of ocean currents and parametric model uncertainty[J]. International Journal of Robust and Nonlinear Control, 2010, 20(14): 1549-1565. DOI:10.1002/rnc.1526 |
| [4] |
LU Y, ZHANG G, SUN Z, et al. Adaptive cooperative formation control of autonomous surface vessels with uncertain dynamics and external disturbances[J]. Ocean Engineering, 2018, 167: 36-44. DOI:10.1016/j.oceaneng.2018.08.020 |
| [5] |
HE H, XU S, WANG L, et al. Mitigating surge–pitch coupled motion by a novel adaptive fuzzy damping controller for a semisubmersible platform[J]. Journal of Marine Science and Technology, 2020, 25(1): 234-248. DOI:10.1007/s00773-019-00643-2 |
| [6] |
DU J, YANG Y, WANG D, et al. A robust adaptive neural networks controller for maritime dynamic positioning system[J]. Neurocomputing, 2013, 110: 128-136. DOI:10.1016/j.neucom.2012.11.027 |
| [7] |
ZHOU X, WU P, ZHANG H, et al. Learn to navigate: cooperative path planning for unmanned surface vehicles using deep reinforcement learning[J]. IEEE Access, 2019, 7: 165262-165278. DOI:10.1109/ACCESS.2019.2953326 |
| [8] |
DAI L, CAO Q, XIA Y, et al. Distributed MPC for formation of multi-agent systems with collision avoidance and obstacle avoidance[J]. Journal of the Franklin Institute, 2017, 354(4): 2068-2085. DOI:10.1016/j.jfranklin.2016.12.021 |
| [9] |
HVAMB O G. A new concept for fuel tight DP control[C]//Dynamic Positioning Conference. 2001.
|
| [10] |
FANNEMEL Å V. Dynamic positioning by nonlinear model predictive control[D]. Institutt for teknisk kybernetikk, 2008.
|
| [11] |
SOTNIKOVA M V, VEREMEY E I. Dynamic positioning based on nonlinear MPC[J]. IFAC Proceedings Volumes, 2013, 46(33): 37-42. DOI:10.3182/20130918-4-JP-3022.00058 |
| [12] |
ZHAO Z Y, TOMIZUKA M, ISAKA S. Fuzzy gain scheduling of PID controllers[J]. IEEE transactions on systems, man, and cybernetics, 1993, 23(5): 1392-1398. DOI:10.1109/21.260670 |
| [13] |
KAYACAN E, PARK S, RATTI C, et al. Learning-based nonlinear model predictive control of reconfigurable autonomous robotic boats: roboats[C]//2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2019: 8230–8237.
|
| [14] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. John Wiley & Sons, 2011.306–306
|
| [15] |
ØVERENG S S, NGUYEN D T, HAMRE G. Dynamic positioning using deep reinforcement learning[J]. Ocean Engineering, 2021, 235: 109433. DOI:10.1016/j.oceaneng.2021.109433 |
 2023, Vol. 45
2023, Vol. 45
