在无人艇的广泛应用中,路径规划始终是其核心技术[1]。无人艇工作海域通常含有较多未知目标,其运动信息通常无法预先掌握,需通过艇载的各类传感器(如雷达、红外、电视等)进行目标探测录取,获取实时局部周边动态。因此,常见的全局路径规划算法(如基于格栅图的REA*算法[2]、基于采样方法的RRT*算法[3]、智能算法AG[4-5]等)并不能与实时变化的场景相适应。而传统动态窗口法(DWA)作为局部路径规划算法,可根据局部态势变化进行机动避障。同时DWA相较于其他局部路径规划算法(如人工势场法PFM、时间弹性带法TEB[6]、向量场直方图法VFH[7]),能充分结合无人艇本身欠驱动特性,划定可行的速度组合生成路径,在编队集结运动中拥有更强的适应性。
Chang等[8]将强化学习的方法应用于传统DWA算法,通过周围环境变化动态调整评价函数权值,进一步提高机器人路径规划能力。王永雄等[9]提出一种参数自适应DWA算法,通过计算机器人周围障碍物距离及障碍物密集度动态变化评价函数权值,较好穿越稠密障碍物。常路等[10]通过修正传统DWA算法中3个评价指标函数和添加2项新评价函数的方法进行改进,增强了机器人导航及全局搜索能力。刘渐道等[11]将COLREs规则融合于动态窗口法,提高了无人艇在海上复杂交通环境中自主避碰能力,进一步保证了在机动过程中的航行安全。
综合以上研究发现,目前DWA在多无人艇编队集结中的应用较少,绝大多数是对单一机器人的避障机动能力进行改进优化。在无人艇编队集结运动中,对各无人艇之间存在运动中相互避碰的情况,而传统DWA算法对移动目标的避障有3项缺陷:一是采样窗口选择策略不够合理,在避障过程中易陷入局部最优,导致目标减速甚至停止;二是障碍物距离计算不够全面,存在碰撞风险;三是未考虑障碍物移动的情况,避障能力不够全面。因此,本文针对传统DWA这3个方面的问题,对算法进行改进,综合提高无人艇对移动障碍避障能力,使其适用于无人艇编队集结任务。
1 传统DWA算法传统DWA算法由Fox等[12]提出,通过机器人自身物理限制的极限速度和极限加速度约束,结合客观环境的障碍物约束,得到一定时间窗口内可行速度组合
| $ {V_s} = \left\{ {\left( {v,w} \right)|{v_{\min }} \leqslant v \leqslant {v_{\max }},{w_{\min }} \leqslant w \leqslant {w_{\max }}} \right\},$ | (1) |
| $ \begin{split} {V_d} =& \left\{ \left( {v,w} \right)|{v_c} - \dot v\Delta t \leqslant v \leqslant {v_c} + \dot v\Delta t,\right.\\ & \left.{w_c} - \dot w\Delta t \leqslant w \leqslant {w_c} + \dot w\Delta t \right\},\end{split} $ | (2) |
| $ {V_a} = \left\{ {\left( {v,w} \right)|{v_a} \leqslant \sqrt {2 \cdot {\rm{dist}}\left( {v,w} \right) \cdot \dot v} ,{w_a} \leqslant \sqrt {2 \cdot {\rm{dist}}\left( {v,w} \right) \cdot \dot w} } \right\} 。$ | (3) |
式中:
这3类约束交集,即为可行速度范围:
| $ {V_r} = {V_s} \cap {V_d} \cap {V_a} 。$ | (4) |
根据设定精度采样所有可行速度组合
| $ E\left( {v,w} \right) = \sigma \left( {\alpha \cdot {\rm{head}}\left( {v,w} \right) + \beta \cdot {\rm{dist}}\left( {v,w} \right) + \gamma \cdot {\rm{vel}}\left( {v,w} \right)} \right)。$ | (5) |
式中:
用传统DWA算法中,对采样窗口的障碍物约束

|
图 1 采样窗口分析 Fig. 1 Sampling window analysis |
图中,障碍物碰撞半径为R,角速度
| $ \begin{split} {V_a}'= & \left\{ \left( {v,w} \right)|{v_a} \leqslant \sqrt {2 \cdot {\rm{dist}}\left( {v,w} \right) \cdot \dot v} \cap |{\rm{cour}}|\geqslant\right.\\ & \left. \arcsin \left( {R/{\rm{dist}}\left( {v,w} \right)} \right),{w_a} \leqslant \sqrt {2 \cdot {\rm{dist}}\left( {v,w} \right) \cdot \dot w} \right\}。\end{split} $ | (6) |
式中,
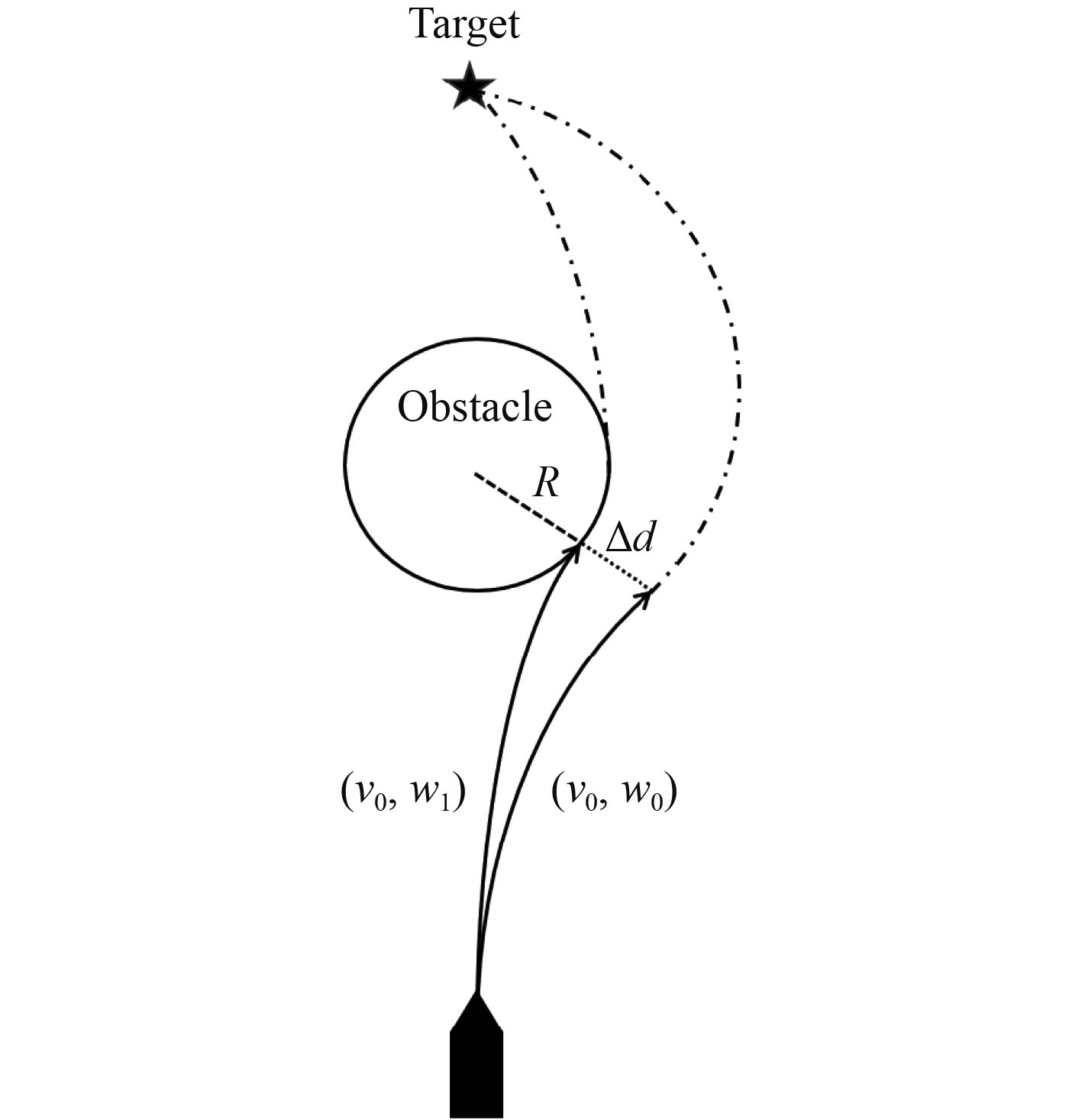
传统DWA算法评价函数
|
图 2 评价函数分析 Fig. 2 Evaluation function analysis |
图中,假设需避开障碍物并抵达目标点,从全局路径规划上看,轨迹
| $ E'\left( {v,w} \right) = \sigma \left( {\alpha \cdot {\rm{head}}\left( {v,w} \right) + \gamma \cdot {\rm{vel}}\left( {v,w} \right)} \right)。$ | (7) |
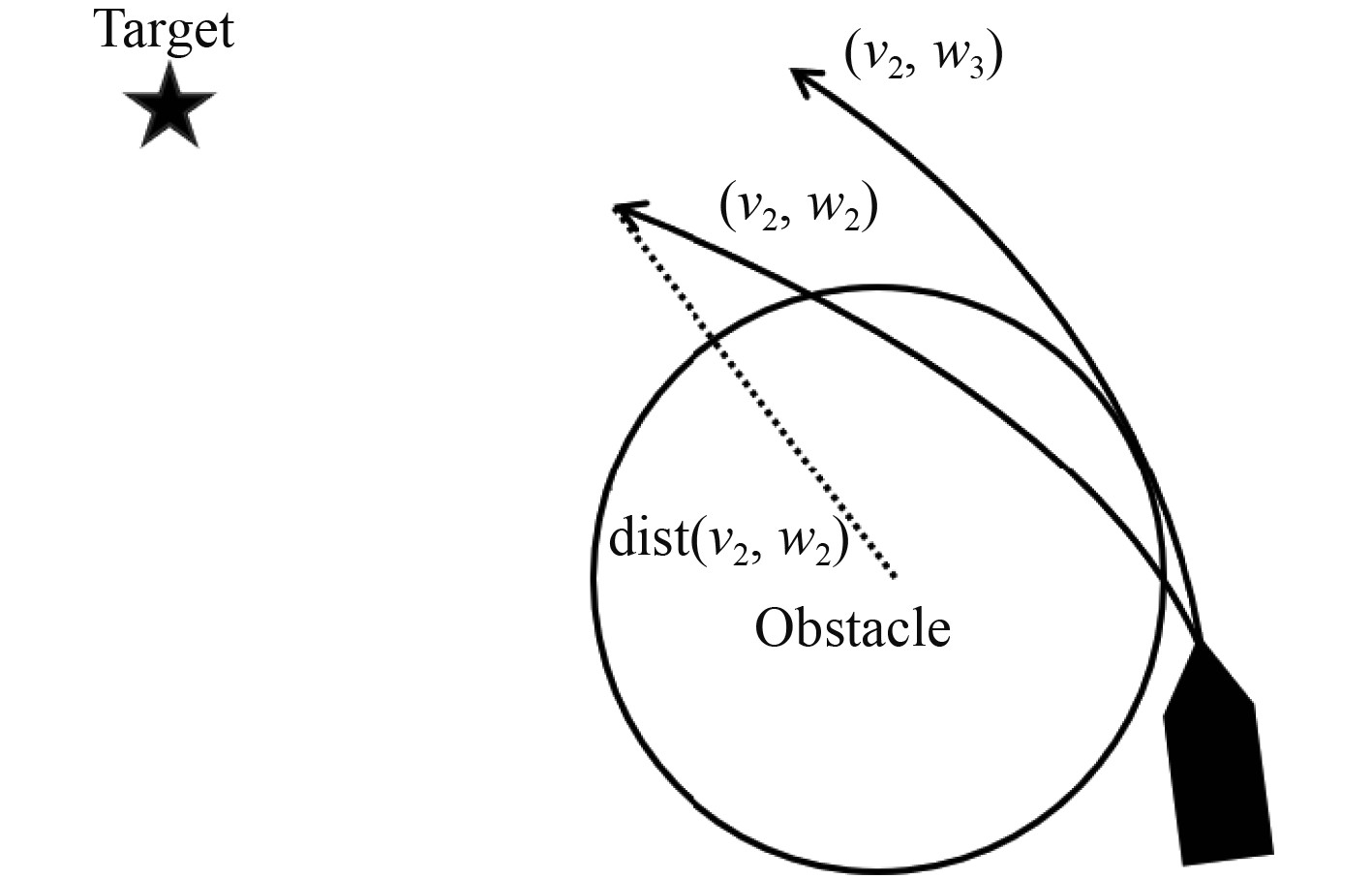
传统DWA算法中,对dist函数计算为预测轨迹终点到障碍物的距离。当与障碍物距离与碰撞半径相近且预测轨迹长度大于碰撞半径时,部分情况下,采样窗口会将发生碰撞的无效轨迹纳入评价范围,最终可能导致无效轨迹被评价为最优可行轨迹,造成避碰失败。具体如图3所示。
|
图 3 传统dist函数计算 Fig. 3 Traditional dist function calculation |
图中,
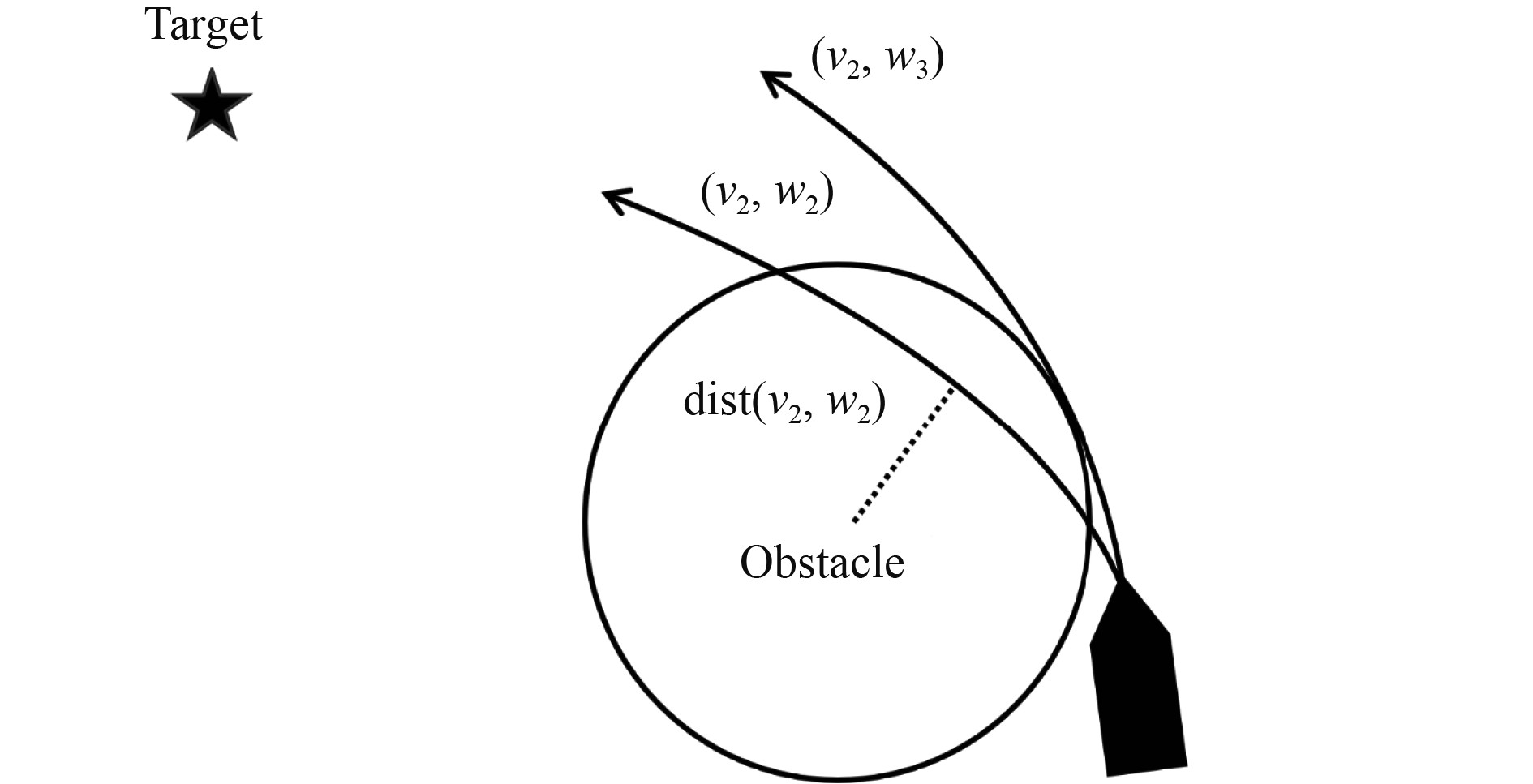
综上,计算预测轨迹终点到障碍物距离的方法存在缺陷,dist函数应完善为计算整条轨迹与障碍物距离的集合,并通过该集合中最小值与碰撞半径进行比较,剔除发生碰撞的无效轨迹。具体如图4所示:
|
图 4 改进dist函数计算 Fig. 4 Improved dist function calculation |
图中,改进后
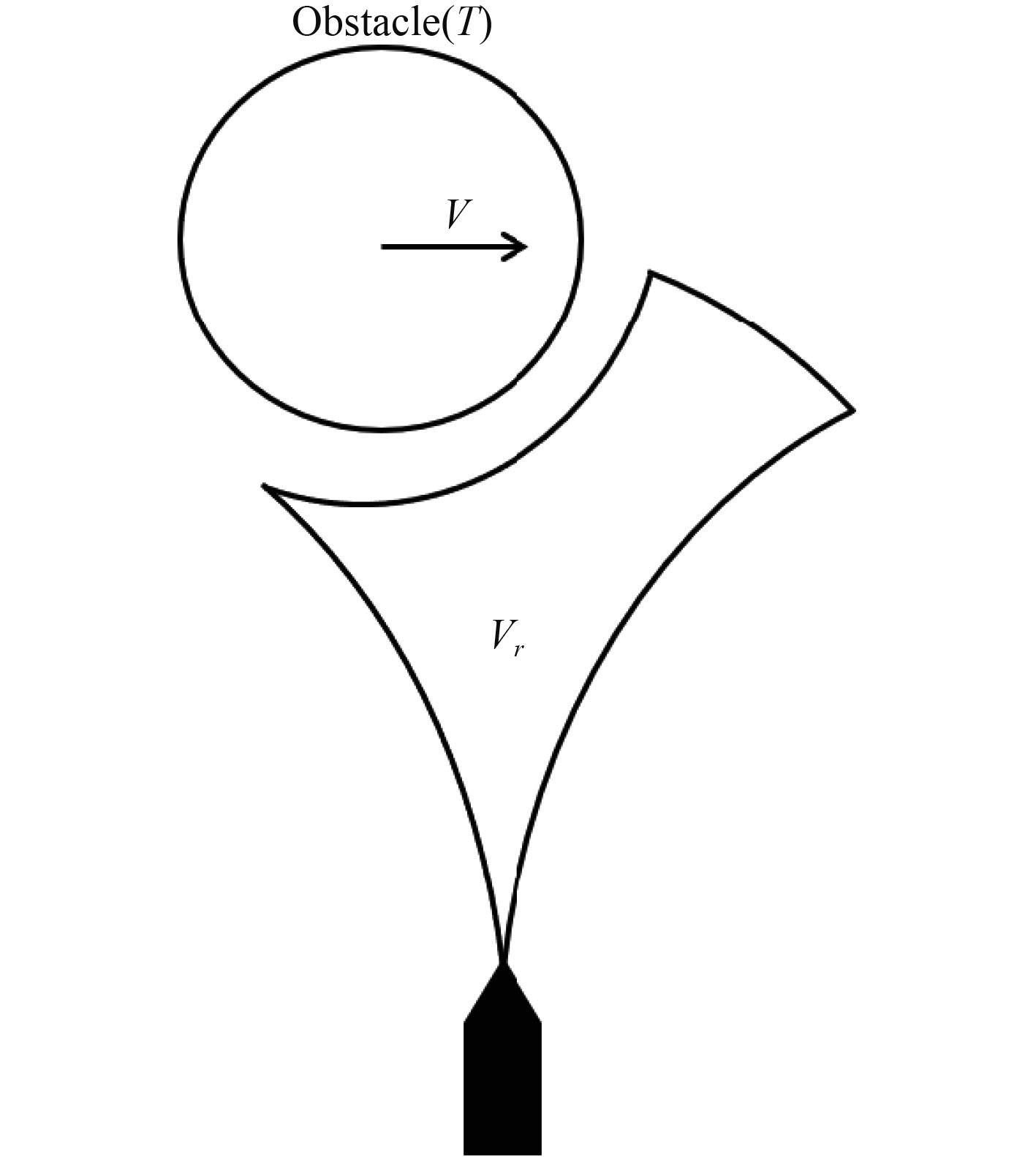
传统DWA算法基于对静止障碍物进行局部路径规划,未考虑对移动障碍物的避碰。因此,为使该算法能适用于存在移动障碍物的路径规划环境,需对障碍物的移动速度
|
图 5 传统DWA速度窗口 Fig. 5 Traditional DWA speed window |
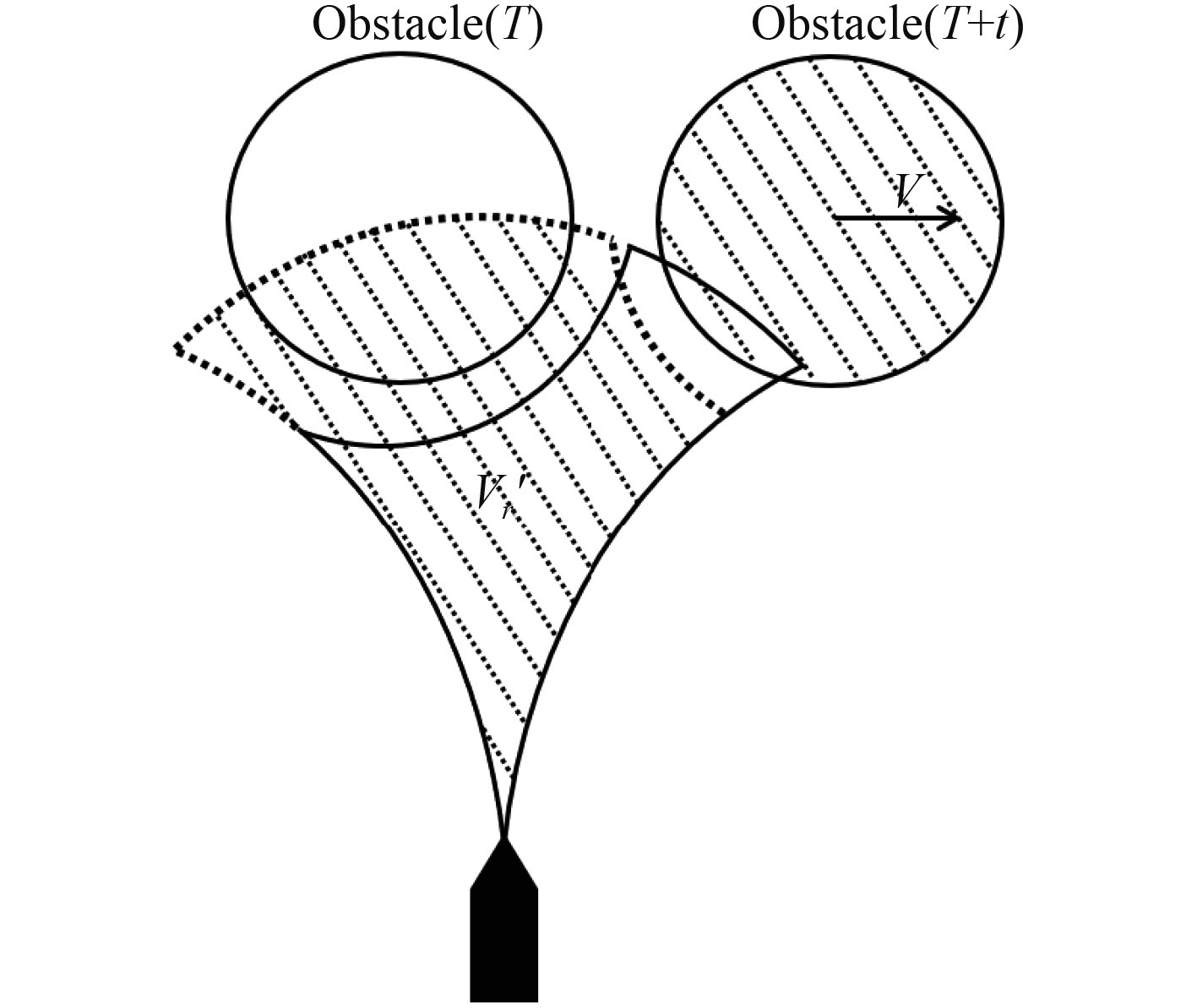
|
图 6 改进DWA速度窗口 Fig. 6 Improve DWA speed window |
通过图4和图5对比,使用障碍物预测终点的改进方法计算的速度窗口
综合对传统DWA算法改进完善,改进后的DWA算法流程如下:
1)设定目标点位置,并根据传感器信息获取周围障碍物实时位置、速度等信息,初步形成总体态势;
2)根据当前时刻USV自身运动性能及预测时间,得到合适大小的原始速度窗口、预测障碍物位置及运动状态;
3)根据预测障碍物位置,利用改进后的速度窗口选择策略剔除无效航迹;
4)通过改进后的评价函数对所有可行航迹进行评分,选择最优航迹
5)根据最优航迹的线速度、角速度执行至下一周期;
6)检查是否到达目标点,若是,则结束运行,若否,则返回第2步。
3 仿真实验与分析为验证改进后的DWA算法可进一步提升USV避障能力,实现USV编队集结,在Matlab 2017a环境下对传统DWA算法和改进DWA算法进行对比仿真实验,并对结果进行分析。USV运动学参数及DWA算法参数如表1和表2所示。
|
|
表 1 USV运动学参数 Tab.1 USV kinematics parameters |
|
|
表 2 DWA算法参数 Tab.2 DWA algorithm parameters |
根据图1和图2所示场景,结合表1和表2参数进行建模仿真,结果如图7所示。

|
图 7 优化前后对比图 Fig. 7 Comparison chart before and after optimization |
由图7可知,经优化后的DWA算法,在相同的评价函数内容和权重系数的情况下,速度窗口更加合理,使无人艇在满足避碰距离的前提下,执行路程更短的避碰轨迹,提高了避障效率。
3.2 完善dist函数计算验证以表1和表2数据为基础,将预测轨迹时间提高至200 s、权重系数
可知,由于传统算法
依据表1和表2的参数,同时模拟4艘USV同时出发并按指定位置集结组成特定队形,具体如图8所示。
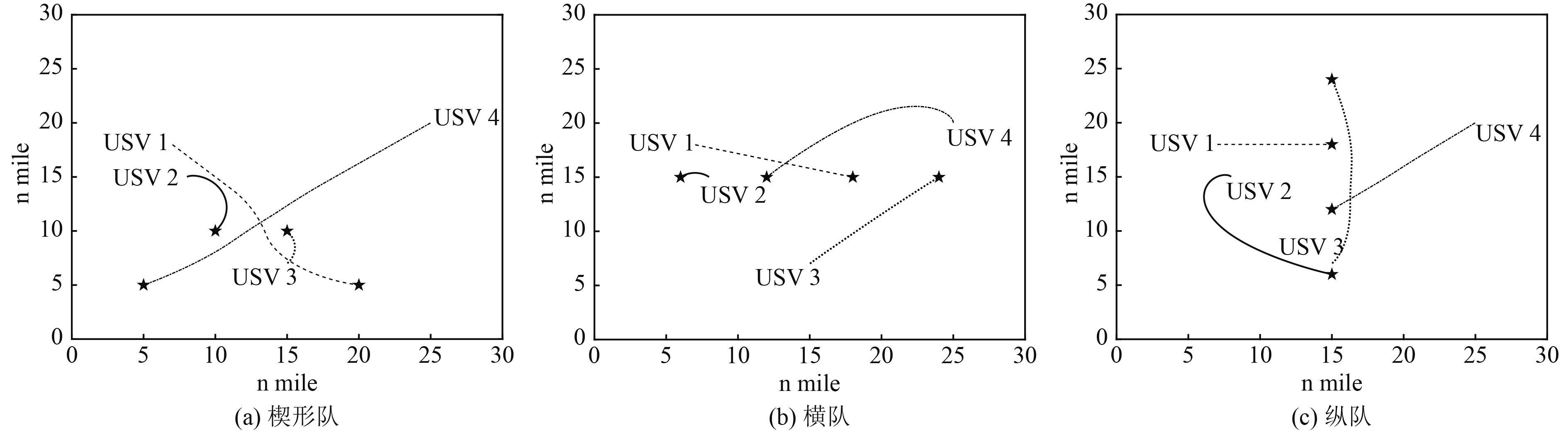
|
图 8 各种队形图 Fig. 8 Various formation charts |
可知,经优化后的DWA算法可在多USV的环境下成功实现编队集结,且任一USV在集结过程中能在自身机动能力范围内对其他USV做出正确的避让机动,各USV航行期间始终保持预先设定的安全距离,未发生碰撞。
4 结 语本文通过分析传统DWA算法,对避碰过程中预测轨迹窗口存在的问题进行分析。通过修改采样窗口范围和评价函数指标,保留更多的优秀轨迹;通过完善
| [1] |
THOA M T, COPOT C, TRAN D T, et al. Heuristic approaches in robot path planning[C]// The Proceedings of 2016 IEEE Robotics an Autonomous Systems, 2016: 13–28.
|
| [2] |
ZHANG An, LI Chong, BI Wenhao. Rectangle expansion A* pathfinding for grid maps[J]. Chinese Journal of Aeronautics, 2016, 29(5): 1385-1396. DOI:10.1016/j.cja.2016.04.023 |
| [3] |
QURESHI A H, AYAZ Y. Potential functions based sampling heuristic for optimal path planning[J]. Autonomous Robots, 2016, 40(6): 1079-1093. DOI:10.1007/s10514-015-9518-0 |
| [4] |
柳长安, 鄢小虎, 刘春阳, 等. 基于改进蚁群算法的移动机器人动态路径规划方法[J]. 电子学报, 2011, 39(5): 1220-1224. |
| [5] |
王晓燕, 杨乐, 张宇, 等. 基于改进势场蚁群算法的机器人路径规划[J]. 控制与决策, 2018, 33(10): 1775-1781. DOI:10.13195/j.kzyjc.2017.0639 |
| [6] |
ROESMANN C., FEITEN W., WOESCH T., et al. Bertram. trajectory modification considering dynamic constraints of autonomous robots[J], ROBOTIK 2012; 7th German Conference on Robotics, 2012, pp. 1–6.
|
| [7] |
STATHEROS T, HOWELLS G, MCDONALD-MAIER K. Autonomous ship collision avoidance navigation concepts, technologies and techniques[J]. The Journal of Navigation, 2008, 61: 129-142. DOI:10.1017/S037346330700447X |
| [8] |
CHANG L, SHAN L, JIANG C, et al. Reinforcement based mobile robot path planning with improved dynamic window approach in unknown environment[J]. Autonomous Robots, 2021, 45(1): 51-76. DOI:10.1007/s10514-020-09947-4 |
| [9] |
王永雄, 田永永, 李璇, 等. 穿越稠密障碍物的自适应动态窗口法[J]. 控制与决策, 2019, 34(5): 927-936. DOI:10.13195/j.kzyjc.2017.1497 |
| [10] |
常路, 单梁, 戴跃伟, 等. 未知环境下基于改进DWA的多机器人编队控制[J]. 控制与决策, 2022, 37(10): 2524-2534. DOI:10.13195/j.kzyjc.2020.1817 |
| [11] |
刘渐道, 刘文, 张英俊, 等. 基于改进动态窗口法的无人水面艇自主避碰算法[J]. 上海海事大学学报, 2021, 42(2): 1-7. DOI:10.13340/j.jsmu.2021.02.001 |
| [12] |
FOX D, WOLFRAM B, SEBASTIAN T. The dynamic window approach to collision avoidance[J]. IEEE Robotics Autom, 1997(4): 23–33.
|
 2023, Vol. 45
2023, Vol. 45
