2. 天津瀚海蓝帆海洋科技有限公司,天津 300462;
3. 天津科技大学 机械工程学院,天津 300222
2. Tianjin Hanhai Lanfan Marine Technology Co.Ltd., Tianjin 300462, China;
3. School of Mechanical Engineering, Tianjin University of Science and Technology, Tianjin 300222, China
波浪是海洋中随处可见的一种现象,如何利用波浪的特性,高效地为无人船提供航行的动力,是近年来针对长航程USV进行研究的一个重点。将波浪作为无人船的动力并非近两年来新诞生的想法,早在1958年Daniel [1]的一篇专利中便提出了一种设想,将水翼布置在船体的两侧,利用船舶随波浪的起伏使水翼产生向前的推力。2016年,Bowker等[2]通过对Autonaut型USV的实验分析得出,前后双翼布置在船体上的水平间距和船体本身的耐波性能都会十分显著地影响船体对波浪的响应能力,但并未形成系统的规律总结。
2018年,Lopes等[3]建立了一种波浪驱动USV的分析方法,将大攻角、不同轴心位置的参数影响加入传统的非线性升力理论中,根据葡萄牙西海岸的波浪特点进行建模,在二维和三维环境下对水翼的推力、阻力、效率进行了计算分析,验证了模型的准确性。
2020年,Diego等[4]在二维平面上对波浪振荡系统进行了模拟分析,考虑到了前翼对后翼的尾流影响,通过调整双翼的水平和垂直间距建立了4组不同的计算模型,得出在海况2(波长大于海况1)的条件下,整体的推进效率要高于海况1,但并未就海况对船体的影响进行详细讨论与分析。
2021年,何广华等[5]基于重叠网格的技术,在二维平面下对波浪推进翼的水动力性能进行了数值计算分析,认为波浪水翼的升沉幅值应当在水翼弦长的1倍左右,并对其他参数进行了数值模拟分析,但并未有实验数据与其仿真结果进行对比验证。2022年,常宗瑜等[6-7]通过Aqwa软件与Adams联合仿真模拟了波浪船的动力学响应过程,之后又针对不同流速不同攻角的情况以单个水翼为模型进行了研究,认为主动控制的水翼可提供更佳的推进效果。
综合来看,大多数学者仅对理想状况下的波浪振荡水翼进行了分析研究,对船体和海况的影响考虑较少。因此,探究在不同海况条件下,船体对波浪的响应规律,并以此为拓展,为不同工况下的USV整体设计提供设计参考十分必要。
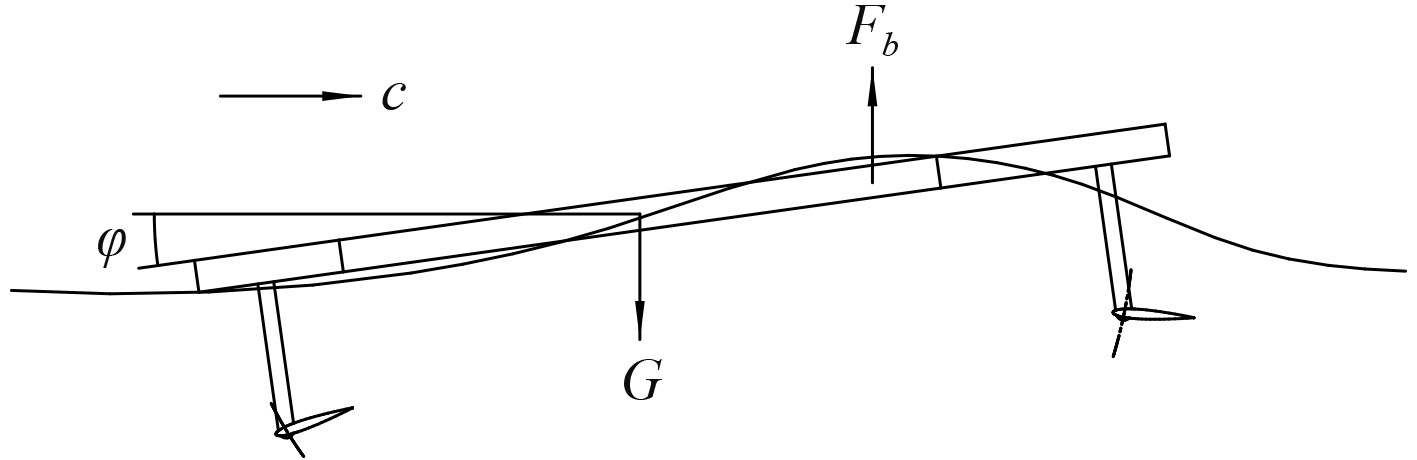
1 船体模型及受力分析船体受到波浪的激励产生一定俯仰角,船体的俯仰运动则带动了水下翼型的姿态变化,水翼两侧因此产生了压力差,产生向前的推力,具体受力情况如图1和图2所示。
|
图 1 船体俯仰受力 Fig. 1 Pitching force on hull |
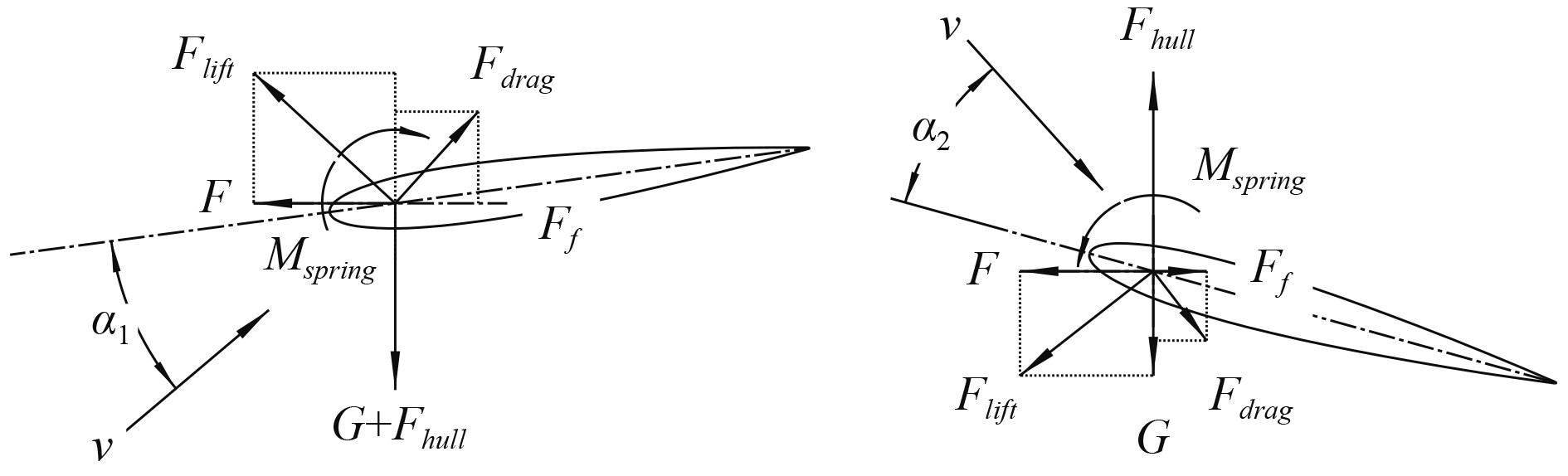
|
图 2 作用在水翼上的力 Fig. 2 Force on the hydrofoil |
波浪的峰谷效应使得船体可大致分作两部分,一侧浸水较深,一侧浸水较浅,打破了船体的平衡条件,当船首位于波谷时(见图1),首部所受浮力减少,尾部浮力增加,使船体产生了一定的俯仰力矩,船体的俯仰又使得水翼与水流产生了相对运动。由于限位和扭簧的存在,水翼与来流形成了一定的攻角
只关注船体俯仰角的变换,则船体所受力矩有:
| $ {\boldsymbol{M}} = \rho gl\Delta V - 2{F_{hull}}s ,$ | (1) |
船体俯仰角变化有:
| $ \varphi = \frac{\boldsymbol{{M}}}{{2J}}{t^2}。$ | (2) |
式中:
线型微幅波认为波高
Stokes五阶波的波面方程为:
| $ \eta {\text{ = }}\frac{1}{k}\sum\limits_{n = 1}^5 {{\lambda _n}{{\cos }^{}}} n(kx - \omega t),$ | (3) |
波速
| $ k{c^2} = C_0^2(1 + {\lambda ^2}{C_1} + {\lambda ^4}{C_2}),$ | (4) |
在Stokes五阶波的表达式中,需确定系数
| $ H = \eta \left| {_{\theta = 0} - } \right.\eta \left| {_{\theta = \text{π} }} \right. ,$ | (5) |
可得:
| $ \frac{{{\text{π}} H}}{d} = \frac{1}{{d/L}}[\lambda + {\lambda ^3}{B_{33}} + {\lambda ^5}({B_{35}} + {B_{55}})],$ | (6) |
再由式(4)可得:
| $ \frac{d}{{{L_0}}} = \frac{d}{L}\tanh kd[1 + {\lambda ^2}{C_1} + {\lambda ^4}{C_2}] 。$ | (7) |
式中,
在CFD模拟中定义Stokes五阶波作为连续体的波浪模型,选择合适的波高,波长,水深及流速即可生成相应的流体域。具体输入参数如表1所示。
|
|
表 1 数值模拟参数 Tab.1 Parameter in numerical simulation |
网格分布如图3所示,数值造波与理论公式得出的结果对比如图4所示。

|
图 3 网格分布 Fig. 3 The grid distribution |
|
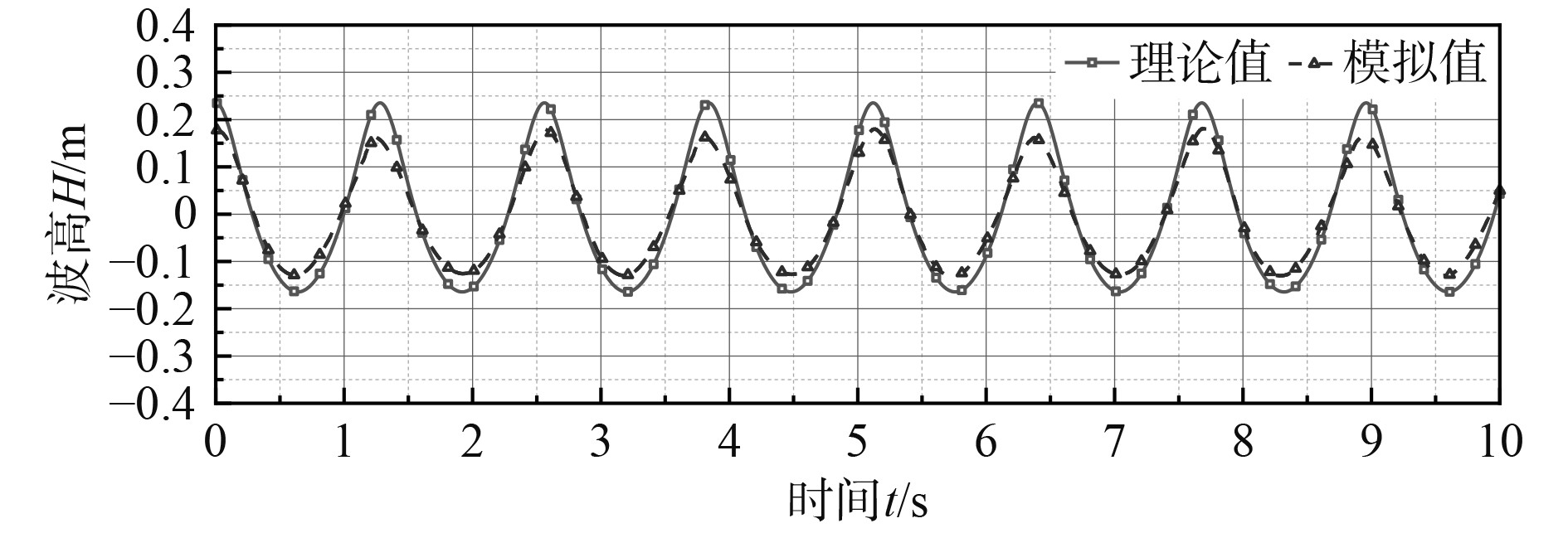
图 4 理论与模拟波浪对比 Fig. 4 Compared with theoretical and simulated wave |
可看出,数值模拟生成的波浪与理论值相比存在一定衰减,最大衰减幅值约为8%,且分布在波峰与波谷处。这是由于波浪受到船体阻碍,产生了一定回流,抵消了部分波浪的能量,使得波浪产生了一定程度的衰减,为此可认为模拟生成的波浪条件符合真实环境下的海况。
3 模拟结果及分析波浪的条件不同,USV的姿态响应也各有出入。针对渤海湾近海海况,参照王晓明等[8]调研的海况参数表,设计了多组实验,具体参数如表2所示。通过数值模拟得到了同一款无人船在相同波长不同波高和不同波长相同波高状态下的振荡响应结果。
|
|
表 2 波浪驱动无人船模拟参数 Tab.2 Parameter of USV in simulation |
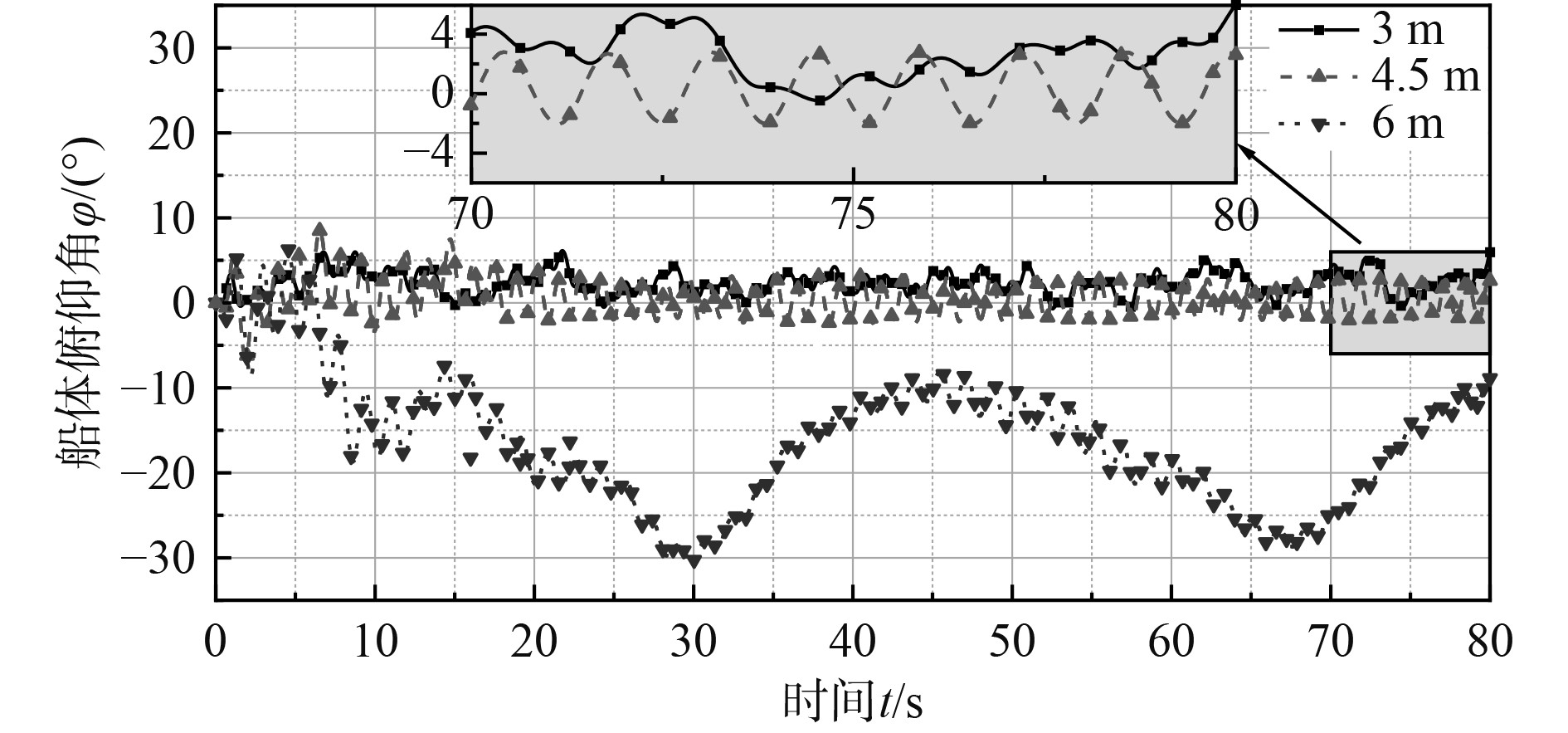
波长是影响船体响应频率的主要因素,船体能否产生周期性的俯仰运动,并与波浪的周期吻合是探讨的主要内容,为此主要针对不同波长的情况下,船体俯仰角的振荡周期与波浪的周期响应关系开展分析。模拟结果如图5所示。
|
图 5 波高0.5 m波长不同时船体俯仰角的响应曲线 Fig. 5 Angle change of hull when H=0.5 m |
可看出,当波长为3 m时,船体的响应角均为正角度,且经过多个波浪周期后才回归0°,说明船体无法与每个波浪形成同步响应,始终为船首受波浪浮力引起振荡,尾部几乎无法对波浪的起伏做出响应。波长为6 m时,在0~5 s内仍在0值上下波动,但随着波浪不断作用,逐渐偏离0值,最终完全变为负角度且跨多个波的起伏。由于偏离过多,且3种波高的案例中,船体响应姿态均与图5所示相似,便不再针对此案例进行对比分析。而波长为4.5 m时,船体则较好的与波浪进行了响应,经过缓冲期后,在20 s开始逐渐呈周期性变化,由图5的局部视图可看出,船体在±2.5°之间表现出周期性的波动。
因船体随波浪的响应是一个瞬态且逐渐趋于动态稳定的过程,为了更加清晰展示响应趋势,截取了模拟趋于稳定时的响应数据做出分析。
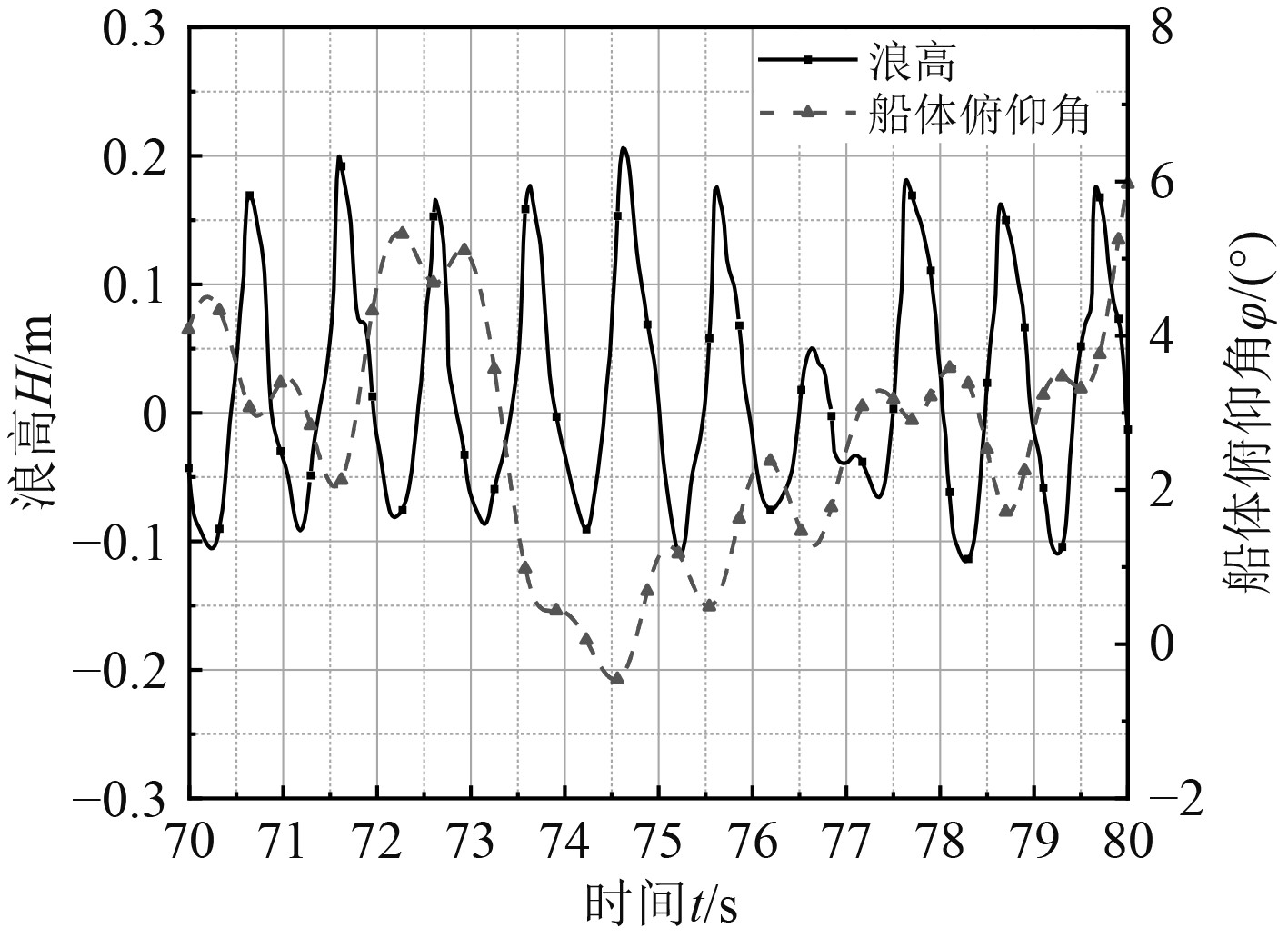
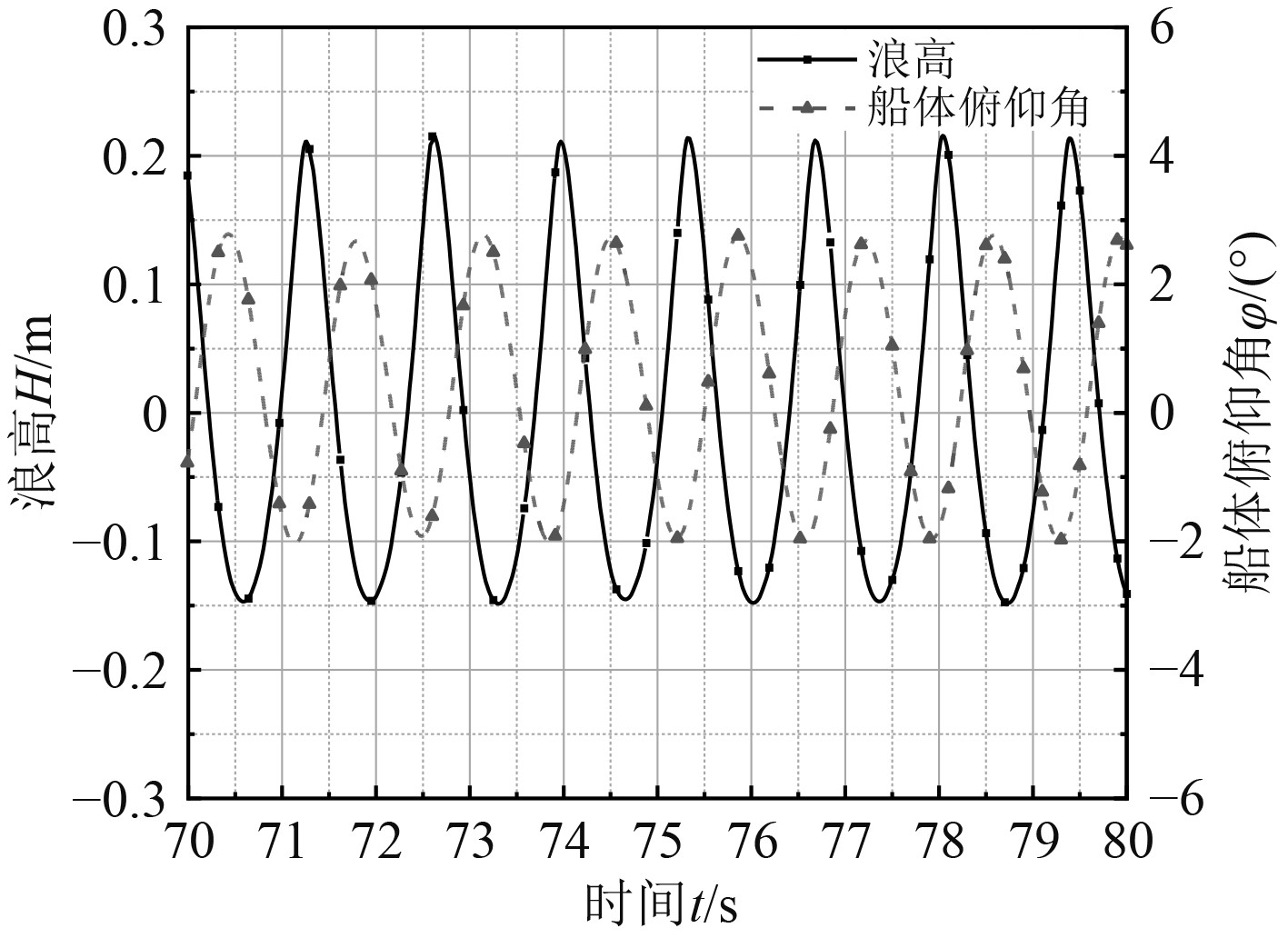
通过监测距船体首部1.5 m处的波高变化,记录了波高的历时变化曲线,并在图6与图7中与船体俯仰角进行对比,进一步清晰展示了船体的响应能力。波长为3 m时,船体的振荡曲线基本无规律可言,一个起伏横跨多个波浪,无法对每一个波浪做出响应。当波长为4.5 m时,俯仰角与波高的频率同步性较高,可对每一次波浪的起伏做出响应,是较为理想的响应模型,由于波浪监测点位于船体前侧,所以曲线存在一定相位差。
|
图 6 波长3 m波高0.5 m波浪与船体响应曲线 Fig. 6 The response of hull in wave when L=3 m H=0.5 m |
|
图 7 波长4.5 m波高0.5 m波浪与船体响应曲线 Fig. 7 The response of hull in wave when L=4.5 m H=0.5 m |
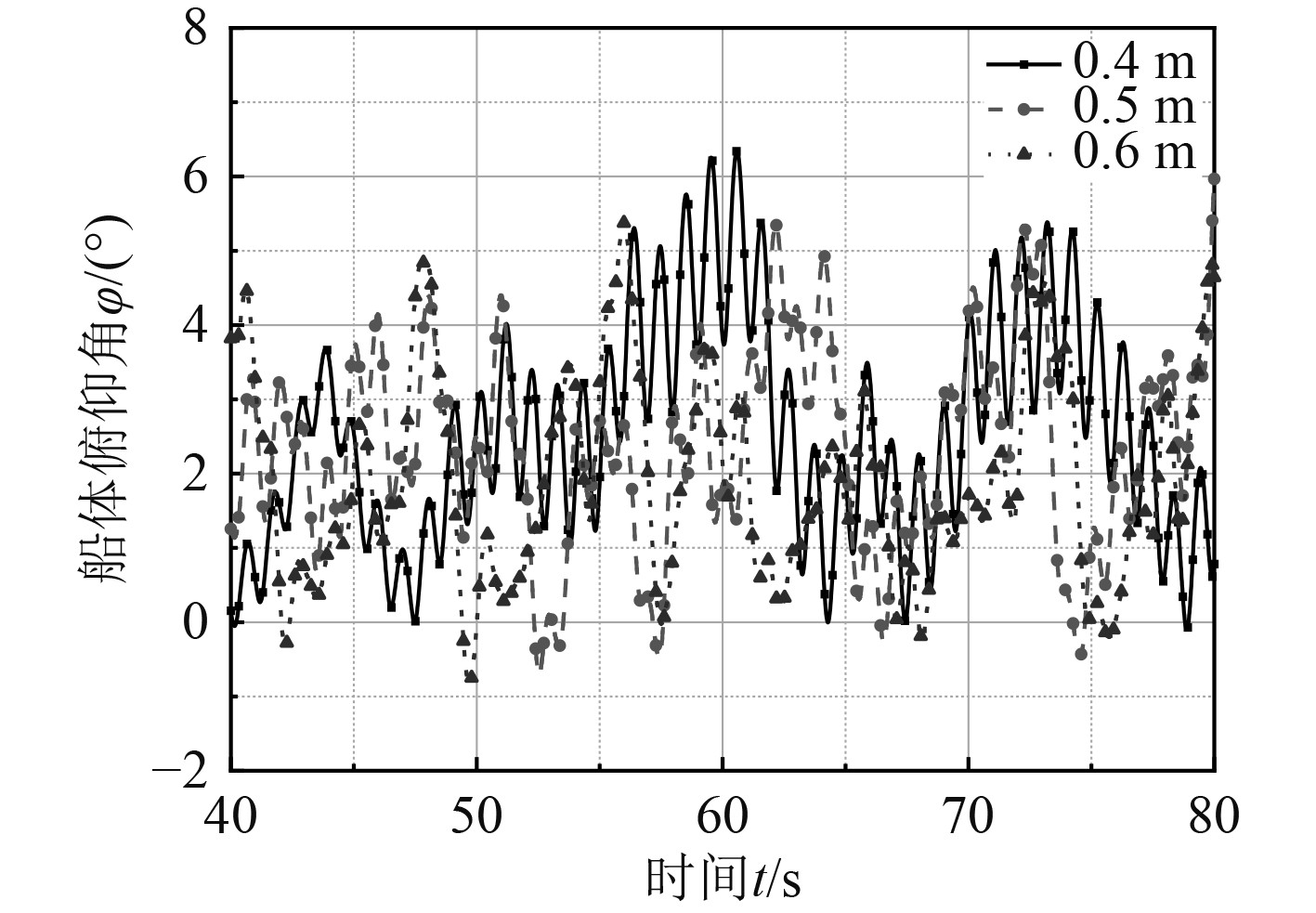
当船体可有效响应波浪的起伏完成俯仰运动时,波高则决定了俯仰角及翼板转角的大小。因此主要分析在不同波高下,船体的振荡幅度及前后侧水翼的振荡变化。模拟结果如图8和图9所示。
|
图 8 波长3 m不同波高下船体俯仰角变化 Fig. 8 Angle change of hull when L=3 m, H=0.4 m, 0.5 m, 0.6 m |

|
图 9 波长4.5 m不同波高下船体俯仰角变化 Fig. 9 Angle change of hull when L=4.5 m, H=0.4 m, 0.5 m, 0.6 m |
图8中,由于船体对波浪响应的同步性较差,无法明确判断波高的影响。图9则可明显看出当波长为1.5倍船长(即4.5 m)时,随着波高的增加,船体的最大俯仰角也随之增加,其中波高为0.6 m时,同比增幅可达225.28%。同时,对比图8与图9可发现,波长3 m时整体响应曲线较为紊乱,而波长4.5 m时则较为规律,说明波高的变化对船体的响应频率无明显影响。
由图10和图11对比可知,船体对波浪响应的同步性对水翼的振荡存在较为明显的影响。波长3 m时,前侧及后侧翼板的角度变化均有一定紊乱,而波长4.5 m时则普遍形成了较为规律的振荡响应。当波长为4.5 m、波高为0.6 m时,水翼的振幅和频率在全部模拟中表现最佳,前侧翼板在±35°区间内稳定变化,与文献[9-11]中期望最优角较为吻合。通过比较前侧与后侧响应曲线,可发现后侧翼板的响应能力弱于前侧翼板,波高0.6 m时最为明显,较前侧振幅的缩减最大可达31.3%。

|
图 10 波长3 m不同波高下翼板攻角变化 Fig. 10 Angle change of hydrofoil when L=3 m, H=0.4 m, 0.5 m, 0.6 m |

|
图 11 波长4.5 m不同波高下翼板攻角变化 Fig. 11 Angle change of hydrofoil when L=4.5 m, H=0.4 m, 0.5 m, 0.6 m |
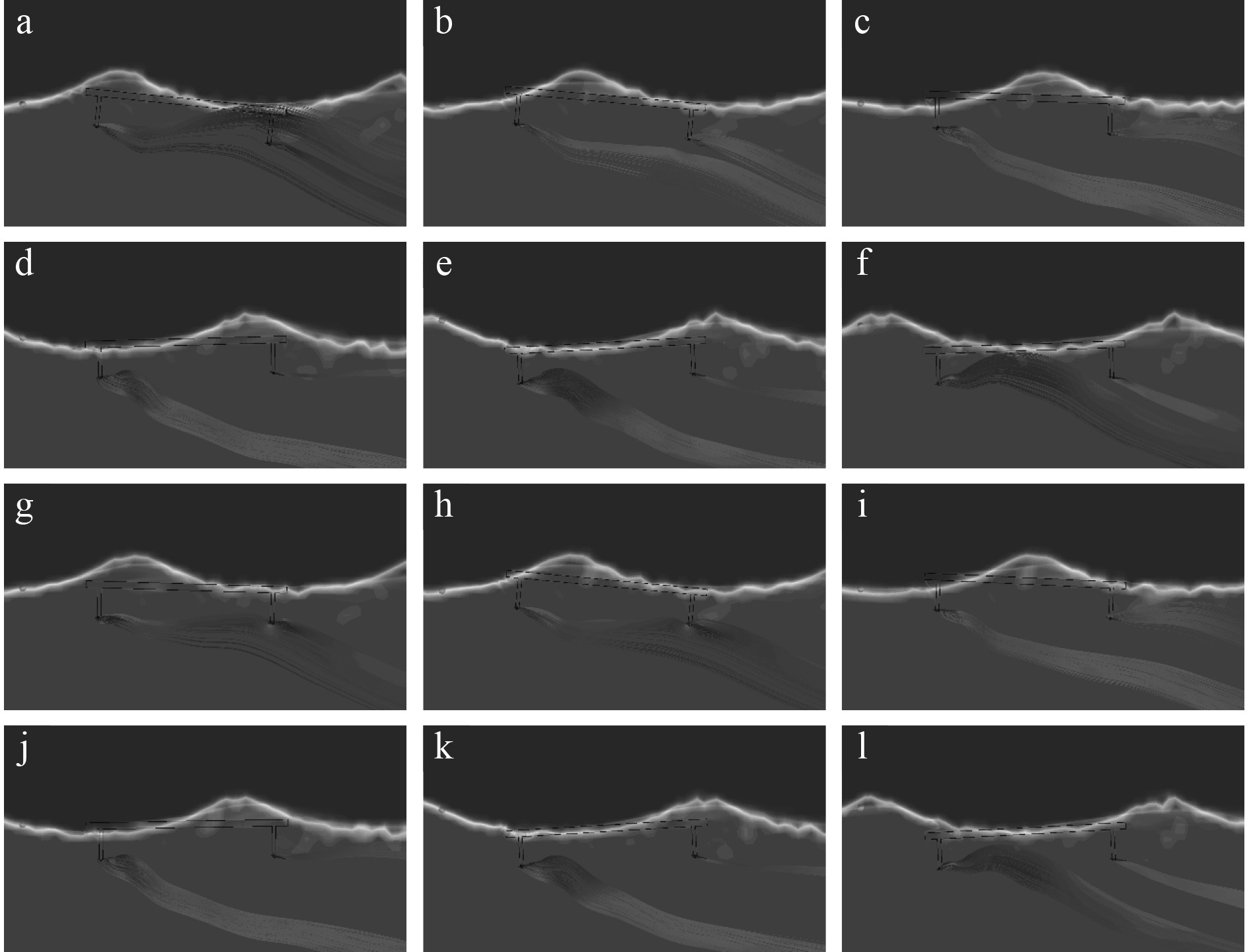
在翼板振荡角度的正负区间内,负角度的区间要略小于正角度,在后侧翼板的响应曲线中尤为明显,波长4.5 m且波高0.6 m时,负角度振幅约为正角度的50.1%~76.5%。为探究产生的原因,在CFD模拟中对经过翼板的流场进行监测,每0.2 s生成一张图像,如图12所示。
|
图 12 波长4.5 m波高0.6 m时船体振荡响应流场图 Fig. 12 The flow field of hull’s oscillatory response when L=4.5 m, H=0.6 m |
可看出,经过前侧翼板的流场大部分时间并未覆盖后侧翼板,不足以对后侧产生明显的影响,因此后侧翼板的响应衰减,并不能以流场干扰解释。除此之外,船体的振荡区间内,正角度的区间总是大于负角度,这也说明,在同一个波浪周期中,首部的响应能力要优于尾部。为此,可认为对于波浪的响应,前侧较后侧也存在一定优先级。
4 实验验证与分析为了验证模拟数据的准确性与可靠性,针对仿真中所使用的波浪驱动无人船设计了完整实验平台,通过在船体、前侧及后侧翼板搭载角度传感器记录运行过程中的角度变化,在天津某出海口进行了多次实验。
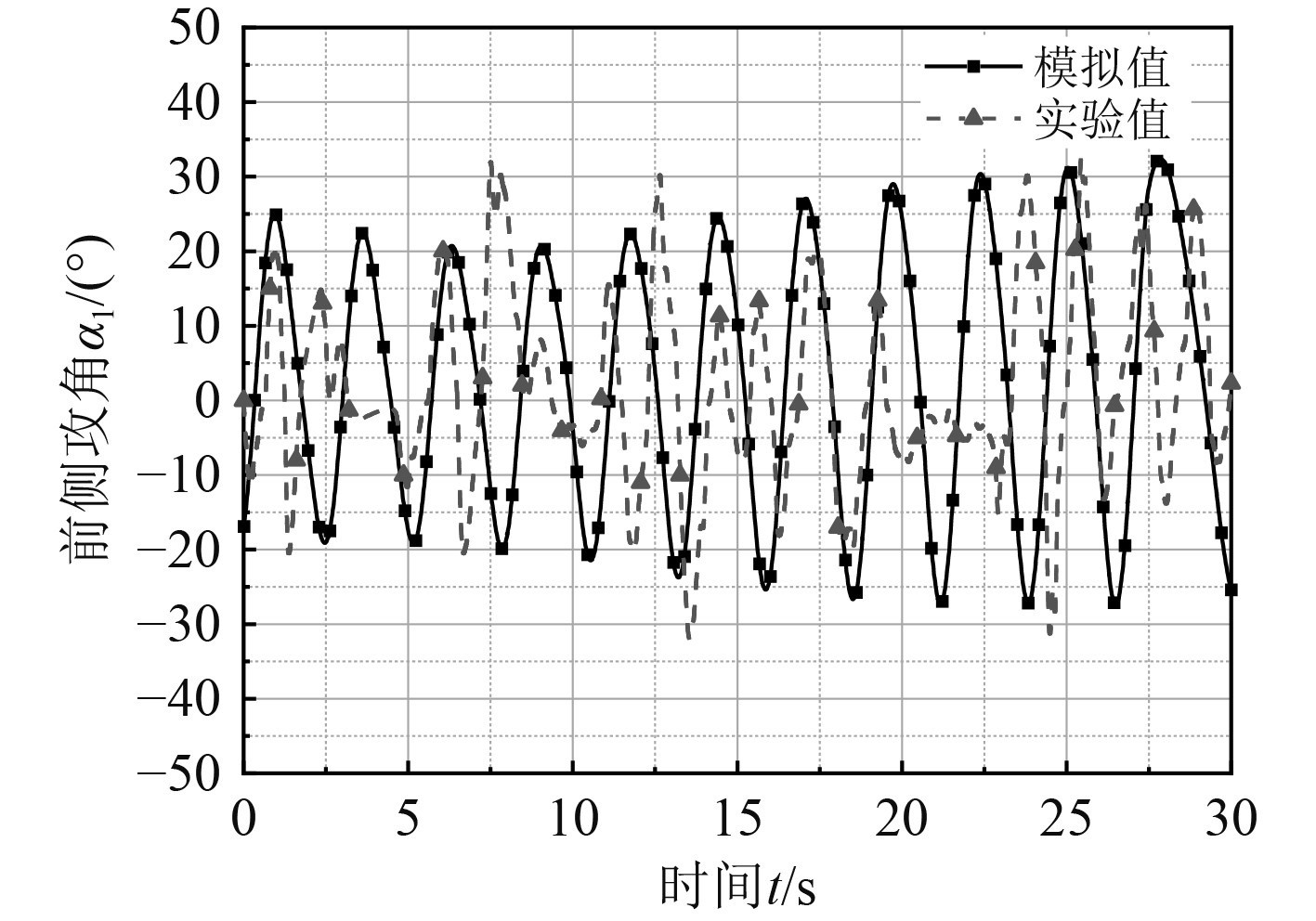
图13为航行路径,由于布放时位置和方向均有变化,故航行轨迹并不连续。由图14可以看出,实验中,船体俯仰角随波浪的振荡频率与模拟值基本吻合,但也存在跨多个波浪的情况出现,因实际中的波浪更加复杂,可能存在多个波浪的重叠交叉,船体的响应也因此出现偏差且属正常现象。图15及图16则描述了前侧及后侧翼板在实验中的响应曲线,与模拟值相对比,响应频率基本一致,呈正负交叉振荡。

|
图 13 实验路径 Fig. 13 Experience track |

|
图 14 模拟与实际船体俯仰角振荡对比 Fig. 14 Angle change of hull between simulation and experiment |
|
图 15 模拟与实际前侧翼板攻角变化对比 Fig. 15 Angle change of front foil between simulation and experiment |

|
图 16 模拟与实际后侧翼板攻角变化对比 Fig. 16 Angle change of back foil between simulation and experiment |
3组数据在相位以及振幅上均存在一定偏差,这是由于模拟与实际中波浪的参数差异导致。因实际海况难以测量,本模拟虽选用了实验当天某气象平台提供的海况参数接近值,但仍存在一定误差,为此结果也有所出入,但整体趋势符合预期。
5 结 语1)船体响应频率的同步性主要由船长与波长之比决定。从本文数据分析可得,船长与波长之比为2∶ 3时,船体响应的同步性较好。
2)波浪水翼的振幅则主要取决于波高,随着波高增加,船体及翼板的振荡范围明显增加。波长4.5 m且波高0.6 m时,响应曲线对比文中其他案例为最佳状态,水翼在±35°内呈周期性振荡。
3)船体首部对波浪的响应能力优于尾部,同时,后侧翼板的响应衰减并非源自前侧翼板的流场干扰,仍是船体对波浪的响应差异导致。
| [1] |
BØCKMANN E. Wave propulsion of ships[J]. 2015–3–5
|
| [2] |
BOWKER J A, TOWNSEND N C, TAN M, et al. Experimental analysis of submerged flapping foils; implications for autonomous surface vehicles (ASVs)[C]//Oceans 2016 MTS/IEEE Monterey. IEEE, 2016: 1–10.
|
| [3] |
LOPES D B S, Falcão de Campos J A C, Sarmento A. An analytical model study of a flapping hydrofoil for wave propulsion[C]//International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2018. 3–7
|
| [4] |
MOREIRA Diego, MATHIAS Nuno, MORAIS Tiago. Dual flapping foil system for propulsion and harnessing wave energy: A 2D parametric study for unaligned foil configurations. [J]. Ocean Engineering, 2020: 5–10
|
| [5] |
何广华, 莫惟杰, 王威, 等. 重叠网格技术下振荡水翼的水动力特性[J]. 哈尔滨工业大学学报, 2021, 53(12): 137–143.
|
| [6] |
CHANG Z Y, DENG C, ZHANG J K, et al. Propulsion performance analysis of wave-powered boats[J]. International Journal of Engineering and Technology, 2020, 10(2): 127-129. |
| [7] |
CHANG Z, DENG C, FENG Z, et al. Performance analysis of wave-powered vehicle by active control of the hydrofoil[J]. Ocean Engineering, 2022, 255: 126-128. |
| [8] |
WANG X, SHANG J, LUO Z, et al. Reviews of power systems and environmental energy conversion for unmanned underwater vehicles[J]. Renewable and Sustainable Energy Reviews, 2012, 16(4): 1958-1970. DOI:10.1016/j.rser.2011.12.016 |
| [9] |
GAUTHIER M. Wave-assisted propulsion for autonomous surface vehicles[D]. Memorial University of Newfoundland, 2018. 36–39.
|
| [10] |
陈福根. 摆动水翼推进的水动力性能影响分析[D]. 哈尔滨: 哈尔滨工业大学, 2020: 32–33.
|
| [11] |
BOWKER J A, TAN M, TOWNSEND N C. Forward speed prediction of a free-running wave-propelled boat[J]. IEEE Journal of Oceanic Engineering, 2020, 46(2): 402-413. |
 2023, Vol. 45
2023, Vol. 45

