2. 武汉理工大学 船海与能源动力工程学院,湖北 武汉 430000;
3. 中国舰船研究设计中心,湖北 武汉 430000;
4. 武汉理工大学 交通与物流工程学院,湖北 武汉 430000
2. School of Naval Architecture Ocean and Energy Power Engineering, Wuhan University of Technology, Wuhan 430000, China;
3. China Ship Research and Design Center, Wuhan 430000, China;
4. School of Transportation and Logistics Engineering, Wuhan University of Technology, Wuhan 430000, China
随着对船舶操作自动化和自主管理的需求日益增多[1],国内外对船舶的研究也朝着智能化方向迅速发展。通过有效的控制手段进行航迹跟踪,是船舶在复杂环境下也能顺利完成任务的重要方法之一。航迹跟踪控制是指自主船舶从任意初始位置出发,驶入期望航迹并沿着期望航迹到达终点。
近年来,随着神经网络的飞速发展,深度强化学习受到了国内外广泛关注[2]。深度学习可实现对任意复杂非线性函数的逼近,学习高维特征;强化学习可在与环境交互过程中学习到最优解,使得其在求解复杂的非线性问题中有独特优势。因此,深度强化学习在航迹跟踪控制中的应用值得探索和研究。针对自主船舶的控制问题,Shen等[3]通过Actor- Critic强化学习方法来解决欠驱动船舶的路径跟随问题。Martinsen等[4]提出一个基于深度确定性策略梯度方法(DDPG)的新框架,用于解决在未知洋流影响下的欠驱动船舶的直线路径跟随问题。Zhao等[5]使用改进的随机制动深度强化学习(DRLRB)解决了欠驱动无人水面舰艇(USV)编队的路径跟踪问题。
为实现自主船舶航迹跟踪的高精度控制,本文在视线制导算法(LOS)的基础上,提出一种基于优先经验回放的SAC算法(PER-SAC)深度强化学习控制器,基于OpenAI gym框架构建的仿真环境中进行训练,通过仿真实验验证了PER-SAC控制器的有效性。
1 船舶建模以及航迹跟踪问题 1.1 欠驱动自主船舶建模通常只考虑三自由度数学模型对欠驱动自主船舶的航迹跟踪问题进行研究,欠驱动自主船舶的运动模型用三自由度运动学方程和三自由度动力学方程来描述。定义向量
| $ \left\{ {\begin{array}{*{20}{l}} {\dot {\boldsymbol{\eta}} = {\boldsymbol{R}}({\boldsymbol{\eta}} ){\boldsymbol{\nu}} },\\ {{\boldsymbol{M}}\dot {\boldsymbol{\nu}} + {\boldsymbol{C}}({\boldsymbol{v}}){\boldsymbol{\nu}} + {\boldsymbol{D}}({\boldsymbol{v}}){\boldsymbol{v}} = {{\boldsymbol{\tau}} _c} + {{\boldsymbol{\tau}} _e}} 。\end{array}} \right. $ | (1) |
式中,
| $ {\boldsymbol{R}}({\boldsymbol{\eta}} ) = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0 \\ {\sin \psi }&{\cos \psi }&0 \\ 0&0&1 \end{array}} \right] 。$ | (2) |
| $ {\boldsymbol{M}}= \left[ {\begin{array}{*{20}{c}} {m - {X_{\dot u}}}&0&0 \\ 0&{m - {Y_{\dot v}}}&{ - {Y_{\dot r}}} \\ 0&{ - {N_{\dot v}}}&{{I_z} - {N_{\dot r}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{m_{11}}}&0&0 \\ 0&{{m_{22}}}&{{m_{23}}} \\ 0&{{m_{32}}}&{{m_{33}}} \end{array}} \right] 。$ | (3) |
式中:m为自主船舶的质量;
| $ \begin{split} {{\boldsymbol{C}}_A}(v) & = \left[ {\begin{array}{*{20}{c}} 0&0&{ - mv + {Y_{\dot v}}v + {Y_{\dot r}}r} \\ 0&0&{mu - {X_{\dot u}}u} \\ {mv - {Y_{\dot v}}v - {Y_{\dot r}}r}&{ - mu + {X_{\dot u}}u}&0 \end{array}} \right]= \\ & \left[ {\begin{array}{*{20}{c}} 0&0&{ - {m_{22}}v - {m_{23}}r} \\ 0&0&{{m_{11}}u} \\ {{m_{22}}v - {m_{23}}r}&{ - {m_{11}}u}&0 \end{array}} \right]。\\[-21pt] \end{split} $ | (4) |
| $ \begin{split} {\boldsymbol{D}}(v) & = \left[ {\begin{array}{*{20}{c}} { - {X_u} - {X_{|u|u}}|u|}&0&0 \\ 0&{ - {Y_v} - {Y_{|v|v}}|v|}&{ - {Y_r} - {Y_{|v|r}}|v|} \\ 0&{ - {N_v} - {N_{|v|v}}|v|}&{ - {N_r} - {N_{||v\mid }}|v|} \end{array}} \right] =\\ & \left[ {\begin{array}{*{20}{c}} {{d_{11}}}&0&0 \\ 0&{{d_{22}}}&{{d_{23}}} \\ 0&{{d_{32}}}&{{d_{33}}} \end{array}} \right] 。\\[-21pt] \end{split} $ | (5) |
式中,
由上述公式总结,标准的自主船舶水平面三自由度运动模型为:
| $ \left\{ \begin{aligned} & {\dot x = u\cos (\psi ) - v\sin (\psi )} ,\\ & {\dot y = u\sin (\psi ) + v\cos (\psi )},\\ & {\dot \psi = r} ,\\ & {\dot u = \frac{1}{{{m_{11}}}}\left( {{m_{22}}ur + {m_{23}}{r^2} - {d_{11}}u + {\tau _u} + {\tau _{eu}}} \right)},\\ & {\dot v = \frac{1}{{{m_{22}}}}\left( { - {m_{23}}\dot r - {m_{11}}ur - {d_{22}}v - {d_{23}}r + {\tau _v} + {\tau _{ev}}} \right)},\\ & \dot r = \frac{1}{{{m_{33}}}}\left( - {m_{32}}\dot v - {m_{22}}uv - {m_{23}}u{\text{r}} + {m_{11}}uv - {d_{32}}v -\right.\\ & \left. {d_{33}}r + {\tau _t} + {\tau _{er}} \right) 。\end{aligned} \right. $ | (6) |
航迹跟踪指的是跟随预定义航迹的任务。对于自主船舶的航迹跟踪,船舶应以所需的航向角通过航路点
LOS制导系统的示意图如图1所示。假设
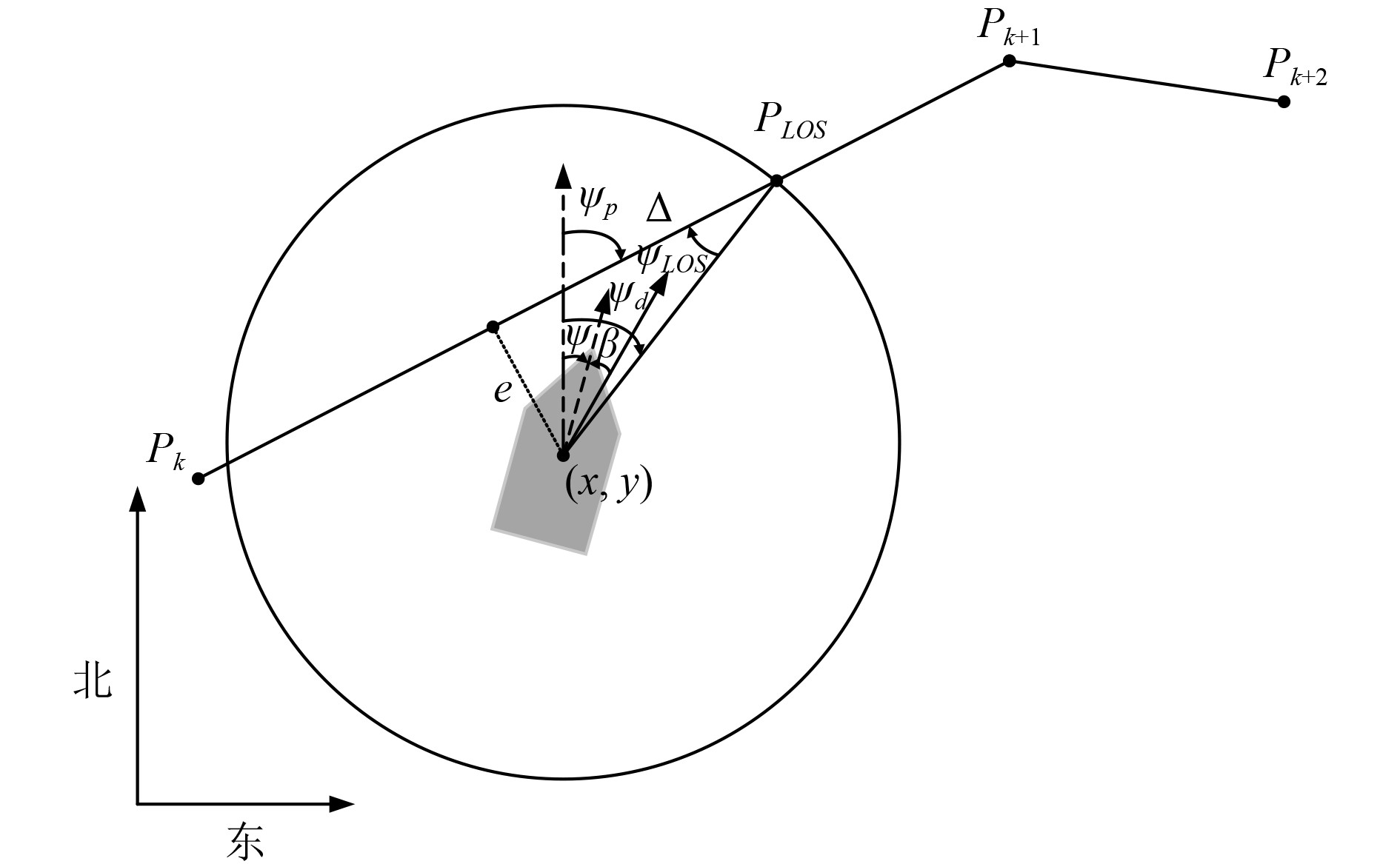
|
图 1 LOS航迹跟踪导航示意图 Fig. 1 LOS trajectory tracking navigation schematic |
| $ {\psi _d} = {\psi _p} + {\psi _{LOS}} = {\psi _p} + \arctan \left(\frac{{ - e}}{\Delta }\right)。$ | (7) |
式中:
自主船舶跟踪当前的期望航路点,进入到一定范围时,则需自动放弃跟踪该航路点,而去跟踪下一个期望航路点
强化学习(Reinforcement Learning)属于机器学习的范畴,是解决马尔科夫决策过程问题的重要方法[6]。深度强化学习(Deep Reinforcement Learning,DRL)是深度学习和强化学习结合,其具备了复杂决策问题的处理能力。近年来,随着对深度强化学习领域的研究不断深入,越来越多的优秀DRL算法被提出,如DQN[7]、DDPG[8]和SAC[9]等。
在DRL算法训练过程中,智能体(Agent)与环境(Environment)进行交互,获得环境的反馈(Reward),然后不断重复这一过程,在重复的交互过程中,会收集大量数据,再利用这些数据不断的学习优化智能体在当前状态下的动作选择,而获得一个最优策略(Policy)。航迹跟踪的控制流程如图2所示。
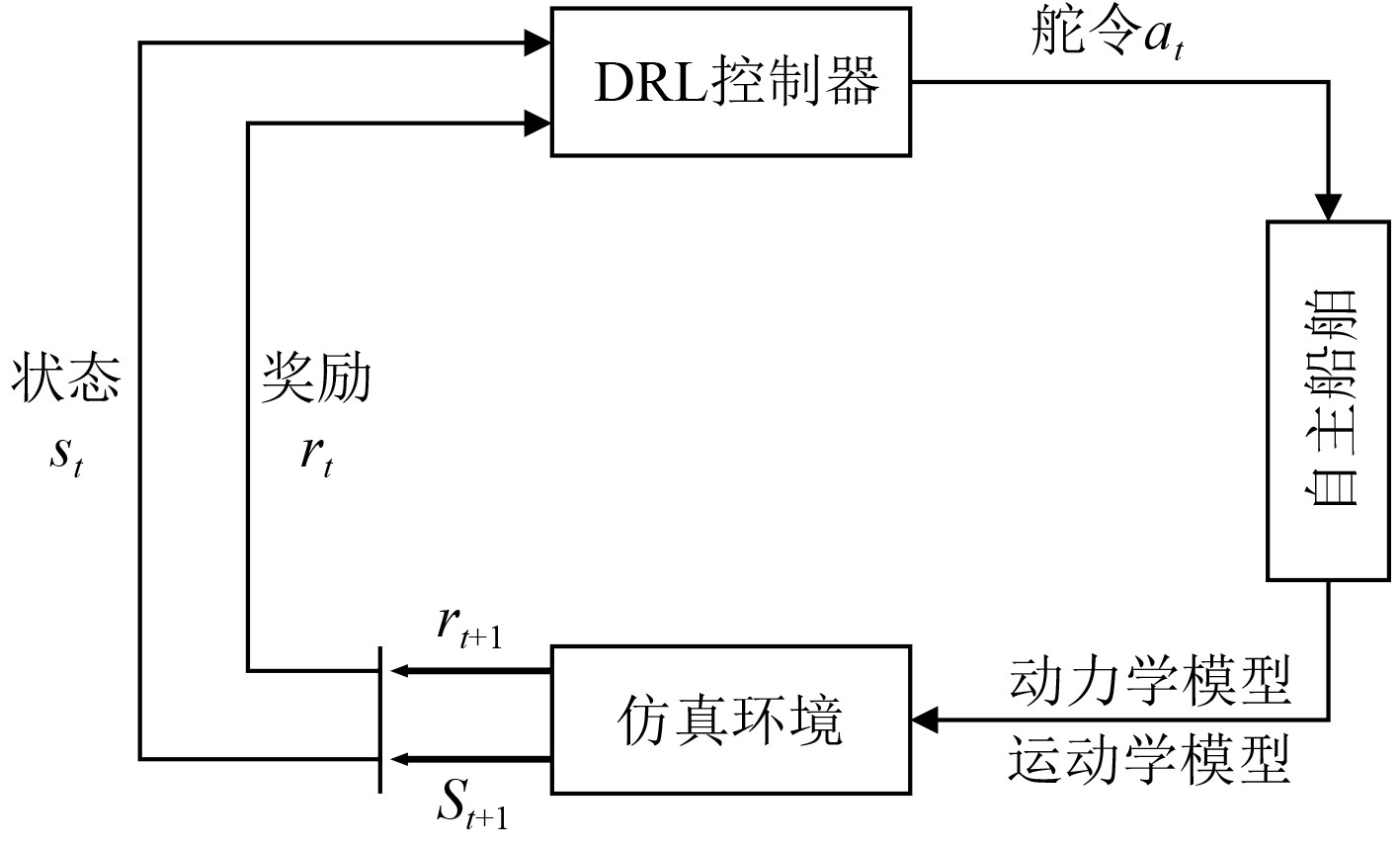
|
图 2 航迹跟踪的控制流程图 Fig. 2 Control flow of track tracking |
仿真环境根据船舶智能体的动力学模型和运动学模型去更新当前时刻的状态
SAC(Soft Actor-Critic)算法是一种off-policy算法。与传统深度强化学习算法不同的是,SAC在优化策略以获得奖励期望最大的同时,还会最大化策略的熵,这样可让策略尽可能随机,防止策略过早的收敛到局部最优值,并且可探索到完成任务的多个策略,提高智能体的抗干扰能力。SAC同时最大化奖励期望和熵值的目标,可表示为:
| $ {\pi }^{\ast }=\mathrm{arg}\underset{\pi }{\mathrm{max}}\sum _{t}{\mathbb{E}}_{\left({s}_{t},{a}_{t}\right)\sim {\rho }_{\pi }}\left[r\left({s}_{t},{a}_{t}\right)+\alpha \mathcal{H}\left(\pi \left(\cdot \mid {s}_{t}\right)\right)\right] 。$ | (8) |
式中,策略
SAC算法一共由5个网络构成,分别为一个Actor网络和4个Critic网络,4个Critic网络又包括动作状态价值估计
| $ \begin{split} {L_Q}(\theta ) = & {\mathbb{E}_{\left( {{s_t},{a_t},{s_{t + 1}}} \right) \sim \mathcal{D}}}\\ & \left[ {\frac{1}{2}{{\left( {{Q_\theta }\left( {{s_t},{a_t}} \right) - \left( {r\left( {{s_t},{a_t}} \right) + \gamma {V_{\bar \theta }}\left( {{s_{t + 1}}} \right)} \right)} \right)}^2}} \right] \\ = & {\mathbb{E}_{\left( {{s_t},{a_t},{s_{t + 1}}} \right) \sim \mathcal{D},{a_{t + 1}} \sim {\pi _\phi }}}\\ & \left[ \frac{1}{2}\Bigr( {Q_\theta }\left( {{s_t},{a_t}} \right) - \Bigr( r\left( {{s_t},{a_t}} \right) + \gamma \Bigr( {Q_{\bar \theta }}\left( {{s_{t + 1}},{a_{t + 1}}} \right) \right. \\ & - \alpha \log \left( {{\pi _\phi }\left( {{a_{t + 1}}\mid {s_{t + 1}}} \right)} \right) \Bigr) \Bigr) \Bigr)^2 ] 。\end{split} $ | (9) |
式中,
在Actor网络中,从经验池中取部分数据来训练Actor网络,Actor网络的损失函数为:
| $ {L_\pi }(\phi ) = {\mathbb{E}_{{s_t} \sim \mathcal{D},\varepsilon \sim \mathcal{N}}}\left[ {\alpha \log {\pi _\phi }\left( {{a_t}|{s_t}} \right) - Q\left( {{s_t},{a_t}} \right)} \right]。$ | (10) |
式中,
SAC算法使用了重参数技巧(reparameterization trick)采样动作,Actor网络更新梯度中的动作就是通过重参数技巧得到,在状态
| $ {a_t} = {f_\phi }\left( {{\varepsilon _t};{s_t}} \right)。$ | (11) |
式中,
SAC算法还可自动调节温度系数,当探索到新的区域时,最优动作未知,需增加温度系数
| $ L(\alpha ) = {\mathbb{E}_{{a_t} \sim {\pi _t}}}\left[ { - \alpha \log {\pi _t}\left( {{a_t}|{\pi _t}} \right) - \alpha {\mathcal{H}_0}} \right]。$ | (12) |
式中,
在SAC算法框架中引入优先经验回放(PER)以提高算法的收敛速度和稳定性,优先经验回放使每个数据被赋予不同优先级,从经验池中采样数据对网络进行训练时,以更大的概率取样到优先级更高的数据,若每次从经验池中采样数据时都根据优先级对所有数据排序,会十分耗费算力,所以引入SumTree存储数据的优先级。
数据的优先级通过TD误差定义,TD误差大的数据就代表该数据的预测精度不高,需提高该数据的出现概率,也就是数据的优先级高。TD误差
| $ {\delta _t} = r\left( {{s_t},{a_t}} \right) + \gamma {Q_{\bar \theta }}\left( {{s_{t + 1}},{a_{t + 1}}} \right) - {Q_\theta }\left( {{s_t},{a_t}} \right)。$ | (13) |
数据
| $ P(i)=\frac{{p}_{i}^{\phi }}{\sum _{i=1}^{k}{p}_{i}^{\phi }}。$ | (14) |
式中,
在PER-SAC算法中,计算TD误差时需同时考虑算法中的
| $ {\delta _j} = abs\left( {TD\left( {{Q_1}} \right)} \right) + abs\left( {TD\left( {{Q_2}} \right)} \right) + \chi abs\left( {TD(\pi )} \right)。$ | (15) |
由于优先级经验回放的引入,样本的采样频率发生了改变,因此需要使用重要性采样权重修正优先经验回放引入的误差。重要性采样权重计算方法为:
| $ ISWeight\text={w}_{j}={\left(N\cdot P(j)\right)}^{-g}/\underset{i}{\mathrm{max}}\left({w}_{i}\right)。$ | (16) |
式中:
最后使用重要性采样权重对Critic网络的损失函数进行更新。对式(9)的更新如下:
| $ {L_Q}^*(\theta ) = {L_Q}(\theta ) \cdot {w_j} 。$ | (17) |
PER-SAC算法的网络结构如图3所示。首先使用Actor网络与环境交互,并使用重参数技巧引入随机噪声加大对环境的探索,然后将当前状态

|
图 3 PER-SAC算法网络结构图 Fig. 3 PER-SAC algorithm network structure |
PER-SAC控制器的Actor网络和Critic网络都使用状态作为输入信息。状态被定义为自主船舶在时刻t可从环境中接收的信息,是自主船舶制定决策和评估其长期奖励的依据。同时要对横向跟踪误差和航向角误差进行调节,使横向跟踪误差和航向角误差趋向于0来达到跟踪效果。为了实现更好的跟踪效果,总的状态由时刻
| $ \begin{split} {s_t} =& \left[ {x_t},{y_t},{e_t},{{\left( {{\psi _e}} \right)}_t},{{\left( {{\psi _c}} \right)}_t},{\zeta _t},{d_t},{x_{t - 1}},{y_{t - 1}},{e_{t - 1}},\right.\\ & \left.{{\left( {{\psi _e}} \right)}_{t - 1}},{{\left( {{\psi _c}} \right)}_{t - 1}},{\zeta _{t - 1}},{d_{t - 1}} \right]。\end{split} $ | (18) |
式中:x、y为自主船舶在二维平面中的位置;
针对航迹跟踪任务的特点,将舵角定义为自主船舶的策略所选择的动作,该角度可改变自主船舶的方向和航迹,其值的选取设定为(−35°,35°)以内。
2.2.5 奖励函数设计在本文中,每个时间步骤能获得的奖励细分为目标奖励
1) 目标奖励
目标奖励是根据自主船舶与LOS点之间的距离所给出的奖励,式(19)给出了目标奖励
| $ \begin{split} & {R}_{goal}=\frac{{L}_{t}-{L}_{t+1}}{{v}_{o}\cdot {\rm{d}}t},\\ & \text{where}\;{L}_{t}=\sqrt{{\left({x}_{t}-{x}_{LOS}\right)}^{2}+{\left({y}_{t}-{y}_{LOS}\right)}^{2}}。\end{split} $ | (19) |
式中,
2) 横向跟踪误差奖励
横向跟踪误差奖励是根据给定的动作
| $ {R_{cross}} = \frac{{\left( {{d_{\max}}/2 - e} \right)}}{{{d_{\max}}/2}}。$ | (20) |
式中,
3) 航路点奖励
航路点奖励被定义为当自主船舶通过给定的动作
| $ {R_{waypo{int} }} = \left\{ \begin{aligned} & 10,{\text{ }}{\text{ }}\left\| {{P_{waypo{int} }} - {P_{t + 1}}} \right\| < {\varepsilon _{Check}} ,\\ & 0,{\text{ }}{\rm{otherwise}} 。\end{aligned} \right. $ | (21) |
式中,
最终,定义每个时间步骤能获得的总奖励表达式为:
| $ r = {R_{goal}} + {R_{cross}} + {R_{waypo{int} }}。$ | (22) |
为验证算法的有效性,基于OpenAI gym框架构建了自主船舶航迹跟踪环境,支持使用tensorboard对训练结果进行可视化展示,并且可通过实时绘制自主船舶的航行航迹来掌握算法的训练情况。训练环境包括了图像引擎模块,物理引擎模块和航迹绘制模块等。
训练平台硬件配置为i7-12700H CPU和RTX3060 GPU,SAC-PER控制器中网络的训练超参数设置如表1所示。
|
|
表 1 超参数设置 Tab.1 Hyperparameter settings |
使用Pytorch作为深度强化学习的训练框架,训练回合为900,每回合的最大步长为800,采样时间为1s。为了更清晰地观察仿真结果,以训练回合数为横坐标,该回合的平均奖励值为纵坐标,绘制PER-SAC控制器训练的每回合平均奖励值图,如图4所示。
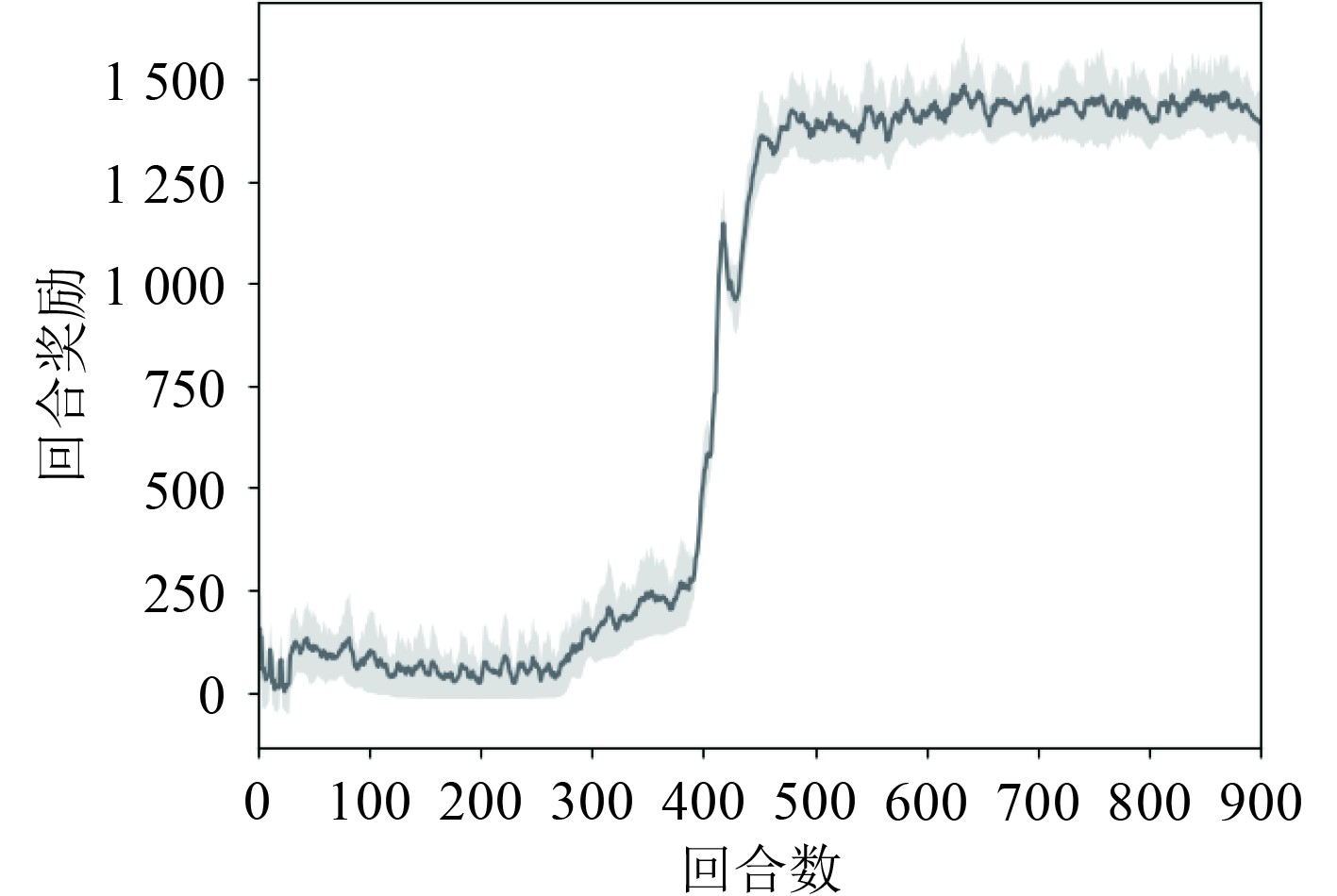
|
图 4 每回合平均奖励值图 Fig. 4 Average reward value per eposide |
从图4可看出,训练初期的每回合平均奖励值较低;当训练到400~500周期时,每回合平均奖励值迅速增加;500周期以后,每回合平均奖励值趋于稳定,算法收敛趋于稳定,展现了快速学习的过程。
3.2 算法对比分析训练完成后,PER-SAC控制器保存了回合奖励最大的参数模型。为验证PER-SAC控制器的有效性,基于OpenAI gym框架构建了2种仿真环境:直线航迹跟踪环境和折线航迹跟踪环境,进行PER-SAC控制器和原始SAC控制器的对比实验。
直线航迹跟踪环境对比试验:设计一条直线航迹,航迹点坐标为(200,0),(200,600),自主船舶从坐标(10,5)出发,单位均为m。
通过观察图5的每回合平均奖励值图,发现在直线航迹跟踪环境中,PER-SAC控制器的回合平均奖励值在390回合左右迅速上升,明显快于SAC控制器的收敛速度。PER-SAC控制器在500回合左右收敛趋于稳定,而SAC控制器在600回合左右收敛趋于稳定,PER-SAC控制器的训练速度更快。通过观察图6直线航迹跟踪图和图7直线航迹跟踪误差图发现,PER-SAC控制器在直线航迹跟踪环境中能快速的进行稳定跟踪,并具有更稳定的控制性能,PER-SAC控制器的航迹存在轻微震荡,而SAC控制器的震荡幅度要明显更大。

|
图 5 直线航迹跟踪每回合平均奖励值图 Fig. 5 Straight track tracking average reward value per eposide |

|
图 6 直线航迹跟踪效果图 Fig. 6 Straight track tracking effect |
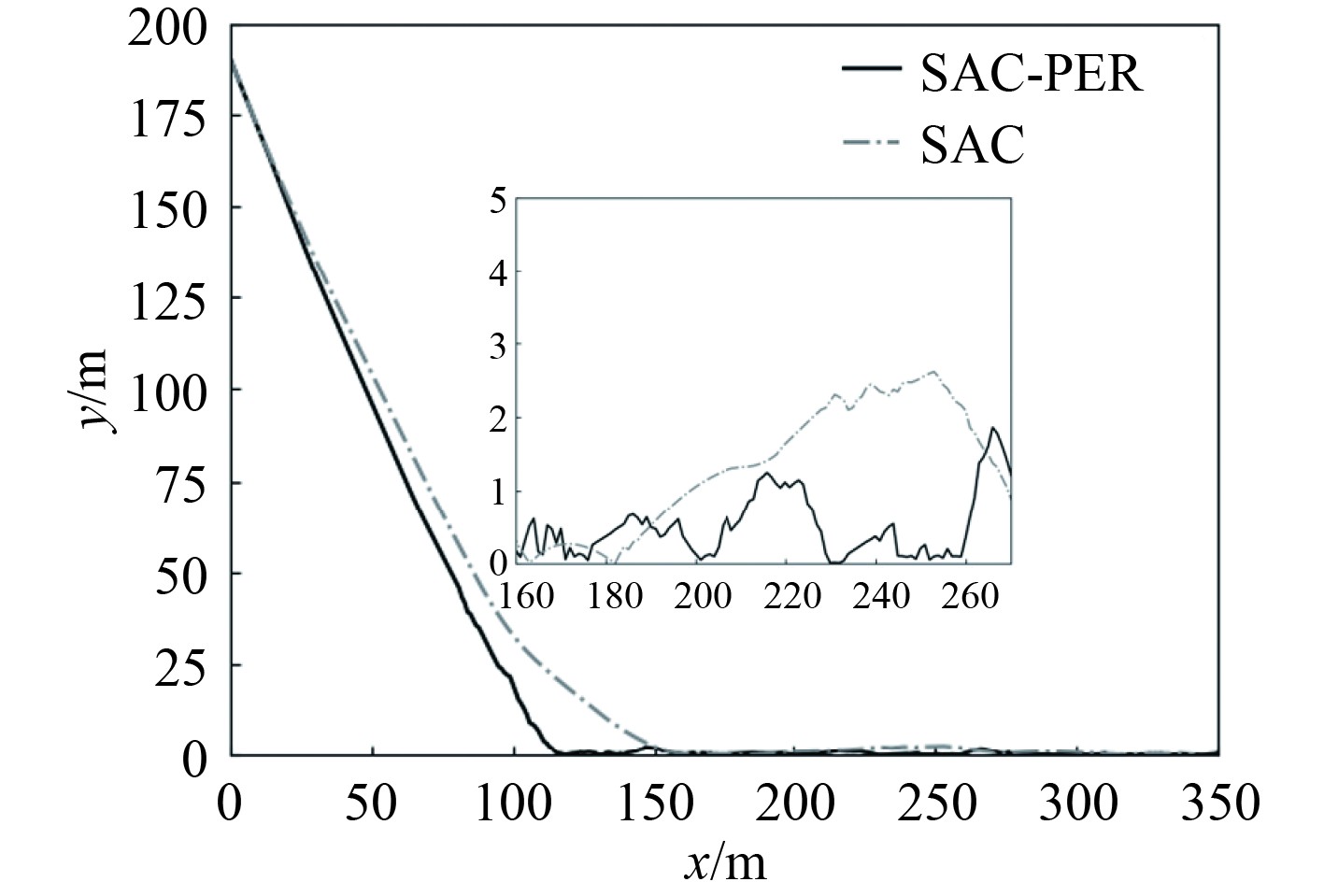
|
图 7 直线航迹跟踪误差图 Fig. 7 Straight track tracking error |
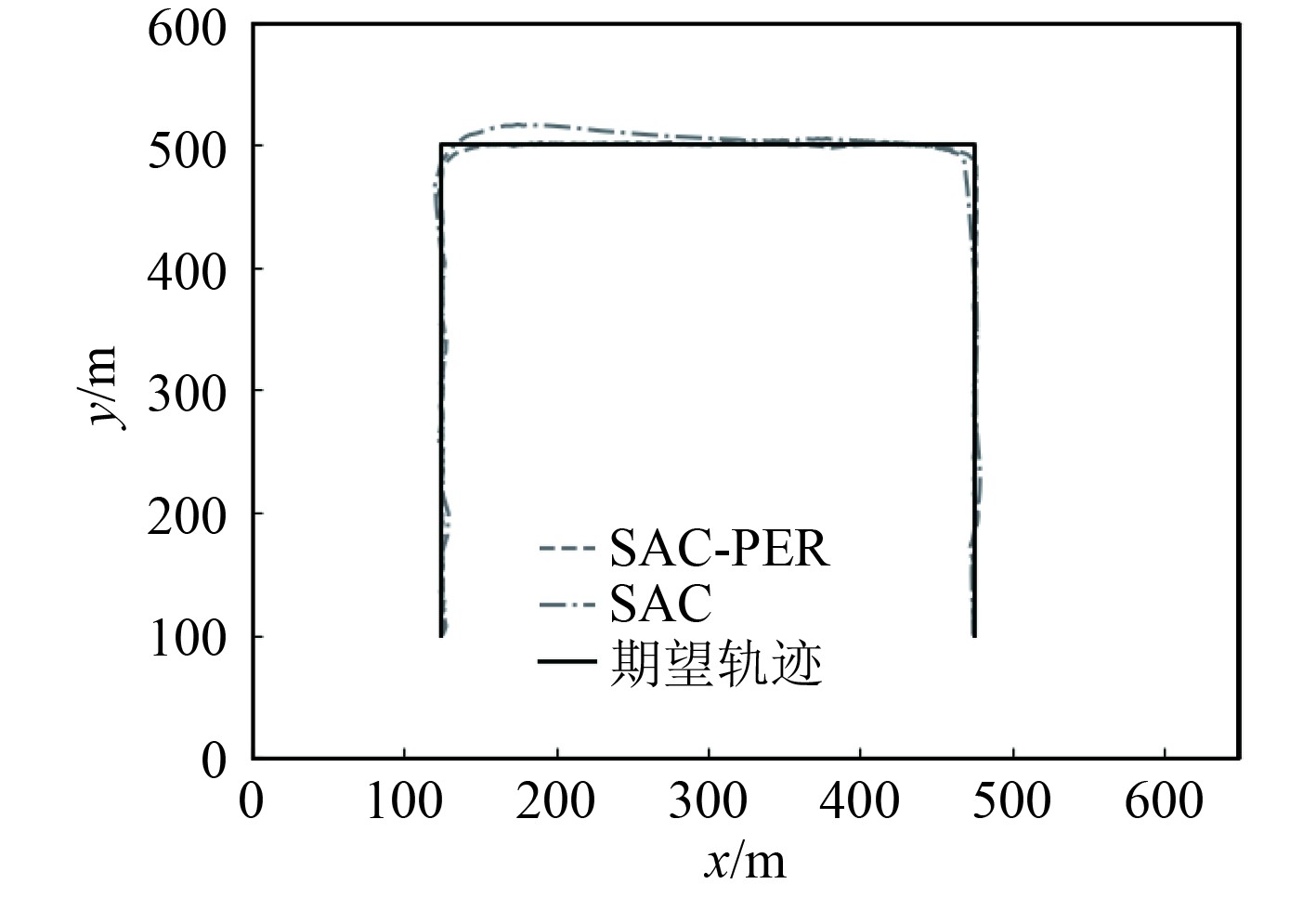
折线航迹跟踪环境对比试验:设计一条折线航迹,航迹点坐标为(125, 0),(125, 500),(475, 500),(475, 100),自主船舶从坐标(475,100)出发,单位均为m。
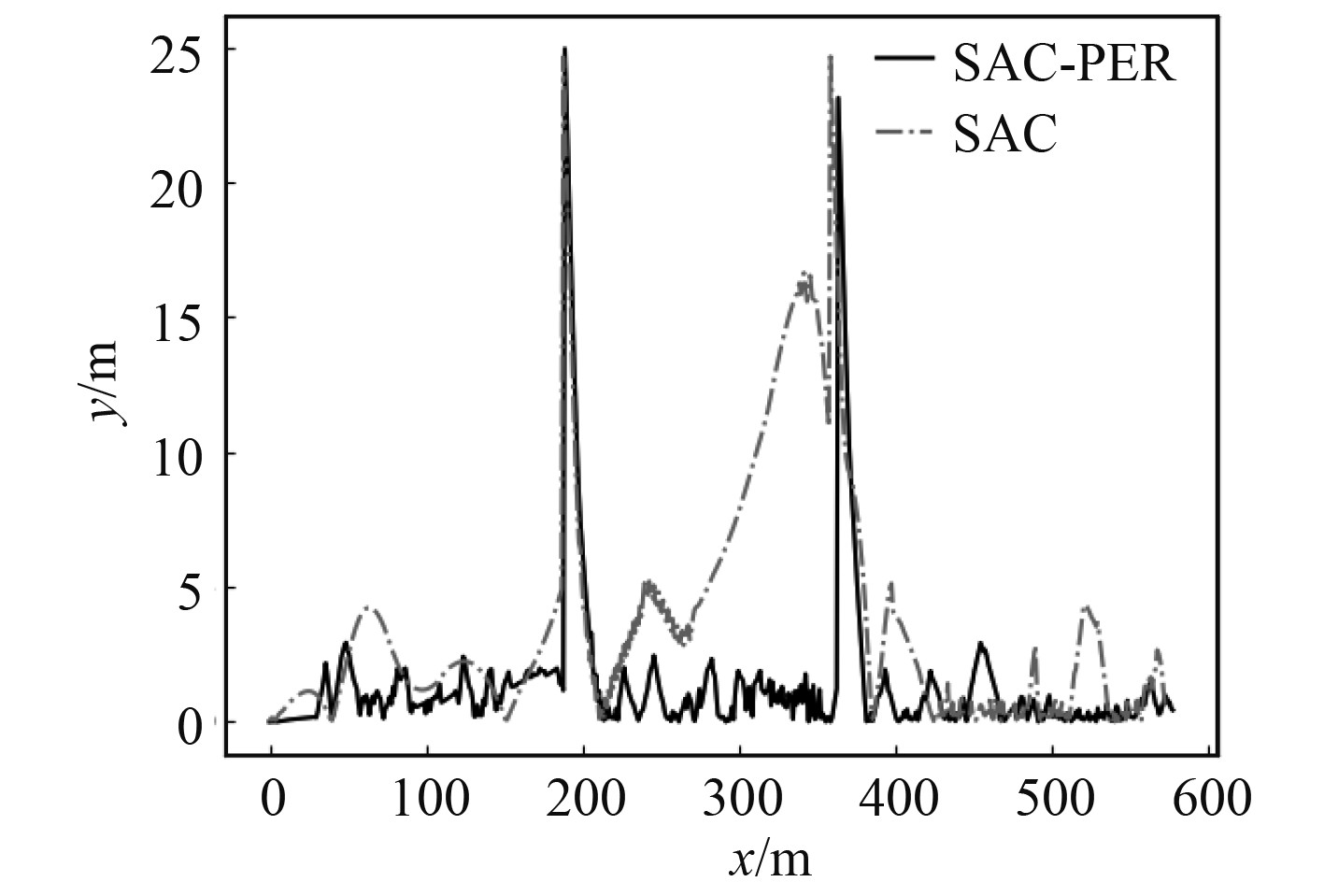
通过观察图8折线航迹跟踪图和图9折线航迹跟踪误差图,可知PER-SAC控制器在转弯处可迅速跟踪到期望航迹,并且相较于SAC控制器有着更高的跟踪精度和更稳定的控制性能。除了在折线转弯处因切换航路点导致横向跟踪误差增大外,PER-SAC控制器的峰值跟踪误差也要明显小于SAC控制器的峰值跟踪误差。
|
图 8 折线航迹跟踪效果图 Fig. 8 Polyline track tracking effect |
|
图 9 折线航迹跟踪误差图 Fig. 9 Polyline track tracking error |
为了进一步评估跟踪误差,对横向跟踪误差的均方根误差进行计算,横向跟踪误差的均方根误差如表2所示。
|
|
表 2 控制性能指标 Tab.2 Control performance indicators |
综上所述,PER-SAC控制器的控制稳定性和控制精度要高于SAC控制器,而且可迅速跟踪到变化的航迹,而SAC控制器无法及时跟踪航迹的变化。由此可见,本文提出的PER-SAC控制器具有控制性能稳定、控制精度高和跟踪及时的特点。
4 结 语本文针对自主船舶的航迹跟踪问题,提出一种基于SAC和PER的深度强化学习控制器,设计了状态、动作空间和奖励函数,并且在基于OpenAI gym框架下构建的不同航迹跟踪环境中进行了仿真实验。通过仿真实验验证了PER-SAC控制器的有效性,同时经过分析发现,PER-SAC控制器在航迹跟踪过程中具有控制精度高,控制性能稳定的特点,对于航迹变化的情况,也可迅速跟踪。整体而言,本文方法可应用到自主船舶的航迹跟踪控制问题中,对船舶的智能控制提供了一定参考。
| [1] |
ZHAO L, ROH M I, LEE S J. Control method for path following and collision avoidance of autonomous ship based on deep reinforcement learning[J]. Journal of Marine Science and Technology, 2019, 27(4): 1. |
| [2] |
王珂, 卜祥津, 李瑞峰, 等. 景深约束下的深度强化学习机器人路径规划[J]. 华中科技大学学报(自然科学版), 2018, 46(12): 77-82. WANG Ke, BU Xiangjin, LI Ruifeng, et al. Deep reinforcement learning robot path planning under the constraint of depth of field[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2018, 46(12): 77-82. |
| [3] |
SHEN H, GUO C. Path-following control of underactuated ships using actor-critic reinforcement learning with MLP neural networks[C]//2016 Sixth International Conference on Information Science and Technology (ICIST). Dalian, China: IEEE, 2016: 317–321.
|
| [4] |
MARTINSEN A B, LEKKAS A M. Straight-path following for underactuated marine vessels using deep reinforcement learning[J]. IFAC-PapersOnLine, 2018, 51(29): 329-334. DOI:10.1016/j.ifacol.2018.09.502 |
| [5] |
ZHAO Y, MA Y, HU S. USV formation and path-following control via deep reinforcement learning with random braking[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(12): 5468-5478. DOI:10.1109/TNNLS.2021.3068762 |
| [6] |
任彧, 赵师涛. 磁导航AGV深度强化学习路径跟踪控制方法[J]. 杭州电子科技大学学报(自然科学版), 2019, 39(2): 28-34. REN Yu, ZHAO Shitao. Magnetic navigation AGV deep reinforcement learning path tracking control method[J]. Journal of Hangzhou Dianzi University (Natural Science Edition), 2019, 39(2): 28-34. |
| [7] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529-533. DOI:10.1038/nature14236 |
| [8] |
LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning[C]//ICLR (Poster). 2016.
|
| [9] |
HAARNOJA T, ZHOU A, HARTIKAINEN K, et al. Soft actor-critic algorithms and applications[J]. arXiv: 1812.05905, 2018.
|
| [10] |
CHUN D H, ROH M I, LEE H W, et al. Deep reinforcement learning-based collision avoidance for an autonomous ship[J]. Ocean Engineering, 2021, 234: 109216. DOI:10.1016/j.oceaneng.2021.109216 |
 2023, Vol. 45
2023, Vol. 45
