2. 嘉兴南湖学院 信息工程学院,浙江 嘉兴 314000
2. Jiaxing Nanhu University, College of Information engineering, Jiaxing 314000, China
和传统的造船金属材料相比,具有高强度、抗冲击力、高刚度、低噪声等优点,这使得碳纤维材料的发展有着十分重要的意义[1]。碳纤维材料随着加工制造技术的提升,在舰船上的应用也越来越广泛[2]。舰船在水面航行过程中,螺旋桨会产生很大的噪声[3]。为了能够降低被敌方探测器探测的概率,各国均在研究可以降低舰船振动噪声的材料,碳纤维复合材料由于其具备较高的声阻尼、质量较轻等优点,已经得到了广泛的使用[4]。由于需要考虑对舰船遭遇到的各类损伤情况,特别是各种破坏性强的弹药产生的爆炸冲击,对舰船的防护能力产生了极大的挑战[5]。为了能够增强舰船在现代战争中的生存能力,对舰船的制造材料以及船体的结构设计提出了更高的要求[6]。本文对船用的碳纤维复合材料合板在水下的抗暴性能进行研究,促进舰船抗暴性材料以及船体结构设计的发展。
1 碳纤维复合材料层合板技术 1.1 碳纤维复合材料模型本文研究的材料是碳纤维复合材料层合板,其纵向以及横向的材料性能一样,为了便于区别,将传统的纤维和基体方向使用1和2表示,为了能够表示碳纤维复合材料铺层之间的损伤,引入层间损伤,同时将碳纤维复合材料的厚度方向用3来表示。模型中引入1方向上的拉伸和压缩损伤、2方向上的拉伸和压缩损伤以及层间损伤5种损伤。因此,其数学模型分别为:
| $ e_{ft}^2 = {\left( {\frac{{{\varepsilon _{11}}}}{{X_t^\varepsilon }}} \right)^2} - 1\left\{ \begin{aligned} { \geqslant 0},&{{\mathrm{failed}}},\\ { \lt 0},&{{\mathrm{elastic}}} 。\end{aligned} \right. $ | (1) |
| $ e_{fc}^2 = {\left( {\frac{{{\varepsilon _{11}}}}{{X_c^\varepsilon }}} \right)^2} - 1\left\{ {\begin{array}{*{20}{c}} { \geqslant 0},&{{\mathrm{failed}}},\\ { \lt 0},&{{\mathrm{elastic}}}。\end{array}} \right. $ | (2) |
| $ e_{mt}^2 = {\left( {\frac{{{\varepsilon _{22}}}}{{Y_t^\varepsilon }}} \right)^2} - 1\left\{ {\begin{array}{*{20}{c}} { \geqslant 0},&{{\mathrm{failed}}} ,\\ { \lt 0},&{{\mathrm{elastic}}} 。\end{array}} \right. $ | (3) |
| $ e_{mc}^2 = {\left( {\frac{{{\varepsilon _{22}}}}{{Y_c^\varepsilon }}} \right)^2} - 1\left\{ {\begin{array}{*{20}{c}} { \geqslant 0},&{{\mathrm{failed}}},\\ { \lt 0},&{{\mathrm{elastic}}}。\end{array}} \right. $ | (4) |
| $ e_{ld}^2 = {\left( {\frac{{{\varepsilon _{33}}}}{{Z_t^\varepsilon }}} \right)^2} + {\left( {\frac{{{\varepsilon _{13}}}}{{S_{13}^\varepsilon }}} \right)^2} + {\left( {\frac{{{\varepsilon _{12}}}}{{S_{12}^\varepsilon }}} \right)^2} - 1\left\{ {\begin{array}{*{20}{c}} { \geqslant 0,} & {{\mathrm{failed}}},\\ { \lt 0},& {{\mathrm{elastic}}} 。\end{array}} \right. $ | (5) |
一旦某种损伤因子大于0时,则碳纤维复合材料就会出现损伤。为了能够更好描述碳纤维复合材料的损伤程度,定义碳纤维复合材料的损伤变量,其数学模型如下式:
| $ {H_i} = \left\{ {\begin{array}{*{20}{c}} 0,&{{e_i} \leqslant 0},\\ {\dfrac{1}{{e_i^n}}},&{{e_i} \gt 0} ,\end{array}} \right. $ | (6) |
当碳纤维复合材料的损伤变量等于0时,则表示此时处于复合材料的损伤起点;当碳纤维复合材料的损伤变量等于1时,则表示此时的复合材料彻底失效了;当复合材料的损伤变量介于0和1之间时候,则表明复合材料的刚度产生了一定的退化,并且损伤变量越大,表示复合材料的刚度退化越严重。
当碳纤维复合材料产生损伤之后,其复合材料的刚度在退化过程中,应力应变之间的关系可以表示为:
| $ \varepsilon = {C_d}\sigma \text{。} $ | (7) |
损伤开始可以通过式(8)来判断。
| $ {\left( {\frac{{{\sigma _n}}}{{{\sigma _N}}}} \right)^2} + {\left( {\frac{{{\sigma _s}}}{{{\sigma _S}}}} \right)^2} + {\left( {\frac{{{\sigma _t}}}{{{\sigma _T}}}} \right)^2} = 1\text{。} $ | (8) |
式中:σN为最大的平面法向拉伸力;σS和σT分别为2个最大的正交面上的剪切力;σn、σs和σt分别为实际测量得到的应力,一旦这些应力的数值满足式(8),则可以判断出碳纤维复合材料开始出现损伤,并且进入材料损伤演化阶段。碳纤维复合材料的损伤演化过程以能量控制为基础,当式(9)成立时,则表示复合材料彻底断裂。复合材料参数如表1所示。
|
|
表 1 复合材料参数 Tab.1 Composite material parameters |
| $ \left( {\frac{{{G_n}}}{{{G_N}}}} \right) + \left( {\frac{{{G_s}}}{{{G_N}}}} \right) + \left( {\frac{{{G_t}}}{{{G_T}}}} \right) = 1\text{。} $ | (9) |
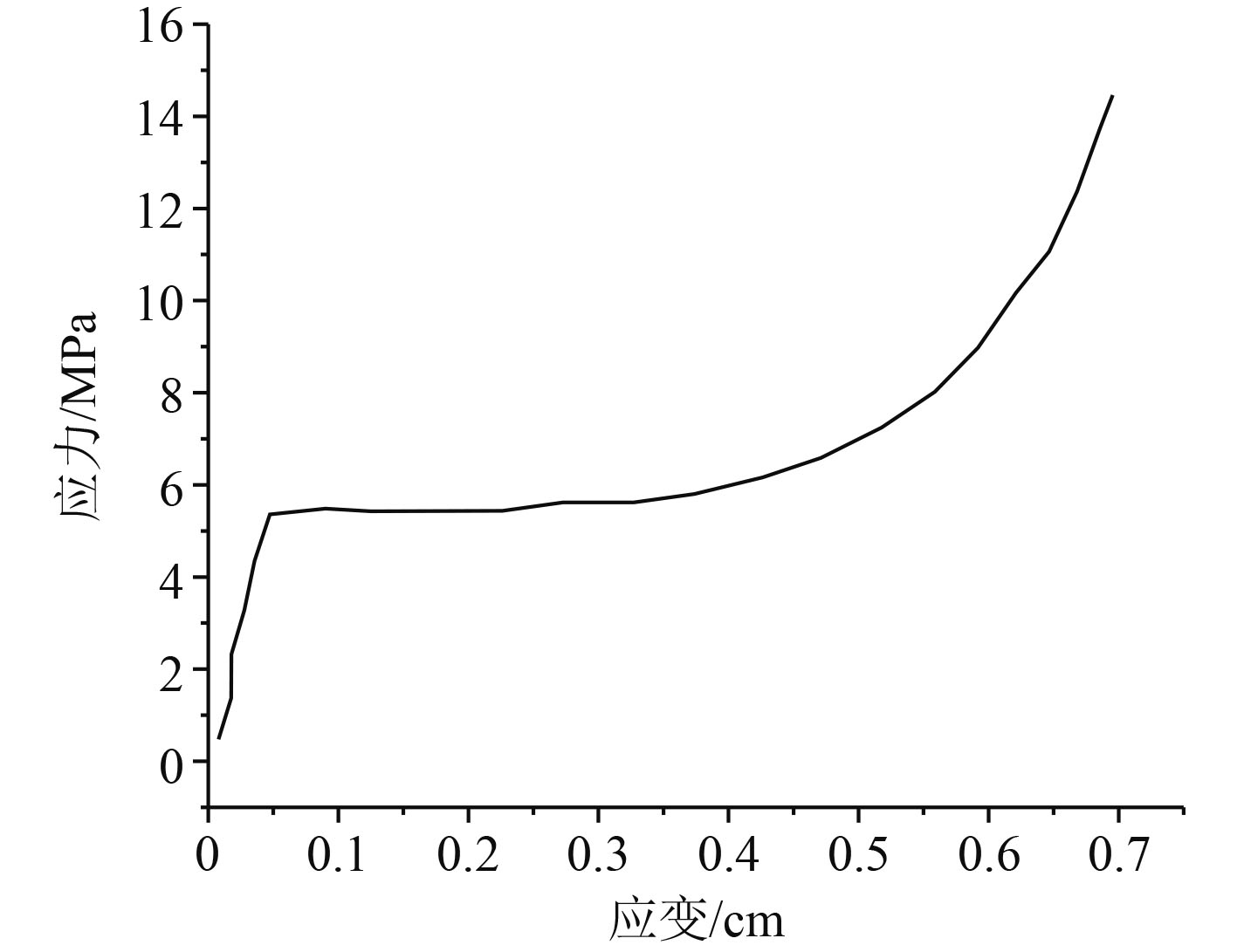
在实际应用过程中,夹芯结构是碳纤维复合材料层合板通常采用的形式。碳纤维复合材料层合板采用夹芯结构的优点在于,夹芯层的厚度从一定程度上提升了复合材料的弯曲以及扭矩刚度,但是其质量只增加了很少,因此复合材料结构的比强度以及比刚度得到了提升。一旦夹芯结构的复合材料层合板受到外部载荷的冲击,则夹芯层可以凭借其柔软性通过压缩变形的方式吸收大量的能量,从某种程度上降低外部冲击造成的损伤。本文研究的夹芯板结构的碳纤维复合材料层合板主要包含迎爆面、背爆面以及芯层3个部分,并使用PVC泡沫作为芯层,PVC泡沫的应力应变曲线如图1所示。
|
图 1 PVC材料的应力应变曲线 Fig. 1 Stress-strain curve of PVC material |
可以看出,当PVC泡沫材料的应变比较小时,PVC泡沫材料显现出线性应力关系。随着应变的继续增大,PVC泡沫材料将会进入一段平台应力阶段,即随着PVC泡沫材料应变的增加,其应力几乎不发生变化。如果继续增大应变,则应力会突然增大。
为了能够更好地对爆炸下的PVC泡沫材料动态力学进行模拟,本文PVC泡沫材料模型使用Crushable Foam塑性模型。Crushable Foam塑性模型使用的是压应力和偏应力为椭圆形的屈服面,并且屈服面是由PVC泡沫材料的实塑性应变控制的,其控制方程如下:
| $ F = \sqrt {{q^2} + {\alpha ^2}{{\left( {p - {p_0}} \right)}^2}} - B\text{。} $ | (10) |
式中,B为屈服椭圆垂直方向上q轴的大小。
| $ B = \alpha A = \alpha \frac{{{p_c} + {p_t}}}{2}\text{,} $ | (11) |
| $ \alpha = \frac{B}{A}\text{。} $ | (12) |
p轴上的屈服椭圆中心的计算方法为:
| $ {p_0} = \frac{{{p_c} + {p_t}}}{2}\text{。} $ | (13) |
在水下爆炸过程中,空气、水以及炸药是常用的3个欧拉体,并且在空间上这3个欧拉体之间是互相独立的。但是在水下发生爆炸的时候,这3个欧拉体之间会产生能量的渗透、力的相互影响等作用[7]。本文使用TNT炸药进行研究,因此用JEL方程来描述炸药的状态,如下式:
| $ {p_T} = A{\left( {1 - \frac{{\omega \eta }}{{{R_1}}}} \right)^{{e^{ - \frac{{{R_1}}}{\eta }}}}} + B{\left( {1 - \frac{{\omega \eta }}{{{R_2}}}} \right)^{ - \frac{{{R_2}}}{\eta }}}\text{,} $ | (14) |
船体的外部流场主要是水介质,在水下爆炸过程中,水介质的状态方程如下式:
| $ {p_w} = \frac{{{\rho _0}{C^2}\mu \left[ {1 + \left( {1 - \frac{{{\gamma _0}}}{2}} \right)\mu - \frac{\alpha }{2}{\mu ^2}} \right]}}{{\left[ {1 - \left( {{S_l} - 1} \right)\mu - {S_2}\frac{{{\mu ^2}}}{{\mu + 1}} - {S_3}\frac{{{\mu ^3}}}{{{{\left( {\mu + 1} \right)}^2}}}} \right]}}\text{。} $ | (15) |
通常使用Linear-Polynomial Model方程来描述空气的状态,如下式:
| $ {p_L} = {c_0} + {c_1}\mu + {c_2}{\mu ^2} + {c_3}{\mu ^3}\text{。} $ | (16) |
炸药在点燃之后,短时间内TNT会快速爆燃,产生高温高压的一团气体,同时迅速地压缩并推动周围的空气,最后由压缩波叠加而形成冲击波。对空间中某个位置的压力变化进行研究,可以给碳纤维复合材料层合板的损伤机理提供依据。TNT炸药爆炸之后产生的冲击波的峰值的预测模型可以描述为:
| $ {p_m} = \left( {\begin{array}{*{20}{l}} {\dfrac{{1.4}}{Z} + \dfrac{{0.56}}{{{Z^2}}} - \dfrac{{0.036}}{{{Z^3}}} + \dfrac{{0.000\;6}}{{{Z^4}}}},&{0.05 \leqslant Z \leqslant 0.3},\\ {\dfrac{{0.62}}{Z} - \dfrac{{0.032}}{{{Z^2}}} + \dfrac{{0.21}}{{{Z^3}}}},&{0.3 \leqslant Z \leqslant 1},\\ {\dfrac{{0.067}}{Z} + \dfrac{{0.405}}{{{Z^2}}} + \dfrac{{0.329}}{{{Z^3}}}},&{1 \leqslant Z \leqslant 10} 。\end{array}} \right. $ | (17) |
式中,Z位比例爆距,其计算方法如下:
| $ Z = \frac{R}{{{W^{\frac{1}{3}}}}}\text{。} $ | (18) |
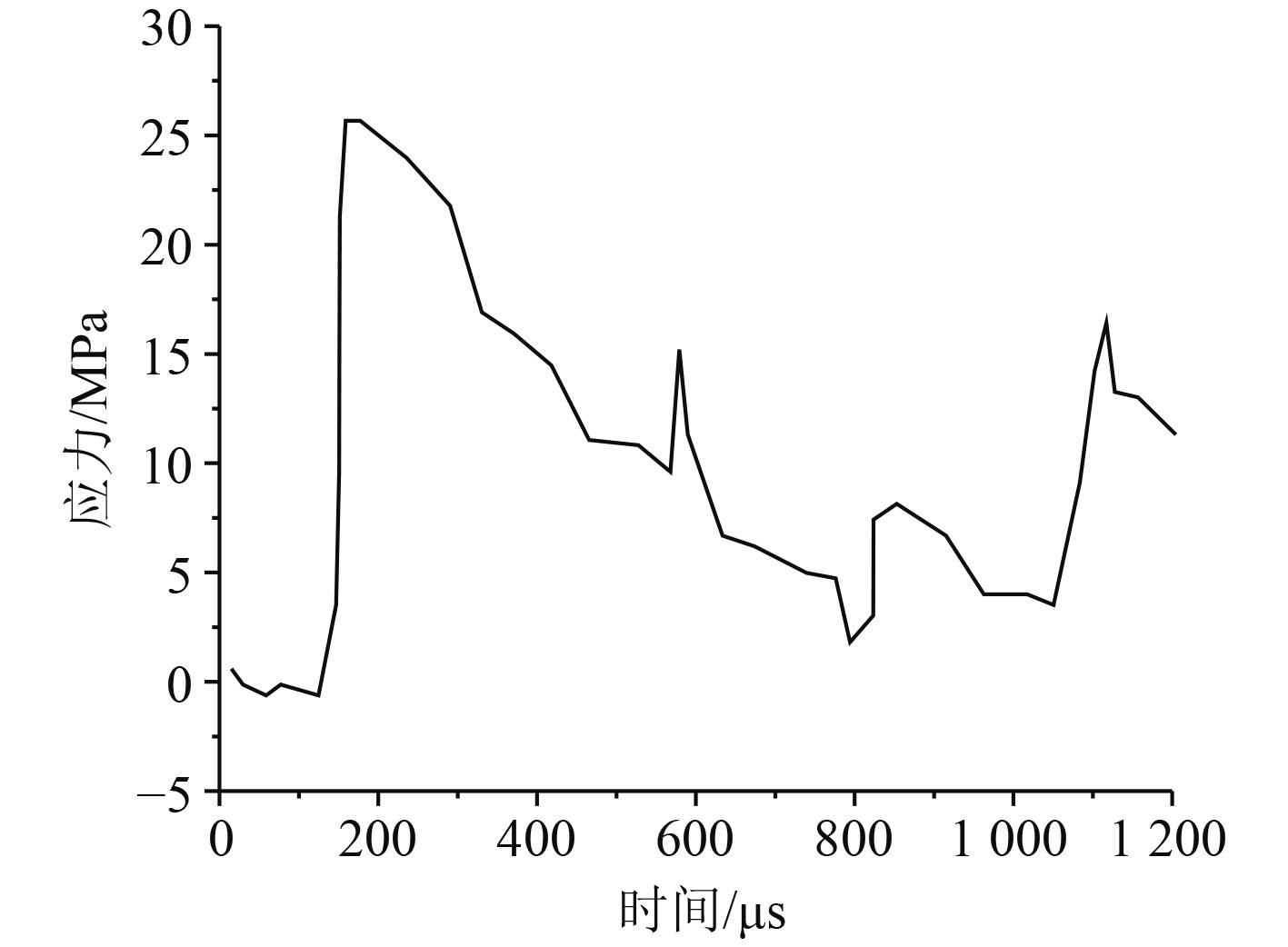
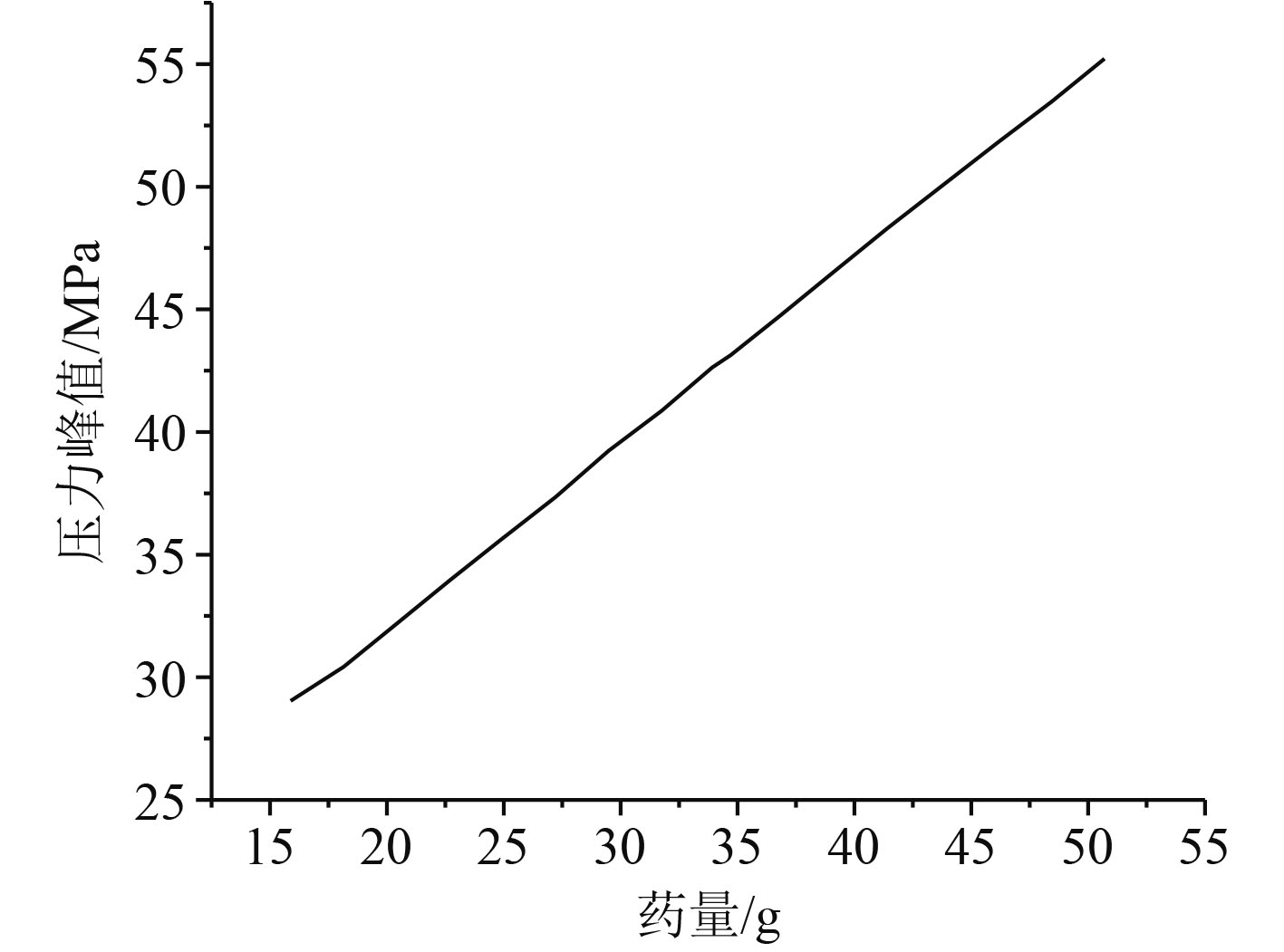
分别取炸药量为16.3g、36g、53.9g,对1500 mm处的冲击波压力随时间的变化进行研究。图2为1500 mm处的压力随时间变化曲线,可知,炸药量一定的情况下,炸药爆炸之后产生的冲击波到达测量点的时候,测量点的压力会突然达到最大值,然后冲击波会随着时间的推移而逐渐下降。1500 mm处的压力最大值会随着药量的提升而变大,如图3所示。
|
图 2 1 500 mm处的压力随时间变化曲线 Fig. 2 Pressure versus time curve at 1 500 mm |
|
图 3 不同药量下1 500 mm处的压力最大值的变化情况 Fig. 3 Change of maximum pressure at 1 500 mm under different dosage |
炸药水下爆炸产生的冲击波随着时间的推移会不断衰减,为了能更好对船体吸能效果进行系统分析,需要对炸药在爆炸过程中产生的能量进行计算,计算方法如下式:
| $ E = me\text{。} $ | (19) |
式中:e为炸药单位质量产生的爆炸能;m为炸药的质量。对于炸药爆炸之后的能量,舰船主要是对动能以及应变能进行吸收,动能的解算方法和应变能的计算方法分别如下:
| $ {E_k} = \int {\frac{1}{2}\rho {v^2}{\mathrm{d}}V} \text{,} $ | (20) |
| $ {E_l} = {E_S} + {E_p}\text{。} $ | (21) |
式中的弹性应变能Es的计算方法和塑性应变能EP的计算方法分别如下:
| $ E_S=\int_0^l\left(\int_V^{ }\sigma^c\cdot\varepsilon^{el}\mathrm{d}V\right)\mathrm{d}\tau\text{,} $ | (22) |
| $ E_P=\int_0^l\left(\int_V^{ }\sigma^c\cdot\varepsilon^{pl}\mathrm{d}V\right)\mathrm{d}\pi\text{。} $ | (23) |
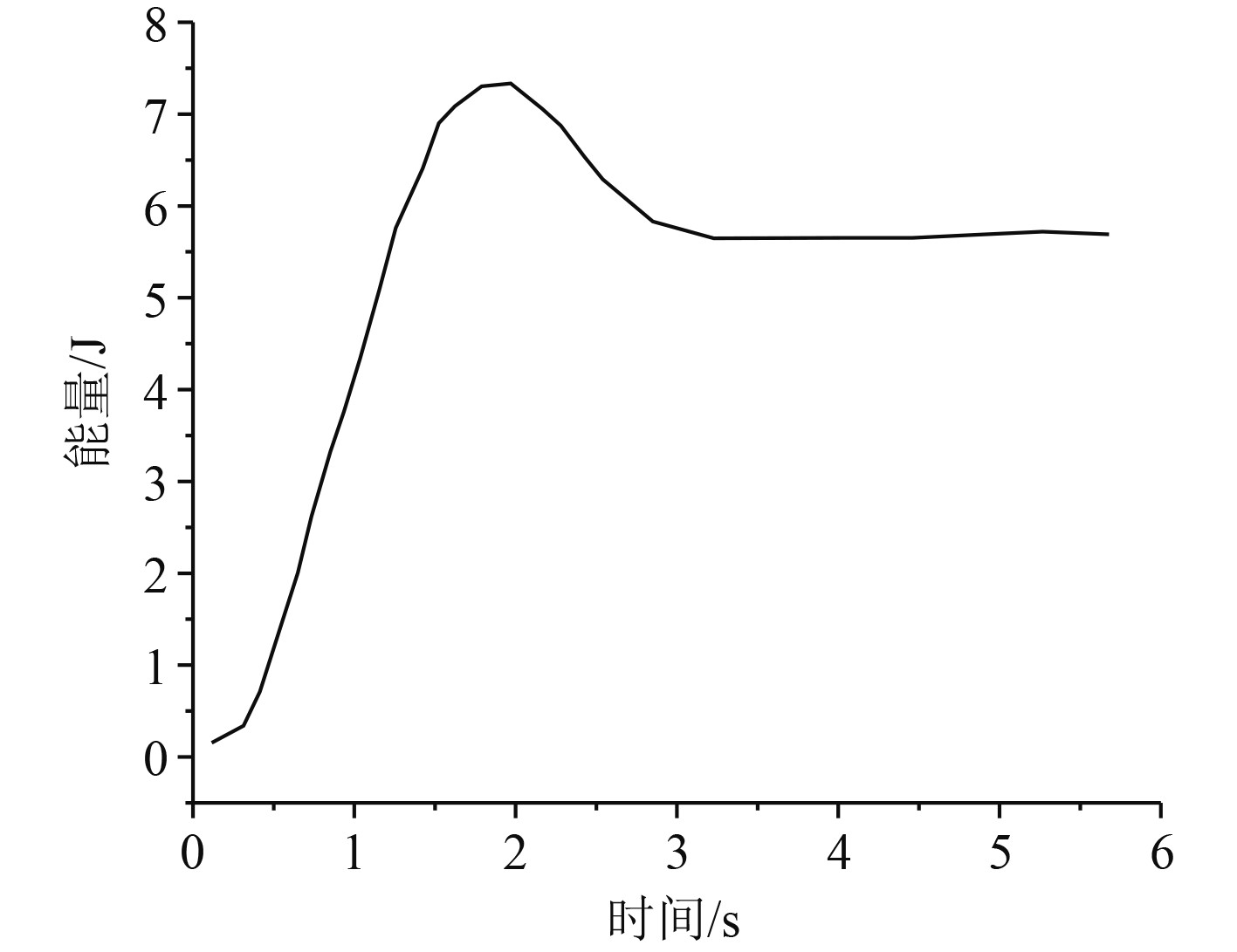
图4给出了碳纤维层合板在7.35 J冲击波能量作用下,其总能量的变化曲线。可以看出,2 s内碳纤维层合板受到的冲击波能量迅速提升,最大可达7.35 J附近,逐渐下降,维持在恒定的数值。
|
图 4 层合板能量变化曲线 Fig. 4 Energy variation curve of laminated plates |
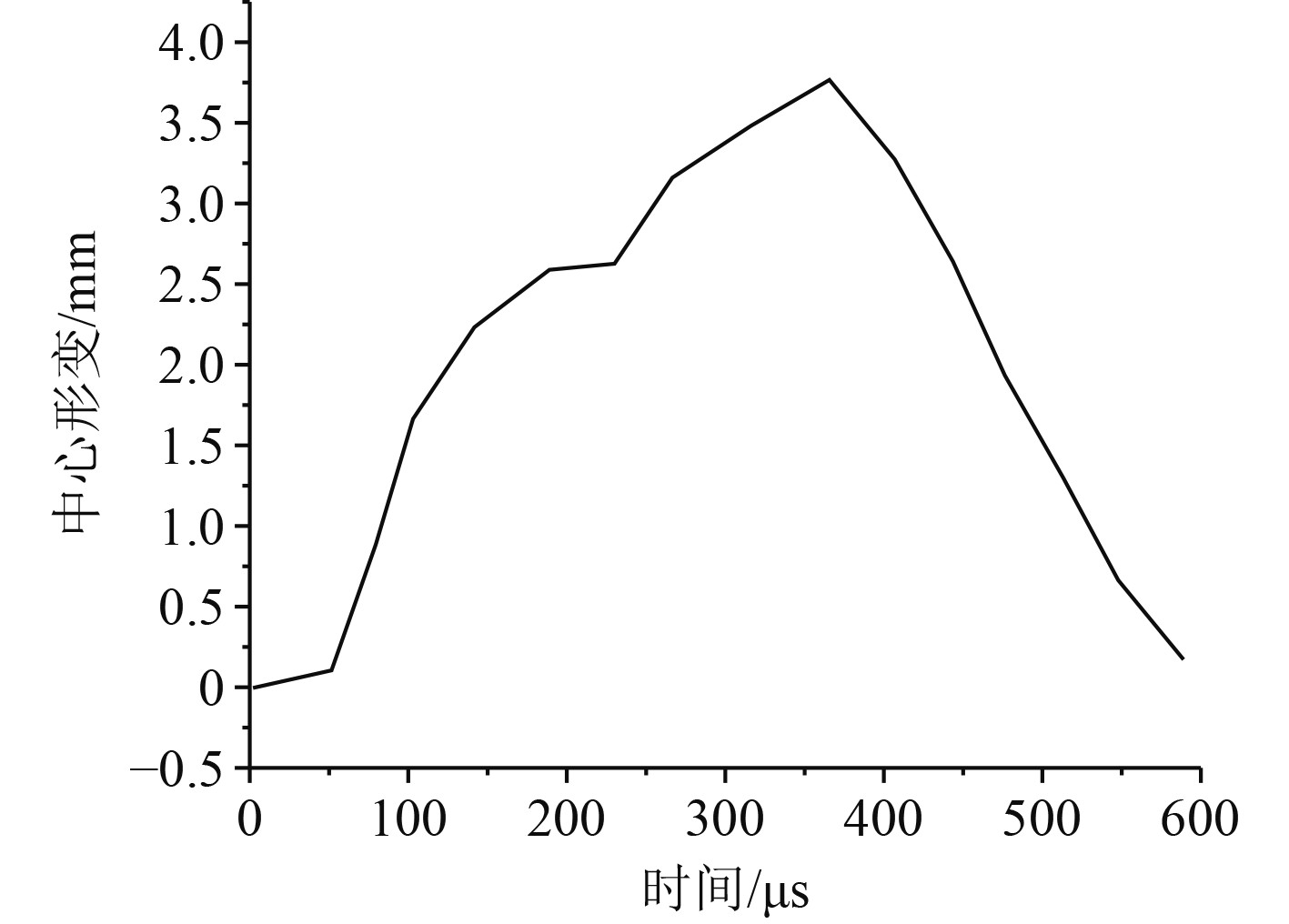
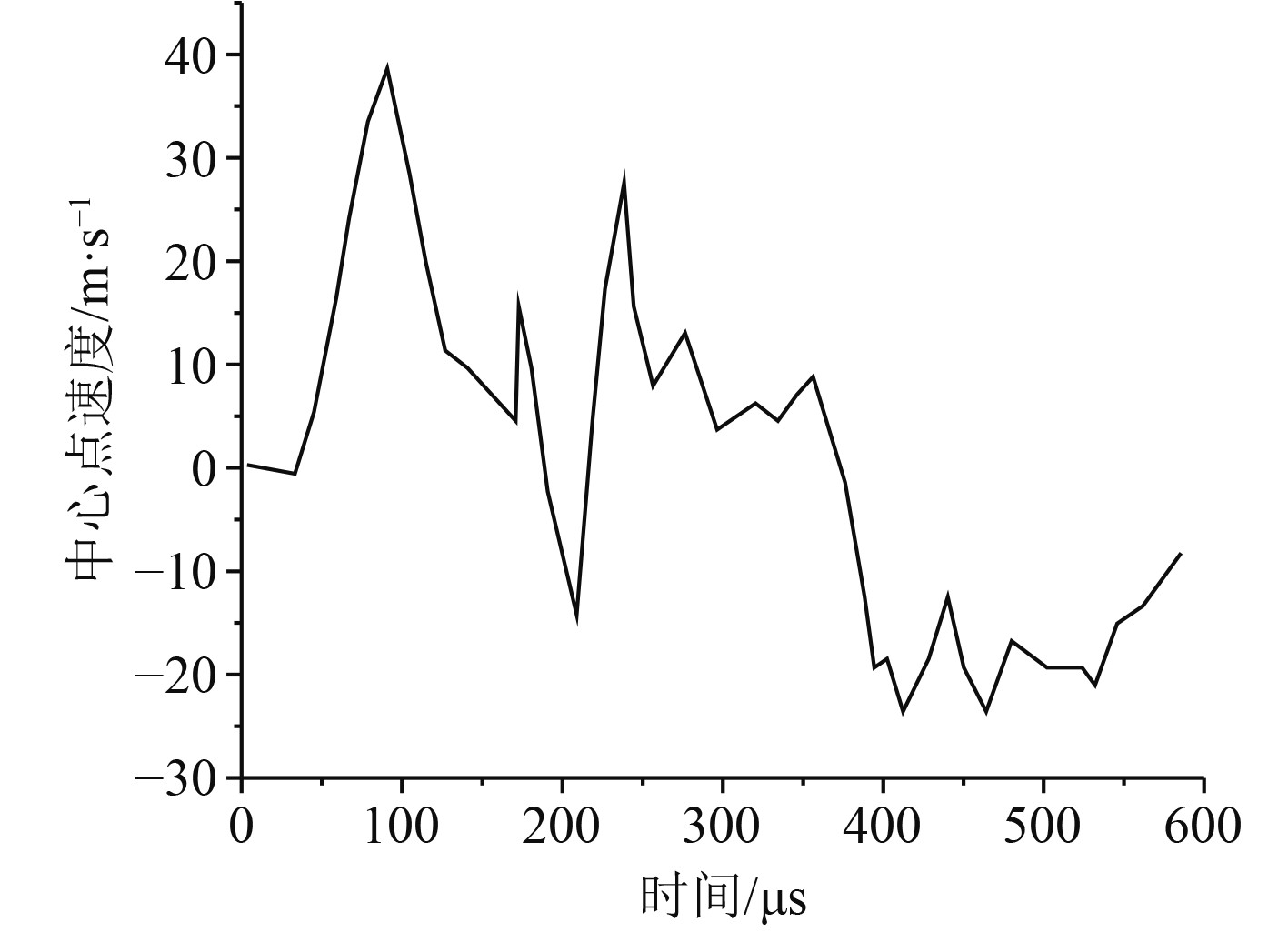
图5和图6分别给出了水下爆炸情况下纤维复合材料层合板中心点的形变以及速度变化的曲线。从图5可以看出,碳纤维复合材料层合板中心点的形变在390 μs后达到最大值,然后随着时间的推移逐渐降低。从图6可以看出,碳纤维复合材料中心点的速度在100 μs达到最大值,然后随着时间的推移震荡下降。
|
图 5 碳纤维复合材料层合板中心形变曲线 Fig. 5 Center deformation curve of carbon fiber composite laminates |
|
图 6 碳纤维复合材料层合板中心速度变化曲线 Fig. 6 Center velocity variation curve of carbon fiber composite laminates |
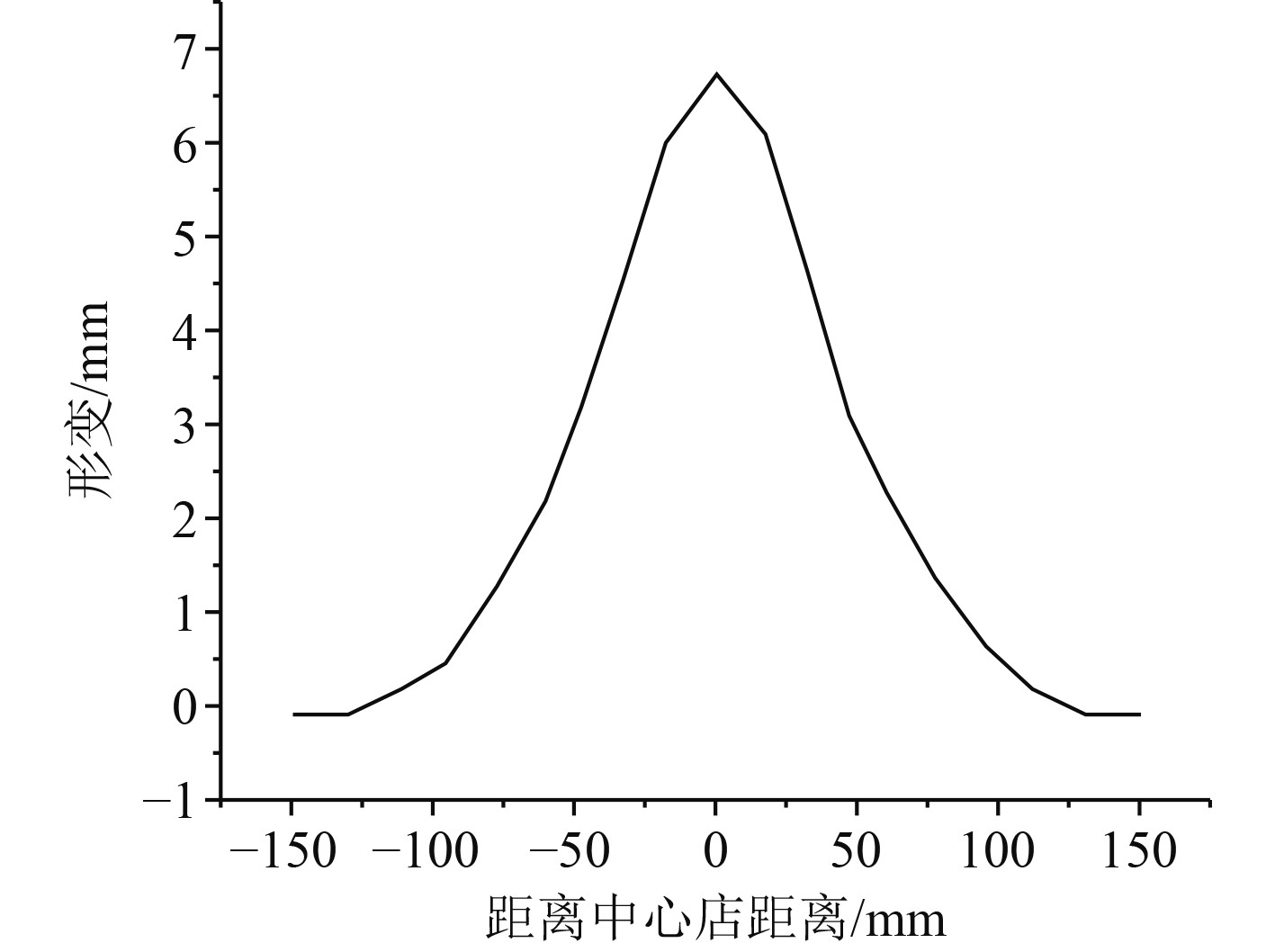
图7给出了水下爆炸情况下碳纤维复合材料层合板剖面形变曲线。可以看出,碳纤维复合材料层合板中心位置的形变最大,距离中心越远的点,其形变越小。
|
图 7 层合板剖面形变曲线 Fig. 7 Deformation curve of laminated plate profile |
和碰撞冲击相比,碳纤维复合材料冲击的过程包含了冲击波、流固耦合等更加复杂的过程,因此对碳纤维复合材料抗爆炸性能的研究很有必要。
| [1] |
张弩, 于馨, 明付仁. 复合材料层合板在水下多层防护结构中的抗暴效能[J]. 兵工学报, 2021(42): 135-141. |
| [2] |
李永正, 朱云笛, 熊小虎, 等. 复合材料无人艇冲击响应及防护结构型式研究[J]. 江苏科技大学学报, 2021(35): 9-16. |
| [3] |
李永正, 朱云笛. 复合材料无人艇在近场水下爆炸载荷下的动态响应研究[J]. 舰船科学技术, 2022(44): 1-5. |
| [4] |
李典, 侯海量, 朱锡, 等. 舰船装甲防护结构抗弹道冲击的研究进展[J]. 中国造船, 2018(59): 237-249+250. |
| [5] |
华康, 王德禹. 连续玄武岩纤维增强复合材料船体水下爆炸响应的数值仿真[J]. 2009(31): 151-155.
|
| [6] |
周昊, 郭锐, 刘荣忠, 等. 碳纤维增强聚合物复合材料方形蜂窝夹层结构水下爆炸动态响应数值模拟[J]. 复合材料学报, 2019(36): 1226-1234. |
| [7] |
卜文俊, 李瑞彪. 新材料技术在潜艇隐身设计中的应用[J]. 舰船科学技术, 2022(44): 1-6. |
 2023, Vol. 45
2023, Vol. 45
