2. 胜利石油管理局有限公司 油气井下作业中心,山东 东营 257000;
3. 江苏科技大学 理学院,江苏 镇江 212100;
4. 上海船舶运输科学研究所有限公司 航运技术交通行业重点实验室/水路交通控制全国重点实验室,上海 200135;
5. 上海交通大学,船舶海洋与建筑工程学院,上海 200240
2. Oil and Gas Downhole Operation Center, Shengli Petroleum Administration Limited, Dongying 257000, China;
3. College of Science, Jiangsu University of Science and Technology, Zhenjiang 212100, China;
4. Key Laboratory of Marine Technology Ministry of Communications/State Key Laboratory of Maritime Technology and Safety, Shanghai Ship and Shipping Research Institute Co., Ltd, Shanghai 200135, China;
5. School of Naval Architecture, Ocean an Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China
在船舶及海洋平台等大型海上结构物的制造过程中,焊接是常用的结构连接方式,其焊接接头质量对结构的强度至关重要。受复杂载荷作用,海上结构物焊接接头部位易产生裂纹等缺陷,严重时会导致结构失效或发生断裂现象[1],产生巨大经济损失。目前,较多学者采用试验方法研究焊接接头的裂纹扩展和断裂失效问题,但试验研究条件限制多,成本高。因此,如何运用数值分析方法合理有效地模拟焊接接头裂纹萌生及扩展显得尤为重要。
内聚力模型(Cohesive Zone Model,CZM)可较好地对裂纹萌生和扩展进行数值模拟分析[2]。其一方面能够较完整地模拟出裂纹萌生及扩展过程,不需要像经验方法那样将裂纹的萌生和扩展分开[3];另一方面,也能较好地解决断裂力学中,裂纹尖端奇异性问题[4-5],不需要对裂尖进行多次网格重划分,可任意放置内聚力单元来模拟裂纹扩展路径。因此,近年来部分学者将CZM理论逐渐应用于金属焊接接头的裂纹萌生和扩展研究中。Morvarid等[6]基于试验获得了内聚能参数,采用CZM理论对低碳钢/铜钎料钎焊接头韧性撕裂过程进行了模拟。Sadigh等[7]模拟了厚度为1 mm的电阻点焊薄壁搭接接头,在拉伸载荷下的断裂情况。谭菊妮[8]和陈兴等[9]虽然使用CZM理论研究了T型钎焊接头的裂纹起裂和扩展过程,但其T型钎焊接头母材和焊缝厚度分别为1 mm和0.08 mm,且焊缝材料与母材不同。从以上文献可看出,CZM目前较多应用于钎焊接头、薄板结构或较小构件的裂纹萌生或扩展分析,而对较大尺寸焊接结构的相关研究较少。
本文基于双线性内聚力模型,以典型焊接接头为例,进行裂纹萌生及扩展的数值仿真计算和研究,获得一套焊接接头的裂纹萌生及扩展分析方法,为后续进行船舶焊接结构安全评估奠定理论基础。
1 基本理论内聚力模型(CZM)是为了模拟裂纹萌生和裂纹扩展而开发的本构模型,其将断裂行为视为一个渐进的过程,在这个过程中,裂纹尖端会形成一个内聚力区,且材料表面的分离受到内聚力阻碍[10]。在有限元中,内聚力模型以界面单元为载体来实现,其形式分为离散状态的内聚力模型单元和连续体内聚力模型单元。对于连续体内聚力单元,单元积分点上都采用内聚力模型本构关系,通过损伤起始准则和损伤演化准则来模拟判定裂纹的萌生和扩展过程。
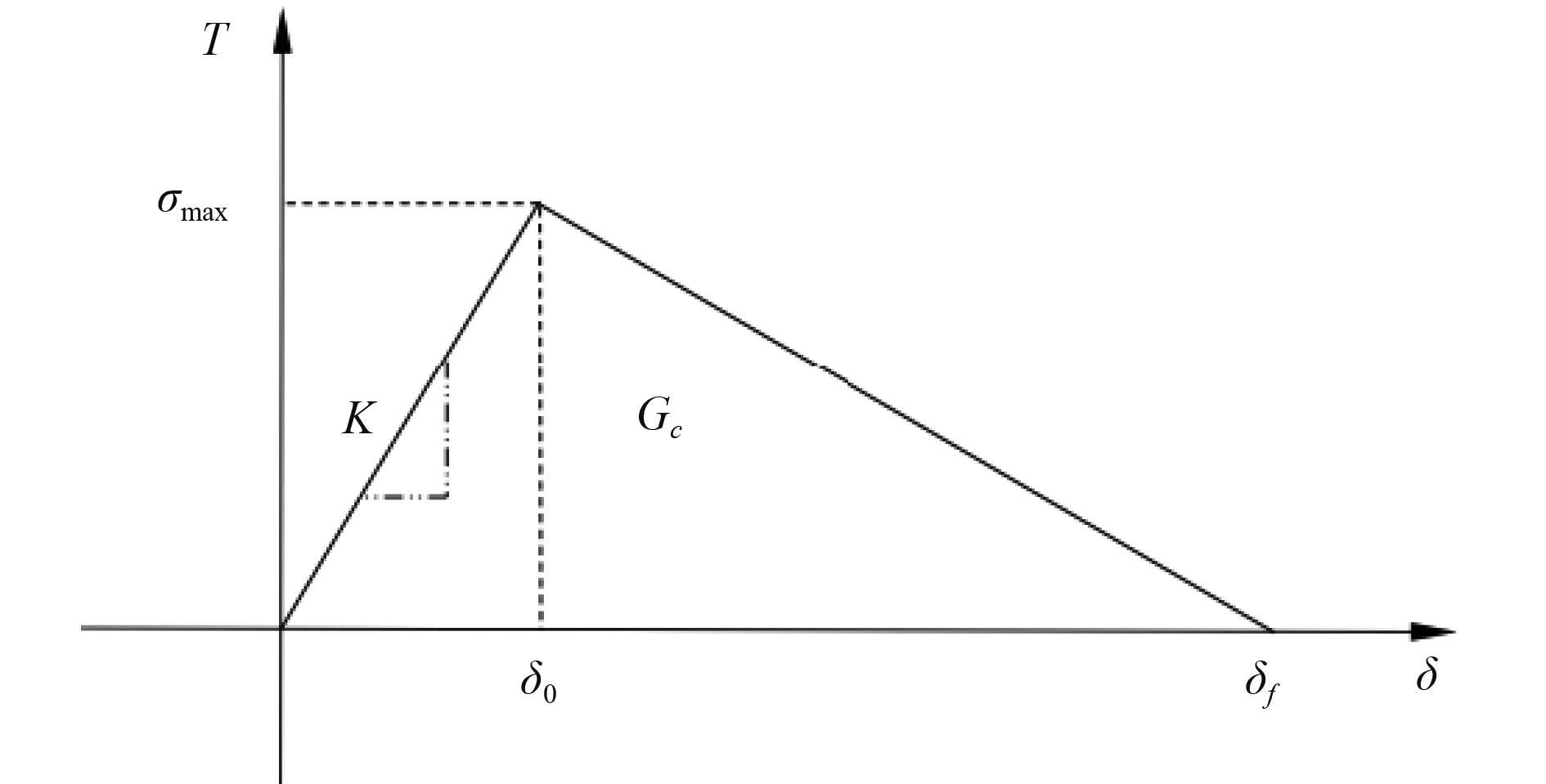
由外载荷引起的使内聚力区材料上下表面处发生开裂的界面应力称为内聚面上的牵引力T,其与内聚力区裂纹尖端上下表面之间的分离位移δ之间的关系称为牵引力-位移法则(Traction-Separation Law,TSL)。对于不同模型的裂纹扩展过程可采用不同的TSL,其中,双线性内聚力模型的牵引力-位移法则被广泛应用于裂纹扩展研究中[11-13],双线性本构模型曲线如图1所示。
|
图 1 双线性内聚力本构模型 Fig. 1 Bilinear cohesive constitutive model |
牵引力位移关系为:
| $ T = K\left( {1 - D} \right)\delta。$ | (1) |
式中:T=(Tn,Ts,Tt),为裂纹扩展垂直方向的法向牵引力和裂纹扩展平面上2个方向的切向牵引力;K为初始刚度;D为损伤因子,在双线性内聚力模型中,是和δ(位移)、δ0(损伤起始位移)、δf(失效位移)有关的参数。当D=0时,内聚力模型的牵引力没达到损伤起始应力σmax,当0<D<1时,说明损伤正处于累积的过程中;当D=1时,代表完全破坏了内聚力单元。损伤因子表示为:
| $ D{\text{ = }}\frac{{\delta - {\delta _0}}}{{{\delta _{\text{f}}} - {\delta _0}}},$ | (2) |
K计算式如下:
| $ K = \frac{{{\sigma _{{\text{max}}}}}}{{{\delta _0}}}。$ | (3) |
材料的应变能释放率G是指双线性内聚力模型牵引力位移曲线下的面积,当完全破坏内聚力单元后,应变能释放率达到临界值Gc,其公式为:
| $ G = \int_0^{{\delta _{\text{f}}}} {T{\rm{d}}s}。$ | (4) |
式中:Gc、K、σmax、δ0及δf为确定内聚模型的5个模型参数,一般基于等效能量的损伤演化准则所需参数为Gc、K和σmax,基于等效位移的损伤演化准则所需参数为σmax、δ0和δf。
在损伤阶段,损伤起始准则用于判断内聚力区材料损伤出现的时间,当应力达到临界应力时,内聚力区材料开始进入软化阶段,材料刚度下降损伤开始累积。其损伤判定包括最大应力、最大应变、二次应力和二次应变等4种准则。损伤起始准则二次应力准则(Quads),当各方向应力与损伤起始应力之比的平方和达到1时,损伤开始累积,其公式为:
| $ {\left\{ {\frac{{\left\langle {{\sigma _{{n}}}} \right\rangle }}{{\sigma _{{n}}^0}}} \right\}^2} + {\left\{ {\frac{{{\sigma _{{s}}}}}{{\sigma _{{s}}^{{0}}}}} \right\}^2} + {\left\{ {\frac{{{\sigma _{{t}}}}}{{\sigma _{{t}}^{{0}}}}} \right\}^2} = 1。$ | (5) |
式中:
损伤演化准则为材料达到损伤起始准则后,材料刚度退化的速率。当材料满足损伤起始准则后,随着载荷的增加,损伤因子D从0逐渐增加到1,内聚力区材料刚度退化,内聚力单元逐渐破坏,裂纹逐渐扩展。基于能量的线性损伤演化BK准则,其公式为:
| $ G_{{n}}^{{c}} + \left( {G_{{s}}^{{c}} - G_{{n}}^{{c}}} \right){\left\{ {\frac{{{G_{{S}}}}}{{{G_{{T}}}}}} \right\}^\eta } = {G_{{c}}} 。$ | (6) |
式中:GS=Gs+Gt ,GT=Gn+Gs ,
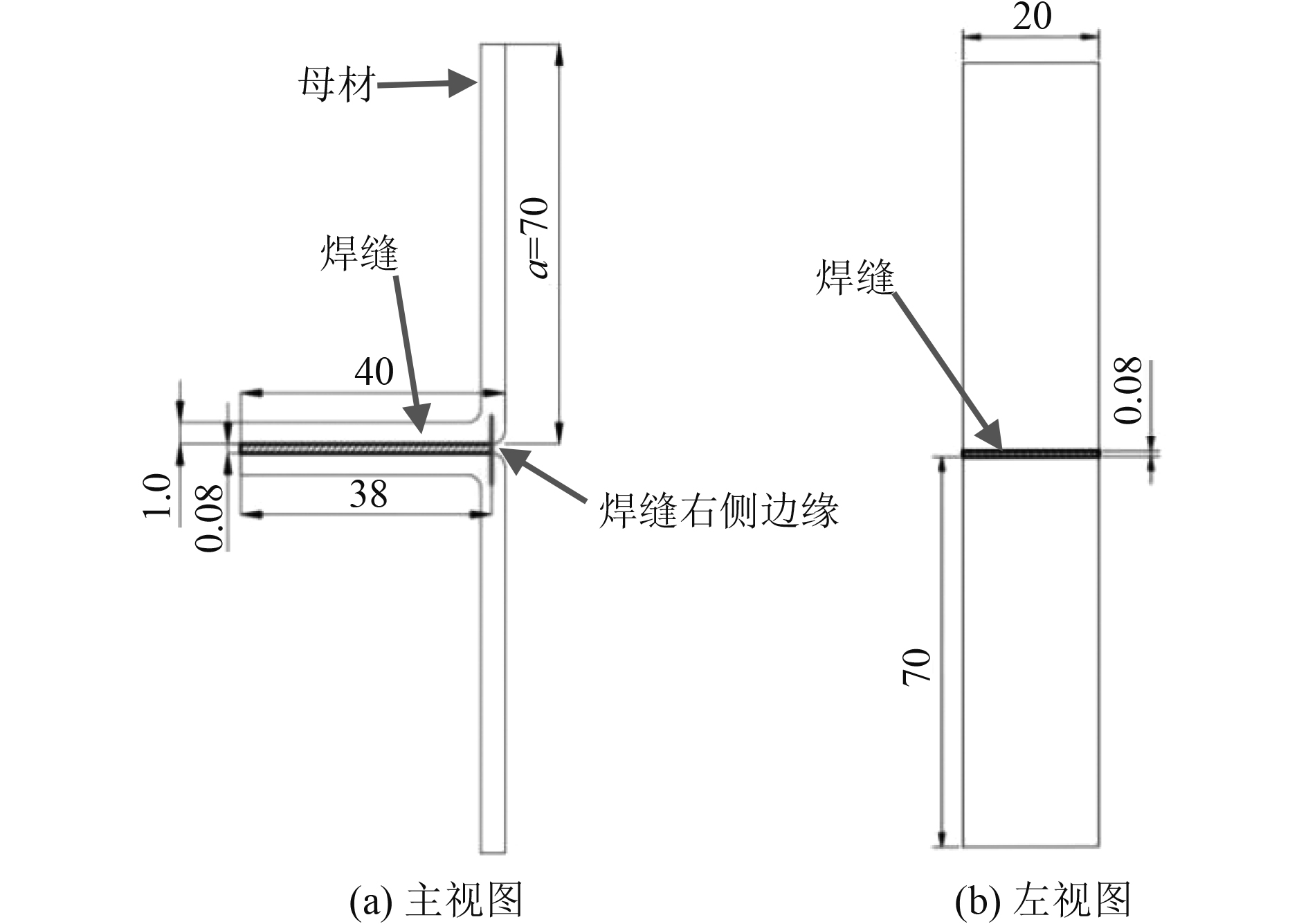
钎焊接头是由长度为70 mm、宽度为20 mm和厚度为1 mm的2个相同的L型304不锈钢(圆角过渡半径均为2 mm)焊接而成,焊缝长度、宽度和厚度分别为38 mm、20 mm和0.08 mm,如图2所示。钎料采用镍基BNi-2箔片,304不锈钢和BNi-2箔片的相关材料属性如图3和表1所示。
|
图 2 304 不锈钢应力-应变关系 Fig. 2 304 stainless steel stress-strain relationship |

|
图 3 有限元网格模型及加载 Fig. 3 Finite element mesh model and loading |
2.2 有限元模型及加载
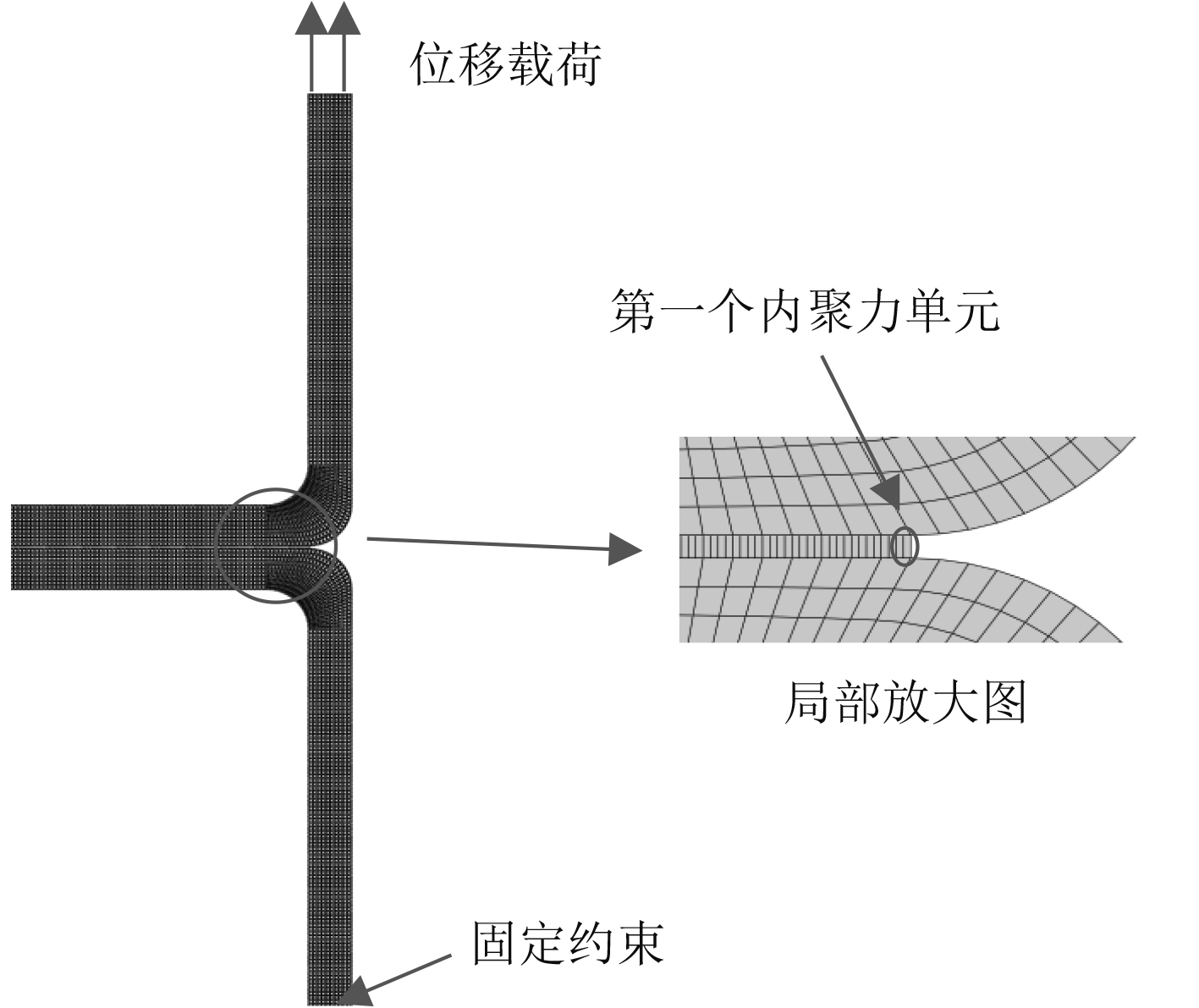
为提高计算效率且考虑到模型结构特点,采用钎焊接头的二维有限元模型在Abaqus/Standard中进行数值模拟研究。由于钎焊接头焊缝处易出现开裂,因此在焊缝部位均采用连续内聚力单元(COH2D4),且采用1个母材单元对应4个内聚力单元的方式[14-16]。通过网格无关性检验,母材单元尺寸为0.1 mm,焊缝单元尺寸为0.025 mm。模型共23340个单元和27066个节点,母材采用平面应变单元(CPE4R),有限元模型如图4所示。钎焊接头模型底端进行固定约束,模型顶端沿图4所示方向施加6 mm恒定位移载荷。
|
图 4 有限元网格模型及加载 Fig. 4 Finite element mesh model and loading |
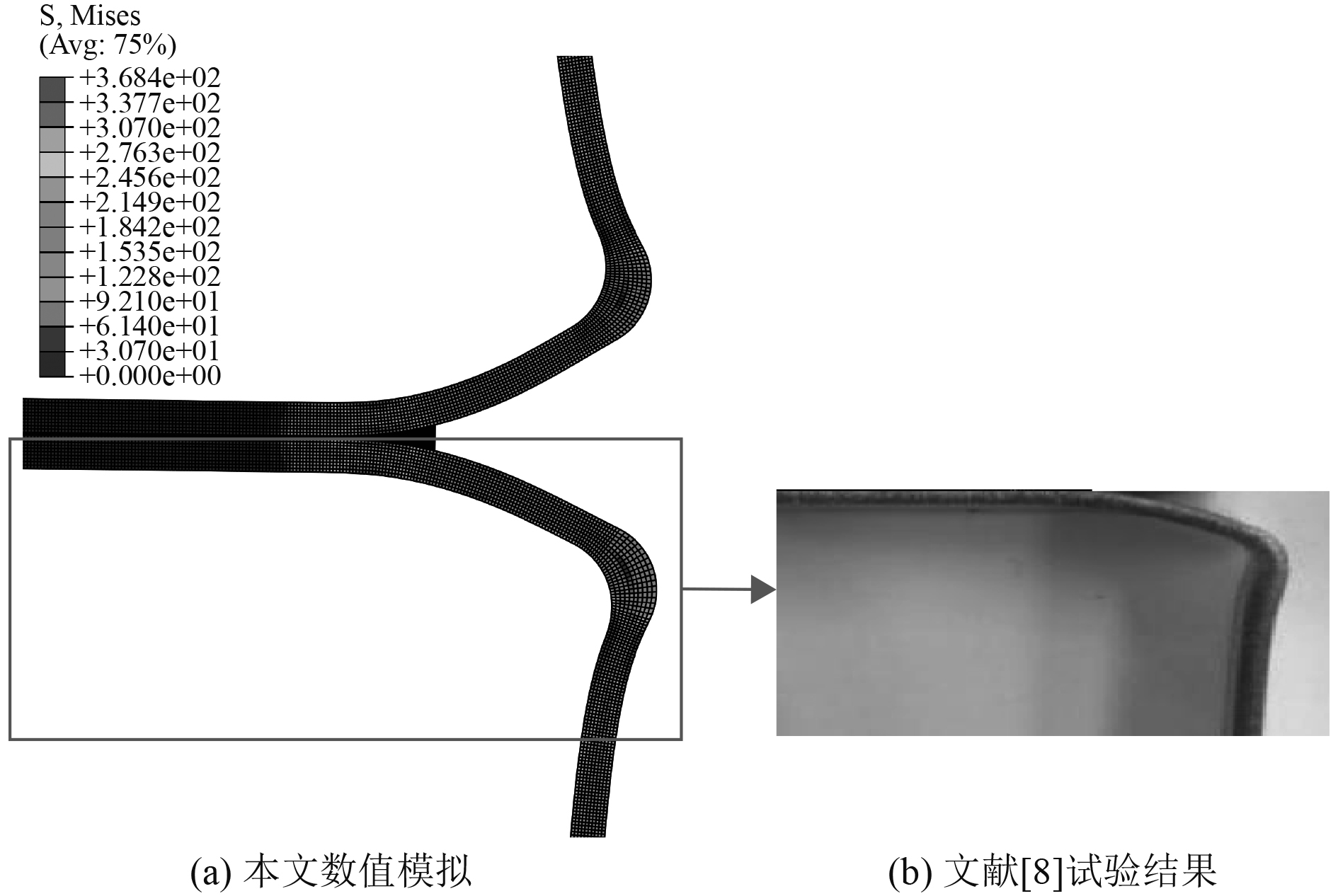
钎焊接头有限元模型的内聚力区域采用基于能量法的双线性内聚力模型,考虑二次应力准则(Quads)作为损伤起始准则,采用BK准则作为损伤演化准则进行数值模拟,计算得到了钎焊接头裂纹扩展的应力云图和裂纹长度随加载位移变化的曲线。图5为钎焊接头裂纹扩展数值模拟结果与文献[8]中试验结果对比,图6为本文钎焊接头裂纹长度随加载位移变化的数值模拟结果与文献[8]的试验和数值模拟结果对比。
|
图 5 数值模拟和文献 [8] 试验裂纹扩展结果对比图 Fig. 5 Comparison of crack propagation results between numericalsimulation and experiment in reference[8] |
从图5(a)可看出,钎焊接头应力最大值出现在L型母材弯折区域,裂纹尖端处应力均超出了材料屈服应力,裂纹沿着钎缝方向进行扩展。图4(a)数值模拟结果与图5(b)文献[8]试验结果较为一致。
由图6看出,随着加载位移的增加,钎焊接头模型裂纹沿厚度方向不断扩展,裂纹长度逐渐增加,本文的数值模拟结果与试验结果较为一致,且相较于文献[8]的数值模拟结果,误差更小。因此,针对钎焊接头模型,本文采用的基于内聚力模型裂纹萌生及扩展数值模拟分析算法是合理可行的,可为后续进行基于内聚力模型的典型焊接接头裂纹萌生和扩展的数值仿真研究奠定理论基础。

|
图 6 裂纹长度随加载位移变化曲线 Fig. 6 Crack length curve with loading displacement |
不锈钢钎焊接头的第1个内聚力单元(见图4)位移损伤如图7所示。可看出:
|
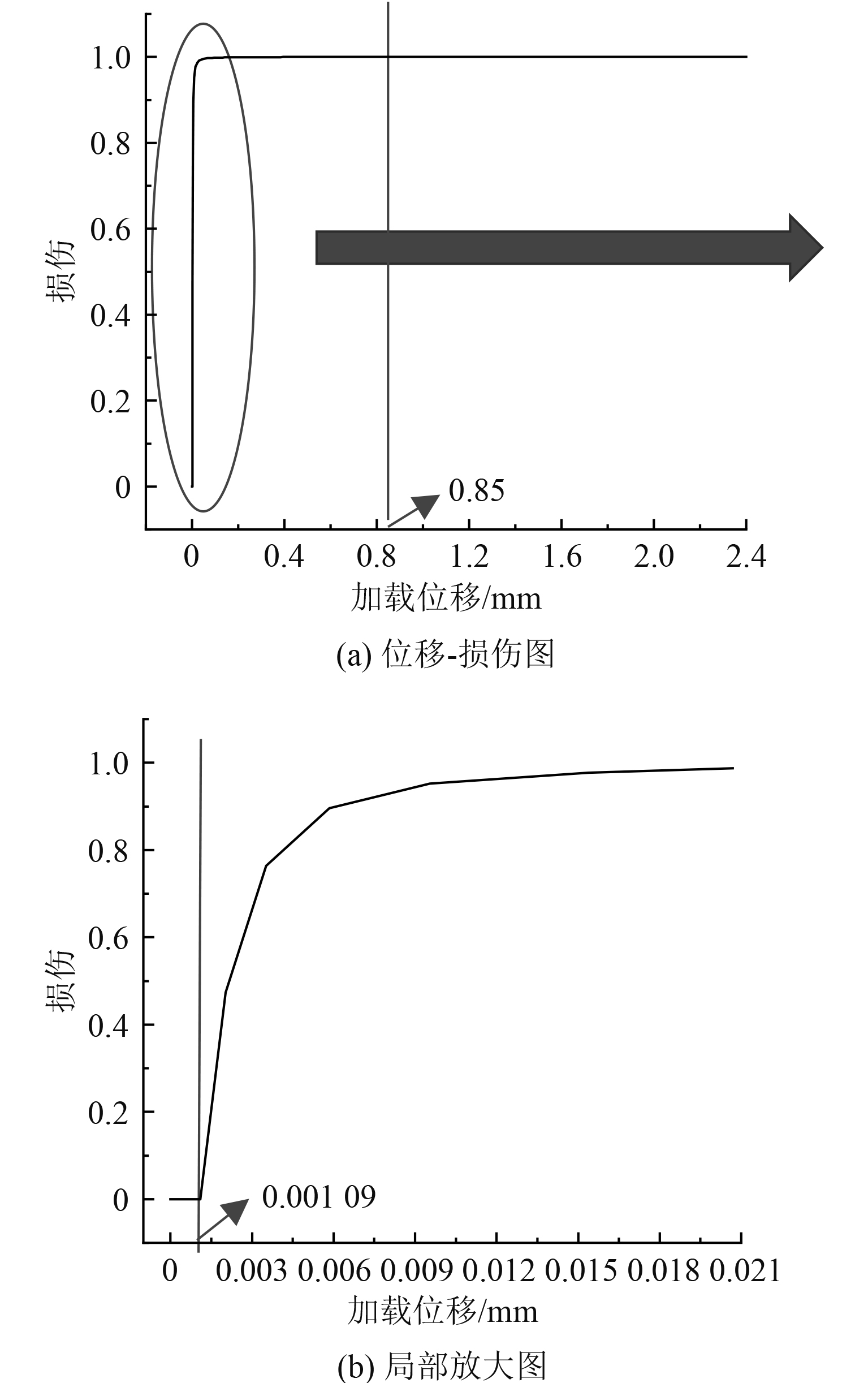
图 7 第一个内聚力单元的位移-损伤曲线 Fig. 7 Displacement-damage of the first cohesive force unit |
1)损伤值在加载位移达到0.00109 mm之前为0(见图7(b)),此时内聚面上的牵引力没有到达临界应力值,没有进行损伤累积;
2)当加载位移到达0.00109 mm(见图7(b))之后,内聚面上的牵引力达到临界应力值30 MPa,损伤开始累积,并随着加载位移的小范围增加,损伤累积迅速增大;
3)随着加载位移逐渐增大,损伤累积速度逐渐变慢,损伤值逐渐趋近于1,当加载位移到达0.85 mm(见图7(a))时,损伤累积到1,裂纹开始萌生。
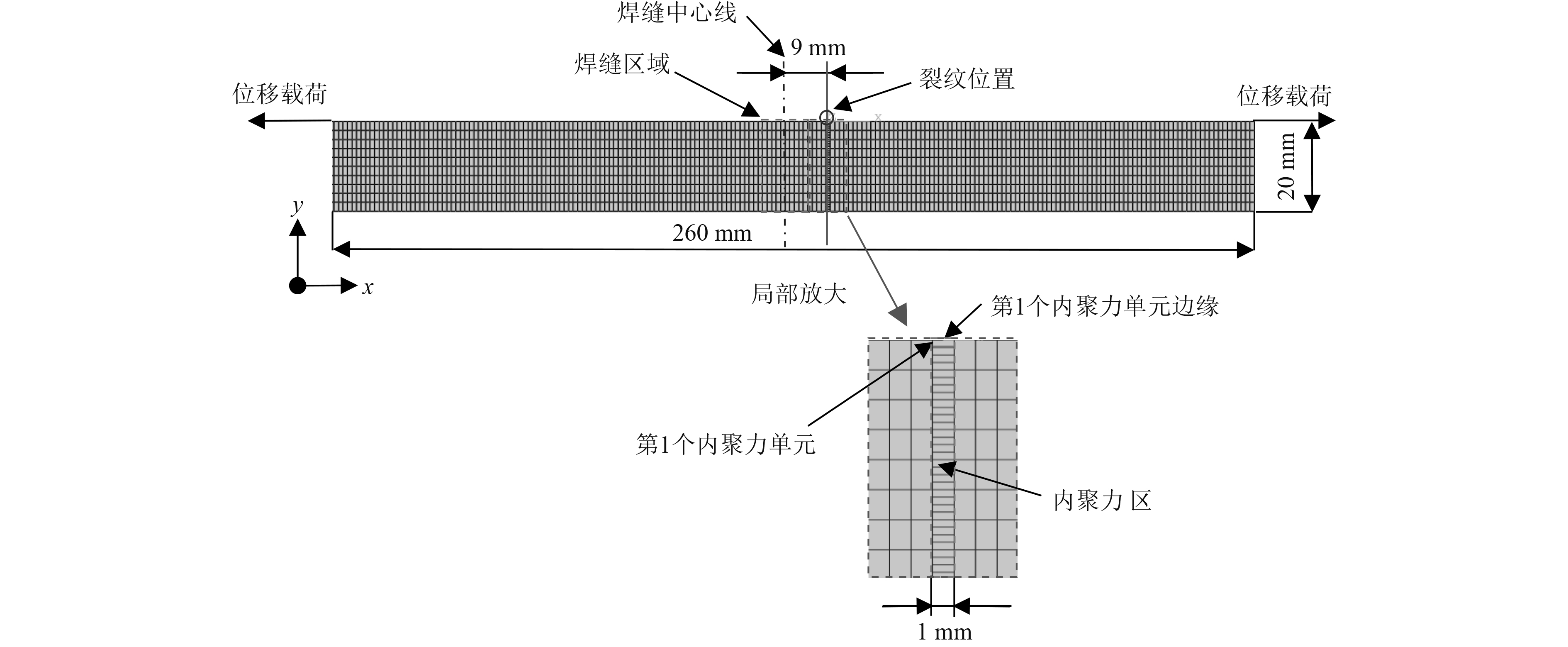
3 典型焊接接头裂纹萌生及扩展数值模拟研究 3.1 有限元模型以典型焊接接头为例,其二维有限元模型长为260 mm沿x方向,宽为20 mm沿y方向,如图8所示。由2块尺寸为250 mm×125 mm×20 mm的304不锈钢板TIG焊接而成,焊缝尺寸为10 mm×20 mm×250 mm。模型材料采用同表1所示的304不锈钢材料。由于焊接接头裂纹较易在焊趾附近萌生,除焊趾附近可能会产生焊接缺陷的原因外,还因为残余拉应力一般较易在该处达到峰值,形成应力集中区域,因此为了便于计算分析,选取距离焊缝熔合线约4 mm处作为内聚力区域,具体位置见图9。
|
图 8 典型焊接接头的网格划分及载荷加载 Fig. 8 Meshing and loading of typical welded joint |
|
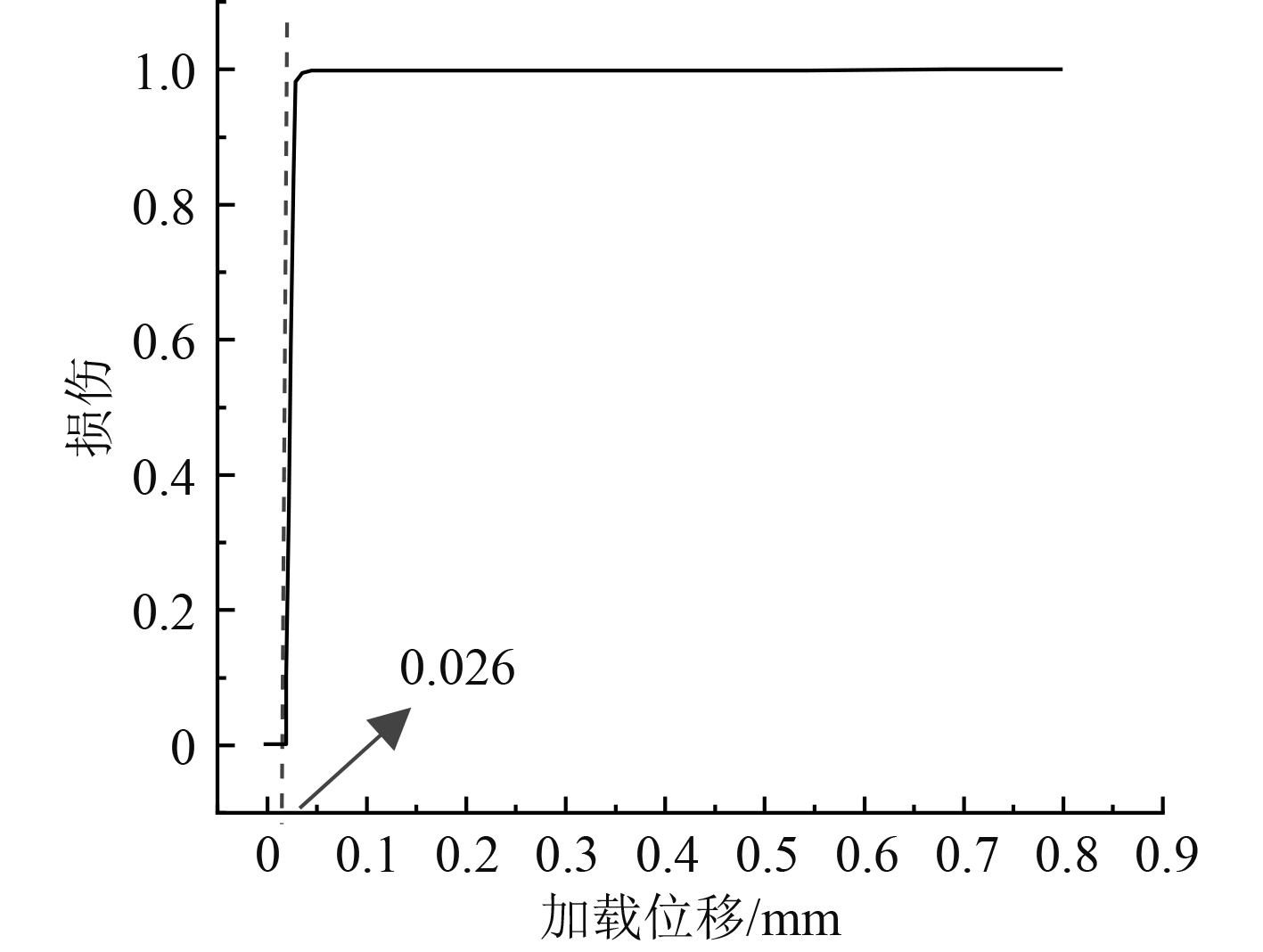
图 9 第一个内聚力单元的损伤 Fig. 9 Damage to the first cohesive unit |
为了更好地显示裂纹扩展情况,采用各实体单独建模的方式,内聚力区域采用连续内聚力单元(COH2D4),通过在单元积分点上采用内聚力模型的本构关系,模拟裂纹萌生及扩展过程,将内聚力界面层与母材接触面进行tie绑定,接触面刚性连接且绑定区域不发生相对运动和变形,使得内聚力单元两侧单元位移和应力协调。对于内聚力区的网格划分,采用4个内聚力单元对应1个母材单元的划分方式,通过网格无关性的检验,母材处网格尺寸为1 mm×2 mm,内聚力区网格尺寸为1 mm×0.5 mm。在模型左右两侧上表面端点处分别施加平行于x方向的2 mm位移载荷(见图8)。
3.2 裂纹萌生及扩展数值模拟分析采用与相同的双线性内聚力模型的非线性分析方法,对典型焊接接头进行裂纹萌生及扩展数值模拟研究,计算得到焊趾处的第1个内聚力单元的损伤曲线如图9所示。
裂纹萌生阶段,加载位移在0.026 mm之前时,损伤数值为0,此时内聚面上的牵引力还没有达到临界应力值,内聚力单元没有进行损伤累积;当加载位移到达0.026 mm后,牵引力达到临界应力值30 MPa,损伤开始非线性累积,开始时牵引力较大,损伤累积速度较快,但随着位移载荷的增加,损伤增大导致牵引力下降,致使损伤累积速率减缓,损伤值趋近于1;当加载位移进一步增加到达0.7 mm时,损伤数值增大为1,此时裂纹开始萌生,并随着加载位移的进一步增加而发生扩展。
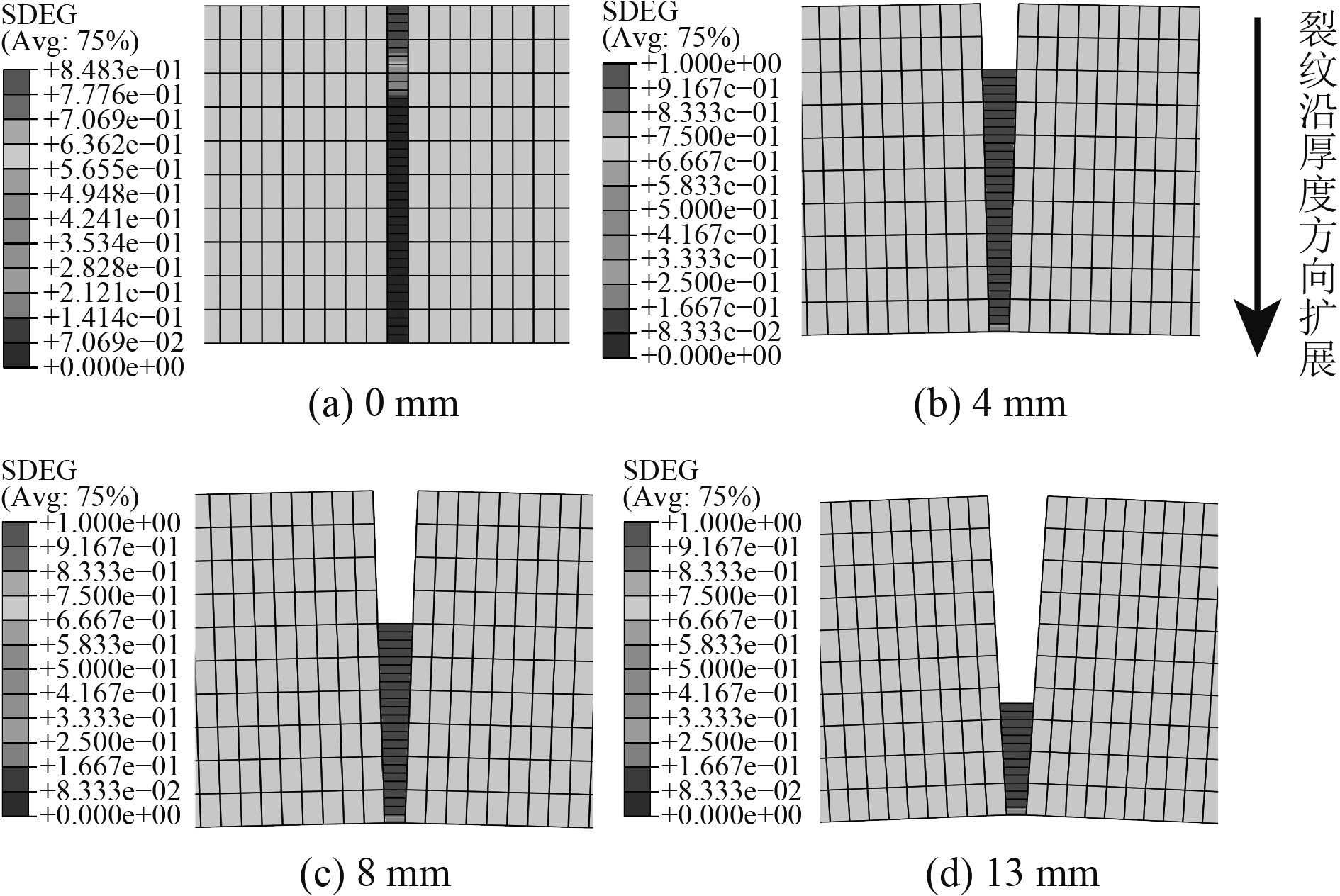
图10为该典型焊接接头从裂纹开始萌生(即裂纹长度为0 mm)到裂纹扩展到4 mm、8 mm和13 mm长度时所对应的损伤值结果。在恒定位移载荷的作用下,损伤值从0逐渐累积,当损伤值增大为1时,裂纹开始从第一个内聚力单元处萌生,且随着位移载荷的增大延板厚方向不断扩展。
|
图 10 焊接接头不同裂纹长度损伤结果图 Fig. 10 Damage results of welded joint with different crack lengths |
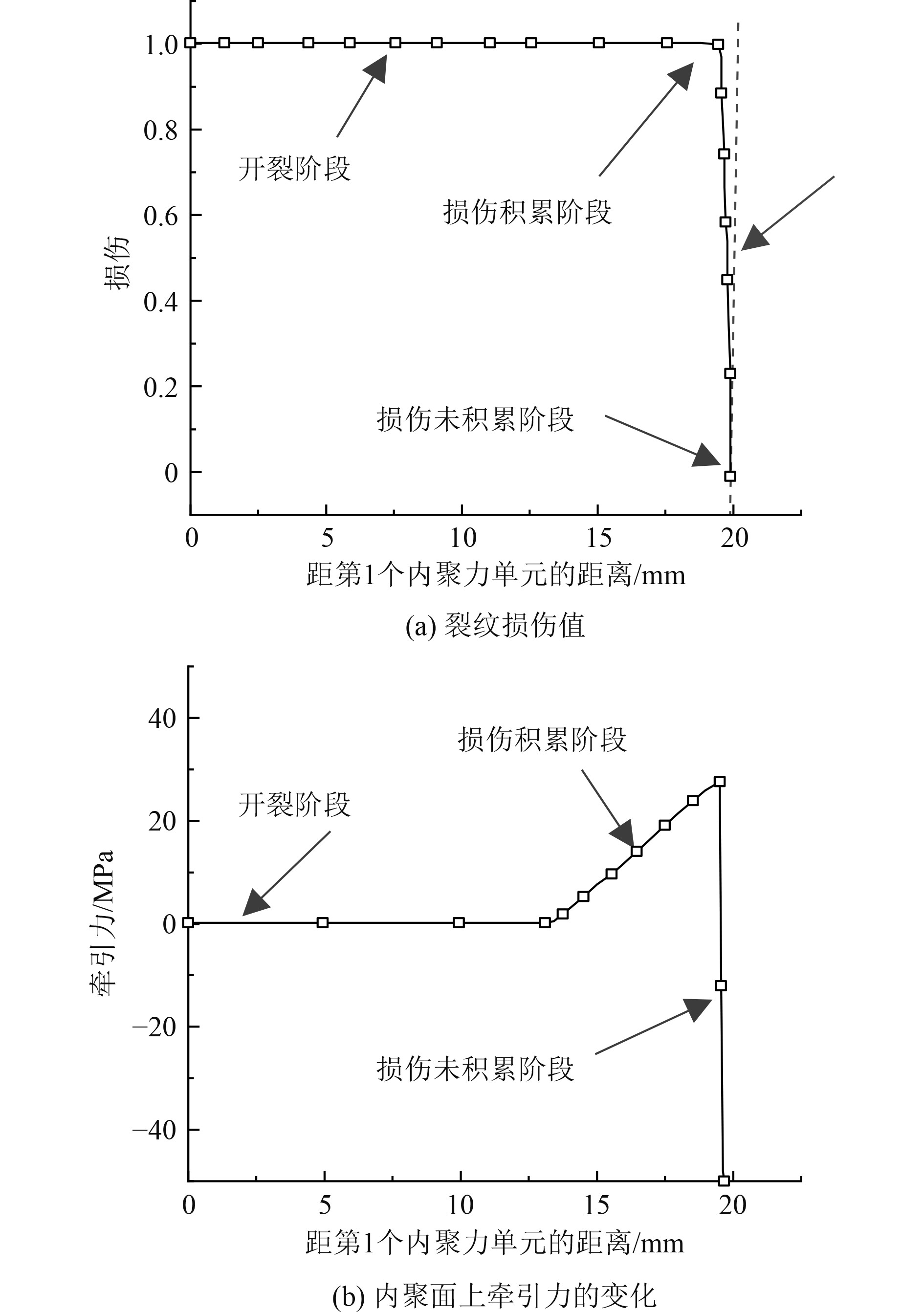
图11为当裂纹扩展长度为13 mm时,该典型焊接接头的裂纹损伤值及内聚面上牵引力的变化。可看出:
|
图 11 裂纹长度为 13mm 时裂纹损伤值及牵引力变化 Fig. 11 The variation of crack damage value and traction forcewhen crack is 13mm |
1)在开裂阶段,内聚力损伤值达到了1(见图11(a)),而对应的内聚面上牵引力变为0(见图11(b)),此时焊趾处裂纹开始萌生,内聚力单元消失,裂纹随着加载位移的增加而继续扩展。
2)随着位移载荷的增加,损伤不断累积,在内聚力区沿板厚方向上距离裂纹尖端越来越远时,内聚面上的牵引力逐渐变大,而损伤与之相反,逐渐减小;当沿板厚方向上距离裂纹尖端有一段距离后,内聚力单元损伤已经无限接近1,此时这部分单元在受到较小的加载位移后就会失效破坏,处在损伤积累阶段。
3)在内聚力区沿板厚方向距离裂纹尖端足够远时,即距离该典型焊接接头上表面19.5mm时,损伤值降为0(见图11(a)),存在压应力(图11(b)),此处内聚力单元还未进行损伤累积,处于损伤未积累阶段。
该典型焊接接头加载位移与裂纹长度呈非线性关系,加载位移未达到0.98mm时,处于裂纹萌生阶段,此时进行损伤累积;当加载位移达到0.98mm时裂纹开始开裂,且在1.2mm的加载位移之前,裂纹扩展速率较快,随着加载位移的增加扩展速率逐渐放缓,在加载位移达到2mm时,裂纹扩展长度为16mm,如图12所示。

|
图 12 裂纹长度随加载位移的变化 Fig. 12 The variation of crack length with loading displacement |
本文基于内聚力模型,采用双线性牵引分离准则,首先对不锈钢钎焊接头在恒定位移载荷作用下的裂纹萌生及扩展过程进行数值模拟分析,在数值模拟与文献试验结果较为一致的基础上,然后采用同样分析方法进行典型焊接接头的裂纹萌生及扩展研究,主要结论如下:
1)基于双线性的CZM裂纹萌生及扩展分析方法能够较好地模拟焊接接头裂纹扩展过程中的开裂、损伤积累及损伤未积累阶段。
2)焊接接头在位移载荷加载初期,损伤数值为0,牵引力还没有达到临界应力值,内聚力单元没有进行损伤累积;当牵引力达到临界应力后,损伤值迅速增加,此时损伤累积速率较大;但随着位移载荷的增加,牵引力下降,致使损伤累积速率减缓,损伤值趋近于1;当加载位移进一步增加时,损伤值到达1,裂纹开始萌生。
3)在开裂阶段,焊接接头内聚力单元损伤值到达1,内聚面上的牵引力为0,此时裂纹随着位移载荷的增加沿板厚方向进行扩展;当在损伤积累阶段时,距离裂纹尖端越远,损伤值越小,而内聚面上的牵引力越大;在损伤未积累阶段,损伤值为0,且由于大变形的存在,出现压应力现象。
| [1] |
TALJAT B, RADHAKRISHNAN B, ZACHARIA T. Numerical analysis of GTA welding process with emphasis on post-solidification phase transformation effects on residual stresses[J]. Materials Science & Engineering A, 1998, 246(1-2): 45-54. |
| [2] |
魏超. 基于内聚力模型的压裂泵泵头体裂纹扩展规律研究[D]. 荆州: 长江大学, 2019
|
| [3] |
杨庆生, 杨卫. 断裂过程的有限元模拟[J]. 计算力学学报, 1997, 14(4): 33-38. YANG Q S, YANG W. Finite element simulation of fracture process[J]. Journal of Computational Mechanics, 1997, 14(4): 33-38. |
| [4] |
HUTCHINSON J W, EVANS A G. Mechanics of materials: top-down approaches to fracture[J]. Acta Materialia, 2000, 48(1): 125-135. DOI:10.1016/S1359-6454(99)00291-8 |
| [5] |
YANG Q D, SHIM D J, SPEARING S M. A cohesive zone model for low cycle fatigue life prediction of solder joints[J]. Microelectronic Engineering, 2003, 75(1): 85-95. |
| [6] |
MORVARID K G, Hamid J, Amir K. Cohesive zone modeling of ductile tearing process in brazed joints[J]. Engineering Fracture Mechanics, 2013, 102: 156-170. DOI:10.1016/j.engfracmech.2012.11.018 |
| [7] |
SADIGH M A S, MARAMI G, PAYGOZAR B. Failure simulation in resistance spot-welded lap-joints using cohesive zone modeling[J]. Journal of Central South University, 2018, 25(11): 2567-2577. DOI:10.1007/s11771-018-3936-z |
| [8] |
谭菊妮. 基于内聚力模型的钎焊接头疲劳裂纹扩展有限元计算[D]. 青岛: 中国石油大学(华东), 2018
|
| [9] |
陈兴, 舒双文, 周帼彦, 等. 基于内聚力模型的T型钎焊接头裂纹扩展数值模拟[J]. 压力容器, 2014, 31(8): 7-13+58. CHEN X, SHU S W, ZHOU Y Y, et al. Numerical simulation of crack propagation of T -type brazed joints based on cohesive zone model[J]. Pressure Vessels, 2014, 31(8): 7-13+58. DOI:10.3969/j.issn.1001-4837.2014.08.002 |
| [10] |
ABDUL-BAQI A, SCHREURS P J G, GEERS M G D. Fatigue damage modeling in solder interconnects using a cohesive zone approach[J]. International Journal of Solids and Structures, 2004, 42(3): 927-942. |
| [11] |
GEUBELLE P H, BAYLOR J. Impact-induced delamination of laminated composite: a 2D simulation[J]. Composites Part B Engineering, 1998, 29(5): 589-602. DOI:10.1016/S1359-8368(98)00013-4 |
| [12] |
CHANDRA N. Evaluation of interfacial fracture toughness using cohesive zone model[J]. Journal of Composites, 2002, 33(A): 1433-1447. |
| [13] |
QIU Y, CRISFIELD M A, ALFANO G. An interface element formulation for the simulation of delamination with bucking[J]. Engineering Fracture Mechanics, 2001, 68(11): 1755-1776. |
| [14] |
TURON A, DAVILA C G, CAMANHO P P, et al. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models[J]. Engineering Fracture Mechanics, 2006, 74(10): 1665-1682. |
| [15] |
ZHOU F H, MOLINARI J F, SHIOYA T. A rate-dependent cohesive model for simulating dynamic crack propagation in brittle materials[J]. Engineering Fracture Mechanics, 2004, 72(9): 1383-1410. |
| [16] |
倪宝玉, 徐莹, 黄其, 等. 修正内聚区长度计算公式在冰Ⅰ型裂纹扩展中的应用[J]. 中国舰船研究, 2022, 17(3): 58-66. NI B Y, XU Y, HUANG Q, et al. Application of improved cohesive zone length formula in ice mode I crack propagation[J]. Chinese Journal of Ship Research, 2022, 17(3): 58-66. |
 2023, Vol. 45
2023, Vol. 45
