2. 江苏科技大学 能动学院,江苏 镇江 212003
2. School of Energy and Power, Jiangsu University of Science and Technology, Zhenjiang 212003, China
三维编织复合材料结合了复合材料和三维编织结构的优点,具备较高的比强度和比刚度以及优良的抗疲劳特性和层间性能,因而可以作为承力部件,在航空航天、医疗、汽车等领域发挥重要作用[1-2]。随着船舶制造水平和材料的发展,三维编织复合材料在船舶领域,尤其在其动力装置方面将会有更大的应用前景。
疲劳失效是发生在工程领域中一类十分普遍的物理现象[3-6]。对金属而言,在交变载荷作用下,局部塑性应变集中引发疲劳裂纹的萌生。随疲劳加载的进行,裂纹会缓慢扩展,使材料性能下降。当裂纹长度扩展到临界尺寸时,材料就会发生失稳疲劳断裂。然而在对三维编织复合材料的研究过程中,除了发现其具有高的疲劳极限外[7-10],还发现了更加奇异的试验现象——周期性循环的疲劳载荷不但没有降低强度,反而随循环次数的增加逐渐提高了强度。朱元林等[11-12]对三维四向编织、0°和±45°层合板碳/碳复合材料进行了室温下的拉/拉疲劳试验研究,并基于Yang[13]的剩余刚度退化公式,建立了考虑应力水平的碳/碳复合材料纤维束纵向和剪切剩余刚度、强度模型。廖晓玲[14]对三维编织碳/碳复合材料进行拉/拉疲劳试验测试,试验结果表明,三维四向碳/碳材料疲劳极限的应力水平可达静强度的93%,拉伸剩余强度可达初始强度的1.3倍。
本文以三维编织复合材料为研究对象,从细观尺寸出发,基于渐进损伤理论,提出一种三维编织复合材料疲劳强化假设,并基于此假设建立了一种能够反映三维编织复合材料在疲劳加载过程中动态变化的三维编织复合材料剩余强度模型。对比分析了试验结果和预测结果,验证了模型的准确性和有效性。
1 编织角-循环数模型及其参数确认通过大量三维编织复合材料疲劳试验发现:三维编织复合材料在疲劳载荷作用下的剩余刚度先增加后减小,是由于三维编织复合材料在疲劳载荷作用下,内部编织角逐渐减小。假设三维编织复合材料内部编织角和循环数遵循以下数学关系式:
| $ \frac{{\gamma \left( n \right)}}{{\gamma \left( 0 \right)}} = {\left[ {a\left( {1 - {e^{ - n}}} \right) + 1} \right]^b}。$ | (1) |
式中:
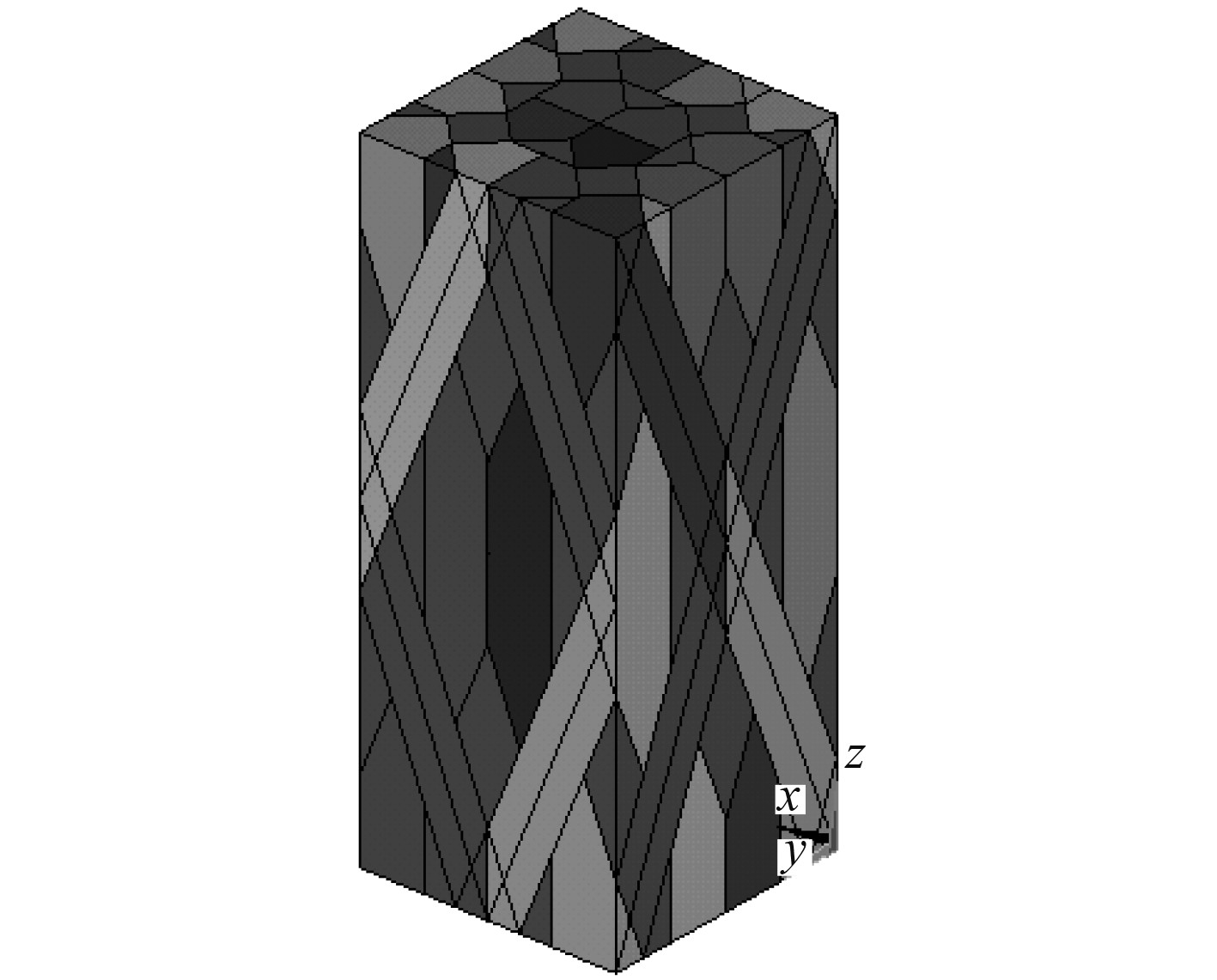
在细观尺度下,考虑纤维束之间的相互挤压,建立截面形状为六边形、纤维束直线走向的三维四向复合材料单胞模型。如图1所示。
|
图 1 内部单胞几何模型 Fig. 1 Geometric model of inner cell |
三维编织复合材料内部结构存在周期性,为保证位移连续和应力连续,需要对所建立的单胞模型施加周期性边界条件。Xia等[15]提出的一种周期性位移边界条件能够满足三维编织复合材料的内部结构要求,其表达式为:
| $ u_i^{j + } - u_i^{j - } = \bar {{\varepsilon _{ik}}} \left( {x_k^{j + } - x_k^{j - }} \right) = \bar {{\varepsilon _{ik}}} \Delta x_k^j。$ | (2) |
式中:j+和j-分别为单胞的第j组相对平行面;
三维四向复合材料内部单胞有3对平行面,约束方程为:
| $ \left\{ \begin{array}{l} {U_{{F_b}}} - {U_{{E_b}}} = 0,\\ {V_{{F_b}}} - {V_{{E_b}}} = 0 ,\\ {W_{{F_b}}} - {W_{{E_b}}} = \bar \varepsilon \left( A \right) \times h,\\ {U_{{B_b}}}-{U_{{A_b}}}=\bar \varepsilon \left( A \right) \times 8{b_1},\\ {V_{{B_b}}} - {V_{{A_b}}} = 0 ,\\ {W_{{B_b}}} - {W_{{A_b}}} = 0 ,\\ {U_{{C_b}}} - {U_{{D_b}}} = 0 ,\\ {V_{{C_b}}}-{V_{{D_b}}}=\bar \varepsilon \left( A \right) \times 8{b_1},\\ {W_{{C_b}}} - {W_{{D_b}}} = 0 ,\\ {U_A} = {V_A} = {W_A} = 0 ,\\ {V_B} = {W_B} = {U_E} = {V_E} = {U_D} = {W_D} = 0 。\end{array} \right. $ | (3) |
式中:U、V、W为节点沿x、y、z方向的位移;
采用对纤维束和基体接触面上的对应单元节点进行x,y,z位移耦合进行界面的模拟。对单胞进行计算过程中,当耦合节点受力小于界面强度时,纤维束和基体的耦合节点不发生变化,材料的受力形式与节点合并相同,当耦合节点受力大于等于界面时,将相应的耦合节点纤维束方向位移耦合删除,保留其他方向位移耦合,以此完成纤维束/基体界面脱黏的模拟。
2.4 疲劳分析中的失效判定 2.4.1 疲劳过程中的纤维束失效判定由于三维Hashin失效准则能够很好描述复合材料中纤维束在损伤中的各种失效形式,因此将三维Hashin静强度失效准则拓展到疲劳中。
纤维束内纤维断裂失效:
| $ {\left[ {\frac{{{\sigma _{11}}}}{{{X_{11}}}}} \right]^2} + \alpha \left[ {\frac{{{\sigma _{12}}}}{{{S_{12}}}}} \right] + \alpha \left[ {\frac{{{\sigma _{13}}}}{{{S_{13}}}}} \right] \geqslant 1 ,$ | (4) |
纤维束内基体失效:
| $ {\left[ {\frac{{{\sigma _{22}} + {\sigma _{33}}}}{{{Y_{22}}}}} \right]^2} + \frac{{\left( {\sigma _{23}^2 - {\sigma _2}{\sigma _3}} \right)}}{{{S_{23}}^2}} + {\left[ {\frac{{{\sigma _{12}}}}{{{S_{12}}}}} \right]^2} + {\left[ {\frac{{{\sigma _{13}}}}{{{S_{13}}}}} \right]^2} \geqslant 1。$ | (5) |
式中:
复合材料在进行疲劳加载时,随着循环数的增加,材料内的纤维损伤逐渐增加。当纤维损伤达到一定程度时,复合材料发生瞬间破坏。因此,对复合材料疲劳分析中的材料最终破坏准则与强度分析相同,即
1)单胞内纤维束沿纵向破坏的有限单元比例超过50%;
2)断裂损伤贯穿整个单胞截面;
3)单胞内应力随应变的增加开始下降。
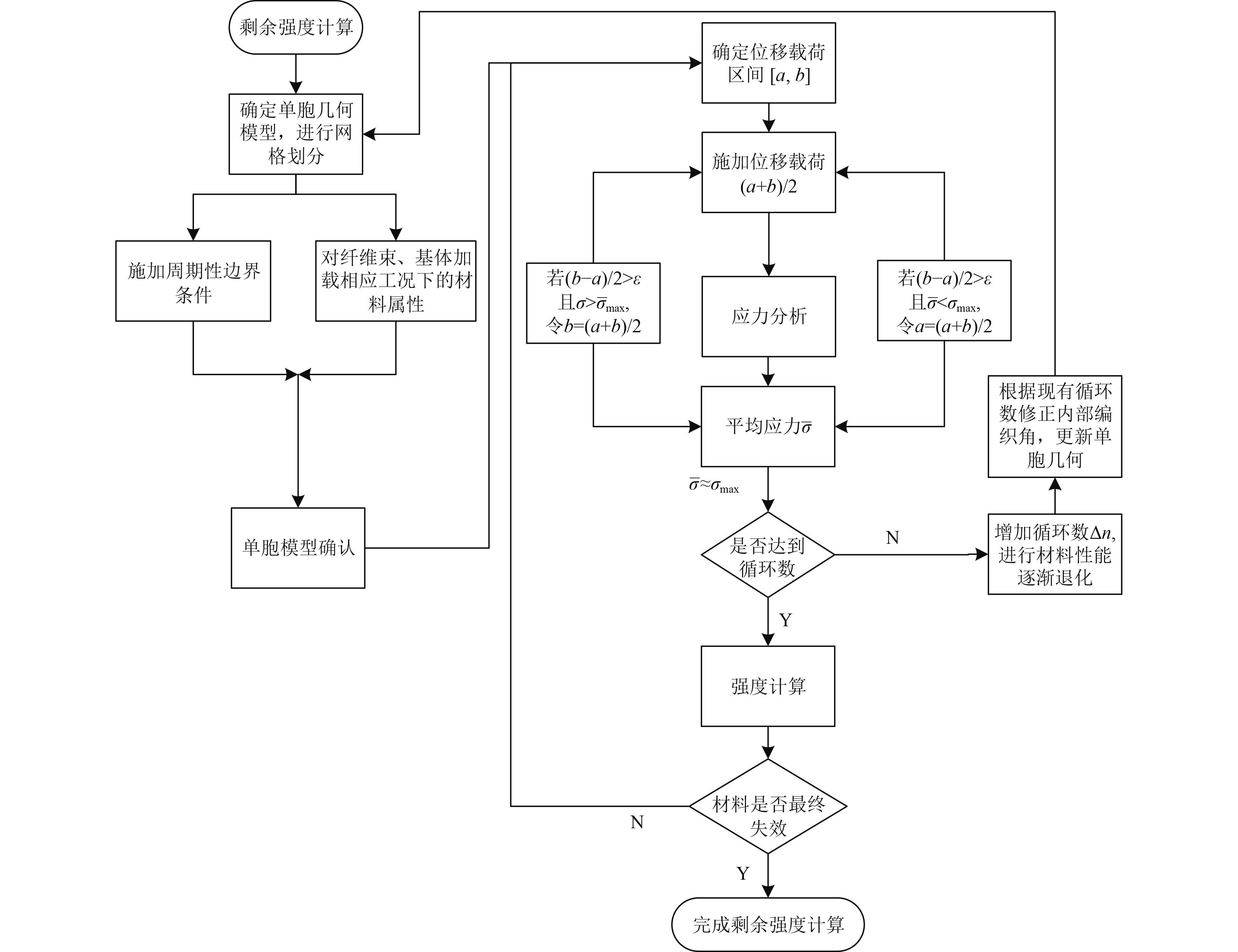
2.6 三维编织复合材料疲劳预测流程采用逐渐损伤研究方法对三维编织复合材料进行疲劳后剩余强度预测研究,计算流程如图2所示。疲劳后剩余强度分析计算过程主要有以下几个方面:
|
图 2 三维编织复合材料进行疲劳后剩余强度预测计算流程图 Fig. 2 Flow diagram for predicting residual strength of 3D braided composites after fatigue |
1)通过输入几何和工艺参数得到三维编织复合材料几何模型,进行网格划分、组分材料的定义及周期性边界条件的加载,完成周期性单胞的建模工作;
2)通过二分法调整载荷,使单胞平均应力达到疲劳最大应力水平,然后在次应力下进行应力分析,采用应力水平、循环数的三维Hashin疲劳失效准则对单元进行失效判定,检查单元是否发生破坏,若所有单元均无破坏,则判定是否达到最大循环数,若达到循环数,则停止计算,若没有达到循环数,则增加循环数增量,进行材料的退化,并进行单胞几何修正,重新进行单元划分、材料定义、载荷施加、应力分析;若单元发生失效,则对单元进行相应刚度退化,如此循环计算,直至到达材料最终失效。
3 模型验证 3.1 编织角-循环数数学模型验证通过采集三维编织复合材料试验件在疲劳过程中的剩余刚度变化,则三维编织复合材料拉-拉疲劳编织角与循环数的关系,即
| $ \frac{{\gamma \left( {{n \mathord{\left/ {\vphantom {n N}} \right. } N}} \right)}}{{\gamma \left( 0 \right)}} = {\left[ { - 0.452\left( {1 - {e^{ - \frac{n}{N}}}} \right) + 1} \right]^{0.183}}。$ | (6) |
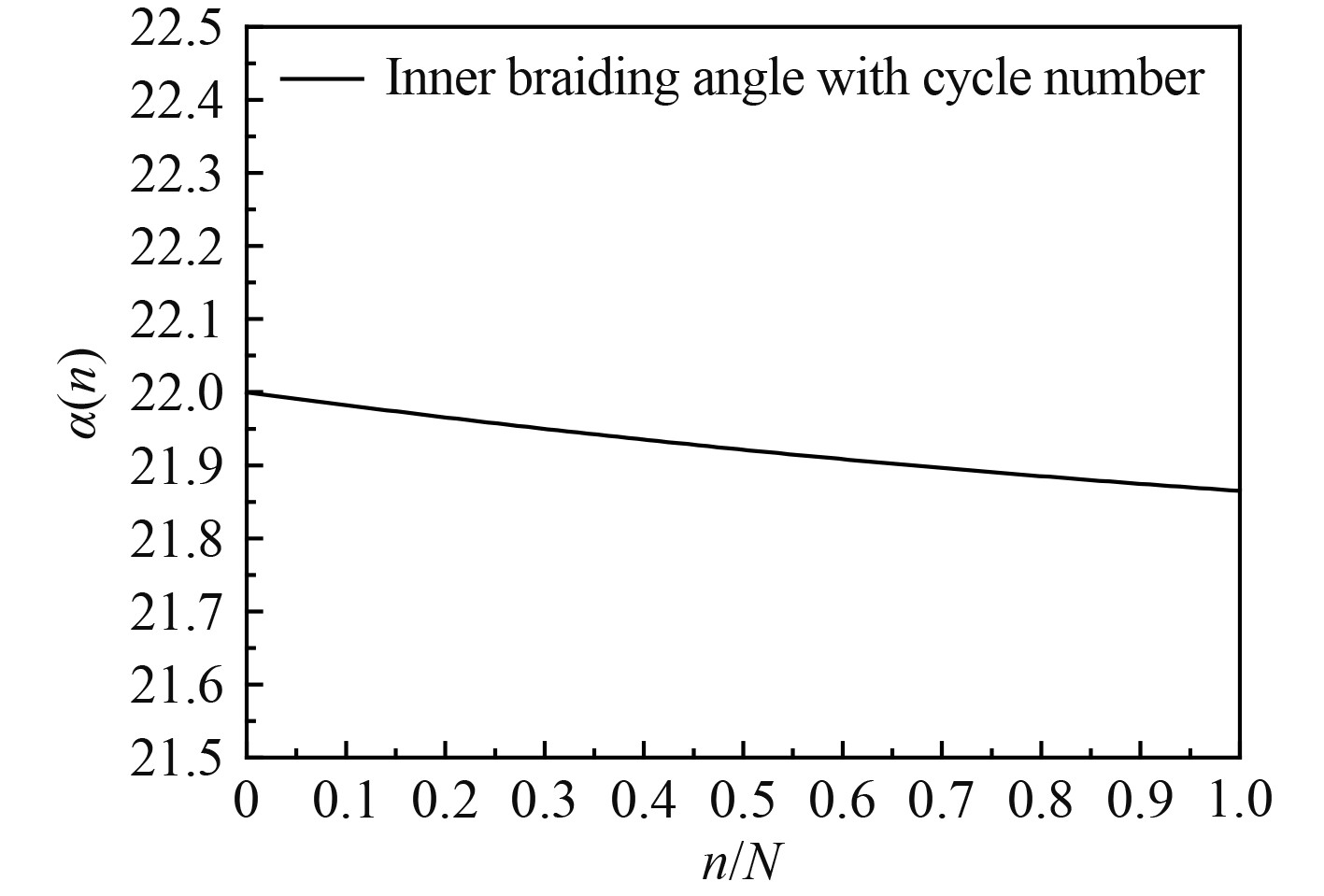
图3给出了单胞内部编织角随循环数的变化。
|
图 3 编织角随循环数的变化 Fig. 3 The change of braided angle with the number of cycles |
三维编织复合材料在105循环数中花节长度、试验件试验段长度变化,如表1所示。
|
|
表 1 三维编织复合材料疲劳加载过程中花节长度、试验件工作段长度变化 Tab.1 The length of flower joint and the length of working section of test specimen change during fatigue loading of 3D braided composites |
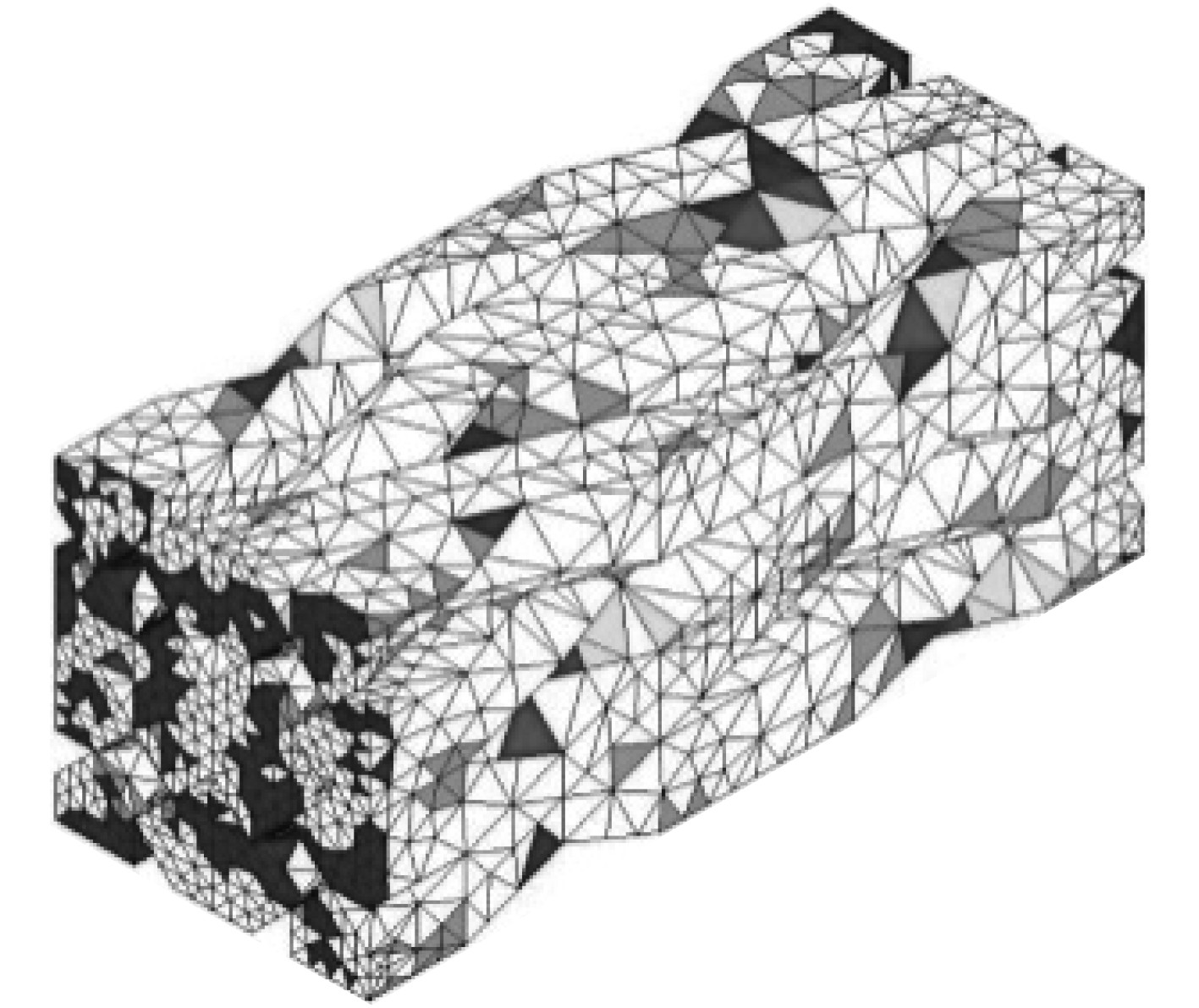
对应力水平为85%,首先进行疲劳分析。三维编织复合材料拉-拉疲劳组分损伤扩展图如图4和图5所示。

|
图 4 循环数1001后纤维的失效状态 Fig. 4 Failure status of the fiber after cycle number 1001 |
|
图 5 循环数为2001失效状态 Fig. 5 Failure status of the fiber after cycle number 2001 |
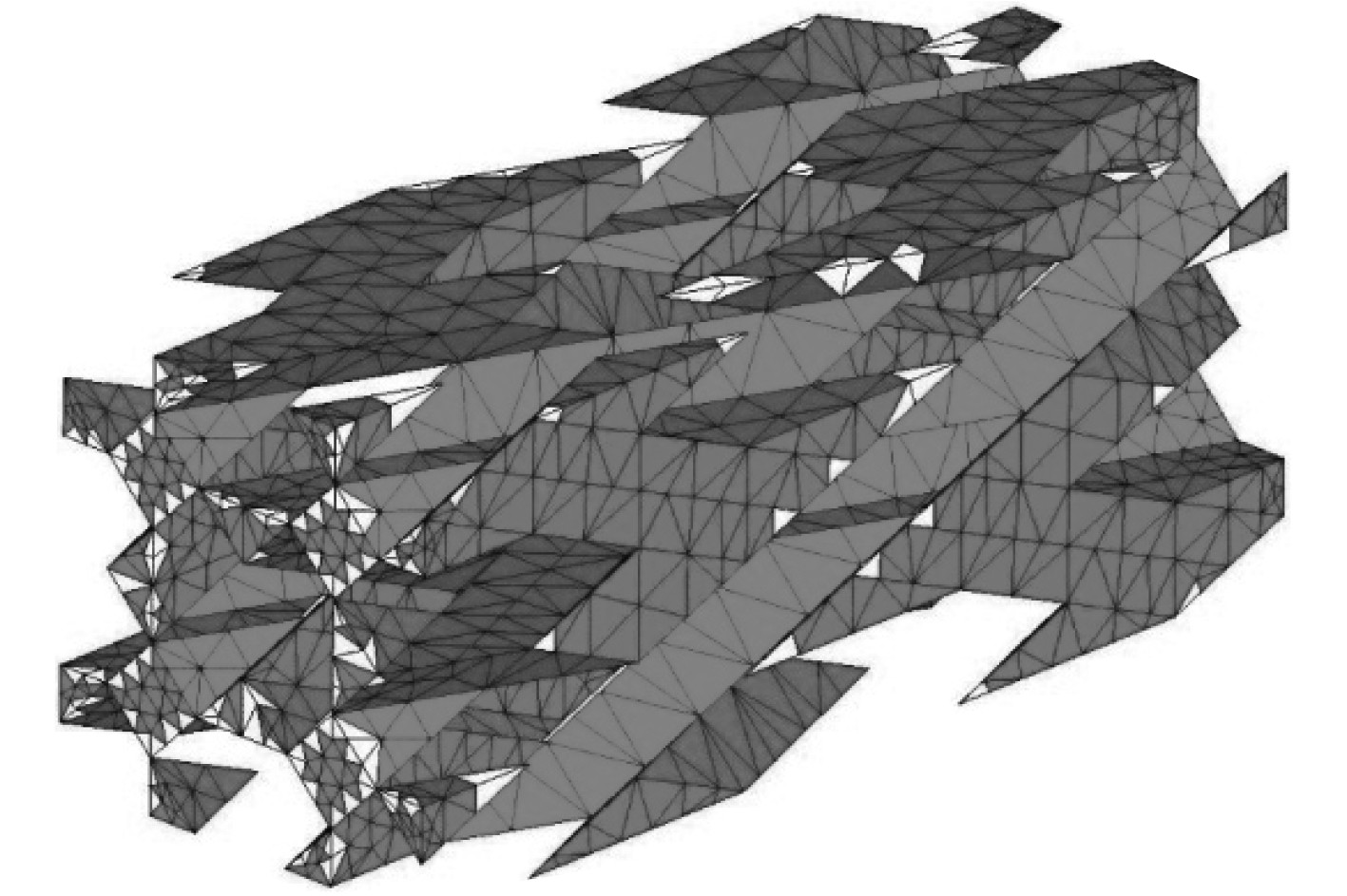
图6和图7为纯基体区域疲劳损伤扩展,表2给出了剩余强度的预测值和试验值对比。
|
图 6 循环数为1001失效状态 Fig. 6 Failure status of the matrix after cycle number 1001 |
|
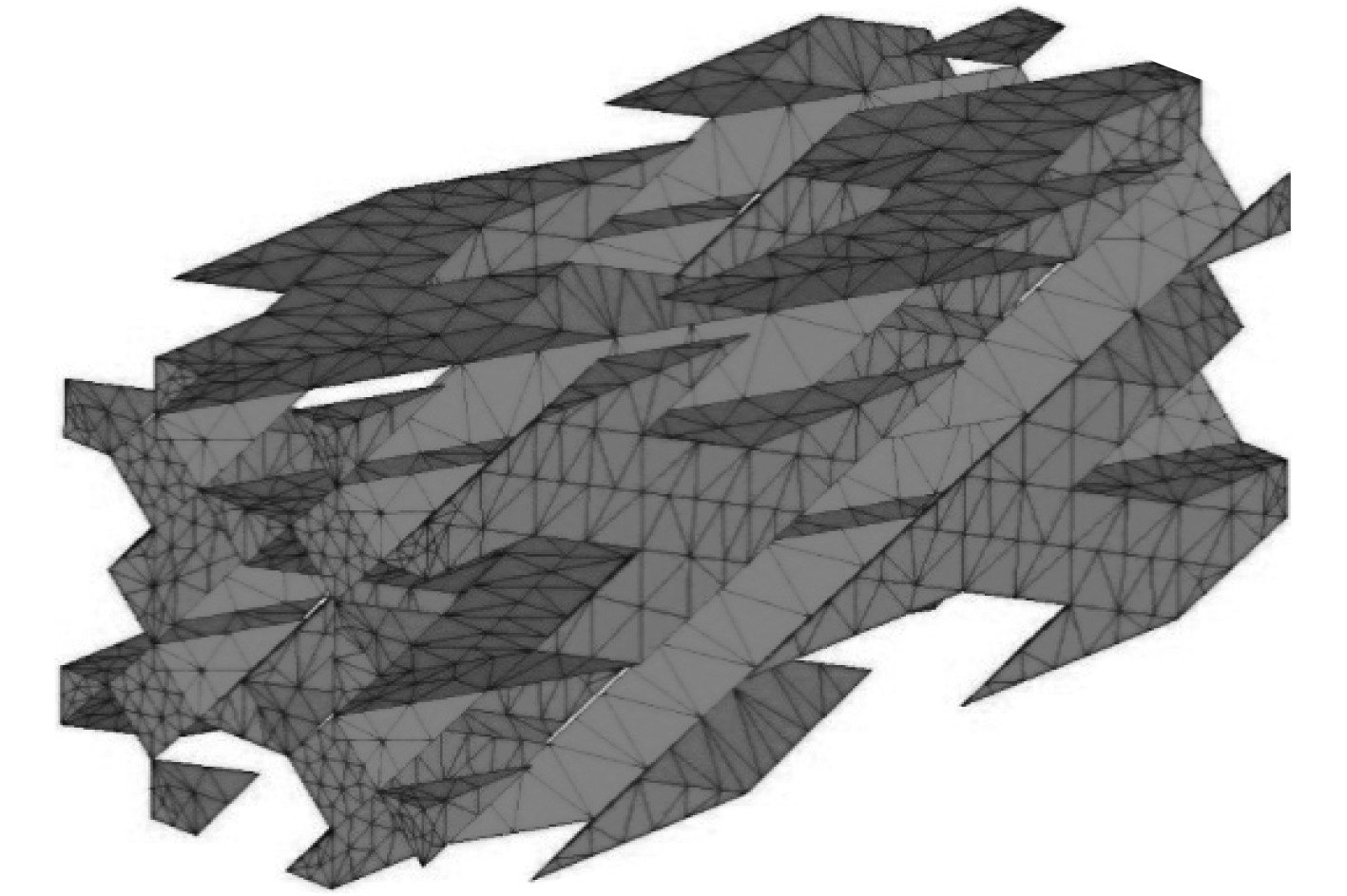
图 7 循环数为2001失效状态 Fig. 7 Failure status of the matrix after cycle number 2001 |
|
|
表 2 三维编织复合材料剩余强度的预测值和试验值对比 Tab.2 Comparison of predicted and tested residual strength of 3D braided composites |
本文提出一种解释三维编织复合材料疲劳强化现象的方法,并将其进行数学描述,即编织角-循环数模型。建立了三维编织复合材料细观单胞模型,考虑了单胞模型的组分结构、周期性,纱线的相互挤压,给出了纤维束和基体的失效模型及三维编织复合材料剩余强度计算方法。
通过刚度采集得到了编织角-循环数模型相关参数,对比试验结果,花节的计算值和测量值之间的误差小于5%。开展了疲劳分析和疲劳加载后的剩余强度计算,得到了不同循环数下的组分损伤情况,以及25%、50%、75%循环数后的剩余强度计算值,计算误差均小于10%,验证了模型的有效性。
| [1] |
李贺军. 碳/碳复合材料[J]. 新型碳材料, 2001, 16(2): 70-80. |
| [2] |
SU J M, ZHOU S J, LI R Z, et al. A review of carbon-carbon composites for engineering applications[J]. Carbon, 2015, 93(2): 1081-1081. |
| [3] |
韩振宇, 梅海洋, 付云忠, 等. 三维编织预成型体的织造及三维编织复合材料细观结构研究进展[J]. 材料工程, 2018, 46(11): 25–36.
|
| [4] |
SHOKRICH M M, LESSARD L B. Progressive fatigue damage modeling of composite materials, part II: material characterization and model verification[J]. Journal of Composite Materials, 2000, 34: 1081–1116.
|
| [5] |
WU W, LEE L J, CHOI S T. A study of fatigue damage and fatigue life of composite laminates[J]. Journal of Composite Materials. 1996, 30: 123–137.
|
| [6] |
CHAO Z, CURIEL-SOSA J L, QUOC B T. Meso-scale progressive damage modeling and life prediction of 3D braided composites under fatigue tension loading[J]. Composite Structures, 2018, 201: 62–71.
|
| [7] |
FAN Z, ZHENGUO L, ZHE W, et al. A new scheme and microstructural model for 3D full 5-directional braided composites[J]. Chinese Journal of Aeronautics, 2010, 23(1): 61–67.
|
| [8] |
SONG J, WEN W, CUI H. Fatigue life prediction model of 2.5D woven composites at various temperatures[J]. Chinese Journal of Aeronautics, 2018, 31(2): 310–329.
|
| [9] |
YAO W X, HIMMEL N. A new cumulative fatigue damage model for fibre-reinforced plastics[J]. Composites Science and Technology. 2000, 60(1): 59–64.
|
| [10] |
HAN K S, HWANG W. Fatigue life prediction and failure mechanisms of composite materials[J]. Advanced Composite Materials. 1992, 2(1): 29–50.
|
| [11] |
朱元林, 温卫东, 刘礼华, 等. 碳/碳复合材料疲劳损伤失效试验研究[J]. 复合材料学报, 2016, 33(2): 386-393. DOI:10.13801/j.cnki.fhclxb.20150420.001 |
| [12] |
朱元林. C/C复合材料疲劳寿命预测与分析方法研究[D]. 南京: 南京航空航天大学, 2012.
|
| [13] |
YANG J N, LEE L J, SHEU D Y. Modulus reduction and fatigue damage of matrix dominated composite laminates[J]. Composite Structures. 1992, 21(2): 91–100.
|
| [14] |
LIAO X, LI H, XU W, et al. Effects of tensile fatigue loads on flexural behavior of 3D braided C/C composites[J]. Composites Science & Technology, 2008, 68(2): 333-336. |
| [15] |
XIA Z, ZHANG Y, ELLYIN F. A unified periodical boundary conditions for representative volume elements of composites and applications[J]. International Journal of Solids and Structures, 2003, 40(8): 1907-1921. DOI:10.1016/S0020-7683(03)00024-6 |
 2023, Vol. 45
2023, Vol. 45
