月池是穿过船舶驳船甲板、船体的垂直开口,用于下降或提升设备。由于外部激励频率(入射波或结构运动)接近月池中流体的固有频率,可激发大振幅的自由表面振荡,造成月池中大振幅的自由表面振荡,导致作用在船上的波浪力发生显著变化。因此,了解共振流体流动中的基本物理现象对海上作业与结构安全极其重要。
预测水动力和发现月池中流体共振行为背后的作用机制这个课题已被广泛研究,Moradi[1]提出了一个准解析近似解,其中垂荡和晃荡模式共振可通过公式表示并且可求得一个近似的特征值方程。Faltinsen等[2]提出了一种在限水深中2个方箱间月池中类垂荡模态共振的区域求解方法。Sun等[3]在并排布置的2艘驳船之间采用二阶波浪绕射模型模拟波浪相互作用。冯等[4]研究了三维非线性势流模型下的两并排驳船间的自由水面的共振。然而,势流模型下的月池中波浪响应共振偏大,已被实验研究广泛证实,Saitoh等[5],Iwata等[6]和Peric等[7]。
随着计算机技术的发展,计算流体动力学方法在这个问题上被采用。Lu等[8]采用VOF自由表面捕捉技术的有限元方法分析了窄缝共振问题。Jiang等[9-10]研究了窄缝中的流体共振和2个不同尺寸并排方箱上的波浪力。Fredriksen等[11]在复杂结构中对月池中的波浪响应进行了实验和数值方法研究。Jiang等[12]进一步对复杂的结构边缘轮廓进行分析,对流体形态分析表明,月池底部周围的旋涡运动会随着不同的边缘轮廓发生明显改变。Moradi等[13]和Feng等[14]的研究中也做了类似工作,尖角和圆角轮廓会对窄缝共振振幅产生影响。所有这些工作表明月池附近的旋涡脱落是研究共振现象的一个重要问题。
本文在Jiang等[12]研究基础上,基于OpenFOAM分析了流速对月池共振现象的影响。旋涡脱落是共振现象上的一个重要问题,流速能影响旋涡的运动,并会对月池中的波浪响应产生进一步影响。
1 理论公式在任意拉格朗日-欧拉(ALE)参考系中,具有再归一化群(RNG)模型的不可压缩湍流中,质量和动量守恒的控制方程为:
| $ \begin{gathered} \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho {u_i}}}{{\partial {x_i}}} = 0, \end{gathered} $ | (1) |
| $ \begin{gathered} \frac{{\partial \rho {u_i}}}{{\partial t}} + \frac{{\partial \rho \left( {{u_j} - u_j^m} \right){u_i}}}{{\partial {x_j}}} = \rho {f_i} - \frac{{\partial p}}{{\partial {x_i}}} + {\mu _e}\frac{\partial }{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)。\\ \end{gathered} $ | (2) |
其中:
RNG k− ε这2个公式用于闭合控制方程:
| $ {\mu _t} = {C_\mu }\frac{{{k^2}}}{\varepsilon }。$ | (3) |
其中,
| $ \begin{split} \frac{{\partial \rho k}}{{\partial t}} + &\frac{{\partial \rho \left( {{u_j} - u_j^m} \right)k}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left( {\frac{{{\mu _t}}}{{{\sigma _k}}}\frac{{\partial k}}{{\partial {x_j}}}} \right) + \\ & {\mu _t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \varepsilon ,\\ \frac{{\partial \rho \varepsilon }}{{\partial t}} +& \frac{{\partial \rho \left( {{u_j} - u_j^m} \right)\varepsilon }}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left( {\frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right) + \\ & {C_{1\varepsilon }}\frac{\varepsilon }{k}{\mu _t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho {C_{2\varepsilon }}\frac{{{\varepsilon ^2}}}{k}。\end{split} $ | (4) |
其中,模型常数
本文采用流体体积(VOF)法(Hirt和Nichols[16])捕捉自由表面运动。VOF中流体的体积量定义为
| $ \varphi = \left\{ {\begin{array}{*{20}{l}} {0,}&{{\text{ in air, }}} \\ {0 < \varphi < 1,}&{{\text{ on free surface }}},\\ {1,}&{{\text{ in water}}}。\end{array}} \right. $ | (5) |
满足以下平流方程:
| $ \frac{{\partial \varphi }}{{\partial t}} + \left( {{u_i} - u_i^m} \right)\frac{{\partial \varphi }}{{\partial {x_i}}} = 0。$ | (6) |
VOF函数中的
| $ \begin{split} &\rho = \varphi {\rho _W} + (1 - \varphi ){\rho_A} ,\\ & {\mu _e} = \varphi {\mu _{e_W}} + (1 - \varphi ){\mu _{e_A}}。\\ \end{split} $ | (7) |
其中,下标
在目前的数值波浪水槽中,辐射波通过海绵层消除。也就是说,在式(2)中物体作用力项引入了人工阻尼:
| $ {f_i} = {g_i} + {R_i} 。$ | (8) |
其中,gi为重力加速度,Ri为人工阻尼。应当注意的是为了数值稳定性,阻尼仅在当前二维问题的垂直方向y上作用。在此处,水平分量Rx = 0,而垂直分量Ry采用以下形式[8]:
| $ {R_y} = - {\left( {\frac{{x - {x_0}}}{{{D_s}}}} \right)^2}\frac{{{y_b} - y}}{{{y_b} - {y_h}}} \cdot v 。$ | (9) |
其中:x和y为网格节点的笛卡尔坐标;x0为海绵层起点处的坐标;v为垂直速度分量;Ds为波传播方向上阻尼区的总长度;yb为海床高;yh为水槽高度;ks为事先通过简单数值试验确定的经验参数。
控制方程式(1)和VOF方程式(7)集成在OpenFOAM中的有限体积法求解。速度和压力由压力隐式分裂算子算法(PISO,Issa[17])分离。使用欧拉方法离散瞬态项。对流项和扩散项分别用高斯有限线性法和高斯线性校正法离散。关于OpenFOAM中数字工具的详细信息,可参考Jasak[18]和Rusche[19]。
数值计算总是从静止状态开始,这意味着静态水压和零速度被指定为初始条件。无滑移边界条件施加在固体壁上,包括体表面和海床表面。在数值波浪水槽的上边界,参考压力p = 0和速度条件
在本数值模拟中,根据Courant-Friedrichs-Lewy(CFL)条件自动确定时间增量:
| $ \Delta t \leqslant {C_r} \times \min \left\{ {\sqrt {{S_e}} /\left| {{u_e}} \right|} \right\}。$ | (10) |
其中,Se和|ue|分别为计算单元中的面积和绝对速度。数值实验证实,使用Cr = 0.20可产生稳定和准确的结果。
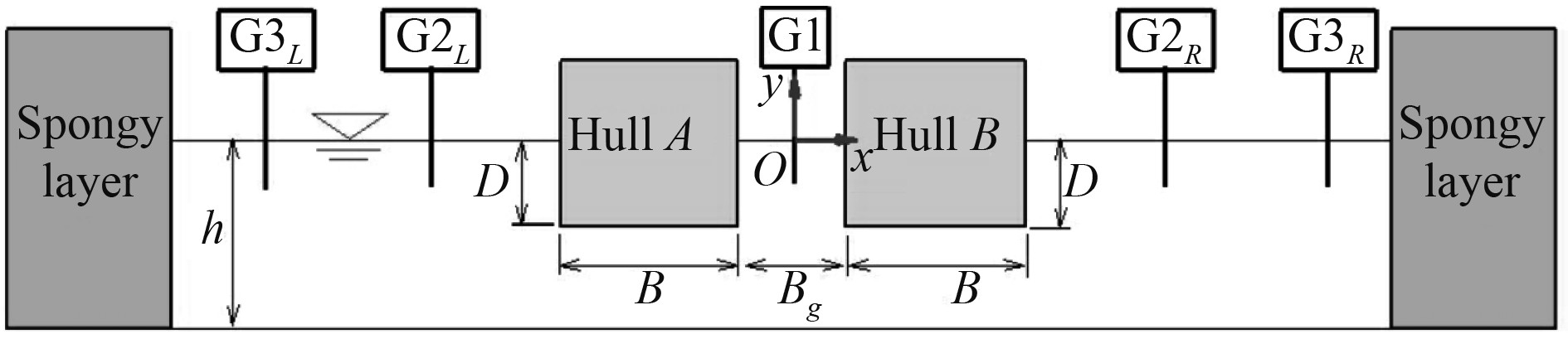
2 数值模型验证如图1所示,考虑由2个相同矩形船体形成的月池中的二维流体共振。宽度B = 0.360 m,吃水深度D = 0.180 m的船体位于恒定水深h = 1.03 m的波浪水槽中。船体之间的月池宽度Bg =0.180 m,当船体的移动频率接近流体固有频率时,可以观察到很大振幅的流体共振。在数值模拟中,定义笛卡尔坐标系oxy,原点位于月池中未扰动自由表面的中心。采用20 m长、1.5 m高的波浪槽,波浪槽两端有2个3 m长的海绵层,用于吸收辐射波。本文考虑了从波浪水槽的左侧到右侧的入流速度U。基于结构总长度的汝德德数定义为:
|
图 1 数值波浪水槽定义示意图 Fig. 1 Sketch of the definition of the numerical wave flume |
| $ {F_n} = \frac{U}{{\sqrt {g\left( {2B + {B_g}} \right)} }}。$ | (11) |
配备6个浪高仪记录波幅变化,其中2个G1L和G1R位于月池,坐标为x = ±0.08 m,另外4个浪高仪G2L和G2R以及G3L和G3R分别位于x = ±0.715 m 和 x = ±1.150 m。双船体的同步位移由垂荡运动引起,如下式:
| $ {\xi _h}(t) = {A_b}\sin (\omega t) 。$ | (12) |
其中,Ab和ω分别为垂荡振幅和频率。
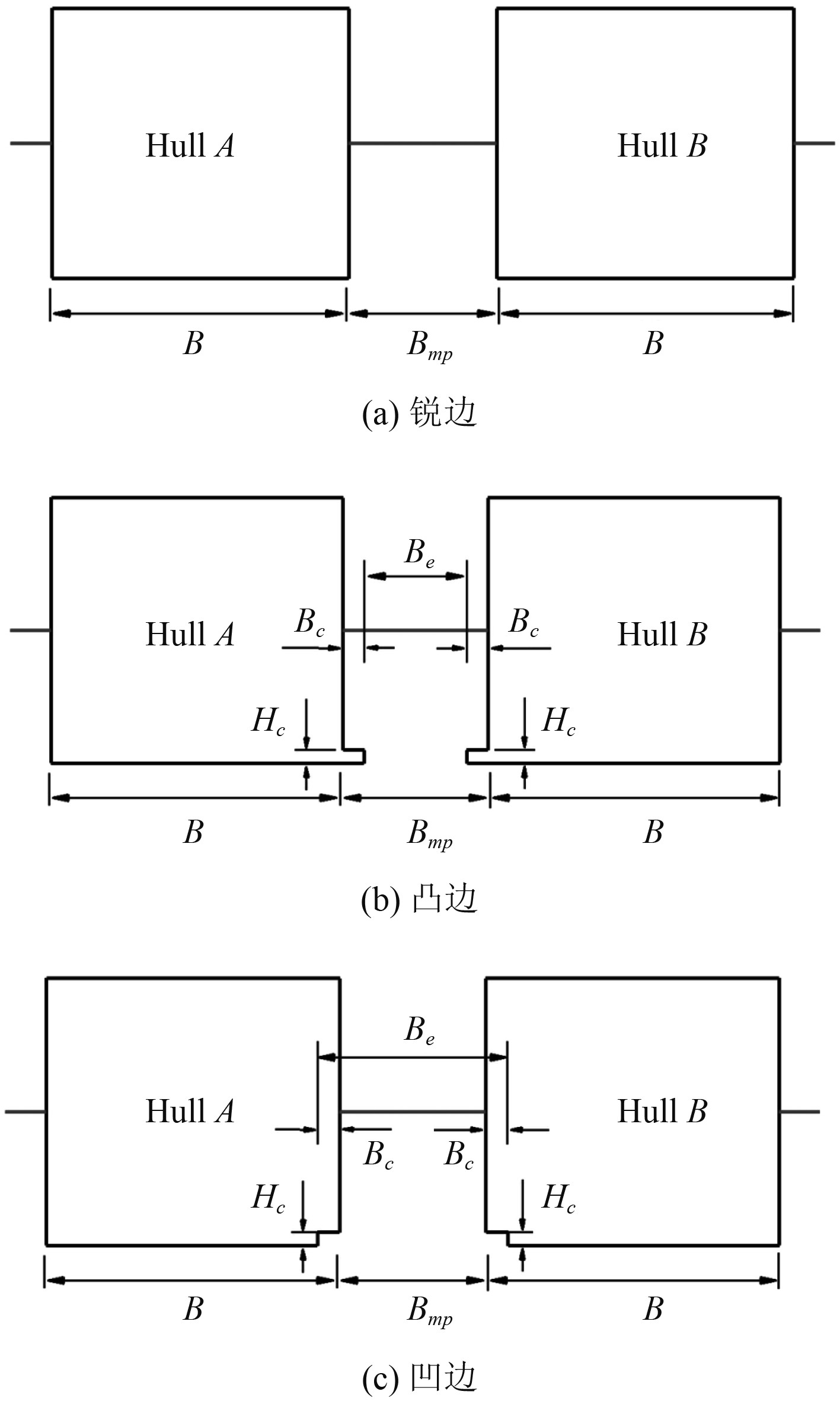
本文根据Jiang等[12]的研究,考虑了双壳的3种边缘轮廓,即锐边、凸边和凹边。图2显示了不同边缘轮廓的概述,包括图标题中的相应名称。凸形或凹形型材的宽度和高度分别由Bc = 27 mm 和 Hc = 18 mm表示。也就是说,凸面轮廓的总长度覆盖了月池宽度的30%,而凹形轮廓的对应物加宽月池尺寸的30%。
|
图 2 不同类型边缘轮廓概述 Fig. 2 Overview of the different types of edge profiles in this study |
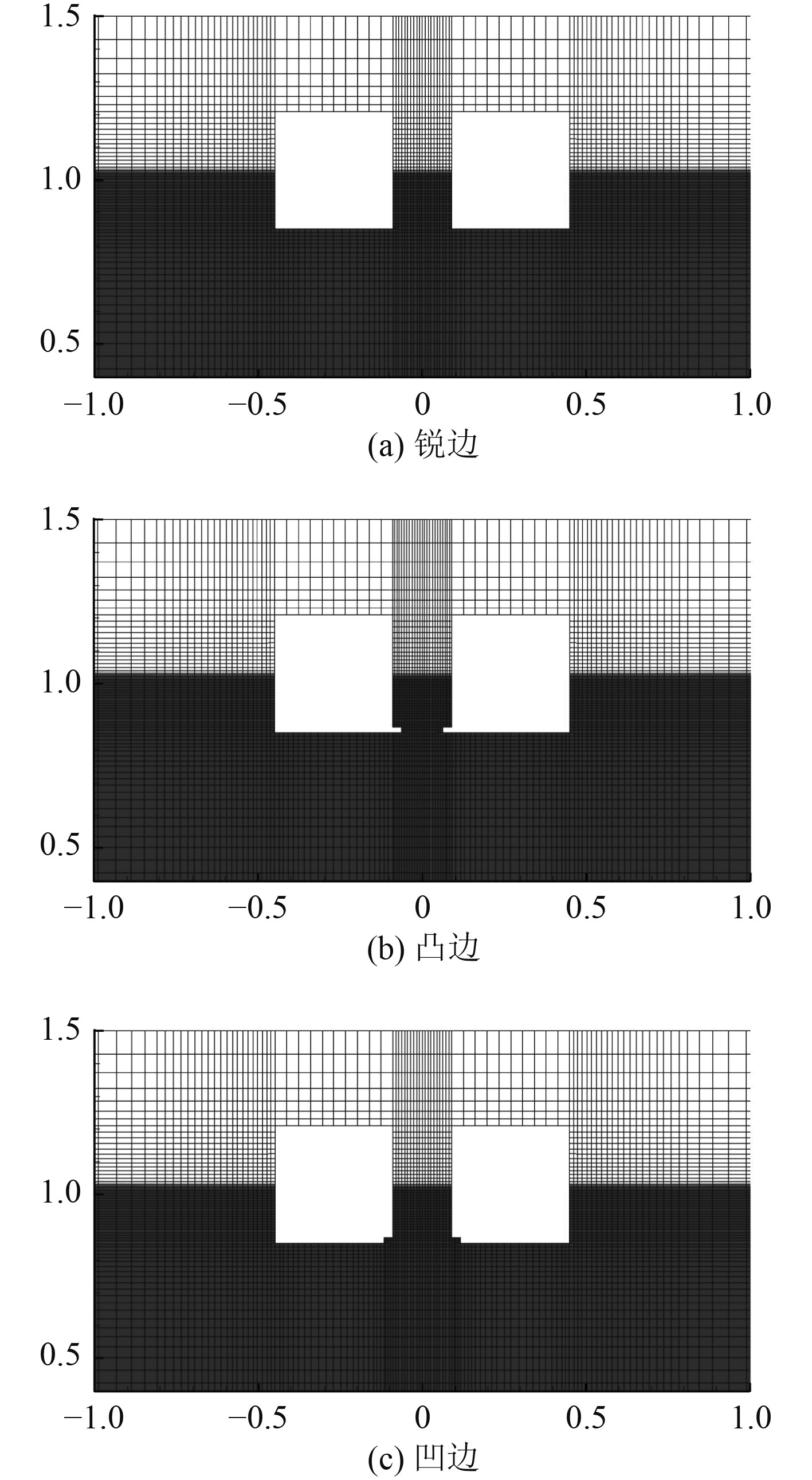
分别用4种不同的网格格式对上述5种构型进行数值收敛实验。采用非均匀网格对计算区域进行离散化,简单来说,在船体周围使用具有高分辨率的方形精细网格来精确捕捉极端波共振,特别是在月池附近。松弛区左右两侧均采用纵横比高达1/20(高度/长度)的粗矩形网格,这有助于消除辐射波。在计算域的其他部分配备了具有中等分辨率的方形精细网格。表1列出了各种边缘轮廓的网格生成细节,图3描绘了双船体周围的典型网格分区,即表1中的网格1。
|
|
表 1 收敛测试的网格分辨率(单元/节点) Tab.1 Mesh resolution for convergent test (Elements/Nodes) |
|
图 3 三种类型边缘轮廓双体船附近的典型计算网格 Fig. 3 Typical computational meshes in the vicinity of the twin hulls for three types of edge profiles |
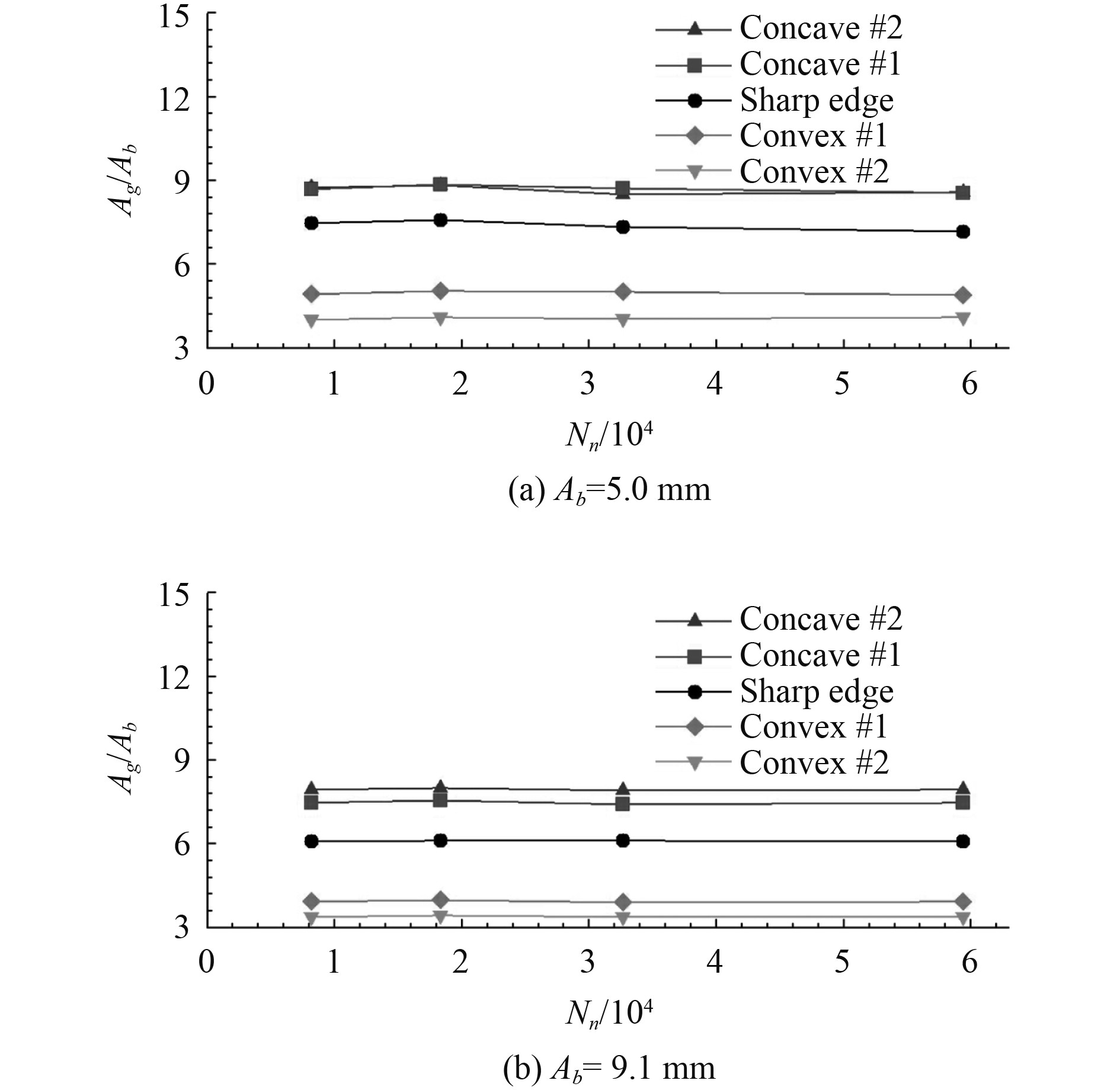
图4为4种不同网格方案,给出了垂荡频率ω = 5.00 rad/s下不同边缘轮廓和垂荡振幅的月池自由表面振幅的数值结果。图中的自由表面振幅是在物体固定坐标系中给出的。可观察到网格3和网格4方案之间的数值结果几乎没有差异,这说明网格3能产生收敛结果。因此,被用作以下数值模拟。
|
图 4 在频率ω=5.00 rad/s下不同几何形状和垂荡振幅的月池自由表面振幅网格收敛测试 Fig. 4 Mesh convergent tests of free surface amplitudes in moonpool for various geometries and heave amplitudes with frequency ω = 5.00 rad/s |
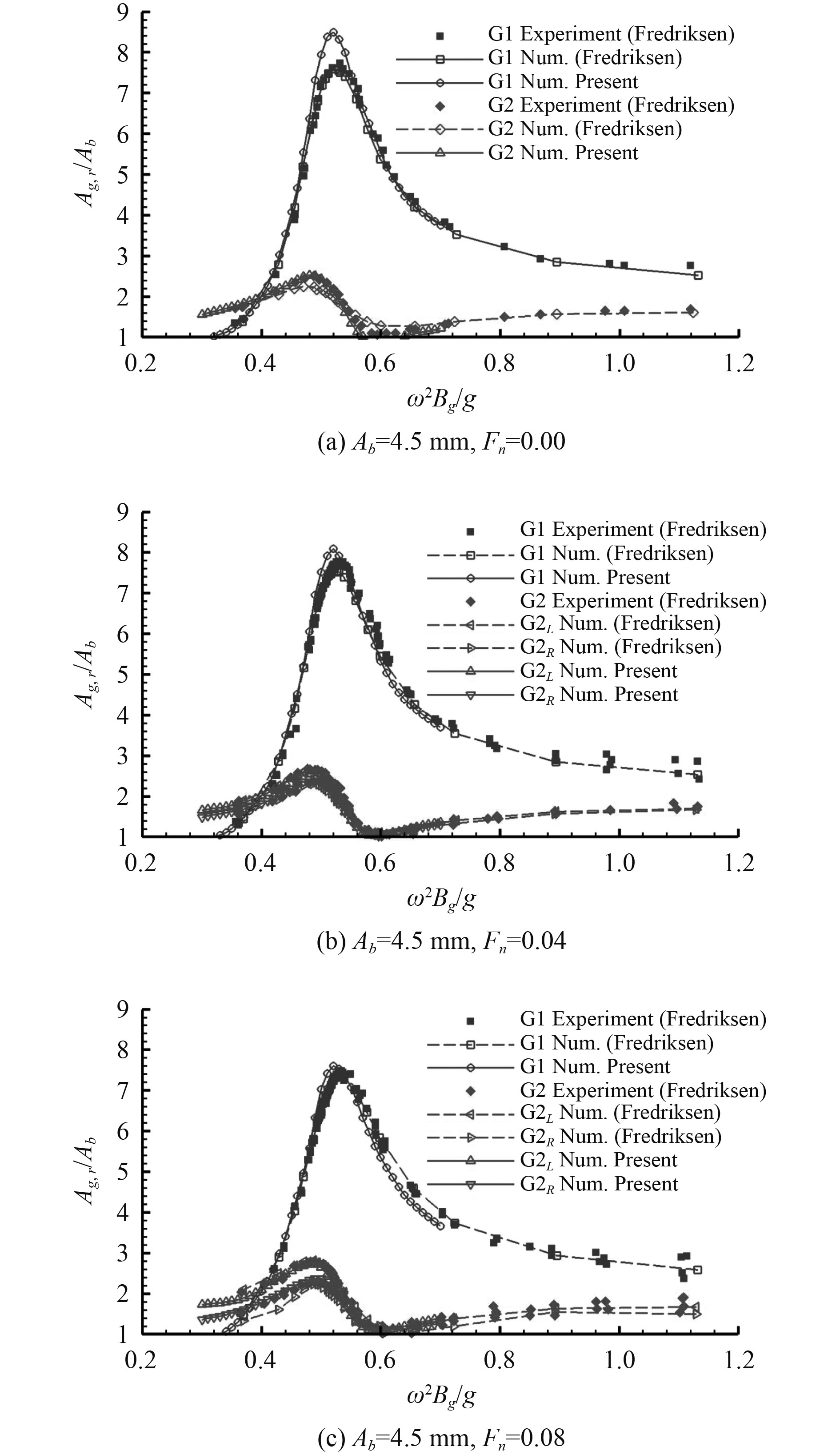
Fredriksen等[11]进行的实验和数值数据可用于验证当前的数值模型,其中进行了尖角边缘轮廓,在流速Fn = 0.00, 0.04 和 0.08下设计了2个波幅Ab = 4.5 mm。由浪高仪G1和G2测得的归一化波幅的比较结果如图5所示。从图中可观察到,当前数值结果与Fredriksen等[11]的实验和数值结果之间具有良好一致性。
|
图 5 不同垂荡频率下锐边剖面的双体船在G1和G2处波幅的数值验证 Fig. 5 Numerical validation of wave amplitudes at G1 and G2 with heave frequency for twin hulls with sharp edge profile |
在共振频率处测点G1测量的2个数值结果有很小的差异,这可能是2个数值模型之间存在差异的原因。在Fredriksen等[11]的研究中,采用了结合势流和粘性流模型的混合数值模型。对于测点G2中的辐射波振幅结果,2个数值结果与实验数据吻合良好。上述模拟表明,目前的数值模型能很好地再现月池中存在不同流速与流体共振的情况。
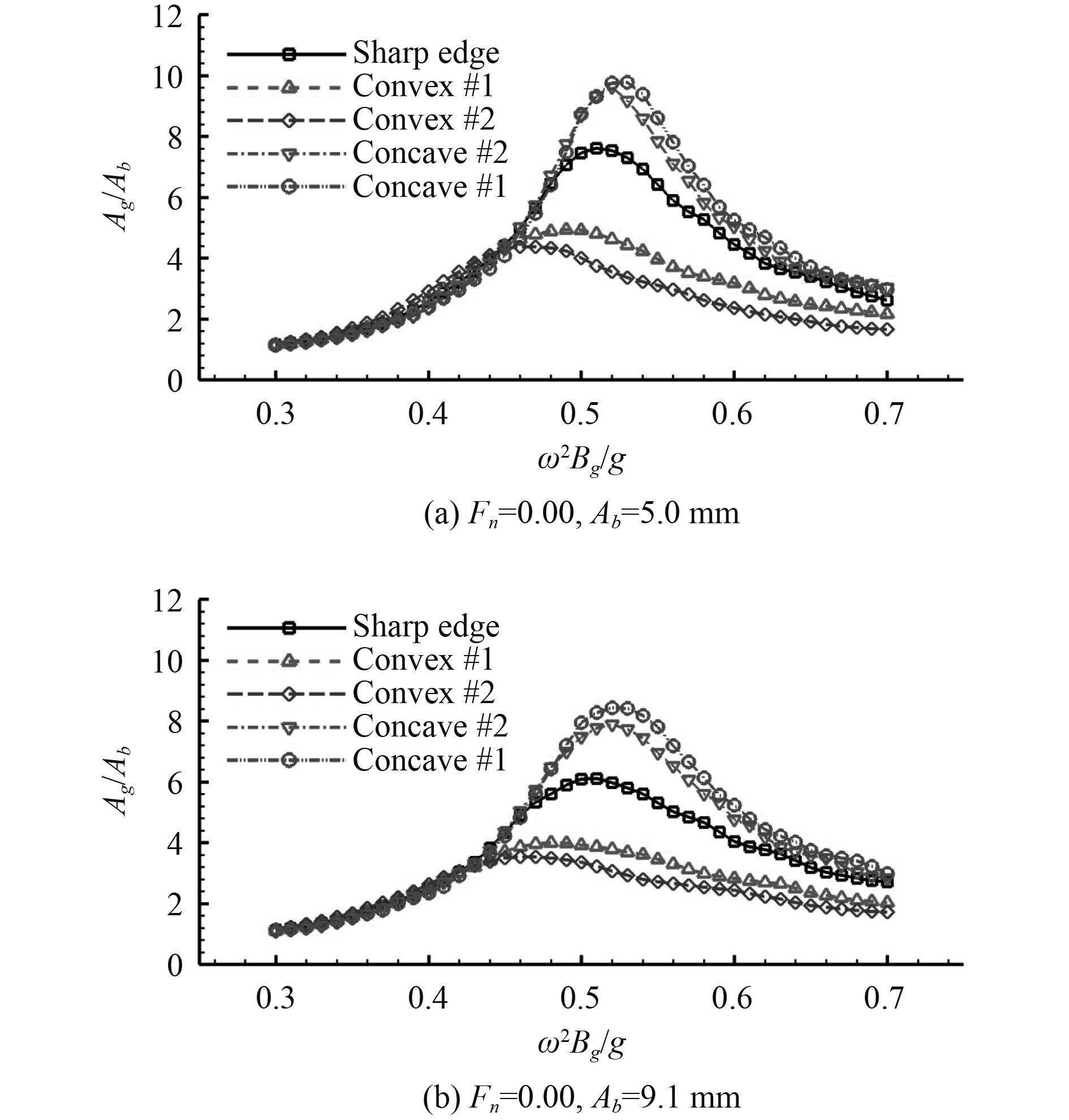
3 数值结果图6考虑了2个垂荡振幅的情况下,边缘轮廓对月池中波幅响应的影响。随着月池底部开口的减小,即从凹面#2、凹面#1、尖角、凸面#1到凸面#2,可观察到月池中共振振幅和共振频率的减小。月池底部开口的减小会减少注入月池的流体,导致自由表面振幅的减小。同时,减小的月池底部开口能增加月池底部外部的共振流体。这实际上增加了流体体积的附加质量,导致共振频率降低。此外,图6还说明了月池中的归一化波浪振幅,随着共振频率附近垂荡振幅的增加而减小。月池周围流体粘度和流动旋转导致的相对能量耗散是造成这种现象的主要原因。
|
图 6 月池中边缘轮廓对波浪响应的影响 Fig. 6 The influence of edge profiles on wave response in moonpool |
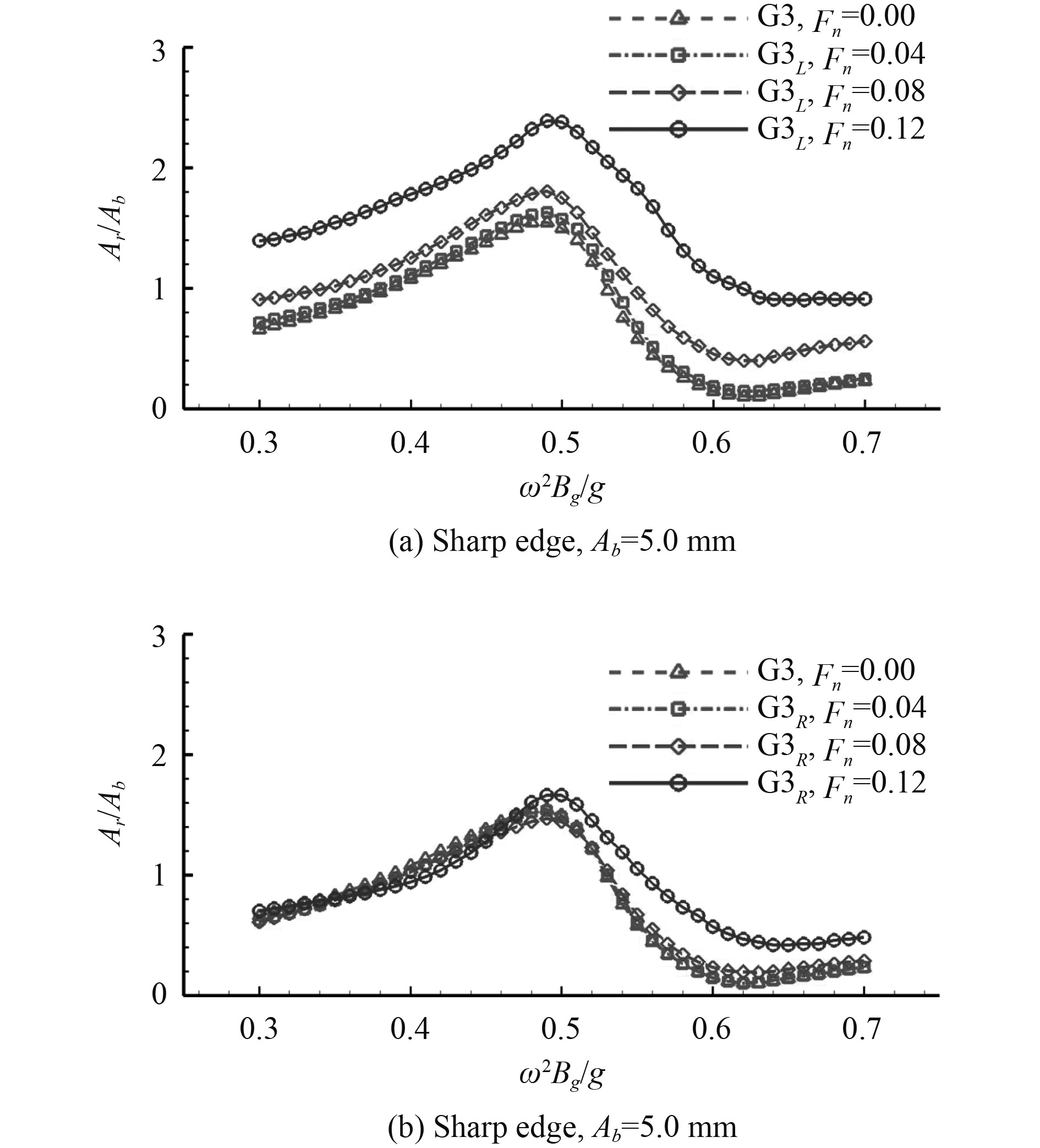
考虑测点G3L和G3R处的辐射波随流速的变化。如图7所示,在所有频率范围内,随着流速的增加,可观察到G3L处船体上游的波幅增加。对于G3R处的下游辐射波,在Fn=0.00、0.04和0.08的情况下,自由表面响应的振幅几乎相同。当流速接近Fn=0.12时,G3R的辐射波增加,这意味着流速的影响很大。
|
图 7 流速对船体上游和下游辐射波的影响 Fig. 7 The influence of current speed on radiation wave in the upstream and downstream of the hulls |
建立流速对月池内流体共振影响的数值计算模型,考虑多种工况下的不同边缘轮廓对月池中波幅响应的影响,比较了不同流速下5种边缘轮廓形成的月池中的自由表面振幅,探究了流速的变化对船体上游与下游波幅产生影响的比较。最后说明了在一个垂荡运动周期内,月池入口附近区域的速度场及涡流轮廓在不同流速下的变化,并得出以下结论:
1)随着月池底部开口的减小,月池内共振振幅和共振频率减小,并且会减少注入月池的流体,导致自由表面振幅的减小。
2)月池中的归一化波浪振幅随着共振频率附近垂荡振幅的增加而减小。月池周围流体粘度和流动旋转导致的相对能量耗散是造成这种现象的主要原因。
3)当流速Fn从0.00~0.08时,流速效应主要在共振频率附近。当流速为Fn=0.12时,在低频范围内也会出现波幅差异,一般来说,共振振幅随着流速Fn从0.00~0.08的增加而减小,当流速为Fn=0.12时,共振振幅通常会增加。通过数值模拟表明月池中流速对波幅的影响不是一个简单的单调关系。
4)随着流速的增加,所有频率范围内船体上游的波幅增加,下游的自由表面响应振幅几乎相同。当流速接近Fn=0.12时,下游的辐射波增加。
| [1] |
MOLIN B. On the piston and sloshing modes in moonpools[J]. Journal of Fluid Mechanics , 2001, 430: 27–50.
|
| [2] |
FALTINSEN O M, ROGNEBAKKE O F TIMOKHA A N. Two-dimensional resonant piston-like sloshing in a moonpool[J]. Journal of Fluid Mechanics, 2007, 575: 359–397.
|
| [3] |
SUN L , EATOCK R, TAYLOR P H. Wave driven free surface motion in the gap between a tanker and an FLNG barge[J]. Applied Ocean Research, 2015, 51: 331–349.
|
| [4] |
FENG X, BAI W. Wave resonances in a narrow gap between two barges using fully nonlinear numerical simulation[J]. Applied Ocean Research, 2015, 50: 119–129.
|
| [5] |
SAITOH T, MIAO G, ISHIDA H. Theoretical analysis on appearance condition of fluid resonance in a narrow gap between two modules of very large floating structure[C]//Proceedings of the Third Asia-Pacific Workshop on Marine Hydrodynamics, 2006: 170–175.
|
| [6] |
IWATA H, SAITOH T, MIAO G. Fluid resonance in narrow gaps of very large floating structure composed of rectangular modules[C]// Proceedings of the Fourth International Conference on Asian and Pacific Coasts, 2007: 815–826.
|
| [7] |
PERIC M, SWAN C. An experimental study of the wave excitation in the gap between two closely spaced bodies, with implication for LNG offloading[J]. Applied Ocean Research, 2015, 51: 320–330.
|
| [8] |
LU, L. , CHENG, L. , TENG, B, et al. Numerical investigation of fluid resonance in two narrow gaps of three identical rectangular structures[J]. Applied Ocean Research, 2010, 32: 177–190.
|
| [9] |
JIANG S C, BAI W, TANG G Q. Numerical simulation of wave resonance in the narrow gap between two non-identical boxes[J]. Ocean Engineering , 2018, 156: 38–60.
|
| [10] |
JIANG S C. , BAI W , CONG P W, et al. Numerical investigation of wave forces on two side-by-side non-identical boxes in close proximity under wave actions[J]. Marine Structures, 2019, 63: 16–44.
|
| [11] |
FREDRIKSEN A G, KRISTIANSEN T, FALTINSEN O M. Experimental and numerical investigation of wave resonance in moonpools at low forward speed[J]. Applied Ocean Research , 2014, 47: 28–46.
|
| [12] |
JIANG S C, CONG P W, SUN L, et al. Numerical investigation of edge configurations on piston-modal resonance in a moonpool induced by heaving excitations[J]. Journal of Hydrodynamics, 2019, 31(4): 682–699.
|
| [13] |
MORADI N , ZHOU T, CHENG L. Effect of inlet configuration on wave resonance in the narrow gap of two fixed bodies in close proximity[J] Ocean Engineering, 2015, 103: 88–102.
|
| [14] |
FENG X, BAI W, CHEN X, et al. Numerical investigation of viscous effects on the gap resonance between side-by-side barges[J]. Ocean Engineering, 2017, 145: 44–58.
|
| [15] |
YAKHOT V, ORSZAG S, THANGAM S, et al. Development of turbulence models for shear flows by a double expansion technique[J]. Physics of Fluids A: Fluid Dynamics, 1992, 4(7): 1510–1520.
|
| [16] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201–225.
|
| [17] |
ISSA R I. Solution of the implicitly discretised fluid flow equations by operator-splitting[J]. Journal of Computational Physics, 1986, 62(1): 40–65.
|
| [18] |
JASAK H Error analysis and estimation for the finite volume method with applications to fluid flows[D]. Imperial College London, 1996.
|
| [19] |
RUSCHE H. Computational fluid dynamics of dispersed two-phase flows at high phase fractions[D]. Imperial College London, 2003:270–5257.
|
 2023, Vol. 45
2023, Vol. 45
