2. 天津瀚海蓝帆海洋科技有限公司,天津 300457
2. Tianjin Hanhai Lanfan Marine Technology Co., Ltd., Tianjin 300457, China
泵喷推进器具有高效和低噪等特性,主要应用于军事领域。目前,除了中国、印度之外,美、英、法、俄已将其用于核潜艇推进。美国在1944年提出了通过泵喷射来减少流过叶片的速度以提高螺旋桨的性能。英国在20世纪80年代率先在“特拉法尔加”级核潜艇上安装了泵喷结构。泵喷推进器包括转子结构、导管结构、定子结构[1]。与普通导管推进器相比,具有前置定子的推进器可改善转子进流状态,称为前置定子泵喷;具有后置定子的推进器可回收转子周向尾流所损失的动能,称为后置定子泵喷[2]。泵喷推进装置中的导流罩结构可分为加速式和减速式2种,加速式导管增加了流体流速,提高了总体效率;减速式导管延缓空泡的发生,改善噪声特性[3]。
不同的定子结构对泵喷推进器的水动力性能具有不同影响。韩瑞德等[4]最早提出泵喷推进器的设计方法及准则,利用不同翼型对转子定子进行设计。刘占一等[5]用CFD对泵喷水动力性能进行数值仿真,成功预报了泵喷推进器水动力性能。胡雷俊等[6]基于数值模拟对推进器性能进行了研究,设计了对转泵喷结构,其结构是串联并且反向旋转的前后转子。谷浪[7]对鱼雷上的泵喷推进器进行分析,认为采用定子后置式可提高推进性能,同时验证了CFD方法在泵喷推进器水动力性能预报方面的可行性及准确性。彭云龙等[8]对前置与后置定子泵喷的敞水性能及空化特性进行了数值模拟。Haiting等[9]通过数值模拟,分析不同定子参数在泵喷推进器推进性能和非定常力中的作用。Han等[10]研究前置定子的预旋作用,结果表明定子的预涡流效应改善了转子的迎面流体,使转子叶片表面波动强度较低。Negin等[11]对泵喷推进系统的流体动力性能进行了数值研究,结果显示在恒定进速比下随着定子厚度的增加,效率提高。武建国等[12]通过改变后置定子结构参数,优化泵喷推进器的效率。
本文基于Ka型7叶螺旋桨及加速性导流罩,设计多种推进器结构,系统分析了增加前置定子、后置定子、前后定子均增加以及对转推进器等5种推进器的推力、扭矩、效率等特性,对比分析各结构部件及推进器整体的推力、扭矩的变化幅值,以及不同推进器尾流场变化,为泵喷推进器的研究、设计和开发提供参考。
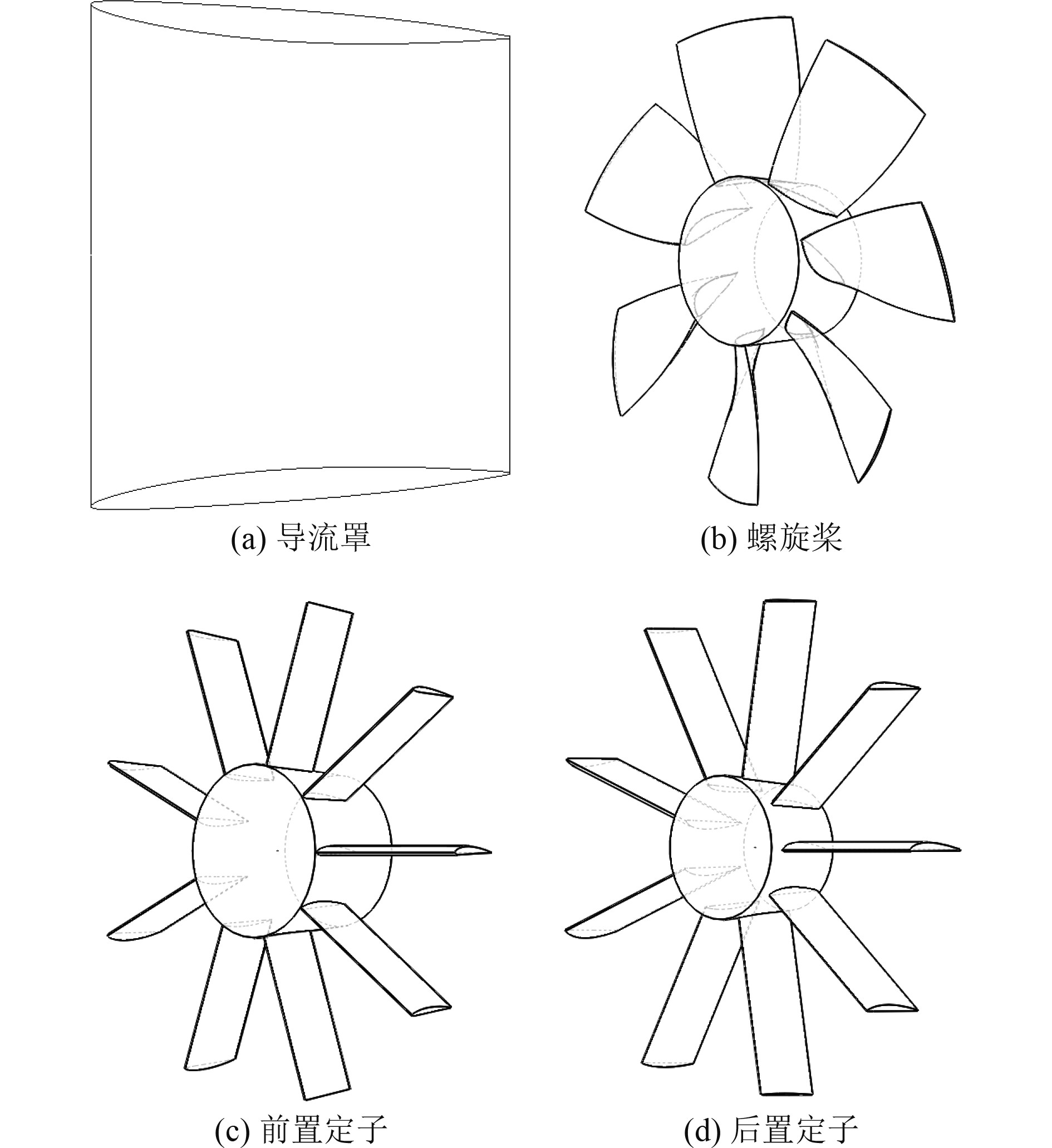
1 推进器结构及尺寸泵喷推进器整体结构包括螺旋桨、前置定子、后置定子以及导流罩。其中,螺旋桨直径D为200 mm,叶片数Z为7,螺距比P/D为0.7,盘面比Ae/A为1;定子翼型采取NACA6412,叶数Zr均为9;导流罩采取加速性结构,直径Dh为240 mm。结构部件三维视图如图1所示,2种定子安装位置如图2所示。
|
图 1 结构部件三维视图 Fig. 1 3D view of structural components |

|
图 2 两型定子的位置 Fig. 2 Position of two types of stator |
通过固定螺旋桨与导管的相对位置,增加不同结构定子的泵喷推进器以及对转推进器的三维视图如图3所示。其中,对转推进器是由2个旋转方向相反的螺旋桨构成,后桨直径是前桨的0.9倍,研究工况下,前桨转速是后桨的0.9倍。后桨能够充分利用前桨转动产生的能量,将旋转涡流转变为轴向动能,提高推进器效率。

|
图 3 推进器三维视图 Fig. 3 3D view of propeller |
所有推进器的流场均为圆柱形的单相流水域,螺旋桨转动时流体流动不涉及热量交换,对于三维不可压流体,流体的运动遵循于质量、动量守恒方程,本文使用 RANS控制方程,表达式如下:
| $ \frac{{\partial \rho {u_i}}}{{\partial {x_i}}} = 0,$ | (1) |
| $\begin{split} \frac{{\partial \left( {{\rho {u_i}}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_j}}} = &\frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\Bigg[ \mu \Bigg( \frac{{\partial {u_i}}}{{\partial {x_j}}} +\\& \frac{{\partial {u_j}}}{{\partial {x_i}}} \Bigg) - \overline {\rho u_i^{'}u_j^{'}} \Bigg] + {S_j}。\end{split} $ | (2) |
式中:t为时间;ρ为流体密度;μ为动力粘度;p为压力;ui和uj为速度分量;
为了模拟复杂的湍流运动,同时保持计算的可靠性和计算精度,采用集合k - ω和k - ε模型优点的SST k - ω作为研究水动力性能的湍流模型。能够准确的预测出流体运动的起始和分离,适合处理边界层问题。基于紊流动能传输方程,k - ω模型引入了紊流脉动频率的传输方程,并对其进行了剪应力修正得到SST k - ω湍流模型[13]。
| $ \begin{split} & \frac{{\partial \rho k}}{{\partial t}} + \frac{{\partial \rho ku}}{{\partial x}} + \frac{{\partial \rho kv}}{{\partial y}} + \frac{{\partial \rho kw}}{{\partial z}} = \frac{\partial }{{\partial x}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial x}}} \right] + \\ & \frac{\partial }{{\partial y}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial y}}} \right] + \frac{\partial }{{\partial z}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial z}}} \right] + {P_k} - \rho {\beta ^*}k\omega,\\ \end{split}$ | (3) |
| $ \begin{gathered} \frac{{\partial \rho k}}{{\partial t}} + \frac{{\partial \rho \omega u}}{{\partial x}} + \frac{{\partial \rho \omega v}}{{\partial y}} + \frac{{\partial \rho \omega w}}{{\partial z}} = \frac{\partial }{{\partial x}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial \omega }}{{\partial x}}} \right] + \\ \frac{\partial }{{\partial y}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial \omega }}{{\partial y}}} \right] + \frac{\partial }{{\partial z}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial \omega }}{{\partial z}}} \right] + \alpha \frac{\omega }{k}{P_k} - \beta \rho {\omega ^2} ,\\ \end{gathered} $ | (4) |
| $ {\mu _t} = \frac{{pk}}{\omega } 。$ | (5) |
式中,σk = 2.0,σω = 2.0,α= 5/9,β = 0.075,β* = 0.09。
湍流动能生产项为:
| $ {P_k} = {\mu _t}{S^2},S = \sqrt {\sum\limits_i {\sum\limits_j {{S_{ij}}{S_{ij}}} } } ,{S_{ij}} = \frac{1}{2}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) 。$ | (6) |
利用Ansys软件对推进器的几何模型进行网格划分,采用多重参考系法(MRF)处理螺旋桨的转动问题。模型中的流域分为2部分:包含螺旋桨的动域和包含其他结构的静域,所有计算域均为圆柱形结构,转子中心到入口处的距离是3D,距离出口为7D,静域直径为5D,减弱静域边界对于推进器的影响,所以可将推进器看作在一个无限宽的范围内运行。其流场分布如图4所示。

|
图 4 流场分布 Fig. 4 The flow field distribution |
在边界条件的设定上,推进器朝向静区域的一侧为速度入口,另一侧设置为压力出口,而在静区域的周围以及推进器表面则是没有滑动的刚性壁面,其余各面默认为内部面interior。计算所设置的压力-速度耦合算法采用SIMPLEC,此算法稳定性较好,在计算中可将亚松弛因子适当放大加速计算速度。
流域采用非结构网格划分,为提高推进器计算精度,设计加密块区域用来加密推进器。其中,动域网格尺寸与转子表面网格相同,加密块采用尺寸增长函数,增长比例为1.1,外表面最大值为10 mm,静域同样采用增长函数,增长比例为1.1,外表面最大尺寸为30 mm。在距离推进器较近的地方,尽可能地精细网格确保计算的准确性,在距离较远的地方设置尺寸更大的网格,以节省计算时间。网格分布如图5所示。

|
图 5 网格分布图 Fig. 5 Grid distribution diagram |
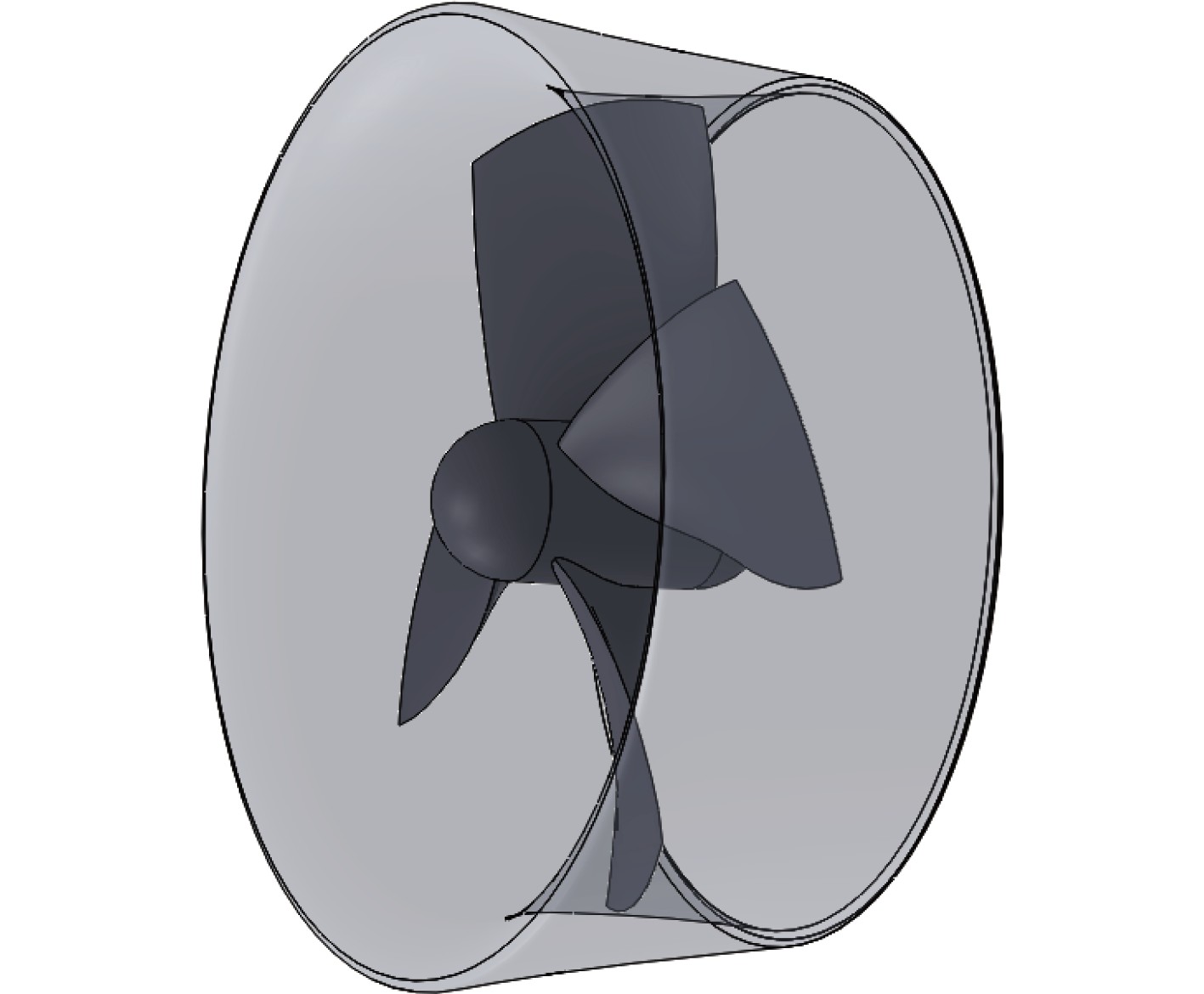
通过对Ka4-70+19A导管桨标模进行CFD仿真计算,验证模拟仿真的准确性。采取SST k-ω湍流模型,螺旋桨导流罩边界层第一层采取0.005 mm,设置速度进口及压力出口,流域边界及推进器表面为无滑移壁面,采用 SIMPLEC算法进行压力速度耦合,动量方程采用二阶迎风模式,选用MRF对流场进行处理,设置各变量的收敛残差为10−5且监视曲线不再变化时认为收敛,标模三维视图如图6所示。
|
图 6 标准模型 Fig. 6 The standard module |
将由Fluent计算所得数据与查找到的标模实验数据对比,判断实验值EXP与仿真值CFD的误差范围是否满足要求,数据结果如表1所示。
|
|
表 1 数据对比结果 Tab.1 Data comparison results |
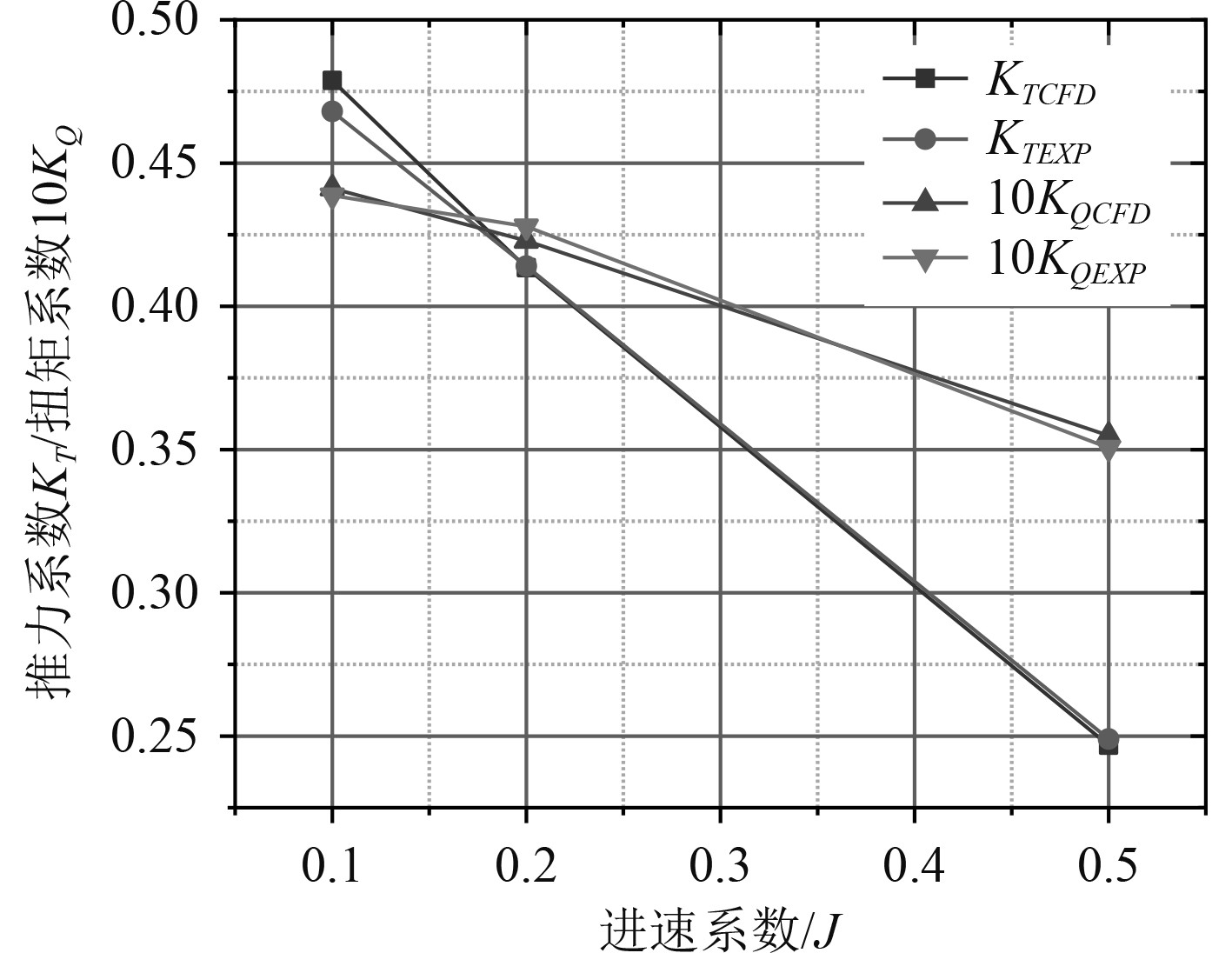
由图7可以看出,通过CFD计算的推力、扭矩系数与通过实验得出结果变化趋势一致,仿真值结果与实验值结果误差仅在3%以内,仿真结果数据可靠。
|
图 7 仿真与实验数据对比图 Fig. 7 Comparison of simulation data and experimental data |
总推力是推进器所有结构共同产生的使潜器前行方向的力。在数据分析时,各部件的推力取值均选取前行方向一致的力,若某部件产生推力为负值,则表明该部件降低推力。扭矩统一为从推进器后面向推进器前方看去,顺时针转动方向为正,逆时针为负。若两部件产生的扭矩值符号相反,则表明2种部件在相互平衡扭矩。所有推进器采取统一工况,进口流速为7 kn,转速范围1000~2000 r/min–1。有关的计算如下式:
| $ J = V/(nD) ,$ | (7) |
| $ 10{K_{Qr}} = 10{Q_r}/(\rho {n^2}{D^5}), $ | (8) |
| $ {K_{Tr}} = {T_r}/(\rho {n^2}{D^4}), $ | (9) |
| $ {K_T} = T/(\rho {n^2}{D^4}) ,$ | (10) |
| $ \eta = \frac{{{K_T}}}{{{K_{Qr}}}} \cdot \frac{J}{{2{\text{π}} }}。$ | (11) |
式中:
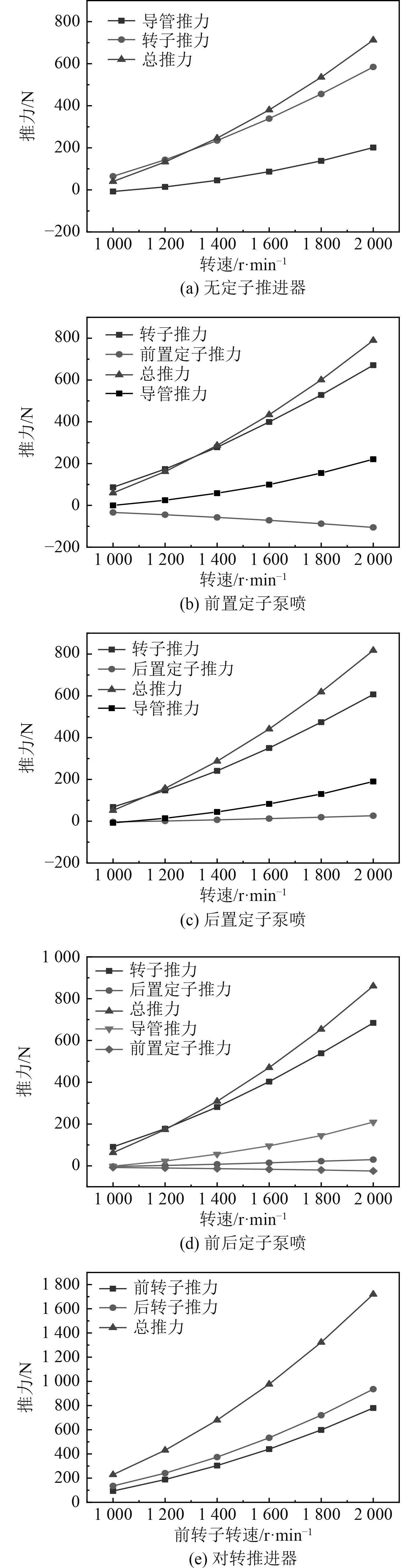
图8为各推进器推力性能变化。可以看出:前置定子一直产生阻力,其阻力大小的绝对值低于螺旋桨及导流罩产生的推力绝对值,但大于后置定子产生推力的绝对值,且随着转速的增加占总推力的比例慢慢减小,最大可达36.16%;后置定子在低转速下产生阻力,随转速升高变成了推力,但占总推力比例都在3%左右,影响非常小;在高速运转状态下,转子及导流罩提供主要推力,且都随转速增加而增大,转子提供的推力占比幅度逐渐减小,导流罩推力占比逐渐增加,最大可达24.33%。
|
图 8 推力性能变化点线图 Fig. 8 Point plot of thrust performance change |
对转推进器推力由前后转子共同提供,后转子产生的推力时刻高于前转子1.2~1.44倍。相比于泵喷推进器,对转推进器在推力方面远高于泵喷推进器,最大可达4倍左右;随着转速的提高,对转推进器相比泵喷推进器增加推力的百分比随之下降。
3.2 扭矩性能变化图9为各推进器扭矩性能变化。可以看出:扭矩主要由转子产生,且随转速增加而增大;导管产生的扭矩占总扭矩1%左右,微小可忽略不计;前置定子及后置定子均产生与转子相反的扭矩,随着转速增加前置定子改变扭矩的百分比逐渐下降,最大仅为48.71%;后置定子变化趋势与转子大小接近,可达完美100.99%平衡状态。后置定子平衡扭矩的幅度高于前置定子,平衡推进器扭矩整体效率非常高。
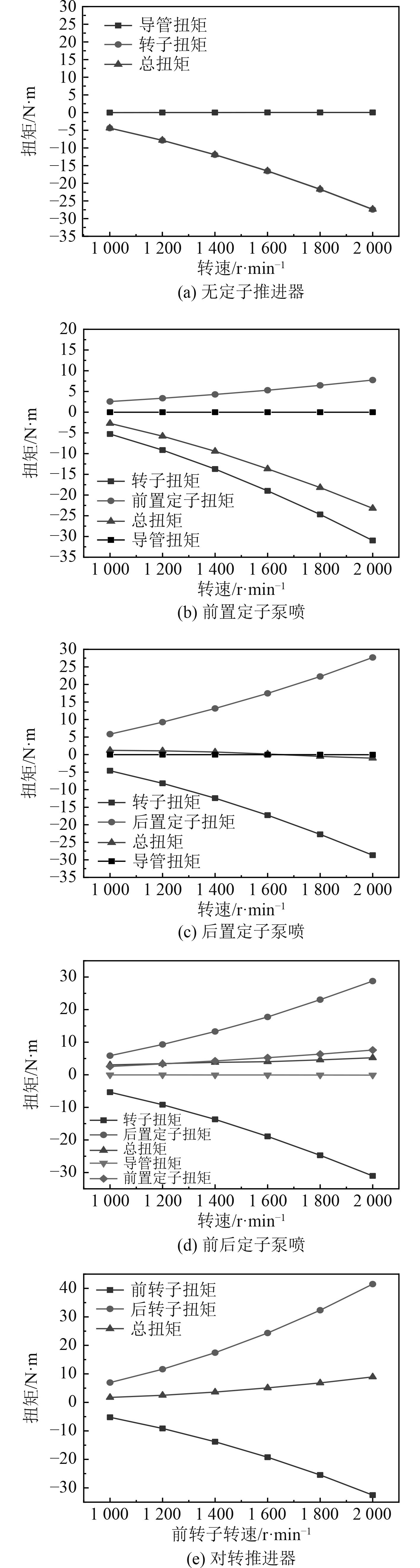
|
图 9 扭矩性能变化点线图 Fig. 9 Point plot of torque performance change |
在前后定子推进器工作时,前后置定子同时产生与转子相反的扭矩,可平衡推进器整体的扭矩,但却使整体的扭矩平衡过量。随着转速增加都逐渐上升,后置定子增加的幅度高于前置定子。
对于对转推进器,前后转子产生方向相反的扭矩,可达到平衡扭矩的目的;后转子产生的扭矩绝对值相比前转子大一些,二者平衡扭矩的幅度保持在75%~79%之间。
3.3 水动力性能对比分析图10分别为各泵喷总推力、总扭矩、效率对比图以及后置定子泵喷与对转推进器效率对比图。

|
图 10 推力、扭矩、效率对比图 Fig. 10 Thrust, torque, efficiency comparison chart |
可知,总推力排名中具有前后定子的泵喷最高,其次是后置定子泵喷、前置定子泵喷,而无定子推进器推力最低。总体扭矩平衡效果是后置定子泵喷强于前后定子泵喷强于前置定子泵喷。总体效率排名中后置定子泵喷为56.86%,高于前后定子泵喷的55.40%、前置定子泵喷的51.37%以及无定子推进器的50.62%。
对转推进器在低转速下,效率要明显高于后置定子泵喷推进器,其中前后转子效率分别可达64%、62%。当转速达到1300 r/min时,后置定子泵喷推进器效率要高于对转推进器,最高可达56.86%。
3.4 流场特性对比湍流动能是衡量湍流强度的一种方法,湍流强度越大代表的流场稳定性越差。由图11可知:后置定子泵喷尾部流场湍流动能为最低的0.316,后置定子具有尾部整流的作用,因此降低了湍流强度;前置定子泵喷尾流场的湍流动能与无定子推进器的几乎无异,可判断前置定子对于尾部湍流动能的影响很微弱;对转推进器的湍流动能最大可达1.11,因2个转子同时做功,尾部流场的稳定性大大降低。

|
图 11 各推进器尾部湍流动能云图 Fig. 11 Turbulent kinetic energy cloud of each propeller tail |
由图12可以看出,具有导流罩的推进器尾部呈现明显喷射状态,具有后置定子结构的推进器尾部喷射流更加集中。同时,由于后置定子可以减弱尾流切向诱导速度,从而减少了旋转的能量损耗,使桨毂尾部产生的毂涡降低,减少了推进器的阻力,因此具有后置定子的推进器有着更高效率。对转推进器尾部流场具有更高流速,但由于尾部湍流动能过大以及喷射流比较分散,导致流场稳定性很差。
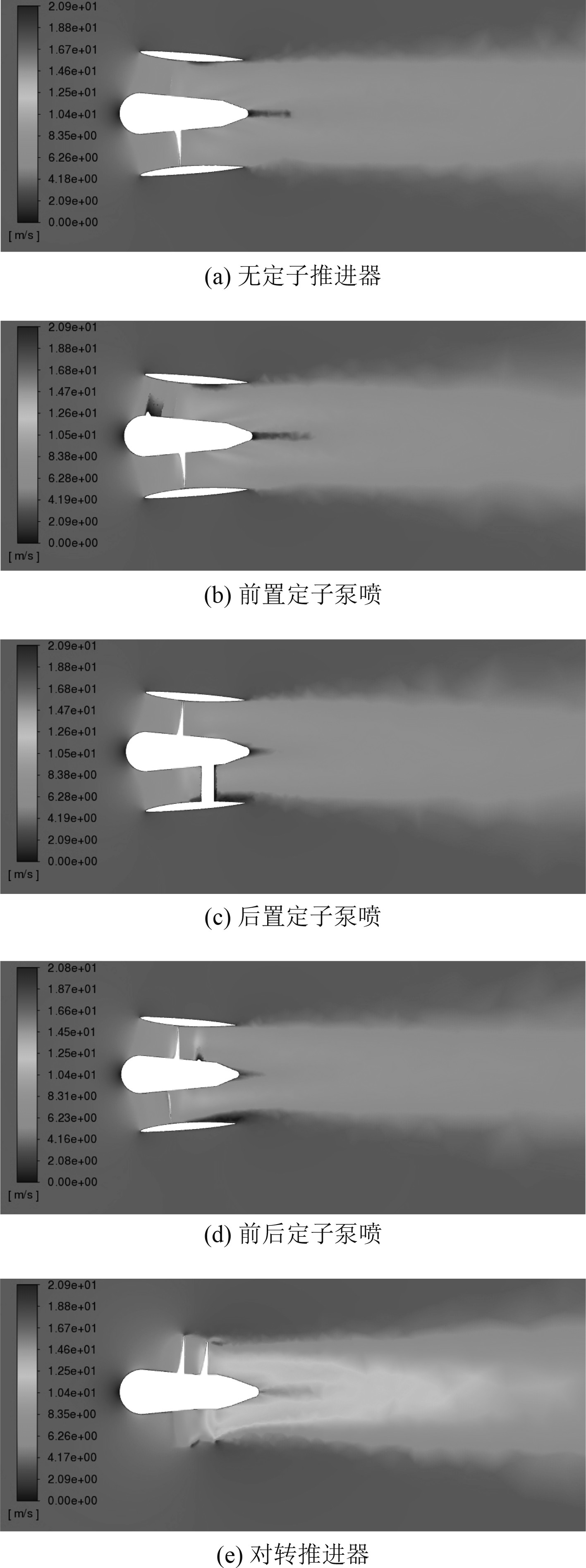
|
图 12 各推进器流场速度云图 Fig. 12 Velocity cloud of each propeller flow field |
1)前置定子可平衡扭矩,但是会降低推力。转速越高,降低推力占总推力的比例慢慢减小,平衡扭矩的幅度也逐渐降低。
2)后置定子平衡扭矩的作用显著,平衡扭矩的能力高于前置定子。同时还能在高转速时提高推力,但占总推力的比例略小。产生的扭矩与转子扭矩相近,从而使整个推进器的转矩保持平衡,且随着转速增加变化趋势与转子大小相同,方向相反。
3)泵喷模型中,后置定子泵喷效率最高为56.86%,平衡扭矩效果最好可达100.99%,同时具有更加稳定的尾流场。相比于泵喷推进器,对转推进器在推力方面远高于泵喷推进器,前者是后者的2~4倍左右。但效率随转速升高一直下降,流场稳定性也远低于泵喷推进器。
| [1] |
刘业宝. 水下航行器泵喷推进器设计方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2013
|
| [2] |
袁建平, 王子路, 王龙滟. 泵喷推进器推进性能及噪声研究综述[J]. 舰船科学技术, 2022, 44(6): 1–7. YUAN J P, WANG Z L, WANG L Y. A review on the performance and noise of pump-jet propulsion [J]. Ship Science and Technology, 2022, 44(6): 1–7. |
| [3] |
胡健, 王楠, 胡洋. 加速导管和减速导管的性能比较[J]. 北京航空航天大学学报, 2017, 43(2): 240-252. HU J, WANG N, HU Y. Performance comparison of accelerating catheter and decelerating catheter[J]. Journal of Beijing university of aeronautics and astronsutics, 2017, 43(2): 240-252. DOI:10.13700/j.bh.1001-5965.2016.0140 |
| [4] |
韩瑞德, 夏长生. 泵喷射推进器的设计方法及设计准则[C]// 中国力学学会, 1999: 122–127. HAN R D, XIA C S. Design method and criterion of pump jet propeller [C]// Chinese Mechanical Society, 1999: 122–127. |
| [5] |
刘占一, 宋保维, 黄桥高. 基于CFD技术的泵喷推进器水动力性能仿真方法[J]. 西北工业大学学报, 2010, 28(5): 724-729. LIU Z Y, SONG B W, HUANG Q G. Hydrodynamic performance simulation method of pump-jet propeller based on CFD technology[J]. Journal of Northwestern Polytechnical University, 2010, 28(5): 724-729. DOI:10.3969/j.issn.1000-2758.2010.05.017 |
| [6] |
胡雷俊, 曹琳琳, 车邦祥. 基于高空化性能的对转泵喷推进器设计[J]. 工程热物理学报, 2017, 38(9): 1877–1881. HU L J, CAO L L, CHE B X. Design of counterrotating pump jet propulaion based on high altitude perfprmance [J]. Journal of Engineering Thermophysics, 2017, 38(9): 1877–1881. |
| [7] |
谷浪. 鱼雷泵喷推进器设计及水动力性能预报方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [8] |
彭云龙, 王永生, 刘承江, 等. 前置与后置定子泵喷推进器的水动力性能对比[J]. 哈尔滨工程大学学报, 2019, 40(1): 132-140. PENG Y L, WANG Y S, LIU C J, et al. Comparative analysis of the hydrodynamic performance of front-stator and rear-stator pump-jets[J]. Journal of Harbin Engineering University, 2019, 40(1): 132-140. DOI:10.11990/jheu.201707018 |
| [9] |
YU Haiting, DUAN Ningyuan, HUA Hongxing, et al. Propulsion performance and unsteady forces of a pump-jet propulsor with different pre-swirl stator parameters[J]. Applied Ocean Research, 2020, 100: 102184.
|
| [10] |
LI Han, HUANG Qiaogao, PAN Guang, et al. The transient prediction of a pre-swirl stator pump-jet propulsor and a comparative study of hybrid RANS/LES simulations on the wake vortices[J]. Ocean Engineering, 2020, 203: 107224.
|
| [11] |
DONYAVIZADEH N, GHADIMI P. Efficacy analysis of thickness and camber size of cross section of the stator on hydrodynamic parameters in linear jet propulsion system[J]. Mathematical Problems in Engineering, 2020: 5861948.
|
| [12] |
武建国, 武天龙. 泵喷推进器扭矩自平衡优化分析[J]. 舰船科学技术, 2022, 44(12): 10–15. WU J G, WU T L, Torque self-balancing optimization analysis of pump - jet propeller [J]. Ship Science and Technology, 2022, 44(12): 10–15. |
| [13] |
EPPLER R. A Computer progam for the desig and analysis of low-sped airfoil [J]. NASA Technical Memoandum, 1980.
|
 2023, Vol. 45
2023, Vol. 45
