水中悬浮隧道(Submerged Floating Tunnel,SFT)代表着一个崭新的特大型水下交通运输体系,这类隧道的特征是其跨越水域两岸,悬浮在水面下的一定深度,而不是完全被埋在或放置在河床上。与传统桥梁相比,水中悬浮隧道具有性价比高、建造灵活、环境干扰小、营运条件优越、快速通行和环保等许多优点[1-2]。水中悬浮隧道面临情况复杂多变的海洋环境,易受到周围环境载荷的影响。对于波流-系泊载荷作用下,悬浮隧道遭受到沉船或者是潜器碰撞之后的动力响应进行深入研究,不仅有利于分析悬浮隧道受撞击之后的运动规律和变形问题,对将来悬浮隧道寿命延长和耐撞性优化有着深远的意义和价值,也能对水中悬浮隧道的安全可靠性给予一定程度的保障,提升水中悬浮隧道的工程应用价值。
近年来,学者们通过简化计算和仿真计算对水中悬浮隧道的碰撞问题进行了研究。Zhang[3]简化了千岛湖拟建的水中悬浮隧道模型,主要研究了隧道受到碰撞过程中结构外表面对碰撞能量的吸收情况。此后张嫄等[4]将隧道简化为等距的弹性支撑梁,分析了锚索刚度、冲击速度等参数对隧道跨中位移的影响。刘迁苹[5]结合前面学者的研究方法,对沉船或潜艇碰撞事故下的悬浮隧道进行了有限元模拟,模拟了碰撞后隧道结构的损伤、能量变化情况,分析了冲击物不同角度和速度对隧道结构各方面的影响。此外,为研究碰撞过程中的能量转化情况,Luo等[6]采用有限元法对锚索、悬浮隧道和潜艇进行了建模。通过罚函数实现了计算过程中的贯穿现象,并在模拟中考虑了流固耦合效应。利用有限元仿真,研究了潜艇对悬浮隧道的撞击过程以及水、潜艇能量与悬浮隧道之间的关系。陈灿鹏等[7]在Luo的基础上,通过CEL流固耦合的方法,对浮筒式悬浮隧道受碰撞的情况进行了建模,分别分析管体跨中、1/4处和浮筒受撞击后隧道管体变形、撞击力、隧道动能等。
目前,针对水中悬浮隧道多场耦合下动力响应的研究较少,同时忽略了系泊系统产生的系泊力。建立双向耦合下水中悬浮隧道碰撞问题的数值仿真分析方法,将系泊力、波流载荷和碰撞载荷综合考虑,研究波流-系泊耦合作用的水中悬浮隧道在碰撞载荷下的运动响应和结构损伤,有效模拟水中悬浮隧道遭受撞击的动态过程。
1 水中悬浮隧道运动性能理论在水中悬浮隧道进行CFD数值模拟过程中,流体流场的湍流模型采用的
雷诺时均N-S方程[8]为:
| $ \frac{{\partial (\rho \bar v)}}{{\partial t}} + \nabla \cdot (\rho \bar v\bar v) = - \nabla \cdot (\bar pI) + \nabla \cdot (T + {T_{RANS}}) + \rho g。$ | (1) |
式中:
| $ \begin{split} \frac{{\partial (\rho k)}}{{\partial t}} +& \frac{{\partial (\rho k{U_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {{\mu _1} + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ &{\mu _t}\frac{{\partial {U_j}}}{{\partial {x_i}}}\left( {\frac{{\partial {U_j}}}{{\partial {x_i}}} + \frac{{\partial {U_i}}}{{\partial {x_j}}}} \right) - \rho \varepsilon ,\end{split} $ | (2) |
| $ \begin{aligned} \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + &\frac{{\partial (\rho \varepsilon {U_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {{\mu _1} + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\ &{C_{1\varepsilon }}{\mu _t}\frac{{\partial {U_j}}}{{\partial {x_i}}}\left( {\frac{{\partial {U_j}}}{{\partial {x_i}}} + \frac{{\partial {U_i}}}{{\partial {x_j}}}} \right) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}。\end{aligned}$ | (3) |
式中:
考虑水中悬浮隧道潜器碰撞问题,采用多自由度体系动力学方程[10]为:
| $ [{\boldsymbol{M}}]\{ \ddot {\boldsymbol{U}}\} + [{\boldsymbol{C}}]\{ \dot {\boldsymbol{U}}\} + [K]\{ {\boldsymbol{U}}\} = \{ {{\boldsymbol{F}}^{ext}}\}。$ | (4) |
式中:
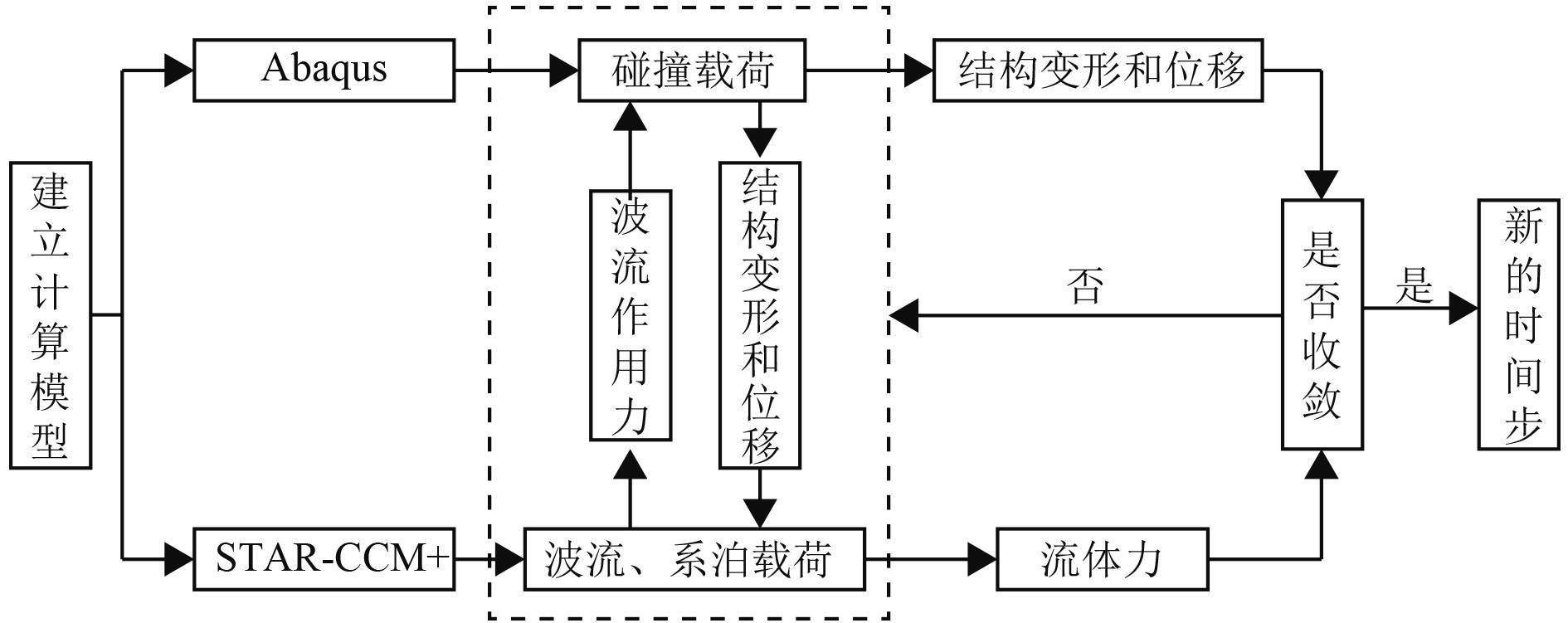
在数值仿真分析方法上,采用STAR-CCM+与Abaqus双向耦合算法[11],相应的实现流程如图1所示。在每一个时间步中,都需在流体网格中计算出水中悬浮隧道结构此时所受的流体力,并通过插值法将流体网格中的力传递到结构网格中,即STAR-CCM+中计算得到的隧道所受波流作用力传输到有限元软件Abaqus内,由此得到在流体力作用下,结构力的收敛解。进行碰撞过程的计算,再将结构网格节点因流体力和碰撞载荷引起的位移插值到流体网格中,引起流体网格的变形,这个过程使隧道表面网格的变形和位移导入回STAR-CCM+中进行波流下隧道运动响应的计算。这一时间步完成关闭了模拟中的一次循环,对于强双向耦合模拟,是不断重复这些循环,直到流体力和结构位移的变化低于规定的量,然后才会进入下一个新的时间步。在计算结束后,处理系统中可得到双向耦合计算过程下水中悬浮隧道的位移、应力应变、损伤情况等。
|
图 1 双向耦合流程图 Fig. 1 Bidirectional coupled flow chart |
王长春[12]试验研究了海洋中洋流对水中悬浮隧道结构的受力和运动响应的影响,将隧道管段模型淹没至预设的固定位置深度并采用锚索进行约束,从而通过调节整流板来模拟隧道所处的洋流环境,具体的试验场景可参见文献[12]。试验所采用的几何相似比为1∶100,隧道管段模型使用的材料是混凝土,锚索则采用钢丝制成,试验所使用的模型具体参数如表1所示。
|
|
表 1 试验模型参数 Tab.1 Test model parameters |
为验证STAR-CCM+中数值仿真计算结果的准确性,参照文献[12]中试验模型参数和环境参数进行数值水槽的建模和数值仿真,相应的数值水槽模型如图2所示。为分析数值模型的有效性,以及网格划分数以及时间步长对计算的影响,建立3种数值水槽进行计算,具体参数如表2所示。其中,H为波高、L为波长、D为隧道直径。

|
图 2 数值水槽模型 Fig. 2 Numerical wave flume model |
|
|
表 2 数值水槽网格[13]及时间步长参数 Tab.2 Numerical flume mesh and time step parameters |
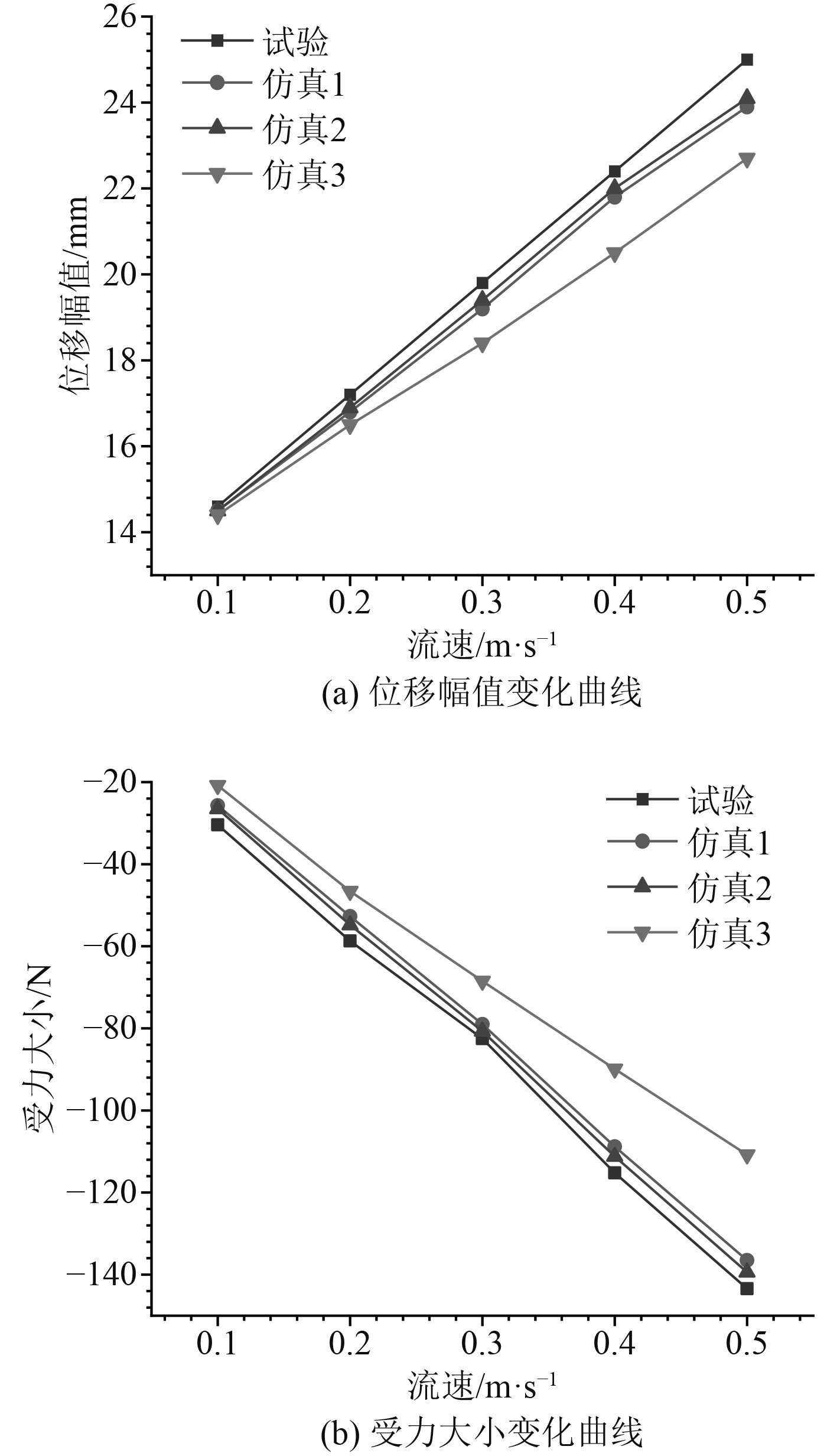
通过调节流速大小计算隧道结构的运动响应和迎流面受力情况,并将计算得到的结果与试验值进行对比,对比结果如图3所示。可知,数值仿真结果与试验结果在位移幅值和受力上均具有较好的一致性,同时当水流速度较小的环境情况下,试验与仿真计算结果的相对差值基本处于很小范围内;而随着水流速度的增大,2种方法所得的位移和受力的相对差值有所增加。从位移幅值和受力情况的整体变化来看,仿真1和仿真2的计算结果与试验结果的变化趋势相同且数值差距较小(误差在5%范围内),而仿真3在流速大的情况下与试验值有较大差异。因此为节约计算成本并保证计算的准确性,数值水槽采取仿真1所选的网格划分尺寸,时间步长均选取0.02 s。
|
图 3 两种计算结果比较曲线 Fig. 3 Comparison curves of two results |
选取典型的圆型断面水中悬浮隧道[14]为仿真计算对象。该隧道断面形式如图4所示,内部主要分为左右2个防护区域和上下2个通行区域,外部防护结构是双层混凝土外壳。该悬浮隧道采用的系泊约束为锚索式系泊,由张紧状态的张力腿支撑系统提供拉力以平衡浮力,使隧道在水中保持稳定。每组支撑系统由2根对称的张力腿组成,张力腿与隧道之间的夹角成45°。隧道模型及张力腿具体参数如表3所示。

|
图 4 隧道断面形式图及几何模型图 Fig. 4 Tunnel section design drawing and finite element model drawing |
|
|
表 3 水中悬浮隧道模型的主要参数 Tab.3 Primary parameters of SFT model |
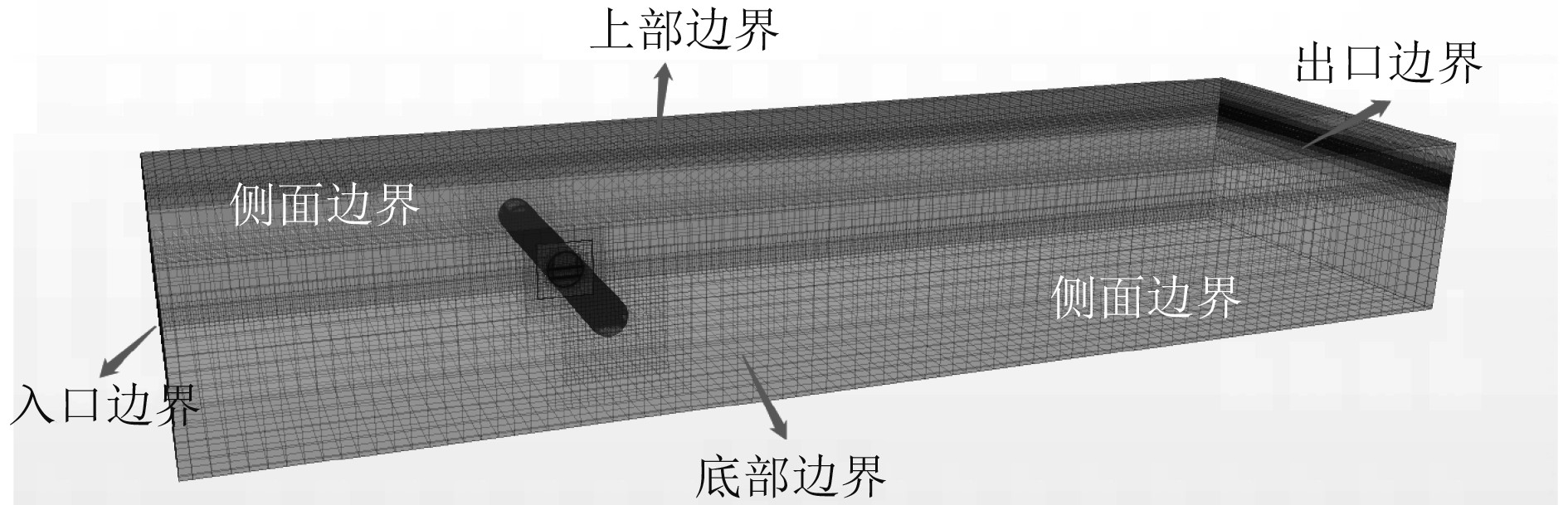
把计算区域设置为有限的长方形区域,近似认为来流对其无影响。该计算模型包含两个侧面边界(对称平面)、一个底部边界(壁面)、一个入口边界(速度进口)、一个出口边界(压力出口)、一个上部边界(压力出口)和管体模型。相应的计算区域示意图如图5所示。数值计算中采用SST k-ε湍流模型,流场动力粘度为0.001067 Pa·s,密度为1 025.0 kg/m3。为了让流体运动得到充分发展,流场范围的长、宽和高分别为1 000 m、80 m和300 m。
|
图 5 计算模型流场区域示意图 Fig. 5 Schematic diagram of flow field area of calculation model |
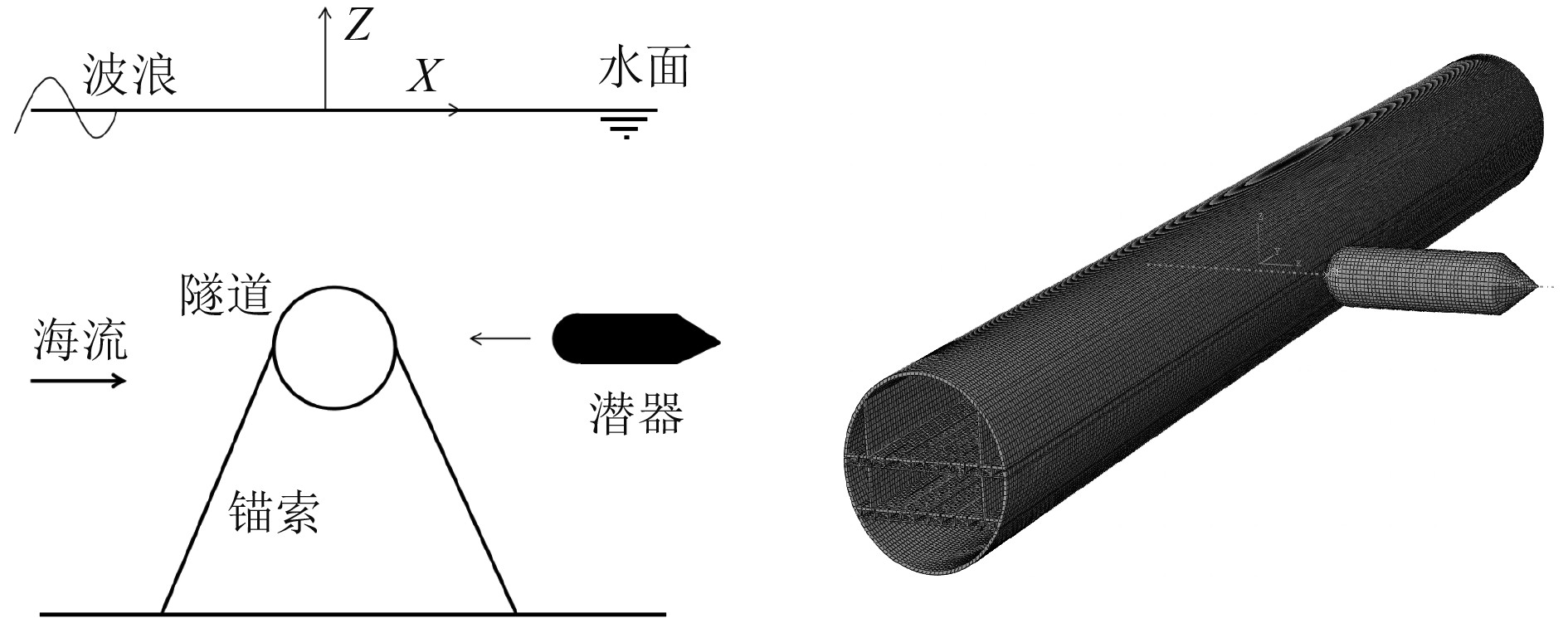
选取的潜器参数如下:长、型宽、型深和总吨位分别为30.0 m、6.7 1 m、6.71 m和800 t[6]。潜器材料选择Q235低碳钢,有限元模型网格单元尺寸为1.0 m,单元类型为S4R。由于计算主要分析水中悬浮隧道在碰撞荷载作用下的结构动力响应,为了减少计算时间,潜器采用刚体建模,并简化部分结构。水中悬浮隧道采用实体建模,网格单元尺寸为0.3 m,单元类型为C3D8R,同时采用混凝土塑性损伤模型,混凝土弹性模量为30 GPa,密度为2 600 kg/m3,泊松比为0.2,初始压缩屈服应力12E6 Pa,抗压强度为24.1E6 Pa,初始抗拉强度2.9E6 Pa,其余塑性损伤参数[15]如表4所示。具体的碰撞场景和水中悬浮隧道的有限元模型如图6所示。
|
|
表 4 混凝土塑性损伤参数[15] Tab.4 Plastic damage parameters of concrete |
|
图 6 碰撞场景有限元模型 Fig. 6 Finite element model of collision scene |
潜器具有结构强、水下运行速度快的特点,因此其所产生的碰撞力可能会对隧道结构造成严重影响。选取的计算工况场景信息如下:波高为8.0 m,周期为13 s,海水流速为1.0 m/s,水深为120 m,悬浮深度–20 m;系泊张力腿成张紧状态,初始预紧力为2E7 N;潜器行进速度为5 m/s;潜器侧向水平撞击作为碰撞场景且碰撞方向与波流方向相反。分析水中悬浮隧道在波流-系泊耦合作用下,遭到潜器碰撞后的运动响应和结构变形情况。
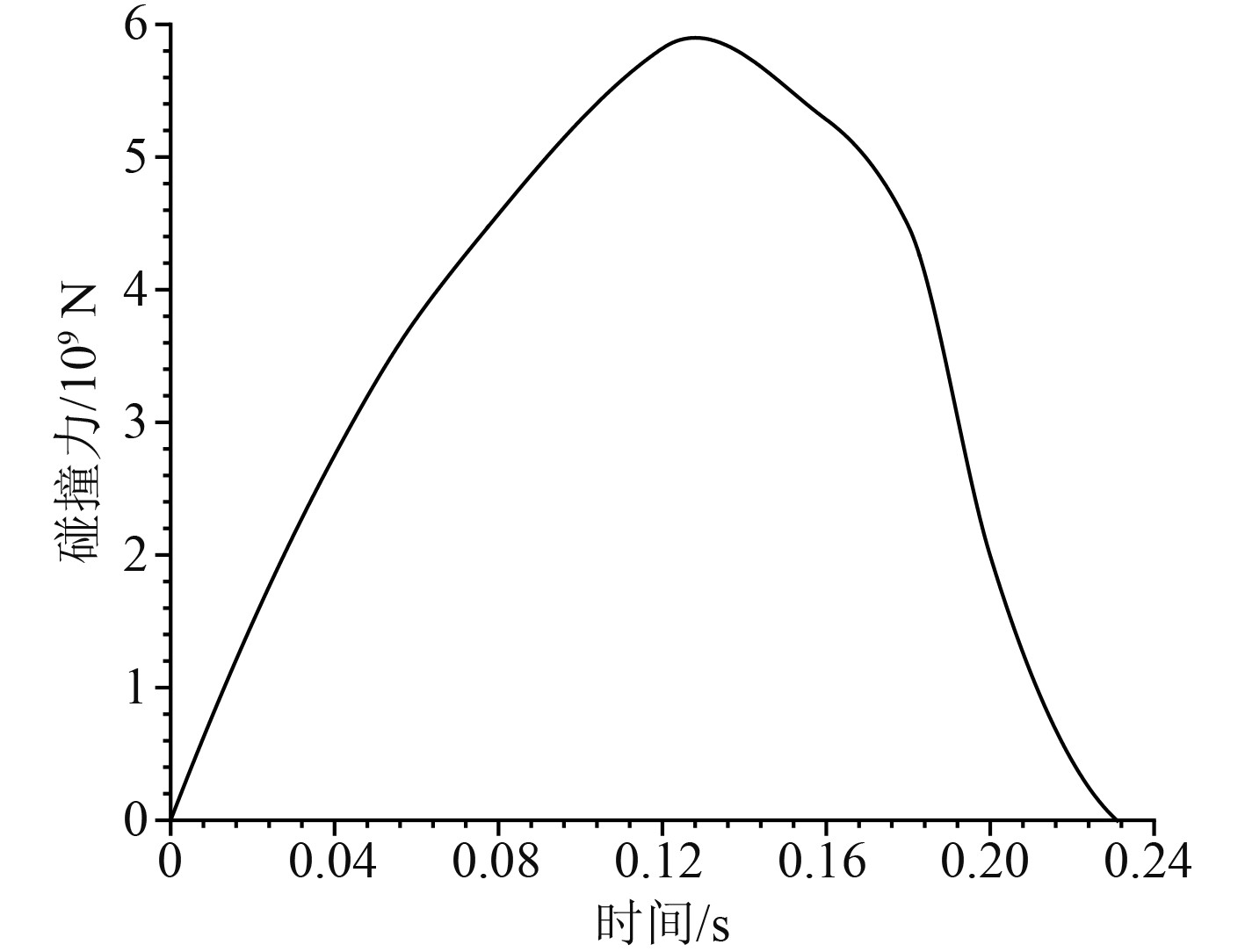
图7为相应的碰撞力曲线。可知,整个碰撞过程发生在较短时间内(0.23 s)。水中悬浮隧道所受的碰撞力首先线性增加达到最大峰值5.96 MN,随后碰撞力快速减小,因为潜器所具有的动能不断被隧道结构吸收,所以碰撞力先增大后变小,总体变化趋势呈明显的非线性。
|
图 7 碰撞力曲线 Fig. 7 Curves of collision force-time |
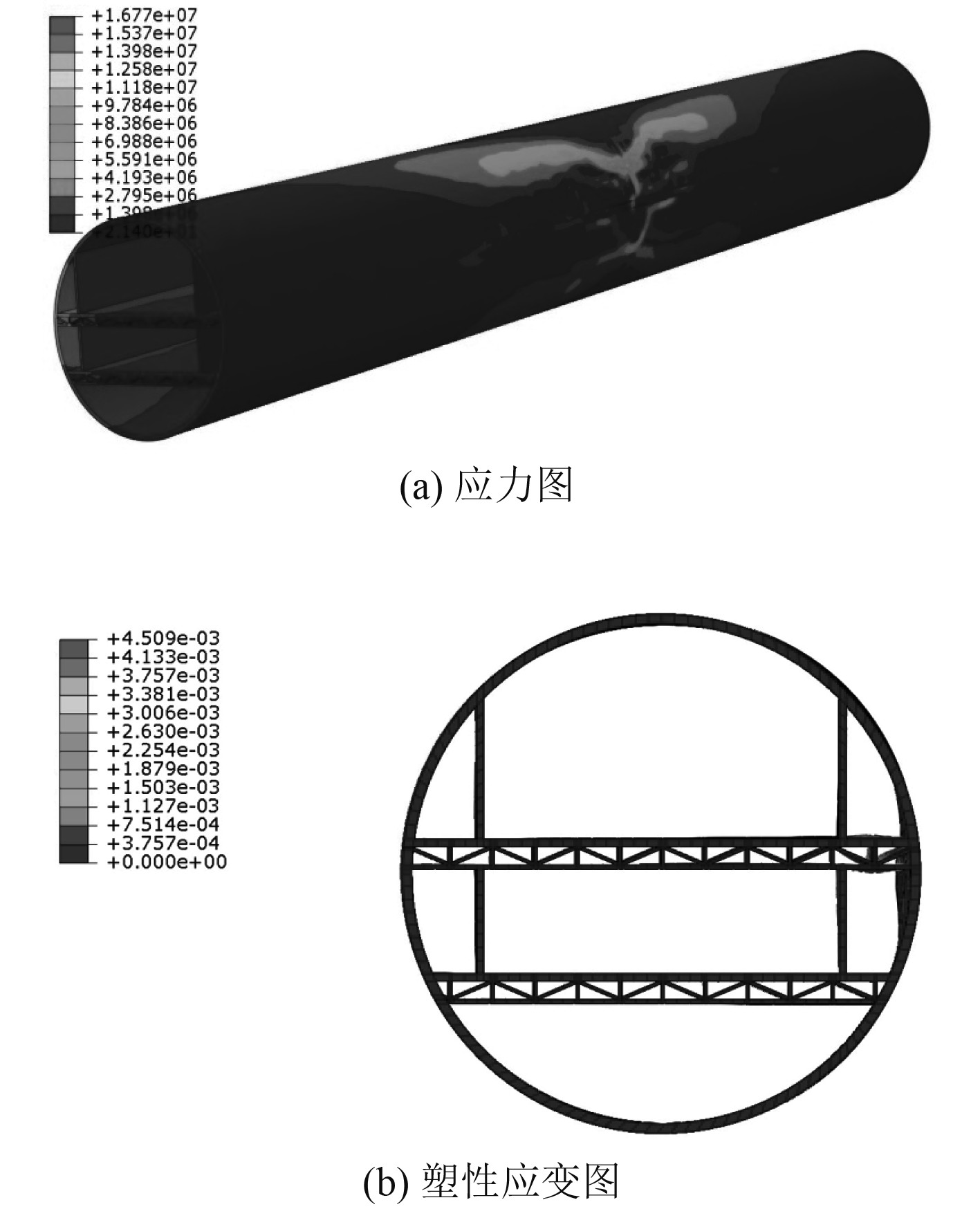
图8为隧道结构应力应变云图。可知,最大应力主要集中在碰撞周围区域,具有明显的局部性,最大应力集中点则在隧道内部结构与隧道外表面连接处。通过塑性应变图可看出,碰撞使隧道结构产生了明显变形,塑性应变大小为0.004 5 m,碰撞并未使隧道结构破裂,不会造成海水进入隧道内部的危险。
|
图 8 隧道结构应力应变云图(变形效果放大50倍) Fig. 8 Stress-strain cloud image of tunnel structure (deformation effect magnified 50 times) |
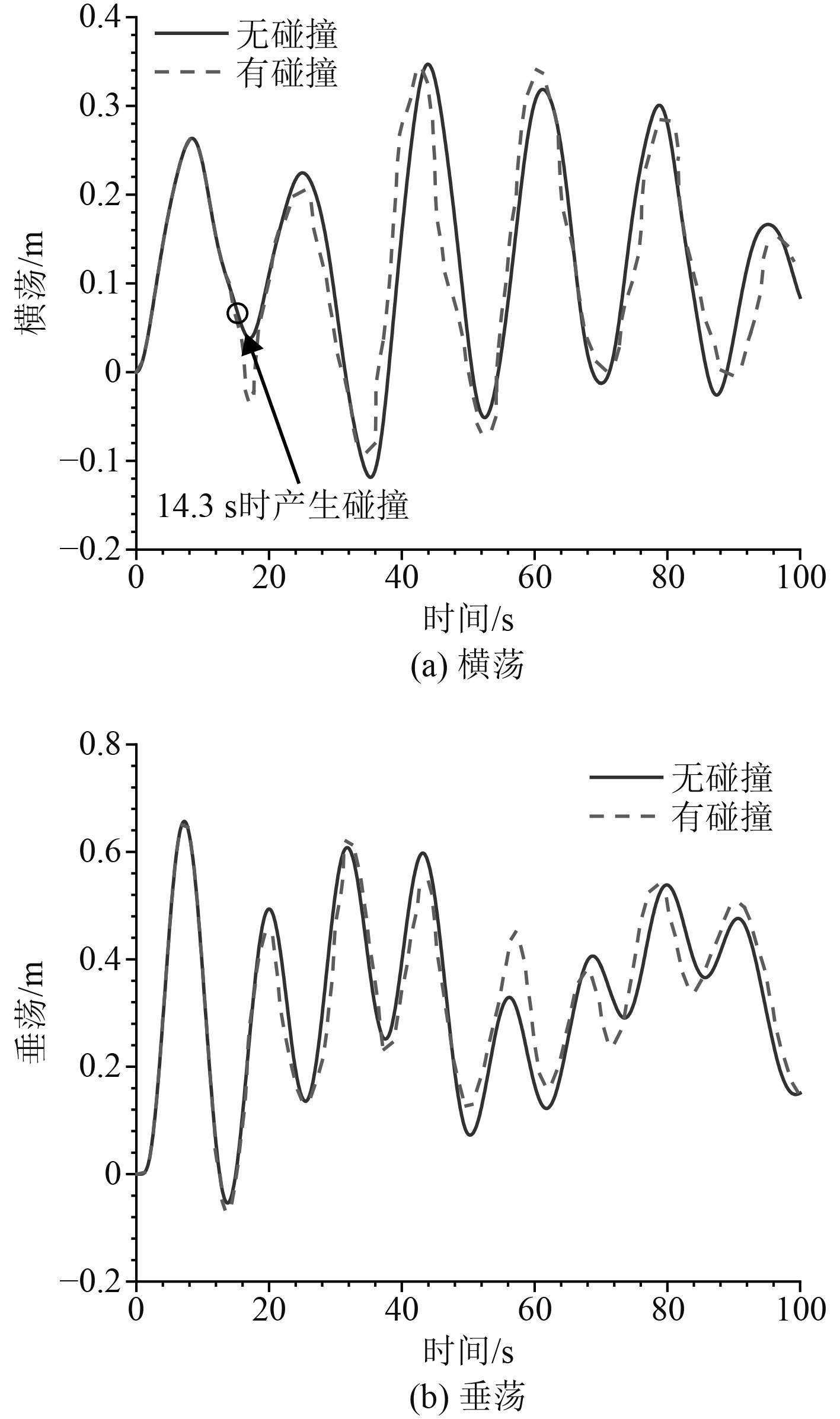
图9为隧道结构在横荡和垂荡方向上的运动响应。可知,碰撞发生时刻为14.3 s时,响应曲线呈周期性变化。在受到潜器撞击下,隧道的横荡和垂荡运动幅度均比无撞击下的运动幅度要大,且横荡运动幅度增加的更为明显。说明撞击荷载对于水中悬浮隧道的运动响应产生了一定的影响,且主要集中在横荡运动上。这是由于潜器沿x方向且所产生的动能大部分转化为了隧道的动能,这些动能导致隧道的运动幅度增大。
|
图 9 运动响应对比图 Fig. 9 Comparison of motion response |
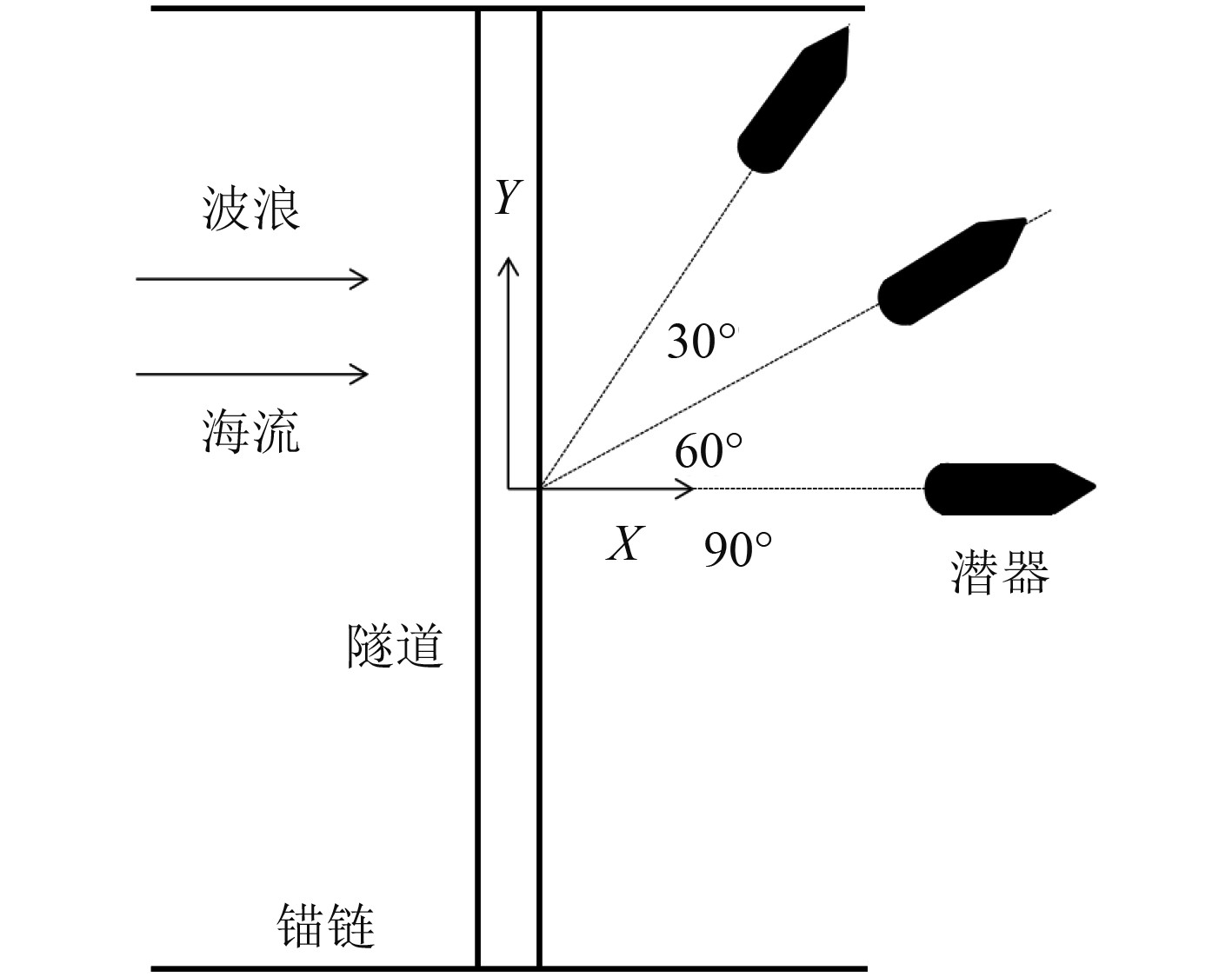
为了探究不同撞击速度和不同撞击角度对水中悬浮隧道碰撞响应的影响。选取潜器撞击速度分别为5 m/s、6 m/s和7 m/s等3组工况来分析撞击速度对于水中悬浮隧道结构动力响应的影响[16](此时碰撞角度为90°)。由于水中悬浮隧道在实际的运营期间,可能出现不同撞击角度碰撞情况,所以选取潜器与隧道成90°、60°和30°等3组角度工况来研究碰撞角度对水中悬浮隧道碰撞响应的影响(此时碰撞速度为5 m/s)。
|
图 10 不同的碰撞角度简化示意图 Fig. 10 Simplified scenarios of different collision angles |
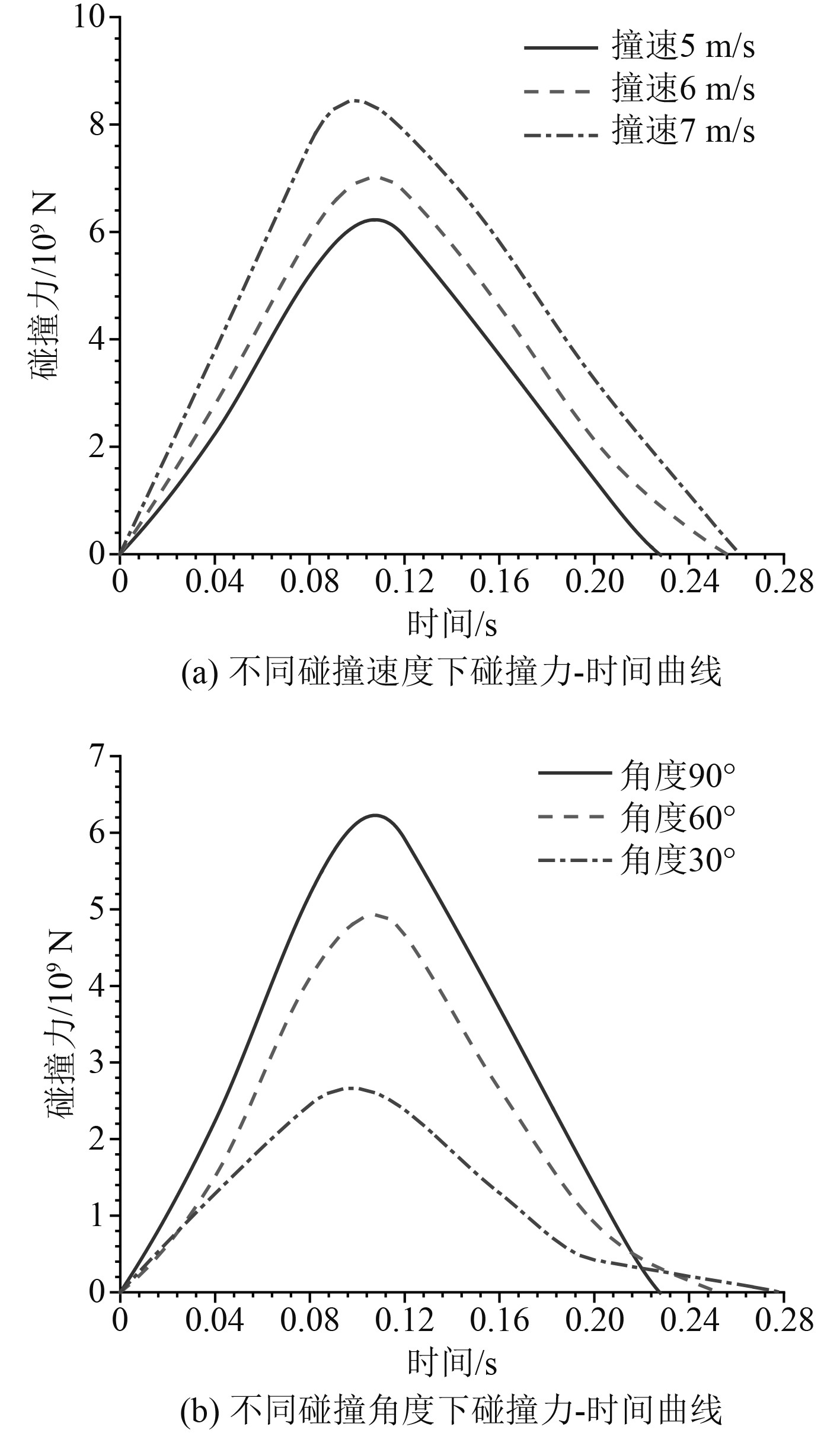
图11为不同碰撞速度和碰撞角度下的碰撞力时程曲线。可知,当潜器撞击隧道的速度和角度增加时,都会使隧道结构受到的最大碰撞力增大。碰撞持续时间随着碰撞速度的增加而变长,随着碰撞角度的增加而变短。这是因为碰撞速度更大时,潜器具有更大的动能。碰撞速度相同,随着角度的减小,垂直于隧道轴线的碰撞速度降低,沿隧道轴线的碰撞速度增大。
|
图 11 两种碰撞参数下的碰撞力-时间曲线 Fig. 11 Curves of collision force-time under two collision parameters |
图12为不同碰撞速度和碰撞角度下的隧道应力应变云图。可知,随着碰撞速度的增加,碰撞区域所受的应力和损伤也在增加。从等效塑性应变的增加程度可看出,撞击速度在达到一定速度时,撞击将会使隧道结构破损,影响隧道整体结构的稳定性。为防止速度过快的水中潜器碰撞对隧道结构造成严重的损害,可在隧道外表面设置一层防撞结构或受到碰撞后自动展开的安全气囊,对隧道最易遭受碰撞的外表面进行防护。经过比较后可发现,撞击角度为90°时的结构性应力和结构损伤最大,所以当撞击角度为90°时,即垂直于隧道轴线碰撞这种情况对水中悬浮隧道的结构损伤最大。尽可能避免隧道受到垂直于轴线的碰撞,降低隧道结构的损伤。

|
图 12 不同碰撞速度、碰撞角度下隧道应力应变云图(变形效果放大50倍) Fig. 12 Stress-strain cloud map of tunnel under different collision velocities and angles (deformation effect magnified 50 times) |
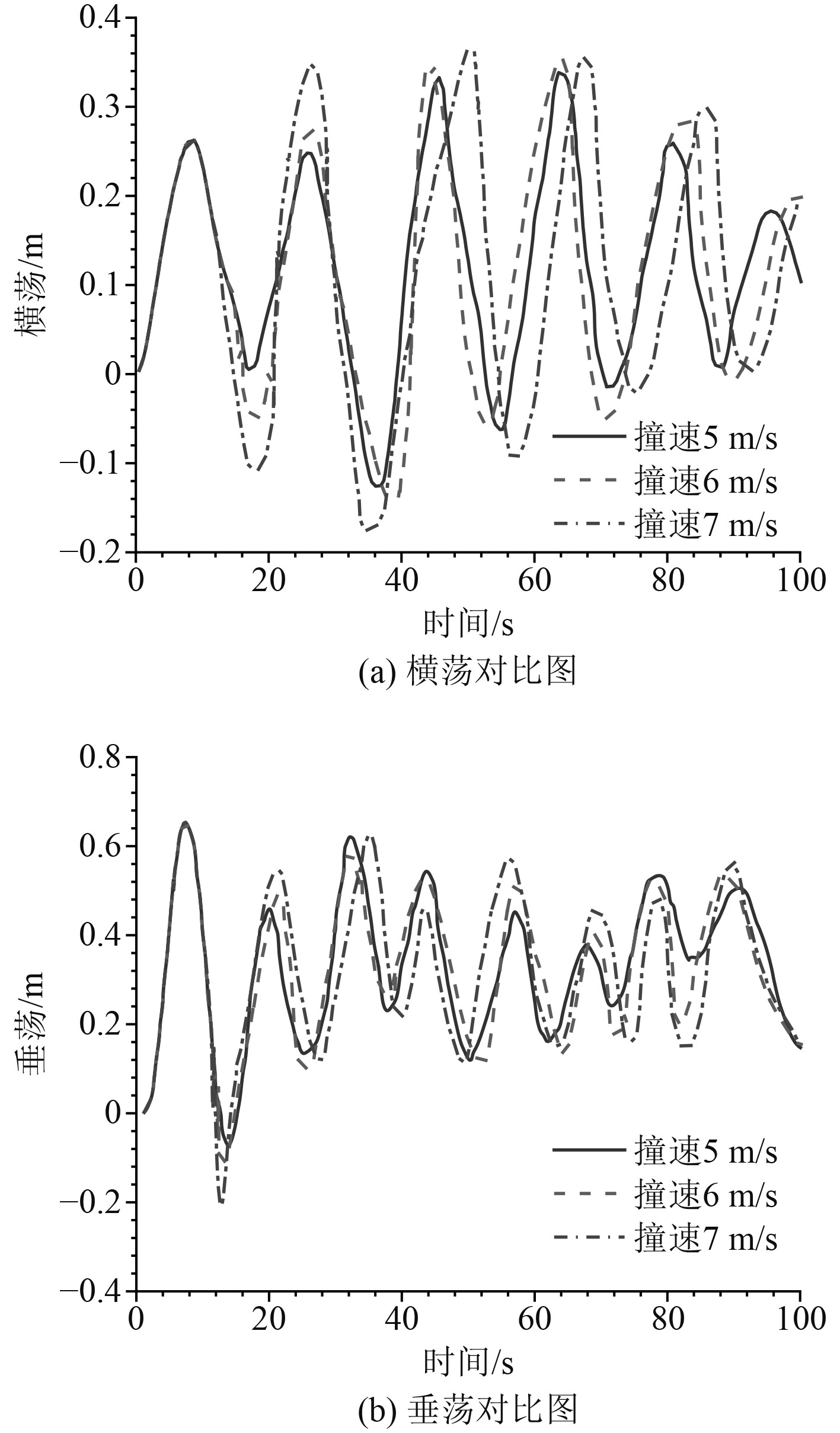
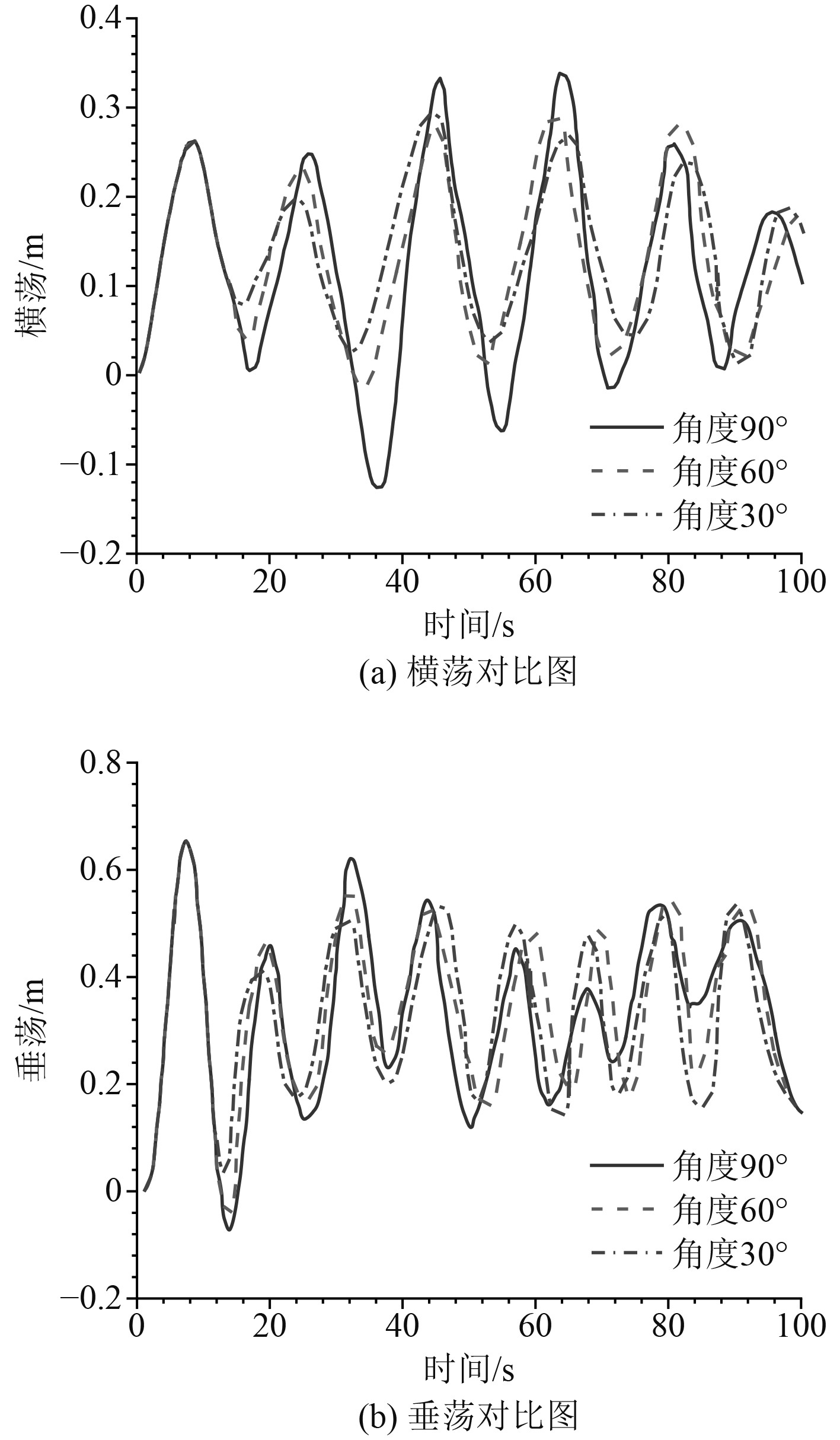
图13和图14分别为不同碰撞角度和碰撞速度下水中悬浮隧道运动响应对比图。由图13可看出,隧道的横荡运动幅度随着撞击速度的增大而增大。这是由于碰撞速度的增大,潜器的动能增大,转化为隧道的动能就越多,这些动能使得隧道的运动幅度增大。图14中,因为90°的撞击使隧道所受的碰撞力最大,所以90°撞击下隧道的横荡和垂荡自由度运动响应最大。碰撞结束后,隧道因处于相同波流环境下,横荡和垂荡运动响应幅值大致相同。本文选取的碰撞方向均与波流方向相反,但通过总结碰撞参数对水中悬浮隧道运动响应的影响规律可推断,碰撞方向与波流方向相同时,碰撞速度和角度的变化对隧道碰撞后运动响应的影响情况应与本文所总结的规律相似。因此水中悬浮隧道在水下运营期间,应对其各个方向都进行充足的防护,减小碰撞事故引起的运动响应和损伤。
|
图 13 不同碰撞角度下水中悬浮隧道运动响应对比图 Fig. 13 Comparison of motion response under different collision angle |
|
图 14 不同碰撞速度下水中悬浮隧道运动响应对比图 Fig. 14 Comparison of motion response under different collision velocities |
本文基于STAR-CCM和Abaqus耦合建立考虑多场耦合的碰撞载荷下,水中悬浮隧道动力响应的数值模型,并通过文献试验结果对模型进行验证。在此基础上,研究潜器碰撞下,水中悬浮隧道运动响应和变形情况,探讨了不同撞击参数对水中悬浮隧道碰撞后,结构损伤和运动响应的影响,主要结论如下:
1)在水中悬浮隧道受到碰撞的过程中,产生的应力主要分布在隧道表面与潜器接触的区域,具有明显的局部性。碰撞虽然使隧道表面产生了变形,但由于变形程度相对较小且隧道结构没有产生裂缝,属于轻度破坏,所以并不会对隧道后期运营阶段的稳定性造成很大影响。
2)在不同撞击速度的情形下,碰撞后隧道的运动响应和结构的损伤程度也都随着撞击速度的提高而增加。但当整个撞击过程完成后,隧道因处于完全相同的波流环境中,运动响应不再有明显差异。
3)在不同碰撞角度的情形下,随着夹角的减小,潜器垂直于隧道轴线的速度降低,沿隧道轴线的速度增大。撞击角度为90°时,结构的应力高于其他2个角度,结构损伤最严重。此外,90°撞击下水中悬浮隧道的横荡和垂荡的运动响应,都大于60°和30°碰撞下的运动响应。
| [1] |
HAVARD O. Submerged floating tunnel(sft), a new type of structure for efficient transport, energy saving, minimizing pollution and environmental impact. Strait Crossing 2001[C]// Krobeborg: Swets&Zeitlinger Publishers Lisse, 2001, 545–546
|
| [2] |
MAZZOLANI F. The waterway strait crossing by means of Submerged Floating Tunnels[J]. Bauingenieur, 2003, 218–223.
|
| [3] |
ZHANG S Y, Vibration behavior and response to an accid-ental collision of SFT prototype in Qiandao Lake (China) [J]. Procedia Engineering, (2010)189–197.
|
| [4] |
张嫄, 董满生, 唐飞. 冲击荷载作用下水中悬浮隧道的位移响应[J]. 应用数学和力学, 2016, 37(5): 483-491. DOI:10.3879/j.issn.1000-0887.2016.05.004 |
| [5] |
刘迁苹. 水下悬浮隧道断索、碰撞的分析模型及动态响应研究[D]. 大连: 大连理工大学, 2021.
|
| [6] |
LUO G, PAN S, ZHANG Y, et al. Response Analysis of Submerged floating tunnel hit by submarine based on smoothed-particle hydrodynamics[J]. Shock and Vibration, 2019, 34(8): 82–88.
|
| [7] |
陈灿鹏, 孙文哲, 王琰, 等. 水中悬浮隧道受撞击作用的数值分析[J]. 水道港口, 2020, 41(2): 191-196. |
| [8] |
邹蓓蕾, 陈淑玲, 王洪富, 等. 规则波中迎浪航行的三体无人监测船阻力性能及片体布局影响研究[J]. 江苏科技大学学报(自然科学版), 2021, 35(3): 16–23. ZOU Bei-lei, CHEN Shu-ling, WANG Hong-fu, et al. Research on resistance performance of three-body unmanned monitoring ship navigating in regular waves and the influence of the body layout[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2021, 35(3): 16–23. |
| [9] |
邹鹏旭, 刘孟源, 陈良志. 波浪作用下悬浮隧道管体-锚索耦合系统水动力特性研究[J]. 现代隧道技术, 2021, 58(3): 154-162. ZOU Peng-xu, LIU Meng-yuan, CHEN Liang-zhi. Study on the hydrodynamic characteristics of the coupling system of submerged floating tunnel tubes and anchor cables under wave action[J]. Modern Tunnelling Technology, 2021, 58(3): 154-162. DOI:10.13807/j.cnki.mtt.2021.03.020 |
| [10] |
孙钦东, 唐怀平. 重力式桥墩与船舶斜向碰撞过程数值仿真[J]. 重庆理工大学学报(自然科学), 2018, 32(7): 67-71. |
| [11] |
王加夏, 周天九, 刘昆, 等. 规则波迎浪砰击下三维船体耦合响应研究[J]. 江苏科技大学学报(自然科学版), 2020, 34(4): 13-18+24. |
| [12] |
王长春. 水中悬浮隧道与洋流耦合作用的模型试验[D]. 成都: 西南交通大学, 2005.
|
| [13] |
陈子和. 浮式防波堤与波浪能发电装置水动力分析[D]. 镇江: 江苏科技大学, 2021.
|
| [14] |
耿宝磊, 刘宇, 胡传琪, 等. 悬浮隧道水动力问题研究概述[J]. 水道港口, 2020, 41(1): 1-8. DOI:10.3969/j.issn.1005-8443.2020.01.001 |
| [15] |
田连波, 侯建国. ABAQUS中混凝土塑性损伤因子的合理取值研究[J]. 湖北大学学报(自然科学版), 2015, 37(4): 7. |
| [16] |
赵岚涛. 波—流耦合作用下悬浮隧道合理断面型式研究[D]. 重庆: 重庆交通大学, 2020.
|
 2023, Vol. 45
2023, Vol. 45
