在船舶结构设计中,大多会采用化整为零及合零为整的做法,即利用规范法或直接设计方法对船舶局部结构进行分类设计,而后进行总体结构设计与衡准。该方法具有较大不确定性且设计精度有限,很难达到最优。即使是在船舶结构优化设计中,应用较多的也主要集中在尺度优化,并没有改变结构的形貌及拓扑构型。这些结构直接设计与优化设计方法仍然具有非常大的局限性,比如局部结构应力集中与结构冗余控制问题等。近年来,随着结构拓扑优化理论所取得的较大发展,使得连续体结构拓扑优化设计方法在汽车、土建及机械制造等领域都有了较为普遍的应用,而在船舶结构设计领域,受限于船体整体结构的大规模、复杂性及设计周期成本控制等多重因素,结构拓扑优化设计应用研究进展缓慢。目前,国内外学者对于单工况或单目标拓扑优化问题的研究已经较为成熟,提出了各种不同的优化方法与求解技术。杨德庆等[1]基于结构拓扑优化均匀化法,通过对比加肋、粘敷阻尼和改变拓扑等条件下结构固有频率和声辐射特性的变化,指出采用结构拓扑优化方法对解谐和减振降噪阻尼材料配置的高效性。李启宏等[2]提出了一种基于改进SIMP法的连续体结构拓扑优化方法,以全体单元中心点应力应变积之和为优化目标函数,基于ISIMP法对悬臂梁进行了不同网格规模下的拓扑优化实验。刘宏亮等[3]体拓扑优化算法引入到油船中剖面横撑结构的优化设计中,分别基于应变与应力约束,得到了取消横撑结构的粗略构型。张会新等[4]以拓扑优化变密度法建立的上层建筑板架结构优化模型,优化后的结构材料分布更为合理,结构重量减轻较显著,提高了结构固有频率。徐飞鸿等[5]考虑单元删除和增加对结构应力约束的影响,提出了一种新的多工况下结构的双方向渐进优化方法。刘辛军等[6]将导重法引入多工况优化问题,并用对偶方法对多约束优化问题的拉格朗日乘子求法进行了改进。
综上,目前多工况优化问题大多转化为多工况下的最小化柔度问题,虽具有较好的收敛效果,并且能够取得较好的优化构型,但大多没有考虑应力约束条件,也加大了后续尺度优化及形貌优化的工作量。另外,单一工况下的最优拓扑构型很难保证在其他载荷工况下同样具备较好的传力路径,特别是对于大型运输船舶,根据作业区域与运用方式不同,存在多种工况,传统船舶结构设计方法显然不能满足其精细化结构设计需求,将多工况拓扑优化方法引入船舶局部结构设计中具有一定意义。大型运输船高双层底结构是船舶横剖面骨架结构的关键部位,而实肋板结构是双层底结构中的主要组成部分,是保证船体载物承重与干船坞维修等工况的关键支撑结构件,双层底结构的高效可靠设计是大型运输船总体结构安全性的重要保障,而采用传统规范法直接设计与部分尺度优化设计对于双层底结构安全裕度的控制能力有限,不利于双层底结构整体重量控制,降低了运输船的有效载重能力。本文将多工况拓扑优化算法引入到船舶结构初步设计中,提出了基于k方法的多工况权因子确定方法,考虑整体化应力约束条件,建立了多工况下拓扑优化数学模型,同时针对某大型运输船舶高双层底典型实肋板结构设计优化应用问题,与有限元分析方法相结合,在获得最终构型的基础上确定可行的实肋板结构初步设计方案,探究了多工况拓扑优化算法进行结构初步设计的一般流程,为船舶结构高效精细化设计提供一种新思路。
1 多工况下拓扑优化数学模型针对多工况问题主要有2种处理方法,一种将其处理为多目标优化问题,另一种为多约束优化问题[6]。针对前一种方式,在拓扑优化问题中一般将多目标优化问题处理为单目标优化问题,这种做法较为高效且能得到满足一定要求的拓扑构型,而难点在于各工况(目标)权因子的确定。对于后一种处理方式,在能够合理确定各约束限的前提下,运用拉格朗日乘子法可以求解该优化问题,难点在于各工况约束函数乘子的确定,无论是采用传统Lemker方法或对偶方法来求解拉格朗日乘子,最终的计算量都非常大。为此,本文尝试将多工况拓扑优化问题转化为多目标问题进行求解,并考虑多目标权因子的确定。
1.1 多目标拓扑优化基本模型以多工况下连续体结构的柔度最小化为目标函数,在给定载荷和边界条件下,考虑体积约束条件,基于SIMP(变密度法)材料插值模型,将多工况拓扑优化问题转化为多目标优化问题。为降低多目标拓扑优化问题的工作量与求解难度,而且多目标同时达到最优解的可能性较小,这里采用权因子法将多目标优化问题转化为单目标优化问题进行求解。
| $ \left\{ {\begin{array}{*{20}{l}} {\rm{Min}}\; C\left( {\rm{X}} \right) = \displaystyle\sum\limits_{j = 1}^m {{\omega _j}} {{{\boldsymbol{U}}}}_j^{\rm{T}}{{{{\boldsymbol{K}}}}_j}{{{{\boldsymbol{U}}}}_j} = \sum\limits_{j = 1}^m {{\omega _j}} {{{\boldsymbol{U}}}}_j^{\rm{T}}{{{\boldsymbol{K}}}}{{{{\boldsymbol{U}}}}_j},\\ {\rm{s.t.}}\quad V - f{V_0} = \displaystyle\sum\limits_{i = 1}^n {{V_i}{x_i} - f{V_0} \leqslant 0},\\ {{{{\boldsymbol{F}}}}_j} = {{{\boldsymbol{K}}}}{{{{\boldsymbol{U}}}}_j},\;\; {j = 1,2,3...,m} ,\\ 0 < {x_{\min }} \leqslant {x_i} \leqslant 1,\;\; {i = 1,2,3...,n} ,\\ \displaystyle \sum\limits_{j = 1}^m {\omega _j} = 1, \;\;0 \leqslant {\omega _j} \leqslant 1 。\end{array}} \right. $ | (1) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{Min}}\; f\left( {\boldsymbol{X}} \right) = {{\left\{ \displaystyle\sum\limits_{i = 1}^m {{\omega _i}^q{{\left[ \dfrac{{{C_i}\left( {\boldsymbol{X}} \right) - {C_i}^{\min }}}{{{C_i}^{\max } - {C_i}^{\min }}} \right]}^q}} \right\}}^{1/q}}},\\ {\displaystyle\sum\limits_{i = 1}^m {{\omega _i} = 1,\;\; 0 \leqslant {\omega _i} \leqslant 1} }。\end{array}} \right. $ | (2) |
式中:q为惩罚系数,q≥2;
在多工况(多目标)结构拓扑优化过程中,如何合理确定各工况对于结构整体刚度的影响程度非常重要,各工况权因子直接影响着最终拓扑构型。目前在大多数情况下,比较常见的做法是根据设计经验与实验数据等进行估算确定,这种做法较为简便,但容易受固有经验影响而造成错误判断,准确性较低。为更加合理确定权重因子,使得最终优化结果具备更好的可靠性,这里根据各工况的拓扑优化结果给出一种基于k方法的权因子确定方法。首先,根据优化准则法单独确定各工况下的最小化柔度计算结果,
与之对应的设计变量取值为
| $ C_i^j = {C_i}\left( {{X_j}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt},i = 1,2,3...,m;j = 1,2,3...,m,$ | (3) |
式中,m为工况数。假定经过以下m个点
| $ \sum\limits_{i = 1}^m {{\omega _i}\left| {\frac{{{C_i} - {C_i}^{\min }}}{{{C_i}^{\max } - {C_i}^{\min }}}} \right|} = {\omega _1}{f_1} + {\omega _2}{f_2} + ... + {\omega _m}{f_m} = k 。$ | (4) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega _1}{f_1}^1 + {\omega _2}{f_2}^1 + ... + {\omega _m}f_m^1 = k},\\ {{\omega _1}{f_1}^2 + {\omega _2}{f_2}^2 + ... + {\omega _m}f_m^2 = k} ,\\ \vdots \\ {{\omega _1}{f_1}^m + {\omega _2}{f_2}^m + ... + {\omega _m}f_m^m = k} ,\\ {{\omega _1} + {\omega _2} + ... + {\omega _m} = 1} 。\end{array}} \right. $ | (5) |
当式(2)不存在绝对最优解时,上式可以得到它的一个可行解k,并可以获得各工况下的一组权因子为:ω1, ω2, ….ωk。
1.3 多工况拓扑优化模型迭代算法上述拓扑优化模型为含不等式约束的非线性规划问题,在拓扑优化中比较常用的求解算法包括数学规划方法、优化准则法与启发式算法。其中:数学规划方法1般具有严格的理论基础,但对于大型结构优化问题重分析次数较多,收敛性不足;启发式算法是一种模拟生物进化过程等的一类算法,它可以进行全局寻优,对函数及变量连续性要求不高,不足之处在于重分析系数较大,对软硬件水平要求较高;优化准则法是从工程上有一定的依据出发,具有收敛快(迭代次数少)的特点,特别适用于大中型结构利用有限元方法进行结构性能约束及求导运算一类的问题。将采用优化准则法,根据式(1)构造包含相关约束的拉格朗日乘数:
| $ \begin{split}L =& C\left( X \right) + {\lambda ^{\rm{T}}}\left( {{\boldsymbol{KU}} - {\boldsymbol{F}}} \right) + {\lambda _0}\left( {\sum\limits_{i = 0}^n {{V_i}{x_i} - f{V_0}} } \right) +\\ &\sum\limits_0^n {{\lambda _{1i}}} \left( {{x_{\min }} - {x_i}} \right) + \sum\limits_0^n {{\lambda _{2i}}} \left( {{x_i} - 1} \right)。\end{split}$ | (6) |
式中:
根据驻值条件,L函数取得极值的K-T条件为:
| $ \frac{{\partial L}}{{\partial {x_i}}} = \frac{{\partial C}}{{\partial {x_i}}} + {\lambda ^T}\frac{{\partial KU}}{{\partial {x_i}}} + {\lambda _0}{V_i} - {\lambda _{1i}} + {\lambda _{2i}} = 0,$ | (7) |
考虑在边界约束内满足极值条件,
| $ \frac{{\partial L}}{{\partial {x_i}}} = \sum\limits_{j = 1}^m {\left( { - {U^T}\frac{{\partial {K_j}}}{{\partial {x_i}}}U} \right)} + {\lambda _0}{V_i} = - {U^T}\frac{{\partial K}}{{\partial {x_i}}}U + {\lambda _0}{V_i} = 0。$ | (8) |
针对多工况问题,根据上述优化准则法可以给出设计变量的迭代公式如下:
| $ {x_i}^{\left( {k + 1} \right)} = {B_i}^{\left( k \right)}x_i^{\left( k \right)}{\kern 1pt} {\kern 1pt} = \frac{{\displaystyle\sum\limits_{j = 1}^m {{\omega _j}{U_j}^{\rm{T}}\frac{{\partial K}}{{\partial {x_i}}}{U_j}} }}{{{\lambda _0}{V_i}}}x_i^{\left( k \right)}。$ | (9) |
式中:
目前在船舶结构优化设计问题求解过程中,考虑拓扑优化方法的运用,通常情况下可以分为两步:首先是基于拓扑优化方法,通过最小化柔度寻找到结构的最佳传力路径;随后利用尺度优化与形貌优化算法等对结构进行应力约束下的优化设计以满足结构强度要求。然而实际情况下,在结构拓扑优化过程对体积约束较为敏感、结构初始应力水平接近于或超过许用应力时,为降低后续修正及设计工作的难度,需要在拓扑优化过程中同步考虑结构应力约束的影响。目前拓扑优化问题中应力约束的处理方法均为采用整体化应力约束,可有效降低由局部应力约束引起的过大计算量,主要有2种处理方法:一是将整体应力水平函数作为约束条件,将拓扑模型转化为对偶问题进行求解;二是将整体应力水平函数纳入到多目标拓扑优化目标函数中。
目前,国内外对于整体化应力函数的处理方法也有一些研究。隋允康等[7-8]将局部的应力约束问题转化为结构整体的应变能约束问题,得到了应力的近似化显示函数,取得了一定效果。另外,运用较多的整体化应力函数方法还包括P准则方法与KS方法[9],P准则法中的应力处理方式为:
| $ {\hat \sigma _{\max }} \approx {\left( {\sum\limits_e {{\sigma _{veg}}^{{P_w}}} } \right)^{\frac{1}{{{P_w}}}}} \leqslant \bar \sigma 。$ | (10) |
式中:
Chau Le[10]在应力约束函数中引入了单元体积项Ve,即
| $ {\hat \sigma _{\max }} \approx {\left( {\sum\limits_e {{V_e}{\sigma _{veg}}^{{P_w}}} } \right)^{\frac{1}{{{P_w}}}}} \leqslant \bar \sigma,$ | (11) |
Erik Holmberg[11]提出了成群应力约束的概念,对于第i个单元集群Φi来说,其整体应力约束为:
| $ {\hat \sigma _{\max \_i}} \approx {\left( {\frac{1}{{{N_i}}}\sum\limits_{e \in {\phi _i}} {{\sigma _{veg}}^{{P_w}}} } \right)^{\frac{1}{{{P_w}}}}} \leqslant \bar \sigma ,$ | (12) |
当
| $ {S_{{P_w}}} = {\left( {\frac{1}{{{V_R}}}\sum\limits_e {{V_e}{{\left( {{S_{eg}}} \right)}^{{P_w}}}} } \right)^{\frac{1}{{{P_w}}}}}。$ | (13) |
式中:VR为体积分数约束;当
为此,同时考虑多工况柔度函数及应力水平函数的多目标无因次函数可以表示为:
| $ \begin{split} \tilde T\left( X \right) = &\left\{ {\omega ^2}\left[ \sum\limits_{j = 0}^m {{\omega _j}\left[ {\frac{{{C_j}\left( X \right) - {C_j}^{\min }}}{{{C_j}^{\max } - {C_j}^{\min }}}} \right]} \right]^2 +\right. \\ &\left.{{\left( {1 - \omega } \right)}^2}{{\left[ {\sum\limits_{j = 0}^m {{\gamma _j}{S_{{P_w}j}}} } \right]}^2} \right\}^{1/2}\times \\ & \left( {\sum\limits_{j = 0}^m {{\omega _j} = 1} ,\sum\limits_{j = 0}^m {{\gamma _j} = 1} ,0 < \omega < 1} \right) 。\end{split} $ | (14) |
式中:ωj、γj分别对应不同工况下无因次柔度函数与等效应力函数的权系数;ω为柔度函数与应力函数之间的权系数。
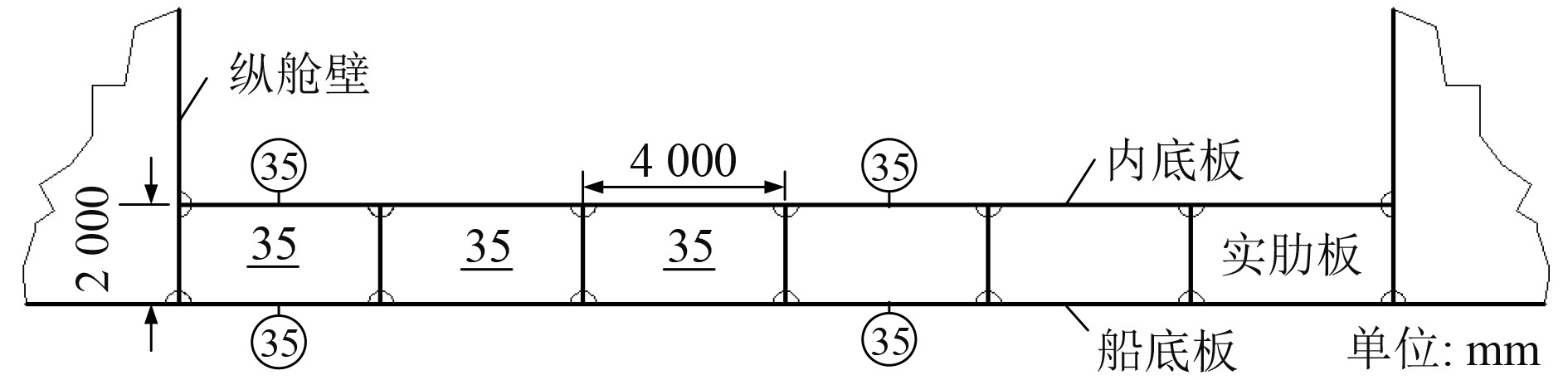
2 船舶高肋板结构拓扑优化设计实例 2.1 船舶高双层底肋板结构介绍以某运输船双层底高肋板结构初步设计为例,其双层底高度2 m,船底设置有1道中纵桁材,两端各有2道旁纵桁材结构对称布置,纵向桁材间距为4 m,横向实肋板间距为0.8 m(由于双层底高度较大且横向受力状态较为复杂,双层底在每一个肋位均设置有实肋板结构),实肋板结构在两端支撑在舷侧纵舱壁上,各板材板厚均为35 mm。船舶所用钢材为普通钢材,其弹性模量为2.0E5 MPa,泊松比为0.3,材料密度为7850 kg/m3,双层底肋板结构(初始)示意图参见图1。
|
图 1 双层底实肋板结构 Fig. 1 Double bottom plate floor structure |
考虑结构设计与施工工艺基本要求,根据作业工况不同,该双层底肋板结构主要有2种受力状态(上下对称),受载工况1:船底板下方作用均布压力载荷为1 MPa;受载工况2:内底板上方作用均布压力载荷为1 MPa。
图2为一个肋距内的实肋板计算有限元模型,单元网格尺寸为100 mm,有限元模型节点总数为9677个,单元总数为9440个。载荷条件根据工况要求进行设置,边界约束条件:实肋板两端在舷侧舱壁处节点作绞支约束,同时约束住纵向构件端部节点沿水平方向的位移。图3给出了工况1对应的实肋板结构应力云图结果,工况2与之类似。可以看出,实肋板应力在靠近端部纵舱壁时较为集中(最大应力值达到262 MPa),满足许用应力要求,在中部区域仍有较大的应力裕度,具有一定的减重潜力。

|
图 2 实肋板结构有限元模型 Fig. 2 Plate floor FE model |

|
图 3 工况1应力云图 Fig. 3 Structure stress distribution |
这种肋板结构一般都会采用开孔处理以减轻结构重量,根据钢制船舶规范#2.6.1.4[12],所有肋板上均应开设减轻孔(人孔),除轻型肋板外,开孔的高度应不大于双层底高度的50%,否则应予加强。在实肋板上开设了半径为500 mm的数个减轻孔,见图4。

|
图 4 实肋板规范法设计 Fig. 4 Plate floor standard design |
为量化肋板减轻效果,定义一个肋板剩余体积分数,即
| $ \eta = \frac{{{V_0} - {V_r}}}{{{V_0}}} 。$ | (15) |
式中:V0为实肋板初始有效体积;Vr对应开孔折减体积。以规范开孔设计方法为例,其剩余体积分数约为0.93,减重效果并不明显。
图5为实肋板按照规范设置减轻孔后的工况1应力云图。可以看出,在靠近端部的第1个减轻孔周围会出现较为明显的应力集中,最大应力达到340 MPa(需要进行局部加强),在中部靠近中桁材区域仍有较大的应力裕度,还存在较大的改进空间。

|
图 5 工况1应力云图(规范法) Fig. 5 Structure stress distribution (Standard) |
考虑到规范方法的不足,将结构拓扑优化方法引入到高双层底实肋板结构开孔设计中,可以更加合理地根据实肋板中的最佳传力路径确定实肋板材料分布,在满足结构强度及刚度需要的基础上达到结构重量最轻。为满足通焊及排水的要求,实肋板在与纵桁相交的上下折角设通焊孔。因此在确定实肋板拓扑优化设计域时需预留出一部分区域作为非设计域,划分情况参见图6。
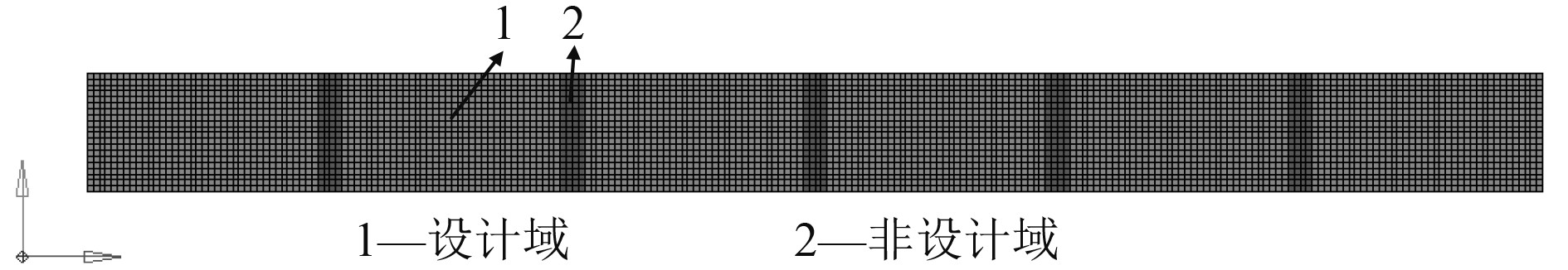
|
图 6 实肋板拓扑优化模型 Fig. 6 Topology optimization model of plate floor |
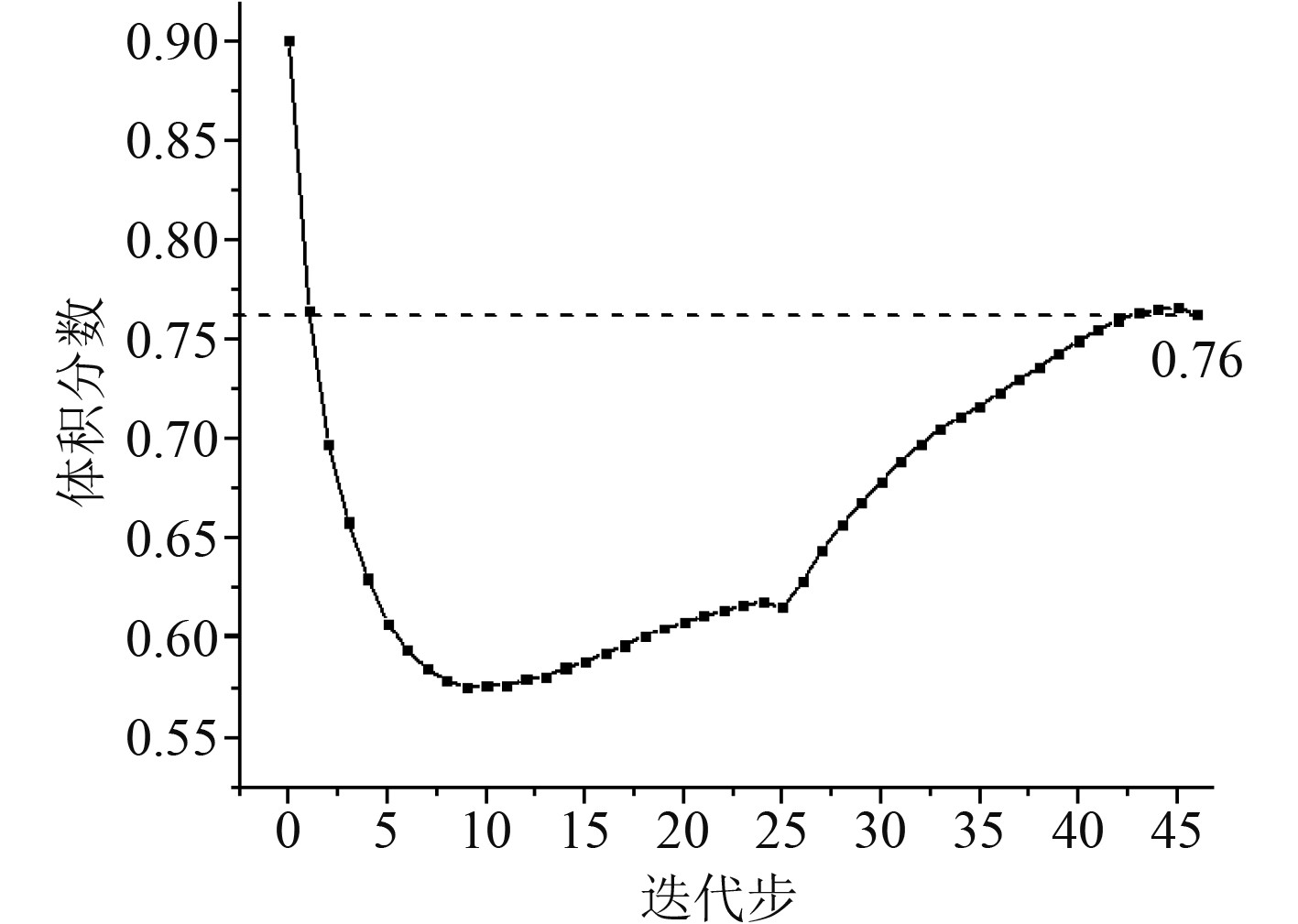
根据钢材许用应力给定整体化应力约束条件为300 MPa,对设计域设置上下对称约束以满足工艺性需要,2种工况下的权系数均取为0.5,根据设计要求取最小成员尺寸约束为600 mm,对实肋板模型进行多工况拓扑优化计算,迭代步数为46步,图7与图8分别给出了实肋板的最终拓扑构型与优化后的工况1应力云图,对部分中间密度单元进行过滤处理,在部分应力集中区域进行适度加强,图9为优化模型的体积分数迭代曲线,图11与图12分别给出了实肋板的最终设计拓扑构型与实肋板结构初步设计方案。
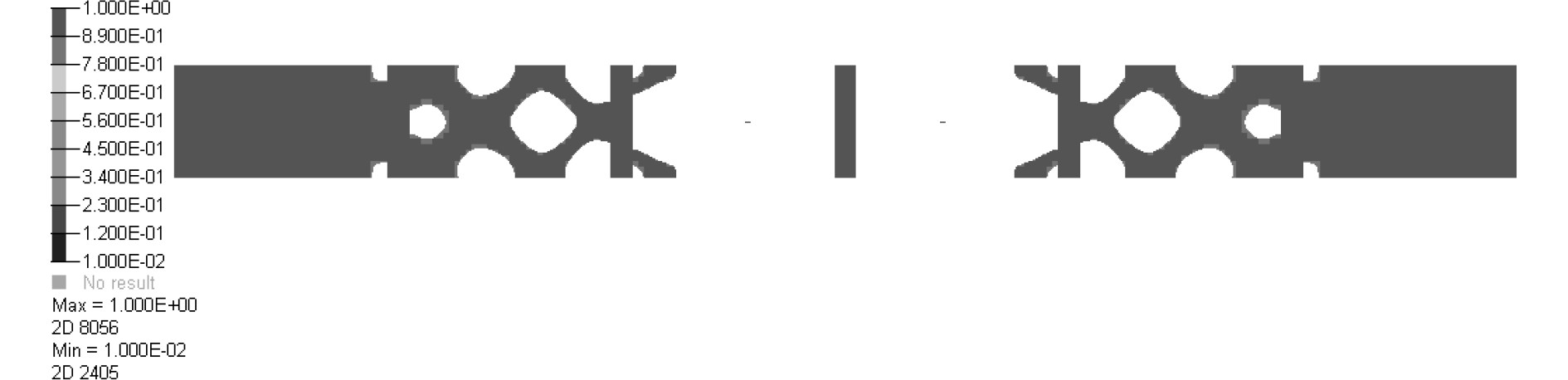
|
图 7 最终拓扑构型 Fig. 7 Final topology configuration |

|
图 8 结构应力云图 Fig. 8 Structure stress distribution |
|
图 9 体积分数迭代过程 Fig. 9 Iterations of volume fraction |

|
图 11 实肋板最终拓扑构型(设计) Fig. 11 Final topology configuration of plate floor (design) |
|
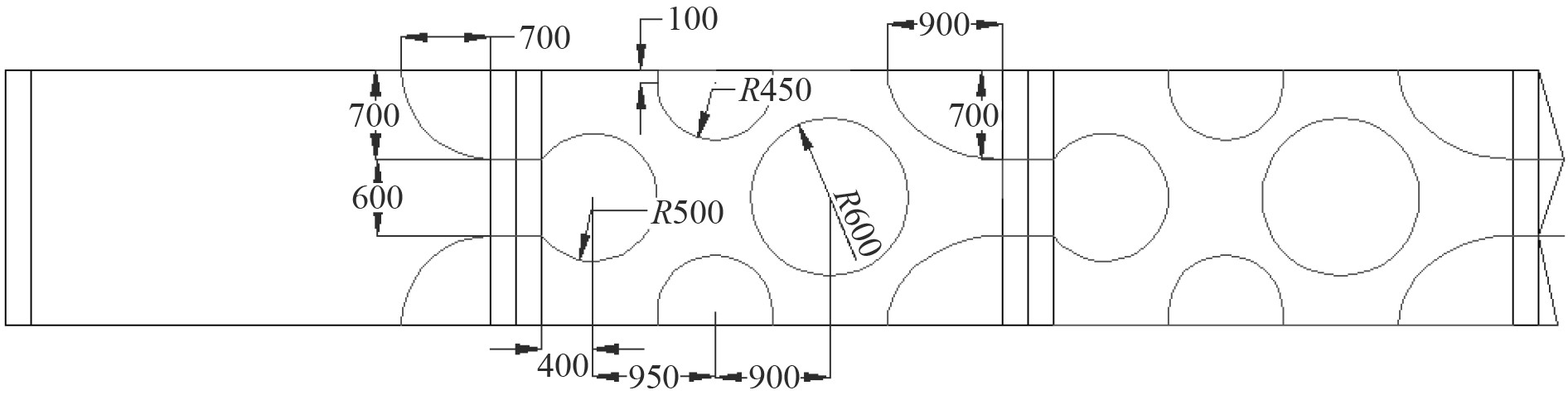
图 12 实肋板设计方案(一半) Fig. 12 Design scheme of plate floor(half) |
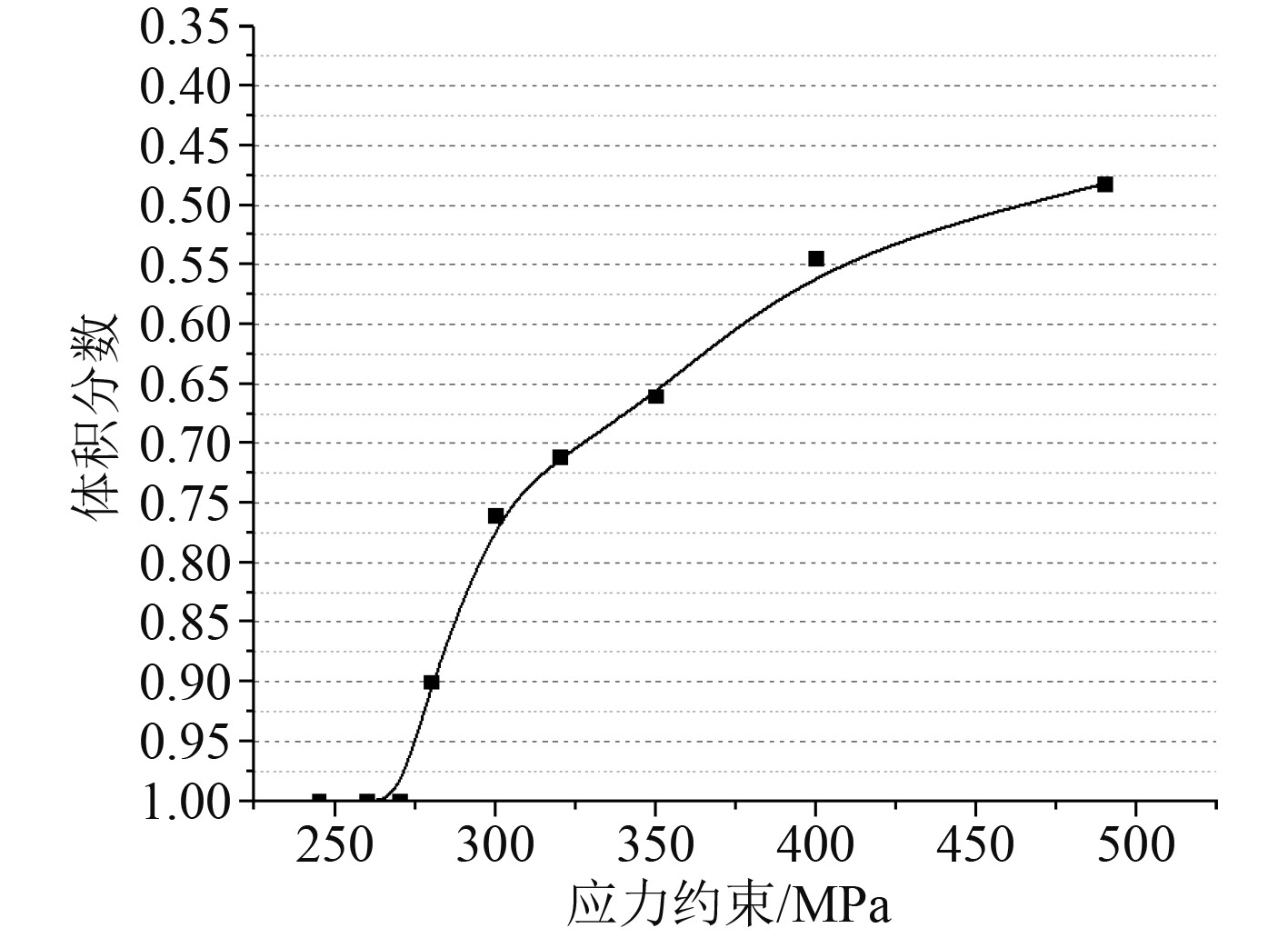
综上,可以看出最终构型较为清晰简明且具有较好的工艺性,剩余体积分数约为0.76(优于规范法设计结果,减重约18.3%),达到了轻量化设计的目的,整体应力水平得到有效控制且分布较为均匀,满足应力应变基本约束条件,这也就验证了上述拓扑优化数学模型及方法在船舶结构初步设计过程中是行之有效。作为对比,图10还给出了不同应力约束条件下的剩余体积分数曲线,可见结构减重效率与所取的应力约束值有关,对结构设计过程中的材料选取、重量控制与结构强度设计等具有一定参考意义。
|
图 10 剩余体积分数曲线 Fig. 10 Residual volume fraction |
本文将多工况优化问题转化为多目标优化问题,提出了基于k方法的权因子确定方法,引入全局化应力约束条件,建立了考虑应力约束的多目标拓扑优化数学模型,并对某高双层底实肋板结构进行静力学拓扑优化研究,结果表明最终构型能够满足应力应变等基本约束条件且具备较好的工艺性,相关研究成果为运用拓扑优化方法进行船舶结构设计提供了一条切实可行的途径。为进一步提升模型与方法的适用范围,还需在以下几方面做研究提升:1)对结构静力强度拓扑优化模型进一步拓展深化,考虑结构动力学约束条件(速度、加速度、振动噪声等),建立考虑静动力约束的多目标拓扑优化数学模型;2)对于全船结构整体优化设计时,由于单元变量多、条件约束多,导致计算量大、不收敛及拓扑构型不清晰,还需进一步改进拓扑优化数学模型,增加优化全过程条件管控;3)在静力拓扑优化数学模型中用到了全局化应力约束条件,对于控制结构最终构型的设计合理性及整体应力水平具有积极作用,但在某些实例中结构局部单元应力水平仍会超过许用应力约束,并没有达到完全控制单元应力水平的目的,有待进一步改进全局化应力函数。
| [1] |
杨德庆, 柳拥军, 金咸定. 薄板减振降噪的拓扑优化设计方法[J]. 船舶力学, 2003, 07(5): 91-97. |
| [2] |
李启宏, 李海艳. 基于改进SIMP法的连续体结构拓扑优化方法研究[J]. 机电工程, 2021, 38(4): 428-433. |
| [3] |
刘宏亮. 油船中剖面结构拓扑优化研究[D]. 上海: 上海交通大学, 2014.
|
| [4] |
张会新, 杨德庆. 典型船舶板架拓扑与形状优化设计[J]. 中国舰船研究, 2015, 10(6): 27-33. DOI:10.3969/j.issn.1673-3185.2015.06.005 |
| [5] |
徐飞鸿, 荣见华. 多工况下结构拓扑优化设计[J]. 力学与实践, 2004, 26: 50-53. |
| [6] |
刘辛军, 李枝东, 陈祥. 多工况拓扑优化问题的一种新解法——导重法[J]. 中国科学: 技术科学, 2011, 41(7): 920–928.
|
| [7] |
杨德庆, 隋允康, 刘正兴. 多工况应力约束下连续体结构拓扑优化设计映射变换解法[J]. 上海交通大学学报, 2000, 34(8): 1061-1065. |
| [8] |
叶红玲, 隋允康. 应力约束下连续体结构的拓扑优化[J]. 北京工业大学学报, 2006, 2(4): 301-305. |
| [9] |
KIYONO C Y, VATANABE S L, SILVA E C N, et al. A new multi-p-norm formulation approach for stress-based topology optimization design[J]. Composite Structures, 2016.
|
| [10] |
CHAU L, JULIAN N, TYLER B. Stress-based topology optimization for continua[J]. Struct Multidisc Optim, 2010, 41: 605-620. DOI:10.1007/s00158-009-0440-y |
| [11] |
HOLMBERG E, TORSTENFELT B, KLARBRING A. Stress constrained topology optimization[J]. Struct Multidisc Optim, 2013, 48: 33-47. DOI:10.1007/s00158-012-0880-7 |
| [12] |
中国船级社. 钢制海船入级规范船体篇[M]. 北京: 人民交通出版社, 2014.
|
 2023, Vol. 45
2023, Vol. 45
