2. 江南造船(集团)有限责任公司,上海 201913
2. Jiangnan Shipyard(Group) Co., Ltd., Shanghai 201913, China
现代战争取胜的关键是以最小成本取得最大战果,而能否达到这一效果的关键在于对战场敌我双方作战力量的精准计算。其中,对于打击敌方目标,评估其毁伤概率成为作战筹划的重要步骤。随着自动化控制技术、通信卫星技术等越来越多的先进技术运用到战场,根据经验评估兵力投入与实时对敌方各方面评估的准确性和时效性已无法满足现实需要。因此研究如何准确、快速计算被打击目标毁伤概率计算方法非常必要。
针对传统目标标准化计算精度低、计算机仿真方法效率低等实际情况,肖元星[1]基于毁伤概率计算的通用积分模型和数值积分方法,开发了通用的毁伤概率计算程序,同时给出了有效的系统流程图。胡建辉等[2]基于蒙特卡罗法对炮弹结合防空武器系统打击空中目标的毁伤概率建立了数学模型,并进行了相应的毁伤分析。Hu jiang等[3]通过蒙特卡罗法模拟出了舰载弹丸的毁伤概率。为弥补蒙特卡罗法的自身缺陷,戴毅等[4]通过公式推导引入了加权蒙特卡罗方法,该方法可在保证精度的条件下,有效提高毁伤概率计算的效率。本文提出一个新的毁伤概率计算公式,对该公式中提出的各概率参数分别进行计算,从而完成舰船目标毁伤概率计算与分析。
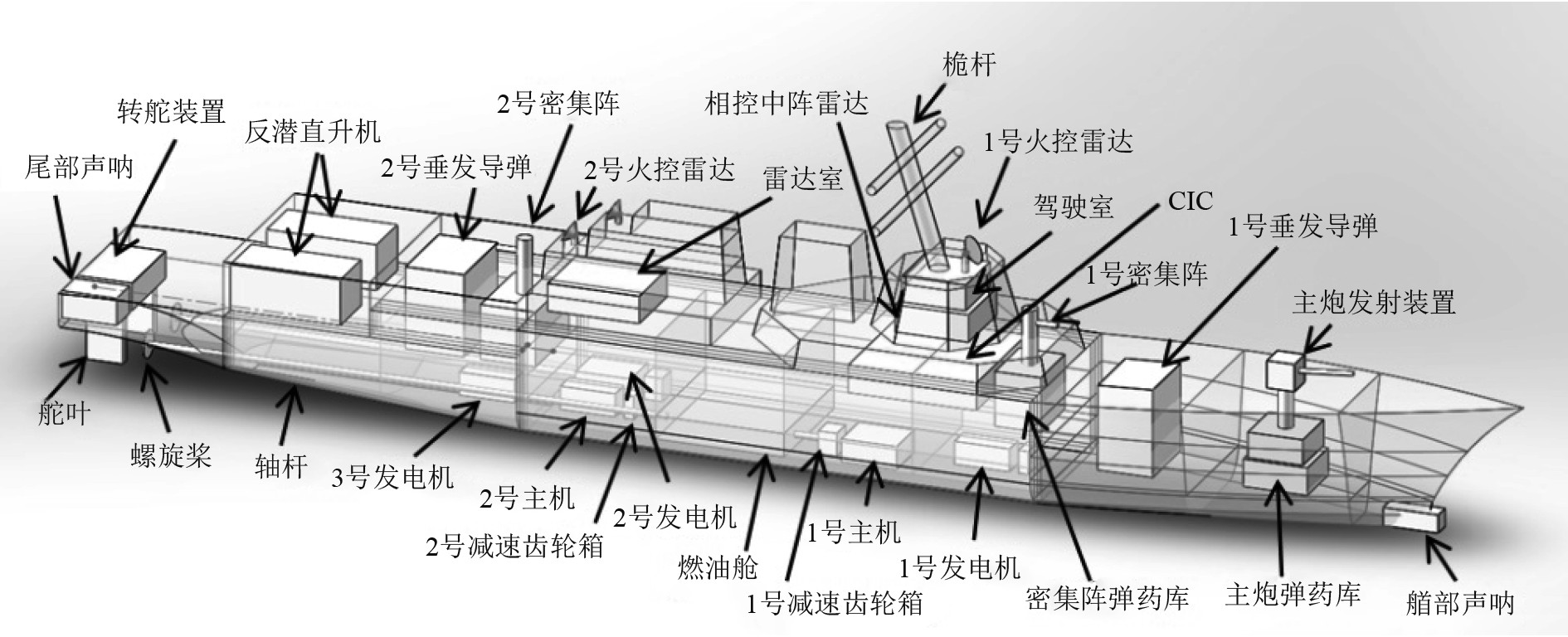
1 舰船目标模型的建立 1.1 典型舰船目标概况选取某典型舰船作为研究对象。该船的总长为155.3 m,船宽20.4 m,吃水深度为6.3 m,满载排水量约为9 238 t。动力输出由4台LM-2500燃汽轮机提供,总输出功率77.23×103 kW。采用宽水线船型,长宽比只有7.5。动力装置采用独特动力组合,螺旋桨为定距桨。上层建筑和同类舰船相比规模略小。桅杆与舷侧都设计为基座倾斜,边角的过渡区为圆弧形。此外,船上的关键位置都安装有“凯芙拉”装甲材料,数据传输系统采用了5条线路的分散布局形式。
1.2 易损性模型的构建根据文献资料确定舰船目标的尺寸及设备所在位置,并通过Solidworks进行三维建模。由于舰船内部设备的复杂性以及相关数据资料的限制,对内部设备及相关的舱室、设备进行简化以方便后续对舰船进行毁伤概率计算研究。用于毁伤评估的易损性可视化模型如图1所示。
|
图 1 典型舰船的易损性可视化模型 Fig. 1 A visual model for the vulnerability of the typical ship |
对于毁伤概率计算方法的研究,引入一个新的毁伤概率计算公式:
| $ P_{q}(x) =P_q(x) \cdot P_a(s)\cdot P_c(x)\cdot P_j(x)。$ | (1) |
式中:
在不同初速度下,弹体侵彻过程的剩余速度也不同,以剩余速度作为弹体是否击穿液舱靶板的判断依据。侵彻概率表达式为:
| $ P_{q}(x)=\left\{\begin{array}{ll} 0, & v \leqslant 0,\\ 1, & v>0。\end{array}\right. $ | (2) |
当弹体的变形过大导致内部压力过大,进而出现弹体早爆的情况时,将无法对舰船目标内部的舱室及设备造成毁伤,可得公式:
| $ P_{a}(x)=\left\{\begin{array}{ll} 1, & \sigma<\sigma_{\max } ,\\ 0, & \sigma \geqslant \sigma_{\max }。\end{array}\right. $ | (3) |
对于
| $ r_{\alpha}=k_{\alpha} \sqrt{w},$ | (4) |
| $ r_{b}=k_{b} \sqrt{w} 。$ | (5) |
式中:
当相对距离
| $ \Delta P_{m}=0.084 \frac{\sqrt[3]{m_{T}}}{R}+0.27\left(\frac{\sqrt[3]{m_{T}}}{R}\right)^{2}+0.7\left(\frac{\sqrt[3]{m_{T}}}{R}\right)^{3}({\rm{M P a}})。$ | (6) |
式中:
当
| $ \Delta P_{m}=0.0106 \frac{\sqrt[3]{m_{T}}}{R}+0.43\left(\frac{\sqrt[3]{m_{T}}}{R}\right)^{2}+1.4\left(\frac{\sqrt[3]{m_{T}}}{R}\right)^{3}({\rm{M P a}})。$ | (7) |
求得这2个距离对应的冲击波峰值超压
| $ P_{c}(x)=\left\{\begin{array}{lc} 0 ,& r(x)>r_{b},\\ \dfrac{\Delta P_{m}(x)-\Delta P_{m b}(x)}{\Delta P_{m a}-\Delta P_{m b}} ,& r_{a}(x)<r(x)<r_{b}(x) ,\\ 1,& r(x)>r_{a}。\end{array}\right. $ | (8) |
计算出
本文基于有限元仿真软件Ansys研究不同初速度下,半穿甲战斗部打击舰船目标的侵彻深度,从而为战斗部的侵彻概率计算提供分析。本文以典型的半穿甲尖卵型战斗部[6]为研究对象,该型战斗部的壳体材料为45#钢,总长度1140 mm,壳体头部长度560 mm,圆柱筒体580 mm,直径为380 mm。内部装有105 kg的TNT炸药,战斗部总质量为375 kg。
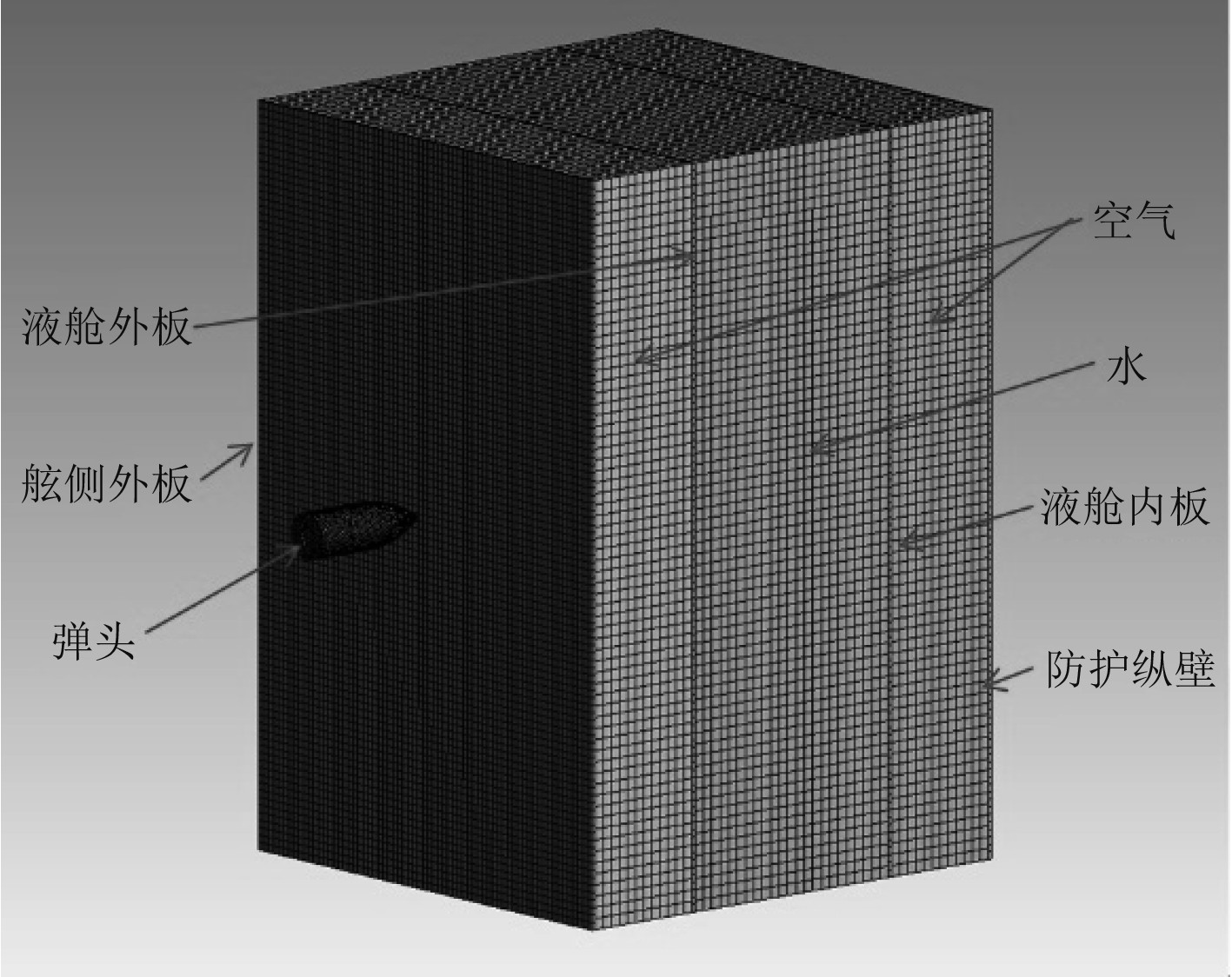
该典型舰船防护液舱靶板的厚度约为30 mm。包括半穿甲战斗部及靶板的其他尺寸均按原尺寸建立有限元模型。弹体和靶板分别设置为30 mm的四面体网格和六面体网格,同时设置为拉格朗日网格。液体区域设置为60 mm的四面体网格,同时设置为欧拉网格。每块靶板的4个侧面设置固定约束,并对欧拉域进行体积控制。具体有限元模型如图2所示。
|
图 2 船体舷侧防护液舱有限元模型图 Fig. 2 Finite element modelling of the protective fluid tanks on the side of the hull |
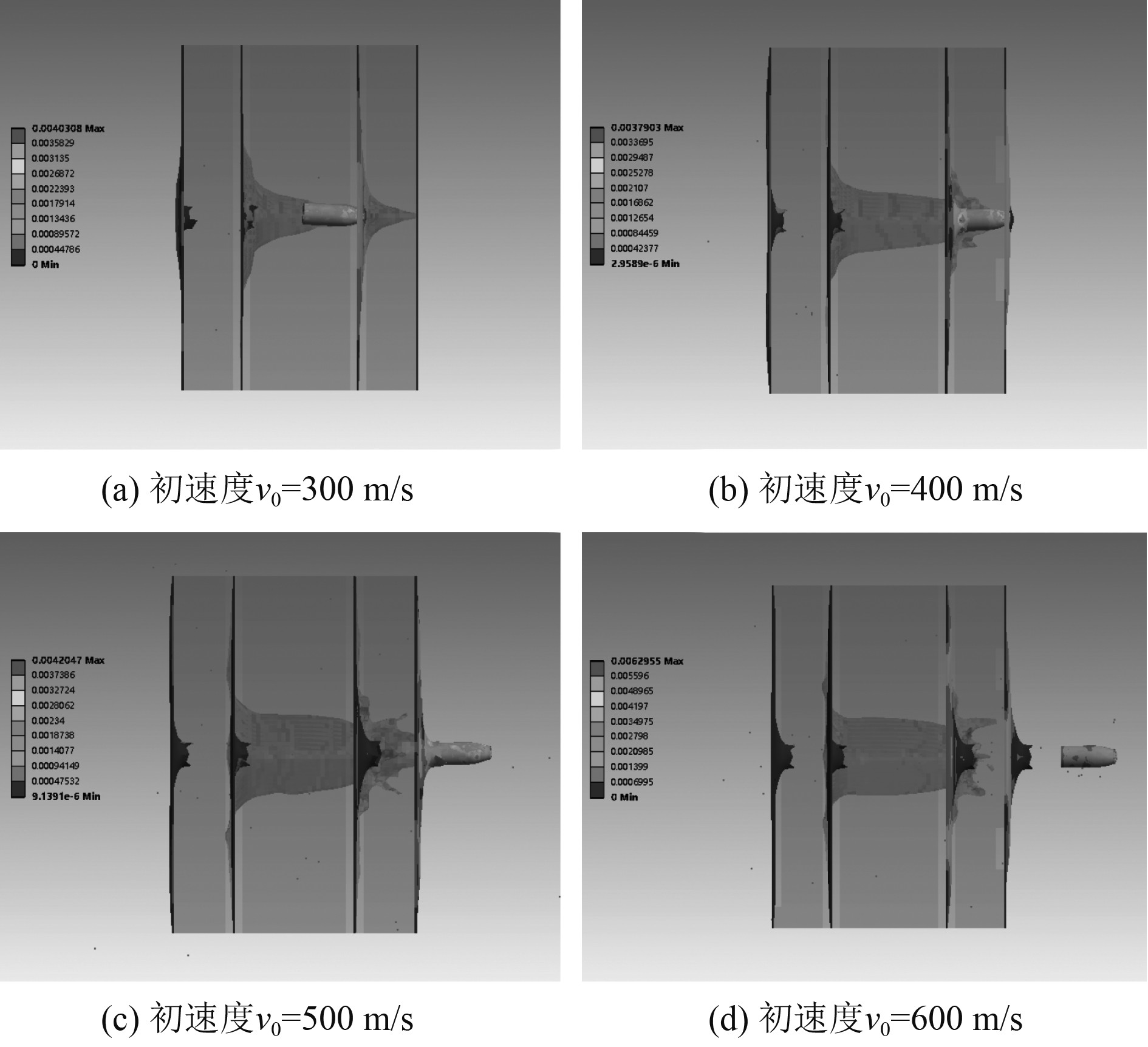
图3为不同初速度下弹体在30 ms后的侵彻深度。在不同初速度下,战斗部的侵彻深度存在明显差异。当初速度为300 m/s时,战斗部在30 ms后只能侵彻到液舱内部便不能继续侵彻;当初速度为400 m/s时,战斗部可击穿液舱,但剩余动能无法侵彻防护纵壁;当初速度为500 m/s时,战斗部刚好可侵彻整个舷侧结构;当初速度设为600 m/s时,战斗部可完全侵彻到舷侧结构,并还有一定剩余速度。
|
图 3 弹体打击液舱侵彻深度 Fig. 3 Depth of penetration of a projectile against a liquid chamber |
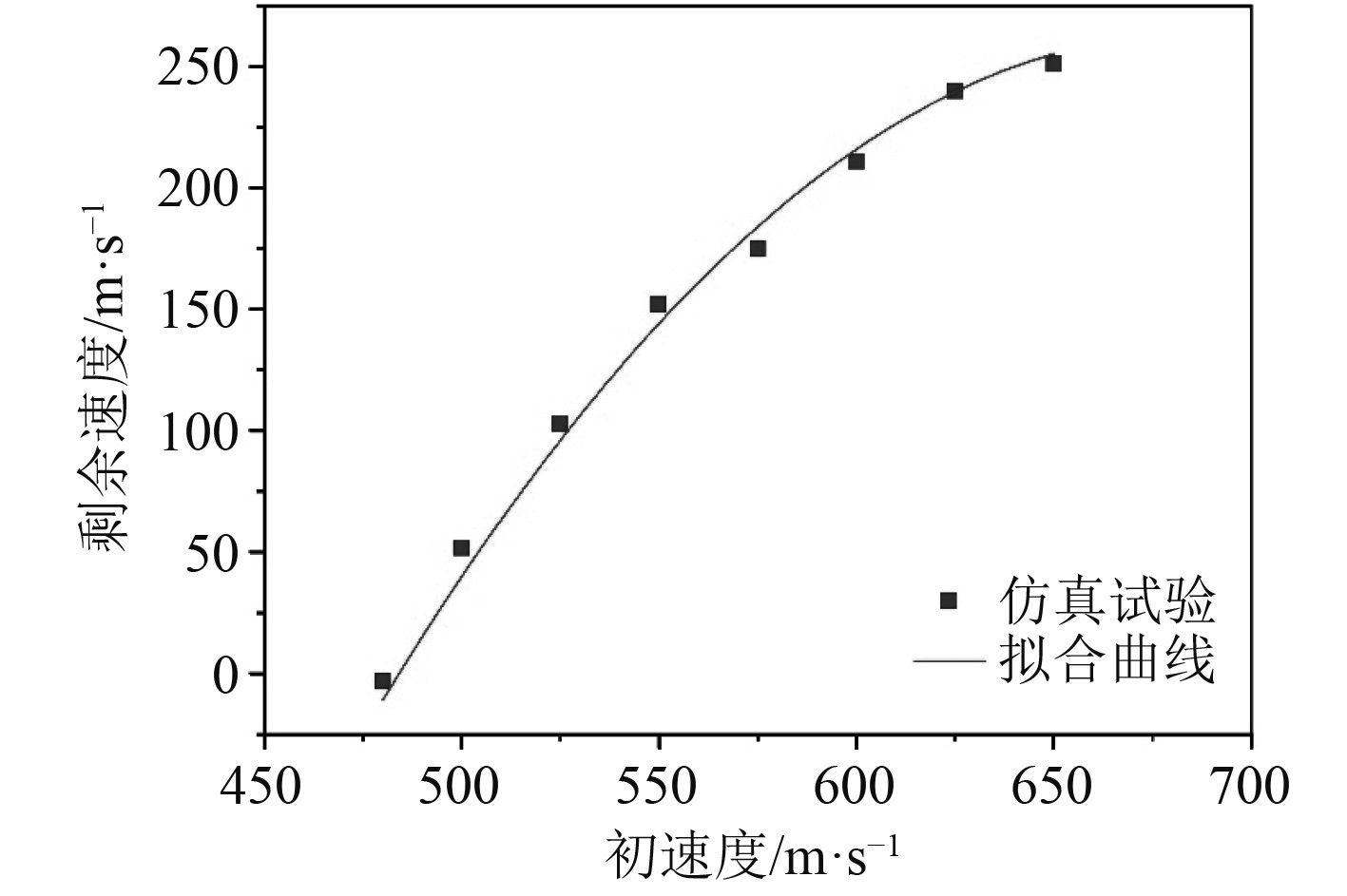
将基于均匀分布的等距抽样方法进行样本点的选取,包括400 m/s、450 m/s、525 m/s、550 m/s、575 m/s、600 m/s、625 m/s及650 m/s的8个样本点,进行有限元仿真计算得到其剩余速度,再通过近似拟合得出每个初速度下的剩余速度。设以30 ms作为延时引信的时间,得出如图4所示的拟合曲线。
|
图 4 初速度与剩余速度关系图 Fig. 4 Diagram of the relationship between initial velocity and residual velocity |
当初速度小于400 m/s时,弹体的剩余速度将小于0,弹体将无法击穿液舱靶板,也将无法对内部舱室及设备造成毁伤。但初速度为400 m/s并不是弹体能否击穿液舱靶板的阈值,通过大量的仿真试验发现,在攻角为0时,其能够击穿液舱靶板的初速度阈值近似480 m/s。但若改变攻角,其击穿阈值也相应发生变化。
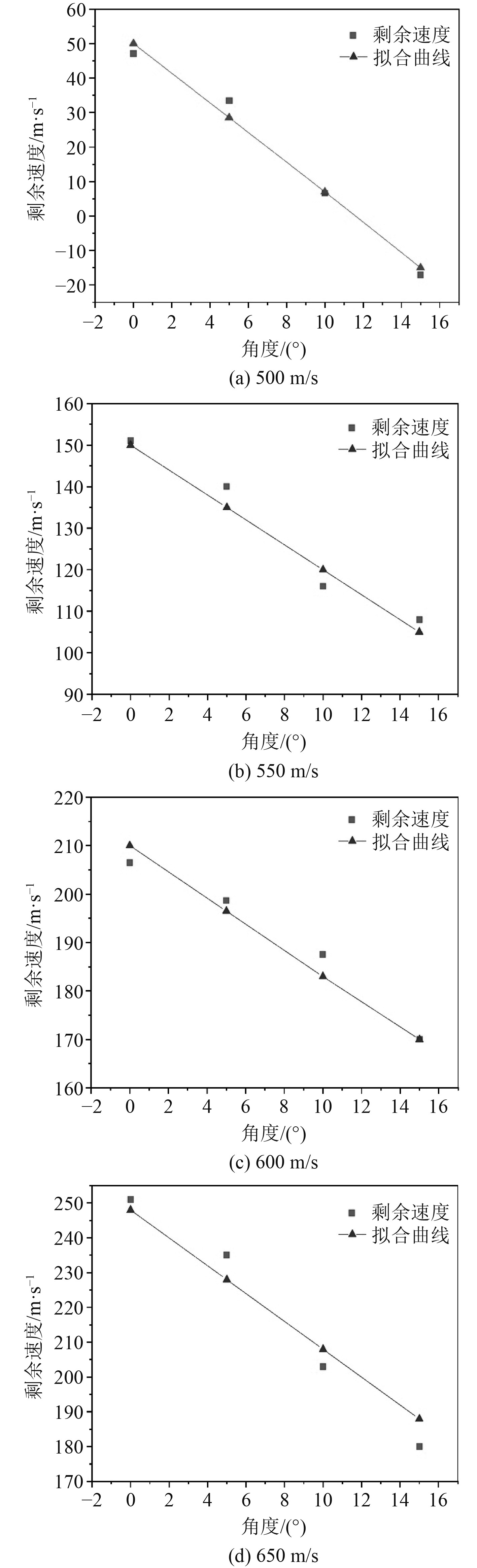
由于攻角对打击位置的影响较小,因此只考虑不同攻角对弹体侵彻深度及剩余速度的影响。在保证初速度不变的条件下,同样采用均匀分布的等距抽样方法分别抽取0°、5°、10°和15°样本点进行有限元仿真和近似拟合,得到不同角度下弹体对剩余速度的影响,如图5所示。
|
图 5 攻角与剩余速度的关系 Fig. 5 The relationship between angle of attack and residual velocity |
可知,相同弹体在初速度一定的条件下,随着攻角增大,剩余速度的减小量也不断增大,并近似为线性关系。通过对比不同初速度条件下,角度与剩余速度关系可知,该线性关系的斜率k可近似为常数3。从而进一步得到不同初速和攻角与剩余速度之间的拟合函数关系,如图6所示。
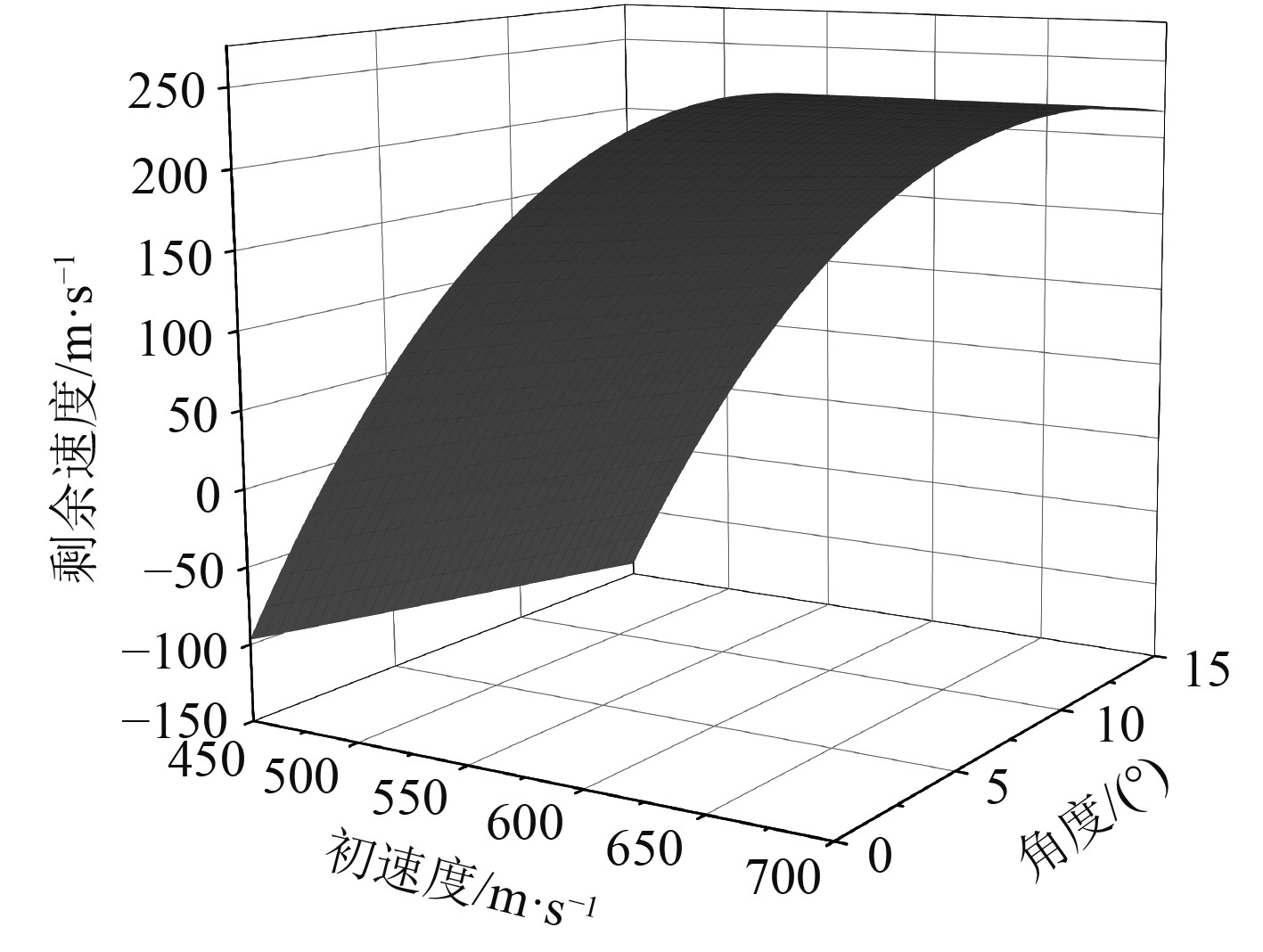
|
图 6 拟合函数三维关系图 Fig. 6 Three-dimensional plot of the fitted function |
蒙特卡罗法[7]基于随机模拟变量进行统计试验。通过这种方法进行足够多次独立重复试验,便能够计算出未知随机变量的一组随机数。同时将计算出来的所有随机样本进行统计处理,便可得到所求随机变量的概率分布以及通过统计得到相关数字特征的概率估值。
如图7所示,定义上甲板以下第一层甲板所在直线为X轴,以第五层横向隔板所在直线为Z轴,以两坐标轴交点为坐标原点O建立直角坐标系。设船体舷侧任意点的坐标为(X,Y),则只要基于确定的概率密度分布函数,统计各个舱室设备的击中次数,便可求得各个舱室及设备的击中概率。
|
图 7 坐标系图 Fig. 7 Coordinate system |
舰船被导弹命中的弹着点分布情况受到多重因素的影响,包括导弹的命中精度、不同海况及舰船的航行姿态。因此,弹着点的概率密度分布函数很难明确表达[8-11]。如图8所示,本文采用在舰船生存能力分析程序MOTISS中提到的以船长方向上的正态分布定义导弹命中点概率分布,高度方向同样也是服从正态分布的概率密度函数[12]。
|
图 8 标准正态分布函数图 Fig. 8 Graph of a function of the standard normal distribution |
基于Pycharm平台进行蒙特卡罗仿真模拟程序的编写。流程图如图9所示,具体步骤如下:

|
图 9 蒙特卡罗仿真模拟流程图 Fig. 9 Flowchart of the Monte Carlo simulation |
1)将舰船模型图导入程序中,并建立以2层甲板中点为原点的X-Z坐标系;
2)利用random库中的内置正态分布函数生成随机x和z值,并根据模型尺寸转换为准确的(X,Z)位置坐标;
3)利用turtle库生成对应(X,Z)的像素点,从而在模型图上确定其具体的打击位置,对于未命中的坐标位置记作黑像素点,命中记为红像素点;
4)利用循环语句进行多次重复的随机像素点生成;
5)通过if条件语句统计舰船目标各个设备位置的打击次数,以此计算出各个设备的打击概率。
图10为进行100次模拟打击点的位置分布图。由于是基于正态分布的概率密度函数,所以图中点的分布呈现了中间多、两边少的分布规律。
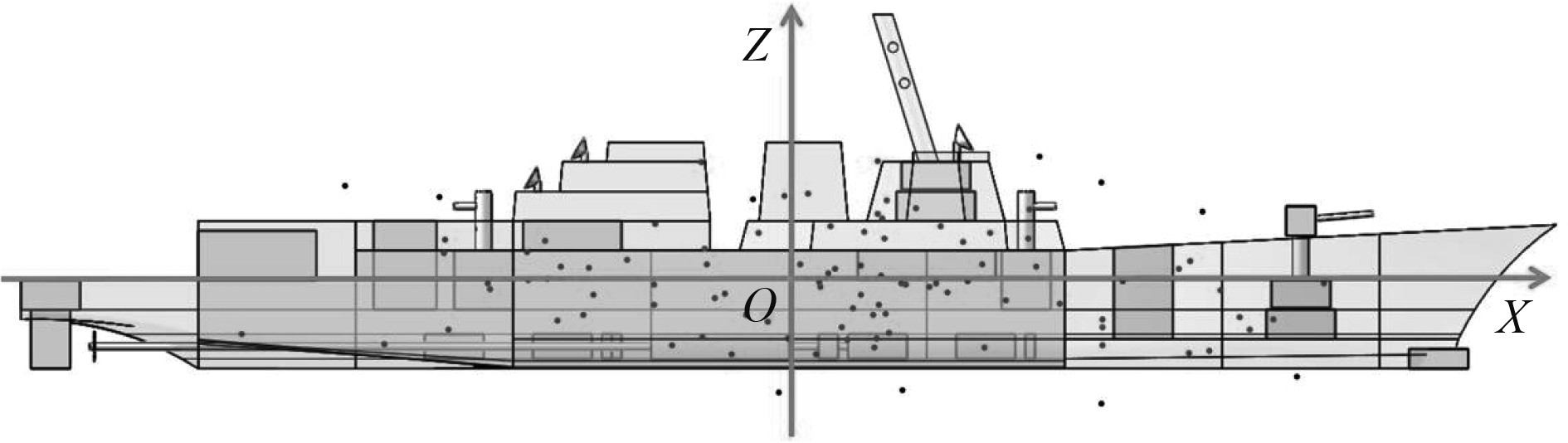
|
图 10 随机样本点生成的弹体打击分布图 Fig. 10 Distribution of projectile strikes generated from random sample points |
为了满足精度要求,进行100次独立重复试验,每次试验进行1000次模拟打击,将各个设备打击次数的平均值作为打击概率计算的依据,各个舱室及设备的平均击中概率如表1所示。
|
|
表 1 各个舱室及设备的平均击中概率 Tab.1 Average probability of hits for each chamber and equipment |
在毁伤概率计算中,
由于侵彻概率
|
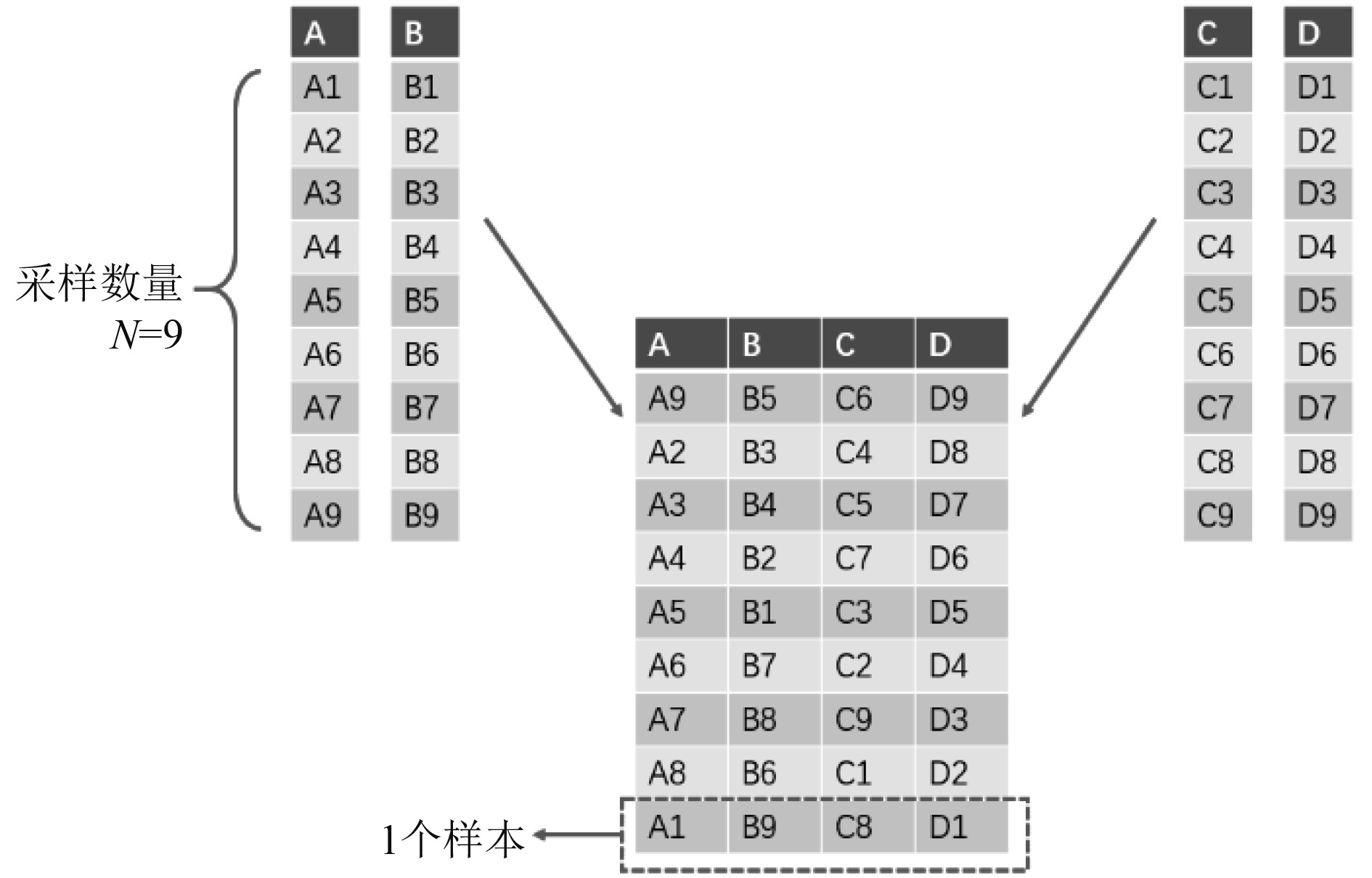
图 11 拉丁超立方抽样方法示意图 Fig. 11 Schematic diagram of the Latin hypercube sampling method |
通过拉丁超立方进行随机抽样需要进行以下几个关键步骤:
1)确定样本元素集,同时对元素集进行等概率分区;
2)从各等概率分区中随机抽取样本点;
3)将各个分区的样本点进行随机组合成一个样本;
4)重复步骤3,直到得到完整的样本集合,结束抽样。
基于拉丁超立方抽样方法进行函数有效性验证。
首先,将初速度和攻角2个参数进行分层,初速度可分为:[400,450]、[451,500]、[501,550]、[550,600]和[601,650],攻角可分为:[0°,7°]和[8°,15°]。然后从每一层随机抽取一个整数,并将初速度的值和攻角的值重新组合成一个样本。同样在Pycharm平台上进行随机样本的生成,并将有限元仿真计算结果与拟合的函数值进行对比,具体如表2所示。
|
|
表 2 仿真结果与拟合函数对比 Tab.2 Comparison between simulation results and fitting functions |
由表2可知,前3个样本点由于初速度没有达到击穿舷侧液舱的阈值,所以仿真试验的结果为负值,说明弹体无法击穿靶板而出现回弹现象。而回弹速度与拟合函数之间没有必然联系,因此在数值上不予对比。通过对其余样本点的对比,可看出仿真试验得到的剩余速度与拟合函数计算的剩余速度之间存在一定误差,但误差在工程允许范围内。因此,可将拟合函数用于计算毁伤概率的研究分析中。
4 结 语本文针对半穿甲战斗部侵彻毁伤舰船目标提出了新的毁伤概率计算公式,对该公式中的侵彻概率、弹体安定性满足要求的概率、冲击波毁伤概率和击中概率分别进行计算分析。
其中,侵彻概率计算基于弹体打击后剩余速度判断,而剩余速度的计算则通过等距抽样的方式确定计算参数。然后,基于有限元仿真结果进行函数的近似拟合,在给定的参数范围内,弹体安定性问题均满足要求。冲击波毁伤概率则通过理论公式计算得出。击中概率计算是基于蒙特卡罗法仿真模拟半穿甲战斗部对舰船目标的打击,为了满足精度要求,仿真计算进行了100次独立重复试验,每次进行1000次模拟打击,求得各个设备被击中的概率。
最后,基于拉丁超立方随机抽样的方法对毁伤概率公式中,相关参数进行有效性验证,验证结果表明拟合的函数关系与仿真结果之间的误差在工程允许的范围内,从而完成了舰船目标毁伤概率的计算分析。
| [1] |
肖元星. 计算着发射击高射武器系统毁伤概率的通用程序[J]. 火力与指挥控制, 1989, 14(4): 65-69. |
| [2] |
胡建辉, 王巨海, 姚光仑. 基于Monte-Carlo方法的弹炮结合防空武器系统毁伤概率仿真研究[J]. 军事运筹与系统工程, 2005, 19(4): 40-44. |
| [3] |
HU Jiang, WANG Wei-song, LIU Yi, et al. The computational model on damage probability of shipborne shrapnel based on Monte Carlo method[J]. Computing, Control and Industrial Engineering (CCIE), 2011 IEEE 2nd International Conference on, 2011, 1: 122–124.
|
| [4] |
戴毅, 苗育红, 周江华. 毁伤概率评估的加权蒙特卡罗方法[J]. 计算机仿真, 2008, 25(3): 115-118. DOI:10.3969/j.issn.1006-9348.2008.03.030 |
| [5] |
王云强. 舰船动力系统生命力评估方法研究及应用[D]. 大连: 大连海事大学, 2015.
|
| [6] |
杨砚世. 侵爆战斗部对航母毁伤评估方法研究[D]. 南京: 南京理工大学, 2015.
|
| [7] |
李建明, 赵富全, 张志勇. 蒙特卡罗法在部件毁伤概率计算中的应用[J]. 火炮发射与控制学报, 2003(z1): 116-118. DOI:10.3969/j.issn.1673-6524.2003.z1.033 |
| [8] |
BALL R E, CALVANO C. Establishing the fundamentals of a surface ship survivability design discipline[J]. Naval Engineers Journal. 2009, 106: 71–74.
|
| [9] |
FRANCE W , LEVADOU M, TREAKLE T, et al, 2003. An investigation of head-sea parametric rolling and its influence on container lashing systems[J]. Marine Technology Soceity Jounal, 2003(40): 1–19.
|
| [10] |
BOGDAN, SZTUROMSKI, KICIŃSKI Radosław. "Material properties of Hy 80 steel after 55 years of operation for fem Applications[J]. Material 2021, 14(15): 81–103.
|
| [11] |
KIM K, HWANG S, LEE J. Naval ship's susceptibility assessment by the probabilistic density function[J]. Journal of Computation Design and Engineering. 2014, 23: 266–271.
|
| [12] |
CHUNG J , KWON J. Survivability analysis of a vaval ship using the MOTISS program(i): theoretical background[C]//Proceedings of the Annual Autumn Meeting of Society of Naval Architects of Korea. 2008: 330–339.
|
 2023, Vol. 45
2023, Vol. 45
