2. 中国船舶集团有限公司第七二二研究所,湖北 武汉 430205
2. The 722 Research Institute of CSSC, Wuhan 430205, China
船体的分段测试以及数据处理方法是一种用于船体分段建造进行高精度检测的实用型技术,在船舶制造过程中,船舶质量的评价参数可以使用配准偏差来表示,利用配准偏差可以对船舶分段建造尺寸的修正提供理论依据[1]。由于船舶的建造工程十分复杂,因此数字化的船舶建造技术在船舶的建造过程中得到了广泛的应用,数字化的船舶建造技术能够极大地提升船舶在制造过程中的效率以及效益[2]。船舶高精度制造的基本准则是以高精度控制为核心,利用先进的工艺以及科学的管理对船舶的建造过程进行全程的高精度尺寸检测、分析以及控制[3]。传统船舶建造方法的改进是以船舶高精度的建造控制技术为基础,从当前的船舶建造管理上来看,存在主动和被动2种高精度管理[4]。高精度主动管理是指船舶在分段组装过程中,均事先设计好防止分段发生形变的措施;高精度被动管理是指船舶在组装过程中,使用全站仪等设备进行实时测试,然后利用实时测试得到的数据对产生形变的船舶分段进行控制。
1 基于计算机的船舶数字化技术 1.1 船舶组合曲线设计作为船体设计的重要成分,船型设计的好坏决定了船舶建造的优劣程度,会直接对船舶的性能计算、制造工艺以及结构设计产生影响,同时船舶开发周期也会受到船型设计效率的影响,是减少船舶建造周期的关键因素[5]。在船舶优化法以及参数设计的基础上,结合计算机技术,分析船舶的曲线特征,可以得到船体的设计参数,并且以船体的主尺度以及横剖线参数为基础,对船体进行优化设计,同时利用船体的曲线平方和生成基于NURBS曲线的船体模型[6]。基于计算机的船舶设计方法能够弥补传统船舶设计方法的缺陷,极大地提升船体的设计效率。由于直线、抛物线、圆弧以及自由曲线等类型的曲线均会出现在船体型线中,考虑到NURBS的优良特性并且引入了权因子,因此可以使用NURBS曲线对船体进行精确的描述。基于插值算法的三次NURBS曲线可以对船体的型线以及特征进行描述,公式为:
| $ P\left( u \right) = \frac{{\displaystyle\sum\limits_{i = 0}^n {{B_{i,3}}\left( u \right){W_i}{V_i}} }}{{\displaystyle\sum\limits_{i = 0}^n {{B_{i,3}}\left( u \right){W_i}} }}\text{。} $ | (1) |
式中,船体型线的三次NURBS曲线为基础,可以采用蒙皮法构建出单一的NURBS曲线,并利用该曲线来描述船体的曲面,公式为:
| $ S\left( {u,v} \right) = \frac{{\displaystyle\sum\limits_{i = 0}^n {\displaystyle\sum\limits_{j = 0}^m {{B_{i,3}}\left( u \right){B_{j,3}}\left( v \right){W_{i,j}}{V_{i,j}}} } }}{{\displaystyle\sum\limits_{i = 0}^n {\displaystyle\sum\limits_{j = 0}^m {{B_{i,3}}\left( u \right){B_{j,3}}\left( v \right){W_{i,j}}} } }}\text{。} $ | (2) |
采用船舶能量优化的方法首先需要获得船体优化的目标函数,船舶的能量物理模型主要有物理形变能量模型以及几何性质能量模型2种。物理形变能量模型可以基于薄板弹性方程得到,如下式:
| $ {E_{curve}} = \int {\left( {\alpha w'{{\left( u \right)}^2} + \beta w''{{\left( u \right)}^2} - 2fw\left( u \right)} \right){\rm{d}}u} \text{。} $ | (3) |
以船体的长度、曲率、形心以及面积为约束,构建出来的模型为几何性质能量模型,本文使用的模型为以船体曲率平方和为基础的几何性质能量模型,如下式:
| $ {E'_{curve}} = \int {{k^2}{\rm{d}}u} \text{,} $ | (4) |
| $ {E_{surface}} = \int {\left( {k_1^2 + k_2^2} \right)} {\rm{d}}u{\rm{d}}v\text{。} $ | (5) |
船舶能量优化模型中至少包含一个非线性的自变量函数,如下式:
| $ \begin{array}{*{20}{l}} {\min f\left( x \right)} \\ {{\mathrm{s.t.}}\left\{ {\begin{array}{*{20}{c}} {{c_i}\left( x \right) = 0,i \in E \in \left\{ {1,2, \cdot \cdot \cdot m} \right\}}\text{,} \\ {{c_i}\left( x \right) \leqslant 0,i \in I \in \left\{ {m + 1, \cdot \cdot \cdot P} \right\}} \text{。} \end{array}} \right.} \end{array}$ | (6) |
针对非线性规划问题,主要有二次逼近法、惩罚函数法、遗传算法等。考虑到本文使用船舶能量优化模型的规模不是特别大,并且其目标函数连续,因此能够得到高精度的梯度值。结合各类求解算法的优缺点,本文使用二次逼近法对船舶能量优化模型进行求解。这使得本文的船舶能量优化模型在解算稳定性、收敛的速度以及结果的精确度上都要比其他模型好。本文改进之后的二次逼近法如下式:
| $ {I_1} = \left\{ {i|{c_i}\left( {{x^{\left( k \right)}}} \right) \geqslant 0,i \in I} \right\}\text{,} $ | (7) |
| $ {I_2} = \left\{ {i|{c_i}\left( {{x^{\left( k \right)}}} \right) \lt 0,i \in I} \right\}\text{。} $ | (8) |
船舶在实际设计的时候,纵向特征线的设计取决于具体的船型。从附加特性来看,船舶的水线设计需要确定漂心纵向坐标等参数。这些参数确定之后,则构建出了几何约束条件,然后再对目标船舶模型进行优化。船舶的设计参数是以NURBS描述的水线为基础的,这些水线包括面积、型点、曲率以及形心等约束条件。为了能够得到光顺的曲线,需要将曲线的曲率均匀变化添加到约束条件中。船舶曲线包围的面积的解算方法和水线面积的计算方法如下式:
| $ S = \int_0^1 {\left[ {y\left( u \right)\frac{{{\rm{d}}x}}{{{\rm{d}}u}}} \right]{\rm{d}}u} \text{,} $ | (9) |
| $ {A_w} = 2S\text{。} $ | (10) |
船舶曲线中心坐标的计算方法如下式
| $ {x_c} = \frac{{\displaystyle\int_0^1 {x\left( u \right)y\left( u \right)\dfrac{{{\rm{d}}x}}{{{\rm{d}}u}}{\rm{d}}u} }}{S}\text{,} $ | (11) |
| $ {y_c} = \frac{{\displaystyle\int_0^1 {y{{\left( u \right)}^2}\dfrac{{{\rm{d}}x}}{{{\rm{d}}u}}{\rm{d}}u} }}{{2S}}\text{。} $ | (12) |
船舶曲线导数的计算方法如下式:
| $ k\left( u \right) = \frac{{{\rm{d}}y\left( u \right)}}{{{\rm{d}}x\left( u \right)}}\text{,} $ | (13) |
船舶曲线曲率的计算方法如下式:
| $ k'\left( u \right) = \dfrac{{\left| {\dfrac{{{{\rm{d}}^2}y}}{{{\rm{d}}{u^2}}}\dfrac{{{\rm{d}}x}}{{{\rm{d}}u}} - \dfrac{{{{\rm{d}}^2}x}}{{{\rm{d}}{u^2}}}\dfrac{{{\rm{d}}y}}{{{\rm{d}}u}}} \right|}}{{{{\left[ {{{\left( {\dfrac{{{\rm{d}}x}}{{{\rm{d}}u}}} \right)}^2} + {{\left( {\dfrac{{{\rm{d}}y}}{{{\rm{d}}u}}} \right)}^2}} \right]}^{\frac{3}{2}}}}}\text{。} $ | (14) |
将船舶曲率跃度的平方和作为船舶设计的约束条件,船舶曲线上的点的曲率跃度的表示方法如下式:
| $ {d_i} = \left| {\frac{{{k_{i + 2}} - {k_{i + 1}}}}{{{l_{i + 1}}}} - \frac{{{k_{i + 1}} - {k_i}}}{{{l_i}}}} \right|\text{。} $ | (15) |
全站仪能够对斜距、高差以及平距等参数进行测量,因此全站仪测试系统集合了电子测距以及经纬仪的特点。全站仪测试系统结构如图1所示,可以看出,测距、测角以及补偿三部分是全站仪的核心部件,全站仪的测试原理为,以电子测距以及电子测角为基础,然后结合计算机计算出三维数据。随着微电子以及光电技术的进一步发展,全站仪的精度以及智能化获得了进一步提升,因此全站仪在船舶分段测量中得到了广泛的应用。

|
图 1 全站仪结构图 Fig. 1 Structure diagram of total station |
电子测距是以电磁波的传播速度恒定为基础的,电子测距是通过测量电磁波的往返时间来求解测量距离的,其计算方法如下式:
| $ D = \frac{\lambda }{2}\left( {N + \Delta N} \right)\text{。} $ | (16) |
式中:λ/2为测尺距离;N为整波数;ΔN为非整波数。在实际测量过程中,电磁波由于频率波长不一样,同时也会受到环境湿度、温度以及灰尘的影响,并进一步对测量距离产生影响,调整之后的距离测量方法如下式:
| $ \Delta D = \frac{{{c_0} \cdot \Delta t}}{{2{n_{REF}}}}\left( {\frac{{{n_{REF}} - n}}{n}} \right)\text{。} $ | (17) |
利用双轴补偿装置,全站仪能够对垂向轴在水平轴以及视准轴上的2个倾斜分量进行测量。水平轴上的倾斜分量的计算方法如下式:
| $ H{Z_k} = H{Z_0} + \frac{C}{{\sin {V_k}}} + \delta \frac{{\sin \theta }}{{\tan {V_k}}} + \frac{K}{{\tan {V_k}}}\text{。} $ | (18) |
式中:HZk为水平方向上的读数;C为视准误差;K为水平轴误差。垂直方向上的倾斜分量计算方法如下式:
| $ {V_k} = {V_0} + i + \delta \cos \theta \text{。} $ | (19) |
船舶目标模型的测量数据和相应工艺模型数据之间的刚性匹配即为对自由位姿的求解,对最优关联矩阵v的搜寻过程即为解算过程,其目的是为了能够获得最佳的配准位姿。利用ICP算法可以构建出点到曲面距离的最小二乘模型,如下式:
| $ f\left( v \right) = \min \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{d_i}\left( v \right)} \right)}^2}} \text{。} $ | (20) |
由于点到曲面的距离是一个概率性问题,因此可以使用MCC构造出最大熵函数,可以从一定程度上减少粗差对配准精度造成的影响。通过MCC构建出的最大熵的配准模型如下式:
| $ {f_*}(v) = \arg \max \frac{1}{N}{\sum\limits_{i = 1}^N {\exp \left( { - \frac{{\left( {R\left( v \right){p_i} + t\left( v \right) - {q_i}} \right) \cdot {n_i}}}{{2{\sigma ^2}}}} \right)} ^2}\text{。} $ | (21) |
为了能够更加形象的对不同配准算法的误差结果进行对比,图2给出了配准之后的正确配准率的曲线,即在不同距离下配准点的数量占总数量的百分比。可以看出,熵函数法的配准精度比ICP法的配准精度要高很多,因此熵函数法能够得到更多的对应点,进一步说明熵函数法可以将粗差配准的权重进行降低,抑制粗差对配准精度的影响。

|
图 2 不同距离下的配准率 Fig. 2 Registration rates at different distances |
本文对船体进行分段测试以及分段调姿,因此以多信息理论和遗传算法为基础对船舶分段测试数据进行处理,以确保船舶分段测试数据的收敛性以及正确性,非线性系统如下式:
| $ y\left( {k + 1} \right) = \frac{{x\left( {k + 1} \right)}}{{\sqrt {0.1 + 0.9{{\left[ {x\left( {k + 1} \right)} \right]}^2}} }} + e\left( {k + 1} \right)\text{。} $ | (22) |
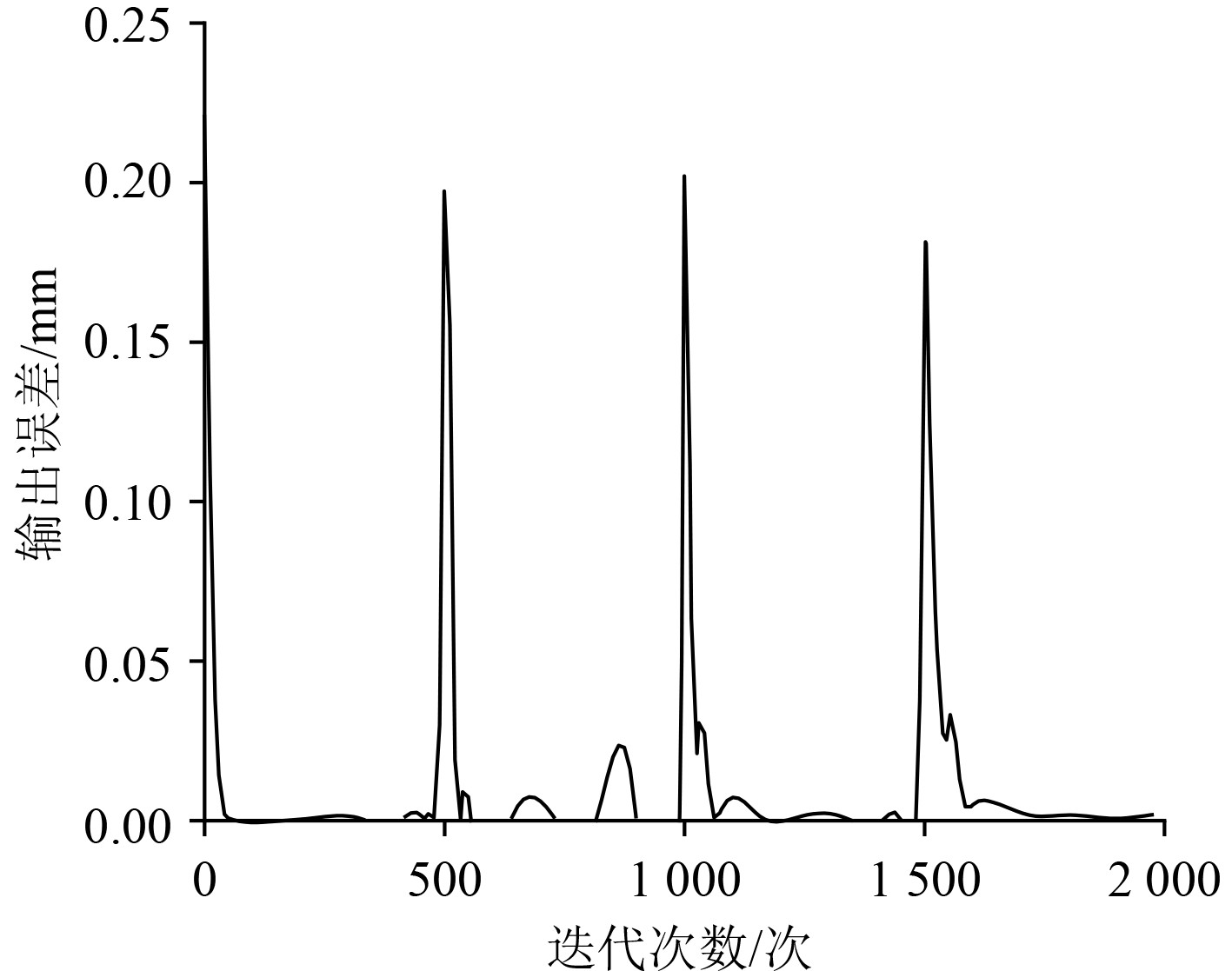
式中:e(k+1)为高斯白噪声,本文使用的以遗传算法为基础的多信息模型数据处理方法中,遗传代数设置成20,则得到的数据输出结果和数据误差的曲线分别如图3和图4所示。

|
图 3 数据处理结果曲线 Fig. 3 Data processing result curve |
|
图 4 数据处理误差曲线 Fig. 4 Data processing error curve |
可以看出,本文提出的以多信息理论模型为基础的、以遗传算法为优化方法的非线性数据处理方法,有利于提升收敛速度,并且能够使得控制参数实现自适应修正,极大地降低了船舶数据测量对人为参数的依赖性,表明本文提出的多信息模型数据处理方法比标准模型处理方法拥有更快的收敛性。
本文提出的多信息模型数据处理方法可以和PID神经网络算法结合起来使用,其非线性数据处理系统可以表示为:
| $ y\left( t \right) = 0.4y(t - 1) + 0.54y(t - 2) + f[u(k - 1)]\text{,} $ | (23) |
| $ u\left( t \right) = 0.2\sin \frac{{2{\text π} t}}{{25}} + 0.3\sin \frac{{{\text π} t}}{{75}}\text{。} $ | (24) |
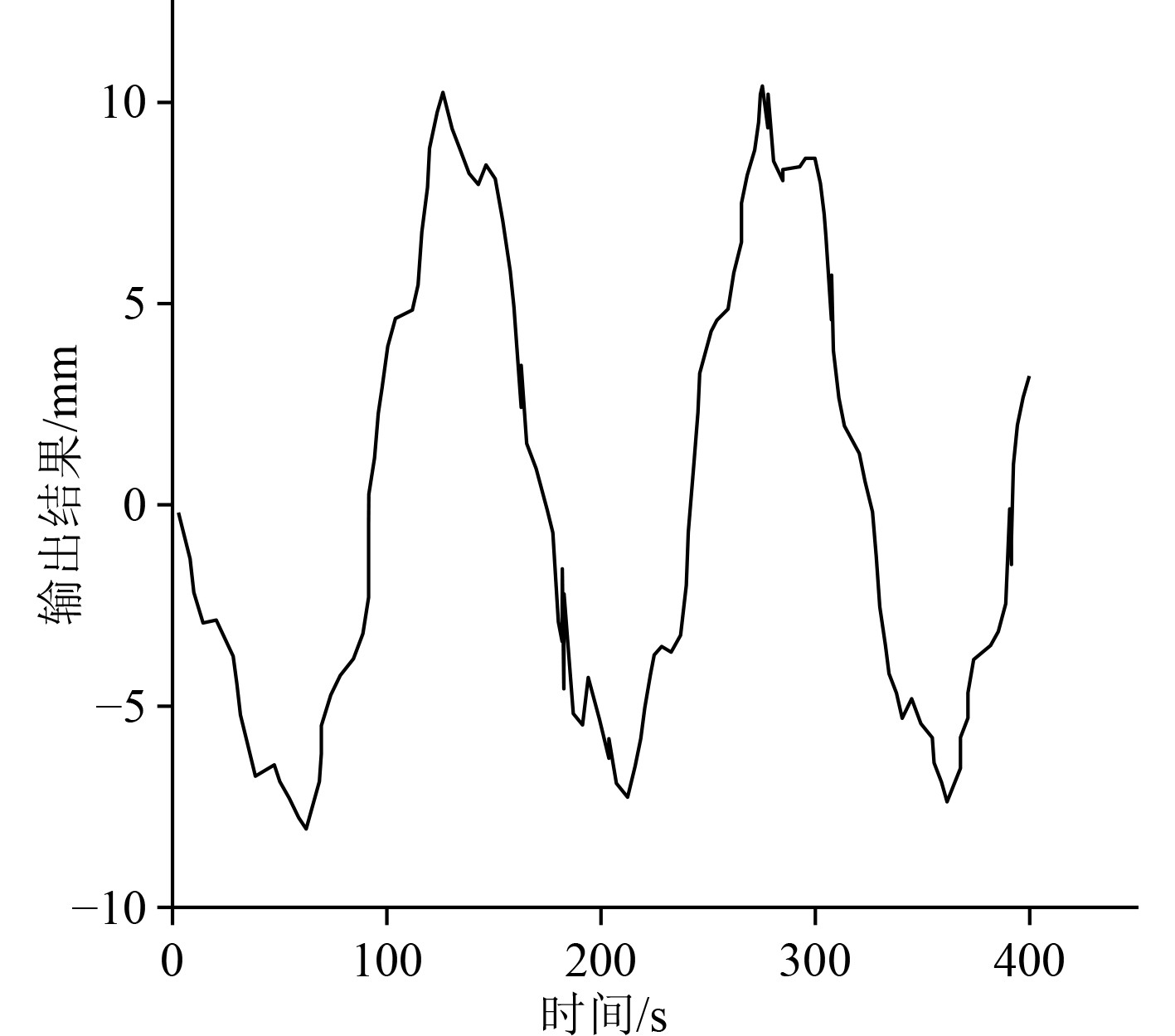
本文使用梯度法进行网格划分,学习效率设置为0.175,学习训练20步之后的数据处理结果如图5所示。
|
图 5 结合PID神经网络算法的数据处理结果 Fig. 5 Data processing results combined with PID neural network algorithm |
可以看出,结合PID神经网络算法之后,本文提出的非线性数据处理方法在拐点处的震荡次数降低、振幅减小。
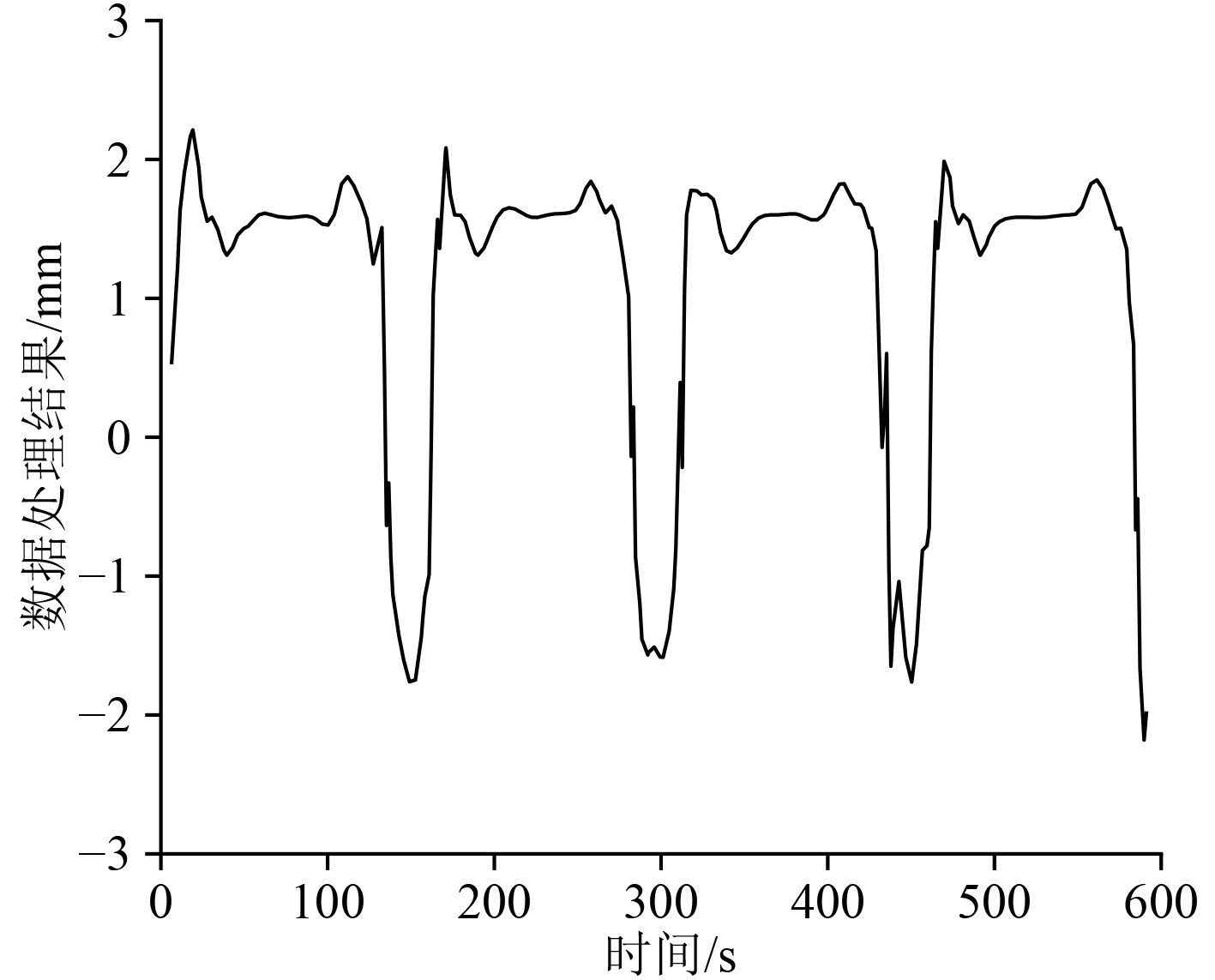
将学习效率改成0.015之后,得到的数据处理结果如图6所示。
|
图 6 高阶非线性数据处理结果 Fig. 6 High order nonlinear data processing results |
采用高阶非线性处理方法,如下式(25)可以看出,使用本文提出的数据处理方法,其震荡的次数以及幅值均在合理范围内,体现出了强大的数据处理能力。
| $ y\left( {t + 1} \right) = f\left[ {y\left( t \right)} \right] + g\left[ {u\left( k \right)} \right]\text{,} $ | (25) |
| $ f\left[ {y\left( t \right)} \right] = \frac{{5y\left( t \right)}}{{2.5 + {y^2}\left( t \right)}}\text{。} $ | (26) |
对船舶进行分段测试的目标是为了能够得到船舶在分段制造过程中产生的尺度误差,以便可以实时精确地对船舶在分段建造过程中的精度情况进行监测,船舶在分段建造过程中的精度会对船体建造的质量产生直接的影响,因此对提升船舶钢材的利用率、减少船舶的建造成本,提升船舶的建造效率、减少船舶的建造周期有着十分重要的意义。
| [1] |
黄晓翔, 吕丽平. 船体外形分段测量数据配准技术优化研究与应用[J]. 舰船科学技术, 2021, 43(6): 28-30. HUANG Xiao-xiang, LV Li-ping. Optimization research and application of data registration technology for hull shape sectional measurement[J]. Ship Science and Technology, 2021, 43(6): 28-30. |
| [2] |
姚明君, 谢菊芳, 王浩君, 等. 基于PLC的船体分段合拢控制系统分析与设计[J]. 湖北大学学报, 2013(35): 79-84. YAO Ming-jun, XIE Ju-fang, WANG Hao-jun et al. Analysis and design of automation assembling system of large ship subsection based on PLC[J]. Journal of Hubei University, 2013(35): 79-84. |
| [3] |
汪浩, 裴大茗, 王爱民等. 基于虚拟流水的多重约束环境下船体分段车间动态调度[J]. 船舶工程, 2019, 43(41): 128-137. WANG Hao, PEI Da-ming, WANG Ai-ming et al. Ship block dynamic scheduling under multi-constraints based on virtual flow[J]. Ship Engineering, 2019, 43(41): 128-137. |
| [4] |
李瑞, 张小明, 张帆等. 计算机辅助船体分段吊装强度计算方法及系统开发[J]. 船舶工程, 2014(36): 162-165. LI Rui, ZHANG Xiao-ming, ZHANG Fan et al. Strength calculation method and system development of computer aided ship block lifting[J]. Ship Engineering, 2014(36): 162-165. |
| [5] |
任晋宇, 徐得志, 吴亮等. 舰艇典型分段焊接工艺仿真及其变形规律分析[J]. 船舶工程, 2020(42): 100-106. REN Jin-yu, XU De-zhi, WU liang et al. Typical subsection welding process simulation and deformation law of naval vessel[J]. Ship Engineering, 2020(42): 100-106. |
| [6] |
管官, 林焰, 申玫等. 考虑工程约束的船体分段测量点集匹配方法[J]. 哈尔滨工程大学学报, 2013(34): 541-548. GUAN Guan, LIN Yan, SHEN Mei et al. Point registration algorithm for hull block measurement with engineering constraints[J]. Journal of Harbin Engineering University, 2013(34): 541-548. |
 2023, Vol. 45
2023, Vol. 45
