随着各类检测技术的发展,水污染、噪声污染以及空气污染等问题不断得到控制。从船舶的角度来看,船舶不仅要具备安全性以及快速性,还必须要具备很好的舒适性[1]。船舶上层建筑的噪声以及振动问题会使得船体出现声振疲劳而受到破坏,还会对船舶上层建筑舱室中的各类设备以及仪器的正常使用产生影响,甚至会对船员的健康产生一定影响[2]。考虑到船舶上层建筑的噪声以及振动等问题造成的严重后果,国际海事组织对噪声的极限值进行了规定,例如船舶上层建筑中的居住舱以及医疗舱等舱室的最大噪声为60 dB,而船舶上层建筑中的驾驶舱以及办公舱等最大噪声为65 dB[3]。对于已建造完毕的船舶进行降噪以及降振动处理,则费用较高并且只能解决部分问题,如果在船舶的建造设计初期对船舶上层建筑中的各个舱室进行噪声以及振动等问题的预测,则可提前对有问题的部分进行减震、降噪处理,这样不但可实现降噪的目的,还能减少造船周期以及造船的成本[4]。
1 非线性回归预测技术 1.1 非线性模型理论支持向量机能够对各种函数进行集中构造,通常情况下也不需要微调,只需进行简单的优化即可[5]。核函数主要有线性、多项式、径向以及两层感知器4种,其数学模型分别如下:
| $ K\left( {x,{x_i}} \right) = {x^T}{x_i}\text{,} $ | (1) |
| $ G\left( {x,{x_i}} \right) = {\left( {{\gamma _i}{x^T}{x_i} + r} \right)^p},\gamma \gt 0\text{,} $ | (2) |
| $ F\left( {x,{x_i}} \right) = \exp \left( { - \gamma ||x - {x_i}|{|^2}} \right),\gamma \gt 0\text{,} $ | (3) |
| $ H\left( {x,{x_i}} \right) = \tanh \left( {\gamma {x^T}{x_i} + r} \right)\text{。} $ | (4) |
支持向量机的功能十分强大,其在处理问题时,存在一个输入以及一个输出,可使用一个映射函数来表示,如下式:
| $ y = f\left( x \right)\text{。} $ | (5) |
在构建预测模型之前,首先需要根据训练集中的x以及y来构造回归模型。支持向量机在进行预测的过程中,能够对输入量和输出量进行自动识别,并且能够通过输入量和输出量之间的关系进行输出量的预测[6]。使用支持向量回归方法可将误差降到最低,如下式:
| $ R\left( \omega \right) = \int {L\left( {y,f\left( {x,\omega } \right)} \right){\rm{d}}F\left( {x,y} \right)} \text{。} $ | (6) |
式中:L(y,f(x,ω))为损失函数,通过损失函数可以对损失程度进行评估;f(x,ω)为一系列含有预测功能的函数,可用来对输出数据Y进行预测;ω为广义系数。在实际情况下,最小的R(ω)数据很难获得,因此通常基于经验风险最小化原则获得近似最小值,其数学模型如下式:
| $ {R_{ERM}}\left( w \right) = \frac{1}{l}\sum\nolimits_{i = 1}^{i = N} {L\left( {{y_i},f\left( {{x_i},y} \right)} \right)} \text{。} $ | (7) |
式中:xi为输入量;yi为期望输出值。当遇到线性判断式无法对数据进行训练的情况,则需将数据映射到高维空间,结合粒子群算法则可获得PSO-SVM模型,其适应度曲线如图1所示。从图1可看出,适应度曲线一开始迅速增大,然后呈现平稳状态。
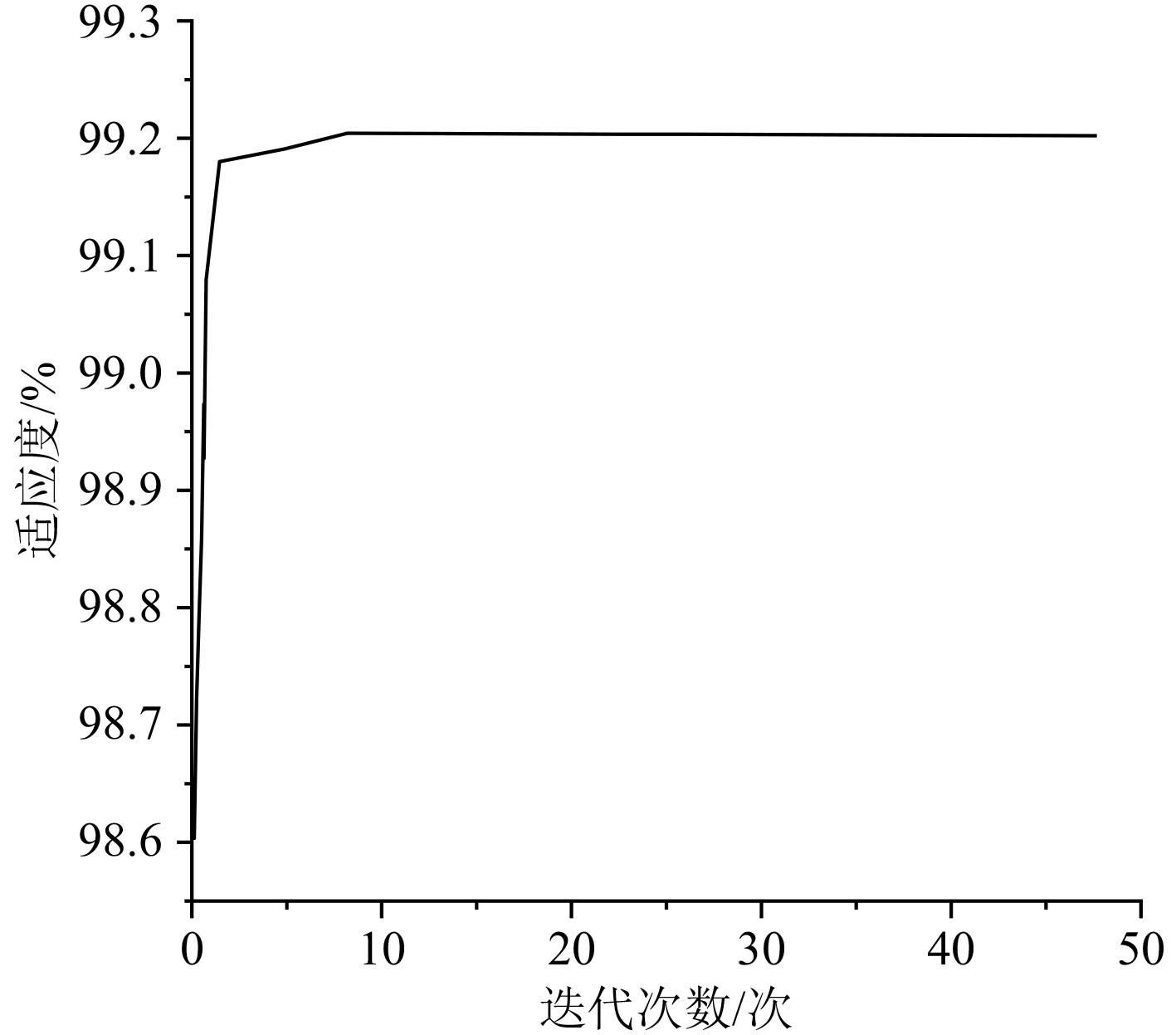
|
图 1 基于粒子群算法的适应度曲线 Fig. 1 Fitness curve based on particle swarm optimization algorithm |
根据非线性回归预测模型的特征,本文构造出一个多输入、单输出以及3层处理结构的多元非线性回归预测模型,如图2所示。图中xp为自变量,y为因变量,fp(xp)为给定函数族构成的函数。从图2可看出,多元非线性回归预测模型是由多个一元非线性函数构成的,因此使用多个一元非线性函数可近似表示多元非线性预测模型,其数学模型如下式:

|
图 2 多元非线性回归预测模型 Fig. 2 Multiple nonlinear regression prediction model |
| $ g = \sum\limits_{l = 1}^p {{c_l}} \sum\limits_{i = 1}^n {{f_{li}}\left( {{x_l}} \right)} \text{。} $ | (8) |
多元非线性回归预测模型在进行结果预测之前,需要一组给定的样本。使用简单并且收敛速度快的最小二乘法,可迅速获得多元非线性回归预测模型的相关参数。
| $ \begin{split} &\left\{ {\left( {{X^{\left( k \right)}},{y^{\left( k \right)}}} \right)|k = 1,2,...,q} \right\} \text{,} \\ &{X^{\left( k \right)}} = \left\{ {x_1^{\left( k \right)},x_2^{\left( k \right)},...,x_p^{\left( k \right)}} \right\} \text{。} \end{split} $ | (9) |
实验值和预测值之间的相关系数r以及标准误差σ,通常作为模型的评估指标,对预测模型的有效性及适应性进行检验。相关系数越大,标准误差越小,则表明模型的预测精度越高。
2 船舶上层建筑结构分析 2.1 船舶尺寸结构分析本文研究的船舶使用的是纵骨架单底结构,船体宽度为18.94 m,长度为68 m,吃水深度为3 m,船型深度为9 m。船体上的肋板采用实肋板,该肋板的纵剖面高度、厚度以及面积的计算方法如下式:
| $ h = 42 \times \left( {B + d} \right) - 70\text{,} $ | (10) |
| $ t = 0.001h + 3\text{,} $ | (11) |
| $ A = \left( {4.8d - 3} \right) \times 100\text{。} $ | (12) |
船体内龙骨腹板的厚度以及剖面积的计算方法分别如下式:
| $ t' = 0.06L + 6.2\text{,} $ | (13) |
| $ A' = \left( {0.65L + 2} \right) \times 100\text{,} $ | (14) |
船体结构中的旁内龙骨高度和肋板高度一致,并且旁内龙骨的厚度以及剖面积的计算公式分别如下式:
| $ t'' = 0.05L + 5\text{,} $ | (15) |
| $ A'' = \left( {0.25L} \right) \times 100\text{。} $ | (16) |
船底纵骨之间的最大距离为1 m,其剖面模数的计算方法如下式:
| $ W = \left[ {\frac{{8.5f}}{{17.3 - {F_b}}}\left( {d + {h_1}} \right)s{l^2}} \right] \times {10^{ - 6}}\text{。} $ | (17) |
式中:s为纵骨之间的距离;d为船体吃水的深度;f为常系数;Fb为衰减系数。船体舷侧的纵骨剖面模数的计算方法如下式:
| $ W' = \frac{{8.5 \times {{10}^{ - 6}}}}{f}ns{l^2}\text{。} $ | (18) |
图3给出了龙骨不同位置受到的应力变化情况。可看出,龙骨在3 m处受到的应力最大。

|
图 3 不同距离下龙骨受到的应力变化曲线 Fig. 3 Stress variation curve of keel under different distances |
利用CDM的渐进损伤分析方法对船舶上层建筑的三维有限元模型进行构建,并对船体在单向压缩载荷影响下的承载力、损伤扩展等因素进行分析。为能确保解算的精度,对船体模型开孔区域的网格进行细化,同时船体流场使用六面体的网格,并且确保船体的网格质量高于0.45。由于船体上层建筑的边界对解算精度存在一定影响,因此船体壁面使用边界层网格,其壁面的网格厚度计算如下式:
| $ {y^ + } = \rho {u_t}\frac{y}{\mu }\text{,} $ | (19) |
最终得到载荷曲线,如图4所示。可看出,船体最大的单向压缩载荷为36.06 kN。
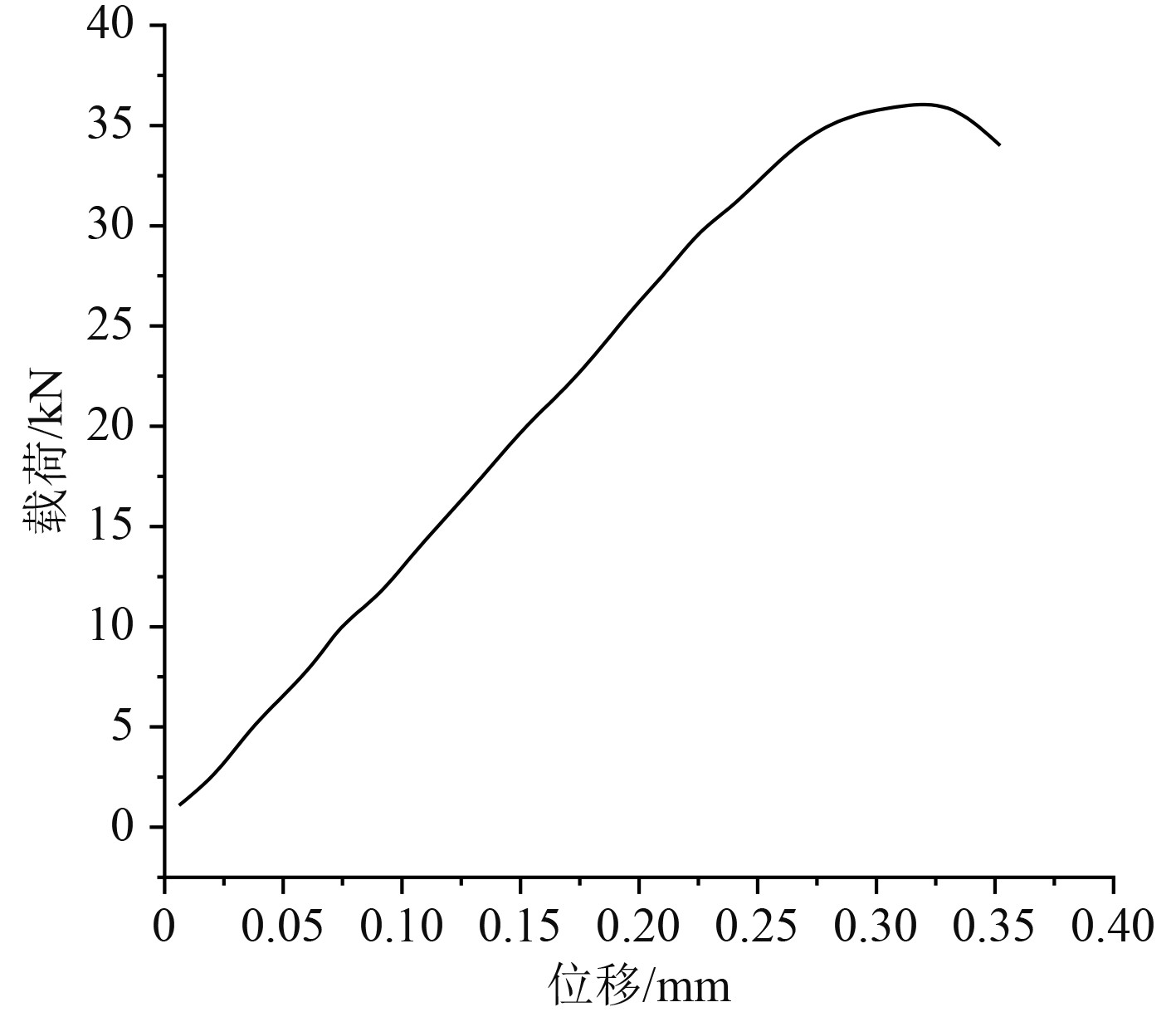
|
图 4 船体单向压缩载荷曲线 Fig. 4 Hull unidirectional compression load curve |
为能更好地对船体上层建筑中的流场压力分布进行分析,将船体上层建筑受到的风载压力进行归一化处理,并且将船体上层建筑和中心线之间的夹角定义为周向角,船体上层建筑的平均压力系数的计算方法如下式:
| $ {C_p} = \frac{p}{{\dfrac{1}{2}\rho {v^2}}}\text{,} $ | (20) |
为了简化处理,直接提取船体上层建筑中相邻甲板高度一致方向上的风载压力,同时以船体的轴向角作为横坐标,得到的平均压力随相对角的变化曲线如图5所示。可看出,相对角度小于35°或大于325°时,船体受到的平均压力较大。
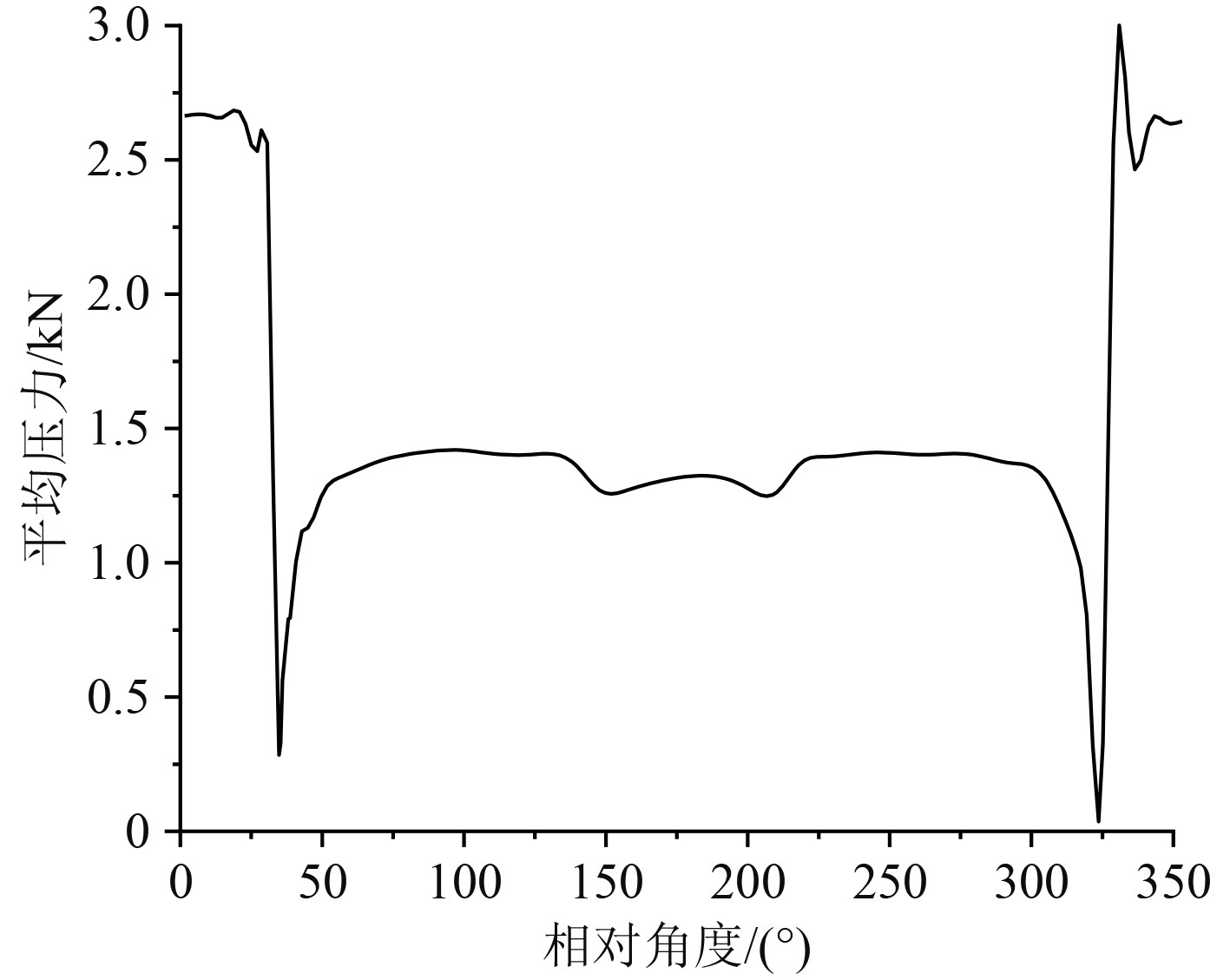
|
图 5 平均压力在不同相对角度下的变化曲线 Fig. 5 The variation curve of average pressure at different relative angles |
船舶上层建筑经常受到甲板上海浪的砰击,尤其是纵摇状态下的船体。船体上层建筑受到的海浪砰击载荷的处理方法如下式:
| $ p = 9.81\Delta \text{,} $ | (21) |
| $ \Delta = 0.01\left[ {1 + 2\left( {\frac{X}{L}} \right) + 8{{\left( {\frac{X}{L}} \right)}^2}} \right] \cdot \frac{L}{{\sqrt {{h_f}} }}\text{。} $ | (22) |
本文基于SVM非线性回归预测方法,对船舶上层建筑的振动噪声进行预测。所采用的拟合数学模型为sin函数,随机噪声的数学模型如下式:
| $ \bar y\left( x \right) = y\left( x \right) + \delta \text{。} $ | (23) |
式中,δ为随机噪声,该随机噪声符合正态分布。产生100个样本,一部分样本进行训练,另一部分则用于预测。训练样本采用样本集(x,y),并且测试样本不包含噪声。支持向量机使用RBF核函数作为内核,则仿真结果如图6所示。
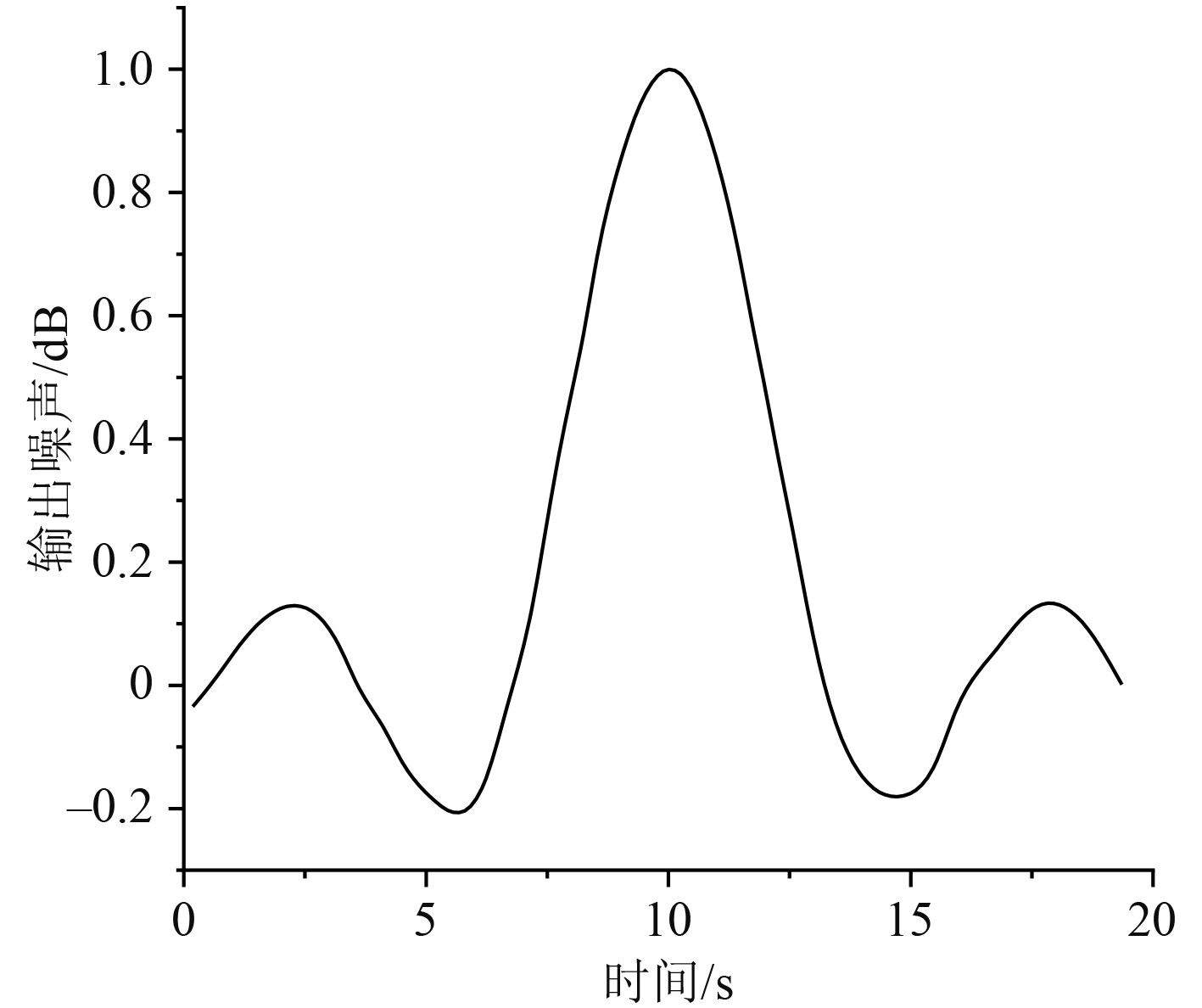
|
图 6 sin函数仿真曲线图 Fig. 6 Function sin simulation curve |
从图6可看出,拟合数学模型sin函数的仿真结果比较理想,因此本文提出的基于支持向量机的非线性回归方程在一维时可以正常使用。
在实际处理船体上层建筑预报问题的时候,其输入空间通常是多维的,同时可获得的数据量是很有限的[7]。输入数据的分布空间十分稀疏,并且包含了大量噪声,本文为了能够使用支持向量机处理这些问题,则采用二维非线性回归函数,其数学模型如下式:
| $ u = \cos \left( {{\text π} {x_1}} \right)\sin \left( {{\text π} {x_2}} \right)\text{,} $ | (24) |
利用不一样的样本数量以及噪声逼近函数,对船体上层建筑进行预报。
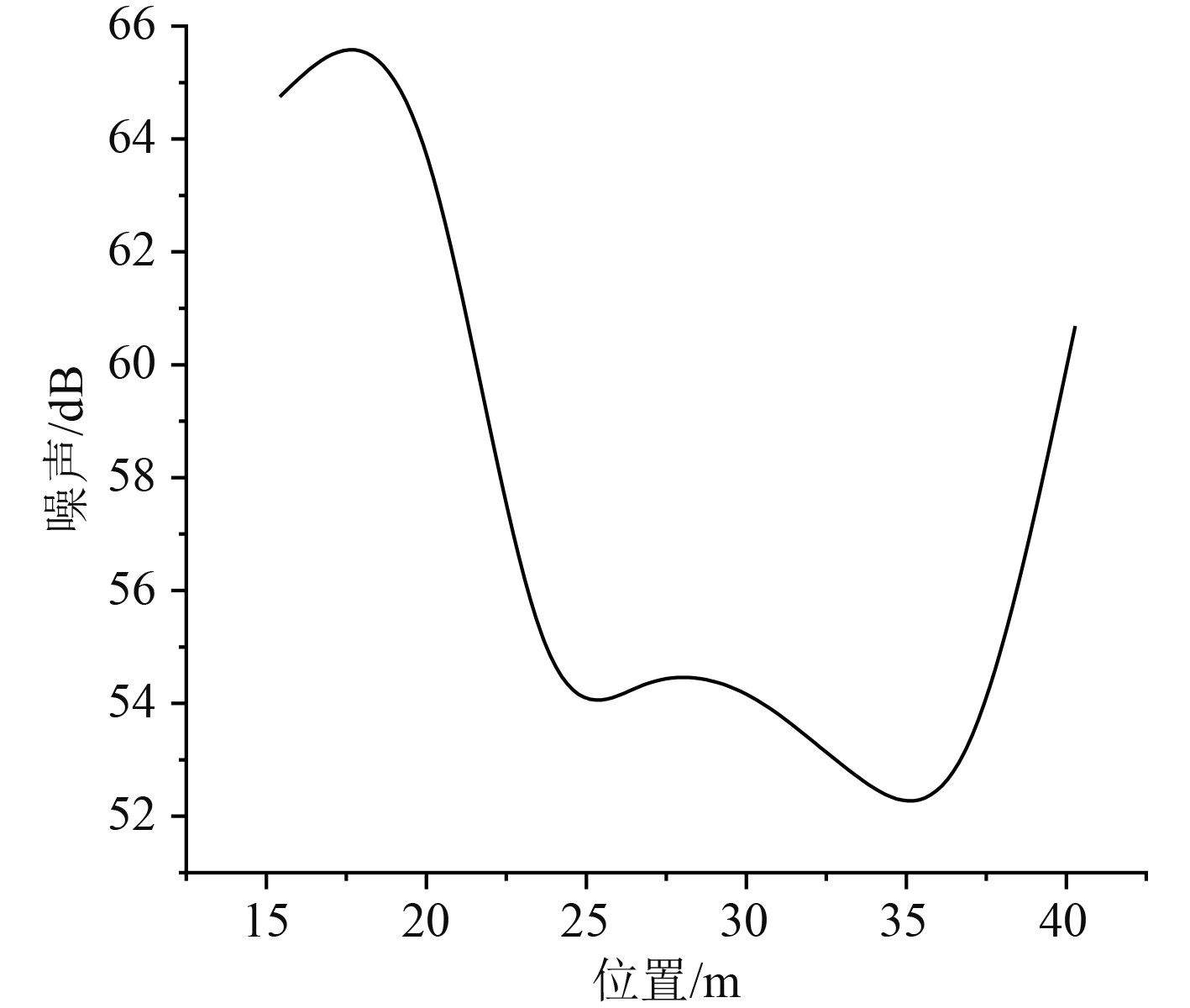
在9×9、7×7个样本点数中添加噪声,同时使用21×21个样本点数用作样本集的检测,这样能对预报的效果进行验证。在建筑进行预报过程中,对船体上层建筑舱室的生成特征参数进行了一定的选取,在空间尺寸上,选择船舶舱室的最大宽度;在声源位置上,选择每个舱室甲板和主机基座之间的垂向距离。得到船舶甲板噪声随距离的变化曲线如图7所示。从图7可看出,在船舶甲板中心位置噪声最小,距离中心越远,噪声越大。
|
图 7 船舶甲板噪声随距离的变化曲线 Fig. 7 Curve of ship deck noise with distance |
船舶建造技术的提升,使得船体结构变得更加轻盈,船体刚度也变得更小,因此船体变得更加容易振动。船舶上层建筑的振动以及噪声过大,会导致船体损害以及各类仪表设备的失灵。由于船舶上层建筑通常布置在船体的尾部,因此船舶上层建筑受到的振动以及噪声的影响主要来自推进轴和螺旋桨两方面,同时船舶上层建筑刚度的降低,又进一步加剧了船体上层建筑的振动。这使得船舶的振动以及噪声作为船舶建造质量的标准之一,受到极大关注。本文借助非线性回归预测技术,预测船舶上层建筑的振动噪声。
| [1] |
姚熊亮, 张林根, 程明亮等. 基于SVM的船舶上层建筑舱室噪声预报方法[J]. 振动与冲击, 2009(28): 85-89. |
| [2] |
姚熊亮, 张宜群, 厉艳才. 基于SVM的大型集装箱船上层建筑振动预测方法[J]. 中国造船, 2008(49): 36-44. |
| [3] |
陈影玉, 索永峰, 杨神化. 基于灰狼优化支持向量回归的船舶航迹预测[J]. 上海海事大学学报, 2021(42): 20-25+46. |
| [4] |
孟凡明, 姚熊亮, 高晓琴等. 基于灰色支持向量机的大型集装箱船上层建筑舱室的噪声预测[J]. 中国舰船研究, 2008(3): 30-33. |
| [5] |
殷玉梅, 赵德有, 崔洪宇等. 基于支持向量机的船舶上层建筑纵向振动特性预报[J]. 中国造船, 2011(52): 115-121. |
| [6] |
张建霞, 许乐平, 何建海. 化学品船运事故分析及其预测模型研究[J]. 安全与环境学报, 2013(13): 276-279. |
| [7] |
孙怡然, 陈伟民, 杜云龙. 基于算法模型的肥大型船艉流场评估方法[J]. 上海传播运输科学研究所学报, 2023(46): 1-7. |
 2023, Vol. 45
2023, Vol. 45
