0 引　言

在海上交通中，航线规划直接影响到船舶的运输效率、运营成本以及海洋环境保护等多个方面^[1−2]。特别是在海上交通高峰期间，由于船舶数量和运输需求的增加，如何合理地规划航线以避免碰撞、减少交通拥堵以及降低环境污染等问题变得尤为重要^[3]。因此，相关学者对海上交通高峰航线船舶疏导路径规划进行仿真分析，为实际航线规划提供有效的决策支持。宁君等^[4]提出改进随机搜索树（Rapidly Exploring Random Tree，RRT）算法的路径规划方法，该方法利用神经网络改进RRT，分析船舶动力学特性，以疏导时间最少作为目标函数，经过模型训练得出最优船舶疏导路径。黄国良等^[5]提出改进蚁群算法的路径规划方法，通过势场函数优化蚁群算法的船舶疏导路径寻优能力，以疏导路径最短作为目标函数，经计算得出最优的船舶疏导路径。上述2种方法因在模型寻优的过程中计算量比较复杂，耗时较长，导致船舶疏导路径规划效果不佳。

针对上述方法的局限性，通过仿真模型来模拟高峰期间的海上交通情况，并利用改进混合遗传算法对船舶疏导路径实施规划和优化，有效地为海上交通管理部门和运营机构提供有益的参考和帮助。

1 海上交通高峰航线船舶疏导路径规划仿真 1.1 海上交通高峰航线船舶疏导路径规划问题描述

海上交通高峰航线船舶疏导路径规划问题是在海图上搜索到最佳航路^[6]，实现海上交通高峰航线船舶疏导，解决海上交通高峰航线拥堵的问题。设置A、B分别代表船舶终点、起点，海上交通高峰航线中船舶设置为障碍物，从A到B需要避开海上交通高峰航线中船舶的航线。将该问题转化为数学模型，构建以航程、安全性、平滑性最小为目标函数，该目标函数表达式如下：

$ \left\{\begin{gathered}\min f_1\left(Q\right)=length\left(Q\right)\text{，} \\ \min f_2\left(Q\right)=safety\left(Q\right)\text{，} \\ \min f_3\left(Q\right)=smoothness\left(Q\right)\text{。} \\ \end{gathered}\right. $

(1)

式中：Q为一条疏导路径；length(Q)为疏导路径Q的航程描述；safety(Q)为疏导路径Q的安全性；smoothless(Q)为疏导路径Q的平滑性。

疏导路径Q上第 $ i $ 个疏导路径点用k_i描述，其坐标是 $ \left( {{x_i},{y_i}} \right) $ ，疏导路径Q为：

$ Q = \left[ {A = {k_0},{k_1},{k_2}, \cdots ,{k_n},{k_{n + 1}} = B} \right] \text{。}$

(2)

式中： $ {k_0} $ 描述疏导路径起点A； $ {k_{n + 1}} $ 描述疏导路径起点B。

疏导路径Q的航程length(Q)求解公式如下：

$ length\left( Q \right) = \sum\limits_{i = 1}^n {dis\left( {{k_i},{k_{i + 1}}} \right)}\text{，} $

(3)

$ dis\left( {{k_i},{k_{i + 1}}} \right) = \sqrt {{{\left( {{x_i} - {x_{i + 1}}} \right)}^2} + {{\left( {{y_i} - {y_{i + 1}}} \right)}^2}} \text{。}$

(4)

式中：疏导路径点 $ {k_i} $ 和疏导路径点 $ {k_{i + 1}} $ 直线距离用 $ dis\left( {{k_i},{k_{i + 1}}} \right) $ 描述。

疏导路径Q的安全性safety(Q)计算公式为：

$ safety\left( Q \right) = - \mathop {\min }\limits_{0 \leqslant i \leqslant n} \mathop {\min }\limits_{0 \leqslant j \leqslant m} \left\{ {MinDis\left( {\overline {{k_i}{k_{i + I}}} ,{G_j}} \right)} \right\}\text{。} $

(5)

式中： $ {G_j}\left( j = 1,2, \ldots ,m \right) $ 描述第 $ j $ 个障碍物即海上交通高峰航线船舶； $ {k_i}{k_{i + I}} $ 描述航段； $ MinDis\left( {\overline {{k_i}{k_{i + I}}} ,{G_j}} \right) $ 描述 $ {G_j} $ 与 $ {k_i}{k_{i + I}} $ 最短距离。

$ smoothness\left( Q \right) = \left( {1/n} \right)\sum\limits_{i = 0}^{n - 1} {\left( {\varepsilon \left[ {{k_i},{k_{i + 1}},{k_{i + 1}}} \right]} \right)} \text{。}$

(6)

$ \begin{split} & \varepsilon[k_i,k_{i+1},k_{i+1}]={\text π}-\cos^{-1} \\ & \left[\frac{(y_{i+1}-y_i)(y_{i+2}-y_{i+1})}{dis\left(k_i,k_{i+1}\right)dis(k_{i+1},k_{i+2})}+(x_{i+1}-x_i)(x_{i+2}-x_{i-1})\right]\text{。}\end{split} $

(7)

式中， $ \varepsilon $ 描述转向角。

1.2 基于混合遗传算法的海上交通高峰航线船舶疏导路径规划方法

分析海上交通高峰航线船舶疏导路径规划问题，采用混合遗传算法求解该模型最优解。为准确描述海上交通高峰航线船舶疏导路径规划过程中，需要采用栅格法仿真模拟出海上交通高峰航线船舶环境，利用仿真软件实施仿真建模，假设路径规划海面为矩形，将海面换分成边长相等的正方形栅格构建海上交通高峰航线船舶疏导路径规划栅格地图。其中，包括可通行栅格与障碍栅格，栅格地图行列分别为 $ row $ 、 $ col $ ， $ \alpha $ 代表一个栅格，关联矩阵值表达式如下：

$ Map\left(\alpha \right)=\;\Biggr\{ \begin{array}{l}D,栅格能通过\text{，}\\ 0,栅格不能通过\text{。}\end{array} $

(8)

其中：当 $ Map\left( \alpha \right) = D > 0 $ 时，代表栅格上无障碍物，此时船舶能通行，常数用 $ D $ 描述；当 $ Map\left( \alpha \right) = 0 $ 时，代表栅格上有障碍物，此时船舶不能通行。在海上交通高峰航线船舶疏导路径规划栅格地图中黑色栅格、白色栅格分别表示障碍物、船舶可移动范围。

在构建仿真栅格图后，利用混合改进遗传算法进行搜索船舶疏导路径。混合改进遗传算法是将非线性规划算法与改进遗传算法相结合，提高算法的寻优效率，并对海上交通高峰航线船舶疏导路径实施优化。第一步利用改进遗传算法寻找海上交通高峰航线船舶疏导路径规划模型的全局最优解，通过在遗传算法中添加安全算子、平滑算子、最短路径算子形成改进遗传算法，疏导路径规划模型的全局寻优具体过程如下：

步骤1　疏导路径编码和进行种群的初始化操作

在已知海上交通高峰环境地图上选取个N×N网格点，各疏导路径均经过网格中心位置，构建疏导路径的编码向量并用 $ \left( {{\varphi _1},{\varphi _2}, \cdots ,{\varphi _n}} \right) $ 描述，海上交通高峰航线船舶在 $ i $ 点转向角用 $ {\varphi _i} $ 描述。当 $ {\varphi _i} < 0 $ 时，船舶向左行驶；当 $ {\varphi _i} > 0 $ 时，船舶向右行驶。在该算法中疏导路径代表由遗传因子组成的染色体，为了降低船舶间碰撞概率，设置遗传因子变量值大于15°。

步骤2　疏导路径适应度函数求解

为了对疏导路径实施评价，需要构建适应度函数，其表达式如下：

$ f = \left\{ \begin{gathered} \chi \left| {{H_c}} \right| + \eta {H_l}{,^{}}{H_l} < {H_s}\text{，} \\ \chi \left| {{H_c}} \right| + \mu {\left( {{H_l} - {H_s}}\right)^{}},{H_l} > {H_s}\text{。} \\ \end{gathered} \right. $

(9)

式中： $ \eta $ 描述惩罚因子； $ \chi $ 描述疏导路径和计划路径偏差度的加权因子； $ {H_c} $ 描述优化后路径结束位置离计划路径目的地距离； $ \mu $ 描述碰撞危险度因子； $ {H_l} $ 描述优化疏导路径上每个点和目标路径点之间的距离； $ {H_s} $ 描述船舶海域半径。

步骤3　搜索疏导路径

① 通过轮盘赌法实施遗传操作选取生命力强的染色体即疏导路径。

② 通过算数交叉操作得出新的基因组，即新的疏导路径组合。

③ 利用变异算子得出均值和方差替换以前基因值，即变异后得出新疏导路径。

④ 安全算子。海上交通高峰航线船舶疏导路径需要规避障碍物，在栅格中选取离障碍物最优栅格并将该栅格节点设置在船舶疏导路径中。

⑤ 平滑算子。利用平滑算子求解船舶疏导路径最大转向角，保证船舶疏导过程的稳定性。

⑥ 最短路径算子。通过最短路径算子寻找海上交通高峰航线船舶疏导路径的最短航程。

通过第一步得出海上交通高峰航线船舶疏导路径规划模型的全局最优解；第二步，利用非性规划求解海上交通高峰航线船舶疏导路径规划模型的局部最优解。

2 结果实验分析

为了验证本文方法的应用效果，通过Matlab R2020a实施仿真实验。分别构建复杂与简单的海上交通高峰航线船舶仿真场景。复杂场景中船舶数量为200条，障碍物数量为100个而简单场景中船舶数量为50条，划方法、文献[5]改进蚁群算法的规划方法。2种场景下，海上交通高峰航线船舶疏导路径进行规划，测试结果见表1。分析可知，针对不同场景下，本文方法的疏导路径拐点数量最少，在疏导过程中船舶碰撞次数为0，疏导路径航程最短，平缓系数低于0.15，安全性系数高达0.98。综合表1参数测评结果，可知本文方法的应用效果明显优于其他2种方法的应用效果，说明本文方法鲁棒性和寻优能力最强。

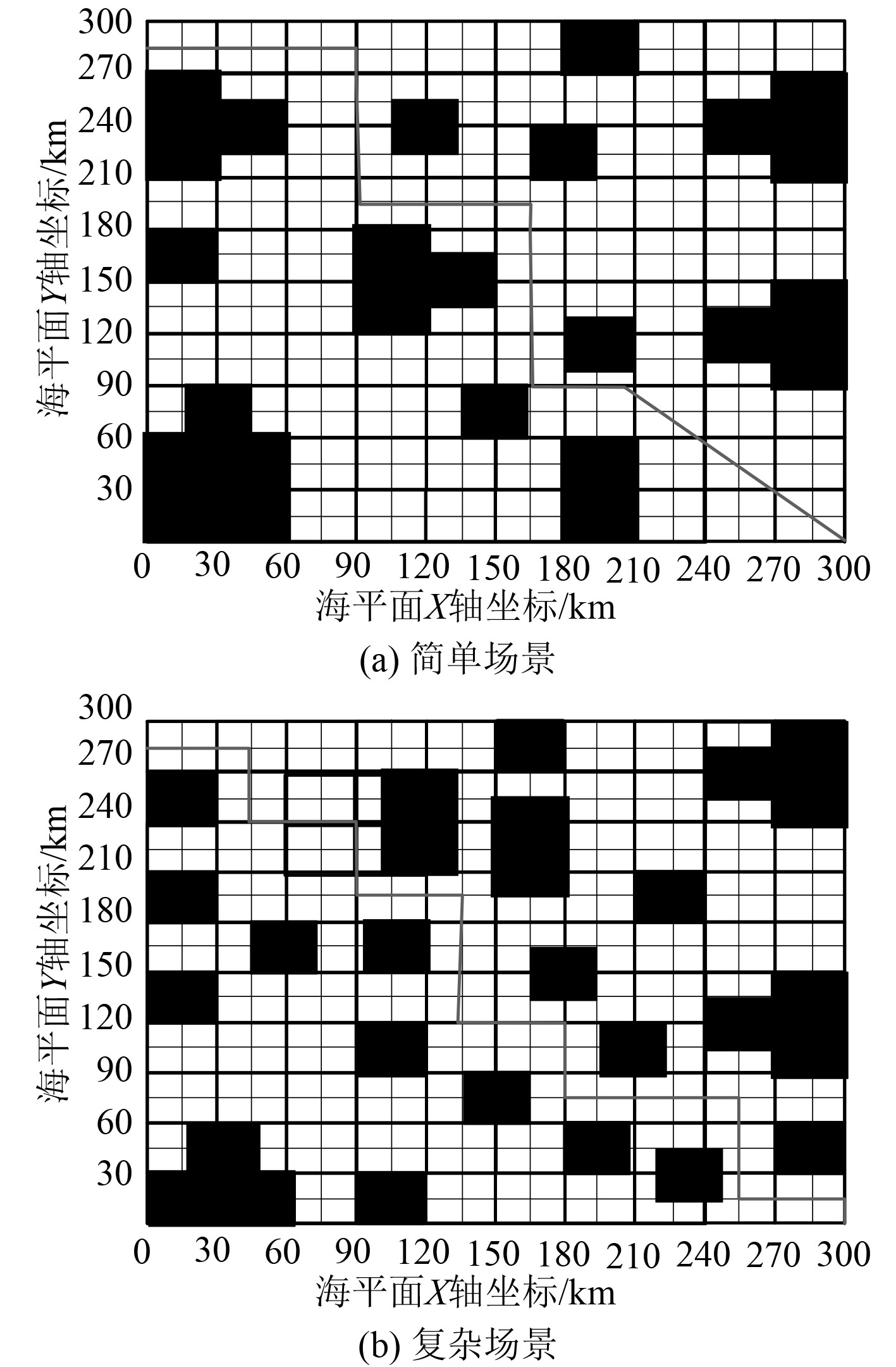
选取其中一艘船作为测试对象，采用本文方法针对2种场景下海上交通高峰航线船舶疏导路径，见图1。分析可知，本文研究方法2种场景下海上交通高峰航线船舶疏导路径具有较好的方向性，结合表1数据可知所规划最优疏导路径安全性、平滑性、航程最少，符合海上交通高峰航线船舶疏导路径目标函数。

以复杂场景为例，本文方法的海上交通高峰航线船舶疏导路径仿真图见图2。分析可知，复杂场景下，本文方法的疏导路径效果较好，以实验船舶为例，本文方法在短时内可规划出最优疏导路径，合理规避障碍物，采用本文方法对其他海上交通高峰航线船舶实施疏导路径规划，可快速实现海上交通畅通。

3 结　语

由于海上交通高峰期间船舶数量和交通流量的增加，对船舶疏导路径的规划显得尤为重要。通过海上交通高峰航线船舶疏导路径规划仿真分析，

将船舶疏导路径规划问题转化为图论中的多目标问题，并利用混合遗传算法得出最优解。仿真实验表明，本文提出的船舶疏导路径规划算法，在不同场景下，通过调整算法参数和约束条件，可以获得较好的规划效果和鲁棒性。