0 引　言

铁磁性目标物在地磁背景场中会被磁化，进而改变背景场原有的分布，产生磁异常现象。通过对磁场的测量，将测量的磁场信息进行一定的处理来判断目标物的有无、实现目标物的定位。磁异常探测技术中测量到的磁场信号含有丰富的噪声。目前磁异常探测常用手段主要是传感器和被探测物相对运动直到彼此错开，再利用生成的完备数据进行建模求解。然而现在的磁异常探测更需要能够及时预判被探测物的具体定位。

如何在有噪声干扰且信噪比极低的情况下，实现对磁性目标的预判定位是磁异常探测技术领域中一个比较棘手的问题。

正交基函数是磁异常探测技术中检测磁性目标物的经典算法。Frumkis等^[1]基于正交基函数的信号能量评估，提出了OBF算法。通过该算法可以提高目标信号的信噪比，从而判断目标信号的有无。Qin等^[2]利用地磁坐标系3个轴向半径的梯度信息，进一步对OBF算法进行改进。使其对目标磁异常检测有了更好的表征，显著提高信噪比。Ginzburg等^[3]利用2个磁传感器测量总场梯度信息，通过改进的正交基函数对磁场信号进行分解，以提高信噪比和信号检测的特性。OBF算法有着噪声与正交基函数不相关的特性，因而有着对噪声不敏感，有效抑制噪声和提高信噪比的优点。但目前对OBF算法的研究大部分用于判断磁异常信号的有无。利用OBF强大的抗噪声性来实现磁目标的定位还不是很普遍。现阶段，利用磁场梯度信息对磁性目标物进行定位的研究越来越多。因其能有效规避背景场的干扰，而广泛应用到磁异常探测定位中。Sui等^[4]通过从旋转磁盘上的单轴磁传感器中提取二阶和三阶梯度张量，以此来实现磁偶极子的高效定位。Huang等^[5]将磁梯度张量和吃水深度结合起来，实现水下航行器的有效定位。Fan等^[6]提出一种基于总磁场梯度定位目标的快速线性算法，实现了静态磁目标的高速定位。大多数利用梯度信息进行目标的定位方法，虽然有着不易受到背景场干扰，能较好描述磁异常场的优点。但是这些方法都是在背景噪声不明显，信噪比较高的情况下才能实现磁性目标的准确定位。

Birsan^[7]通过传感器阵列，将正交基函数与单一梯度信息结合，将普遍用于判断磁异常有无的OBF算法运用到磁异常定位中。目前这种利用OBF实现磁异常探测定位的算法，针对的是信噪比大于0的情况。对于信噪比小于0，甚至更低的复杂噪声背景下的定位效果还没有研究。

本文利用声呐系统提供测量的大致方位和距离，结合正交基函数天然的规避噪声的特性，将OBF算法结合L-M算法改进，成为可以运用到磁异常探测定位领域中的一种基于声磁复合的磁探测高效算法，有效提升声呐定位精度。

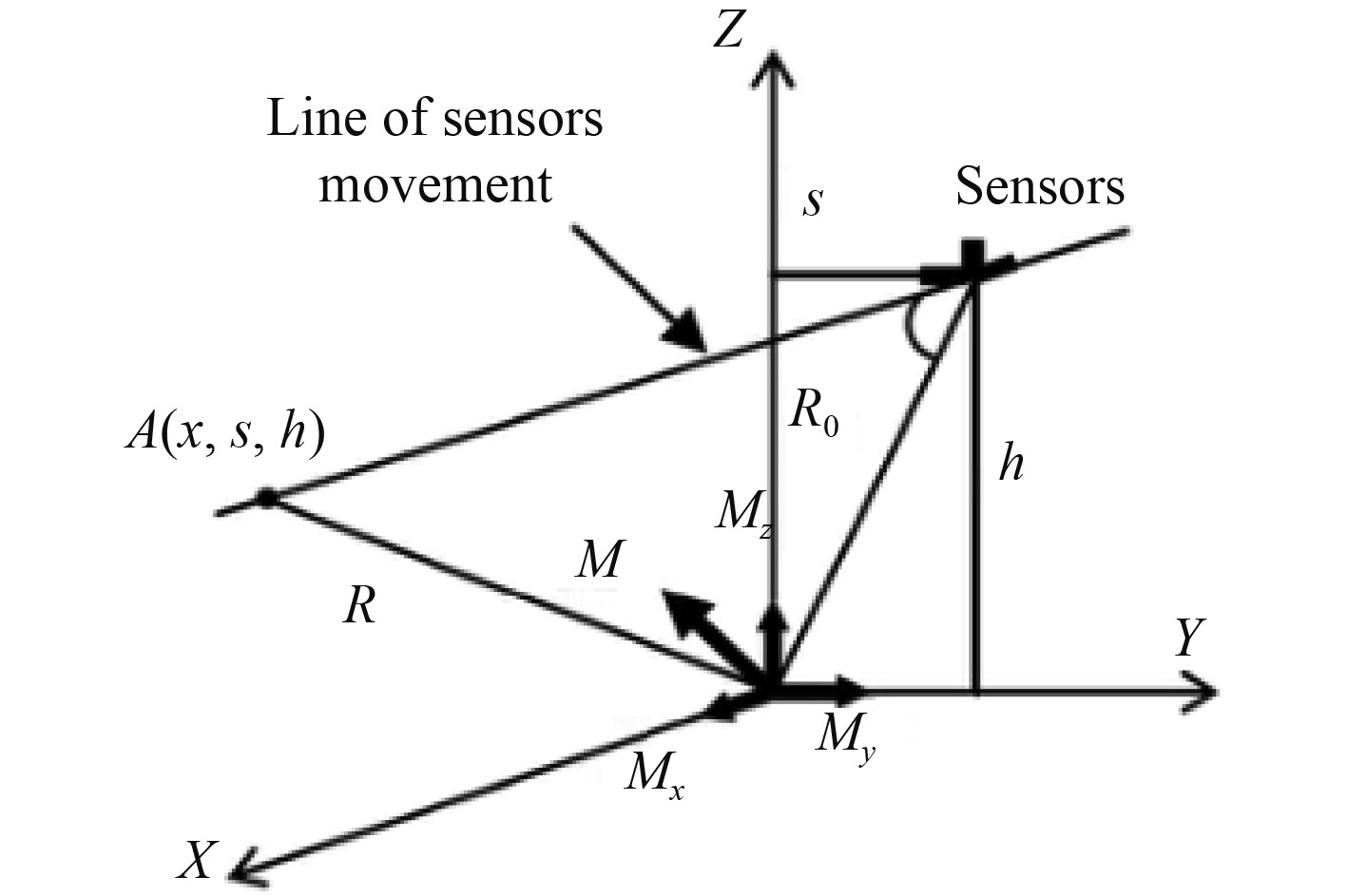
1 OBF算法

在传统的MAD系统中, 如图1搭载有2个标量磁强计的探测平台沿着笛卡尔坐标系的X轴方向移动，路径的方程见式（1）。其中 $ {x_1} $ 为探测平台在X轴的分量初始值，且为负数，探测平台沿着平行于X轴的直线匀速以 $ v $ 向X轴正方向行进，经过声呐的初步探测定位点，把目标暂时假定为坐标系原点^[8-13]。

$ \left\{ \begin{aligned} & x = {x_1} + vt(t \leqslant - \frac{{{x_1}}}{v}) ，\\ & y = s，\\ & z = h 。\end{aligned} \right. $

(1)

假定铁磁目标静止不动。当传感器距离铁磁目标大于目标尺寸3倍时,铁磁目标产生的异常场可以视为偶极子场，并且可以描述为：

$ {\overline{{B}}}=\frac{{\mu }_{0}}{4\text{π} }\left(\frac{3(\overline{{\boldsymbol{r}}},\overline{M})\overline{{\boldsymbol{r}}}}{|\overline{{\boldsymbol{r}}}{|}^{5}}-\frac{\overline{M}}{|\overline{{\boldsymbol{r}}}{|}^{3}}\right) 。$

(2)

式中， $\overline M $ 为磁偶极矩， ${\boldsymbol{r}}$ 为偶极子到传感器的位置矢量， ${\mu _0}$ 是真空的磁导率。磁强计在轨道上以匀速v平行于x轴的直线上运动: $ \overrightarrow {R\left( t \right)} = \overrightarrow {{R_0}} + {\text{ }}(t - {t_0})\overrightarrow v $ ，在t = t₀时刻，传感器处于离目标最近的接近点 R₀(也即为最短横距CPA值)。将 $ \overrightarrow {R\left( t \right)} $ 代入式（2）化简，将 $ \stackrel{\rightharpoonup }{B} $ 的每个分量都可以写成3个Anderson函数的线性组合

$ \left\{ \begin{gathered} {A_0}(\tau ) = \frac{1}{{{{(1 + {\tau ^2})}^{\frac{5}{2}}}}}，\\ {A_0}(\tau ) = \frac{\tau }{{{{(1 + {\tau ^2})}^{\frac{5}{2}}}}}，\\ {A_0}(\tau ) = \frac{{{\tau ^2}}}{{{{(1 + {\tau ^2})}^{\frac{5}{2}}}}}。\\ \end{gathered} \right. $

(3)

其中， $ \mathrm{\tau } $ 为归一化时间， ${{t}}_{0}$ 为传感器和被测物最近的时候（最短横距为CPA）。

$ \tau = \frac{{(t - {t_0})v}}{{{R_0}}} = \frac{{x - {x_0}}}{{{R_0}}}，$

(4)

$ {R_0} = \sqrt {{y^2} + {z^2}} = \sqrt {{s^2} + {h^2}} 。$

(5)

将 $\overline {{\boldsymbol{B}}}$ 化简为：

$ \left[ \begin{gathered} Bx \\ By \\ Bz \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{l}} {{a_{{x_0}}}}&{{a_{{x_1}}}}&{{a_{{x_2}}}} \\ {{a_{{y_0}}}}&{{a_{{y_1}}}}&{{a_{{y_2}}}} \\ {{a_{{z_0}}}}&{{a_{{z_1}}}}&{{a_{{z_2}}}} \end{array}} \right]\left[ \begin{gathered} {A_0} \\ {A_1} \\ {A_2} \\ \end{gathered} \right]。$

(6)

其中：

$ \begin{gathered} \left[ {\begin{array}{*{20}{l}} {{a_{{x_0}}}}&{{a_{{x_1}}}}&{{a_{{x_2}}}} \\ {{a_{{y_0}}}}&{{a_{{y_1}}}}&{{a_{{y_2}}}} \\ {{a_{{z_0}}}}&{{a_{{z_1}}}}&{{a_{{z_2}}}} \end{array}} \right]{\text{ = }}\frac{{{\mu _{\text{0}}}}}{{{\text{4}}\text{π} {R_0}^{\text{5}}}} \cdot \\ \left[ {\begin{array}{*{20}{l}} {{{ - }}{M_X}{R_0}^2}&{3(y{M_Y} + zMz){R_0}}&{2{M_X}{R_0}^2} \\ {3yz{M_Z} + (2{y^2} - {z^2}){M_Y}}&{3{R_0}y{M_X}}&{ - {M_Y}{R_0}^2} \\ {3yz{M_Y} + (2{z^2} - {y^2}){M_z}}&{3{R_0}z{M_X}}&{ - {M_Z}{R_0}^2} \end{array}} \right] 。\end{gathered} $

(7)

按照OBF理论， ${\overline{M}}$ 为偶极子的磁偶极矩， ${\overline{{{m}} }}$ 为偶极矩方向上的单位矢量，在地磁场 $\overline{{\boldsymbol{T}}}$ 中， $\left|\overline {{\boldsymbol{B}}} \right|\ll \left|\overline {{\boldsymbol{T}}} \right|$ 时传感器测得的异常场大小 $\overline {S}$ 为 $\overline {{\boldsymbol{B}}}$ 在 $\overline {{\boldsymbol{T}}}$ 的投影，即

$ S=\frac{\overline {{\boldsymbol{B}}} \cdot \overline {{\boldsymbol{T}}}} {\left|\overline {{\boldsymbol{T}}} \right|}，$

(8)

此时 $S$ 可以由3个线性无关的基函数的加权和表示。

$ S = \sum\limits_{i = 1}^3 {{a_i}{\psi _k}} (\tau ) 。$

(9)

可以使用朗斯基行列式证明这3个函数之间是线性无关的。

$ \left\{ \begin{gathered} {\psi _1}(\tau ) = \frac{1}{{{{(1 + {\tau ^2})}^{5/2}}}}, \\ {\psi _2}(\tau ) = \frac{\tau }{{{{(1 + {\tau ^2})}^{5/2}}}}, \\ {\psi _3}(\tau ) = \frac{{{\tau ^2}}}{{{{(1 + {\tau ^2})}^{5/2}}}}，\\ {R_0} = \sqrt {{{({x_s} - {x_0})}^2} + {{({z_s} - {z_0})}^2}}。\end{gathered} \right. $

(10)

代入测量的数据，可以解出 ${y_0}$ 、 ${R_0}$ 和 ${a_i}(i =1,2,3)$ 这5个未知数，而且上述过程假定地磁背景场是均匀的，使用2个标量传感器取均值来计算更加准确。

2 探测定位流程框图

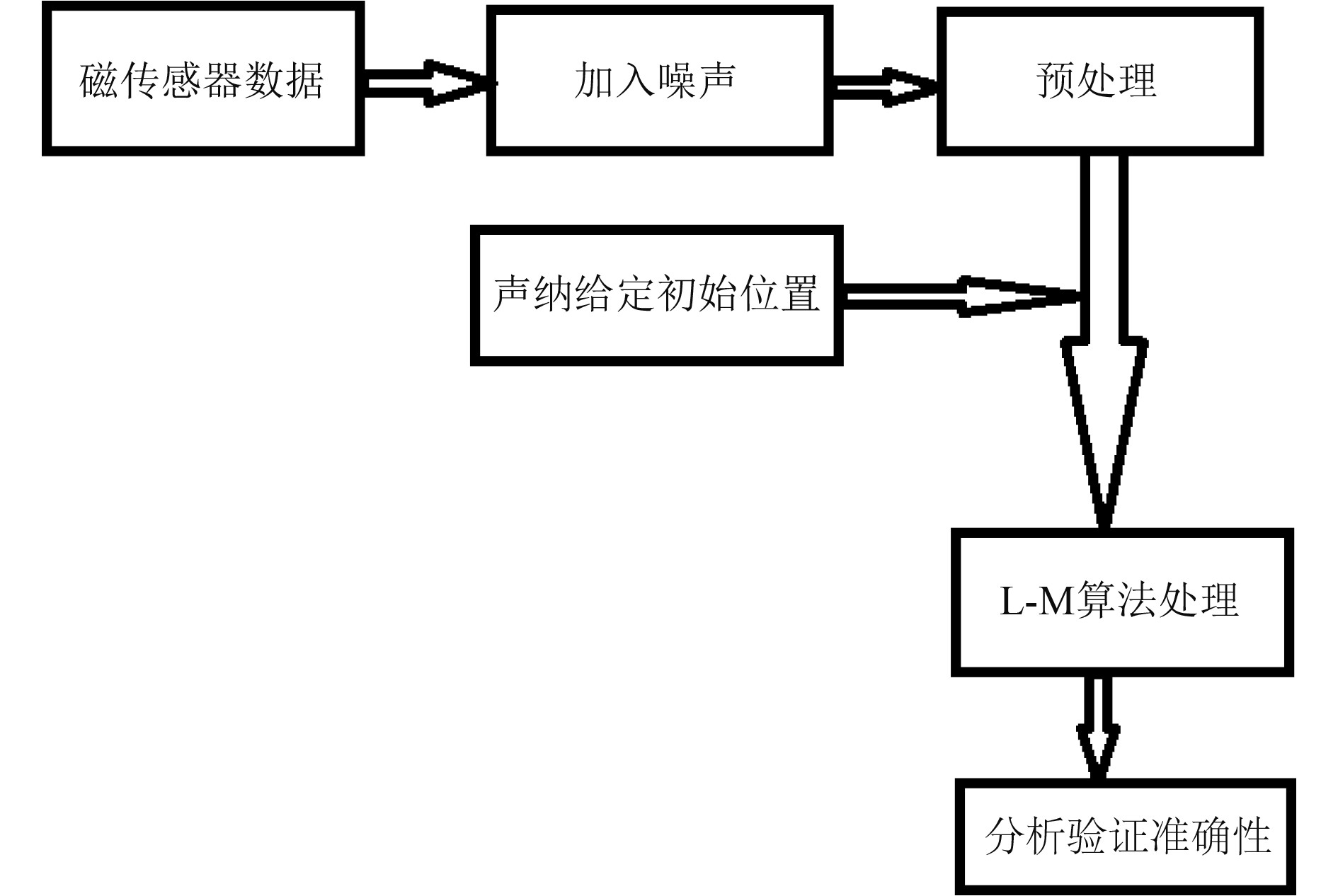
本文设计探测流程如图2所示。由2个标量磁性传感器测得的数据加入不同噪声，再经过数据预处理，结合声呐给定初始位置，进行L-M算法的迭代处理，从而得出磁异常的具体参数，并根据结果分析验证准确性。

磁异常目标位置坐标为 $ （{x}_{0},{y}_{0},{z}_{0}） $ ，2个磁传感器相距1 m，且S₁和S₂平行于水平面移动，磁强计的排布如图3所示。将移动的方向定义为X轴正方向，则2个磁强计采集的磁异常信号可以表示为：

$ \begin{split} & {S_1} = \mathop \sum \limits_{i = 1}^3 {a_i}\psi ({\tau _1}),{\tau _1} = \frac{{y - {y_0}}}{{\sqrt {{{({x_s} - {x_0})}^2} + {{({z_s} - {z_0})}^2}} }}，\\ & {S_2} = \mathop \sum \limits_{i = 1}^3 {b_i}\psi ({\tau _2}),{\tau _2} = \frac{{y - {y_0}}}{{\sqrt {{{({x_s} - {x_0} + \Delta X)}^2} + {{({z_s} - {z_0})}^2}} }}。\end{split} $

(11)

对于测量轨迹上的偶极子异常信号 $S$ ，其在 $X$ 方向上的梯度为：

$ \begin{split} \frac{{\partial S}}{{\partial x}} =& \frac{{\partial S}}{{\partial \tau }} \cdot \frac{{\partial \tau }}{{\partial x}} ={b_1}({\phi _1} + {\phi _3}) +\\ & {b_2}({\phi _2} + {\phi _4}) + {b_3}({\phi _3} + {\phi _5}) - \frac{{(x - {x_0})\tau }}{{R_0^2}} \times \\ &\left( { - 5{a_1}{\phi _2} + {a_2}({\phi _1} - 4{\phi _3}) + {a_3}(2{\phi _2} - 3{\phi _4})} \right) 。\end{split} $

(12)

其中：

$ \left\{ \begin{gathered} {\phi _1}(\tau ) = \frac{1}{{{{(1 + {\tau ^2})}^{7/2}}}},\quad \\ {\phi _2}(\tau ) = \frac{\tau }{{{{(1 + {\tau ^2})}^{7/2}}}}，\\ {\phi _3}(\tau ) = \frac{{{\tau ^2}}}{{{{(1 + {\tau ^2})}^{7/2}}}},\quad \\ {\phi _4}(\tau ) = \frac{{{\tau ^3}}}{{{{(1 + {\tau ^2})}^{7/2}}}} 。\end{gathered} \right. $

(13)

可以使用朗斯基行列式证明这4个函数之间是线性无关的^[14-17]。

沿X轴方向的梯度可以由2个传感器的差分近似表达为：

$ \frac{{\partial S}}{{\partial x}} \approx \frac{{{S_2} - {S_1}}}{{\Delta X}}, $

(14)

至此根据 $x$ 方向上的梯度得到了如上方程，未知数仍是 ${x_0}$ ， ${y_0}$ ， ${z_0}$ ， ${R_0}$ ， ${a_i}(i = 1,2,3)$ ，因而可以根据最小均方误差的标准，使用Levenberg-Marquardt算法求解^[18-20]。但由于 ${z_0}$ 只存在于 ${({z_s} - {z_0})^2}$ 这一项中，即 ${z_0} = - |{z_0}|$ 或者 ${z_0} = |{z_0}|$ 都满足最优解，在此不直接用LM算法求出 ${z_0}$ ，而是使用得到的 ${R_0}$ 、 ${x_0}$ 以及 ${z_0} < {z_s}$ 这一条件唯一确定 ${z_0}$ 。

3 实验验证

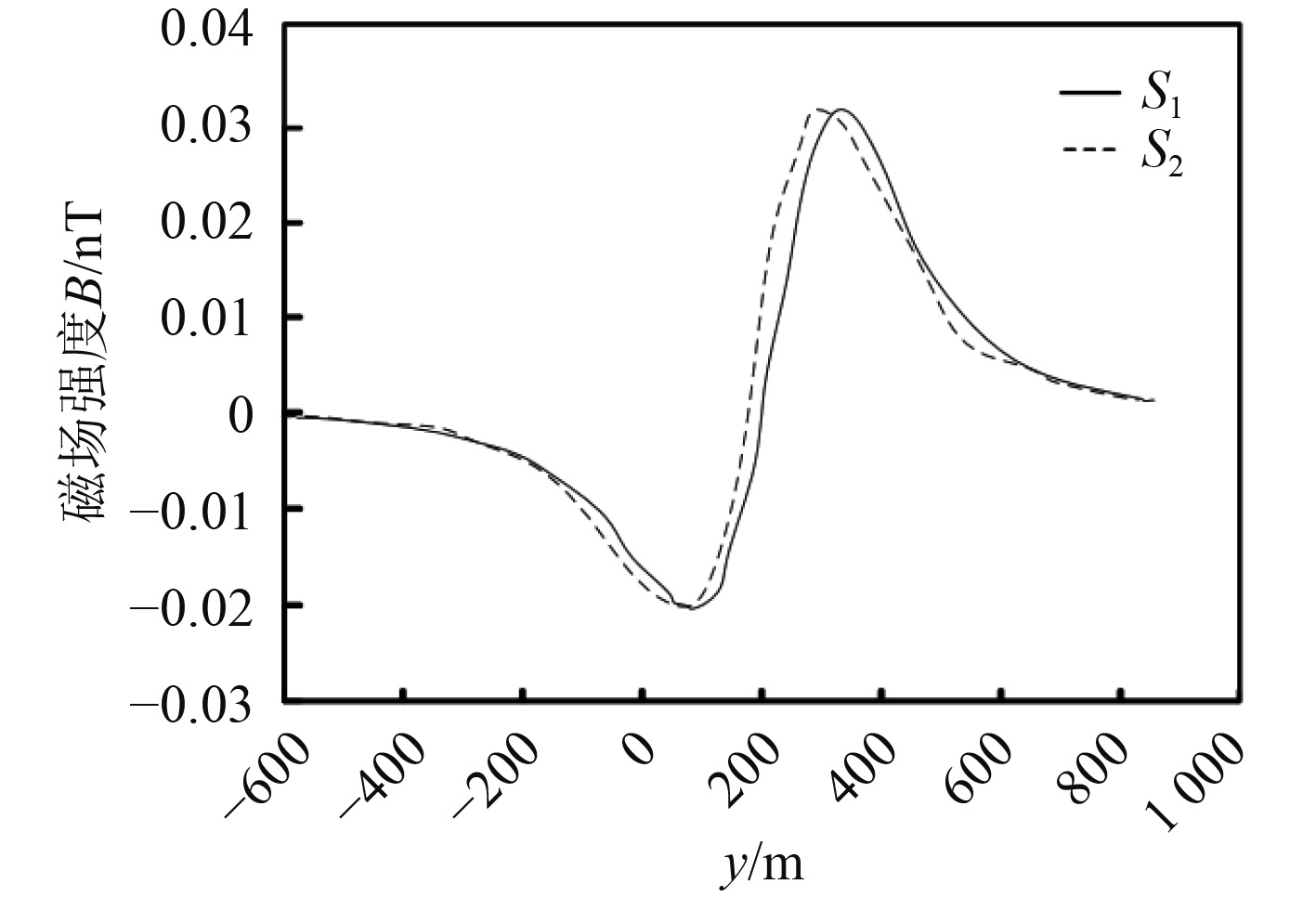
在数值验证部分将地磁场视为背景场，且认为信号中没有噪声，2个磁强计的数据由传感器测量得到，如图4所示。

可以看出由于间距比较小，2个磁强计的数据差别非常小。

计算过程中 ${z_s} = 100\;{\rm{m}}$ ， ${x_s} = 100\;{\rm{m}}$ ，偶极子位置为(0,0,0)，地磁场的磁倾角 $I = {70^\circ }$ ，磁偏角 $D = {81^\circ }$ 。传感器间距 $\Delta Y = 1\;{\rm{m}}$ 。使用Levenberg-Marquardt算法求解，但由于 ${z_0}$ 只存在于 ${({z_s} - {z_0})^2}$ 这一项中，即 ${z_0} = - |{z_0}|$ 或者 ${z_0} = |{z_0}|$ 都满足最优解，在此不直接用LM算法求出 ${z_0}$ ，而是使用得到的 ${R_0}$ 、 ${x_0}$ 以及 ${z_0} < {z_s}$ 这一条件确定唯 ${ - }{z_0}$ 。

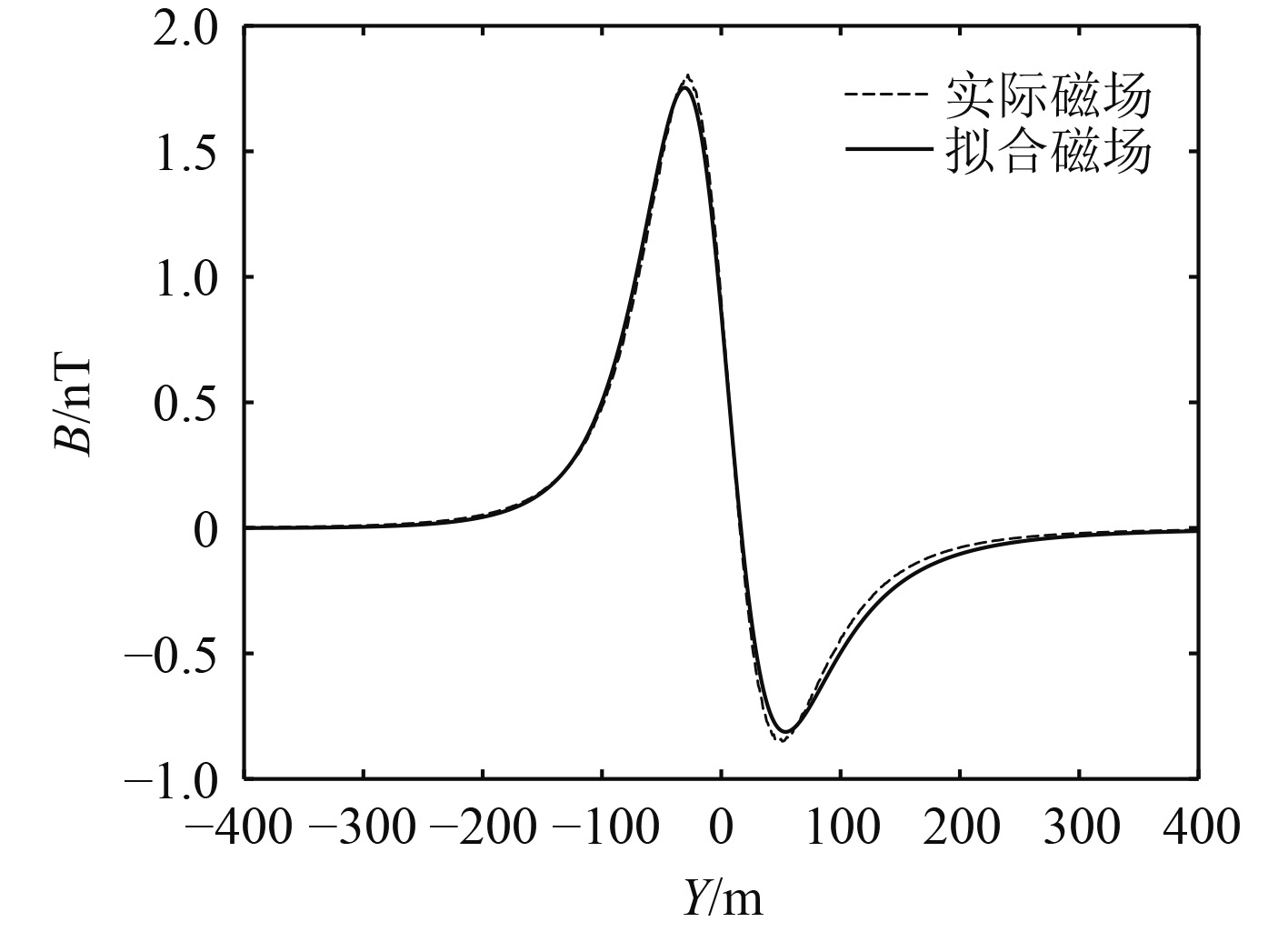
可以看出在声呐系统辅助下，将初始值设定为0.1，传感器和被测物垂直方向距离定位110 m，在运算过程中将b₀，b₁，b₂都定初值为1时（b₀，b₁，b₂为L-M算法中自主定义的3个参数），Levenberg-Marquardt算法经过501次迭代，拟合效果很好，如图5所示。

接下来进行磁场梯度的验证，按照L-M算法计算的结果(197.90,296.38,−52.19)，估计的误差较小。使用求解出的系数代入式(12)、式(8)与式(9)、式(14)，得到的梯度与原始数据对比如图6所示，拟合的结果与真实值非常接近。

再考虑偶极子朝向的不同，角度的变化也会导致磁场的结果随之发生改变。随机设置32组偶极子朝向 $({\theta _d},{\beta _d})$ 组合，并生成仿真数据，使用算法反演磁异常位置结果如图7所示。

可知，在 ${R_0} = 269.26\;{\rm{m}}$ 的情况下，对于不同的 $({\theta _d}, {\beta _d})$ 组合， ${x_0}$ 的求解误差在 $\pm 25\;{\rm{m }}$ ， ${y_0}$ 和 ${z_0}$ 的求解误差在 $\pm 5\;{\rm{m}}$ ，说明本文方法具有较好的求解精度。

而在实际探测到的信号一般包含各种噪声。为了检验本文方法在低信噪比情况下的表现，现在对仿真生成的偶极子信号人为添加不同强度的噪声，以模拟不同信噪比下采集到的信号。所加的噪声是标准的高斯白噪声，此处信噪比定义为：

$ SNR = 10\lg \left( {\frac{{{P_{signal}}}}{{{P_{nosie}}}}} \right)。$

(15)

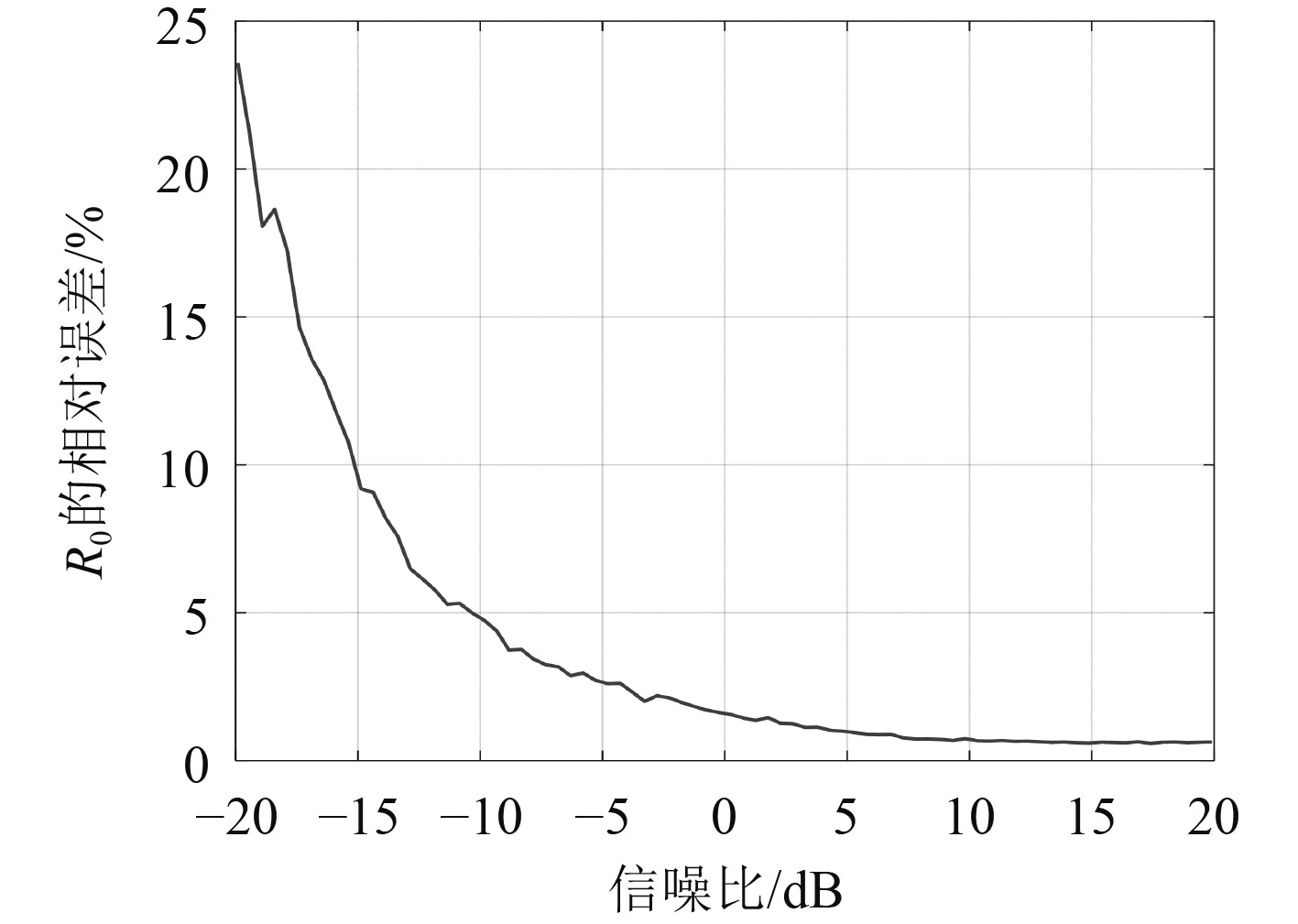
由于磁强计之间的距离比较近，差分求梯度能在一定程度上减弱噪声的影响。图8为信噪比在 $- 10$ ～ $10\;{\rm{dB}}$ 的范围内，式(6)中 ${R_0}$ 的计算结果。

可以看出，本文的解算方法对噪声具有一定的适应能力。在信噪比为 $- 10\;{\rm{dB}}$ 的情况下 ${R_0}$ 的求解相对误差小于5%。说明算法对于低信噪比的环境具有很好的适应能力^[21-25]

4 结　语

本文提出一种信号处理技术，用于定位和识别一个模拟为磁偶极子的目标。该算法同时利用了在配备2个磁强计的飞机上同时测量的总磁场和标量梯度。对于不同的实验情况和噪声水平，这2个量都可以通过一组安德森型函数很好地建模。从大量的计算机模拟得到的结果表明，对目标位置的估计和磁矩精度的预测是可以接受的，即使在相当低的信噪比−10 dB的情况下，从2个磁力计的信号依然可以较好反演出实际的磁异常信号位置。