海底布设磁传感器广泛用于海洋勘探、水中目标探测、舰船磁场防护等领域,在使用磁传感器进行磁场采集之前,获取磁传感器的精确位置、姿态信息是必不可少的环节[1-5]。尤其是对于临时布放的海底磁传感器,受施工工艺、水文气象、海底环境等因素的影响较大[6],很难在预定位置精确部署,更难以精确确定其姿态,因此需要采用一定的技术手段方便地对水下磁传感器进行位置和姿态的精确校准。采用动态电磁线圈对水下磁传感器进行校准是一种有效的技术方法[7],O’donoghue等[8-9]采用多个平面方形线圈对磁传感器进行定位校准,应用于虚拟支气管镜导航中的肺导管定位。Pfeiffer等[10]采用多个磁偶极子状的电磁线圈作为磁源,对脑磁图磁传感器阵列进行位置和方向校准。这些研究仅对小尺度(分米级)问题进行了研究,没有研究大尺度(数十米量级)问题的可行性和适用性。
本文设计并制作了一种水下磁传感器校准装置场地试验装置,采用动态电磁线圈作为磁源,采用组合导航设备测量电磁线圈的位置和姿态,采用差分进化(Differential Evolution,DE)算法和Levenberg-Marquardt(LM)算法对磁传感器的位置和姿态进行优化求解。对设计制作的校准装置场地试验样机分别进行了数值仿真实验和场地验证实验,证明该装置能够同时实现水下磁传感器位置和姿态的高精度校准。并且最优化求解过程不需要设置初始值,便于使用。
1 水下磁传感器校准原理水下磁传感器校准装置主要由电磁线圈、稳流电源、组合导航设备、校准软件等组成,如图1所示。电磁线圈由稳流电源供电,作为磁源。电磁线圈和组合导航设备同时固定安装在无磁载具(例如橡皮艇等)上。无磁载具搭载电磁线圈、稳流电源和组合导航设备,按照一定的轨迹从水下磁传感器上方的水面航行通过。测磁仪和组合导航设备分别同步采集磁场数据、无磁载具(电磁线圈)的位置姿态数据,与线圈电流一起提供给磁传感器校准软件。校准软件采用差分进化算法对水下磁传感器的位置和姿态进行最优化解算。

|
图 1 水下磁传感器校准装置工作原理 Fig. 1 Diagram of underwater magnetic sensor calibration device |
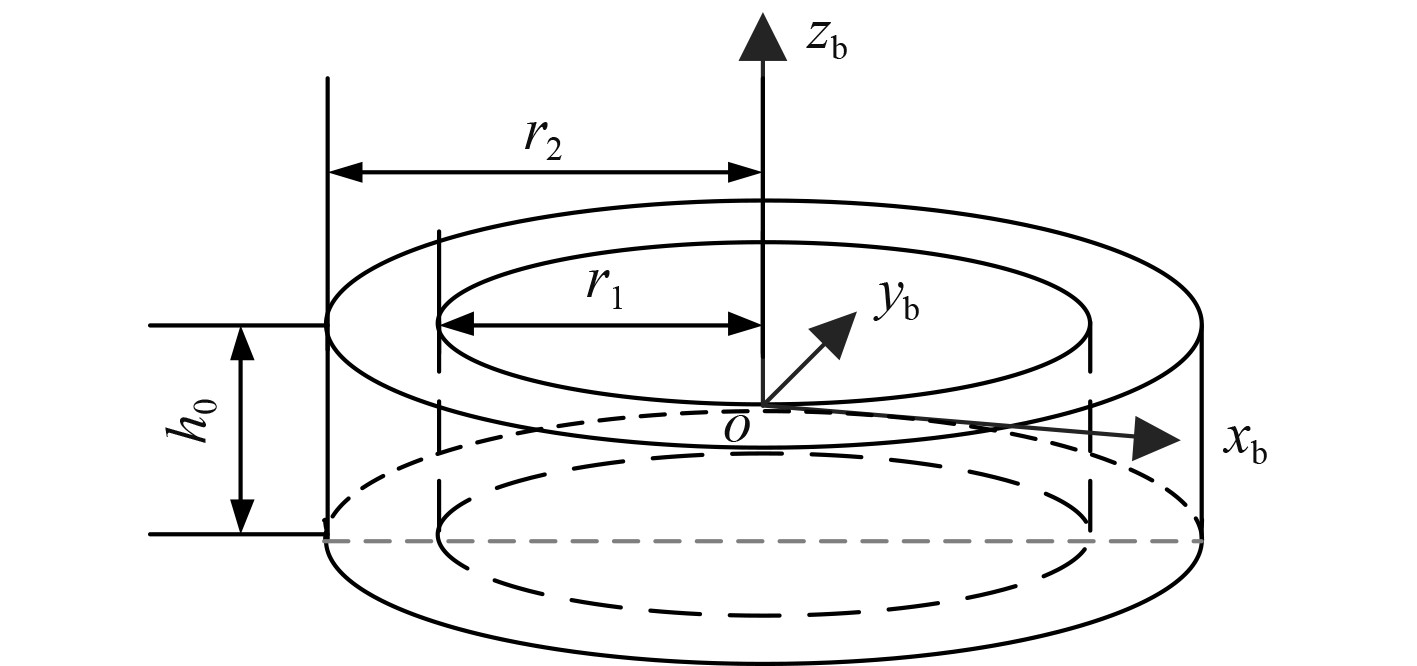
电磁线圈采用圆柱形螺线管线圈,设其内半径r1,外半径r2,高度h0,匝数为N,导线电流为I。建立如图2所示的线圈坐标系oxbybzb,原点o为线圈中心,xb、yb、zb轴分别指向线圈的右方、前方、上方方向。
|
图 2 圆柱形线圈及其坐标系 Fig. 2 Cylindrical coil and its coordinate system |
设圆柱形螺线管线圈为均匀密绕线圈,线圈的等效截面积为
| $ {m_{\text{z}}} = \int_{ - \frac{{{h_0}}}{2}}^{\frac{{{h_0}}}{2}} {\int_{{r_1}}^{{r_2}} {J{{\text π}}{r^2}{\rm{d}}r{\rm{d}}h} } = \frac{{{\text π}}}{3}J\left( {{r_2}^3 - {r_1}^3} \right){h_0} = \frac{{{{\text π}}NI(r_2^3 - r_1^3)}}{{3({r_2} - {r_1})}} 。$ | (1) |
由于水下磁传感器与电磁线圈间的距离远大于电磁线圈的尺度,可将螺线管线圈产生的磁场等效为线圈中心点(原点o)处的一个磁偶极子产生的磁场,其偶极矩为mz(方向沿zb轴方向)。该磁偶极子在场点P(x,y,z)处产生的磁感应强度三分量为:
| $ \left\{ \begin{gathered} {{B} _x} = \frac{{{\mu _{\text{0}}}{{m} _{\text{z}}}}}{{4{{\text π}}}}\frac{{3{xz} }}{{{{r} ^5}}} ,\\ {{B} _y} = \frac{{{\mu _{\text{0}}}{{m} _{\text{z}}}}}{{4{{\text π}}}}\frac{{3{yz} }}{{{{r} ^5}}},\\ {{B} _z} = \frac{{{\mu _{\text{0}}}{{m} _{\text{z}}}}}{{\text π}}\left(\frac{{3{{z} ^2}}}{{{{r} ^5}}} - \frac{1}{{{{r} ^3}}}\right)。\end{gathered} \right. $ | (2) |
式中:
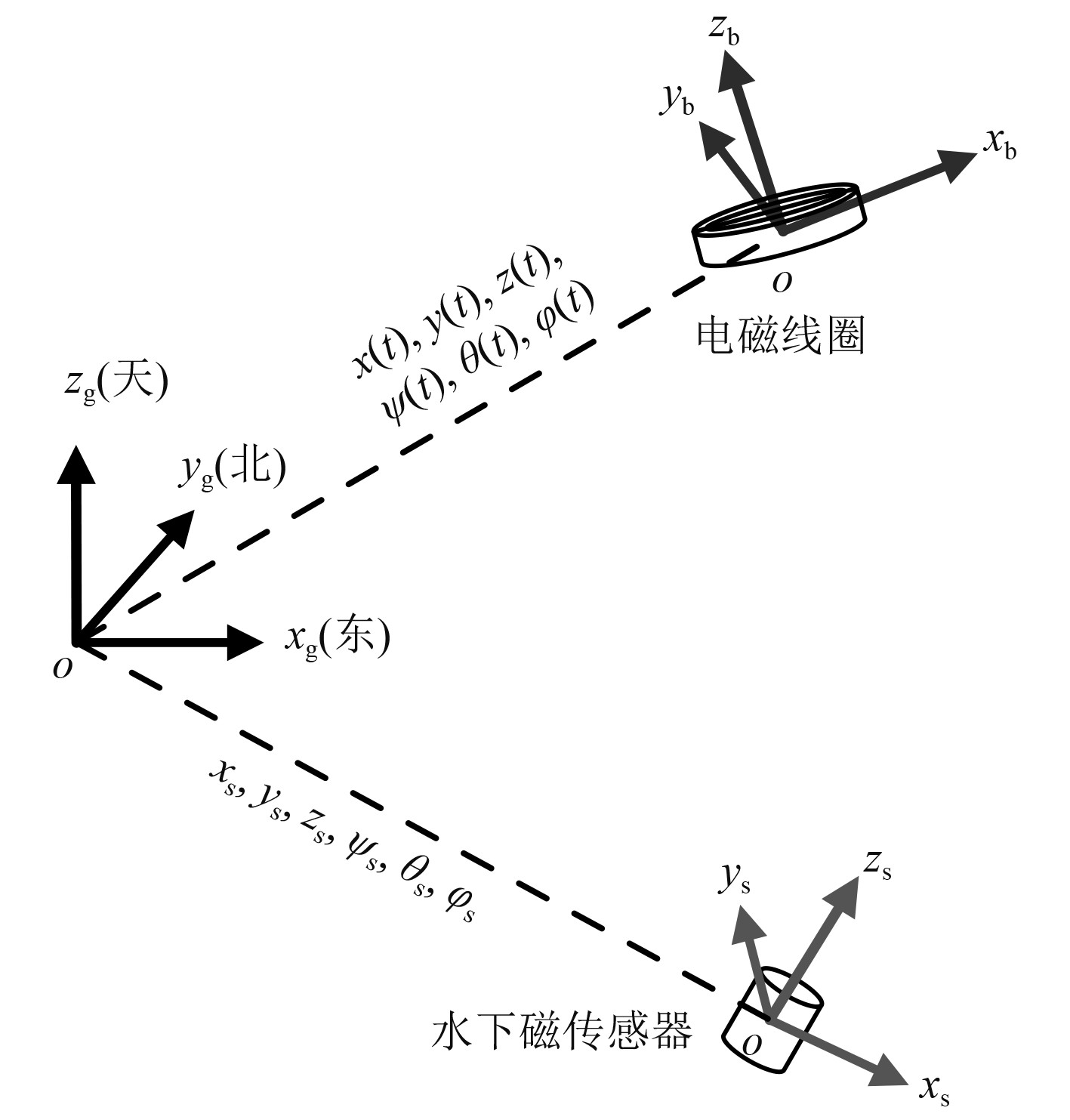
系统的坐标系定义如图3所示。其中,oxgygzg、oxbybzb、oxsyszs分别为地理坐标系、线圈坐标系和磁传感器坐标系。
|
图 3 系统坐标系定义 Fig. 3 Definition of system coordinate systems |
定义线圈在地理坐标系下的位置和姿态c=(x, y, z, ψ, θ, ϕ)。线圈姿态角(ψ, θ, ϕ)是由线圈坐标系oxbybzb与地理坐标系oxgygzg之间的关系确定的,由航向角ψ、俯仰角θ和横滚角ϕ三个欧拉角组成。航向角ψ为线圈yb轴在地面上的投影与yg轴间的夹角,以线圈前部右偏航为正;俯仰角θ为线圈yb轴与地平面(平面xgoy g)间的夹角,以线圈前部抬头为正;横滚角ϕ为线圈zb轴与包含线圈yb轴的铅垂面间的夹角,以线圈向右倾斜为正。
通过线圈的姿态角可以得到线圈坐标系与地理坐标系间的转换矩阵,线圈坐标系与地理坐标系间的转动关系按航向角ψ、俯仰角θ、横滚角ϕ的顺序进行。即先绕zb轴转过角度ψ(航向角),再在此基础上绕xb轴转过角度θ(俯仰角),最后在前2次旋转的基础上绕yb轴转过角度ϕ(横滚角)。由此得到由地理坐标系到线圈坐标系的坐标转换矩阵
| $ \begin{split} {\boldsymbol{C}}_g^b =&\left[ \begin{array}{*{20}{c}} {{\cos}\varphi {\cos}\psi + {\sin}\varphi {\sin}\theta {\sin}\psi } \\ {{\cos}\theta {\sin}\psi } \\ {{\sin}\varphi {\cos}\psi + {\cos}\varphi {\sin}\theta {\sin}\psi } \end{array} \right. \\ &\left. \begin{array}{*{20}{c}} { - {\cos}\varphi {\sin}\psi + {\sin}\varphi {\sin}\theta {\cos}\psi }&{ - {\sin}\varphi {\cos}\theta } \\ {{\cos}\theta {\cos}\psi }&{{\sin}\theta } \\ { - {\sin}\varphi {\sin}\psi - {\cos}\varphi {\sin}\theta {\cos}\psi }&{{\cos}\varphi {\cos}\theta } \end{array} \right]。\end{split} $ | (3) |
同理,可定义被校准磁传感器在地理坐标系下的位置和姿态s=(xs, ys, zs, ψs, θs, ϕs),由线圈坐标系到地理坐标系、由地理坐标系到磁传感器坐标系、由磁传感器坐标系到地理坐标系的坐标转换矩阵分别为
通电螺线管线圈搭载无磁载具(如橡皮艇),按照一定轨迹通过被校准磁传感器附近,同步采集线圈的位置、姿态信息和磁传感器测量数据。t时刻的线圈运动的位置、姿态用c(t)=(x(t), y(t), z(t), ψ(t), θ(t), ϕ(t))表示;磁传感器输出的磁场数据减去地磁背景场,可获得磁传感器坐标系下的包含地磁波动的线圈磁场测量值Bms(t)=[Bmsx(t), Bmsy(t), Bmsz(t)]T;同理,可得到地磁监测传感器测量的地理坐标系下的地磁波动值ΔBmg(t)=[ΔBmgx(t), ΔBmgy(t), ΔBmgz(t)]T。
3.3 校准解算方法根据线圈磁矩mz、位置姿态c(t)=(x(t), y(t), z(t), ψ(t), θ(t), ϕ(t)),磁传感器位置姿态s=(xs, ys, zs, ψs, θs, ϕs),坐标转换矩阵
地磁监测传感器与被校准磁传感器所处的地磁环境相同,二者测得的地磁波动相同,只是所在坐标系不同。根据磁传感器的姿态(ψs, θs, ϕs),可将地理坐标系下的地磁波动值ΔBmg(t)转换为磁传感器坐标系下的地磁波动值ΔBms(t)=
设开始数据采样的时刻t=0,采样间隔为ts,采样点数为K,那么整个采样时间序列为(0, ts, 2ts,…, (K−1)ts)。对时间序列上的每个时刻t,计算线圈磁场计算值Bcs(t)与测量值(Bms(t)−ΔBms(t))之间的差值Bcs(t)−(Bms(t)−ΔBms(t)),写成矩阵形式为Bcs−(Bms−ΔBms)。将目标函数定义为矩阵Bcs−(Bms−ΔBms)的F范数的平方:
| $ f{\text{(}}s{\text{)}} = \left\| {{{\boldsymbol{B}}_{{\text{cs}}}} - {\text{(}}{{\boldsymbol{B}}_{{\text{ms}}}} - \Delta {{\boldsymbol{B}}_{{\text{ms}}}}{\text{)}}} \right\|_{{F}}^2 。$ | (4) |
在给定的搜索范围内寻找目标函数
采用DE算法和LM算法作为水下磁传感器校准优化求解算法。
LM算法的具体实现步骤为:从初始值X0 =(xs0,ys0,zs0,ψs0,θs0,ϕs0)开始,在给定的在给定的搜索上限Xu和搜索下限Xl内,先假设一个可以信赖的最大位移r。以当前点为中心,以r为半径的区域内,寻找目标函数f(s)的近似函数(忽略二阶以上的导数项)的最优点,求解得到真正的位移。接着再计算目标函数值,如果目标函数的下降满足条件,表示该位移可靠,继续按照此规则迭代计算;如果不满足条件,则缩小r重新计算。重复进行上述过程,直至目标函数值达到收敛阈值或者达到最大迭代次数,得到目标函数的最优解,即为磁传感器阵列位置姿态的计算值。
DE算法是一种高效的自适应全局优化算法,主要用于求解实数优化问题[13-15]。该算法是一类基于群体的启发式搜索算法,群中的每一个个体对应一个解向量。与粒子群优化算法、蚁群算法、人工蜂群等智能算法相比,DE算法所需的参数少,优化能力强。
应用DE算法求解水下磁传感器位置姿态校准优化问题时,每个个体代表式(4)的一个候选解。设种群规模为NP,最大进化代数为Gm。进化至第g代的第i个个体表示为:
| $ {{\boldsymbol{s}}_i}(g) = [{s_{i1}}(g),{s_{i2}}(g),{s_{i3}}(g),{s_{i4}}(g),{s_{i5}}(g),{s_{i6}}(g)]。$ | (5) |
其中,i=1,2,…,NP,g=1,2,…,Gm。
计算流程如下:
步骤1 初始化
置g=0,在解空间内,均匀随机生成NP个初始个体si(0),i=1,2,…,NP,并根据式(4)计算每个个体适应度。
步骤2 变异操作
应用DE/rand/1/bin策略生成变异个体,表达式为:
| $ {{\boldsymbol{v}}_i}{\text{(}}g + 1{\text{)}} = {{\boldsymbol{s}}_{r1}}{\text{(}}g{\text{)}} + {{F}} \times {\text{(}}{{\boldsymbol{s}}_{r2}}{\text{(}}g{\text{)}} - {{\boldsymbol{s}}_{r3}}{\text{(}}g{\text{))}},$ | (6) |
式中,i≠r1≠r2≠r3,i=1,2,…,NP,r1、r2、r3均为区间[1,NP]内的随机整数,F为缩放因子。
步骤3 交叉操作
对第g代种群si(g)及其变异的中间种群vi(g+1)进行相应个体间的交叉操作。
| $ {u_{ij}}(g + 1) = \left\{ \begin{gathered} {v_{ij}}(g + 1){\text{,}}i{f_{}}(rand \leqslant {{CR {\rm{or}} }}j = {j_{{\text{rand}}}}) ,\\ {s_{ij}}(g),{\rm{otherwise}} 。\end{gathered} \right. $ | (7) |
其中,i=1, 2,…, NP,j=1, 2,…, 6,rand为区间(0, 1)内均匀分布的随机数,CR为交叉概率,jrand为区间[1, 6]内的随机整数。
步骤4 选择操作
采用贪婪策略,根据目标函数的大小来选择进入新种群的个体:
| $ {s}_{i}(g+1)=\left\{\begin{array}{l}{u}_{i}(g+1){\text{,}}_{}i{f}_{}{}_{}f({u}_{i}(g+1))\leqslant f({u}_{i}(g)),\\ {s}_{i}(g)\text{,}\text{otherwise}。\end{array}\right. $ | (8) |
步骤5 终止条件
若g<Gm,则置g=g+1,返回步骤2;否则,输出最优解,结束。
重复计算5次,取目标函数最小的一组结果作为最终结果输出。
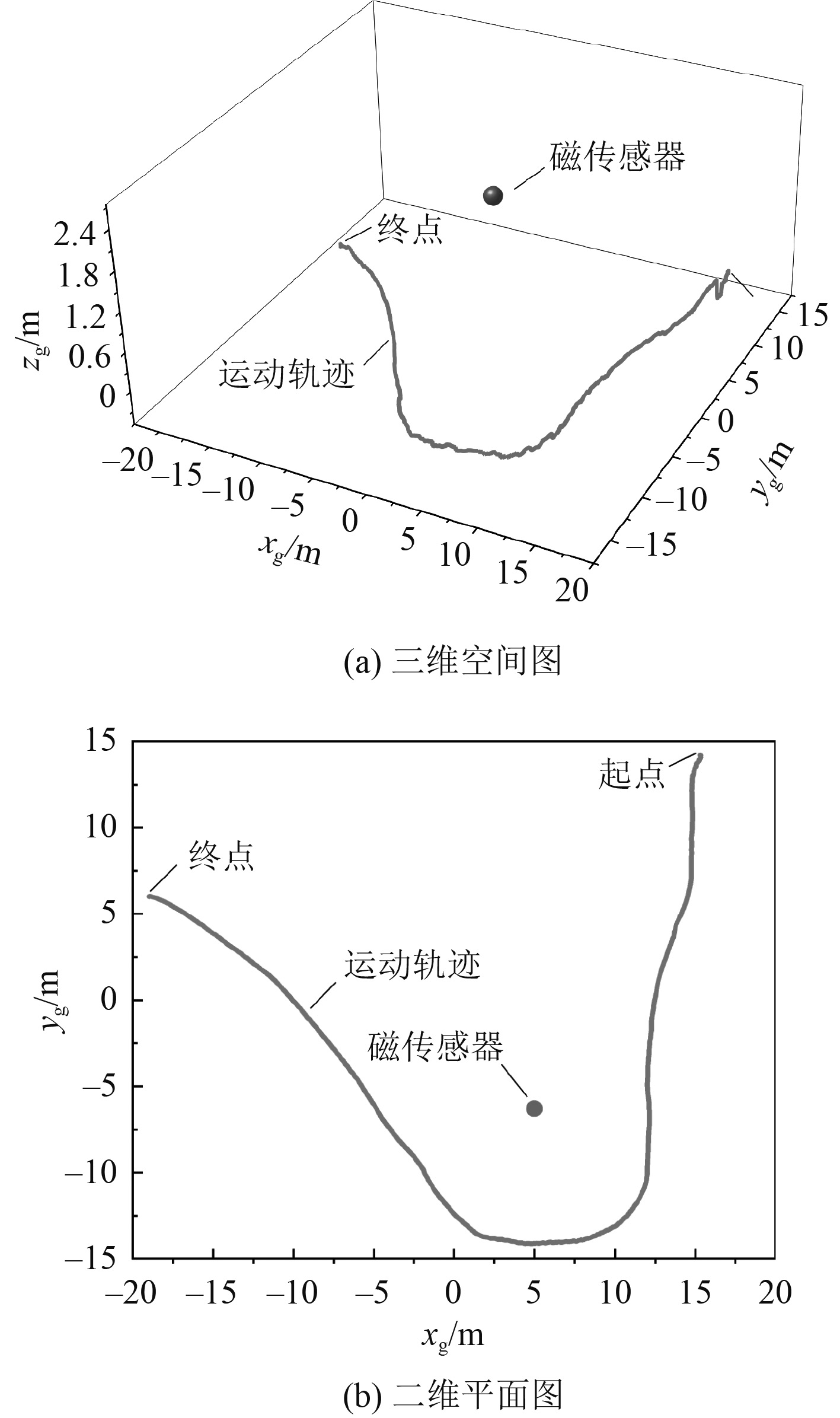
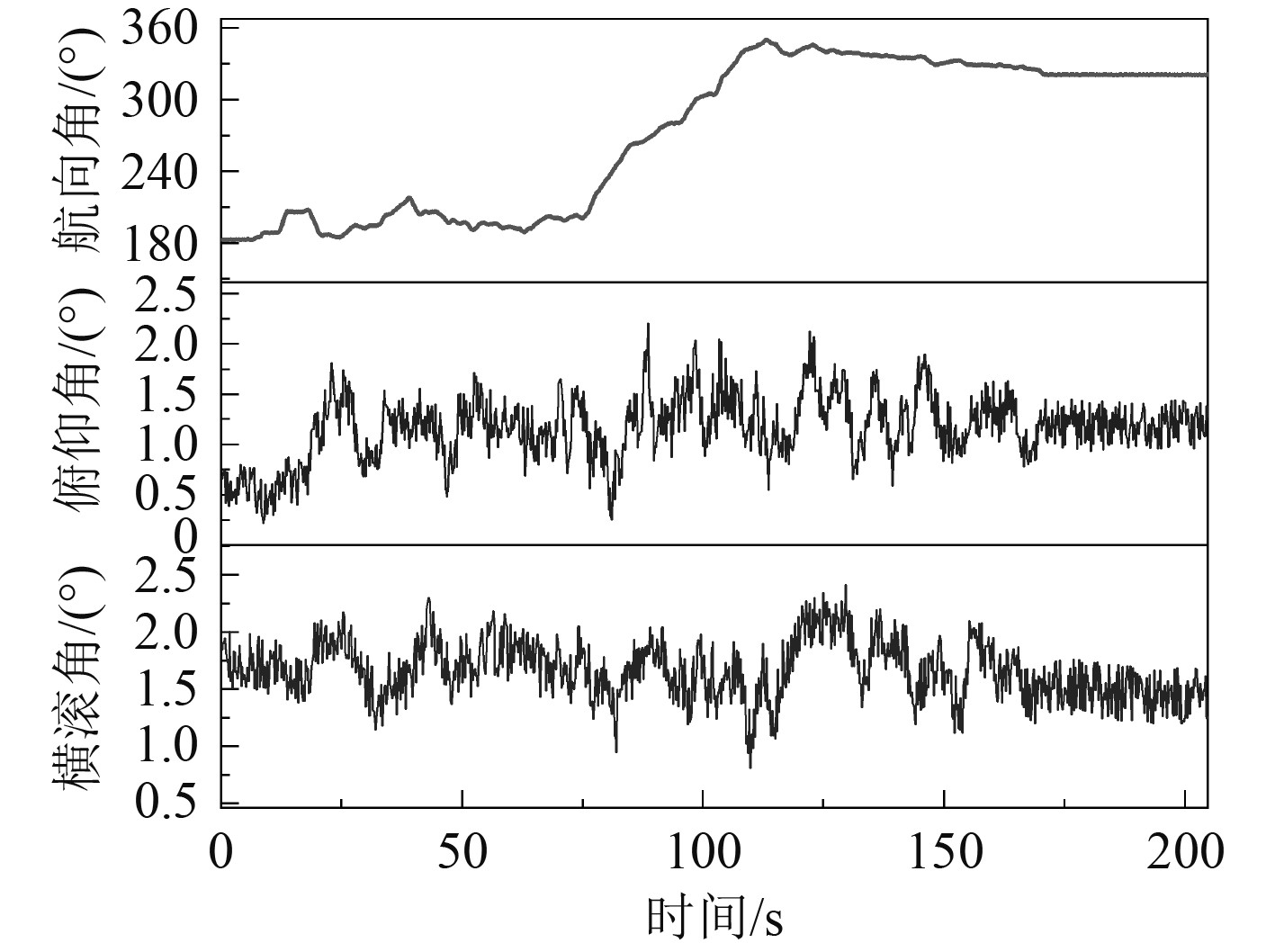
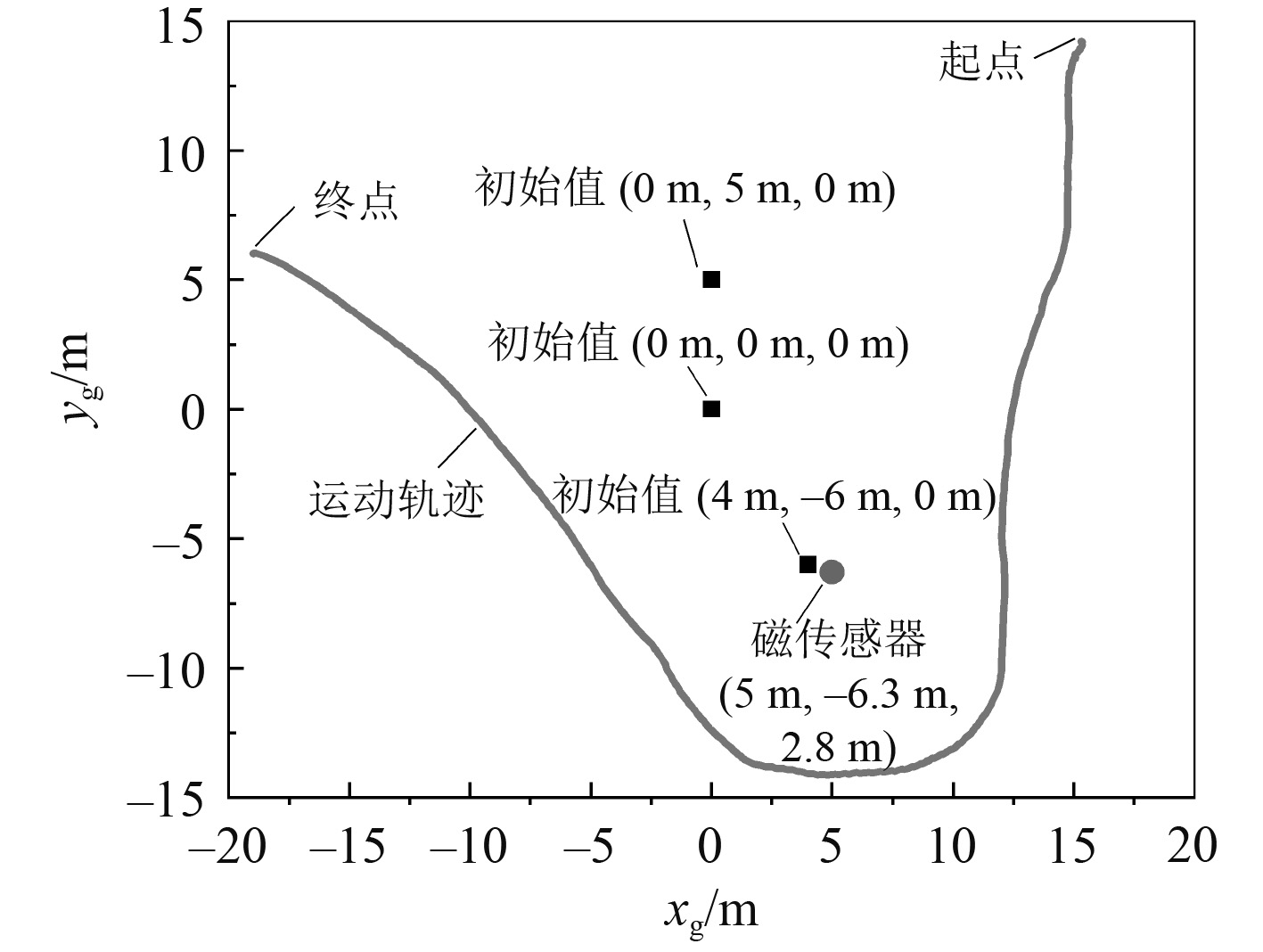
4 数值仿真实验 4.1 实验配置设被校准磁传感器位置、姿态为s=(5m, −6.3m, 2.8m, 20°, 3°, 170°)。校准装置沿着弧形轨迹运动,通过被校准磁传感器附近,如 图4所示。线圈运动过程中的姿态角变化如图5所示。
|
图 4 线圈运动轨迹及磁传感器位置 Fig. 4 Motion trajectory of coil and position of magnetic sensor |
|
图 5 线圈运动过程中的姿态角变化 Fig. 5 Attitude angle change during coil movement |
被校准磁传感器位于线圈轨迹上方2.8 m处,线圈轨迹与磁传感器的距离大于7 m。线圈运动速度约为0.4 m/s,采样间隔为ts=0.2 s,数据点数为K=1 025,运动时间为204.8 s。在线圈轨迹数据中加入定位噪声0.05 m,在姿态数据中加入姿态偏差0.1°和姿态噪声0.5°,得到校准装置(电磁线圈)的位置、姿态信息c(t)。
设圆柱形螺线管线圈的内半径r1=0.175 m,外半径r2=0.215 m,高度h0=0.100 m,匝数为N=1 100,导线电流为I=3 A。安匝量NI=3 300 AT,根据式(1)可得线圈磁矩为mz=395.6 A·m2。
根据线圈和被校准磁传感器位置、姿态数据(无噪声),利用圆柱形螺线管线圈磁场计算模型(见式(2))和坐标转换矩阵
考虑被校准磁传感器存在正交误差0.5°、标度误差0.5%和系统噪声0.5 nT,得到磁传感器的系统误差值。
考虑被校准磁传感器和地磁监测传感器共同所在的地磁环境中,存在幅值20nT以内的随机噪声和±15nT以内的渐变噪声[6],可得到地磁监测传感器测量得到的地理坐标系下的地磁波动值ΔBmg(t)=[ΔBmgx(t),ΔBmgy(t),ΔBmgz(t)]T,以及被校准磁传感器测量得到的磁传感器坐标系下的地磁波动的模拟值。
线圈磁场真实值、磁传感器系统误差值以及地磁波动模拟值相加,可得到被校准磁传感器上测量的线圈磁场测量数据的模拟值Bms(t)。
将仿真产生的线圈位置、姿态数据模拟值c(t)、被校准磁传感器的磁场测量数据模拟值Bms(t)以及地磁监测传感器的地磁波动测量数据模拟值ΔBmg(t)作为输入数据,对被校准磁传感器进行位置、姿态校准优化求解。
4.2 数据分析参数的定义将定位误差es定义为被校准磁传感器位置的真实值(xs, ys, zs)与计算值(xc, yc, zc)之间的欧几里德距离:
| $ {e_{\text{s}}} = \sqrt {{{{\text{(}}{x_{\text{c}}} - {x_{\text{s}}}{\text{)}}}^2} + {{{\text{(}}{y_{\text{c}}} - {y_{\text{s}}}{\text{)}}}^2} + {{{\text{(}}{z_{\text{c}}} - {z_{\text{s}}}{\text{)}}}^2}} ,$ | (9) |
被校准磁传感器姿态的真实值(ψs,θs,ϕs)和计算值(ψc, θc, ϕc)之间的姿态误差为:
| $ \left\{ \begin{gathered} {e_\psi } = \left| {{\psi _{\text{c}}} - {\psi _{\text{s}}}} \right| ,\\ {e_\theta } = \left| {{\theta _{\text{c}}} - {\theta _{\text{s}}}} \right|,\\ {e_\varphi } = \left| {{\varphi _{\text{c}}} - {\varphi _{\text{s}}}} \right|。\\ \end{gathered} \right. $ | (10) |
相对残差RRE反映线圈磁场计算值对测量值的拟合程度,代表算法的收敛程度。RRE计算公式如下:
| $ {{RRE}} = \frac{{{{\left\| {{{\boldsymbol{B}}_{{{cs}}}} - \left( {{{\boldsymbol{B}}_{{{ms}}}} - \Delta {{\boldsymbol{B}}_{{{ms}}}}} \right)} \right\|}_{\rm{F}}}}}{{{{\left\| {{{\boldsymbol{B}}_{{{ms}}}}} \right\|}_{\rm{F}}}}} \times 100\%。$ | (11) |
校准优化计算时,搜索上限Xu=(20 m, 20 m, 20 m, 360°, 90°, 180°),搜索下限Xl=(−20 m, −20 m, 0 m, 0°, −90°, −180°)。
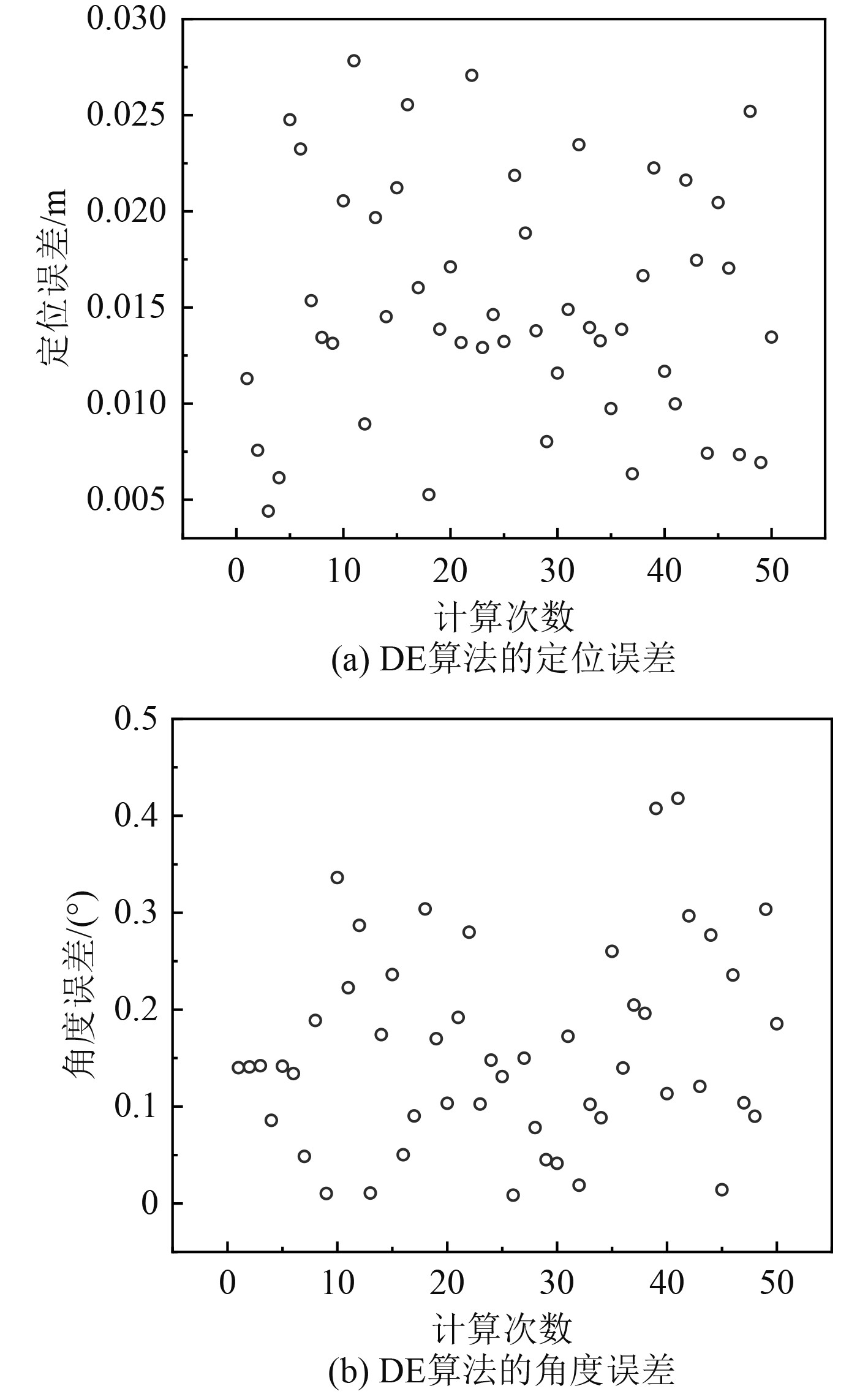
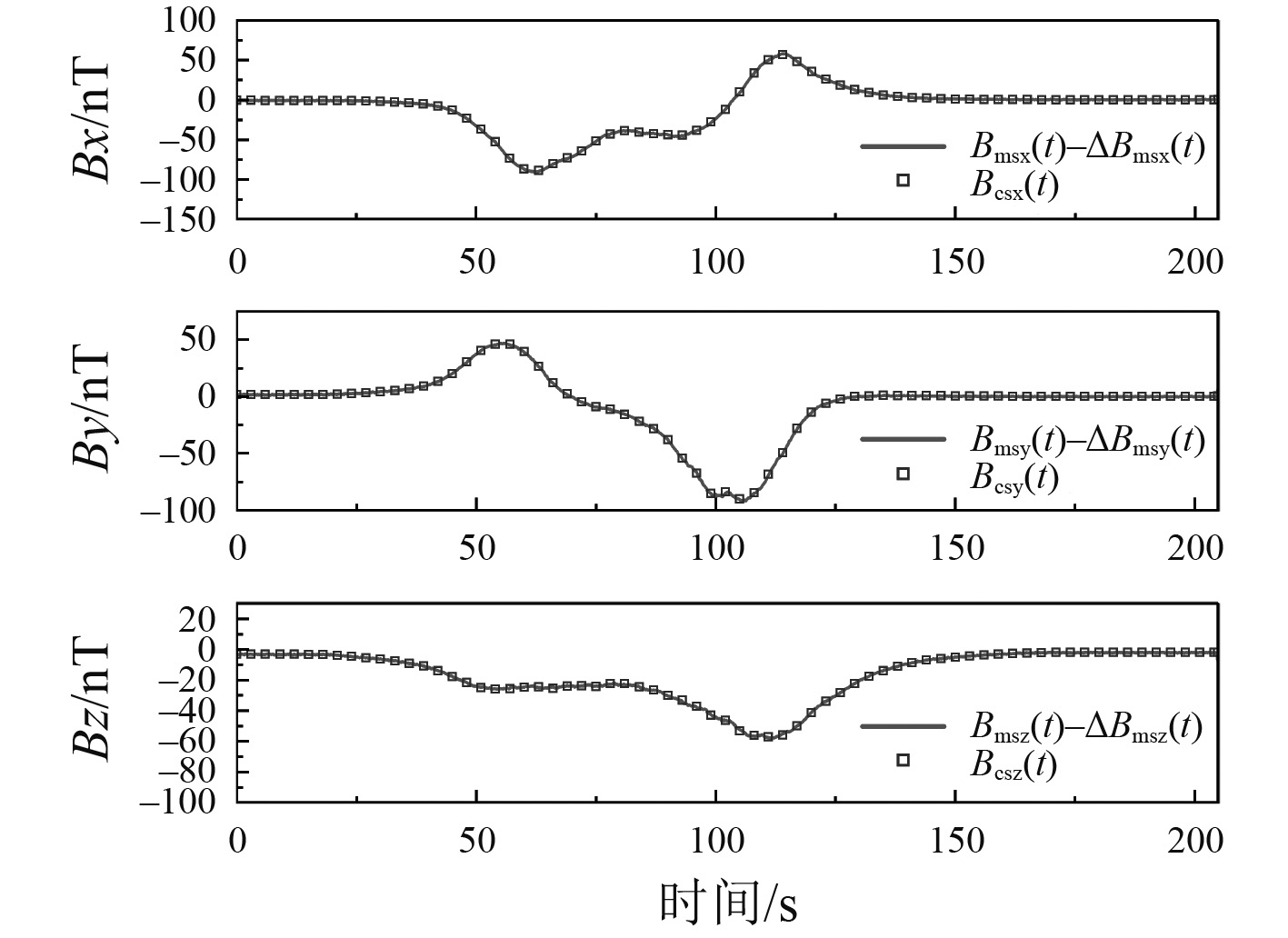
采用DE算法计算时,设置NP=60,F=0.7~0.9,CR=0.7,Gm=500,目标向量初始值无需预设。重复50次仿真计算,得到的误差区间为RRE=[1.66%, 1.95%],es=[0.01 m, 0.03 m],eψ=[0.00°,0.43°],eθ=[0.00°,0.27°],eϕ=[0.01°,0.36°],线圈磁场计算值Bcs(t)与测量值(Bms(t)−ΔBms(t))之间吻合程度较好。DE算法的定位误差如图6(a)所示,角度误差如图6(b)所示。例如,某次计算得到的相对残差RRE=1.95%,定位误差es=0.02 m,姿态角误差eψ=0.27°,eθ=0.21°,eϕ=0.02°,校准精度较高。线圈磁场计算值Bcs(t)与测量值(Bms(t)−ΔBms(t))之间对比如图7所示。
|
图 6 DE算法的定位误差和角度误差 Fig. 6 Positioning error and angle error of DE algorithm |
|
图 7 线圈磁场测量值与计算值对比 Fig. 7 Comparison between measured and calculated values of coil magnetic field |
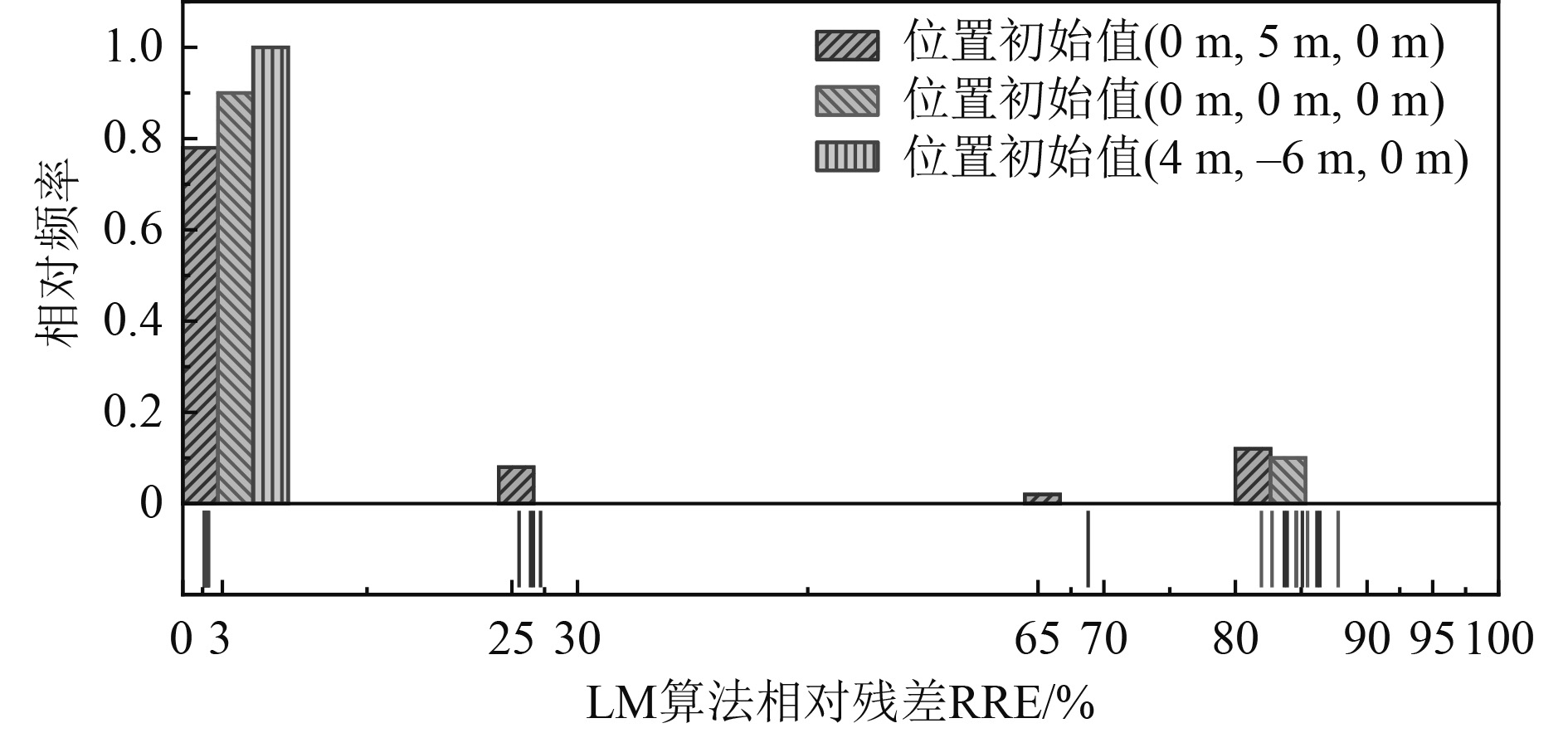
采用LM算法计算时,最大迭代次数mmax=500,收敛阈值为10−8。设置姿态角初始值为(ψs0= 0°, θs0= 0°, ϕs0= 0°)。分别设定磁传感器位置坐标为(4 m, −6 m, 0 m)、(0 m, 0 m, 0 m)和(0 m, 5 m, 0 m),如 图8所示。对每个位置坐标初始值独立进行50次仿真实验,将不同初始值的LM算法得到的相对残差RRE区间进行对比,如表1所示。可以看出,当LM算法的位置坐标初始值非常接近真实值时,即(xs0,ys0,zs0)为(4 m, −6 m, 0 m)时,LM算法没有出现不收敛的情况。此时得到的误差区间为RRE∈[1.66%, 1.98%],es∈[0.01 m, 0.03 m],eψ∈[0.01°,0.41°],eθ∈[0.01°,0.34°],eϕ∈[0.01°,0.35°],能够实现精确校准。当位置坐标初始值远离真实值时,LM算法计算结果不稳定,容易出现无法收敛的情况。其相对残差分布如图9所示,其中相对频率为结果出现的次数除以实验的总次数。
|
图 8 磁传感器坐标初始值设定 Fig. 8 Initial value setting of magnetic sensor coordinates |
|
|
表 1 DE算法与LM算法的相对残差(RRE)对比 Tab.1 Comparison of relative residual error (RRE) from DE and LM algorithms |
|
图 9 渐变噪声幅值为±15 nT时的RRE分布图 Fig. 9 RRE distribution with gradient noise amplitude of ±15 nT |
从图9可以看出,只有在位置初始值最接近真实值时,即(xs0,ys0,zs0)=(4 m, −6 m, 0 m)时,相对残差在1%~3%之间(LM算法收敛)的相对频率为1,没有出现不收敛的情况。位置初始值( xs0,ys0,zs0)为(0 m, 0 m, 0 m)时,相对残差在1%~3%之间(LM算法收敛)的相对频率为0.90。位置初始值(xs0,ys0,zs0)为(0 m, 5 m, 0 m)时,相对残差在1%~3%之间(LM算法收敛)的相对频率为0.78。
实验中设置地磁波动噪声时,由于渐变噪声较大(±15 nT以内),可能难以通过算法迭代消除,导致LM算法无法收敛。为进一步考察影响LM算法稳定性的相关因素,将地磁波动中的渐变噪声设置为±10 nT以内和±5 nT以内,LM算法采用3种初始值,每种情况独立进行50次实验。渐变噪声为±10 nT时,设置不同位置初始值,LM算法的相对残差分布如图10所示。渐变噪声为±5 nT时,设置不同位置初始值,LM算法的相对残差分布如图11所示。

|
图 10 渐变噪声幅值为±10 nT时的RRE分布图 Fig. 10 RRE distribution with gradient noise amplitude of ±10 nT |

|
图 11 渐变噪声幅值为±5 nT时的RRE分布图 Fig. 11 RRE distribution with gradient noise amplitude of ±5 nT |
渐变噪声在±10 nT以内随机变化时,位置初始值(xs0,ys0,zs0)为(4 m, −6 m, 0 m)、(0 m, 0 m, 0 m)、(0 m, 5 m, 0 m)时,相对残差在1%~3%之间(LM算法收敛)的相对频率均为1,没有出现不收敛的情况。
渐变噪声在±5 nT以内随机变化时,位置初始值为(4 m, −6 m, 0 m)、(0 m, 0 m, 0 m)、(0 m, 5 m, 0 m)时,相对残差在1%~3%之间(LM算法收敛)的相对频率均为1,没有出现不收敛的情况。
通过对比图9~图11,不同渐变噪声下,LM算法分别设置3种位置初始值时的相对残差,可知在渐变噪声较大时,LM算法更加依赖初始值的设定,初始值越接近真实值,LM算法稳定性和精度越好。当渐变噪声较小时,初始值设定对LM算法的影响不大。因此在地磁噪声干扰较大时,不宜采用LM算法对水下磁传感器位置姿态进行求解。
5 校准装置制作和验证实验 5.1 实验装置校准装置由圆柱形螺线管线圈、稳流电源、组合导航设备、无磁小车、计算机和校准软件等构成,结构示意图如图12所示。
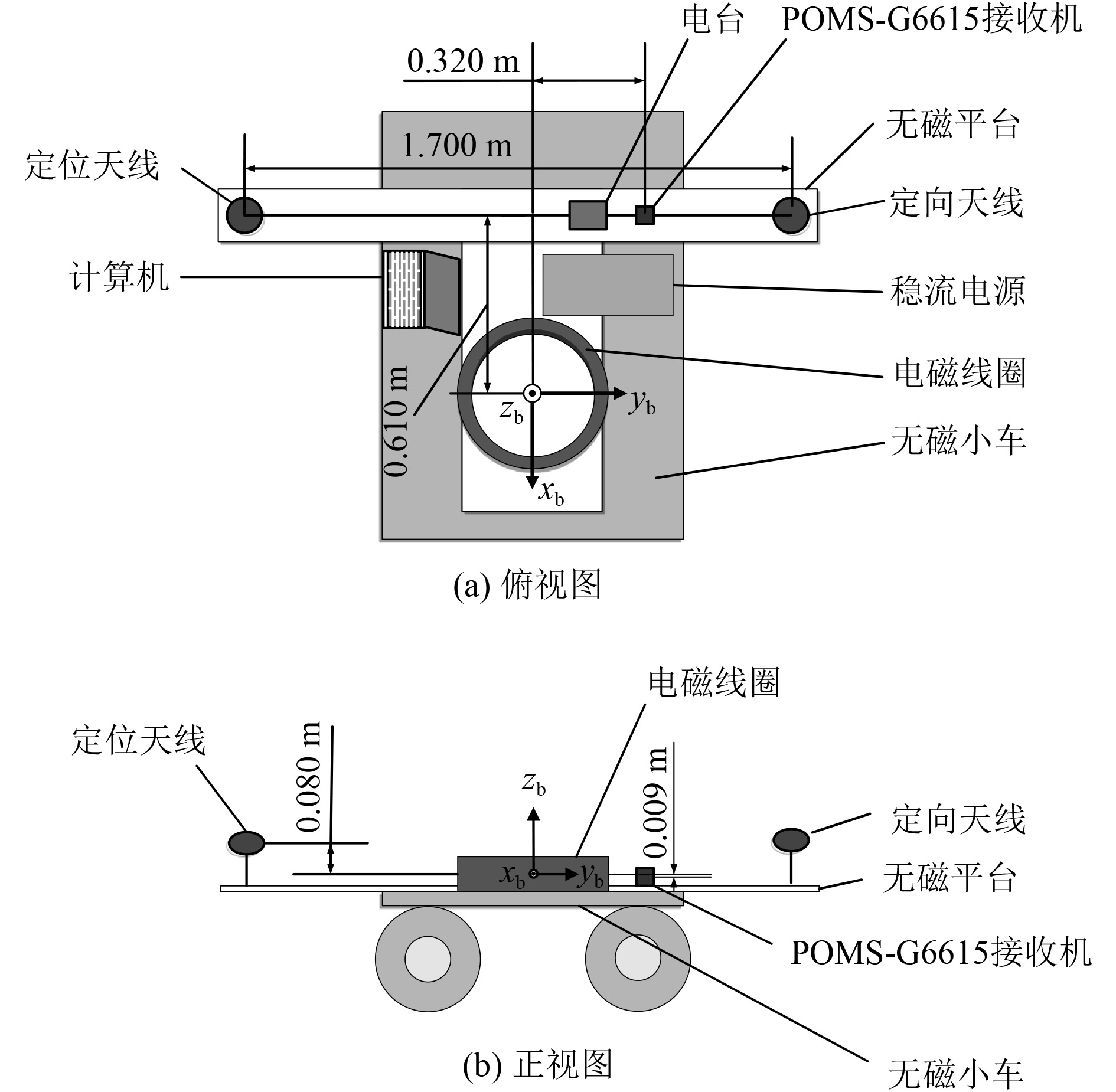
|
图 12 校准装置结构示意图 Fig. 12 Structural diagram of calibration device |
被校准磁传感器为典型的三轴磁通门传感器,其主要技术参数如表2所示。
|
|
表 2 磁传感器主要技术参数 Tab.2 Main Technical parameters of magnetic sensor |
实验场地选择在开阔无遮蔽的户外区域,校准装置运动范围为20 m×25 m的平面,地磁监测传感器布置在距离实验区域25 m外的位置。
在实验开始前,使用POMS-G6615组合导航系统测量被校准磁传感器的位置(xm, ym, zm),组合导航设备的位置测量误差为0.02 m。使用HWT905-485姿态角度传感器测量被校准传感器的横摇角、纵摇角和磁航向角(横摇角和纵摇角的测量误差小于0.05°,磁航向角的测量误差小于1°)。根据当地地磁偏角(可获得的地磁偏角数据可能存在0.3°左右的误差),可进一步得到地理坐标下的真航向角,从而得到被校准磁传感器在地理坐标系下的姿态角测量值(ψm, θm, φm)。
校准装置通电前,利用被校准磁传感器和地磁监测传感器测量一段时间的环境磁场,取平均值作为背景磁场。校准装置通电后,以约0.4 m/s的速度沿弧形轨迹经过磁传感器附近;装置中的线圈通电作为移动磁源;组合导航系统采集线圈的位置姿态信息;被校准磁传感器同步测量磁场信息;地磁监测传感器测量地磁背景场,采样率为5 Hz。将线圈的位置姿态数据c(t)、被校准磁传感器的磁场测量数据Bms(t)、地磁监测传感器测量数据ΔBmg(t)作为输入,采用校准软件进行解算,最后输出被校准磁传感器的位置及姿态数据。
实验分别在白天和凌晨进行。白天地磁环境较差,实验场地周边地铁、大型工业设施等正在运行,地磁波动幅值约30 nT,如图13(a)所示。凌晨地磁环境较好,实验场地周边的地铁、大型工业设施等已停止运行,地磁波动幅值约2 nT,如图13(b)所示。
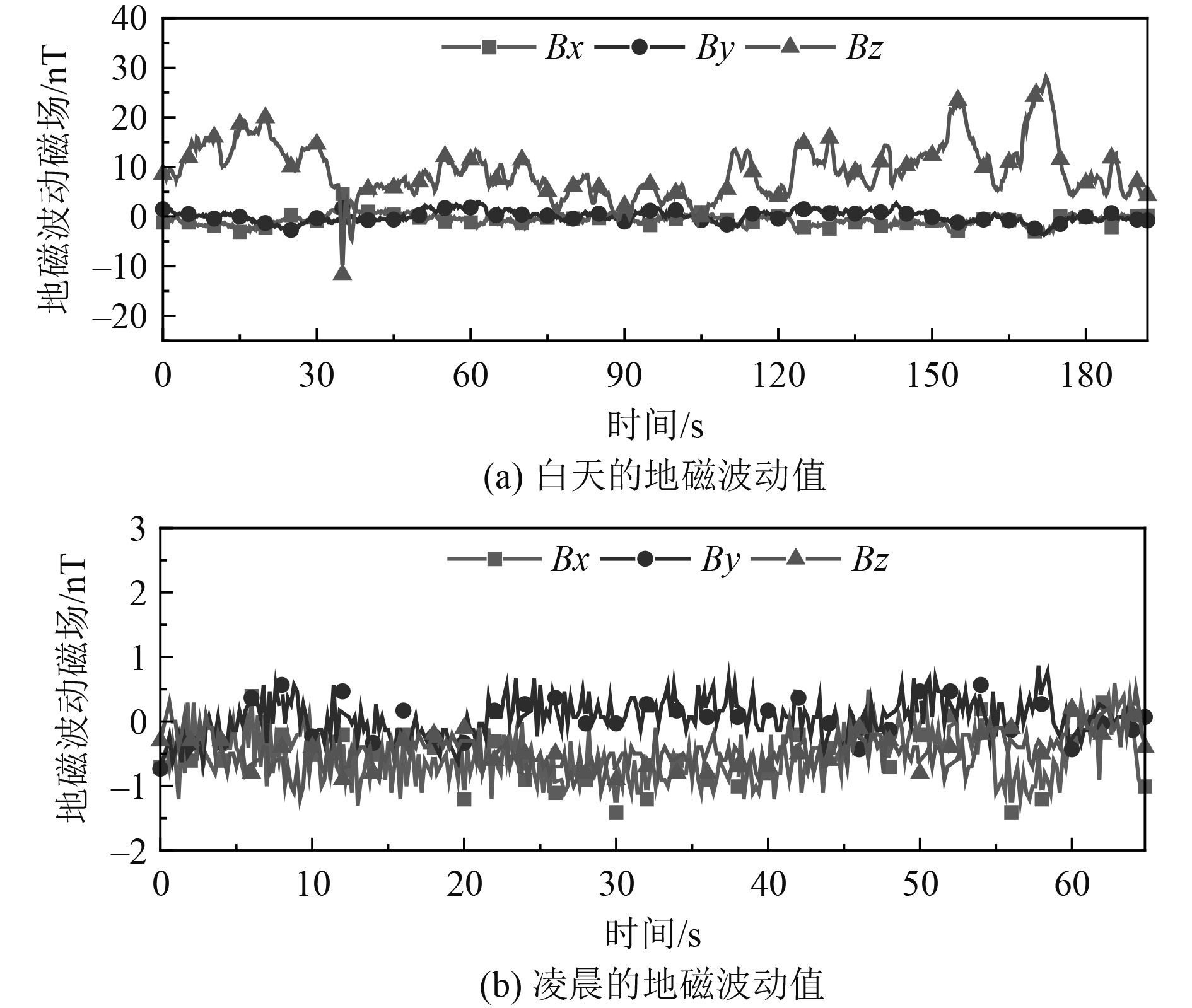
|
图 13 白天和凌晨的地磁波动值 Fig. 13 Geomagnetic fluctuations of daytime and daybreak |
白天进行的实验中,磁传感器位于线圈上方约2.5 m,线圈轨迹与磁传感器距离大于7 m。凌晨进行的实验与白天进行的实验配置相同,只是线圈运动轨迹稍有区别。
白天进行的实验中,使用组合导航设备和姿态角度传感器,测得在地理坐标系下,被校准磁传感器的位置姿态测量值为(xm =4.37 m, ym=−7.62 m,zm=2.63 m, ψm=350.57°, θm=0.13°, ϕm=177.70°)。凌晨进行的实验中,地理坐标系下,被校准磁传感器的位置姿态测量值为(xm=6.13 m, ym=−4.19 m,zm=2.61 m, ψm=350.60°, θm=0.39°, ϕm=177.25°),其余设置与白天进行的实验配置相同,只是线圈运动轨迹稍有区别。
将定位误差es定义为被校准磁传感器位置的测量值(xm, ym, zm)与计算值(xc, yc, zc)之间的欧几里德距离:
| $ {e_{\text{s}}} = \sqrt {{{{\text{(}}{x_{\text{c}}} - {x_{\text{m}}}{\text{)}}}^2} + {{{\text{(}}{y_{\text{c}}} - {y_{\text{m}}}{\text{)}}}^2} + {{{\text{(}}{z_{\text{c}}} - {z_{\text{m}}}{\text{)}}}^2}} ,$ | (12) |
被校准磁传感器姿态的真实值(ψm,θm,ϕm)和计算值(ψc, θc, ϕc)之间的姿态误差为:
| $ \left\{ \begin{gathered} {e_\psi } = \left| {{\psi _{\text{c}}} - {\psi _{\text{m}}}} \right|,\\ {e_\theta } = \left| {{\theta _{\text{c}}} - {\theta _{\text{m}}}} \right|,\\ {e_\varphi } = \left| {{\varphi _{\text{c}}} - {\varphi _{\text{m}}}} \right| 。\end{gathered} \right. $ | (13) |
采用DE算法分别对白天实验数据和凌晨实验数据进行了优化计算,算法参数设置与数值仿真实验一致,计算结果如表3所示。可以看出,白天实验数据未进行地磁波动消除措施时,拟合较差(RRE=13.11%),校准精度较低;采取地磁波动消除措施后,拟合较好(RRE=3.63%),校准精度较高(es=0.07 m,eψ=1.37°,eθ=0.79°,eϕ=0.78°)。凌晨实验数据的拟合较好(RRE=2.56%),校准精度最高(es=0.05 m,eψ=1.34°,eθ=0.27°,eϕ=1.17°)。较大的地磁波动对磁传感器的校准精度影响较大,采取地磁波动消除措施后,可显著提高校准精度,已经接近地磁波动值较小情况下的校准精度。
|
|
表 3 场地实验数据的DE算法计算结果 Tab.3 Calculation results of DE algorithm from data of field tests |
根据白天实验数据,采取地磁波动消除措施后,计算得到的磁场线圈磁场计算值Bcs(t)与测量值(Bms(t)−ΔBms(t)),如图14所示。可以看出,二者吻合程度较高。
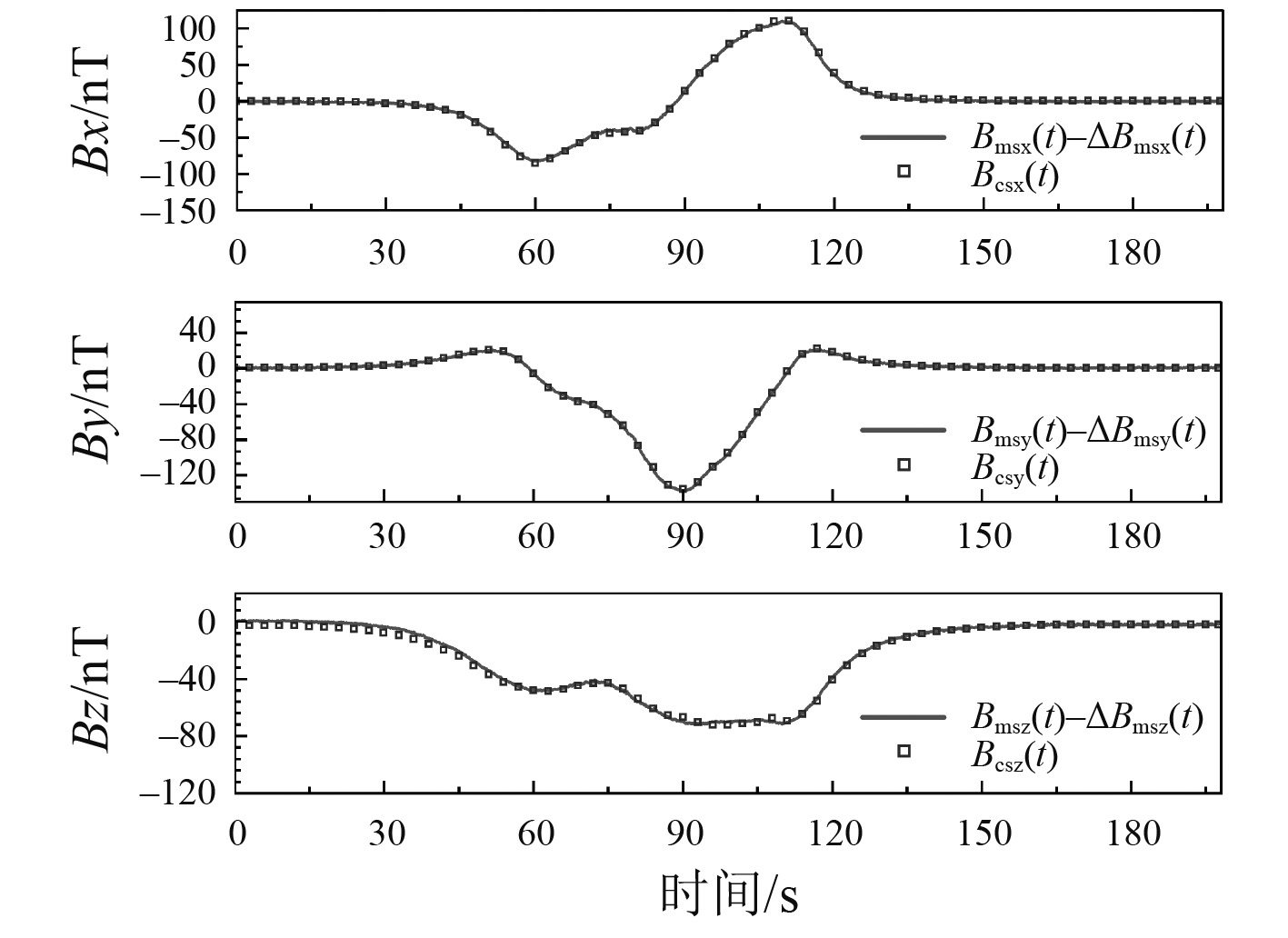
|
图 14 白天实验数据消除地磁波动值后得到的线圈磁场计算值与测量值 Fig. 14 Calculated and measured values of coil magnetic field from data of daytime test after removing geomagnetic fluctuations |
LM算法参数设置与数值仿真实验一致,考虑到LM算法受位置初始值影响较大,分别设置被校准磁传感器的坐标位置初始值为(4 m, −6 m, 0 m)、(0 m, 0 m, 0 m)和(0 m, 5 m, 0 m)三种情况。
对于白天和凌晨2组实验数据,LM算法的计算结果如表4所示。使用LM算法对白天和凌晨的实验数据进行校准解算时,在3种不同初始值设置的情况下,均能较好地收敛,且校准精度较高。
|
|
表 4 场地实验数据的LM算法计算结果 Tab.4 Calculation results of LM algorithm from data of field tests |
从图13可知,即使在地磁噪声较大的白天,地磁波动磁场中的渐变噪声的幅值也远小于±15 nT,因此LM算法受初始值影响较小,设置的3种初始值均能实现磁传感器的精确定位定姿。LM算法计算结果与DE算法差别不大,说明在地磁环境噪声不大的时候,LM算法能够对磁传感器实现精确校准。
6 结 语水下磁传感器广泛应用于多种场合,对其进行位置和姿态的校准是非常重要的。本文设计和制作了基于动态电磁线圈的水下磁传感器校准装置场地试验样机,进行了数值仿真实验和实际装置场地验证实验,并采取措施消除地磁波动的影响。仿真实验结果表明,所设计的装置能对7 m外的磁传感器实现精确校准,定位误差不超过0.03 m,姿态误差不超过0.43°。场地实验结果表明,实际装置能对7 m外的磁传感器实现精确校准,定位误差0.07 m,姿态误差1.37°。利用地磁监测传感器的测量数据,可有效消除和降低地磁波动对校准结果的不利影响。当渐变噪声较大时,LM算法受初始值影响较大,容易出现不收敛的情况,导致校准精度较低;而DE算法则未出现不收敛的情况。由于DE算法具有更好的鲁棒性,且无需设置初始值,仍具有一定优势。
| [1] |
HOLMES J J. Modeling a ship’s ferromagnetic signatures[M]. Maryland: Morgan & Claypool Publishers, 2007: 1−3.
|
| [2] |
候希晨, 孙玉东, 吴江海. 基于PSO算法的磁偶极子阵列舰船磁场模拟研究[J]. 舰船科学技术, 2022, 44(18): 159-164. HOU Xichen, SUN Yudong, WU Jianghai. Magnetic field modelling of ship using magnetic dipole array based on PSO algorithm[J]. Ship Science and Technology, 2022, 44(18): 159-164. DOI:10.3404/j.issn.1672-7649.2022.18.033 |
| [3] |
郭成豹, 殷琦琦. 舰船磁场磁单极子阵列法建模技术[J]. 物理学报, 2019, 68(11): 114101. GUO Chengbao, YIN Qqiqi. Magnetic monopole array model for modeling ship magnetic signatures[J]. Acta Physica Sinica, 2019, 68(11): 114101. DOI:10.7498/aps.68.20190201 |
| [4] |
孙兴凯, 胡平, 吕俊军, 等. 基于时谐电偶极子模型的交变磁场定位技术[J]. 舰船科学技术, 2022, 44(7): 132-137. SUN Xingkai, HU Ping, LV Junjun, et al. Research on alternating magnetic field location based on time-harmonic electric dipole model[J]. Ship Science and Technology, 2022, 44(7): 132-137. DOI:10.3404/j.issn.1672-7649.2022.07.026 |
| [5] |
郭成豹, 胡松, 王文井, 等. 利用磁传感器阵列磁场差值的舰船磁场反演建模方法[J]. 兵工学报, 2022, 43(1): 111-119. GUO Chengbao, HU Sao, WANG Wenjing, et al. Ship magnetic field inversion modeling method utilizing the magnetic field difference between magnetic sensors[J]. Acta Armamentarii, 2022, 43(1): 111-119. DOI:10.3969/j.issn.1000-1093.2022.01.012 |
| [6] |
吕俊军, 陈凯, 苏建业, 等. 海洋中的电磁场及其应用[M]. 上海: 上海科学技术出版社, 2020: 296−300.
|
| [7] |
郭成豹, 刘大明, 肖昌汉, 等. 一种磁传感器定位方法[P]. 中国: 102928884, 2015-07-22.
|
| [8] |
O’DONOGHUE K, EUSTACE D, GRIFFITHS J, et al. Catheter position tracking system using planar magnetics and closed loop current control[J]. IEEE Transactions on Magnetics, 2014, 50(7): 5100209. |
| [9] |
O’DONOGHUE K, CANTILLON-MURPHY P. Low cost super-Nyquist asynchronous demodulation for use in EM tracking systems[J]. IEEE Transactions on Instrumentation and Measwement, 2015, 64(2): 458-466.
|
| [10] |
PFEIFFER C, RUFFIEUX S, ANDERSEN L M, et al. On-scalp MEG sensor localization using magnetic dipole-like coils: a method for highly accurate co-registration[J]. Neuroimage, 2020, 212: 116686. DOI:10.1016/j.neuroimage.2020.116686 |
| [11] |
倪光正, 杨仕友, 邱捷. 工程电磁场数值计算[M]. 北京: 机械工业出版社, 2010: 67−69.
|
| [12] |
严恭敏, 翁浚. 捷联惯导算法与组合导航原理[M]. 西安: 西北工业大学出版社, 2019: 244−245.
|
| [13] |
PRICE K, STORN R, LAMPINEN J. Differential evolution[M]. Berlin: Springer, 2005: 157−159.
|
| [14] |
STORN R, PRICE K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 |
| [15] |
PARK T Y, KIM H J, PARK S H, et al. Differential evolution method to find optimal location of a single-element transducer for transcranial focused ultrasound therapy[J]. Computer Methods and Programs in Biomedicine, 2022, 219: 106677. |
| [16] |
FORST W, HOFFMANN D. Optimization-Theory and practice[M]. New York: Springer, 2008: 23-25.
|
| [17] |
CHONG E, ZAK S. An introduction to optimization[M]. New York: John Wiley & Sons, Inc. , 2001: 145−148.
|
 2023, Vol. 45
2023, Vol. 45

