随着近年来声呐探测技术的发展,如何进行水下防御成为了国内外的研究热点。主动声呐利用发射脉冲信号在目标上的回波来探测目标,为了防止敌方探测到我方目标,就要削弱或者完全抵消目标回波。通过估计目标回波的参数,包括中心频率、初相位等,利用估计得到的参数发射反相信号可对目标回波进行抵消,但当信噪比降低时,参数估计会产生较大的误差,从而降低对目标回波的抵消性能。如何在低信噪比情况下提高目标回波参数估计性能是急需解决的问题。
传统的降噪方法有相干平均和滤波,相干平均通过将多次观测信号相加取平均以抵消噪声,该方法虽然简单、运算量小,但对非平稳随机噪声的降噪效果不佳,并且该方法需要大量的观测数据,处理进程较长。滤波方法是假定信号和噪声处在不同的频带上,通过滤波器将通带外的噪声进行滤除,但在未知信号频率范围时,无法设计滤波器参数。近年来,国内外学者提出许多通过将信号分量与噪声分量进行分离从而降噪的方法,如奇异值分解[1](SVD)、独立分量分析[2-3](ICA)、小波变换[4-7]、经验模态分解[8](EMD)等。奇异值分解利用含噪信号构造Hankel矩阵,对此矩阵进行奇异值分解,所得到奇异值中较大的对应信号成分,较小的对应噪声成分,但当信噪比较低时,信号成分与噪声成分奇异值的分界不明显,导致信号与噪声难以分离。ICA通过构造解混系统将信号分量与噪声分量进行盲分离达到降噪目的,但由于ICA的不确定性,分解出的信号分量幅度和相位可能产生变化。小波变换利用不同尺度的小波基将信号分解成许多子带信号,将信号能量集中到某些频带的少数系数上,通过将其他频带上的小波系数置零或是给予小的权重,即可达到抑制噪声的目的。然而,小波基的选取及分解层数的确定存在一定的盲目性。EMD是根据信号自身特性,将一个复杂的信号自适应地分解为一系列固有模态函数(IMF),通过将噪声所在的IMF置零达到降噪的目的,但当信噪比较低时,EMD分解容易产生模态混叠问题,导致信号分量与噪声分量难以分离。为解决模态混叠问题,Wu[9]和Yeh[10]分别提出了集总经验模态分解(EEMD)和互补集总经验模态分解(CEEMD)算法。EEMD虽然可以通过向信号中不断添加白噪声改变信号极值分布来避免模态混叠问题,但其集总平均次数一般要在几百次以上,非常耗时,并且会在每个IMF分量中残留一些白噪声。而CEEMD通过向信号中添加许多对符号相反的白噪声,可以在集总次数较少的情况下解决模态混叠问题,大大节约计算时间,并且可以基本上去除残留在IMF分量中的白噪声。
本文针对低信噪比情况下参数估计误差增大问题,提出一种基于CEEMD-MI的目标回波参数估计算法。首先利用CEEMD对目标回波进行自适应分解,通过MI选取信号成分所在固有模态函数对信号进行重构,再对重构后的信号进行参数估计。仿真及试验数据处理结果表明,所提算法能有效提高目标回波参数估计性能。
1 基于CEEMD-MI的目标回波参数估计 1.1 算法流程利用CEEMD-MI对目标回波进行参数估计可分为3个步骤。首先利用CEEMD对目标回波进行自适应分解,再通过MI重构目标回波,最后对重构后的信号进行参数估计。
1.2 基于CEEMD-MI的目标回波去噪 1.2.1 CEEMD算法互补集总经验模态分解(CEEMD)是依据信号自身特点来对信号进行自适应分解的方法,其原理是通过向信号中施加N组正负噪声,不断地减去由信号局部极大值点和局部极小值点构造的包络均值,当满足IMF条件,即极值点数目和过零点数目相等或最多差一个并且在该时间区间任一点包络均值为0,即可分离出添加正负噪声后信号的各个IMF,对其取平均。最后将N组噪声情况下分离出的IMF进行集总平均,即可得到最终的IMF分量,具体步骤如下:
步骤1 对信号
| $ \left[ \begin{gathered} x_i^ + (t) \\ x_i^ - (t) \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} 1&{ 1} \\ 1&{ - 1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {x(t)} \\ {{u_i}(t)} \end{array}} \right] \text{,} i = 1,2,...,N ,$ | (1) |
可得到加入正负噪声后的信号为:
| $ \left[ \begin{gathered} x_i^ + (t) \\ x_i^ - (t) \\ \end{gathered} \right] = \left[ \begin{gathered} x(t) + {u_i}(t) \\ x(t) - {u_i}(t) \\ \end{gathered} \right] \text{,} i = 1,2,...,N 。$ | (2) |
步骤2 对信号
| $ h_i^ + (t) = x_i^ + (t) - m_i^ + (t),$ | (3) |
| $ h_i^ - (t) = x_i^ - (t) - m_i^ - (t) 。$ | (4) |
步骤3 同理,找出
| $ h_{i1}^ + (t) = h_i^ + (t) - m_{i1}^ + (t) ,$ | (5) |
| $ h_{i1}^ - (t) = h_i^ - (t) - m_{i1}^ - (t) 。$ | (6) |
检查
| $ h_{ik}^ + (t) = h_{i(k - 1)}^ + (t) - m_{ik}^ + (t) ,$ | (7) |
| $ h_{ik}^ - (t) = h_{i(k - 1)}^ - (t) - m_{ik}^ - (t)。$ | (8) |
式(7)和式(8)中的
| $ c_{i1}^ + (t) = h_{ik}^ + (t) ,$ | (9) |
| $ c_{i1}^ - (t) = h_{ik}^ - (t) 。$ | (10) |
则
步骤4 令
| $ r_{i1}^ + (t) = x_i^ + (t) - c_{i1}^ + (t),$ | (11) |
| $ r_{i1}^ - (t) = x_i^ - (t) - c_{i1}^ - (t) 。$ | (12) |
将
| $ \begin{split} & r_{i2}^ + (t) = r_{i1}^ + (t) - c_{i2}^ + (t),\\ & r_{i2}^ - (t) = r_{i1}^ - (t) - c_{i2}^ - (t) ,\\ &\vdots \\ & r_{im}^ + (t) = r_{i(m - 1)}^ + (t) - c_{im}^ + (t),\\ & r_{im}^ - (t) = r_{i(m - 1)}^ - (t) - c_{im}^ - (t)。\end{split} $ | (13) |
式中:
| $ x_i^ + (t) = \sum\limits_{k = 1}^m {c_{ik}^ + (t) + } r_{im}^ + (t) ,$ | (14) |
| $ x_i^ - (t) = \sum\limits_{k = 1}^m {c_{ik}^ - (t) + } r_{im}^ - (t),$ | (15) |
对
| $ IM{F_{ik}} = {{[c_{ik}^ + (t) + c_{ik}^ - (t)]} \mathord{\left/ {\vphantom {{[c_{ik}^ + (t) + c_{ik}^ - (t)]} 2}} \right. } 2},$ | (16) |
再对加入N组噪声下得到的
| $ IM{F_k} = {{\sum\limits_{i = 1}^N {IM{F_{ik}}} }/ N}。$ | (17) |
式中,
互信息(MI)是2个随机变量间相互依赖性的度量,可以看成是一个随机变量中包含的关于另一个随机变量的信息量。假设存在一个随机变量
| $ I(X;Y) = \sum\limits_{x \in X} {\sum\limits_{y \in Y} {p(x,y)} } \log \left(\frac{{p(x,y)}}{{p(x)p()y}}\right)。$ | (18) |
式中:
令重构后的信号
| $ {y_R}(t) = {x_R}(t) \cdot \frac{1}{{\text{π} t}}。$ | (19) |
由式(19)可得
| $ {z_R}(t) = {x_R}(t) + j{y_R}(t) = {a_R}(t){e^{j{\varphi _R}(t)}} 。$ | (20) |
其中:
假设信号
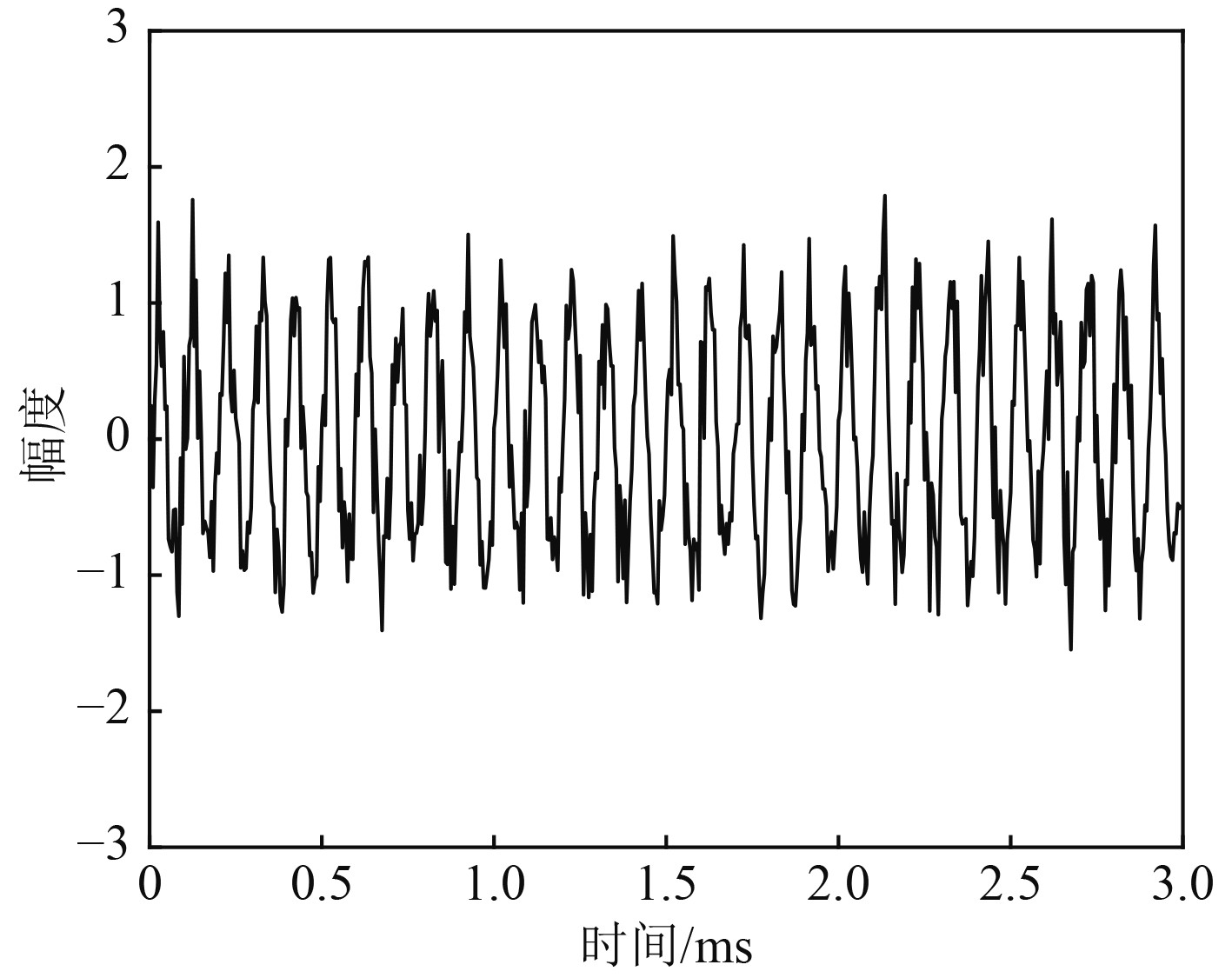
|
图 1 去噪前信号 Fig. 1 Signal before denoising |
对
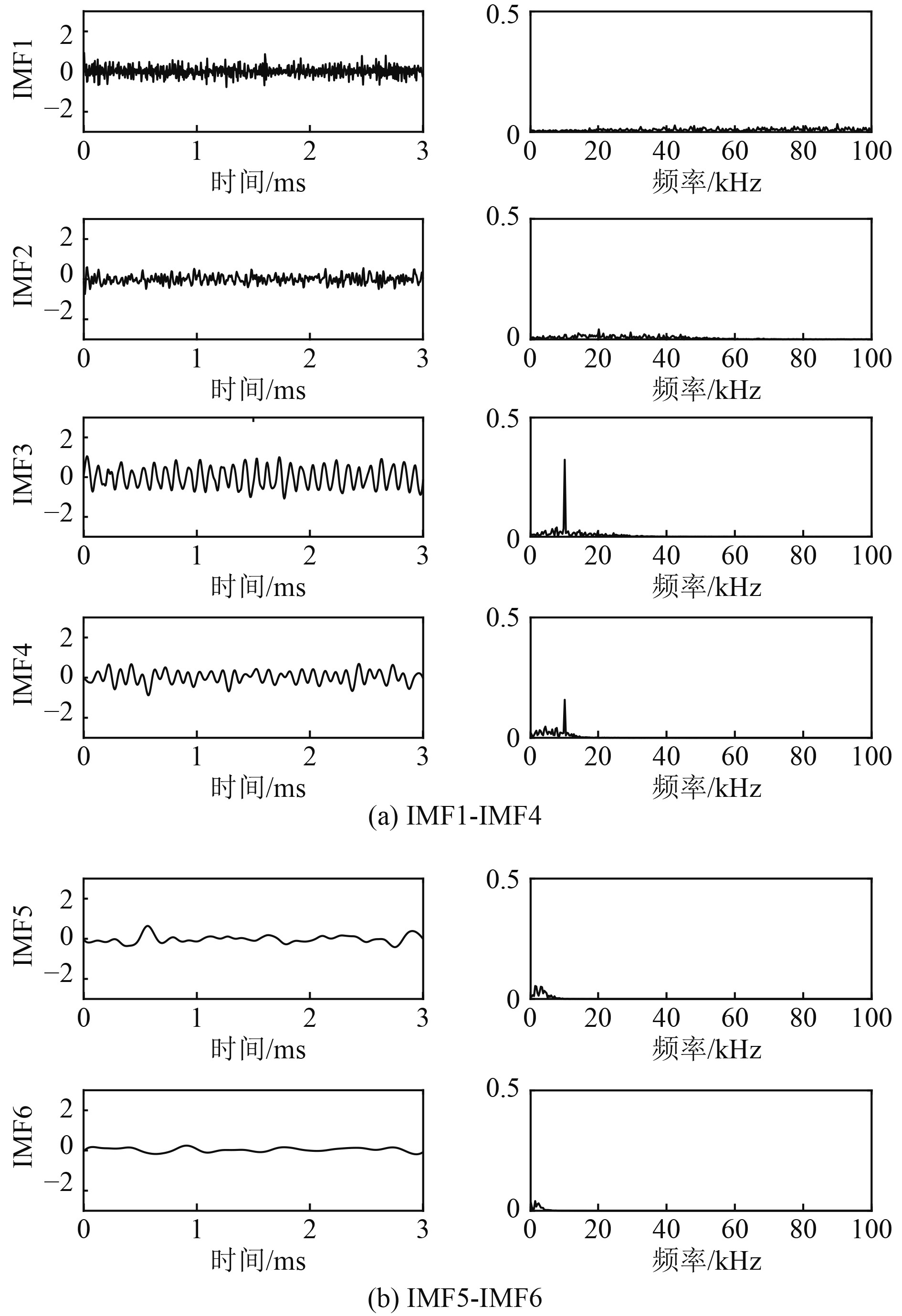
|
图 2 固有模态函数 Fig. 2 Intrinsic mode function |
图2中IMF1~IMF6分量与
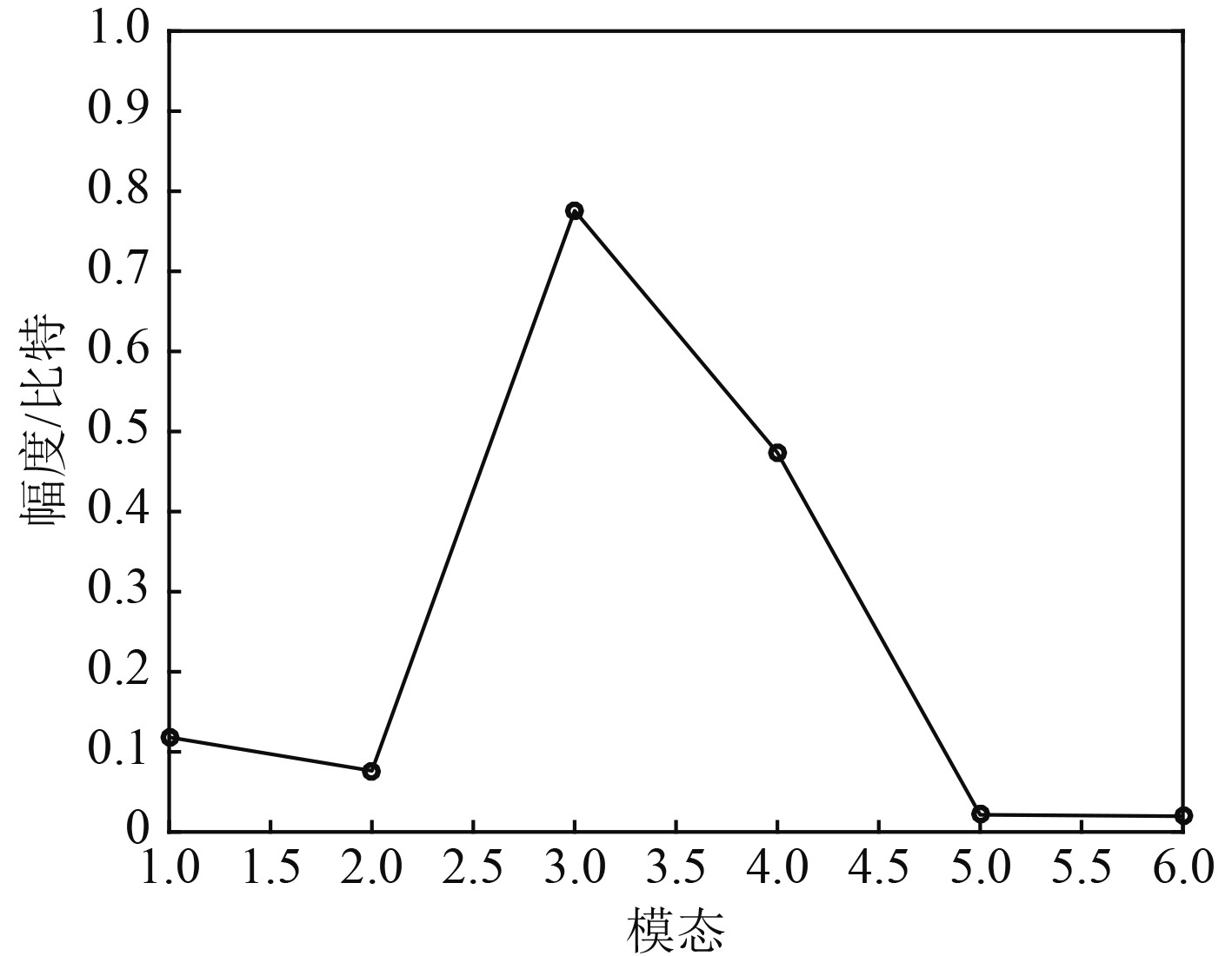
|
图 3 各个固有模态函数分量与原信号互信息 Fig. 3 Mutual information of IMFs and original signal |
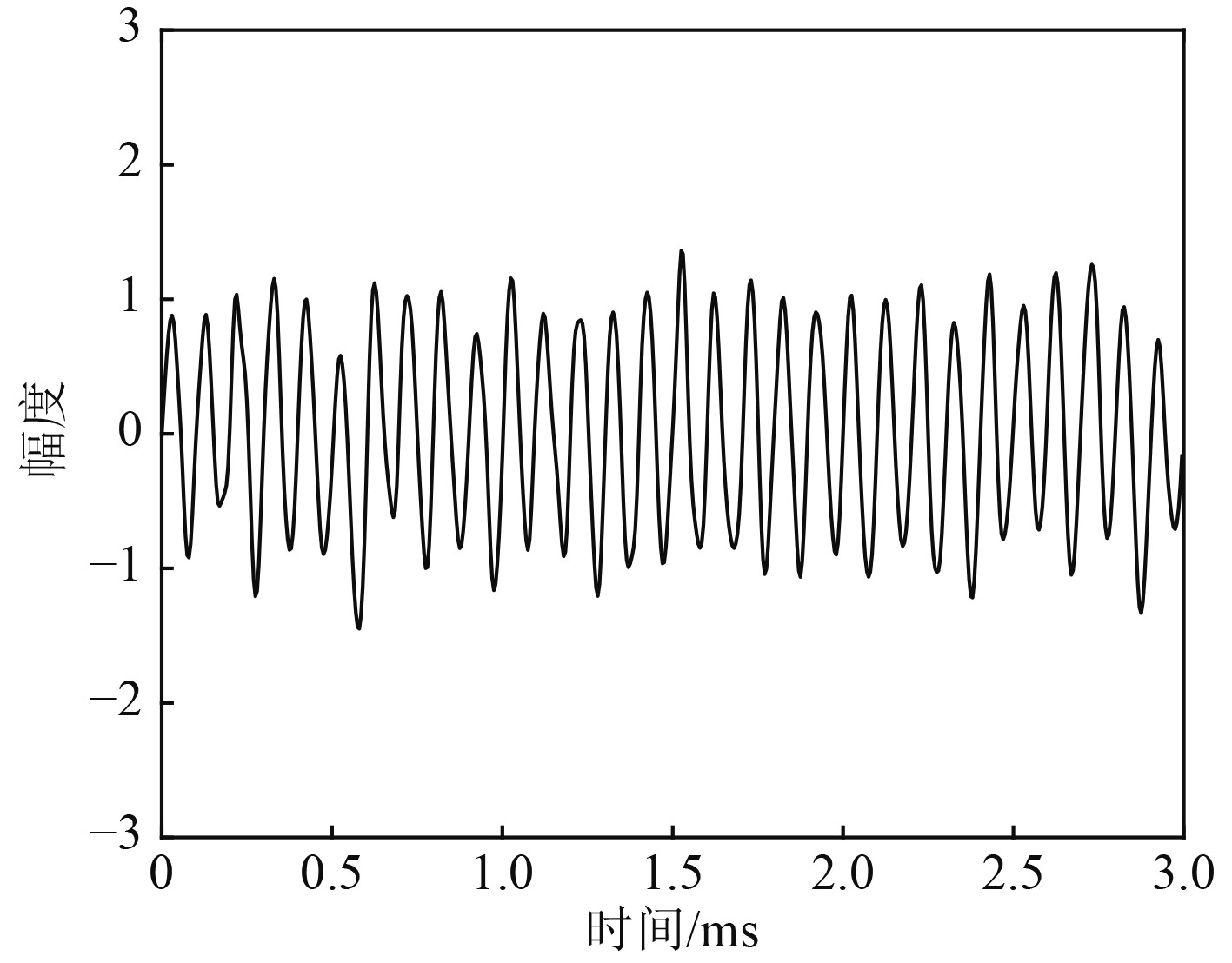
|
图 4 重构信号(CEEMD-MI去噪处理) Fig. 4 Reconstructed signal(CEEMD denoising) |
将图4与图1对比可得,通过CEEMD-MI算法对信号进行自适应分解,根据各个IMF分量与原信号互信息量的大小对信号进行重构可在很大程度上去除原信号中的噪声分量,得到较好的降噪效果。
2.2 不同信噪比下参数估计性能分析假设信号
|
|
表 1 估计信号参数 Tab.1 Estimated signal parameters and echo cancellation |
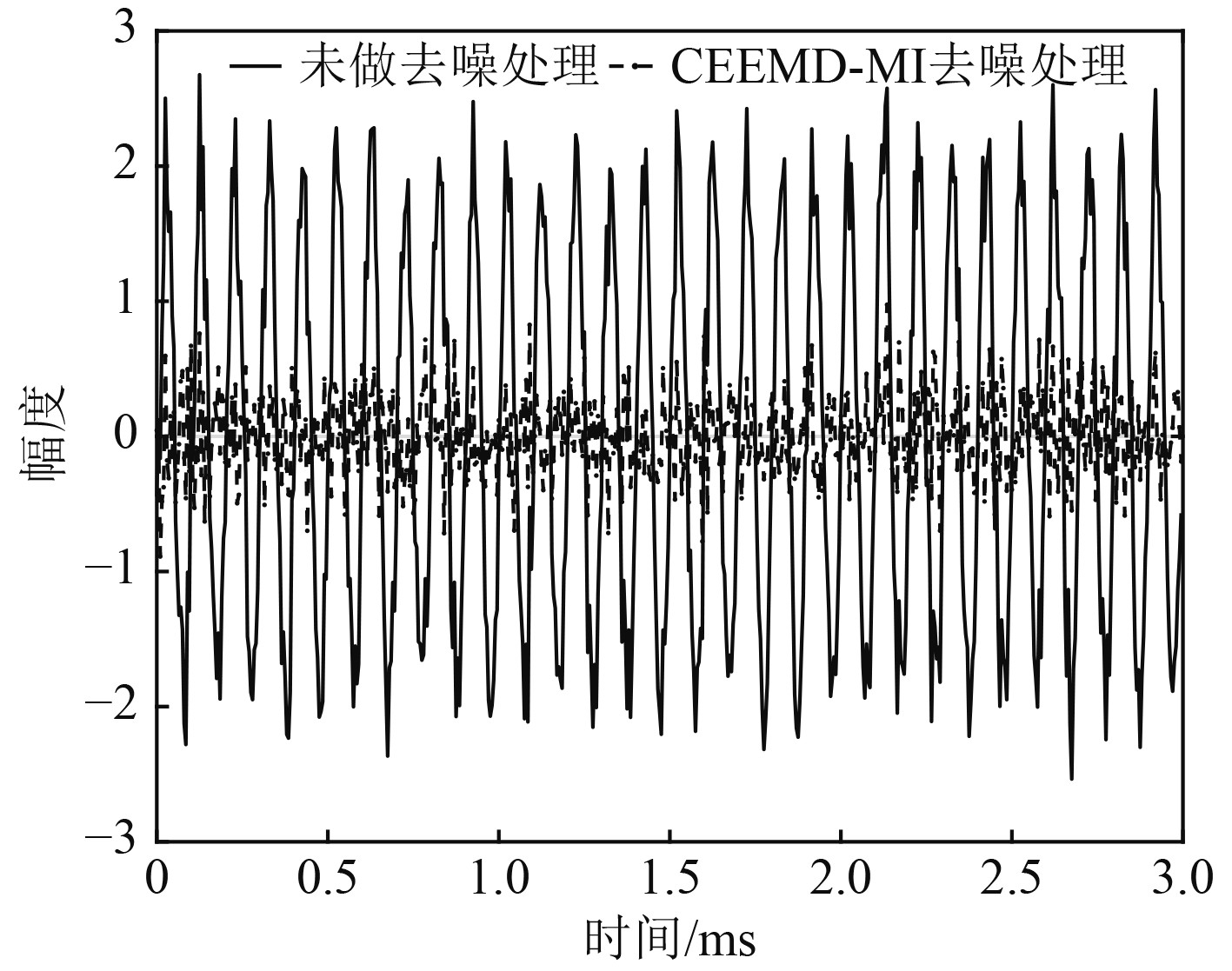
如图5 所示,当信噪比是10 dB时,实线和虚线分别代表利用表1中未进行去噪处理和利用CEEMD-MI去噪处理后估计所得参数生成的信号与
|
图 5 估计信号与原信号差值 Fig. 5 Difference between estimated signal and original signal |
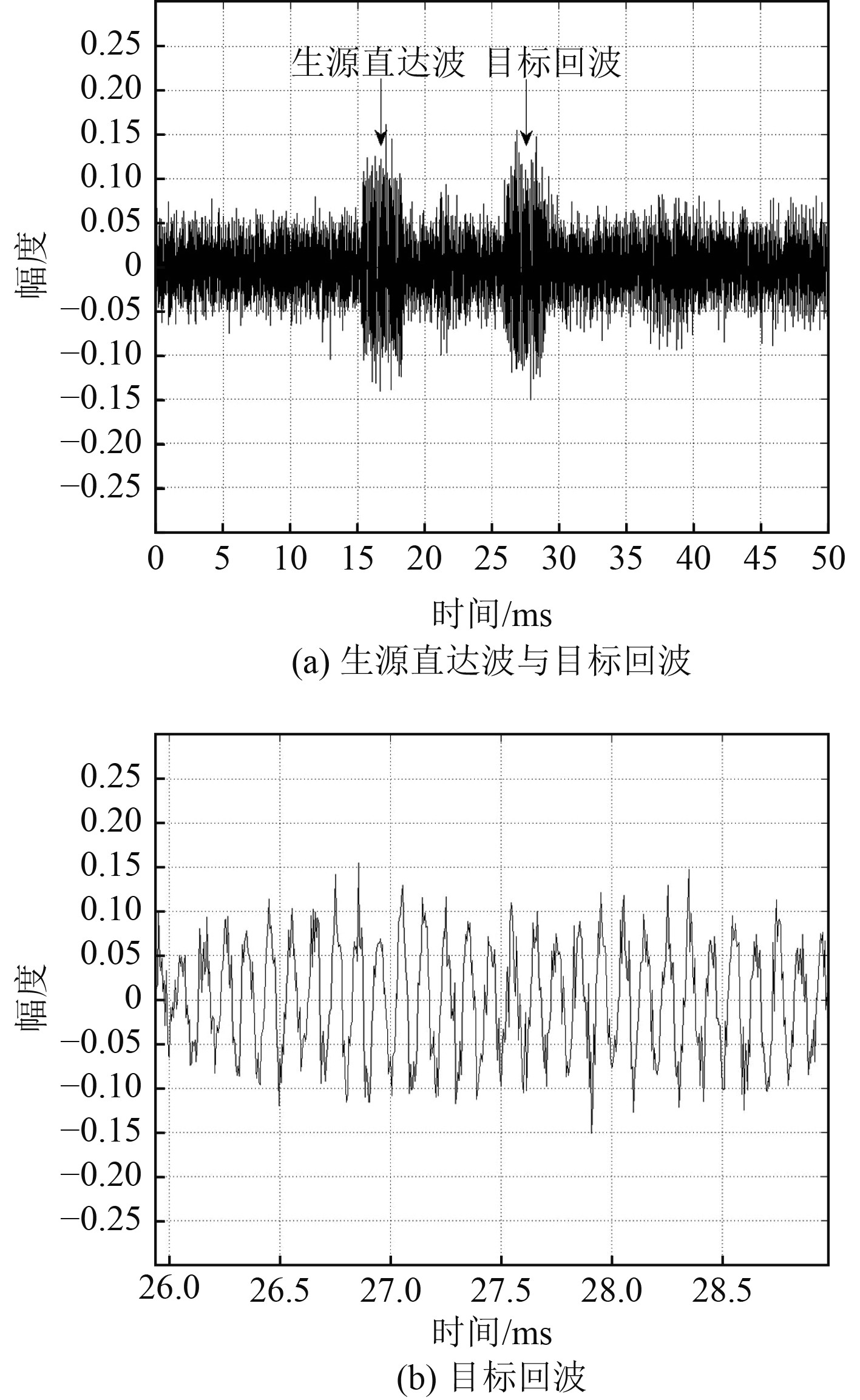
图6为水听器接收信号图,图7为对目标回波未进行去噪处理及经CEEMD-MI去噪处理后,利用估计所得参数生成的信号对与目标回波信号的差值。从图中可以得到,在低信噪比情况下,对目标回波未进行去噪处理估计所得参数生成的信号与目标回波差值很大,由于中心频率估计的不准确使得估计信号与回波信号的差值产生了其他频率的信号成分,而利用CEEMD-MI对目标回波进行去噪处理后估计所得参数生成的信号与目标回波差值很小,几乎只剩噪声成分。
|
图 6 水听器接收信号 Fig. 6 Hydrophone receive signal |

|
图 7 估计信号与目标回波差值 Fig. 7 Difference between estimated signal and target echo |
本文提出一种基于CEEMD-MI的目标回波参数估计算法,该算法首先利用CEEMD对低信噪比情况下的目标回波进行自适应分解,再利用MI对分解得到的各个IMF进行筛选并进行信号重构,有效地去除了信号中的噪声成分。最后对重构后的信号进行参数估计。仿真结果和湖试试验结果表明,本文所提算法可在低信噪比情况下对目标回波参数进行有效估计。
| [1] |
李亚安, 王洪超, 陈静. 基于奇异谱分解的水声信号降噪方法研究[J]. 系统工程与电子技术, 2007(4): 524-527. LI Ya-an, WANG Hong-chao, CHEN Jing. Research on denoising of underwater acoustic signal based on singular spectrum decomposition[J]. System Engineering and Electronics, 2007(4): 524-527. DOI:10.3321/j.issn:1001-506X.2007.04.006 |
| [2] |
WEI K, BIN Y. De-noising of underwater acoustic signals based on ICA feature extraction[C]// 10th Iberoamerican Congress on Pattern Recognition, 2005: 917–924.
|
| [3] |
鲍雪山. 潜艇自噪声自适应有源抵消技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2007.
|
| [4] |
DONOHO D L. Denoising by soft-thresholding[J]. IEEE Trans on Information Theory, 1995, 41(3): 613-627. DOI:10.1109/18.382009 |
| [5] |
DONOHO D L, JOHNSTONE I M, KERKYACHARIAN G, et al. Wavelet shrinkage: Asymptopia?[J]. Journal of the Royal Statistical Society, Series B, 1995, 57(2): 301-369. |
| [6] |
DONOHO D L, JOHNSTONE I M. Ideal spatial adaptation via wavelet shrinkage[J]. Biometrika, 1994, 81: 425-455. DOI:10.1093/biomet/81.3.425 |
| [7] |
DONOHO D L, JOHNSTONE I M. Ideal denoising in an orthogonal basis chosen from a library of bases[J]. C R Acad Sci I-Math, 1994, 319: 1317-1322. |
| [8] |
杨宏. 经验模态分解及其在水声信号处理中的应用[D]. 西安: 西北工业大学, 2015.
|
| [9] |
WU Z H, HUANG N E. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 |
| [10] |
YEH Jia-rong, SHIEH Jiann-shing. Complementary ensemble empirical mode decomposition: a novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156. DOI:10.1142/S1793536910000422 |
 2023, Vol. 45
2023, Vol. 45
