2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
水声通信是水下远距离信息传输的主要技术手段,在海洋环境监测、资源开发、工程建设以及军事领域等方面都发挥了重要作用。前导信号检测是水声通信中的一个关键环节,也是接收机进行后续处理的前提条件,前导信号检测的准确性对通信性能具有重要影响[1-2]。水声信道具有低带宽、大延迟、高噪声、强干扰、信号起伏、多途和多普勒双扩展、时变-频变-空变等特征,是目前已知最复杂的无线信道之一[3],给前导信号检测带来了极大的困难与挑战。
目前常用的前导信号检测算法分为基于相关检测和基于能量检测两类。基于相关检测包括匹配滤波法(MF)、归一化匹配滤波法(NMF)和累积和检验法(PT),MF的判决门限受信噪比影响严重,NMF通过归一化解决上述问题,但不能有效克服水声信道的多径效应,PT通过多径累积提高抗多径能力,但需要一定的先验知识,且门限设定困难,限制了实际应用[4]。基于能量检测包括时域能量检测[5]、频域能量检测[6]和时频域能量检测[7]。与单一时域或频域能量检测相比,时频域检测采用时频分析技术,能够同时提取信号的时域和频域特征,获得更好筛选特性和识别的能力。如何从时频谱图中实现特定信号的检测与识别是时频域检测的核心问题。文献[8-11]分别采用模板匹配、特征识别、支持向量机、决策树自动设计方法解决这一问题,但普遍存在复杂度高和鲁棒性低的缺点。
卷积神经网络(CNN)是一类包含卷积计算且具有深度结构的前馈神经网络,仿造生物的视觉机制构建,能够通过大量数据自动提取图像特征,算法通用性强、网络结构简单高效、准确度和效率较大提升,在图像识别领域获得广泛应用。本文采用CNN技术解决时频谱图的目标识别问题,提高复杂水声信道环境下前导信号检测的准确性,对提升通信质量和通信效率具有重要意义。
1 前导信号检测算法 1.1 前导信号形式线性调频信号(LFM)和双曲调频信号(HFM)具有良好的相关性和多普勒不变性,是水声通信系统中最常用的前导序列。使用HFM信号,发射前导信号的数学表达式为:
| $ b=\frac{{f}_{1}-{f}_{2}}{{f}_{1}{f}_{2}T} ,$ | (1) |
| $ s\left(t\right)=A\left(t\right)\mathrm{e}\mathrm{x}\mathrm{p}\left[j\frac{2 {\text{π}} }{b}\mathrm{ln}\left(1+b{f}_{1}t\right)\right],0\leqslant t\leqslant T 。$ | (2) |
式中:
根据式(2)求导可知,HFM信号的瞬时频率表达式为:
| $ {f}_{i}\left(t\right)=\frac{{f}_{1}}{1+b{f}_{1}t} 。$ | (3) |
式中:
若
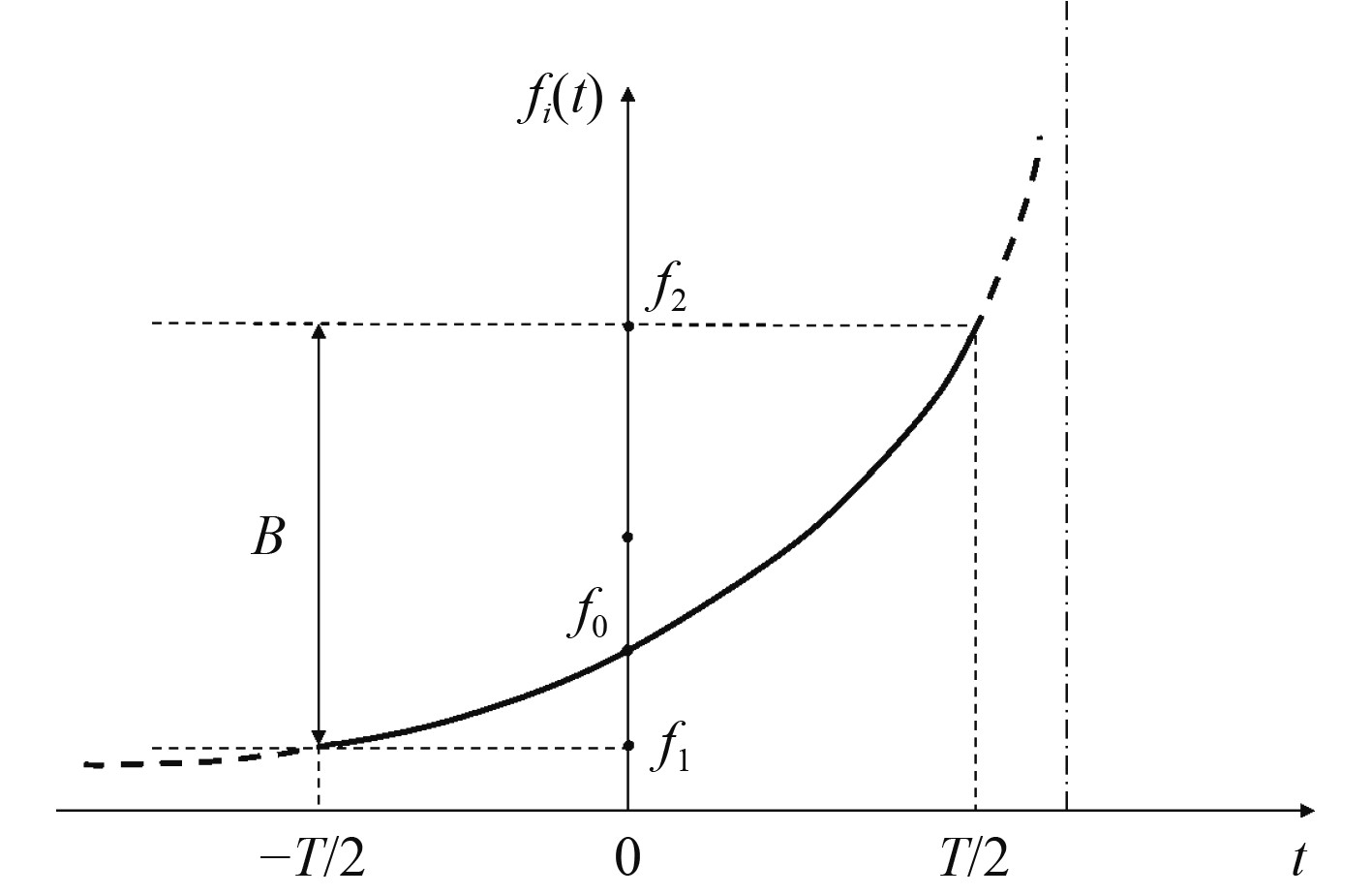
|
图 1 HFMU调频规律示意图 Fig. 1 Frequency variation of HFMU signal |
水声信道是多途-多普勒双扩展的时变信道,信道冲击响应可表示为:
| $ h\left(t;\tau \right)=\sum _{p=1}^{{N}_{pa}}{A}_{p}\mathrm{\delta }(\mathrm{\tau }-\left({\tau }_{p}-{a}_{p}t\right))。$ | (4) |
式中:
经过水声信道后,前导信号
| $ y\left(t\right)=\sum _{p=1}^{{N}_{pa}}{A}_{p}s(\left(1+{a}_{p}\right)t-{\tau }_{p})+w\left(t\right) 。$ | (5) |
式中,
短时傅里叶变换是最常用的时频分析工具。通过窗函数对信号当前时刻进行截断,然后对截断后的数据进行傅里叶变换。不断移动窗函数,分别对各个时刻进行处理,最终得到全时段的分布情况。离散形式短时傅里叶变换(STFT)可表示为:
| $ {STFT}_{x}\left(n,\omega \right)=\sum _{m=-\infty }^{\infty }x\left(m\right){g}^{*}\left(m-n\right){e}^{-jm\omega }。$ | (6) |
式中:
时频谱图为STFT模的平方,即
| $ {SPEC}_{x}\left(n,\omega \right)={\left|STFT(n,\omega )\right|}^{2}。$ | (7) |
采用时频谱图对信号进行分析,描述信号强度和分布随时间和频率的变换,能够直观地呈现出信号的时频特性。图2为4种不同类型信号的时频谱图,用灰度表示能量,没有坐标轴,可将横轴视为时间,纵轴视为频率。

|
图 2 信号时频谱图 Fig. 2 Time-frequency spectrum |
可看出,HFM信号的时频谱图特征明显,与噪声和其他信号的区分度很高,能够实现接收信号的检测。
1.2.2 均值滤波无论是在时域还是频域,噪声总是普遍存在且不可避免。噪声与信号相叠加,会造成目的信号能量起伏,增加检测难度;当噪声能量较高时,还会造成很大程度的虚警。因此在信号检测中,经常需要进行预处理滤除噪声。
采用均值滤波算法对时频谱图进行去噪。均值滤波是典型的线性滤波算法,在图像上对目标像素给一个模板,该模板包括了其周围的临近像素,再用模板中的全体像素的平均值来代替原来像素值。均值滤波表达式为:
| $ g\left(x,y\right)=\frac{1}{m}\sum f(x,y)。$ | (8) |
式中,m为该模板中包含当前像素点在内的像素总个数。
对信噪比为5 dB的HFM信号进行STFT,得到时频谱图,然后用4×4的矩形作为邻域模板,对时频谱图进行均值滤波,图3为均值滤波前后的时频谱图对比图。

|
图 3 均值滤波前后的时频谱图对比图 Fig. 3 Time-frequency spectrum before and after mean-filtering |
可看出,均值滤波能够快速有效抑制加性噪声,增加信号与背景噪声的对比度,经过均值滤波处理后,背景噪声中“亮点”减少,HFM信号变得更为突出。
1.3 卷积神经网络 1.3.1 神经网络结构用于分类的卷积神经网络一般包括卷积层、池化层、激活函数、全连接层、Softmax层5种结构,并由此组成特征提取模块和分类模块2个功能模块。卷积层、池化层、激活函数这3种结构交替出现组成特征提取模块,全连接层、Softmax层依次连接组成分类模块,2个功能模块连接组成完整的卷积神经网络。图4为本文所用的卷积神经网络结构示意图。

|
图 4 卷积神经网络结构示意图 Fig. 4 Convolutional neural network structure |
对数据进行预处理。用4倍于前导信号长度的窗函数截取原始信号,对截取后的信号做STFT,得到时频谱图,并进行均值滤波。为了方便训练网络,还对时频谱图进行像素点归一化、减去均值、缩放图片尺寸等处理。
将预处理后得到的时频谱图输入到特征提取模块。通过2个卷积层提取其不同尺度的特征,采用ReLU激活函数增强网络的非线性拟合能力,利用最大池化层对特征进行降维,同时减少参数数目和计算量。
将特征提取模块提取出的抽象特征输入到分类模块。利用展平层将二维特征图调整为一维特征向量,随后连续通过2个全连接层,得到一个
先对数据集进行处理。对数据集打标签,将包含HFM前导信号的数据视为正样本,标签值为0,其余为负样本,标签值为1。将数据集划分为训练集、验证集、测试集3部分,划分比例为6∶2∶2。其中,训练集用于训练网络,验证集用于实时评估网络性能,以找到提前停止训练的最优轮数,测试集用于最终测试网络性能。
用数据集对卷积神经网络进行训练。将训练集数据输入网络,前向传播得到预测结果,用损失函数量化预测结果和标签的差异,用优化算法找到使得损失函数值最小的最优网络参数。训练过程采用了随机失活(Dropout)和提前停止(Early-stopping)两个技术,防止网络出现过拟合现象。当达到一定训练次数或网络在验证集上性能开始变差时,停止更新网络训练参数,训练阶段结束。
2 试验数据处理分析用上述算法处理试验数据验证性能。试验在千岛湖开展,水深约50 m,采用单发单收方式,分别在试验艇和母船上安置发射换能器和接收换能器,布放深度均为5 m。试验信号为HFM信号,信号带宽6 kHz,中心频率12 kHz,采样率96 kHz,信号长度为21.3 ms。试验过程中,母船静止不动,试验艇分别移动到距离母船300 m、700 m、1000 m、1500 m、2000 m、2500 m和3000 m位置处,开展试验。
将接收信号与本地信号相关,测量各个位置的信道冲激响应,图5为部分位置信道测量结果,颜色表示相关系数,横轴表示信道时延,纵轴表示时间。测量结果显示,本次试验水声信道环境极为复杂,时间空间变化明显,多途、混响和噪声严重,随着距离增加主径逐渐变弱,距离超过1500 m不再存在明显主径,极大增加了前导信号检测难度。
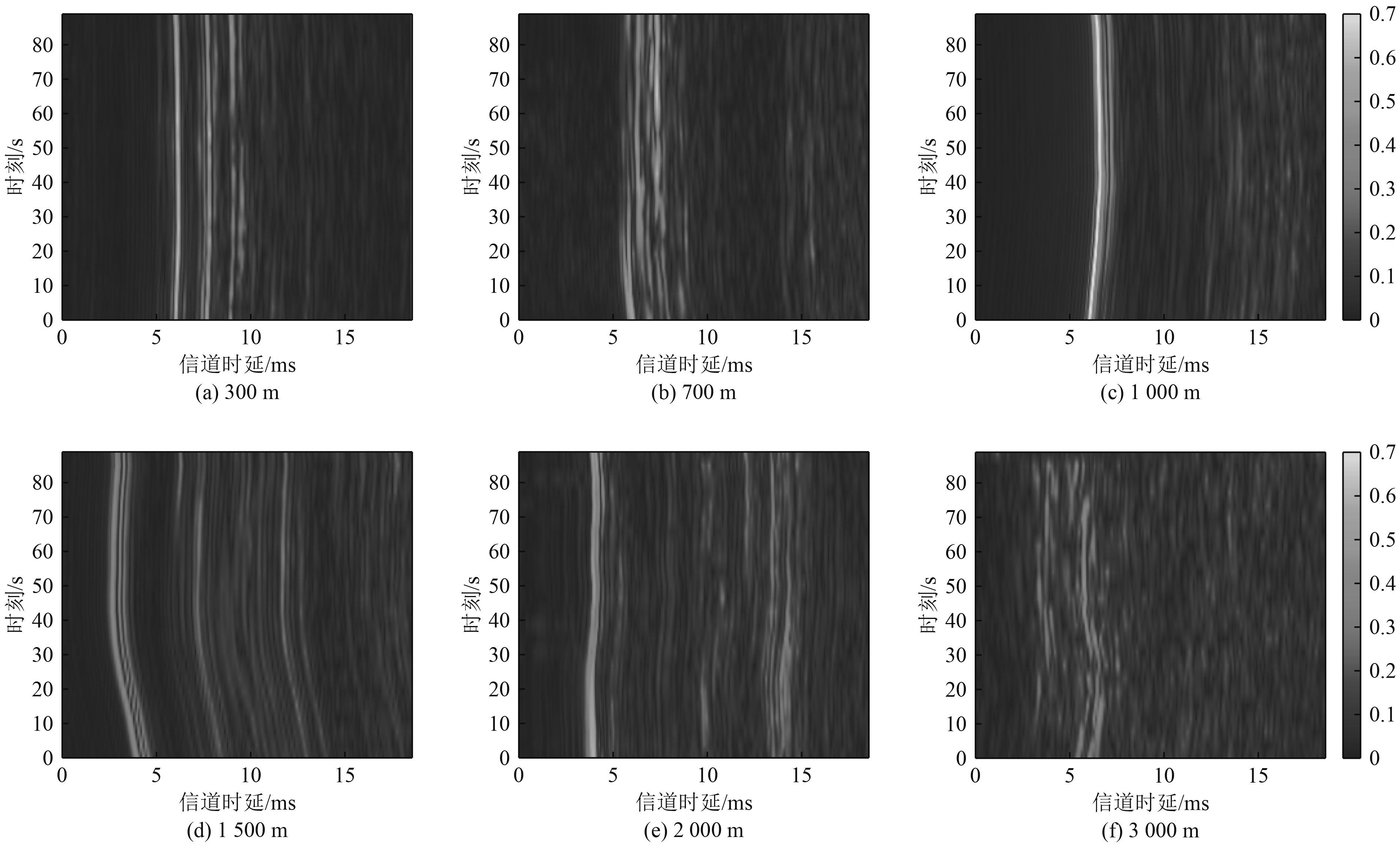
|
图 5 信道冲激响应测量结果 Fig. 5 Estimation of channel impulse response |
分别用传统NMF算法和本文STFT-CNN算法处理试验数据,测试算法性能。测试数据包括1260个正样本和2240个负样本,在各个位置平均分布。图6为试验数据检测结果。
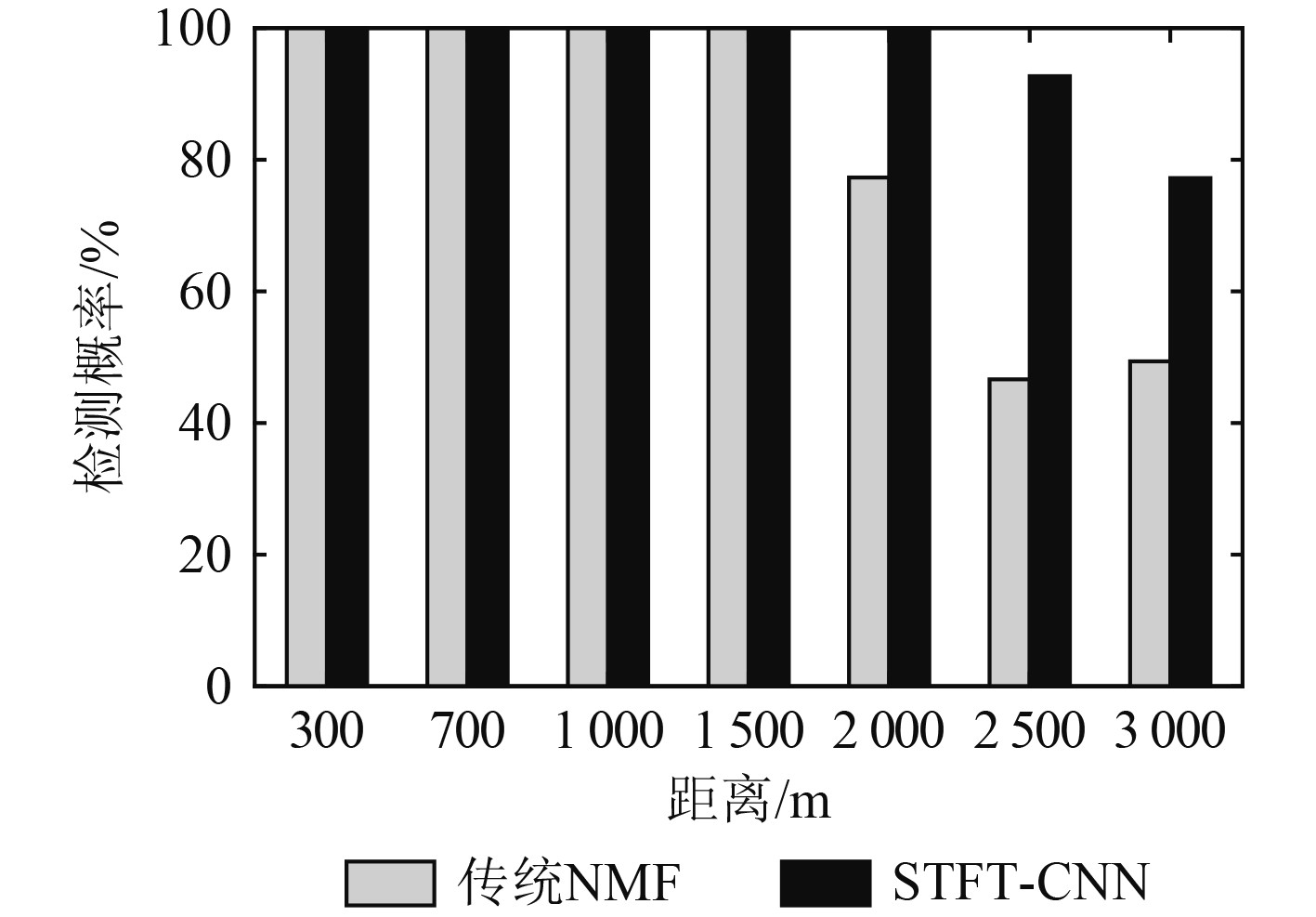
|
图 6 HFM前导信号检测结果 Fig. 6 Detection results of HFM preamble |
在距离超过1500 m的位置,传统NMF算法检测性能明显变差,而STFT-CNN算法仍能保持较好的性能,检测概率提升约30%。此外,NMF算法在2000 m和3000 m位置各出现一次虚警,而STFT-CNN算法则没有虚警。
3 结 语本文针对复杂水声信道环境下,通信信号前导检测问题,提出一种基于卷积神经网络与时频分析的检测方法,使用时频分析技术同时观测信号时域和频域信息,然后用卷积神经网络解决时频谱图中特定信号的检测与识别问题。利用千岛湖试验数据,对比传统NMF算法和STFT-CNN算法的检测性能。结果表明,STFT-CNN算法能够有效对抗水声信道多径、噪声和干扰的影响,在复杂水声信道环境下,检测性能明显提升。
| [1] |
TAN Q Y, WANG Y Y, MA X L. Preamble detection based on cyclic features of zadoff-chu sequences for underwater acoustic communications[J]. IEEE Signal Processing, Lett, 2019, 26(8).
|
| [2] |
LI W, ZHOU S L, Peter Willett, et al. Preamble detection for underwater acoustic communications based on sparse channel identification[J]. IEEE Journal of Oceanic Engineering, 2019, 44(1).
|
| [3] |
QIAO G, ZEESHAN Babar, MA L, et al. MIMO-OFDM underwater acoustic communication systems-A review[J]. Physical Communication, 2017, 23.
|
| [4] |
赵方真. 水声通信系统中的前导信号检测与识别性能分析[D]. 哈尔滨: 哈尔滨工业大学, 2020.
|
| [5] |
王大宇, 王志欣, 张光普. 基于改进谱减算法的水声通信信号检测方法[J]. 应用科技, 2020, 47(3): 69-73. WANG Dayu, WANG Zhixin, ZHANG Guangpu. Detection method of underwater acoustic communications signal based on improved spectral subtraction algorithm[J]. Applied Science and Technology, 2020, 47(3): 69-73. DOI:10.11991/yykj.202005006 |
| [6] |
叶辉. 宽带频谱检测技术研究以及FPGA实现[D]. 成都: 电子科技大学, 2020.
|
| [7] |
孙伟, 彭华, 李天昀, 等. 基于时频图像处理的宽带特定信号检测方法[J]. 信息工程大学学报, 2020, 21(5): 545-551. SUN Wei, PENG Hua, LI Tianyun, et al. Broadband specific signal detection method based on time-frequency image processing[J]. Journal of Information Engineering University, 2020, 21(5): 545-551. |
| [8] |
Xl A , TO B , MK A , et al. An effective method for laboratory acoustic emission detection and location using template matching[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2022.
|
| [9] |
袁冠杰, 王虹, 陈静, 等. 基于特征提取融合判决的卫星干扰识别算法[J]. 微波学报, 2021, 37(S1): 241-244. YUAN Guanjie, WANG Hong, CHEN Jing, et al. Satellite jamming recognition algorithm based on feature extraction and fusion decision[J]. Journal of Microwaves, 2021, 37(S1): 241-244. |
| [10] |
S. Raghu, Natarajan Sriraam, Yasin Temel, et al. Performance evaluation of DWT based sigmoid entropy in time and frequency domains for automated detection of epileptic seizures using SVM classifier[J]. Computers in Biology and Medicine, 2019, 110: 127−143.
|
| [11] |
魏煜宁, 张劲东, 李勇, 等. 雷达干扰信号识别决策树的自动化设计方法[J]. 电光与控制, 2020, 27(4): 82–86. WEI Yuning, ZHANG Jingdong, LI Yong, et al. A method for automatic design of decision tree in radar jamming signal recognition[J]. Electronics Optics & Control, 2020, 27(4): 82–86. |
 2023, Vol. 45
2023, Vol. 45
