随着全球经济的快速增长以及人们对环境保护意识的不断增强,船舶在水面航行过程中排放的废气对周围的海洋环境产生的影响逐渐得到了人们的重视[1]。由于船舶电力推进系统有着可以提升船舶的能效、实现机舱的灵活布置等优点,得到了广泛的关注,并且船舶的电力推进系统可以进行变速发电,因此该系统可以十分方便接到各类新能源系统中[2]。以燃料电池为基础的船舶电力混合动力系统实现了多种新能源的耦合,但是采用这类混合动力系统,船舶在航行过程中也出现了能效优化、多能源协调等优化控制问题,这些问题对船舶混合动力系统的应用提出了更高的要求,设计高效的混合动力系统成为提升船舶能量使用效率的重要方法[3]。
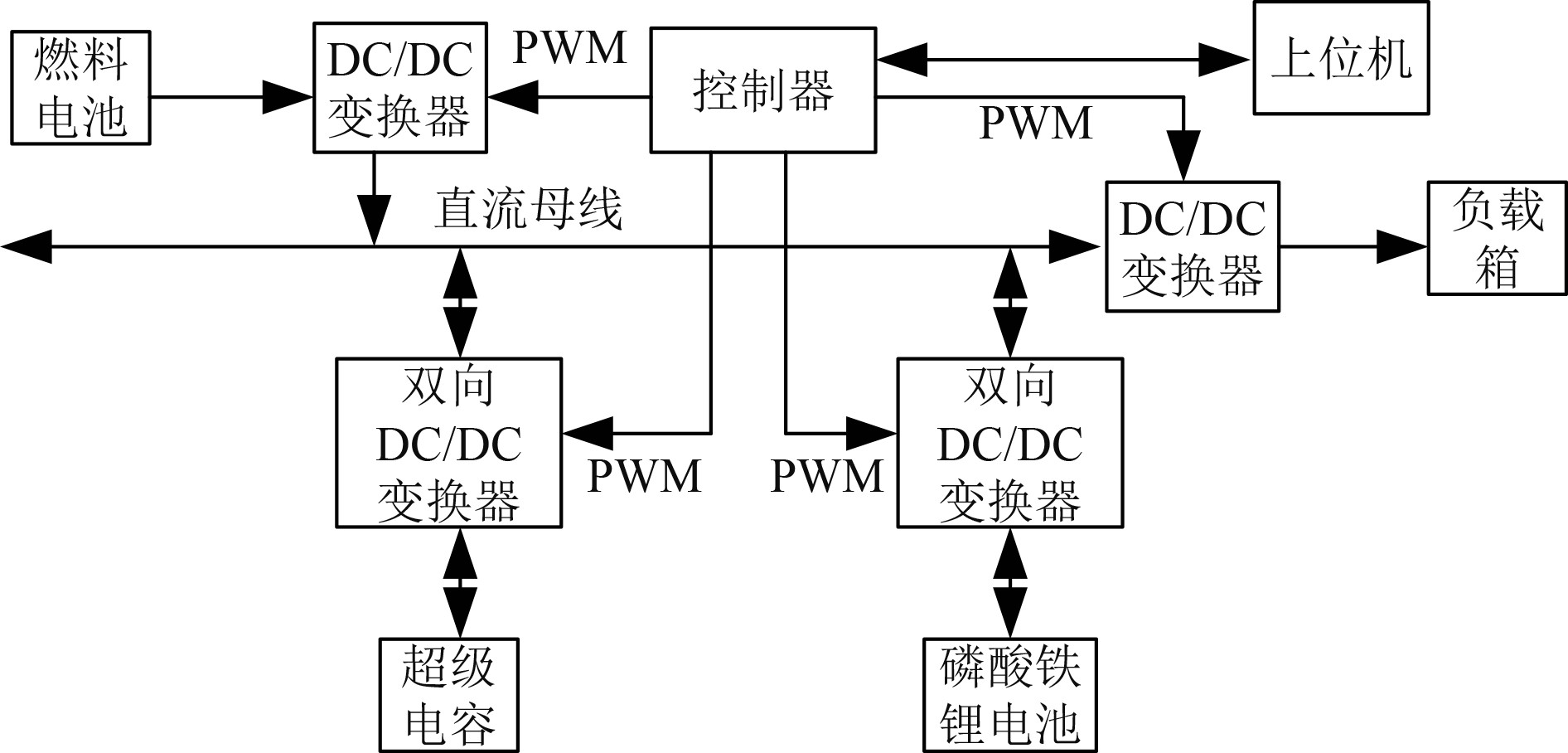
1 船舶复合储能系统设计 1.1 复合储能系统结构分析根据船舶自身特点可知,船舶在正常航行过程中,输出的功率比较稳定,一旦遇到风浪等情况,输出的功率波动范围则会比较大,这会增大船舶电力系统的不稳定性[4]。当船舶的负载功率出现较大的波动或者频率比较快的时候,为了能够确保船舶可以稳定输出功率,则需要使用储能系统进行能量调节,以便可以对船舶电机的输出效率进行优化,并且确保船舶上电网的稳定性[5]。化学、物理以及电磁储能是最常见的3种储能形式。船舶电力系统中通常使用电化学、飞轮、超级电容器以及超导磁等储能设备。虽然超导磁储能包含了上述3种储能系统的所有优点,但是其价格昂贵。船舶复合储能系统结构如图1所示。
|
图 1 船舶复合储能系统结构图 Fig. 1 Structure diagram of ship composite energy storage system |
磷酸铁锂电池PNGV模型的特点在于,在电池模型的支路中串联了一个电容,利用该电容可以十分便利模拟电池的极化现象,同时在电容频繁的充放电过程中,电池的模型精度比较高,因此采用PNGV模型来模拟磷酸铁锂电池的充放电过程,其数学模型为:
| $ \left\{ \begin{aligned} & {U = {U_{OC}} - {U_{TP}} - \frac{1}{C}\int {{I_L}{\rm{d}}t - R{I_L}} }\text{,} \\ & {{I_L} = \frac{{{U_{TP}}}}{{{R_1}}} - C\frac{{{\mathrm{d}}{U_{TP}}}}{{{\mathrm{d}}t}}} \text{。} \end{aligned} \right. $ | (1) |
超级电容在充电的过程中,其数学模型为:
| $ C = \frac{Q}{V}\text{,} $ | (2) |
式中,C为电容大小。其计算公式为:
| $ C' = \frac{{{\varepsilon _0}{\varepsilon _1}A}}{D}\text{。} $ | (3) |
式中:ε0和ε1为介质常数;A为电容面积;D为电容两极间距。可以看出,电容的C值和面积A以及介电常数成正比例关系。超级电容的电压、电荷状态以及能量可以分别表示为:
| $ U' = I{R_s} + \frac{1}{C}\int {I{\rm{d}}t} \text{,} $ | (4) |
| $ SoC = \frac{{{U_0} + \frac{1}{C}\int_0^1 {I{\rm{d}}t - {U_{\min }}} }}{{{U_{\max }} - {U_{\min }}}}\text{,} $ | (5) |
| $ W = \frac{1}{2}C\left( {U_{\max }^2 - U_{\min }^2} \right)\text{。} $ | (6) |
当船舶上负载消耗的功率比较大的时候,船舶上的电网系统则可以使用复合储能系统来稳定船舶发电机的输出功率,并且提升船舶上的电网对船舶负载供电的可靠性程度,这需要对船舶上的复合储能系统进行容量优化[6]。在对船舶上的复合储能系统进行最优配置的过程中,首先需要知道每个储能单元承担的平均功率,船舶复合储能系统的补偿功率取决于船舶负载需要的功率和船舶发电机输出功率之间的差,计算公式为:
| $ {P_{HESS}} = {P_{load}} - {P_G}\text{,} $ | (7) |
| $ {P_{SC}} = {P_{HESS}} - {P_b}\text{。} $ | (8) |
式中,PHESS为船舶复合储能系统的功率补偿值。船舶复合储能系统的电荷状态在充电和放电过程中的变化情况,可以分别表示为:
| $ SO{C_t} = SO{C_{t - 1}} \cdot \left( {1 - \sigma } \right) - \frac{{P \cdot \Delta t \cdot \eta }}{E}\text{,} $ | (9) |
| $ SO{C_t}^\prime = SO{C_{t - 1}}^\prime \cdot \left( {1 - \sigma } \right) - \frac{{P \cdot \Delta t}}{{E \cdot \eta }}\text{。} $ | (10) |
船舶复合储能系统中的电池以及电容的折旧系数主要和工作年限、自身的折旧率有关,计算方法为:
| $ {f_p} = \frac{{d{{\left( {1 + d} \right)}^l}}}{{{{\left( {1 + d} \right)}^l} - 1}}\text{。} $ | (11) |
式中:d为折旧系数;l为工作年限。
在对储能系统进行优化配置的过程中,可以将船舶复合储能系统的成本Cp作为优化目标,其计算方法为:
| $ \min {C_p} = \frac{1}{{365}}\left( {{C_T} + {C_Y} + {C_W}} \right)\text{。} $ | (12) |
当船舶发电机和复合储能系统的输出功率比船舶负载的功率低的时候,这种情况称作负荷缺电,其计算方法如下式:
| $ LPSP=\frac{\displaystyle\sum\limits_{t=1}^{t=24}P_{lock.t}}{\displaystyle\sum\limits_{t=1}^{t=24}P_{load.t}}\text{。} $ | (13) |
当船舶发电机和复合储能系统的输出功率比船舶负载的功率高的时候,这种情况称作能量溢出,其计算方法如下式:
| $ SPSP = \frac{{\displaystyle\sum\limits_{t = 1}^{t = 24} {{P_{waste.t}}} }}{{\displaystyle\sum\limits_{t = 1}^{t = 24} {{P_{G.t}}} }}\text{。} $ | (14) |
负荷缺电和能量溢出均可以用来描述船舶电网的可靠性程度,负荷缺电和能量溢出的值越小,则表示船舶电网系统越可靠。
2 船舶混合动力系统建模仿真船舶混合动力系统中蓄电池的特征参数主要包括容量、放电倍率、荷电状态、端电压、内阻、充电效率以及开路电压等[7]。电池的容量为在一定条件下可以释放出的所有电量,其计算方法为:
| $ {Q_{bat.a}} = \int_{{t_0}}^{{t_{cut}}} {{i_{bat}}{\rm{d}}t} \text{。} $ | (15) |
船舶的电荷状态是指电池当前的容量,其表示方法为:
| $ So{C_{bat}} = \left( {1 - \frac{{{Q_{bat.a}}}}{{{Q_{bat}}}}} \right) \times 100 \text{%。} $ | (16) |
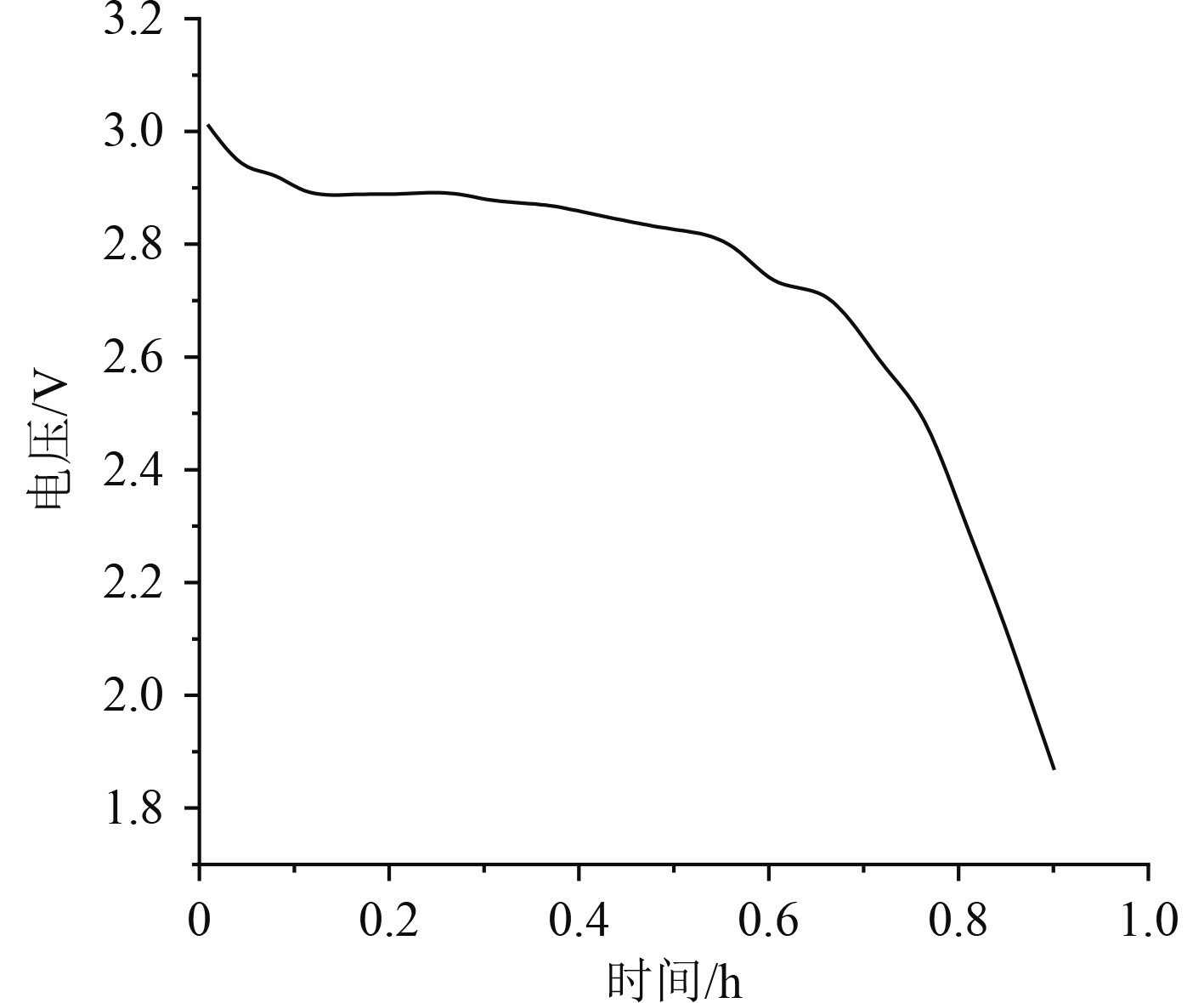
接入实际电网之后,电池两端输出电压的变化情况如图2所示。可以看出,电池的端电压会在一定时间内维持稳定,超过一定的时间之后,端电压会迅速下降。
|
图 2 电池放电特性曲线 Fig. 2 Battery discharge characteristic curve |
电池的充电效率为电池放电期间输出的能量和恢复到放电前所需能量的比值,其计算方法如下式:
| $ 充电效率=\frac{输出能量}{充电容量}\times 100 \text{%。} $ | (17) |
超级电容在以一定的电流恒定放电的过程中,可以用超级电容放电的电量和超级电容两极之间的电压变化量的比值来表示该超级电容的容量,计算方法如下式:
| $ {C_{sc}} = \frac{{{i_{sc}}t}}{{{V_{sc1}} - {V_{sc2}}}}\text{。} $ | (18) |
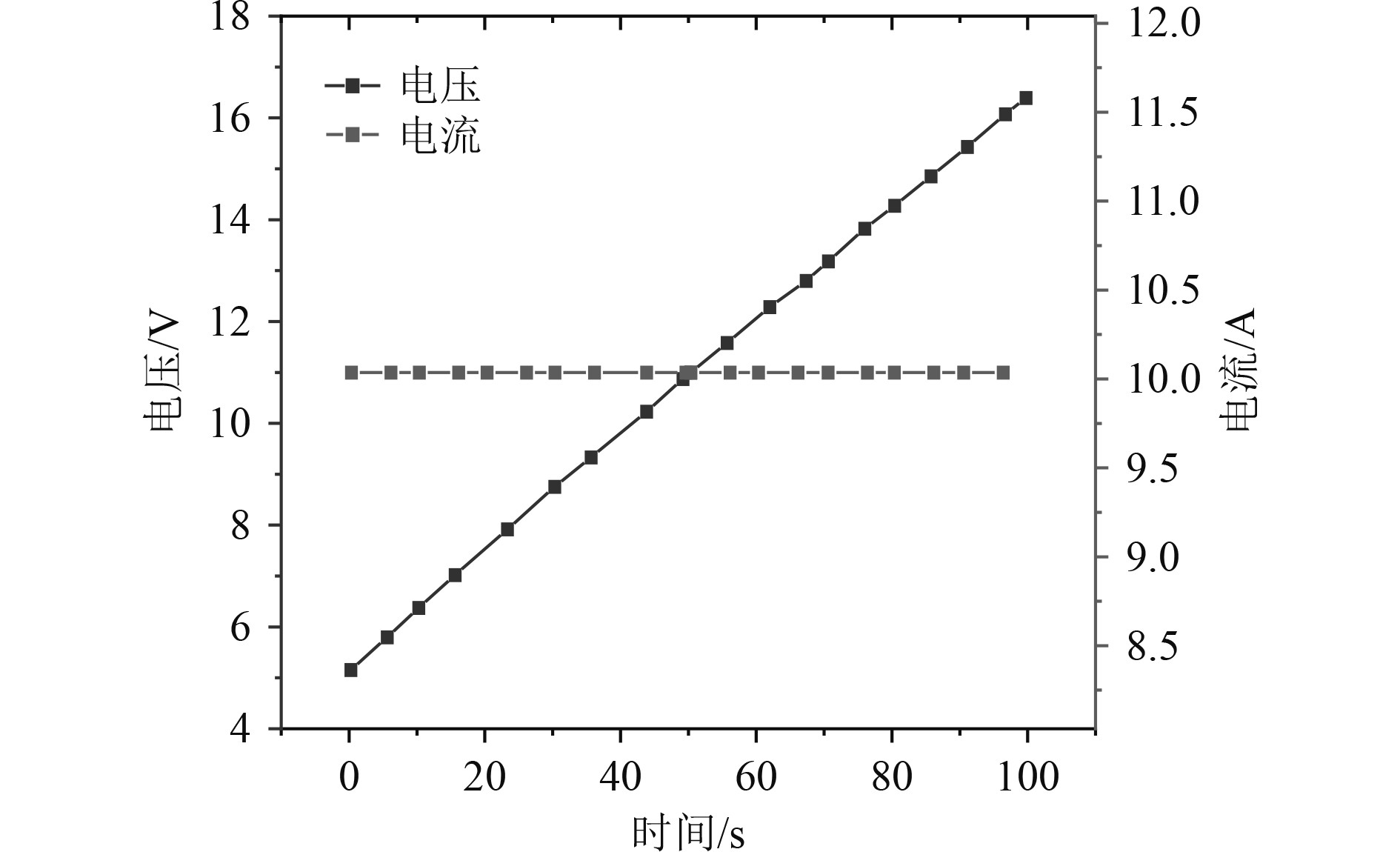
在以恒定电流的方式充电的情况下,超级电容两极之间的电压变化曲线如图3所示。可以看出,超级电容的端电压随时间呈线性变化。超级电容中的能量值:
|
图 3 超级电容两极之间的电压变化曲线 Fig. 3 The voltage change curve between the two poles of a supercapacitor |
| $ {E_{sc}} = \frac{1}{2}{C_{sc}}V_{sc}^2\text{。} $ | (19) |
通过DC/DC得到的电压波形如图4所示。可以看出,经过双向DC/DC电压变换器之后,电压能够上升到527 V。使用PEMFC堆栈模型来模拟燃料电池,PEMFC模型融合了电气模型以及化学模型的特征,并且将电池内的流体忽略掉,因此得到了广泛应用。

|
图 4 固定移相角下的DC/DC输出电压 Fig. 4 DC/DC output voltage under fixed phase shift angle |
本文采用的智能能效管理方法为,首先对船舶上的发电机组的工作状态进行定义,然后将船舶上发电机组的实时运行状态以及船舶负荷需要的能量信息发送给船舶能量优化调配模块,船舶能量优化调配模块根据这2个信息,给不同的动力源发送各自的输出参考功率,最后通过信号转换之后,控制船舶上的电子调速器以及DC/DC变换器,最终实现船舶上各个动力源功率的优化输出。将船舶上发电机和动力源进行分开,这样有利于降低船舶能量优化分配的复杂程度。
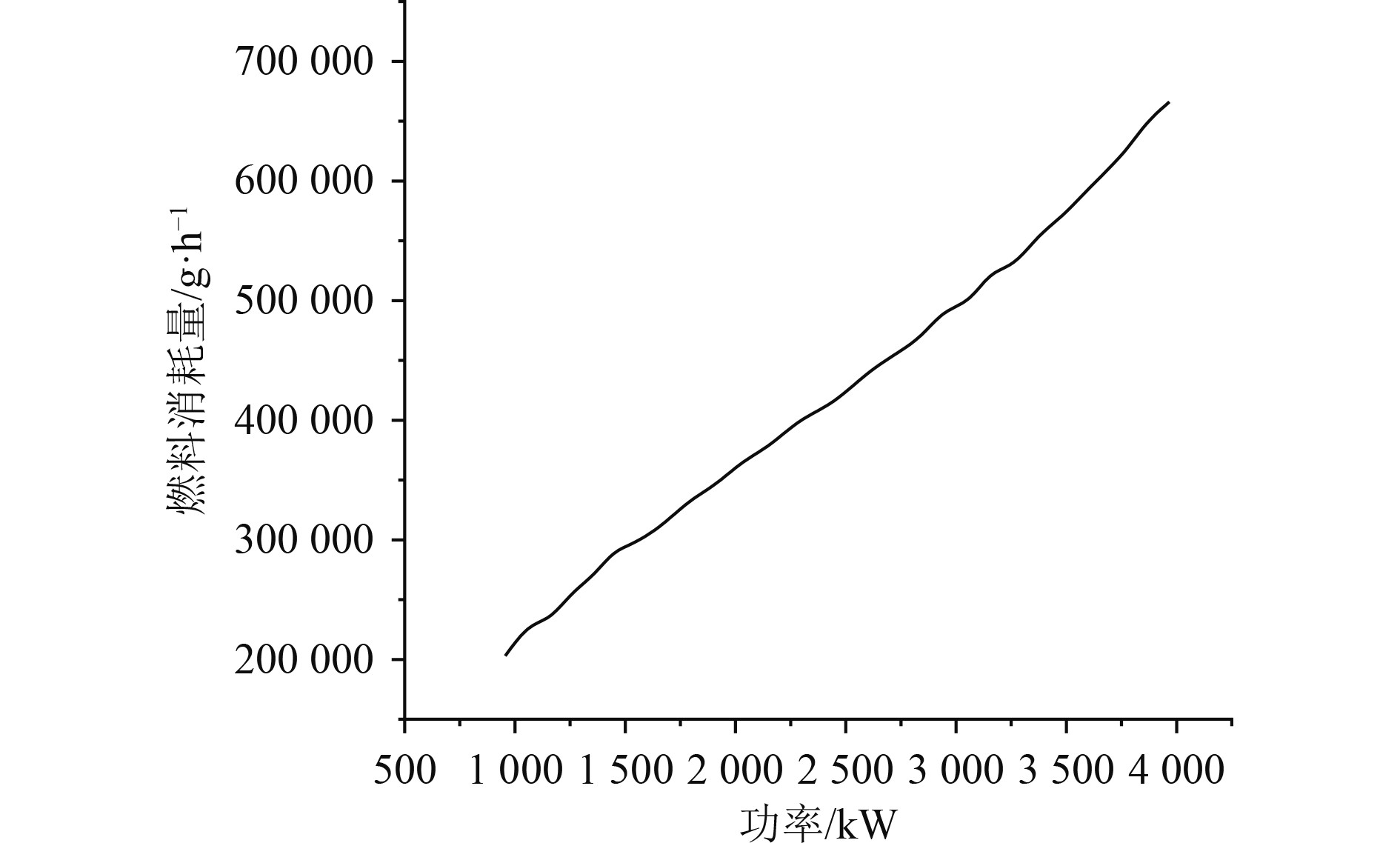
结合船舶发电机组的工况、船舶电力系统的稳定性以及船舶储能系统的安全性等因素,本文构建了船舶智能能量优化分配的数学模型。船舶发电机的燃料消耗量和船舶发电机的输出功率成正比,如图5所示。控制船舶发电机的总燃油消耗量最低是船舶能量优化分配的目标,该目标方程为:
|
图 5 船舶燃料消耗量随功率变化的曲线关系 Fig. 5 Curve relationship between ship fuel consumption and power variation |
| $ \min {f_0} = \sum\limits_{x = 1}^3 {{f_{v,x}}} \text{。} $ | (20) |
式中:x为船舶发电机编号;fv,x为船舶发电机燃料消耗率,船舶发电机的燃料消耗率为:
| $ {f_{v,x}} = ap_{g,x}^2 + b{P_{g,x}} + c\text{。} $ | (21) |
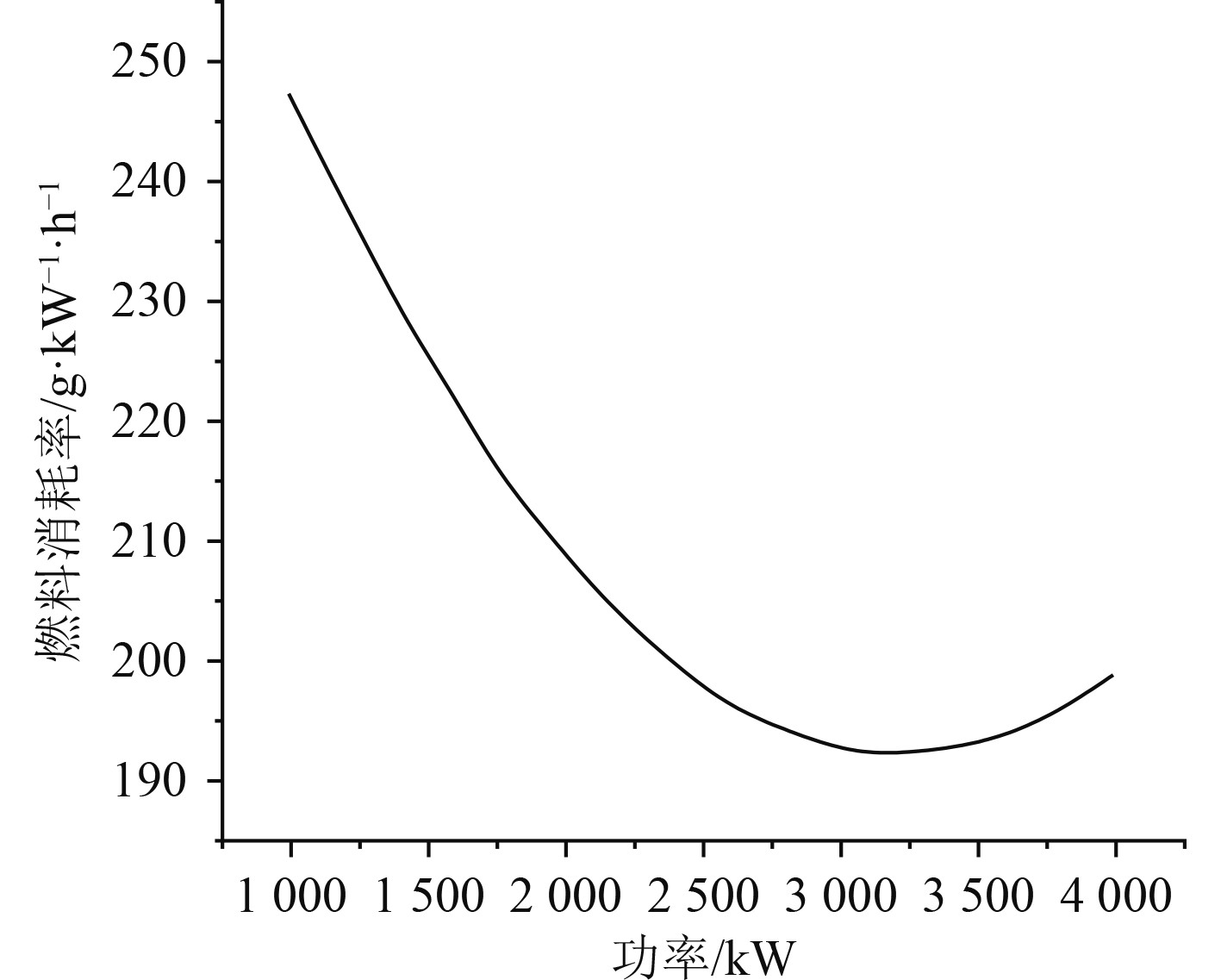
式中:Pg,x为船舶发电机的输出功率。根据船舶发电机的测试数据,可以得到船舶发电机的燃料消耗率和功率的关系曲线如图6所示。可以看出,随着功率的增大,船舶发电机的燃料消耗率会逐渐降低,最终会达到一个最低值,然后随着船舶发电机功率的进一步增加,船舶的燃料消耗率存在一定程度的上升。
|
图 6 燃料消耗率和功率的关系曲线 Fig. 6 Relationship curve between fuel consumption rate and power |
船舶混合动力技术的快速提升,对船舶混合动力系统的经济性提出了更高的目标,因此相关研究机构对多种类型的船舶混合动力系统及其控制方法进行了多角度的研究,特别是针对船舶储能设备容量、能效的提升以及多种能量源的协调与控制等。对船舶混合动力系统及其主要构件的特性进行分析,同时设计出高效的能量管理方法,这对提高船舶混合动力系统的能效,实现船舶的节能减排等目标,有重要的理论意义。
| [1] |
王凯, 卢博闻, 李仁祥, 等. 船舶多清洁能源混合动力系统及其关键技术[J]. 舰船科学技术, 2020(42): 6-11. WANG Kai, LU Bo-wen, LI Ren-xiang et al. Research progress on multi-clean energy hybrid system and the key technologies of ships[J]. Ship Science and Technology, 2020(42): 6-11. |
| [2] |
张程, 贾宝柱. 船舶混合电力推进系统设计及优化控制仿真[J]. 舰船科学技术, 2020(42): 134-139. ZHANG Cheng, JIA Bao-zhu. Research on design and optimization control of ship hybrid electric propulsion system[J]. Ship Science and Technology, 2020(42): 134-139. |
| [3] |
孙晓军, 宋恩哲, 姚崇. 船用混合动力推进系统能量管理系统关键技术[J]. 中国机械工程, 2022(33): 469-481+495. SUN Xiao-jun, SONG En-zhe, YAO Chong. Research status of key technology for energy management system of marine hybrid propulsion system[J]. China Mechanical Engineering, 2022(33): 469-481+495. |
| [4] |
魏莱, 朱志宇, 张哲卿. 基于航速优化的电推渡轮能量管理策略[J]. 船舶工程, 2022(44): 100-105+114. WEI Lai, ZHU Zhi-yu, ZHANG Zhe-qing. Energy management strategy of electric propulsion ferry based on electric power optimization[J]. Ship Engineering 2022(44): 100-105+114. |
| [5] |
潘钊, 商蕾, 高海波等. 燃料电池混合动力船舶复合储能系统与能量管理策略优化[J]. 大连海事大学学报, 2021(47): 79-85. PAN Zhao, SHANG Lei, GAO Hai-bo et al. Optimization of composite energy storage system and energy management strategy for fuel cell hybrid ships[J]. Journal of Dalian Maritime University, 2021(47): 79-85. DOI:10.16411/j.cnki.issn1006-7736.2021.03.010 |
| [6] |
唐道贵, 严新平, 袁裕鹏. 综合电力系统船舶能量管理技术[J]. 中国航海, 2017(40): 56-60. TANG Dao-gui, YAN Xin-ping, YUAN Yu-peng. Power management technology in ship’s integrated power system[J]. Navigation of China, 2017(40): 56-60. DOI:10.3969/j.issn.1000-4653.2017.04.012 |
| [7] |
陈剑龙, 刘俊峰, 王振刚等. 基于DRL的无人船混合动力系统能量管理策略研究[J]. 中国测试, 2020(46): 9-15. CHEN Jian-long, LIU Jun-feng, WANG Zhen-gang et al. Energy management strategy of hybrid ship based on deep reinforcement learning[J]. China Measurement & Test, 2020(46): 9-15. |
 2023, Vol. 45
2023, Vol. 45
