船舶燃气轮机具有功率密度大、机动性优越等优势,燃气轮机控制效果,直接影响燃气轮机的运行安全性、经济性以及稳定性。控制功能主要包括转速控制、排气温度控制、限制保护控制等。转速控制属于船舶燃气轮机控制的核心问题,在燃气轮机启停时期、加减载阶段,转速的合理控制,可保证燃气轮机运行状态平稳[1 − 2]。
为此,船舶燃气轮机转速的控制研究成为当下船舶智能控制问题的研究热点。宋武健等[3]在分析船舶电力推进系统负载特性的基础上,使用转速环控制器,调节转速环带宽,实现船舶电力推进系统转速控制。虽然此方法可控制电机的转速响应无超调,但在多变工况中,此方法的自适应控制效果不好。宋恩哲等[4]在研究船舶混合动力系统控制问题时,以动态协调的方式,控制天然气发动机转速,但此方法在提出使用“功率/扭矩闭环”的方式,调节转速的过程中,对此方面的具体操作方法一语带过,研究层次有待提升。
本文提出基于状态观测的船舶燃气轮机转速自适应模糊控制方法,此方法有效结合已有经验,在准确观测船舶燃气轮机转速状态的前提下,利用模糊自适应PID控制器,完成船舶燃气轮机转速自适应模糊控制。
1 船舶燃气轮机转速自适应模糊控制 1.1 状态观测器船舶燃气轮机转速控制时,可将船舶燃气轮机构建为非线性控制模型:
| $ \left\{ \begin{gathered} {y_h} = f\left( {{y_h},{\phi _h}} \right)\text{,} \\ {x_h} = f\left( {{y_h},{\phi _h}} \right) + {c_h}\text{。} \\ \end{gathered} \right. $ | (1) |
式中:
船舶燃气轮机运行时,运行工况出现变动后,船舶燃气轮机运行参数也随之变化。此时燃油流量这一指标,可体现船舶燃气轮机的运行状态,燃油流量和燃气轮机转速之间具有明显的映射关系[5 − 7],则
| $ {x_{h - 1}} = {f^{ - 1}}\left( {{y_{h - 1}},{\phi _{h - 1}}} \right) \text{,}$ | (2) |
将式(2)代入式(1),则
| $ {x_{h - 1}} = f\left( {{y_{h - 1}},{\phi _{h - 1}},{\phi _h}} \right) + {c_h}\text{。} $ | (3) |
使用式(3)构建船舶燃气轮机转速状态观测器时,因燃气轮机的不确定项存在约束值,为此设置转速观测器的观测结果为:
| $ {x_h} = f\left( {{y_{h - 1}},{\phi _{h - 1}},{\phi _h}} \right) \text{。}$ | (4) |
由式(4)可知,当掌握船舶燃气轮机的初始状态值、历史的燃油流量,便可实时估计观测后续时刻的转速状态量。在此过程中,需设定转速跟踪矢量误差
| $ {d_h} = \frac{{{a_h}}}{{{x_h}}}\text{,} $ | (5) |
则结合
针对观测的异常转速问题,使用基于模糊自适应PID控制器的转速控制模型,解决船舶燃气轮机转速自适应模糊控制问题。
模糊控制能通过计算机模拟人类思维方式、操作经验,应用于问题分析过程之中。其利用控制规则便可解决非线性控制问题。控制过程中,把模糊控制与PID控制结合,实现自适应控制。图1为基于模糊自适应PID控制器的转速控制模型结构图。

|
图 1 基于模糊自适应PID控制器的转速控制模型结构 Fig. 1 Structure of speed control model based on fuzzy adaptive PID controller |
如图1所示,此模型根据实时观测的速度状态量,设置转速偏差与偏差变化率分别是
船舶燃气轮机转速的模糊自适应PID参数调节运算方法为:
| $ {k_P} = {k_{P0}} + \Delta {k_P} \text{,}$ | (6) |
| $ {k_I} = {k_{I0}} + \Delta {k_I}\text{,} $ | (7) |
| $ {k_D} = {k_{D0}} + \Delta {k_D}\text{。} $ | (8) |
式中:
构建转速控制的模糊规则表时,由模糊隶属度函数,把转速给定值输入量映射至模糊集区间中,为保证转速控制的自适应性、灵敏性,使用归一量化因子,把模糊控制器输入量映射至模糊集论域[正大、正中、正小、零、负小、负中、负大]中,模糊隶属函数示意图如图2所示。

|
图 2 模糊隶属函数示意图 Fig. 2 Schematic diagram of fuzzy membership function |
模糊逻辑推理使用Mamdani模型,引入加权平均解模糊法,求解转速控制器的输出值,则转速控制律
| $ q = \left\{ \begin{gathered} \frac{{W\varepsilon }}{{{d_h}\varepsilon }} \text{,} \\ {k_P},{k_I},k{}_D \text{。} \\ \end{gathered} \right. $ | (9) |
式中,
为实现转速自适应控制,使用Lyapunov函数设置自适应率,则
| $ L\left( {{x_h},{{\hat x}_h}} \right) = x_h^{\rm{T}}{\boldsymbol{Z}}{\hat x_h} + \frac{1}{q}\hat x_h^{\rm{T}}{\boldsymbol{Z}}_1^{ - 1}{\hat x_h} \text{。}$ | (10) |
式中:
船舶燃气轮机运行时,转速控制效果需符合预期给定状态,为了保证船舶燃气轮机安全运行,且具备较好的发电能力,需要动态、自适应调节转速。为测试本文方法的使用效果,以某型燃气轮机为实验对象,此燃气轮机信息如表1所示。
|
|
表 1 实验研究对象详情 Tab.1 Details of experimental research subjects |
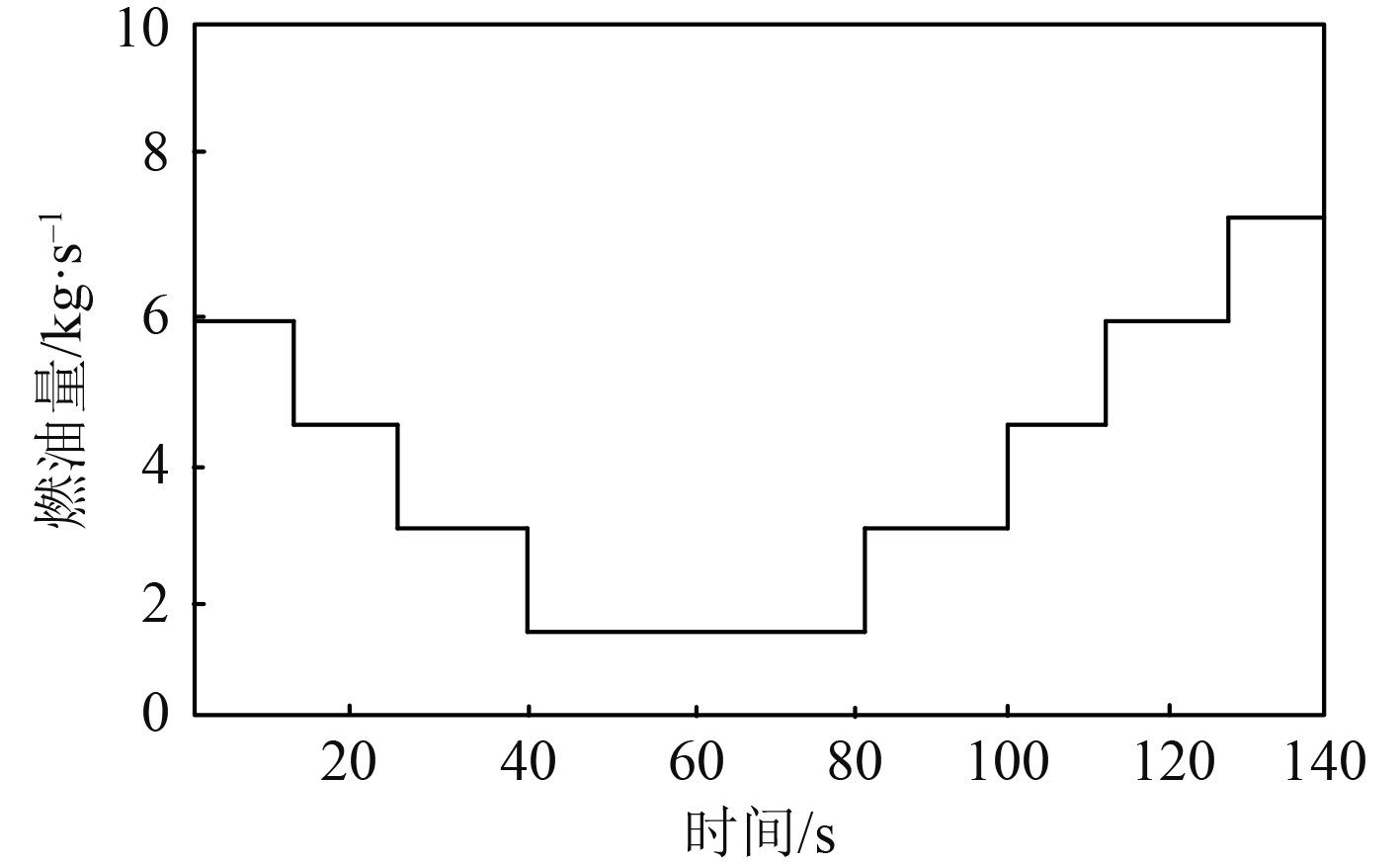
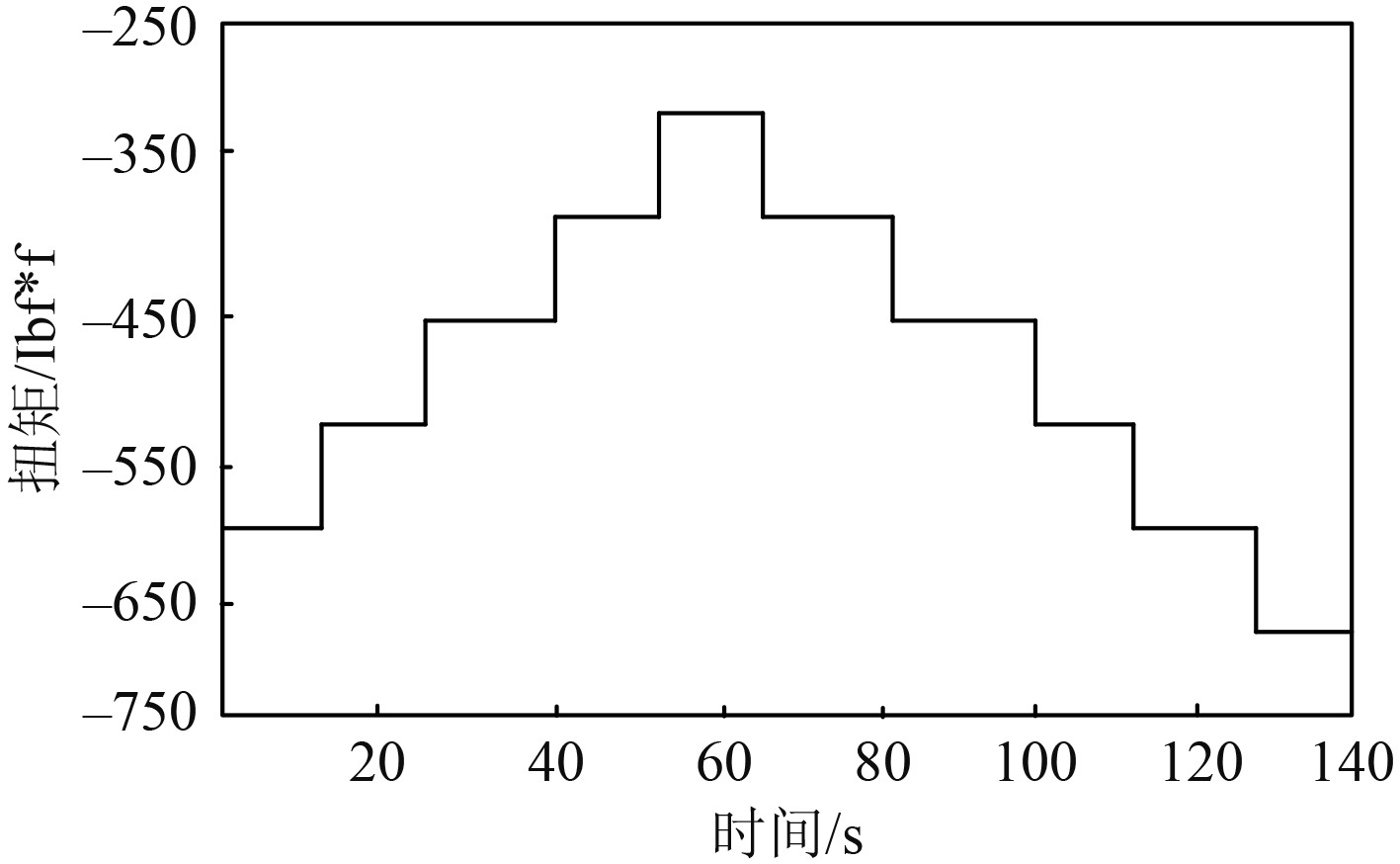
实验中,燃气轮机的给定连续阶跃燃油与负载情况如图3和图4所示。
|
图 3 燃气轮机的给定连续阶跃燃油输入详情 Fig. 3 Details of given continuous step fuel input for gas turbines |
|
图 4 燃气轮机的给定连续阶跃外部负荷输入详情 Fig. 4 Details of the given continuous step external load input for a gas turbine |
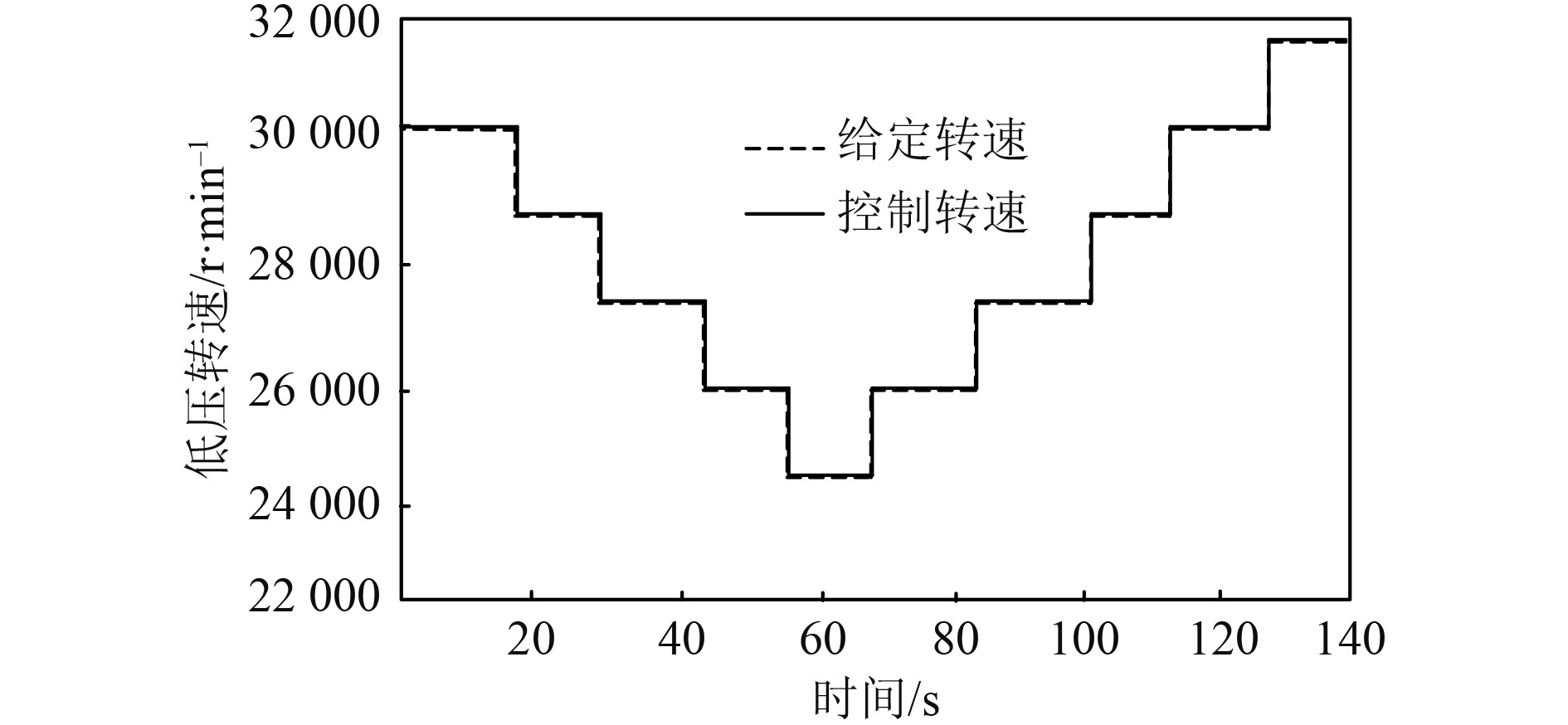
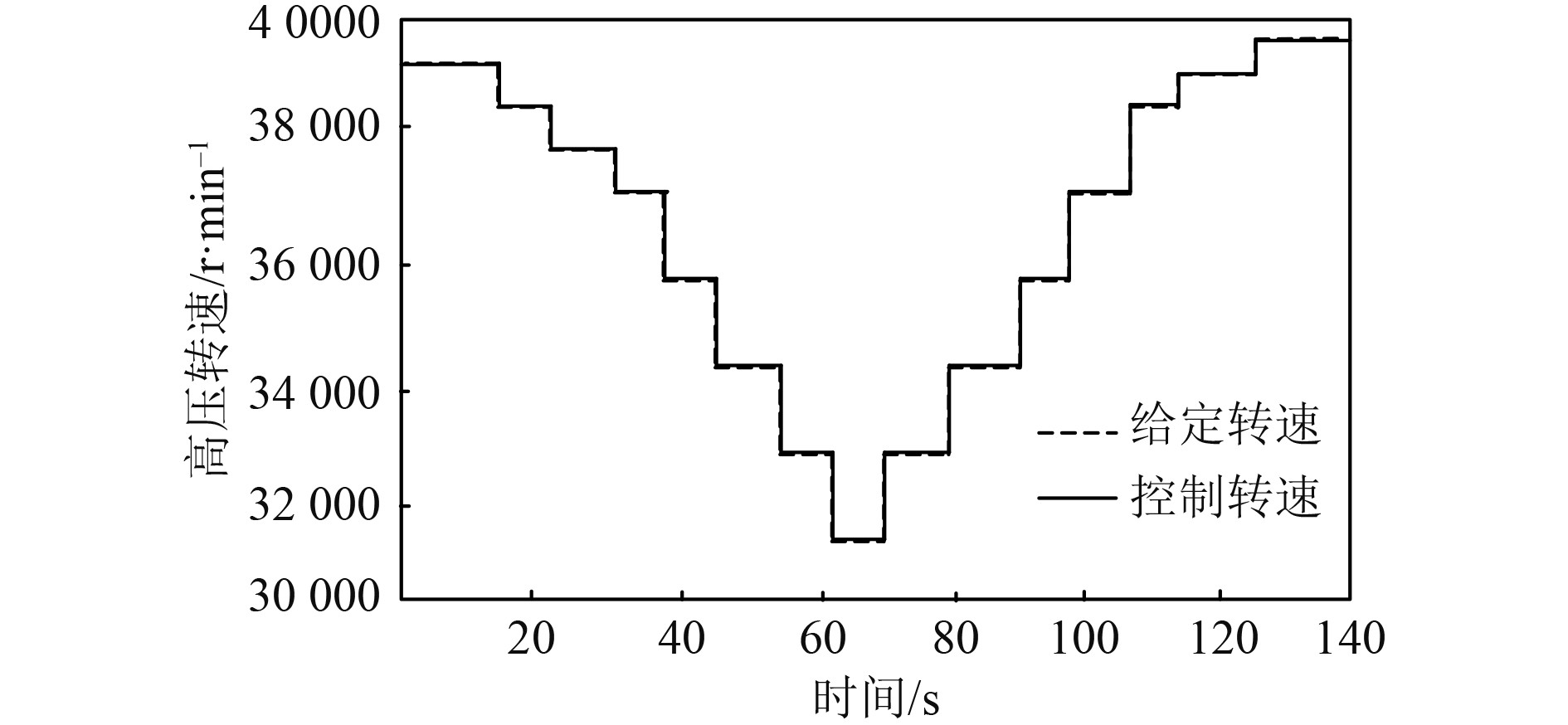
在图3、图4所示工况中,本文方法使用后,船舶燃气轮机低压转速、高压转速的控制效果如图5和图6所示。
|
图 5 船舶燃气轮机低压转速控制效果 Fig. 5 Low pressure speed control effect of ship gas turbine |
|
图 6 船舶燃气轮机高压转速控制效果 Fig. 6 High pressure speed control effect of ship gas turbine |
可以看出,本文方法使用下,船舶燃气轮机低压转速、高压转速的控制均与给定值匹配,转速的变化趋势不存在明显超调状态。
为更直观分析本文方法的使用价值,使用雷达图分析本文方法使用后,船舶燃气轮机转速偏差率、转速稳定时间参数,雷达图中,面积较小,则表示转速控制稳定性越高。测试结果如图7和图8所示。
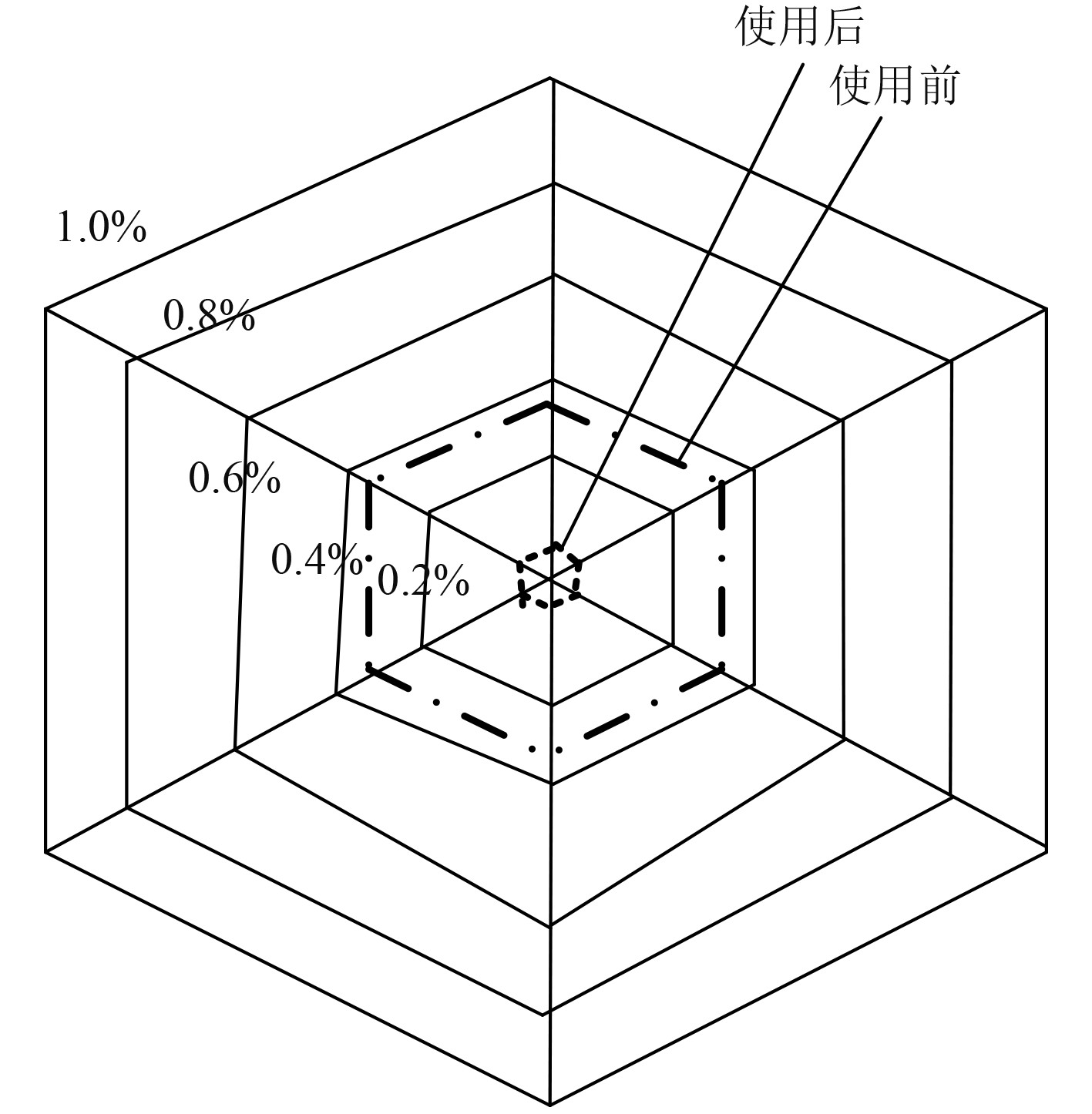
|
图 7 转速偏差率测试结果 Fig. 7 Speed deviation rate test results |

|
图 8 转速稳定时间测试结果 Fig. 8 Speed stability time test results |
可以看出,本文方法使用后,船舶燃气轮机转速偏差率最小,控制在0.1%之内,转速稳定时间最短,控制在1 min之内。对比可知,本文方法的使用,可优化船舶燃气轮机转速控制精度、控制速度,转速控制稳定性较高。
3 结 语燃气轮机凭借效率高、可靠性显著等优点,被广泛使用在船舶上。燃气轮机转速控制,是燃气轮机发电机组可靠运行的重点问题。本文针对船舶燃气轮机转速控制问题进行专题研究,提出了基于状态检测的船舶燃气轮机自适应模糊控制方法,并在实验中对本文方法进行性能测试,测试结论如下:
1)本文方法使用下,船舶燃气轮机低压转速、高压转速的控制均与给定值匹配,转速的变化趋势不存在明显超调状态。
2)本文方法使用后,船舶燃气轮机转速偏差率最小,控制在0.1%之内,转速稳定时间最短,控制在1 min之内,具有使用价值。
| [1] |
戴日辉, 宋子刚, 董辉, 等. 船用燃气轮机输出轴对中状态监测装置[J]. 热能动力工程, 2021, 36(3): 13-18. DAI Rihui, SONG Zigang, DONG Hui, et al. Monitoring device for the alignment condition of marine gas turbine output shaft[J]. Journal of Engineering for Thermal Energy and Power, 2021, 36(3): 13-18. DOI:10.16146/j.cnki.rndlgc.2021.03.002 |
| [2] |
赵松涛, 王南, 王鑫, 等. 水下爆炸作用下船舶结构与燃气轮机动态响应的数值研究(英文)[J]. 船舶力学, 2021, 25(6): 815-827. ZHAO Songtao, WANG Nan, WANG Xin, et al. Numerical investigation of dynamic responses of ship structure and gas turbine subjected to underwater explosion[J]. Journal of Ship Mechanics, 2021, 25(6): 815-827. DOI:10.3969/j.issn.1007-7294.2021.06.013 |
| [3] |
宋武健, 王国玲, 罗成汉, 等. 船舶氢储直流电力推进系统控制器转速环带宽设计方法[J]. 中国舰船研究, 2023, 18(1): 260-268. SONG Wu-jian, WANG Guo-ling, LUO Cheng-han, et al. Speed-loop bandwidth design method for controller parameters of ship hydrogen storage DC electric propulsion system[J]. Chinese Journal of Ship Research, 2023, 18(1): 260-268. |
| [4] |
宋恩哲, 孙晓军, 姚崇, 等. 船舶混合动力系统模式切换与动态协调控制[J]. 哈尔滨工程大学学报, 2022, 43(4): 522-528. SONG Enzhe, SUN Xiaojun, YAO Chong, et al. Mode switching and dynamic coordination control of ships with a hybrid power system[J]. Journal of Harbin Engineering University, 2022, 43(4): 522-528. DOI:10.11990/jheu.202104057 |
| [5] |
徐涛, 李晖, 祁昱豪. 船舶参数横摇抑制的神经网络逆/内模控制[J]. 船舶工程, 2022, 44(6): 109-116. XU Tao, LI Hui, QI Yuhao. Neural network inverse/internal model control for ship parametric roll suppression[J]. Ship Engineering, 2022, 44(6): 109-116. DOI:10.13788/j.cnki.cbgc.2022.06.18 |
| [6] |
张青山, 陈伟民, 杜云龙, 等. 基于实尺度船舶自航数值模拟的航速预报[J]. 中国造船, 2022, 63(5): 11-21. ZHANG Qingshan, CHEN Weimin, DU Yunlong, et al. Speed prediction based on full scale numerical simulation of self-propulsion[J]. Shipbuilding of China, 2022, 63(5): 11-21. DOI:10.3969/j.issn.1000-4882.2022.05.002 |
| [7] |
谢嘉令, 施伟锋, 兰莹, 等. 基于幂次指数趋近律的船舶电力推进控制研究[J]. 计算机仿真, 2022, 39(6): 279-283. XIE Jialing, SHI Weifeng, LAN Ying, et al. Research on sliding mode control of ship electric propulsion based on power exponent reaching law[J]. Computer Simulation, 2022, 39(6): 279-283. |
 2023, Vol. 45
2023, Vol. 45
