作为船舶系统重要的组成部分,柴油机的可靠性和安全性得到了越来越多的关注[1]。在整个航运过程中,船舶柴油机运行性能发挥着至关重要的作用。因为处于恶劣环境中,船舶柴油机在工作时出现了越来越多故障。如果船舶柴油机发生重大故障,会导致船舶停运,造成严重经济损失[2]。为实现船舶系统视情维护,保障船舶稳定运行,及时对船舶柴油机进行故障诊断,并根据故障诊断结果进行合理维修,具有极其重要的意义。
神经网络基于对故障样本的学习,对所学习的故障诊断知识,以连接权值形式进行描述,解读故障征兆和故障之间一对多的非线性关系,从而实现对故障的联想记忆、模式匹配和相似归纳,在复杂系统故障诊断中应用越来越广泛,优势也越来越明显[3]。目前,在故障诊断领域,被广泛采用的神经网络模型有反向传播(Back Propagation,BP)神经网络[4-6]、自组织映射(Self-organized Mapping,SOM)神经网络[7-10]等。但各神经网络因算法局限性、所需样本数量大、网络结构未知等因素,在故障诊断过程中都存在一定缺陷。基于上述问题,本文阐述了BP神经网络和SOM神经网络模型结构和算法学习步骤,将二者融合构建SOM-BP神经网络,并阐述该网络的模型结构和算法学习步骤,通过仿真试验验证了该网络在船舶柴油机故障诊断中的有效性。
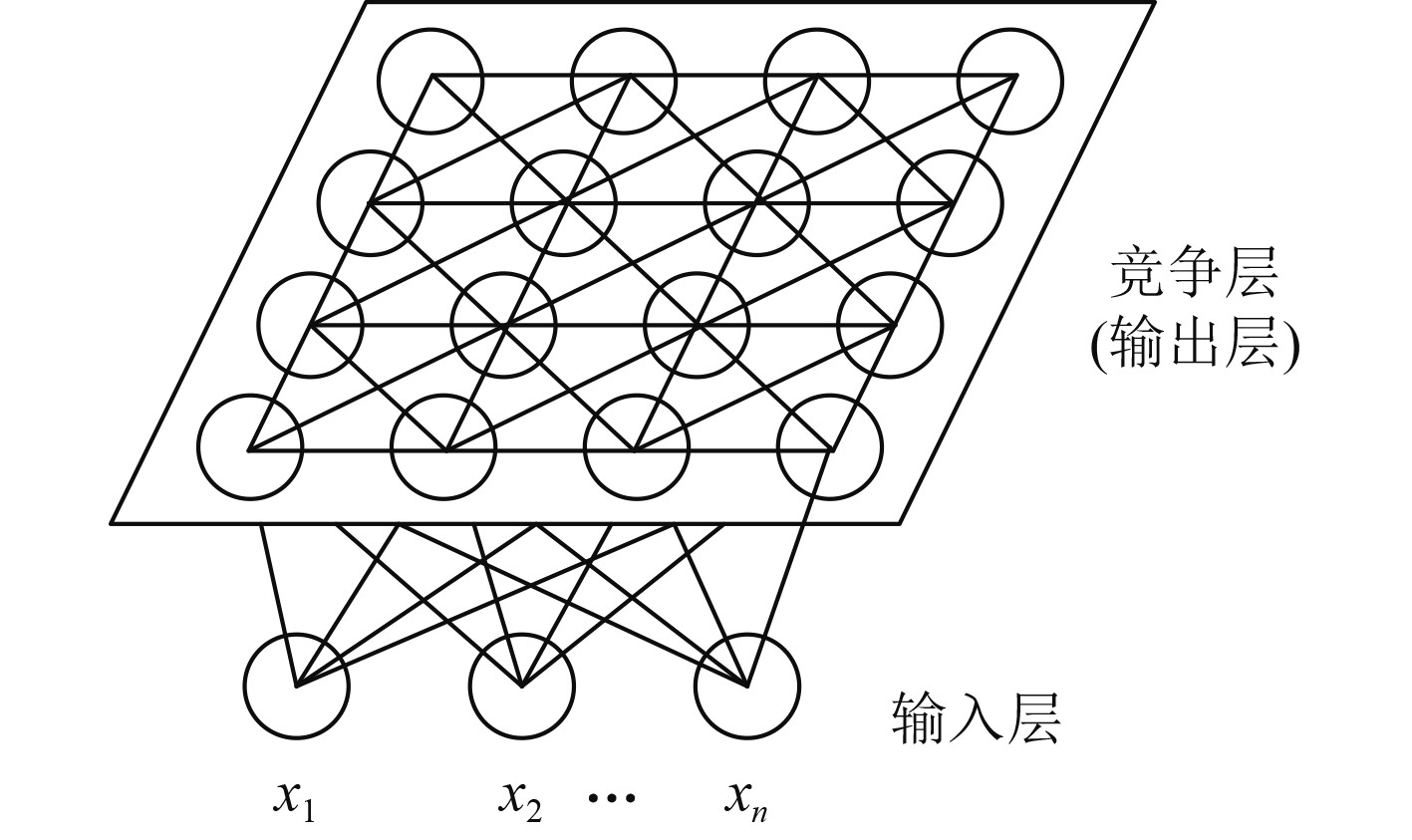
1 SOM神经网络 1.1 SOM神经网络模型结构SOM神经网络是无监督、自学习网络[11],通过对故障样本数据进行聚类,将其映射至多维空间不同的位置,从而实现对故障样本数据的分类,其网络结构如图1所示。SOM神经网络由2层神经元构成,即输入层和输出层神经元。通过权向量,故障样本数据经输入层传输到输出层神经元。输入层神经元个数与故障样本维数保持一致,输出层神经元结构以二维形式呈现。
|
图 1 SOM神经网络结构图 Fig. 1 Structure diagram of SOM neural network |
当样本数据输入网络模型,故障样本输入向量与神经元权值向量间的欧式距离就可通过计算得出,获胜神经元可通过比较所计算出的欧式距离大小来确定。通过获胜神经元位置,可确定其邻域范围,依据学习率、故障样本数据更新此范围内所有神经元的权值,模型经过不断更新迭代,直至收敛。
1.2 SOM神经网络算法学习步骤步骤1 SOM神经网络初始化。随机设定输入层神经元i与竞争层神经元j的初始权值
步骤2 训练样本向量输入。首先进行归一化处理,并选取一组训练样本k,将输入样本
步骤3 获胜神经元确定。计算输入样本
| $ {d}_{jk}=\left|\right|{X}_{k}-{w}_{j}\left|\right|=\sqrt{{\sum _{i=1}^{n}({x}_{ik}-{w}_{ij}(t\left)\right)^{2}}}。$ | (1) |
其中:
步骤4 获胜神经元邻域范围确定。获胜神经元领域范围随着更新次数不断缩小。
步骤5 权值更新。确定获胜神经元邻域范围后,对此范围内的神经元进行权值更新,其更新公式为:
| $ {w}_{ij}(t+1)={w}_{ij}\left(t\right)+\eta(t)[{x}_{ik} -{w}_{ij}\left(t\right) ],j=1,2,...,m。$ | (2) |
其中:
步骤6 竞争神经元
| $ {o}_{k}=f\left(\min\right||{X}_{k}-{w}_{j}|\left|\right) 。$ | (3) |
其中,
步骤7 判断SOM神经网络是否收敛。收敛结束训练,未收敛则重新返回步骤2。
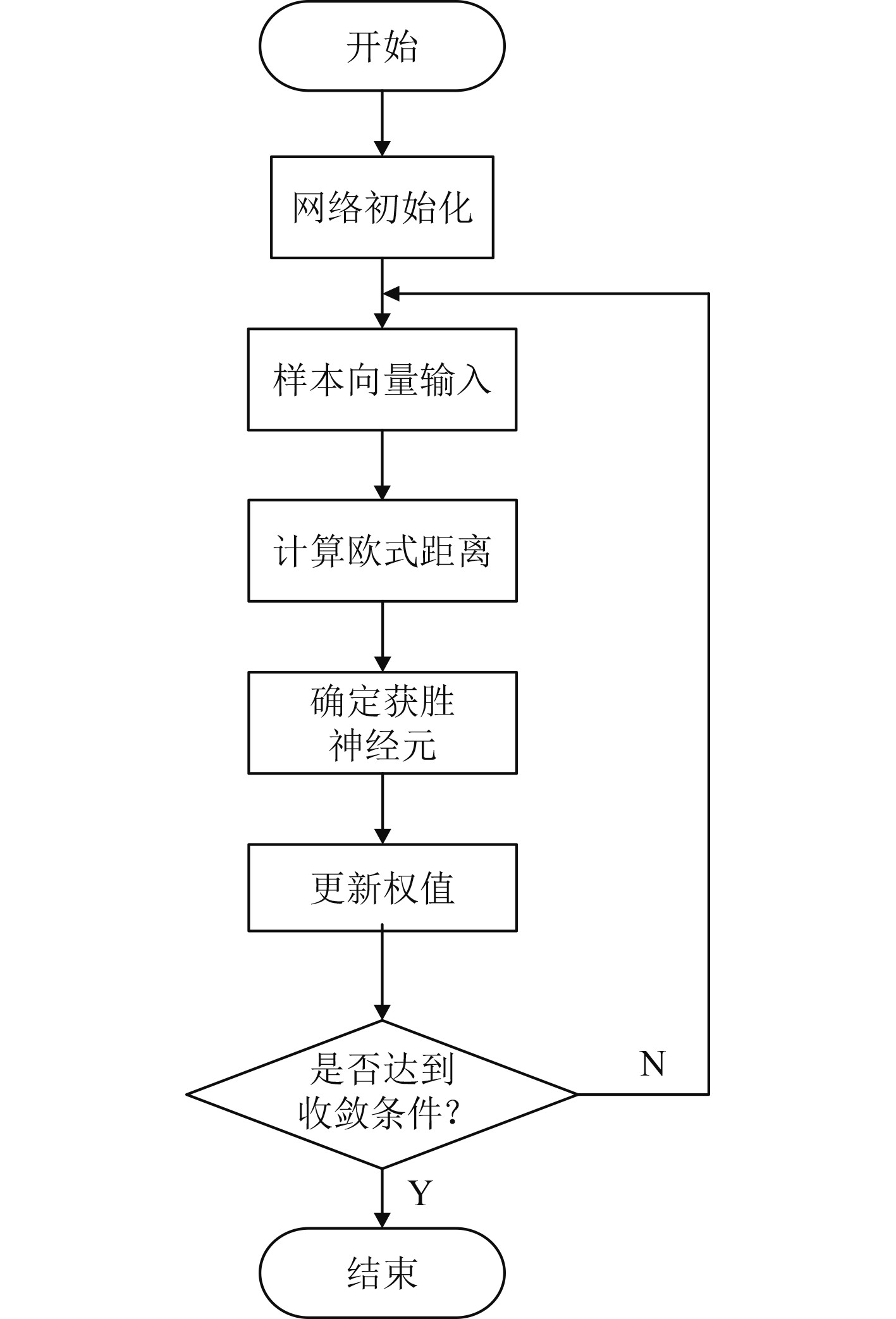
SOM神经网络学习流程图如图2所示。
|
图 2 SOM神经网络算法流程图 Fig. 2 Flow chart of SOM neural network algorithm |
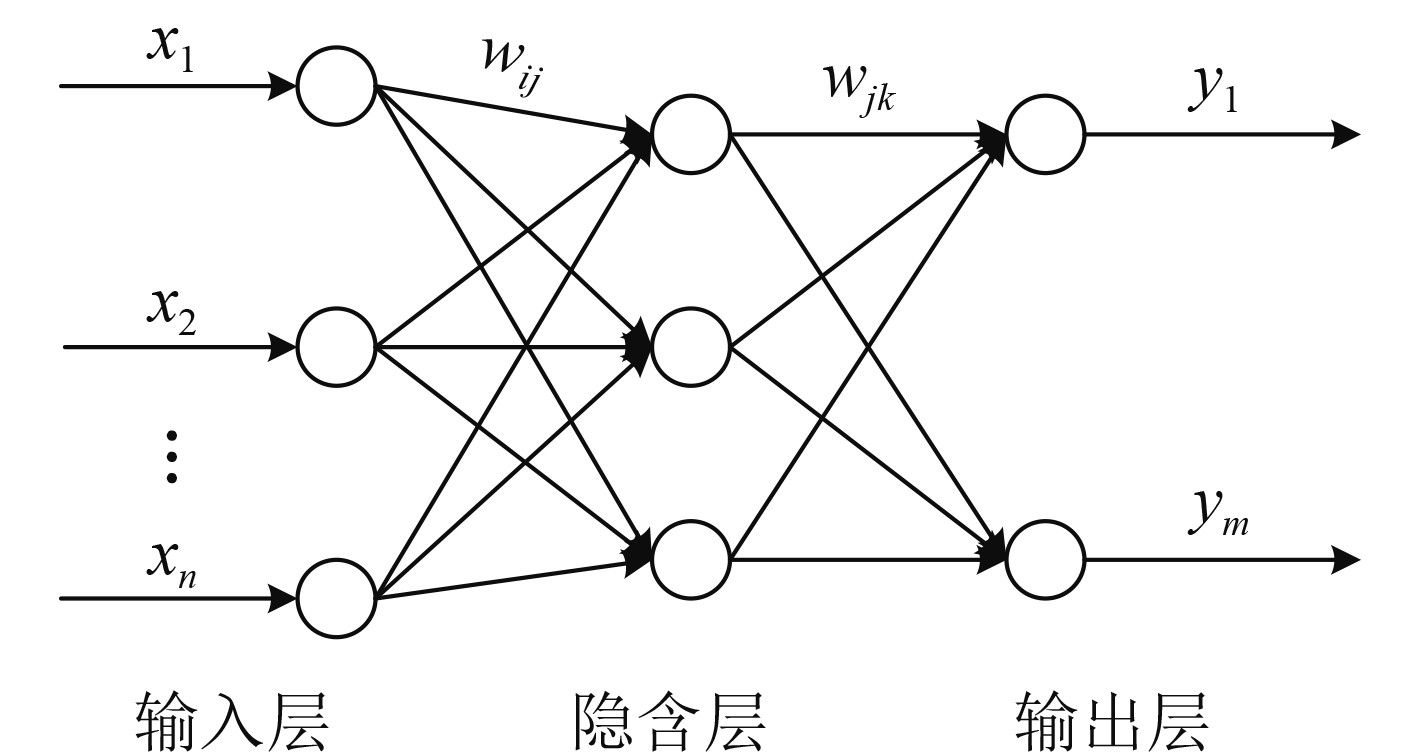
BP神经网络是一种前馈网络,其结构如图3所示,由输入层、隐含层和输出层构成。该网络的主要特点是各层神经元仅与相邻层神经元之间相互全连接,同层内神经元之间无连接,各层神经元之间无反馈连接。
|
图 3 BP神经网络结构图 Fig. 3 Structure diagram of BP neural network |
图中,
步骤1 网络初始化。确定BP神经网络输入节点数n,隐含层节点数l,输出节点数m。初始化权值
步骤2 隐含层输出计算:
| $ {H}_{j}=f\left(\sum _{i=1}^{n}{w}_{ij}{x}_{i}-{a}_{j}\right) \text{,}j=1,2,...,l。$ | (4) |
其中:
步骤3 神经网络预测输出计算:
| $ {O}_{k}=\sum _{j=1}^{l}{H}_{j}{w}_{jk}-{b}_{k} \text{,}j=1,2,...,l 。$ | (5) |
步骤4 网络预测误差计算:
| $ {e}_{k}={y}_{k}-{O}_{k} \text{,}j=1,2,...,l 。$ | (6) |
步骤5 更新网络权值:
| $ \begin{split} & {w}_{ij} = {w}_{ij}+\eta {H}_{j}\left({1-H}_{j}\right){x}_{i}\sum _{k=1}^{m}{w}_{jk}{e}_{k} \text{,}i=1,2,...,n\text{;}\\ & j=1,2,...,l,\end{split} $ | (7) |
| $ {w}_{jk}={w}_{jk}+\eta {H}_{j}{e}_{k} \text{,}j=1,2,...,l\text{;}k=1,2,...,m 。$ | (8) |
其中,
步骤6 更新阈值:
| $ {a}_{j}={a}_{j}+\eta {H}_{j}(1-{H}_{j})\sum _{k=1}^{m}{w}_{jk}{e}_{k} \text{,}j=1,2,...,l,$ | (9) |
| $ {b}_{k}={b}_{k} + {e}_{k} \text{,}k=1,2,...,m。$ | (10) |
步骤7 判断是否达到终止条件。判断误差是否在允许范围内,如果满足要求,则结束训练,否则返回步骤2。
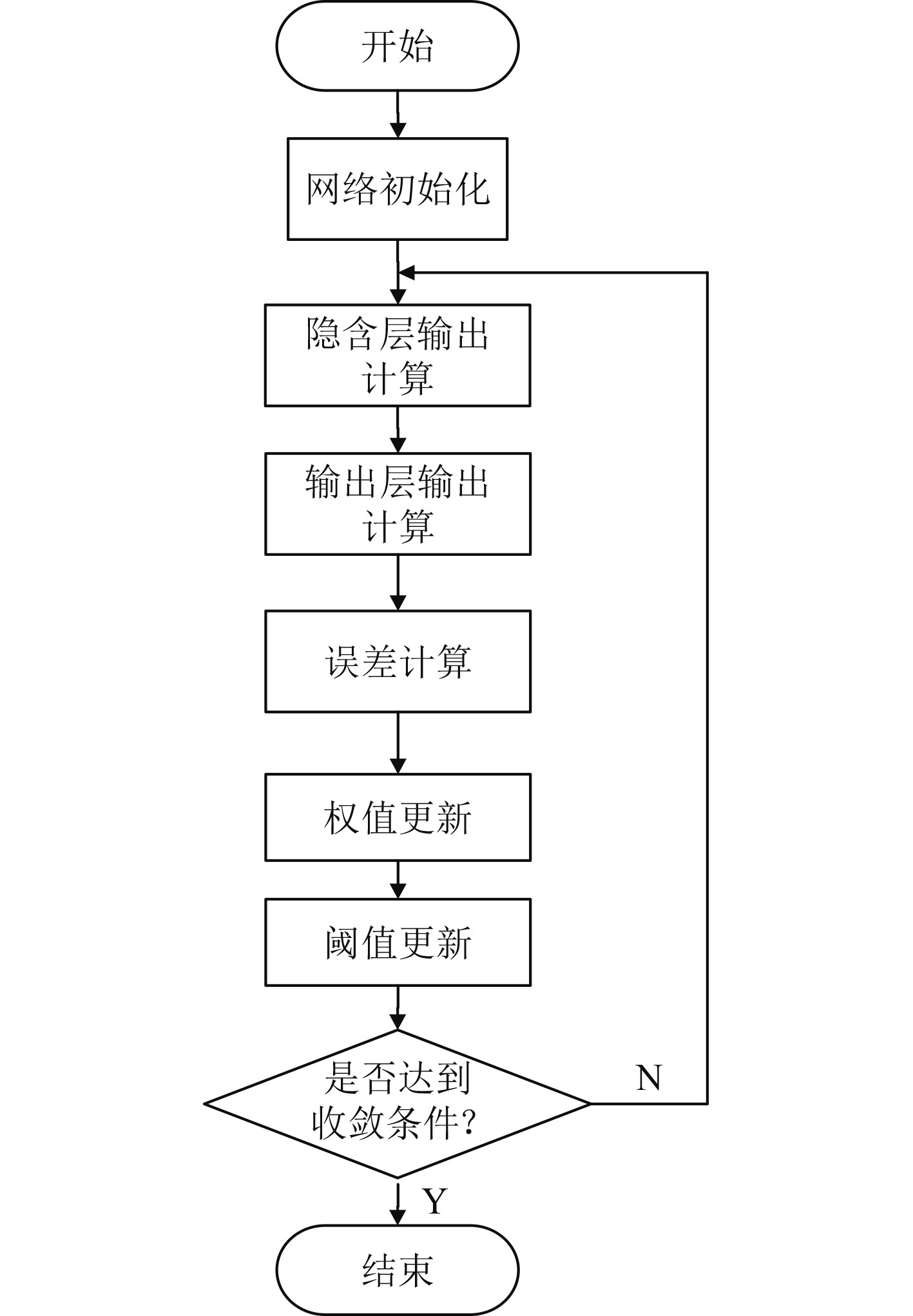
BP神经网络学习流程图如图4所示。
|
图 4 BP神经网络算法流程图 Fig. 4 Flow chart of BP neural network algorithm |
BP神经网络具有自学习、非线性映射能力,但需进行大量的故障样本数据训练,会导致网络训练时间较长,实时性较差。SOM神经网络能够对数据进行聚类,无需大量样本数据和人工干预,实时性强,但SOM神经网络分类的准确性依赖于采集故障样本数据的完整性以及数据量的多少。考虑到单一网络在故障诊断中的局限性,将二者进行融合,构建SOM-BP组合神经网络。
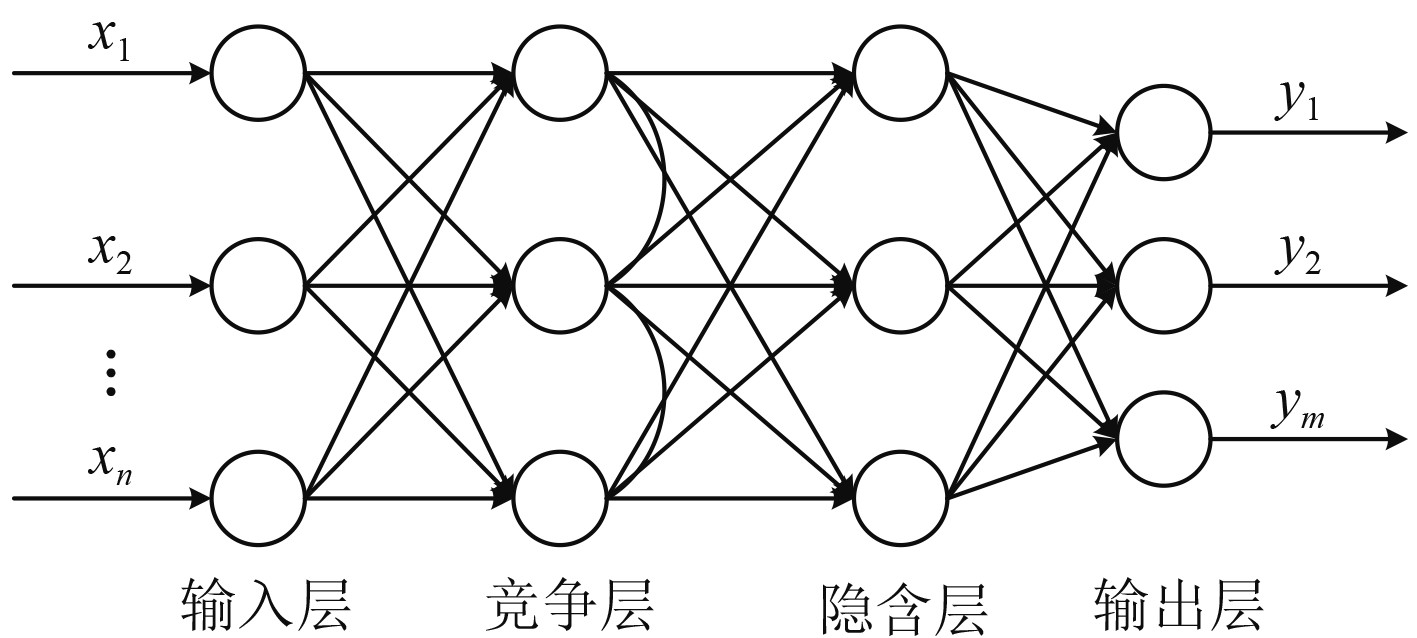
3.1 SOM-BP神经网络模型结构SOM-BP组合神经网络融合有串联、并联2种方式。结合二者在故障诊断中各自优缺点,本文将二者串联来实现故障诊断。将SOM网络作为第一级网络,将输入样本进行自聚类,目的是减轻BP网络识别压力,降低识别难度。将BP网络作为第二级网络,对故障样本进行有导师学习,图5为SOM-BP组合网络结构图。
|
图 5 SOM-BP神经网络结构图 Fig. 5 Structure diagram of SOM-BP neural network |
步骤1 样本数据预处理,选取故障样本数据,进行归一化处理。
步骤2 初始化SOM神经网络,输入故障样本数据,经过模型训练,得到初步聚类结果。
步骤3 将SOM神经网络竞争层输出的结果进行归一化处理。
步骤4 初始化BP神经网络,将归一化后的结果输入到BP网络中再次进行训练。
步骤5 进行多次训练,形成SOM-BP神经网络分类模型。
步骤6 判断模型是否达到收敛条件。如果达到收敛条件,则终止训练。如果未达到收敛条件,则返回步骤4。
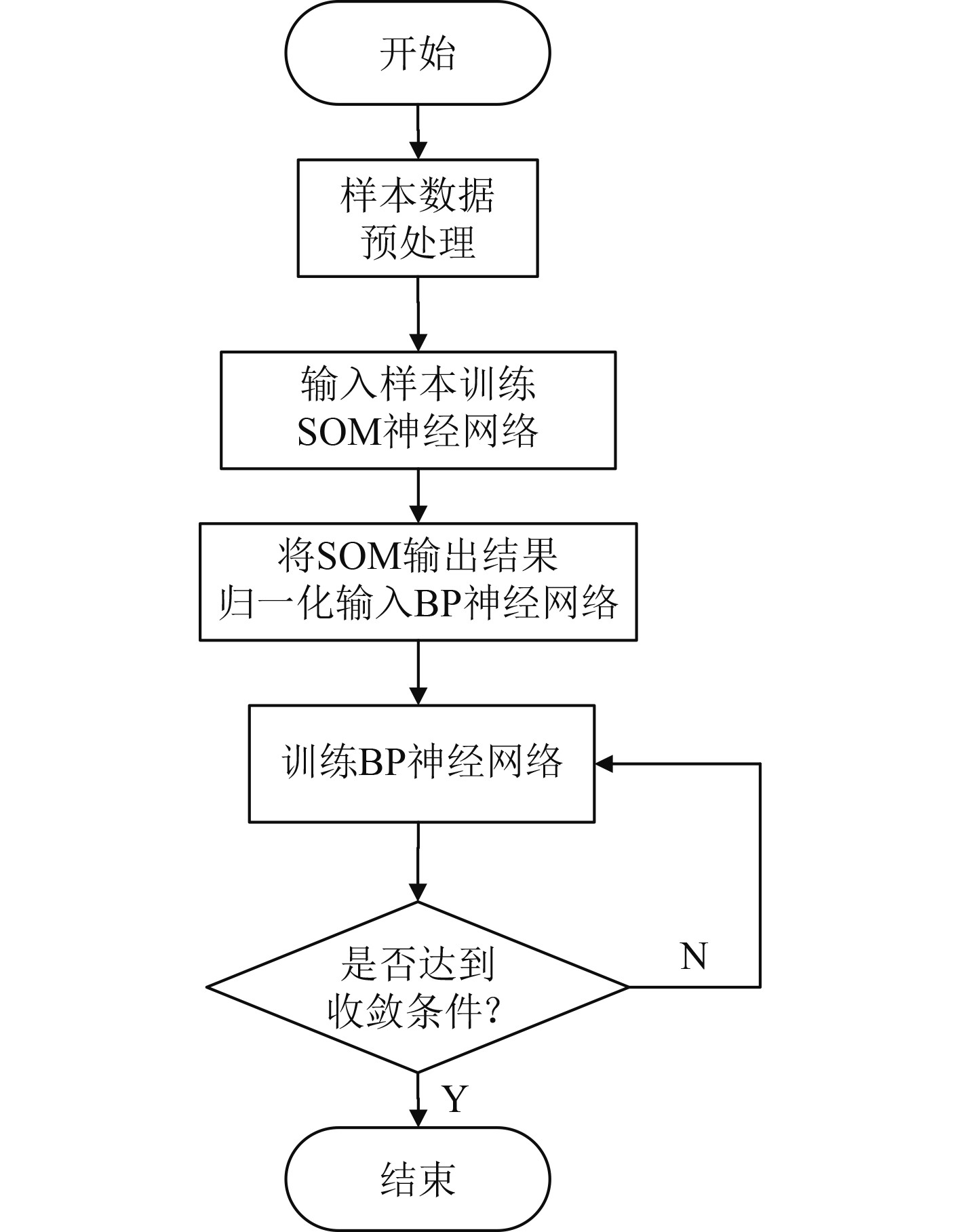
|
图 6 SOM-BP神经网络算法流程图 Fig. 6 Flow chart of SOM-BP neural network algorithm |
根据船舶柴油机压力波形曲线,提取8种故障特征(P1~P8),汇集船舶柴油机8种故障类型(T1~T8)数据,形成训练集和测试集,如表1和表2所示,SOM-BP网络期望输出如表3所示。
|
|
表 1 SOM-BP神经网络训练数据集 Tab.1 Training data of SOM-BP neural network |
|
|
表 2 SOM-BP神经网络训练数据集 Tab.2 Testing data of SOM-BP neural network |
|
|
表 3 SOM-BP神经网络期望输出 Tab.3 Desired output of SOM-BP neural network |
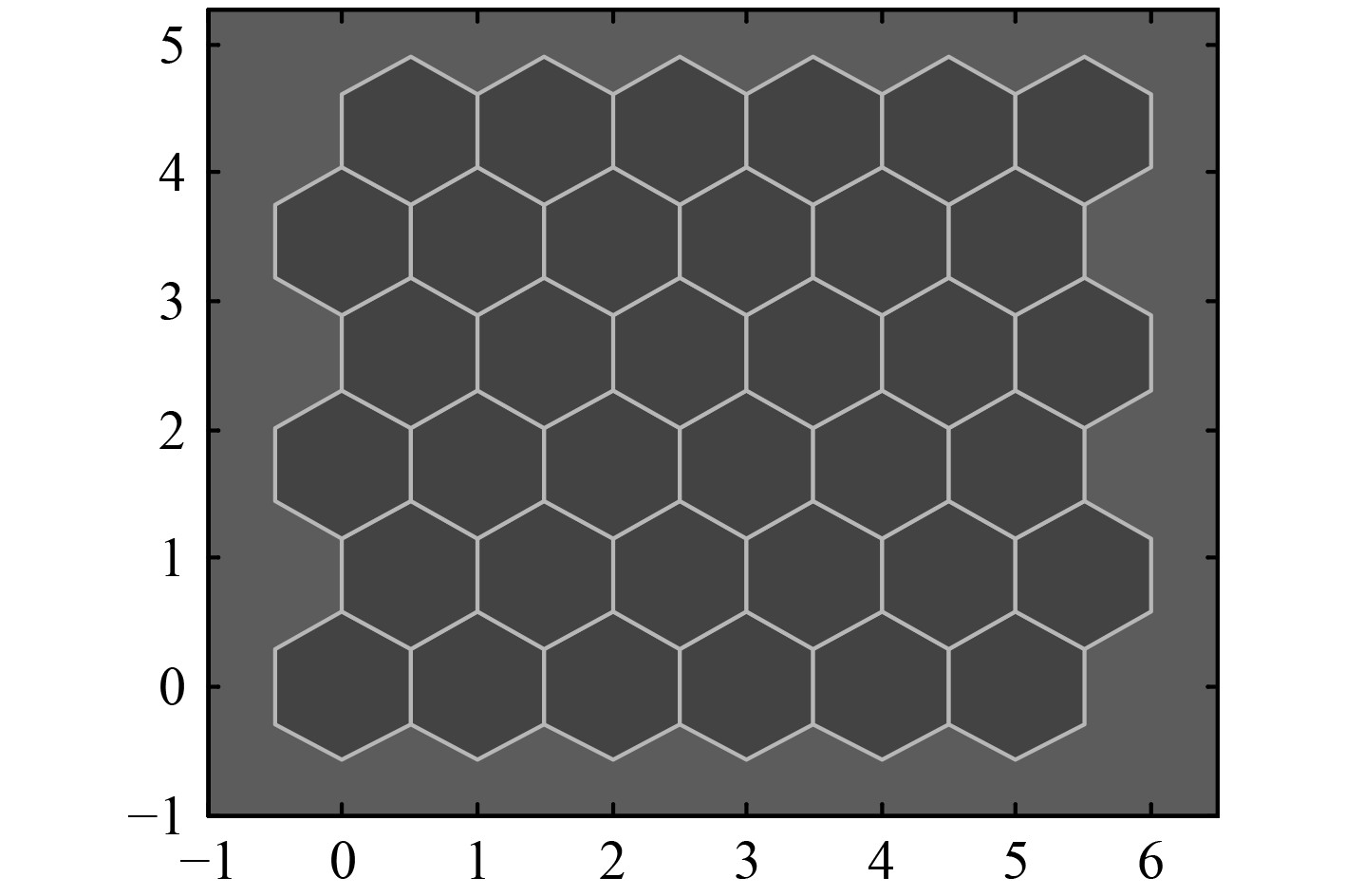
将初级神经网络即SOM神经网络输入神经元个数设置为8,对应8种船舶柴油机故障类型。竞争层网络选用6×6结构,采用六角形拓扑结构,如图7为SOM神经网络竞争层36个神经元网络拓扑结构。
|
图 7 SOM神经网络拓扑结构 Fig. 7 SOM neural network topology |
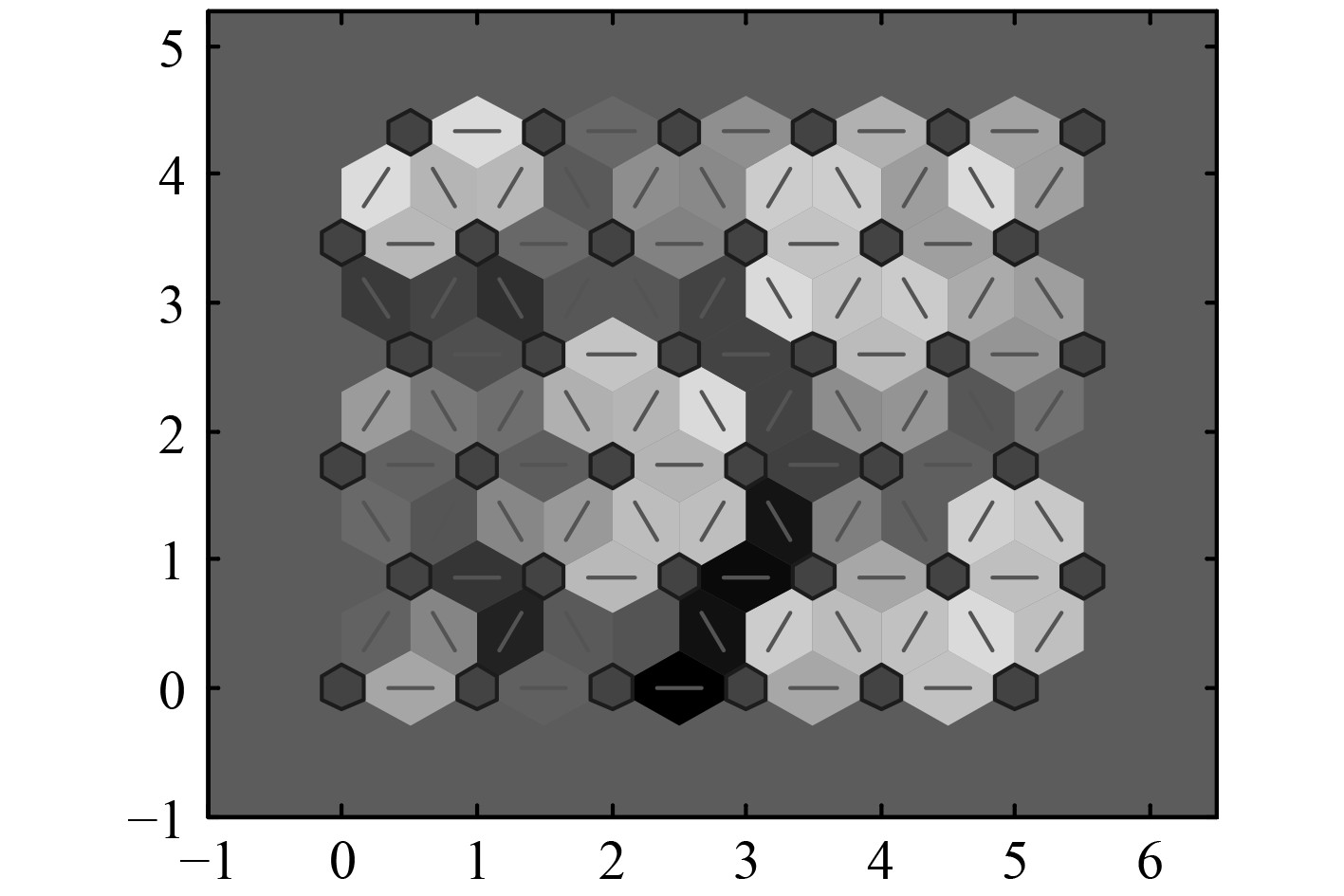
故障样本数据经过SOM神经网络处理之后,邻近神经元之间的距离如图8所示,神经元分类情况如图9所示,聚类结果如表4所示。
|
图 8 SOM神经网络邻近神经元距离 Fig. 8 SOM neighbor weight distances |

|
图 9 SOM神经网络分类情况 Fig. 9 SOM neural network classification |
|
|
表 4 SOM神经网络聚类结果 Tab.4 Cluster result of SOM neural network |
将表4归一化结果输入到BP神经网络中,BP神经网络采用3层结构。经过多次试验,隐含层神经元个数取13,传递函数采用S型正切函数;输出层神经元个数设置为8,对应8种故障类型,传递函数采用S型对数函数。
当BP神经网络模型达到收敛条件时,终止训练。输入表2故障样本数据进行检测,诊断该故障样本数据为T1类型故障,故障诊断类型与实际故障类型一致。此外,SOM-BP神经网络在模型训练阶段不依赖于大量样本,网络稳定性较好,收敛速度也很快,达到了预期效果。
5 结 语1)基于SOM神经网络和BP神经网络理论基础,构建SOM-BP神经网络模型,用于船舶柴油机故障诊断,通过仿真试验验证SOM-BP神经网络在船舶柴油机故障诊断中的正确性和准确性。
2)避免了单一神经网络模型在复杂系统故障诊断中的局限性,复杂系统故障诊断提供理论依据。
| [1] |
吴瑞莉. 船舶柴油机机械磨损故障诊断方法[J]. 舰船科学技术, 2018, 40(7): 109-111. |
| [2] |
陈颖. 自适应RBF神经网络在船舶柴油机故障诊断系统中的应用[J]. 舰船科学技术, 2021, 43(11): 85-87. DOI:10.3404/j.issn.1672-7649.2021.11A.029 |
| [3] |
罗亮, 李国璋, 杨权, 等. SOM-BP神经网络在机械故障诊断中的应用研究[J]. 车用发动机, 2008, 2(174): 72-75. |
| [4] |
JI Mengran, CHEN Gang, YANG Qing, et al. Fault diagnosis of analog circuit based on PSO and BP neural network[J]. Journal of Shenyang Ligong University, 2014, 33(5): 90-94. |
| [5] |
SUN Y J, ZHANG S, MIAO C X, et al. Improved BP neural network for transformer fault diagnosis[J], Journal of China University of Mining and Technology, 2007, 17(1): 138-142.
|
| [6] |
余锋, 许开熙, 黄俊, 等. 基于 BP 神经网络的高压断路器故障诊断[J]. 真空科学与技术学报, 2019, 39(1): 249-253. |
| [7] |
陈时游, 陆海, 张少泉, 等. SOM 神经网络对永磁同步电机的故障诊断[J]. 软件, 2018, 39(8): 70-73. |
| [8] |
黄金波, 杨萍. 基于SOM神经网络的矿井提升机故障诊断技术研究[J]. 设备监理, 2019, 7: 53-54. |
| [9] |
刘兆炜, 王汉军, 李丹, 等. 改进SOM神经网络在电力调度故障诊断中的应用[J]. 计算机系统应用, 2018, 27(3): 179-185. |
| [10] |
CHEN Xin-yi, YAN Xue-feng. Using improved self-organizing map for fault diagnosis in chemical industry process[J]. Chemical Engineering Research and Design, 2012, 90(12): 2262-2277. DOI:10.1016/j.cherd.2012.06.004 |
| [11] |
赵文均. 基于SOM和BP网络的K均值聚类算法分析[J]. 电脑知识与技术, 2020, 16(9): 24-26. |
 2023, Vol. 45
2023, Vol. 45
