管道系统作为水利、交通运输等领域内重要流体介质的运输媒介,由于大高差、停泵、闭阀等原因,会产生水锤效应,水锤对管道系统的寿命、安全性等方面有着很大影响,因此准确的水锤计算对管系十分重要[1-2]。Xi等[3]对石油工程油管的偏心水锤特性,通过测试装置、粒子图像测速仪和瞬态压力测量系统进行分析,发现随着偏心距的增大,油套环空内外壁的压力增大,出现水锤现象。Micha等[4]通过在管道内插入弹性管,利用理论分析、实验测试和数值模拟等方法,发现加入弹性管的管道水锤压力增长明显降低。张巧玲等[5]基于特征线法,建立了考虑非恒定摩阻的含气瞬变流模型,对含气疏水管道的水锤特性进行了分析;郭强等[6]对厚壁输水管道在考虑流固耦合情况下的水锤和振动特性进行了分析。王祺武等[7]通过实例计算,对调节阀门全开工况下的关阀水锤进行计算分析,并对管路中的水锤压强进行改善,分析不同控制方式下,对于水锤情况的改善效果,表明单阀,双阀以及三阀调节对于管路中水锤问题都有出色的控制效果。
水锤效应在很多领域都有至关重要的影响,因此各国的专家学者对于水锤现象都进行了大量研究,对水利、交通运输等领域的发展起着重要的推动作用[8-10]。通过对相关文献阅读可发现,目前的研究只考虑了管道与管道内流体对水锤效应的影响,而忽略了管系中管道支架这一影响因素。本文为简化复杂的管路停泵水锤模拟过程,以某深水通用型FPSO管路系统参数为设计依据,设计了一种管型以简化数值仿真难度,并对典型的停泵水锤情况下,支架对水锤效应的影响情况进行分析,为实际工程中对水锤效应的准确分析提供参考。
1 模型建立 1.1 数值模型本文涉及的管系参数均来源于某深水通用型FPSO压载水管路系统,系统中的流体介质为水,可视为不可压缩流体。其中,管路截面上的流动差异对计算结果影响较小,是可忽略的[11]。基于一维水锤方程和特征线法,建立实验研究的数值计算模型。流体的动量方程和连续性方程为[12]:
| $ g\frac{{\partial H}}{{\partial x}} + \frac{{\partial v}}{{\partial t}} + \frac{{{\lambda _f}}}{{2D}}v\left| v \right| = 0 \text{,} $ | (1) |
| $ \frac{{\partial H}}{{\partial t}} + \frac{{{a^2}}}{g}\frac{{\partial v}}{{\partial x}} = 0 \text{。} $ | (2) |
式中:g为重力加速度;H为水头压力;v为流速;x为轴向间距;t为时间;
引入特征值
| $ {C^ + } = \left\{ \begin{gathered} \frac{g}{a}\frac{{{\rm{d}}H}}{{{\rm{d}}t}} + \frac{{{\rm{d}}v}}{{{\rm{d}}t}} + \frac{{{\lambda _f}}}{{2D}}v\left| v \right| = 0 ,\\ \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = + a 。\\ \end{gathered} \right. $ | (3) |
| $ {C^ - } = \left\{ \begin{gathered} - \frac{g}{a}\frac{{{\rm{d}}H}}{{{\rm{d}}t}} + \frac{{{\rm{d}}v}}{{{\rm{d}}t}} + \frac{{{\lambda _f}}}{{2D}}v\left| v \right| = 0 ,\\ \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = - a 。\\ \end{gathered} \right. $ | (4) |
通过式(3)和式(4)可知,管道中水流的压力会以波的形式传递,其传递速度为a。而压力值的大小则等于2个方向(+a/-a)的水锤波叠加。将管道在x方向离散成N等分,每等份的长度为
| $ \left\{ \begin{gathered} {H_i} = \frac{1}{2}({C_{Pi}} + {C_{Mi}}),\\ {Q_i} = \frac{1}{{2B}}({C_{Pi}} - {C_{Mi}})。\\ \end{gathered} \right. $ | (5) |
| $ \left\{ \begin{gathered} {C_{Pi}} = {H_{i - 1}} + {Q_{i - 1}}(B - R\left| {{Q_{i - 1}}} \right|),\\ {C_{Mi}} = {H_{i + 1}} + {Q_{i + 1}}(B - R\left| {{Q_{i + 1}}} \right|)。\\ \end{gathered} \right. $ | (6) |
| $ \left\{ \begin{gathered} B = a/gA,\\ R = {\lambda _f}\Delta x/2gD{A^2} 。\\ \end{gathered} \right. $ | (7) |
式中:A为管道截面积;B和R为常数;
为更好地分析管道支架对水锤效应的影响,利用Ansys软件进行管系与管道水流的流固双向耦合计算,由于常见管系停泵水多产生于水泵处,需重点研究的边界面属于变界面情况,水泵处的水锤压力监测以及双向流固耦合的过程十分复杂,对计算机的运算能力要求太高。因此提出一种基于某深水通用型FPSO压载水管系参数设计的简化水锤计算模型,在简化计算的同时,更好地模拟水锤产生的过程及不同算例形式对水锤大小的影响,以得出具有普遍参考意义的研究结果。
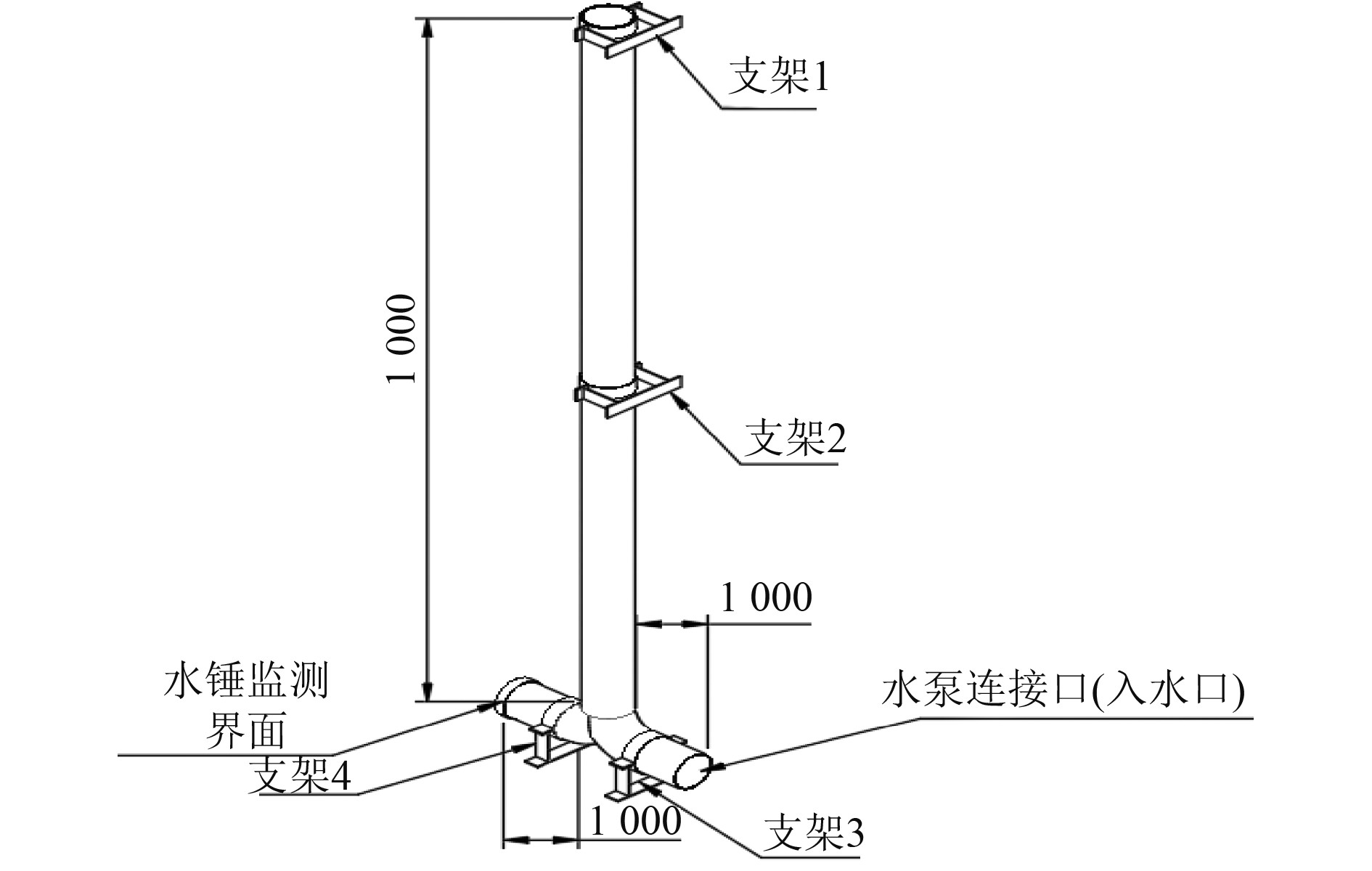
如图1所示,模型为对称三通管结构,有水泵连接口(入水口)提供泵水压力,在水锤监测界面监测水锤压力,其管系各部分参数如表1所示。此外,由《海上移动平台入级规范》及相应计算准则,FPSO压载水管网系统水泵扬程为45 m,因此可选择泵压为450000 Pa的水泵[13]。
|
图 1 水锤计算简化模型示意图 Fig. 1 Simplified model of water hammer calculation |
|
|
表 1 管系各部分参数表 Tab.1 Parameters of all parts of the pipeline system |
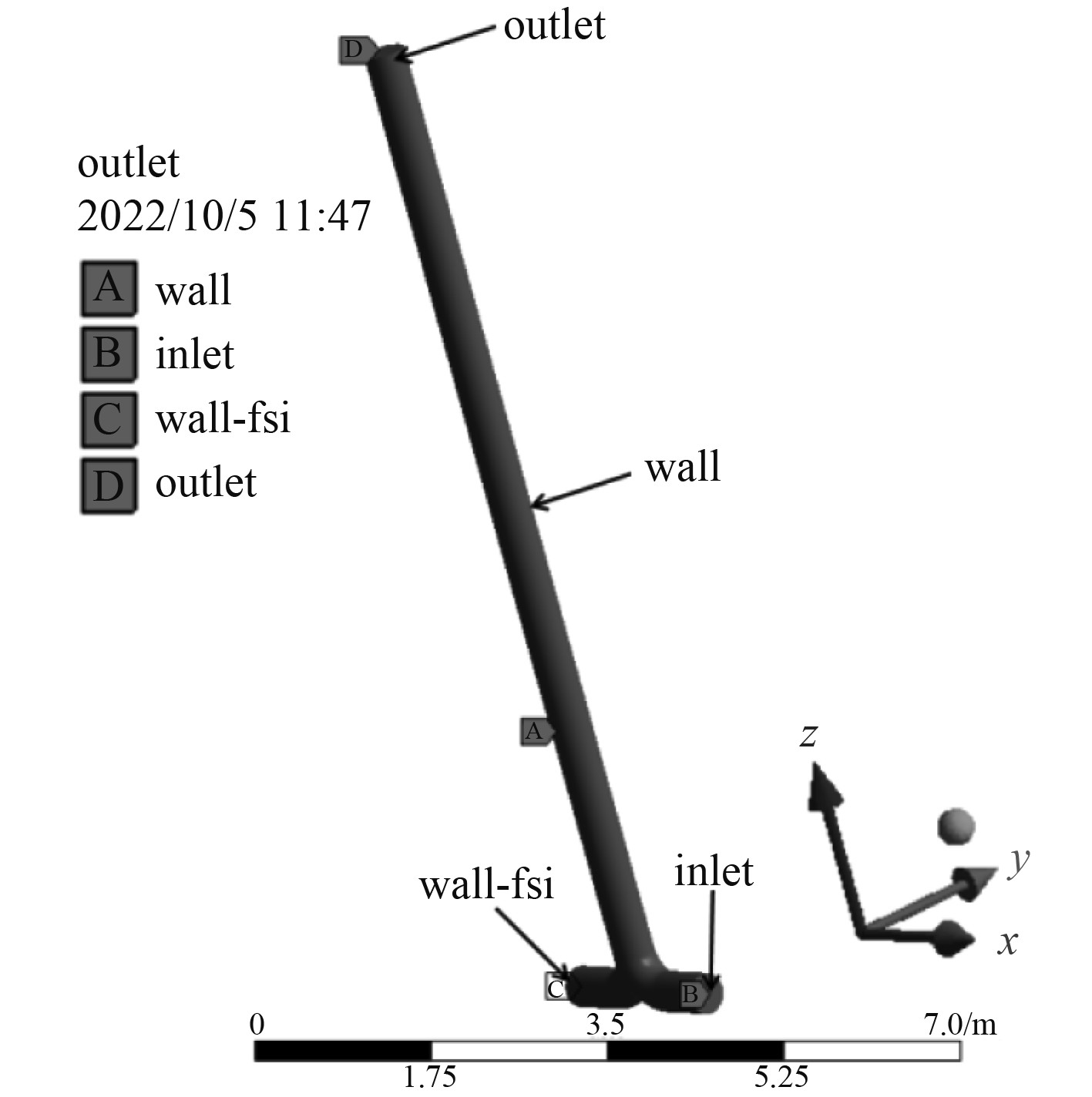
通过SolidWorks建模软件,基于图1建立三维模型,导入Fluent软件中,抑制掉管道和支架部分,进行流体仿真(计算模型见图2)。设置其入口压力为45000 Pa,时间步为2000步,步长0.01 s,在管系正常运行10 s后闭阀(Fluent中通过Event命令进行模拟)以进行试算。
|
图 2 Fluent流体仿真计算模型 Fig. 2 Fluent fluid simulation calculation model |
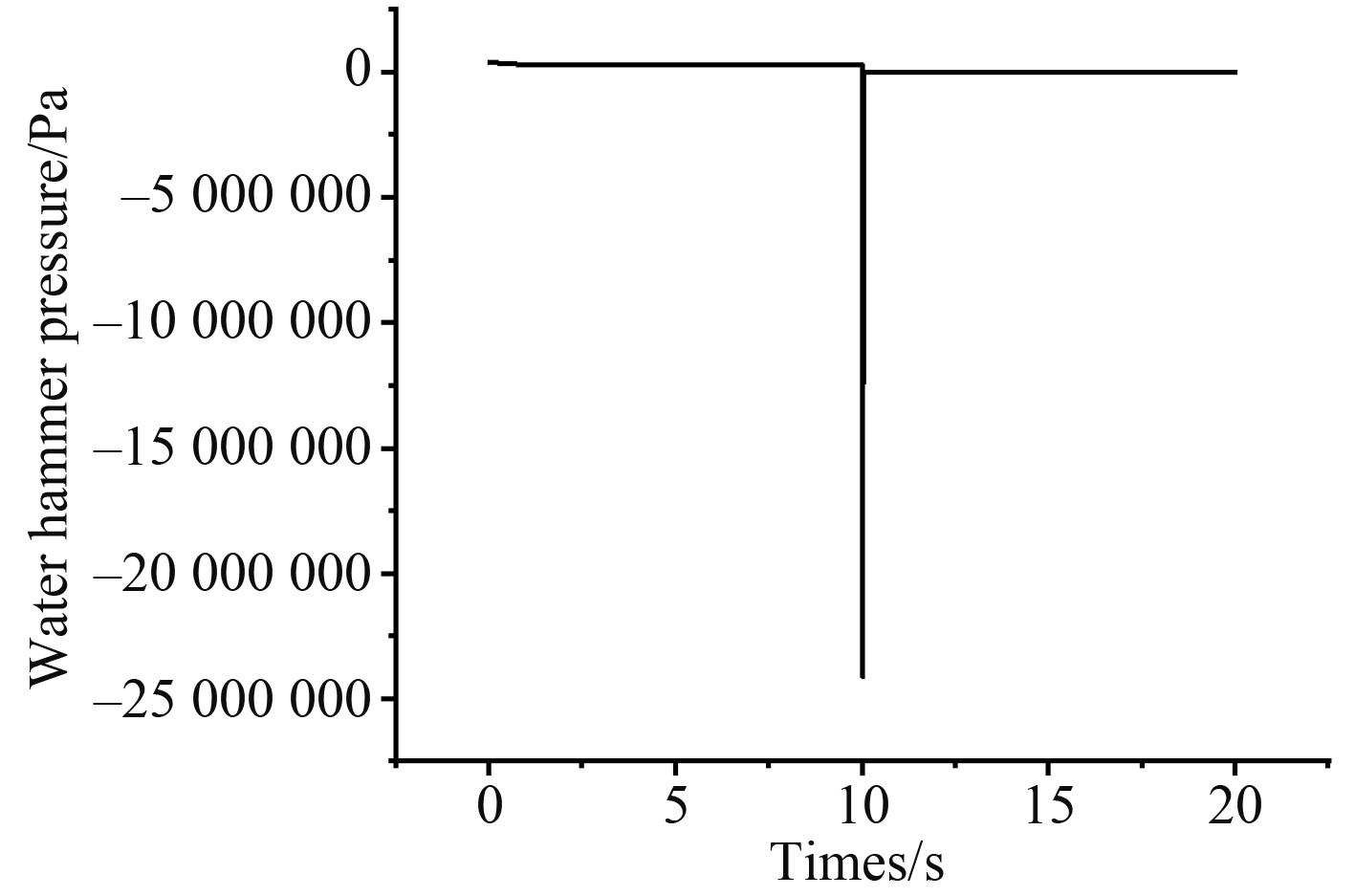
为更好地了解水锤情况,选择wall-fsi界面进行压力监测,其结果如图3所示。通过监测数据其水锤压力最值为−2.409×107 Pa,出现在10.01 s时刻。此外,由图3及监测具体数据可知,当管系运行6 s时,管系内水流水压趋于稳定,因此在6 s时刻停泵即可模拟管系水流稳定后停泵较为准确的水锤压力值。在后续的双向流固耦合计算中为减小运算量,设置运算时间为12 s,在6 s时停泵。
|
图 3 管系流体仿真wall-fsi界面水锤压力随时间变化图 Fig. 3 Water hammer pressure at wall-fsi interface of pipe system fluid simulation versus time |
通过Ansys Workbench模块,利用System Coupling 建立Fluent与Transient Structure的双向流固耦合系统,将由图1建立的计算模型导入模块当中,并在Fluent与Transient Structure模块中分别抑制固体和流体部分并将支架以固定约束的形式代替。通过表1数据建立Engineering Data后,设置其时间步数为1200步,时间步长为0.01 s,在6 s时刻停泵,计算12 s的管系水锤情况,并监测wall-fsi界面的水锤压力,通过监测数据其水锤压力最值为−2.405×107 Pa,出现在6.01 s时刻。
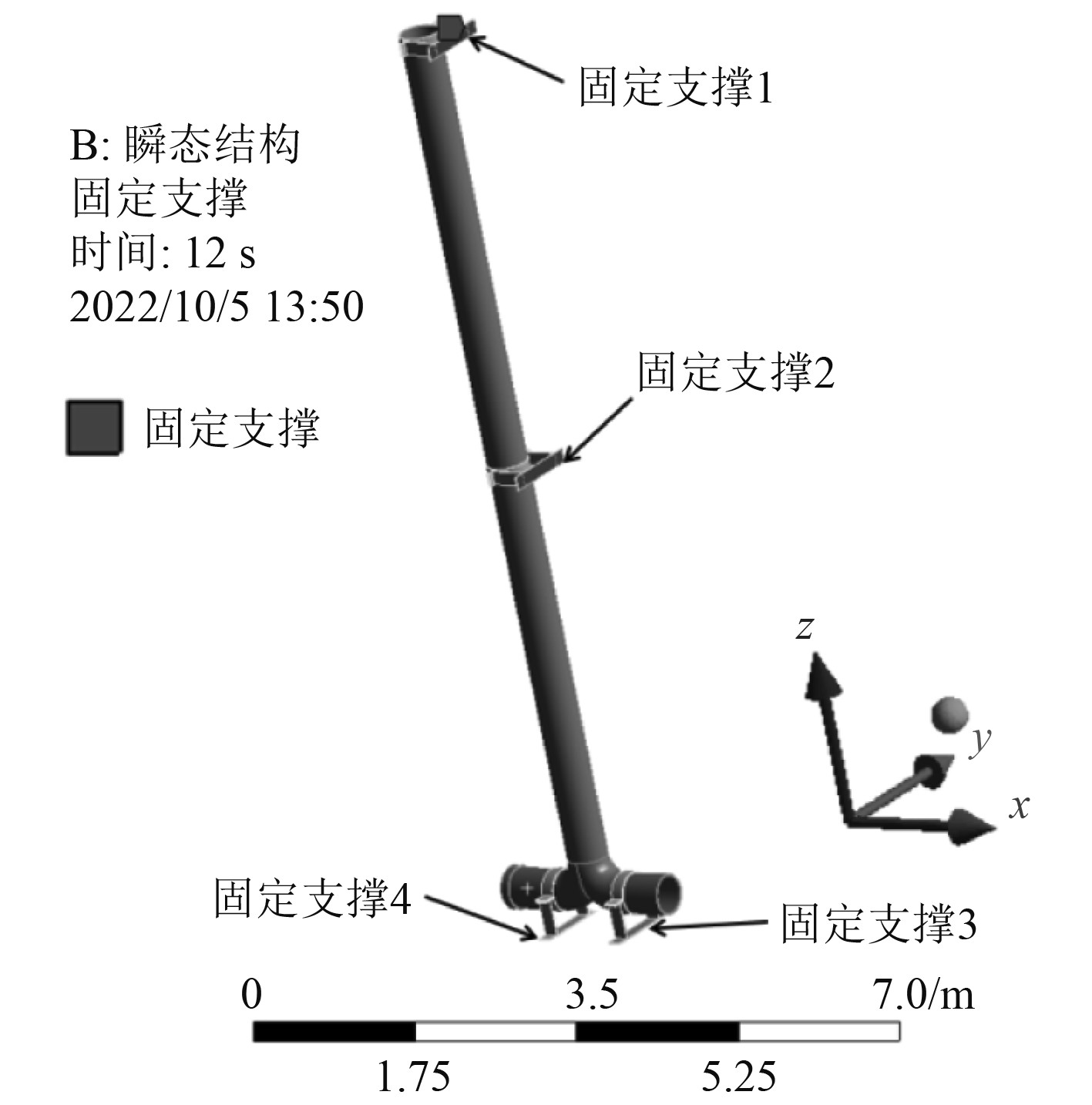
2.3 考虑管道支架整体性的双向流固耦合管系水锤仿真考虑支架的影响,将固定支撑施加在支架管托地面上,如图4所示。设置其时间步数为1200步,时间步长为0.01 s,在6 s时刻停泵,计算12 s的管系水锤情况,可得其wall-fsi界面的水锤压力随时间变化情况,并通过监测数据可得其水锤压力最值为−2.263×107 Pa,出现在6.01 s时刻。
|
图 4 考虑管道支架整体性耦合仿真Transient Structure模块计算模型 Fig. 4 Calculation model of transient structure module considering integrated coupling of pipe support |
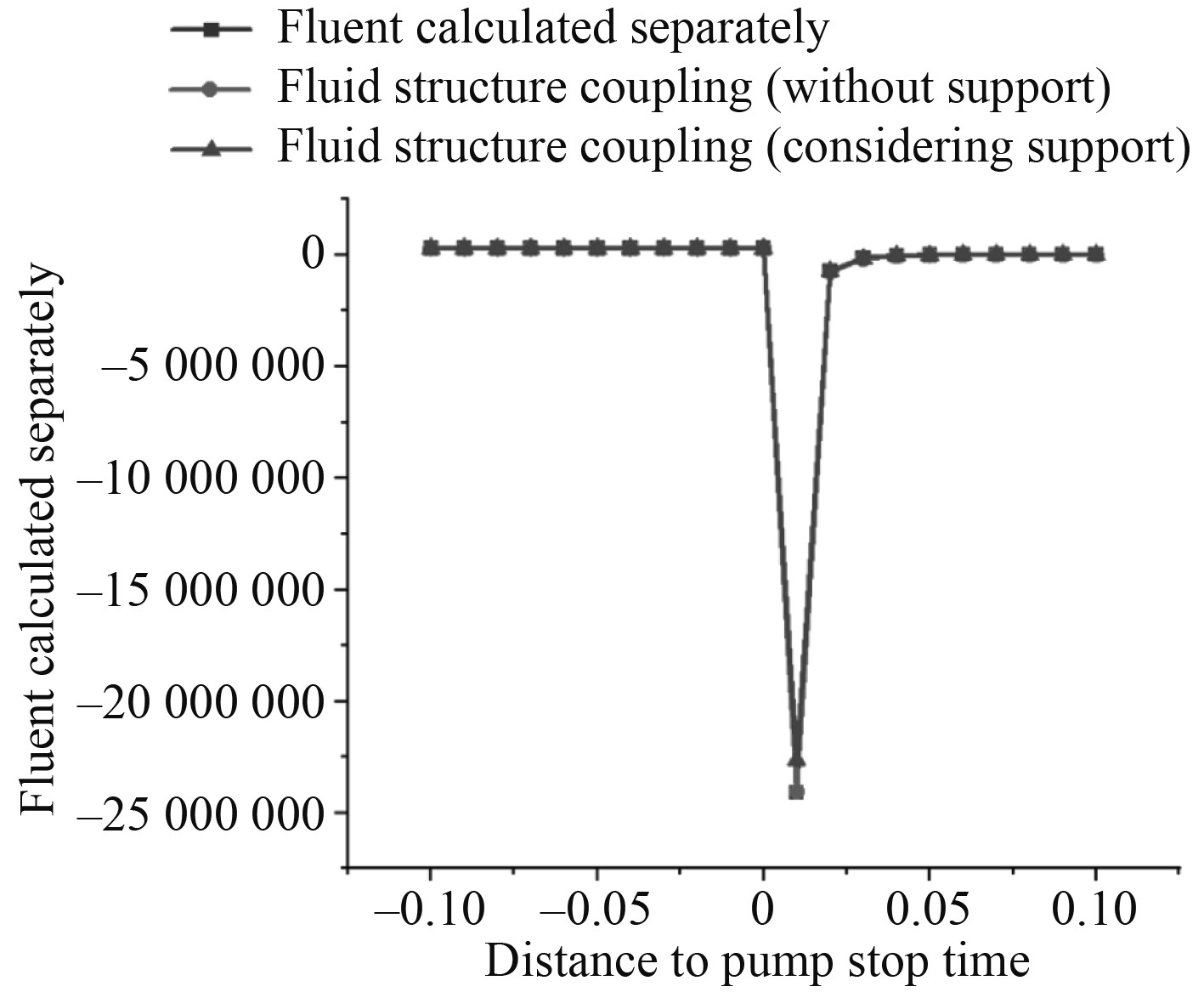
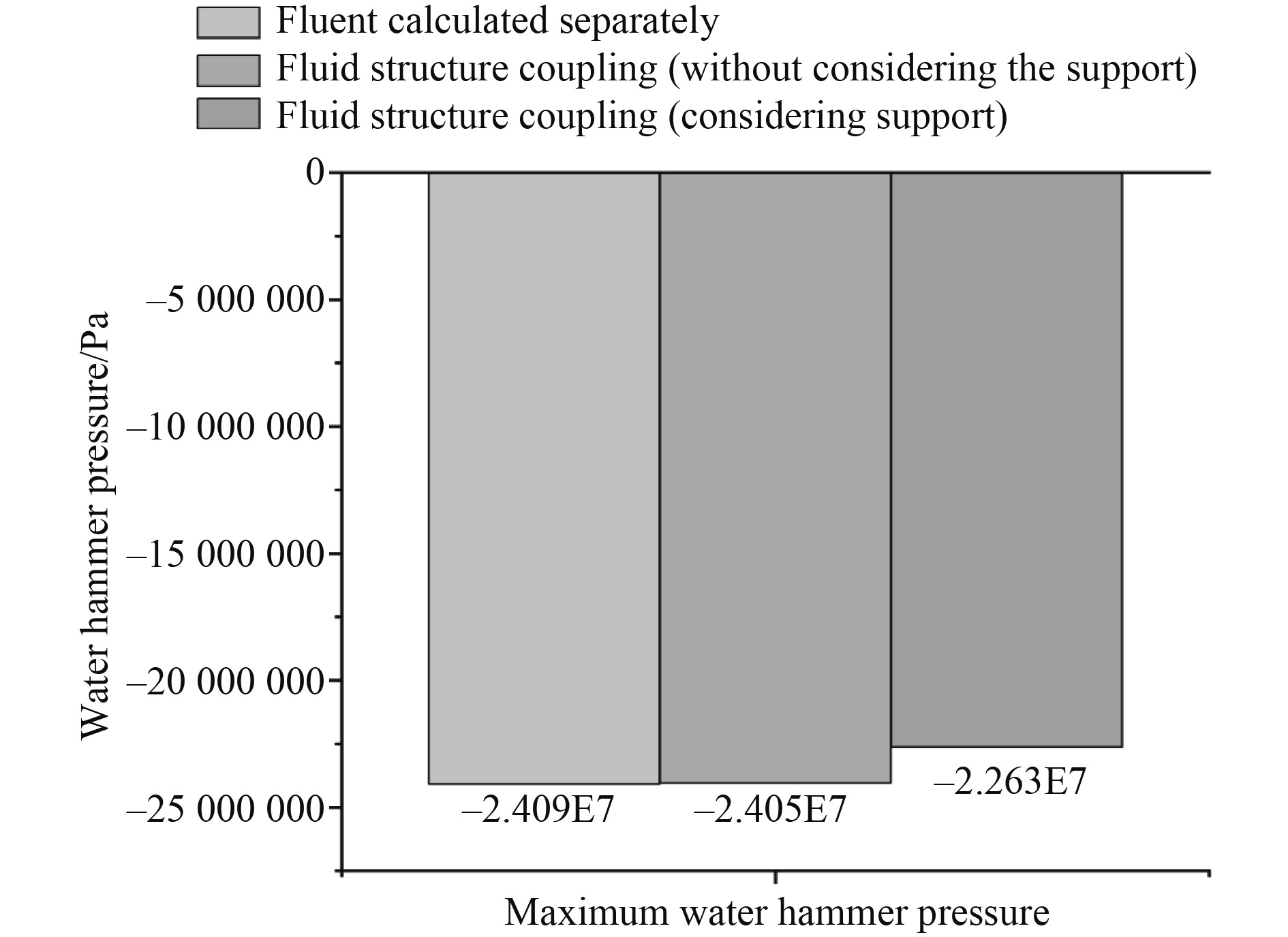
通过计算结果可知,监测界面的水锤压力变化主要集中在停泵(6 s时刻)前后的1 s时间范围(5.91~6.10 s),将该时间段的结果进行整理,如表2所示,其结果如图5所示。通过表2、图5可得,在Fluent单独计算、不考虑支架影响的流固耦合计算以及考虑支架影响的流固耦合计算,不考虑支架影响(将支架简化为约束)的计算结果与采用单独Fluent计算的结果差异性很小,但当考虑支架影响时,监测界面水锤压力有所下降。如图6,在Fluent单独计算、不考虑支架影响的流固耦合计算以及考虑支架影响的流固耦合计算时,其监测界面的最大水锤压力分别为−2.409×107 Pa、−2.405×107 Pa、−2.263×107 Pa。在考虑支架影响的流固耦合计算时,最大水锤压力相较于Fluent单独计算,其水锤压力减小了6.06%。
|
|
表 2 不同计算方式下监测界面水锤压力数据表 Tab.2 Water hammer pressure data of monitoring interface under different calculation methods |
|
图 5 不同计算方式下监测界面水锤压力数据图 Fig. 5 Water hammer pressure data of monitoring interface under different calculation methods |
|
图 6 不同计算方式下管系最大水锤压力值图 Fig. 6 Maximum water hammer pressure of pipeline system under different calculation methods |
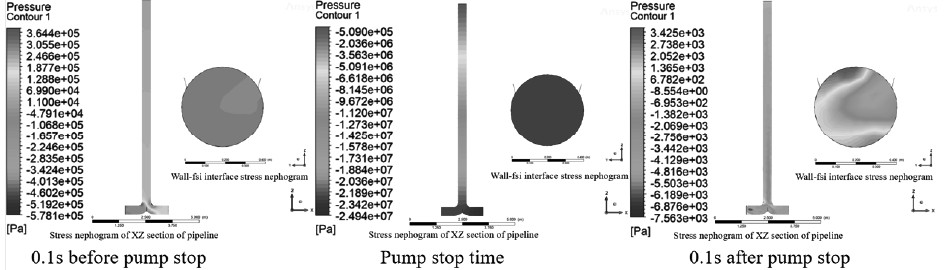
为进一步了解其水锤压力结果差异的原因,对表2停泵前后0.1 s时间段监测界面wall-fsi的压力进一步探究,结合停泵前后0.1 s时刻和停泵时刻的压力云图(见图7),可发现在停泵前后的0.1 s时刻内,管系的压力变化请况是非常明显的,在停泵之后,管系内的压力迅速由正压变成负压,且最大压力出现在停泵处和wall-fsi监测界面。而后,管道内压力逐渐稳定,水锤效应消失。另外,通过压力云图可知,管系内的水压沿Z轴基本对称,这也表明了简化的计算模型计算的可行性;对3种不同计算方式下的计算结果整体观察可发现,在Fluent单独计算、不考虑支架影响的流固耦合计算的各个时间点应力大小是相似的,而在考虑支架影响的计算形式中在停泵(发生水锤效应)前的应力情况与前2种计算形式是相似的,但在水锤产生后应力大小与前2种计算形式差异较大。这也表明,管道本身与管道内部流体的相互作用对水锤大小的影响很小,而管道支架是一个相对而言较大的影响因素。
|
图 7 考虑支架影响的流固耦合计算时管道水压力图 Fig. 7 Water pressure diagram of pipeline during fluid structure coupling calculation considering support influence |
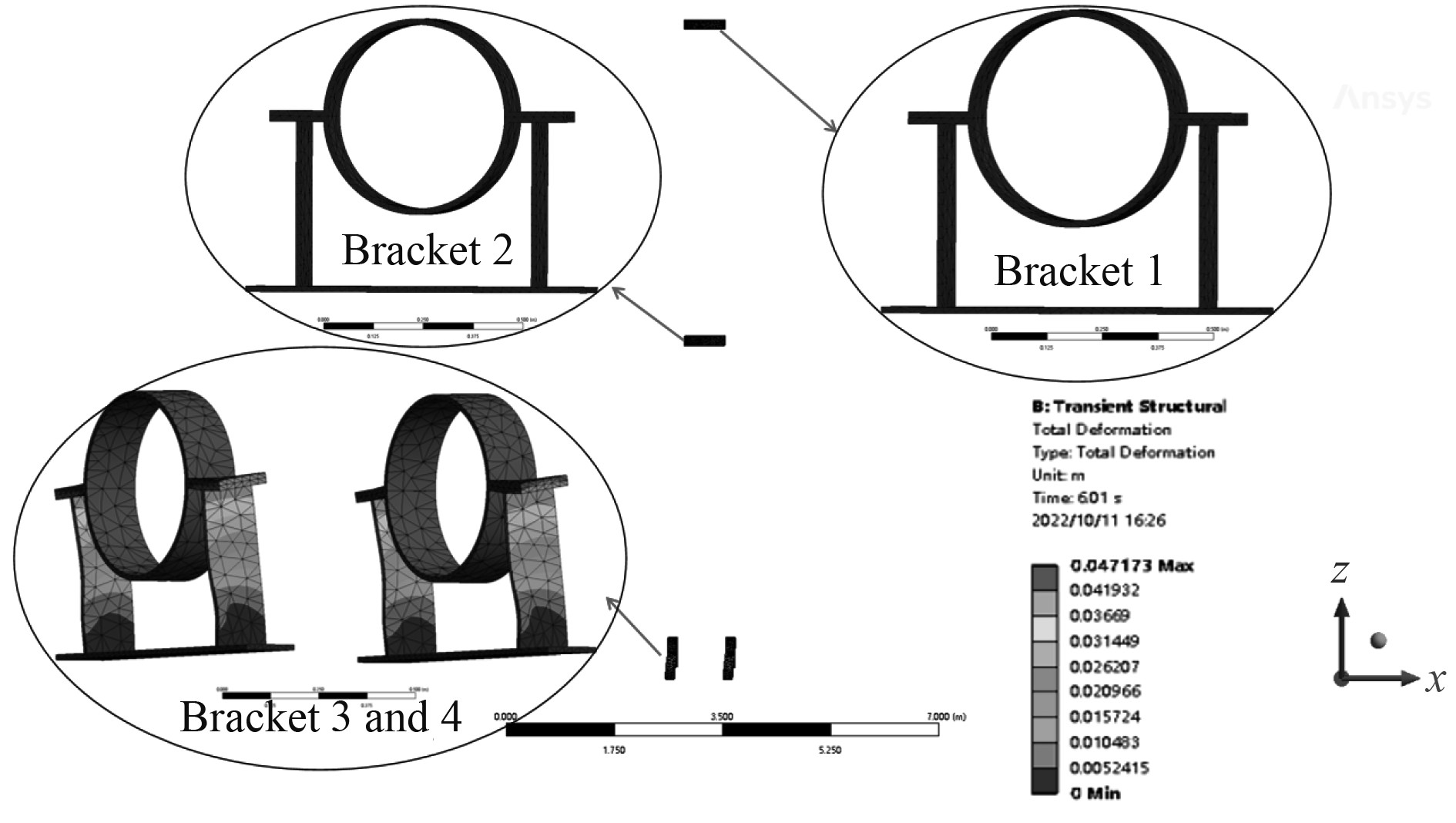
对于考虑支架影响的流固耦合情况下计算形式,在Transient Structure模块中观察其管道支架的变形情况,如图8所示。垂向布置的2个管道支架(支架1和支架2)基本无变形产生,而位于水锤发生界面附近所布置的管道支架(支架3和支架4)发生了较大变形,且最大变形发生在管道支架的管卡处,其中最大变形量达到了0.0472 m。表明,在发生水锤时,支架发生一定的变形量,有一定缓冲作用,会消减水锤效应产生时水锤压力的大小,从而对管系水锤情况产生影响。
|
图 8 水锤效应发生时管系中各支架变形情况图 Fig. 8 Deformation of supports in pipe system when water hammer effect occurs |
本文基于某通用型FPSO压载水管段参数,设计了一种易于计算的简化管系水锤压力计算模型,通过Fluent单独计算、不考虑支架影响的流固耦合计算以及考虑支架影响的流固耦合计算等计算形式,对特定工况下监测界面(wall-fsi)和管道水压力进行了计算仿真。通过计算分析,可得出以下结论:
在Fluent单独计算形式和不考虑支架影响的流固耦合计算形式下,管系的监测界面(wall-fsi)的水锤压力以及管系在停泵前后0.1 s的管系水压力大小差异不大;而考虑支架影响的流固耦合计算的计算形式表明监测界面的水锤压力大小有所下降,相较于Fluent单独计算,其水锤压力减小了6.06%,表明支架对管系水锤压力具有消减作用。
通过对考虑支架影响的流固耦合计算时,支架变形情况进行研究,可发现位于水锤发生界面附近所布置的管道支架(支架3和支架4)发生了较大的变形。其最大变形为0.0472 m,表明支架对管系水锤压力具有消减作用主要是由于在水锤产生时,支架产生变形,缓解了管系的水锤压力。
| [1] |
LI Y, HU X, ZHOU F, et al. A new comprehensive filtering model for pump shut-in water hammer pressure wave signals during hydraulic fracturing[J]. Joumal of Petroleum Scionce and Engineering, 2021: 109796.
|
| [2] |
MIAO Y, QIU Z, ZHANG X, et al. Effects of a water hammer and cavitation on vibration transients in a reservoir-pipe-valve system[J]. Polskie Towarzystwo Mechaniki Teoretycznej i Stosowanej (PTMTS), 2021,59(4). 611−622.
|
| [3] |
XI B, WANG C, XI W, et al. Experimental investigation on the water hammer characteristic of stalling fluid in eccentric casing-tubing annulus[J]. Energy, 2022, 253: 1−13.
|
| [4] |
MICHA, KUBRAK, APOLONIUSZ, et al. Water hammer phenomenon in pipeline with inserted flexible tube[J]. Journal of Hydraulic Engineering, 2020, 146(2): 1−11.
|
| [5] |
张巧玲, 黄铋匀, 杨振东, 等. 基于特征线法的含气输水管道水锤特性分析[J]. 农业工程学报, 2022, 38(5): 79−86.
|
| [6] |
郭强, 周建旭, 黄亚, 等. 考虑流固耦合的厚壁输水管水锤和振动特性分析[J]. 农业工程学报, 2020, 36(21):137−144.
|
| [7] |
王祺武, 李志鹏, 朱慈东, 等. 重力流输水管路阀门调节与水锤控制分析[J]. 流体机械, 2020, 48(6): 38−43+50.
|
| [8] |
GROUP L W. Pipeline pressure[J]. LPG World, 2011(21): 17. |
| [9] |
陈旭云, 张健, 俞晓东, 等. 考虑爆管工况的长距离供水工程水锤防护研究[J]. 人民黄河, 2021, 43(7): 145−148+159.
|
| [10] |
孙哲豪, 吴旭敏, 陈丽芬, 等. 高扬程小流量加压供水工程水锤防护设计研究[J]. 灌溉排水学报, 2020, 39(S2): 66−71+75.
|
| [11] |
陈亚飞, 顾卫国, 王德忠, 等. 球型调节阀关阀水锤效应的试验研究与数值计算[J]. 排灌机械工程学报, 2021, 39(10): 1027−1032.
|
| [12] |
王学芳. 工业管道中的水锤[M]. 北京: 科学出版社, 1995.
|
| [13] |
杨豪杰. 通用型FPSO关键管网系统水锤分析及优化防护研究[D]. 镇江: 江苏科技大学.
|
 2023, Vol. 45
2023, Vol. 45
