2. 三亚崖州湾深海科技研究院,海南 三亚 572000
2. SJTU-Sanya Yazhou Bay Institute of Deepsea Science and Technology, Sanya, 572000, China
海洋油气开发已然成为现今深海开发的重要一环,各类海上平台正在向大型化、综合化、智能化多方向发展[1-2],大型海上结构物安装越来越复杂,其上部结构的重量不断增加的同时,整体尺寸也在不断增大,原始安装方法的安装难度不言而喻。模块安装法作为一种新型安装选择,可以减少海上安装作业时间,降低安装难度并且减少安装费用,目前主流的模块安装法有浮吊法和浮托法,浮吊法需要用到价格昂贵的大型起重船,成本较高,浮托安装则只需要普通的驳船,节约成本的同时也节省时间,不需要在海上集成和调试模块。
浮托安装具体流程如下:在定位装置的辅助下,利用驳船将上部组块运输到相应的安装位置,缓慢增加驳船吃水,将上部组块的重量从驳船逐渐转移到下部支撑结构上[3],当上部组块重量完全转移到下部结构后,此时驳船与上部组块无接触,操作驳船缓慢退出。根据使用的驳船数量不同,浮托安装可简单分为单船浮托和双船浮托[4]。与浮吊法相比,浮托安装法绝大多数所需装置可在陆地上进行调试,可快速开展安装作业,大幅缩短海洋平台安装工期[5]。国外浮托安装的研究开展得较早,在中东、西非和墨西哥湾等地就曾多次实地尝试浮托法,已有很多成功的实际工程经验[6],如最早的Zakum导管架平台,国内也有KL3-2CEPA、QHD32-6CEPI、荔湾3-1CEP[7]等浮托安装成功案例。
由于天气条件的敏感性和多体相互作用的复杂性,大型水上漂浮装置面临各种挑战。在过去的几十年里,通过数值模拟、模型试验和现场测量,用来估计浮体的动态响应[8]。在模拟浮托安装过程中的多体相互作用方面,建立了基于线性势流理论和脉冲理论的数值模型[9]。在数值模型中,上层组块和驳船通常被简化为具有六自由度的刚体,而系泊系统通常采用细长梁理论进行模拟[10],LMU、DSU和护舷通常被建模为线性或非线性弹簧[11-14]。许鑫[15]以一座导管架平台实际安装为研究对象,分别从频域和时域两方面进行分析,将系泊缆分成若干段,每部分按照悬链线方法计算。杨光[16]以渤海锦州9-3油田新建导管架平台为研究对象,考虑极浅水条件下驳船运动响应,针对驳船触底的可能性展开研究,对驳船的浅水效应产生原因进行分析。现有研究多是针对导管架平台等固定平台上部组块浮托安装,缺少以半潜平台浮托安装为研究对象的相关研究。半潜式平台作为一种稳定性较好的浮式平台,常见于海洋石油天然气开发中钻井和生产作业中。相较于固定的导管架平台,半潜平台浮托安装还需要考虑到平台的运动响应,以及平台与驳船之间多体系统耦合动力响应,因此开展相关研究具有现实意义。
在浅水海域浮托安装作业过程中,更需要关注浮体触底风险,触底现象会带来极大的安全隐患,若对浮体结构带来损伤,则会造成经济损失。研究表明,随着水深的减小,浮体所受波浪漂移力会增加,即浅水效应。Pinkster[17]提出浅水效应的明显特征是低频长波对二阶波浪力的影响大于一阶波浪力。针对二阶波浪力的预报,Newman提出一种近似方法得到二次传递函数(Quadratic Transfer Function,QTF)。相较于直接计算完整的QTF矩阵,Newman近似方法利用定常二阶力近似低频二阶力,计算效率更高。Naciri[18]的研究表明在谱峰周期较短的海况中,全QTF法和Newman近似的方法均可以很好模拟浅水中的LNG运输船。但针对具体作业海况,两者的浮体运动预测效果不得而知。因此,本文以半潜平台上部组块浮托安装过程为研究对象,针对不同海况条件,分别使用全QTF法和Newman近似的方法对浮体六自由度运动进行数值模拟,与物理模型实验结果进行对比,探究半潜平台在浮托安装船进船过程中的水动力响应特性,并对半潜平台是否会发生触底进行评估。
1 数值理论 1.1 势流理论在实际海洋环境条件的作用下,浮体的运动响应较为复杂,常见方法有理论计算和水池模型试验。风、浪、流条件中,通常由经验公式可以计算得出风载荷和流载荷,而波浪载荷作为对浮体最复杂和重要的影响因素,可通过势流理论进行求解,即通过求解流场中的速度势,从而计算需要的各类波浪力。
对于海洋工程实际工程中的大型结构物,通常可以认为其周围流场中的流体是均匀的、不可压缩的、无粘性的,其流动是无旋的。流场中用非定常的速度势
| $ \varPhi (x,y,z,t) = {\varPhi ^I}(x,y,z,t) + {\varPhi ^D}(x,y,z,t) + {\varPhi ^R}(x,y,z,t) 。$ | (1) |
根据不同的边界条件,分别求解速度势,得到流场速度势后,根据伯努利方程计算作用在浮体上的动压力,对湿表面进行积分,可以得到作用在浮体上的流体作用力。其中,需要重点关注的是二阶波浪力,二阶波浪力共分为3个部分,平均部分、差频部分和高频部分。其中,平均波浪漂移力和低频慢漂力的大小与入射波波高的平方成正比,其关系可以用二阶波浪力的二次传递函数(QTF)表示。除了直接计算完整的QTF矩阵(全QTF法),还可以通过近似的方式得到QTF矩阵,最常用的方法为Newman近似。
不规则波的表达式为:
| $ \zeta (t) = \sum\limits_{i = 1}^N {{\zeta _i}\cos ({\omega _i}t + {\varepsilon _i})} 。$ | (2) |
二阶波浪力表达式为:
| $\begin{split} {F^{(2)}}(t) = & \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\frac{1}{2}{\zeta _i}{\zeta _j}} } {P_{ij}}\cos \left\{ {({\omega _i} + {\omega _j})t + ({\varepsilon _i} + {\varepsilon _j})} \right\} + \\ & \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\frac{1}{2}{\zeta _i}{\zeta _j}} {Q_{ij}}\sin \left\{ {({\omega _i} - {\omega _j})t + ({\varepsilon _i} - {\varepsilon _j})} \right\}}+ \\ & \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\frac{1}{2}{\zeta _i}{\zeta _j}} } {{\bar P}_{ij}}\cos \left\{ {({\omega _i} + {\omega _j})t + ({\varepsilon _i} + {\varepsilon _j})} \right\}+ \\ & \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\frac{1}{2}{\zeta _i}{\zeta _j}} {{\bar Q}_{ij}}\sin \left\{ {({\omega _i} - {\omega _j})t + ({\varepsilon _i} - {\varepsilon _j})} \right\}} 。\end{split}$ | (3) |
式中:
求解得出波浪力后,可运用刚体运动理论计算浮体在波浪中的运动,其时域方程如下:
| $\begin{split} & \sum\limits_{j = 1}^6 \Biggr\{M_{ij}^{\left( m \right)}\ddot x_j^{\left( m \right)}\left( t \right) + \sum\limits_{l = 1}^2 \left[ \mu _{ij}^{\left( {lm} \right)}\ddot x_j^{\left( l \right)}\left( t \right) + \int_0^t K_{ij}^{\left( {lm} \right)}\left( {t - \tau } \right)\dot x_j^{\left( l \right)}\left( \tau \right)d\tau \right] +\\ & C_{ij}^{\left( m \right)}x_j^{\left( m \right)}\left( t \right) \Biggr\} = F_{wi}^{\left( m \right)} + F_{cu}^{\left( m \right)} + F_{wa}^{\left( m \right)} + F_{md}^{\left( m \right)} + F_{ot}^{\left( m \right)},\\ & \quad i,j = 1,2,3,4,5,6; m = 1,2。\\[-15pt] \end{split}$ | (4) |
式中:
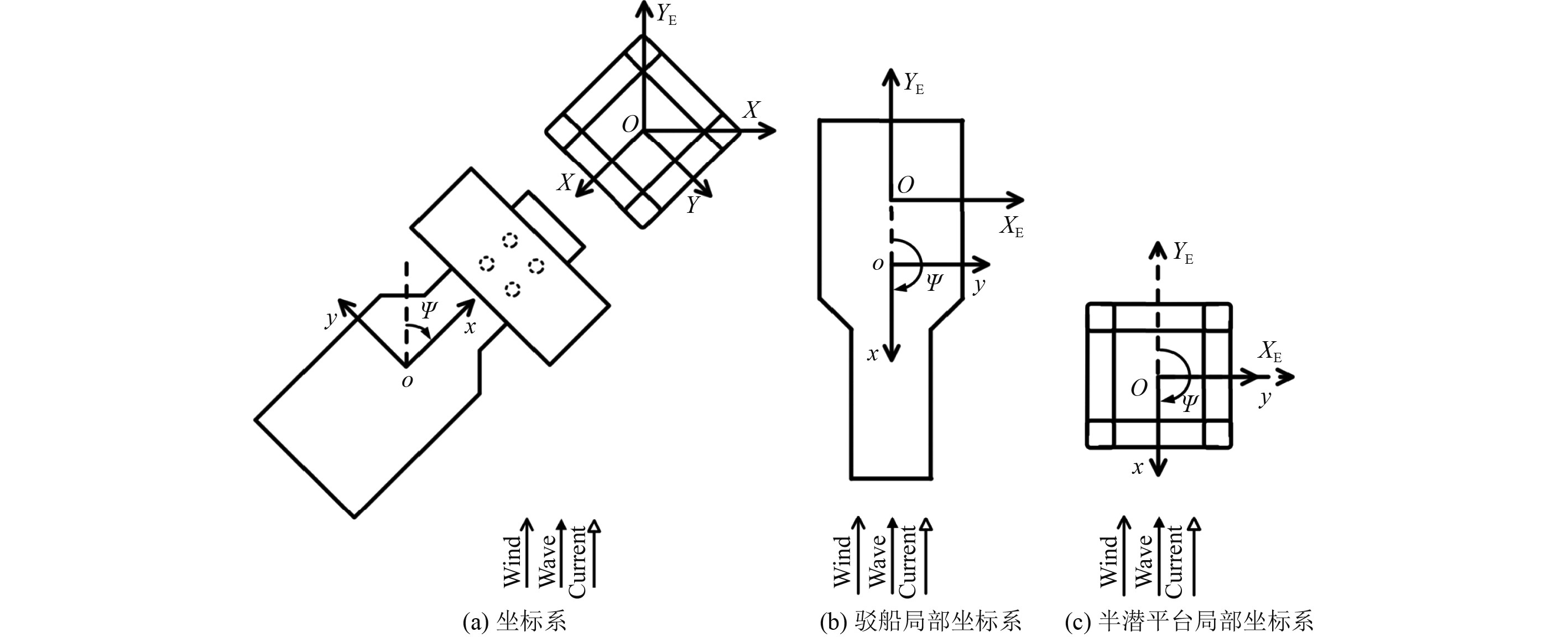
模型试验中共涉及3个坐标系,包括大地坐标系、驳船局部坐标系和半潜平台局部坐标系。其中大地坐标系原点位置通常选择浮托安装的目标点,作为浮托安装的位置参考,风、浪、流的入射角也基于大地坐标系。
处于浮托安装进船阶段,可将浮托安装驳船和其运输的上部组块视作整体,此时驳船局部坐标系的坐标原点位于两者共同的重心,记录其六自由度运动;而半潜平台坐标系的坐标原点则位于半潜平台重心。
比号根据相似准则,本试验模型线性缩尺比选取为1∶50,海水和水池水的密度比γ=1.025。
|
图 1 坐标系的定义 Fig. 1 Definition of coordinate systems |
基于“陵水17-2半潜平台”和“海洋石油229船”开展半潜平台浮托安装试验,研究适用于半潜平台浮托的集成技术,通过理论和模型试验手段进行研究。浮托安装模型试验在海洋工程水池完成,水池长为50 m,宽为30 m,深为6 m。
正式试验前已对所有测试仪器进行校准,分别对相关物理量进行了测量与数据采集,主要包括半潜平台和驳船重心处的六自由度运动、运动加速度、系泊缆载荷等。
2.3 模型设计与模拟模型包括1艘浮托作业驳船模型(海洋石油229)、1艘半潜平台模型(陵水17-2)、1座上部组块模型、8个LMU模型、4个DSU模型、护舷模型、若干辅助缆绳与系泊缆。
试验模型缩尺比为1∶50,根据半潜平台与驳船主尺度制作相关模型。表1为驳船模型的主尺度,半潜平台与上部组块主尺度如表2和表3所示。为提高模型试验的准确性,模型重量、重心、惯性半径误差均要求小于3%,可以根据调节重块的位置与重量以减少相关误差。
|
|
表 1 HYSY-229主尺度 Tab.1 Properties of HYSY-229 |
|
|
表 2 陵水17-2半潜平台上部组块主尺度 Tab.2 Properties of SEMI topside |
|
|
表 3 陵水17-2半潜平台下浮体主尺度 Tab.3 Properties of SEMI floating body |
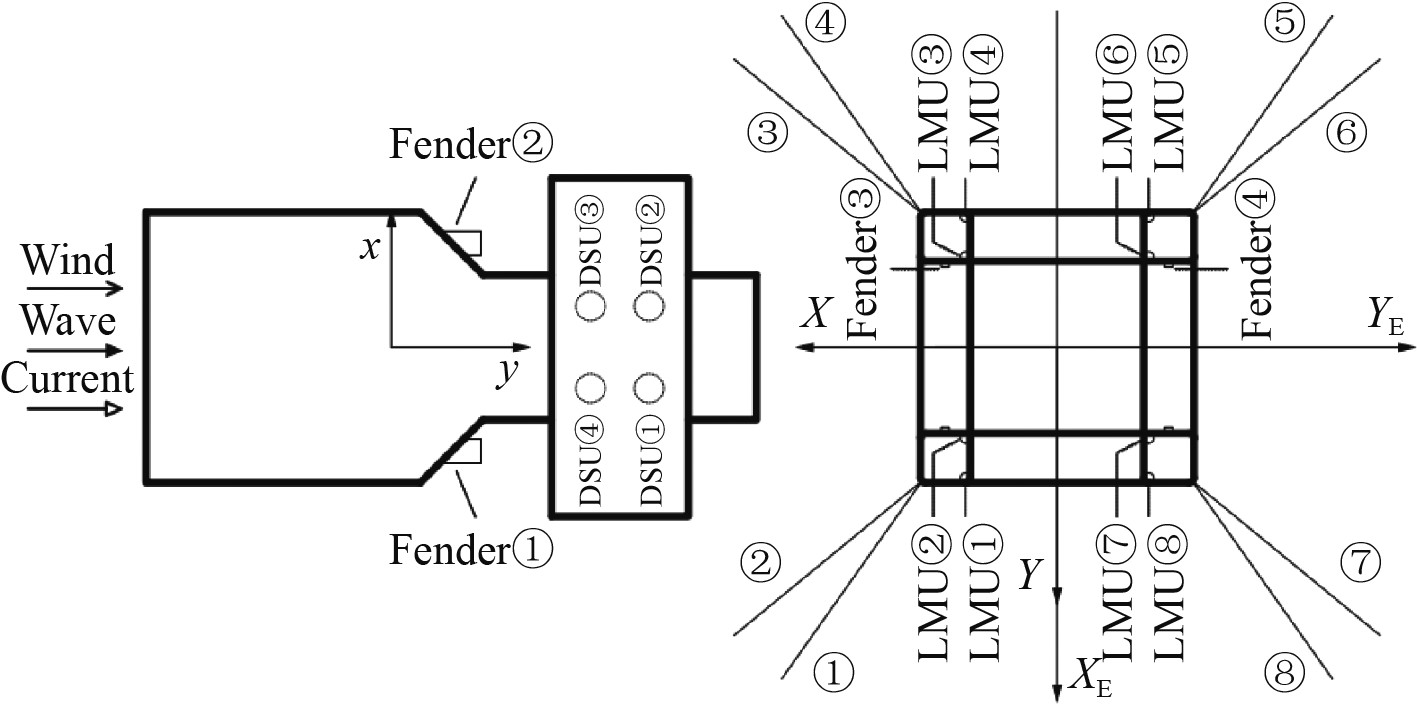
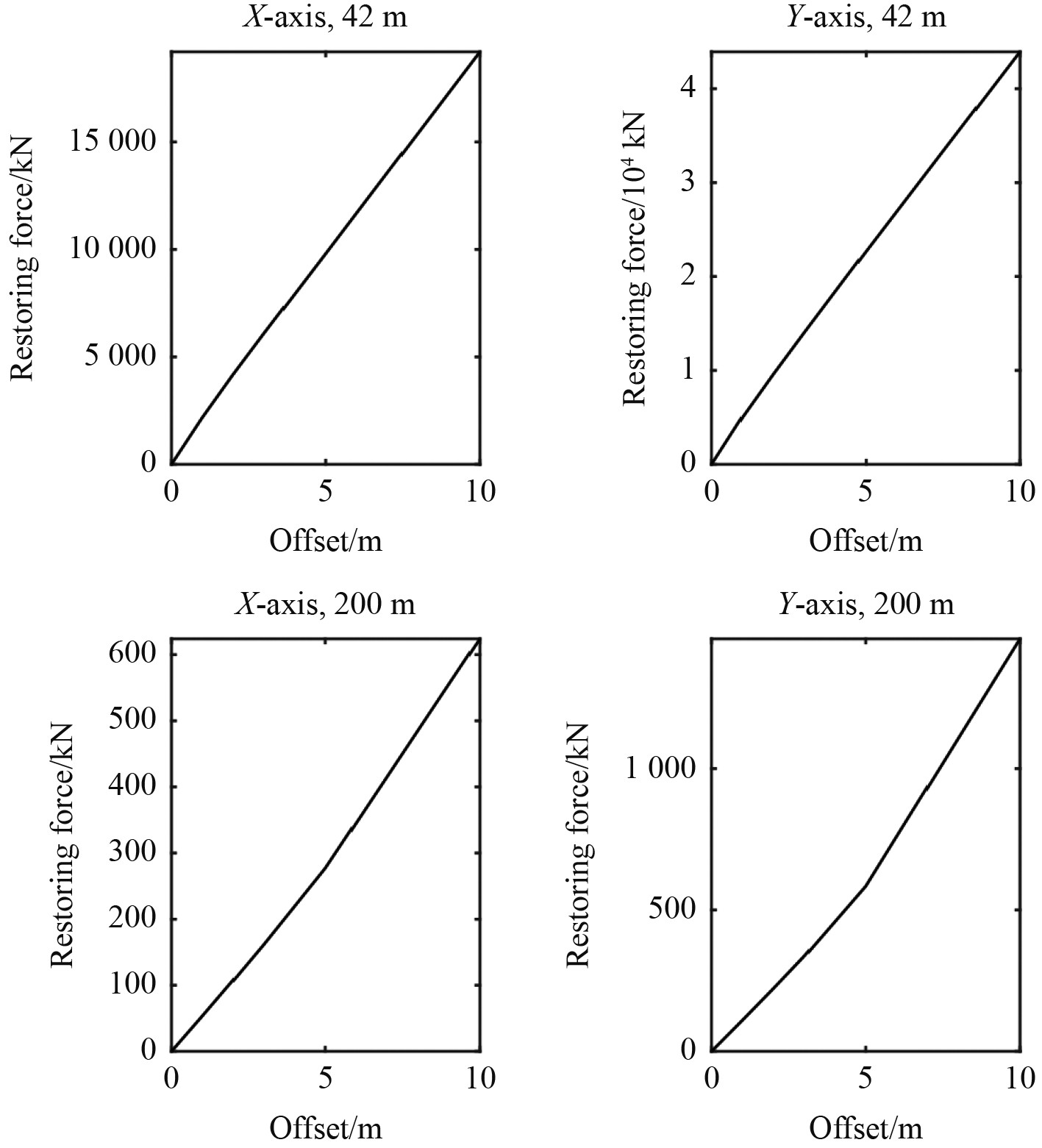
LMU模型共有8个,其基座安装在半潜平台顶部,浮托安装的对接端则安装在上部组块的底部,安装时,LMU模型的对接端和三分力传感器相连接;DSU模型共有4个,安装在浮托安装驳船的甲板上,用于支撑上部组块。LMU模型与DSU模型均采用钢质材料制作。图2为LMU、DSU、护舷及系泊系统的布置图,图3为对应的系泊系统刚度曲线图。
|
图 2 LMU、DSU、护舷及系泊系统的布置图 Fig. 2 Arrangement drawing of LMU, DSU, fender and mooring system |
|
图 3 系泊系统刚度曲线 Fig. 3 Mooring system stiffness curves |
|
|
表 4 锚链主要物理属性 Tab.4 Material property of the mooring lines |
模拟2个水深条件下的浮托安装作业,模型试验中通过调整假底的位置,以实现对不同水深的模拟,水深分别为42 m和200 m,换算成模型值分别为0.84 m和4 m。风的模拟采用定常风,通过控制造风系统风机的转速,从而获得不同的风速大小,流的模拟通过造流系统实现。模型试验中模拟的波浪包括白噪声波浪和不规则波浪,其中不规则波浪谱采用Jonswap波谱,目标谱公式如下:
| $ S(f) = \alpha H_s^2T_p^{ - 4}{f^{ - 5}}\exp \left[ { - 1.25{{({T_p}f)}^{ - 4}}} \right]{\gamma ^{{{\exp }^{\left[ { - {{({T_P}{f^{ - 1}})}^2}/2{\sigma ^2}} \right]}}}} 。$ | (5) |
式中:S(f)为谱密度,m2s;Hs为有义波高m;f为波浪频率Hz;fp为谱峰频率Hz;γ为谱形参数。
| $ \gamma = 3.3,$ |
| $\begin{aligned} \sigma = \left\{ \begin{aligned} 0.09,\;\; f > f_p ,\\ 0.07, \;\; f < f_p 。\end{aligned}\right.\end{aligned}$ | (6) |
| $ \alpha = \frac{{0.0624}}{{0.230 + 0.0336\gamma - 0.185/(1.9 + \gamma )}} 。$ | (7) |
波浪模拟中的数据采样频率为25 Hz。从开始造波到正式试验采样,安排至少间隔90 s,目的是让模型有足够的时间到达稳定的运动状态,不规则波浪试验的海洋环境条件实际值如表5所示。
|
|
表 5 海洋环境条件 Tab.5 Marine environmental conditions |
图4给出了不规则波与白噪声波浪环境条件测量所得到的实际波浪谱与目标谱对比。可以看出,测量值与目标值拟合较好,满足相关试验规范。

|
图 4 目标波浪谱与实际波浪谱对比 Fig. 4 Target and measured wave spectrum |
使用SESAM软件计算浮体的水动力响应,首先根据半潜平台与驳船的主尺度在GeniE模块中建立湿表面模型,划分网格后生成FEM文件,将其导入HydroD模块进行水动力计算。模型试验中已对半潜平台与驳船进行3 h的白噪声波浪试验,将数据导出并进行对比。
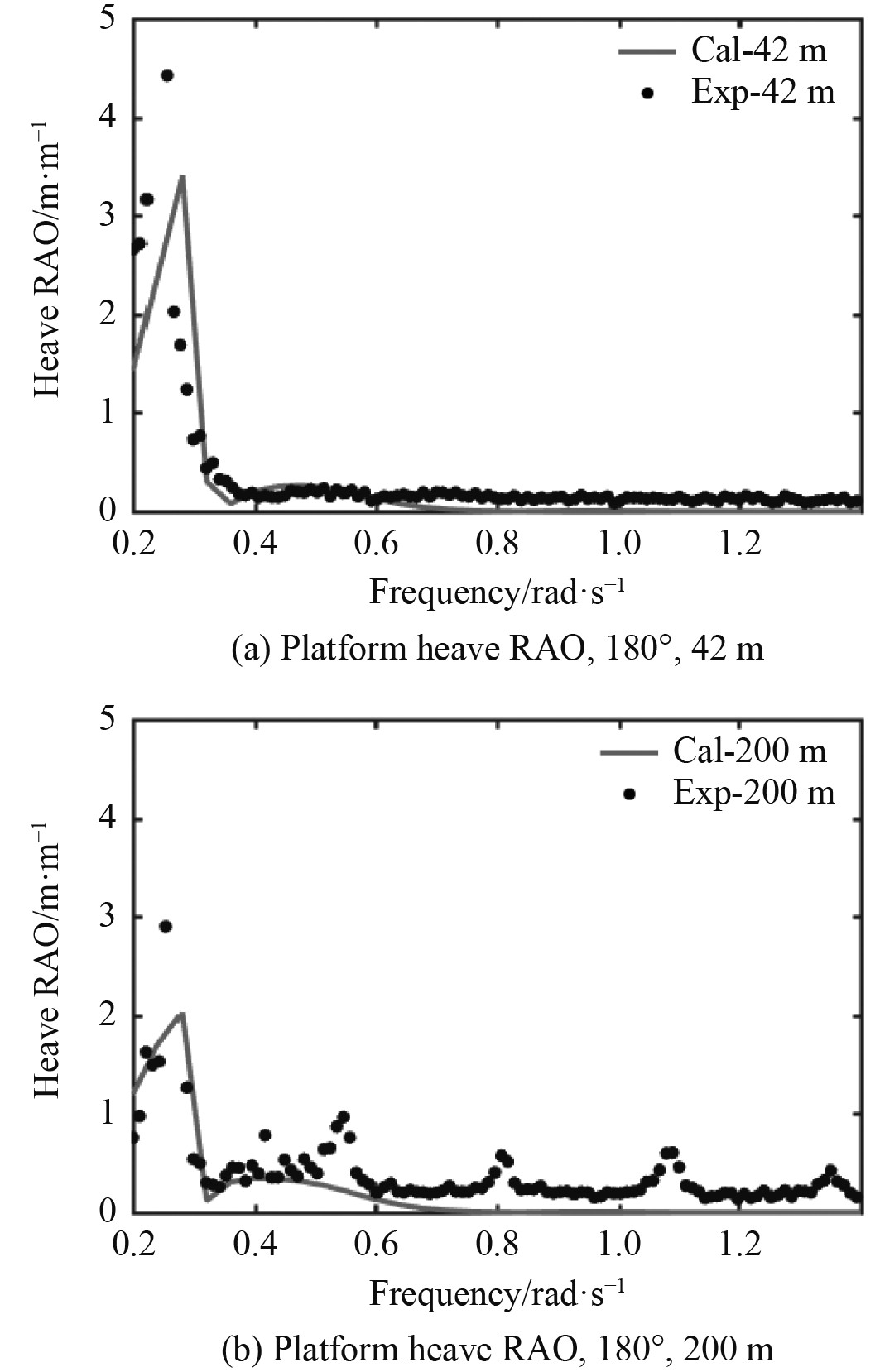
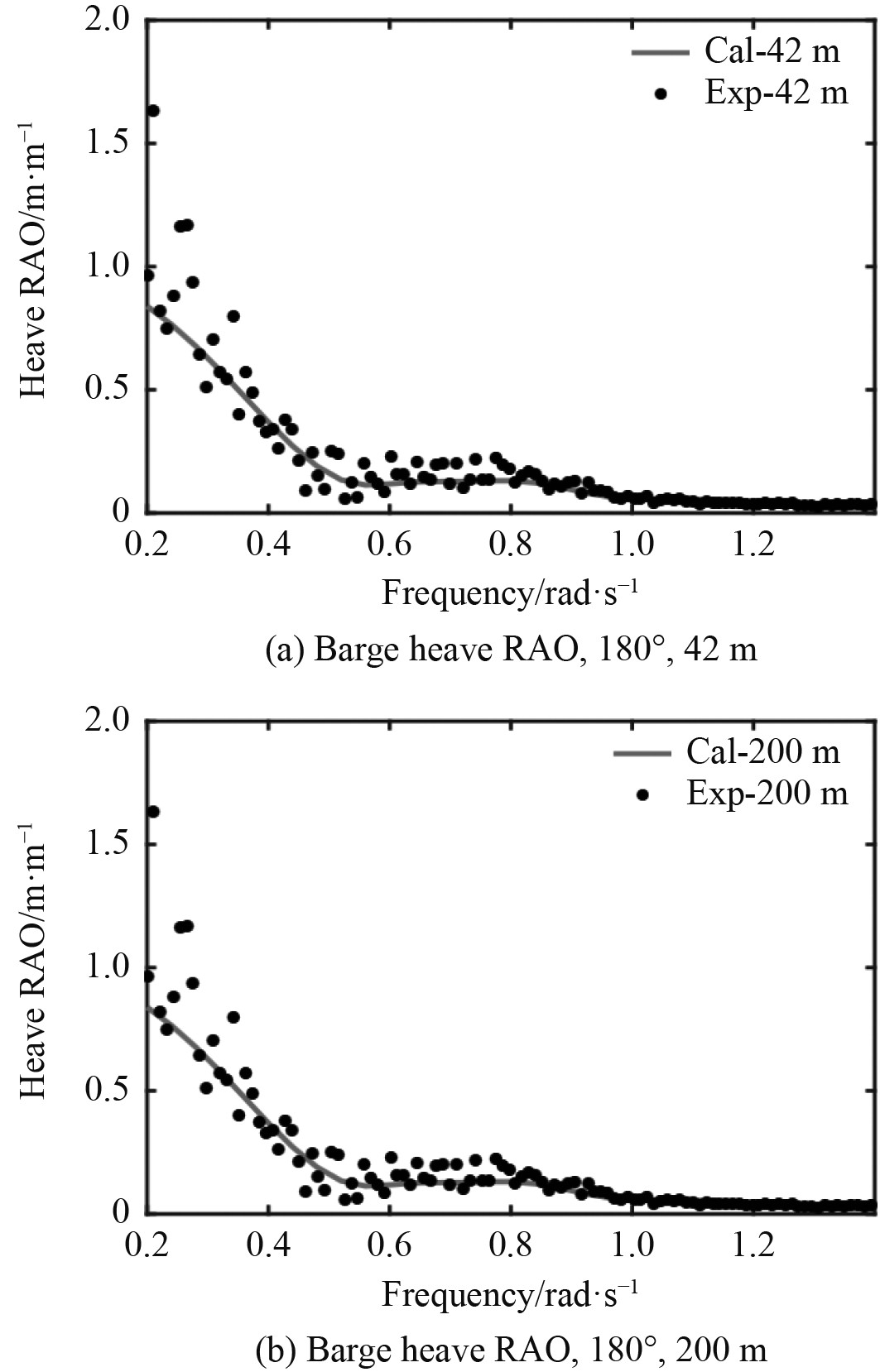
图5和图6为水深为浅水情况(42 m水深)和深水情况(200 m水深)时,数值计算和模型试验所得到的半潜平台与驳船的垂荡运动传递函数(RAO)。可以看出,在45°与180°的风浪流情况下,不管是半潜平台还是驳船,频域模拟得到的运动传递函数结果与模型实验结果的拟合效果都较好,除几个明显坏点外,偏差较小,表明可以通过数值计算较为准确地预报浮体的运动响应,为后续的时域模拟提供参数。
|
图 5 半潜平台的运动传递函数(RAO)对比 Fig. 5 Response amplitude operator (RAO) of SEMI |
|
图 6 驳船的运动传递函数(RAO)对比 Fig. 6 Response amplitude operator (RAO) of the barge |
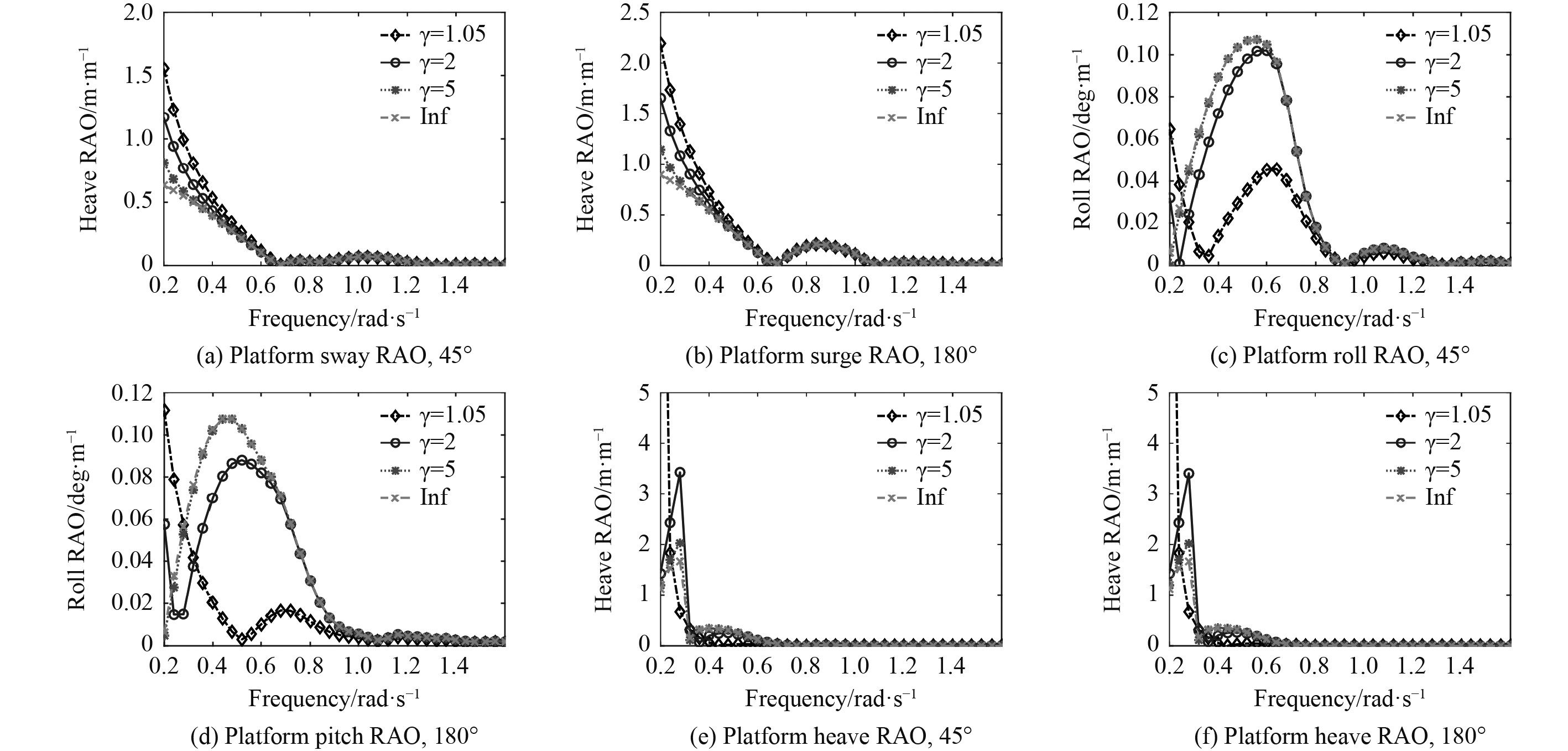
为了进一步验证水深对浮体运动响应的影响,比较水深吃水比γ为1.05、2、5和接近无限水深(3000 m水深)时的半潜平台运动RAO,包括平台六自由度运动,频率为0.2~1.6 rad/s,风浪流同向,入射角分别为45°与180°。如图7所示,可以看出针对水平面运动,浅水效应主要体现在低频部分,随着γ的变小,平台的纵荡、横荡RAO也逐渐减小;高频部分则基本重合,水深影响较小。而针对垂直面的低频运动,考虑到随着水深的减小,受边界条件的影响,垂直面运动的附加质量会显著增加,造成固有频率变大。
|
图 7 不同水深吃水比条件下,半潜平台的运动传递函数 Fig. 7 Response amplitude operator (RAO) of SEMI with different γ |
进船试验的目的是得到浮托安装时,浮体的水动力性能参数,以及平台和驳船的六自由度运动响应,为后续实际工程方案和数值计算提供参考。模型试验中已对半潜平台与驳船进行3 h的进船试验,将数据导出并进行对比。
在Orcaflex中进行一次完整的3 h不规则波试验模拟,直接读取.OUT结果,会自动导入计算得出的浮体的RAO、二阶波浪力、阻尼等参数,首先按照海洋环境参数设置好相应的风浪流入射角度、波浪参数、水深等;然后布置锚链的位置,输入坐标点、长度、刚度和重量参数,考虑到锚链的不规则形状,合理选择锚链分段长度。最后,选择合适的数值计算方法,本文选取的数值计算方法是显式积分迭代算法,模拟时长设置为10800 s(3 h)。
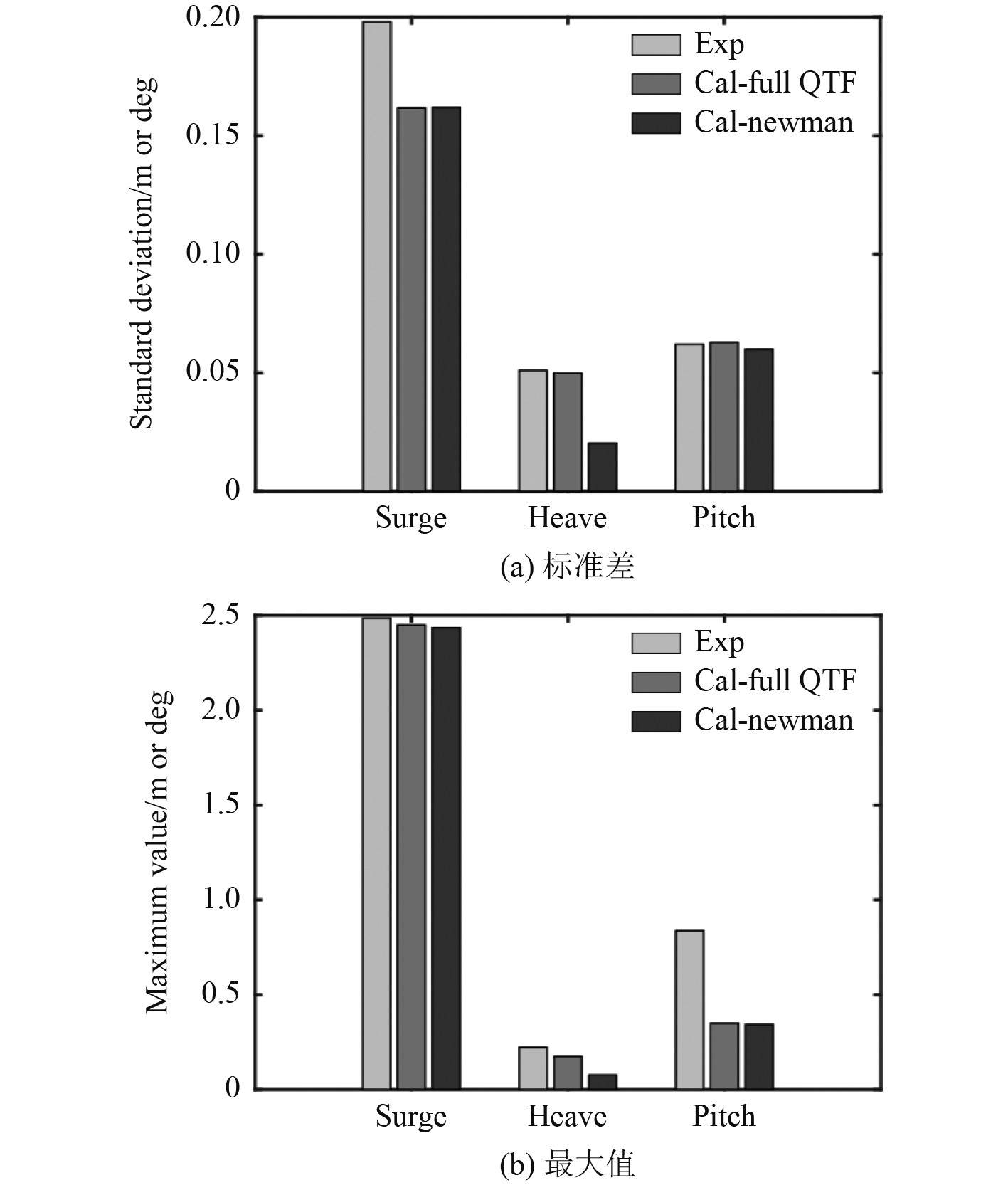
本文数值计算均采用全QTF法。相较于全QTF法,Newman近似忽略了二阶速度势的影响,利用定常二阶力近似低频二阶力,计算效率更高,但在某些情况下并不够准确。图8给出了全QTF法、Newman近似数值计算和模型试验结果的对比。设置水深为42 m,风浪流入射角度为0°,波浪条件为工况3。
|
图 8 半潜平台的运动响应标准差和最大值 Fig. 8 Standard deviation and maximum value of SEMI motion response |
将采用全QTF法的时域模拟结果与模型试验结果进行对比,可以看到数值模拟与试验结果较为相近,垂荡与纵摇的标准差偏差很小,纵摇最大值略有偏差,考虑到试验不可避免地受到外界因素的影响,可能是试验与数值中流载荷作用形式不同而产生的,试验中平台底部流场变化也可能会导致较大运动响应,具体原因需要进一步的研究。
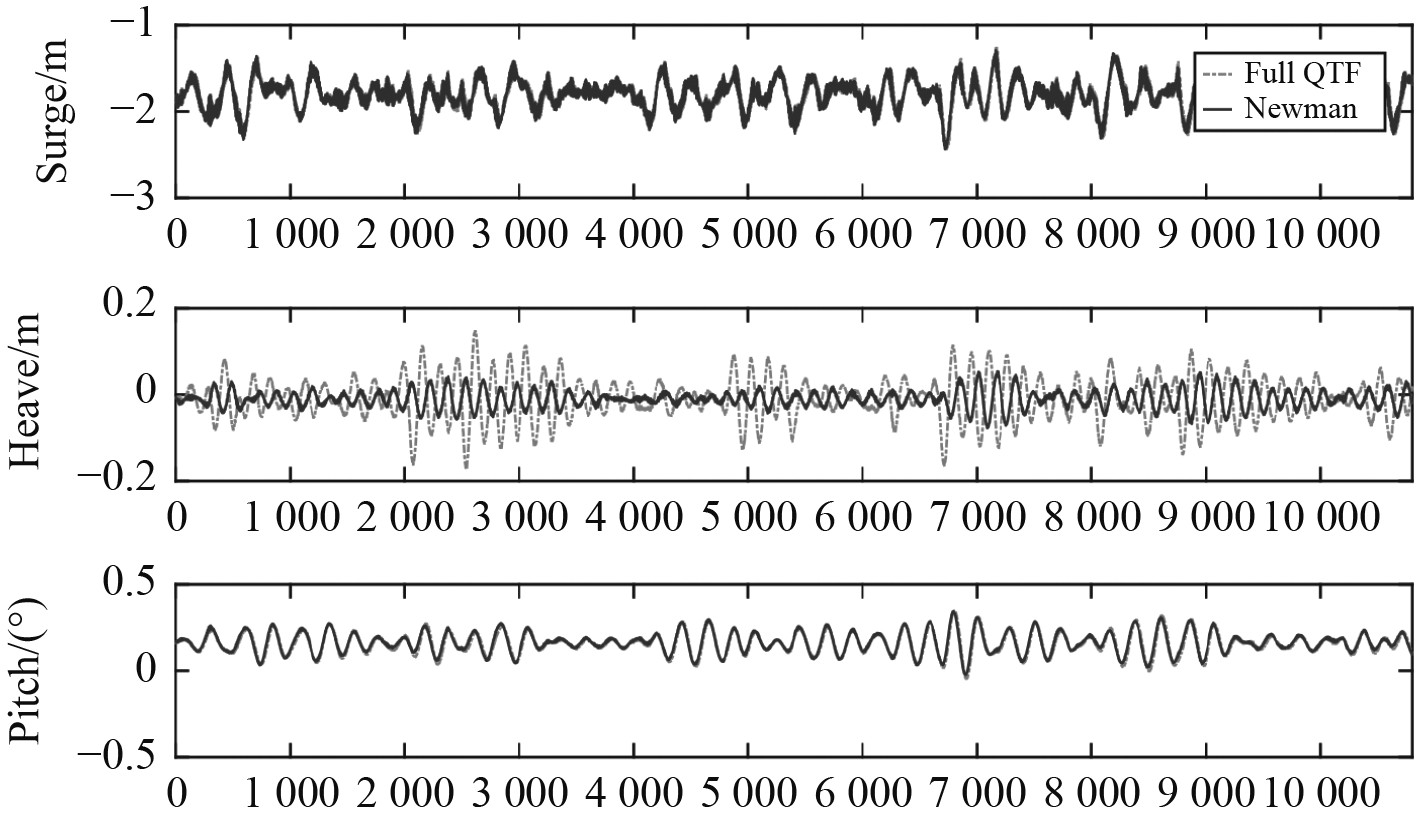
数值模拟的时历结果如图9所示。可以看出,全QTF法和Newman近似方法数值计算得出的纵荡和纵摇运动响应拟合效果较好,但垂荡运动两者误差较大,这是因为2种计算方式不同,Newman近似低估了垂荡方向的二阶波浪力,已知浅水效应对波浪漂移力影响较大,Newman近似并不适用于浅水海况。对比模型试验垂荡运动最大值与标准差,Newman近似得出的标准差不到模型试验结果的一半,偏差较大。故得出结论:相较于Newman近似,全QTF法对浅水中浮体运动可以给出更佳的预测,而本文旨在研究深浅水对浮体的影响,其中必须考虑到平台的触底风险,所以采取全QTF法有助于得到更为准确的数值模拟结果。
|
图 9 全QTF法与Newman近似的平台运动时历对比 Fig. 9 Comparison of platform motion time history between full QTF and Newman’s approximate |
同时,当安装水深为42 m时,半潜平台的吃水可达40 m,需要考虑到半潜平台触底的可能性,若半潜平台与底部发生碰撞,会影响到作业人员的安全,也可能损伤平台结构,对安全问题与经济效益都会造成不可估量的损害。因此,需要特别关注浮体的垂向运动,浮托安装驳船吃水较小,水深吃水比γ值大于20,暂不考虑其触底的可能性。在数值模拟中,考虑浮托安装所在海域的实际海况条件,表6列出了典型的计算工况。考虑到不同浪向角的影响,将风浪流入射角度设置为45°与180°,模拟时长设置为10800 s。
|
|
表 6 不规则波浪条件 Tab.6 Irregular wave conditions |
如图10所示,当浪向角相同,平台垂荡的剧烈程度随波高的增加而增大;当波浪条件相同,浪向角不同时,浪向角45°平台的垂荡运动更加剧烈。当波高为3 m时,平台垂荡运动的最大值可达到0.665 m,标准差为0.208 m,而42 m水深情况下,平台吃水为40 m,数值计算得到的最大值小于2 m,避免了触底的风险。
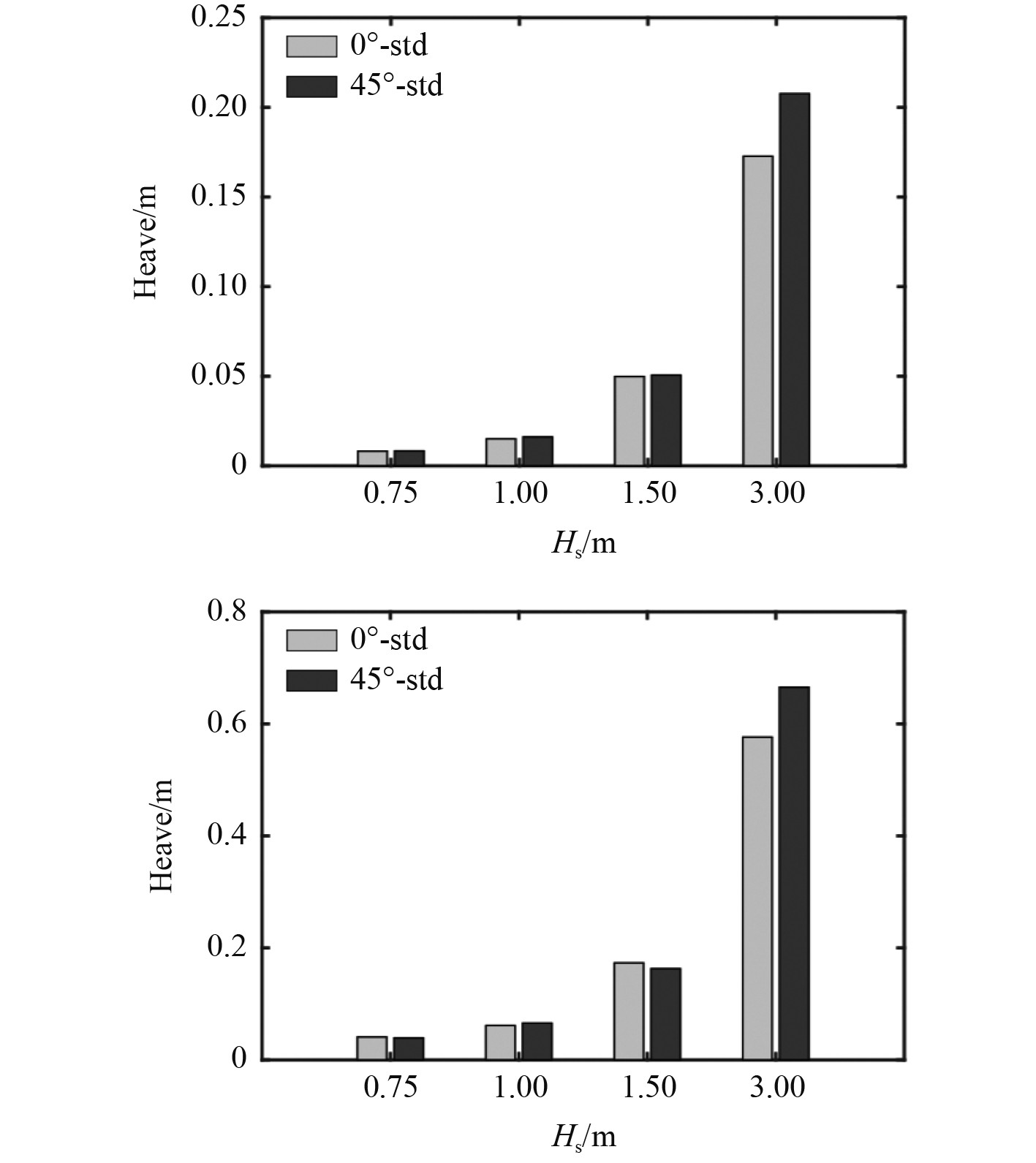
|
图 10 不同波浪条件下,半潜平台的垂荡运动 Fig. 10 SEMI heave motion response in different wave conditions |
本文基于“陵水17-2半潜平台”和“海洋石油229船”的浮托安装,以半潜平台上部组块浮托安装过程为研究对象,以数值模拟和模型试验为研究手段,针对浅水中半潜平台浮托安装进船过程展开研究,得到以下结论:
1)数值计算和模型实验得出的总体运动响应结果吻合较好,都可以较为准确地预报浮体的运动,证明数值计算方法的可靠性。对比不同水深吃水比下平台RAO,结果表明,低频部分浅水效应更为显著。
2)对比全QTF法与Newman近似数值计算结果,2种方法的纵荡和纵摇模拟结果拟合效果较好,但Newman近似低估了垂荡方向的二阶波浪力。浅水海况下,全QTF法与模型试验拟合效果更佳。
3)当浪向角相同,平台垂荡的剧烈程度随波高的增加而增大;当波浪条件相同,浪向角不同时,浪向角为45°的平台垂荡运动比0°时更加剧烈。数值计算得到的最大值小于2 m,实际作业中可避免触底的风险。
| [1] |
KOO B, MAGEE A, LAMBRAKOS K, et al. Model tests for floatover installation of Spar topsides[C]// Shanghai, China: American Society of Mechanical Engineers (ASME), 2010.
|
| [2] |
张铎, 王磊, 李博, 等. 动力定位平台协同运动控制与栈桥运动响应研究[J]. 海洋工程, 2019, 37(5): 16–27. ZHANG D, WANG L, LI B, et al. Cooperative motion control of dynamic positioning platforms and motion responses analysis of a gangway[J]. The Ocean engineering, 2019, 5. |
| [3] |
邱荷珍. 基于动力定位方法的浮托安装时域模拟与模型试验研究[D]. 上海: 上海交通大学, 2015.
|
| [4] |
XU X, YANG J, LI X, et al. Investigation on hydrodynamic performance of t-shaped barge in topside transportation[J]. Journal of Ship Mechanics, 2013, 17(12): 1426-1438. |
| [5] |
宋青武, 王圣强, 高本金, 等. 大型组块整体浮托安装法研究[J]. 天然气与石油, 2020, 38(5): 13-17. SONG Q, WANG S, GAO B, et al. Research on float-over installation of large integrated marine platform topside module[J]. NATURAL GAS AND OIL, 2020, 38(5): 13-17. DOI:10.3969/j.issn.1006-5539.2020.05.003 |
| [6] |
秦立成. 我国海洋平台浮托安装技术现状及未来[J]. 海洋工程装备与技术, 2019, 6(S1): 189-194
|
| [7] |
许鑫, 杨建民, 李欣. 浮托法安装的发展及其关键技术[J]. 中国海洋平台, 2012, 27(1): 44-49. DOI:10.3969/j.issn.1001-4500.2012.01.010 |
| [8] |
TAO W, WANG S, SONG X, et al. Experimental investigation on continuous load transfer process of twin-barge float-over installation[J]. Ocean engineering, 2021, 234: 109309. DOI:10.1016/j.oceaneng.2021.109309 |
| [9] |
SONG X, WANG S, HU Z, et al. A hybrid rayleigh and weibull distribution model for the short-term motion response prediction of moored floating structures[J]. Ocean Engineering, 2019, 182: 126-136. DOI:10.1016/j.oceaneng.2019.04.059 |
| [10] |
CHEN M, EATOCK TAYLOR R, CHOO Y S. Investigation of the complex dynamics of float-over deck installation based on a coupled heave-roll-pitch impact model[J]. Ocean engineering, 2017, 137: 262-275. DOI:10.1016/j.oceaneng.2017.04.007 |
| [11] |
ZOU M, ZHU L, CHEN M. Numerical simulation of the complex impact behavior of floatover deck installation based on an efficient two-body heaving impact model[C]// Madrid, Spain: American Society of Mechanical Engineers (ASME), 2018.
|
| [12] |
TIAN X, WANG P, LI X, et al. Design and application of a monitoring system for the floatover installation[J]. Ocean Engineering, 2018, 150: 194-208. DOI:10.1016/j.oceaneng.2017.12.030 |
| [13] |
ZHU L, ZOU M, CHEN M, et al. Nonlinear dynamic analysis of float-over deck installation for a GBS platform based on a constant parameter time domain model[J]. Ocean engineering, 2021, 235: 109443. DOI:10.1016/j.oceaneng.2021.109443 |
| [14] |
TAHAR A, HALKYARD J, STEEN A, et al. Float over installation methods - Comprehensive comparison between numerical and model test results[J]. Journal of Offshore Mechanics and Arctic Engineering, 2006, 128(3): 256-262. DOI:10.1115/1.2199556 |
| [15] |
许鑫, 杨建民, 吕海宁. 导管架平台浮托法安装的数值模拟与模型试验[J]. 上海交通大学学报, 2011, 45(4): 439-445. XU X, YANG J, LV H, et al. Experimental and numerical analysis for floatover installation on jacket[J]. Journal of Shanghai Jiaotong University, 2011, 45(4): 439-445. DOI:10.16183/j.cnki.jsjtu.2011.04.001 |
| [16] |
杨光, 吕海宁, 熊凌志, 等. 大型浮托安装驳船在极浅水中的运动特性和触底条件分析[J]. 船舶力学, 2018, 22(7): 827-837. YANG G, LV H, XIONG L, et al. Motion response and bottom grounding of a large floatover barge moored in ultra-shallow water[J]. Journal of Ship Mechanics, 2018, 22(7): 827-837. DOI:10.3969/j.issn.1007-7294.2018.07.006 |
| [17] |
PINKSTER J. Wave drift forces in directional seas in shallow water[C]// In ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering, 2009: 831–842.
|
| [18] |
NACIRI M, BUCHNER B, BUNNIk T, et al. Low frequency motions of LNG carriers moored in shallow water[C]// In ASME 2004 23rd International Conference on Offshore Mechanics and Arctic Engineering, 2004: 995–1006.
|
 2023, Vol. 45
2023, Vol. 45
